Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Brittle fracture in associative polymers: the case of ionomer melts†‡
Aamir
Shabbir
a,
Qian
Huang
a,
Quan
Chen§
b,
Ralph H.
Colby
b,
Nicolas J.
Alvarez
c and
Ole
Hassager
*a
aTechnical University of Denmark, Department of Chemical and Biochemical Engineering, Kgs. Lyngby 2800, Denmark. E-mail: oh@kt.dtu.dk
bPenn State University, Department of Material Science and Engineering, University Park PA 16802, USA
cDrexel University, Department of Chemical and Biological Engineering, Philadelphia PA 19104, USA
First published on 9th August 2016
Abstract
Ionomers are interesting due to their applications in coatings, adhesives, films and packaging materials. A study of the underlying mechanisms for fracture in ionomers is consequently of both practical as well as theoretical interest. In this study, we employ high speed imaging coupled with uniaxial extensional rheometry to delineate the mechanics leading to the brittle fracture of ionomer melts. When these ionomers are elongated at a rate higher than the inverse relaxation time of physical crosslinks, an edge fracture occurs at a critical stress. Parabolic fracture profiles provide evidence that the phenomenon is purely elastic and bulk dissipation has little impact on the crack profile. Experimental results are interpreted within the Griffiths theory for linear elastic materials and the de Gennes theory for viscoelastic materials.
1 Introduction
Viscoelastic fluids are complex materials with properties intermediate between a solid and a liquid. They behave as solid like on fast time scales and liquid like on slow time scales compared to the characteristic relaxation time.1 Fracture is expected at high deformation rates compared to the inverse of the relaxation time of the material.2 In solids this phenomenon is referred to as brittle fracture.3 Amongst viscoelastic fluids, associative polymeric systems including self-healing rubbers4 and physical hydrogels5 have attracted the interest of researchers recently due to their importance in processing and application as polymeric materials. Consequently, understanding fracture is important for tailoring such materials that are tougher and stronger for practical applications.When a crack exists in a material, any external applied stress undergoes a large amplification at its tip.6 For linear elastic materials, the stress field close to an infinitely sharp line crack takes the form 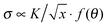 , where K is the stress intensity factor, x is the distance from the crack tip and f(θ) is a function of the angle to the crack.6,7 Displacements normal to the crack direction predicts a parabolic crack tip opening
, where K is the stress intensity factor, x is the distance from the crack tip and f(θ) is a function of the angle to the crack.6,7 Displacements normal to the crack direction predicts a parabolic crack tip opening 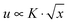 where x is the distance along the crack.6 For real materials, the stress singularity must be cut off to a finite value at least at the atomic scale, where it may or may not be large enough to snap bonds. Hence the prediction of a singular stress is itself insufficient to make a crack propagate. This leads to the early works of Griffith who provided a condition to determine whether the crack would propagate or not by noting that new surface must be created and that requires energy.8 On the other hand, fracture in viscoelastic materials has received less attention compared to solid materials. Modifications to Griffith's theory have been adapted to help understand fracture in viscoelastic materials.9,10
where x is the distance along the crack.6 For real materials, the stress singularity must be cut off to a finite value at least at the atomic scale, where it may or may not be large enough to snap bonds. Hence the prediction of a singular stress is itself insufficient to make a crack propagate. This leads to the early works of Griffith who provided a condition to determine whether the crack would propagate or not by noting that new surface must be created and that requires energy.8 On the other hand, fracture in viscoelastic materials has received less attention compared to solid materials. Modifications to Griffith's theory have been adapted to help understand fracture in viscoelastic materials.9,10
Several groups have reported fracture in the extensional deformation flow field for associative polymers.9,11–13 Most of the work concerns either networks or solutions of worm-like micelles.11,12 Recently, Ligoure et al.13 have studied fracture mechanisms of oil-in-water emulsions linked by telechelic polymers using pendant drop experiments. More recently, Huang et al. have reported an experimental framework capable of quantifying time resolved crack propagation together with true stress measurements and applied this for linear homo-polymer melts.14 We use this framework to perform fracture experiments for ionomers at different viscoelastic regimes by employing different temperatures and strain rates.
Ionomers represent a family of polymers where ionic groups are covalently attached to the polymer backbone.15 Due to strong dipolar interactions, the ionic groups have a tendency to associate into ionic clusters.16 These ionic clusters act as temporary crosslinks and restrict the motion of polymer chains thus leading to a delay in stress relaxation relative to the nonionic polymer. The terminal response of ionomers is governed by an association lifetime, τs, which is the average time for an ion pair to reside in the ionic cluster before its dissociation. The isolated pair can associate back to its original cluster or randomly move to a nearby cluster: the latter process leads to stress relaxation of the portion of chains between the ionic associations.17 Ionomers fracture in a brittle fashion under extensional deformation flow fields.18,19 Although some work has been conducted to understand the fracture of ionomers, it has primarily focused on deformation and fracture below the glass transition temperature.20,21 Fracture in the rubbery and flow states of ionomers has not been investigated at all. In the light of applications of ionomers as materials for toughening systems, coating and adhesives, batteries, and their importance in processing, it is surprising that no study has considered the fracture mechanisms from either theoretical or experimental perspectives.22
In this paper, we provide an experimental framework to investigate the fracture mechanism of ionomer melts synthesized via condensation of sulfonated pthalates with poly(tetramethylene glycol).23 Linear viscoelastic and structural properties have been extensively studied by Colby et al.17,23 This system provides an excellent model associative polymer melt (unentangled) where ionic associations attached to the polymer backbone act as physical crosslinks thus giving rich viscoelastic properties. The linear rheological response of the material resembles that of a well entangled polymer melt with a discernible plateau modulus. Despite being viscoelastic the material exhibits brittle fracture. Using a state of the art filament stretching rheometer coupled with a high speed imaging camera, we demonstrate that the ionomer filaments rupture via edge fracture. Analysis of the fracture profiles provide evidence that bulk viscous dissipation is minimal during the fracture event and has little impact on the crack profile. Results are in accordance with the viscoelastic trumpet model of de Gennes.24 Crack propagation velocities are quantified and compared to the speed of a shear wave in the medium.25 We employ Griffith's theory using Pomeau's criterion26 which reasons that the energy barrier to achieve crack growth can be overcome by thermal fluctuations. This allows for an estimation of the fracture energy needed to create two new air/polymer surfaces (dry fracture), which is found to be comparable to the surface tension of the ionomer. The use of Pomeau's criterion for such transient systems depends on the association/disassociation kinetics of temporary crosslinks (stickers) compared to the experimental time scales. When the average sticker lifetime, τs, is shorter than the experimental time scale, Pomeau's criterion is readily applicable. However, when the average sticker lifetime is much larger than the experimental time scale the material acts as a non-self-healing material within the experimental window and fractures. The driving force for fracture is not thermal energy, and the origins of the problem become solid mechanics related. Finally, we examine the extensional rheological response over a wide range of flow rates to provide a rationale for understanding the nature of fracture for ionomer melts under uniaxial extensional flows.
2 Materials and methods
2.1 Description of the ionomer melt
The amorphous polyester ionomer synthesized via condensation of sulfonated phtalates with poly(tetramethylene glycol) having M = 650 g mol−1 with Na as the counterion was provided by Chen et al.17 The PTMO-Na ionomer exhibits microdomain separation as confirmed by X-ray scattering whereby Na+ forms dense aggregates of the order of 15 ion pairs. The PTMO-Na ionomer exhibits a glass transition temperature, Tg, of −60 °C.232.2 Rheological experiments
The extensional stress growth coefficient as a function of time was measured using the VADER 1000 (versatile accurate deformation extensional rheometer) from Rheo Filament ApS. Cylindrical stainless steel plates with a diameter of 5.4 mm were used for all measurements. The Hencky strain in the mid-filament is defined as ε = − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(D(t)/D0), where D0 is the initial diameter. The diameter is measured by a laser micrometer during stretching and a control loop27 is used to adjust the plate motion to ensure a constant Hencky strain rate defined as
ln(D(t)/D0), where D0 is the initial diameter. The diameter is measured by a laser micrometer during stretching and a control loop27 is used to adjust the plate motion to ensure a constant Hencky strain rate defined as ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = dε/dt. Samples were heated under nitrogen for 2 hours at 120 °C prior to performing experiments. At such a temperature the ionomer flows easily and forms a nice axisymmetric shape when the top rheometer plate is brought in contact with the sample. All experiments were performed in a nitrogen controlled environment.
= dε/dt. Samples were heated under nitrogen for 2 hours at 120 °C prior to performing experiments. At such a temperature the ionomer flows easily and forms a nice axisymmetric shape when the top rheometer plate is brought in contact with the sample. All experiments were performed in a nitrogen controlled environment.
2.3 Fracture experiments
Fracture experiments were performed using a Photron Mini UX100 high speed camera with a Navitar Zoom6000 lens coupled with VADER 1000 operating in an open loop control scheme configuration (at 60 °C and 80 °C). The imposed stretching rate was 1 s−1 (see open orange circles in Fig. 5). The feedforward control parameters27 which define the kinematic trajectory of the top plate motor were obtained by performing constant rate experiments on the VADER in a control loop scheme with an active feedback control and without coupling a high speed camera. Only after that, VADER was coupled with the high speed camera to perform fracture experiments. Operating the VADER in a open loop ensures avoiding interference between the laser micrometer and the light emitted from the illuminator that is used for the camera. Since the crack can nucleate and propagate in any direction of the filament surface, around 40 experiments were performed in order to capture crack propagation profiles orthogonal to the camera lens for the experimental data analysis.3 Results
Shear rheology results were obtained from previous studies on PTMO-Na ionomer melts.17,23The linear viscoelastic (LVE) response shown in Fig. 1a resembles that of a well entangled polymer melt with a distinct plateau modulus. Since the PTMO-Na is unentangled, the plateau modulus, G0N, results from the ionic cluster density and is approximately 107 Pa. Polydispersity in molecular weight leads to a broadening in the lower crossover frequency because of a distribution in the number of polymer modes each associated with a contribution to the moduli.17,28 The PTMO-Na ionomers used in this study are polydisperse (polydispersity ≈ 2.0), and they exhibit terminal tails (slope of 1 and 2 for loss modulus G′′ and storage modulus G′, respectively) at low frequency, ω. The terminal relaxation time can be determined as,
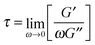 | (1) |
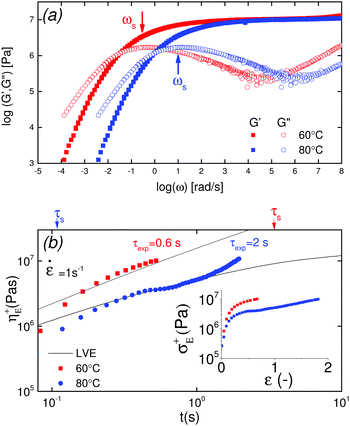 | ||
Fig. 1 (a) LVE master curves of the PTMO-Na ionomer at Tref = 60 °C and Tref = 80 °C,17,23 (b) stress growth coefficient as a function of time at the Hencky rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 s−1, for PTMO-Na at 60 °C, and 80 °C. The inset plot shows transient extensional stress as a function of Hencky strain. Solid lines represent the LVE envelope. = 1 s−1, for PTMO-Na at 60 °C, and 80 °C. The inset plot shows transient extensional stress as a function of Hencky strain. Solid lines represent the LVE envelope. | ||
The association lifetime can thus be obtained as ref. 23
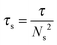 | (2) |
The extensional rheological response of the PTMO-Na ionomer is shown in Fig. 1b. It shows the transient stress growth coefficient, η+E, as a function of time for a fixed strain rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 s−1, at two different temperatures, 60 °C and 80 °C. The LVE envelope obtained using a multimode Maxwell fit from LVE oscillatory shear data is plotted as solid lines. The extensional data are seen to be consistent with the predictions of linear viscoelasticity. The inset shows transient extensional stress, σ+E, as a function of Hencky strain, ε. The end of each experiment represents brittle fracture of the PTMO-Na filament. From Fig. 1b, it is interesting to note the temperature dependent extensional rheological response. At T = 60 °C, the experimental time scale is smaller compared to the association lifetime, τs, and the material fractures at relatively low Hencky strain without showing any departure from the LVE envelope (often termed as strain hardening). By contrast, at T = 80 °C, the experimental time scale exceeds the association lifetime, τs, and a noticeable strain hardening is observed before brittle fracture. From the inset, it is evident that the material fractures at the same level of stress 107 Pa which corresponds to the shear plateau modulus, G0N.
= 1 s−1, at two different temperatures, 60 °C and 80 °C. The LVE envelope obtained using a multimode Maxwell fit from LVE oscillatory shear data is plotted as solid lines. The extensional data are seen to be consistent with the predictions of linear viscoelasticity. The inset shows transient extensional stress, σ+E, as a function of Hencky strain, ε. The end of each experiment represents brittle fracture of the PTMO-Na filament. From Fig. 1b, it is interesting to note the temperature dependent extensional rheological response. At T = 60 °C, the experimental time scale is smaller compared to the association lifetime, τs, and the material fractures at relatively low Hencky strain without showing any departure from the LVE envelope (often termed as strain hardening). By contrast, at T = 80 °C, the experimental time scale exceeds the association lifetime, τs, and a noticeable strain hardening is observed before brittle fracture. From the inset, it is evident that the material fractures at the same level of stress 107 Pa which corresponds to the shear plateau modulus, G0N.
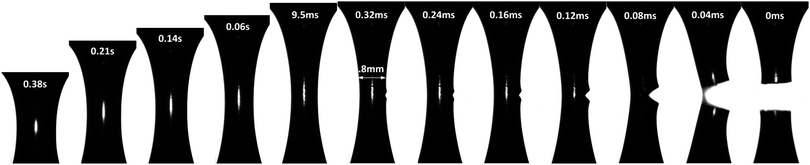
A complete evolution of the PTMO-Na ionomer filament at a Hencky strain rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 s−1 and T = 60 °C during extensional deformation is shown in Fig. 2 (see also Movie in the ESI‡). During extensional deformation, a notch appears from the right edge of the filament orthogonal to the camera lens 0.32 ms before it fractures into two halves. A close inspection of the images reveals multiple cracks initially, but the crack shown in the picture prevails over the other cracks (see the ESI‡). The sequence of images demonstrates the decoupling of time scale associated with extensional deformation (of the order of seconds) from the fracture event time which is of the order of ms. The crack propagation at T = 80 °C is shown in the ESI.‡ In both cases, the fracture profile exhibits a parabolic shape from the beginning of crack propagation to complete fracture of the filament into two halves. This is an attribute associated with the fracture of solids under tension.8 It is worth mentioning that the position of fracture along the filament axis is completely random. This observation may indicate the stochastic nature of reversible microcracks. A microcrack corresponds to a domain across which there is no connection of polymer chains between crosslinks.
= 1 s−1 and T = 60 °C during extensional deformation is shown in Fig. 2 (see also Movie in the ESI‡). During extensional deformation, a notch appears from the right edge of the filament orthogonal to the camera lens 0.32 ms before it fractures into two halves. A close inspection of the images reveals multiple cracks initially, but the crack shown in the picture prevails over the other cracks (see the ESI‡). The sequence of images demonstrates the decoupling of time scale associated with extensional deformation (of the order of seconds) from the fracture event time which is of the order of ms. The crack propagation at T = 80 °C is shown in the ESI.‡ In both cases, the fracture profile exhibits a parabolic shape from the beginning of crack propagation to complete fracture of the filament into two halves. This is an attribute associated with the fracture of solids under tension.8 It is worth mentioning that the position of fracture along the filament axis is completely random. This observation may indicate the stochastic nature of reversible microcracks. A microcrack corresponds to a domain across which there is no connection of polymer chains between crosslinks.
A quantitative analysis of fracture profiles is shown in Fig. 3. Fig. 3a and b shows fracture profiles (shifted to have the same crack tip position) at each moving frame with a time spacing of 0.04 ms (corresponds to the frame rate = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps). The overall fracture profile can be fit using an equation for a parabola
000 fps). The overall fracture profile can be fit using an equation for a parabola 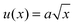 , where a is a constant adjusted to fit the parabolic profile. The parabolic fit is shown by the solid line. The fitting constant a, which is an indirect representation of the amount of crack opening is higher for T = 60 °C compared to T = 80 °C.
, where a is a constant adjusted to fit the parabolic profile. The parabolic fit is shown by the solid line. The fitting constant a, which is an indirect representation of the amount of crack opening is higher for T = 60 °C compared to T = 80 °C.
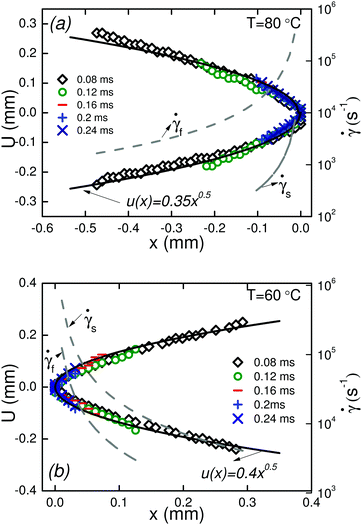 | ||
| Fig. 3 Fracture profiles u(x) in the moving frame at different times before complete fracture of the filament at T = 60 °C, and T = 80 °C. | ||
Crack length as a function of remaining time for the filament to disconnect into two halves is shown in Fig. 4 at T = 60 °C, and T = 80 °C. We use the diameter of the filament just before opening of the crack, D, as the reference to define the crack length L from the crack tip. The velocity of the crack, V, is obtained from the slope of the plot. Two velocity regimes are evident:
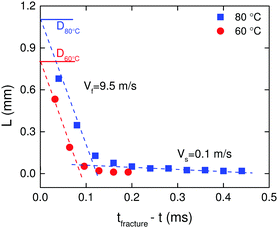 | ||
| Fig. 4 Variation of crack length as a function of time remaining for complete fracture of the filament at T = 60 °C, and T = 80 °C. | ||
(i) For L < 0.05D, a slow velocity regime, Vs, is noticed where the crack moves at almost V = 0.1 m s−1.
(ii) For L > 0.05D, a fast velocity regime, Vf, is observed in which the crack propagates dynamically at almost V = 9.5 m s−1.
The crack velocities are almost independent of temperature. An increase in crack velocity during crack propagation is to be expected because the stresses near the tip will increase thus driving faster crack growth. In addition, we speculate that in the slow velocity regime, multiple cracks shield one another from the external applied stress whereby they all propagate slowly together,29 while in the fast velocity regime the leading crack takes off alone. While cracks achieve quite large velocities particularly close to complete fracture, the highest velocities are still an order of magnitude smaller than the elastic shear wave velocity for an incompressible material (cR ≈ (|G*|/ρ)1/2 = 96 m s−1), where ρ is the density and |G*| = (G′2 + G′′2)1/2 is the absolute value of the complex modulus.25 Slow crack velocities compared to shear wave velocity have been reported previously for non-associative polymers.5,13,30 What is different here compared to other reversible systems like gelatin5 and gels made from oil-in-water droplet emulsions bridged by telechelic polymers13 is the absence of solvent drag. As a consequence the crack propagation velocities are in the range of 1–2 orders of magnitude faster compared to those in solvent containing reversible networks. It should be mentioned that the quantification of crack velocity was made assuming a 2D symmetry of the crack front and that the crack front is flat.
4 Discussion
It was noted above that the shape of the fracture profile was parabolic which is indicative of elastic like behavior. To provide a rationale of such a behavior of the PTMO-Na ionomer during fracture, the viscoelastic trumpet model of de Gennes is employed.24,31,32 This model demonstrates through scaling laws that the shape of the crack depends upon a characteristic relaxation time, τ, and crack propagation velocity, V. For a viscoelastic material, during crack propagation a transition from a solid to liquid like response can be distinguished,(i) L ≤ Vτ: a strong elastic response is noticed and the viscous dissipation is negligible. For this case, 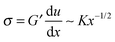 yields
yields
| u(x) ∼ K/G′x1/2 | (3) |
(ii) L > Vτ: in this region the modulus is purely imaginary and a Newtonian liquid response is expected. This region contributes to the bulk viscoelastic dissipation processes. For this case, 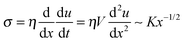 yields
yields
| u(x) ∼ (K/ηV)x3/2 | (4) |
If we define τ = τs, then the characteristic length scale, Vτ, for the PTMO-Na ionomer is 10 mm and 300 mm at T = 80 °C and T = 60 °C, respectively. Since the fracture length Lmax = D ∼ 0.8–1.1 mm, a purely elastic response is expected with the fracture profile given by a classical parabolic shape using eqn (5).
During crack propagation, the local shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , experienced at the crack surface is high near the fracture tip, and lowers as the distance x to the tip increases because the material has time to relax the stresses.32 We may thus define a relationship for
, experienced at the crack surface is high near the fracture tip, and lowers as the distance x to the tip increases because the material has time to relax the stresses.32 We may thus define a relationship for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) as a function of distance x to the tip. For an elastic material, the local shear strain, γ, is defined as
as a function of distance x to the tip. For an elastic material, the local shear strain, γ, is defined as
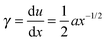 | (5) |
The local shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , during crack propagation is then given simply as
, during crack propagation is then given simply as
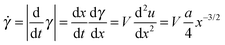 | (6) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) s, corresponds to the slow velocity regime (V = 0.1 m s−1) while the shear rate,
s, corresponds to the slow velocity regime (V = 0.1 m s−1) while the shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) f, corresponds to the fast velocity regime (V = 9.5 m s−1).
f, corresponds to the fast velocity regime (V = 9.5 m s−1).
A remarkable elastic recoil of the filament or strain recovery, defined as r = (fracture strain-recovered strain)/(fracture strain-initial strain), of about 92% and 72% at T = 60 °C and T = 80 °C, respectively, after the fracture was noticed. This observation and the fact that the fracture profile exhibits a parabolic shape provide motivation to analyze data using Griffith's theory of brittle fracture.8 According to this theory, a surface energy, Fs, is required for the creation of free surface within the body counterbalanced by the bulk elastic energy released because of unloading of the newly created surface. Ligoure et al.9 considered a disk-like crack for radius R. They stated the energy to be
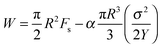 | (7) |
| Rc = 2FsY/σ2 | (8) |
The term σ2/2Y in eqn (7), represents the elastic energy density, E, that may be released by the fracture opening. Since we have measured the stress as a function of strain we prefer to use measurements to calculate this quantity directly in the form,
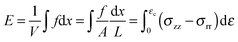 | (9) |
Only a fraction, r, of this energy is available for opening of the crack since part of the energy will be dissipated. We take, r, to be the fractional strain recovery. We therefore replace σ2/2Y by rE.
The modified energy expression yields,
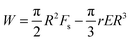 | (10) |
Likewise, eqn (8) is modified as Rc = Fs/rE which may be substituted in the modified energy expression to obtain the critical energy,
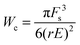 | (11) |
The critical energy derived above represents an energy barrier which can be overcome either by existing cracks of length, Rc, or by thermal fluctuations. The latter scenario would correspond to self-healing materials where the transient nature of physical crosslinks causes the crack length to reversibly increase. Microcracks in self-healing materials always exist because of thermal energy fluctuations.9 Recall that a microcrack is a domain without polymers connecting physical crosslinks. A crack can reversibly explore states with different crack lengths between the initial and critical ones.33 For self-healing materials, we may thus assume that the critical energy can be overcome by thermal fluctuations as suggested by Pomeau26 which implies,
| Wc = βkBT | (12) |
| Fs = (6/πβkBT(rE)2)1/3 | (13) |
Recalling from Fig. 1b, the comparison of the average sticker lifetime with the experimental time scale, τexp, during a constant rate experiment. Clearly, the notion of self-healing works well for the PTMO-Na ionomer at T = 80 °C since τs ≪ τexp. In other words, the kinetics of association/dissociation is faster than the experimental time scale. The activation energy barrier can be overcome by thermal fluctuations. From previous works,17 the activation energy is approximated to be Ea = 20kBT at T = 80 °C for the PTMO-Na ionomer. Plugging β = 20 in eqn (12) yields Fs = 20 mJ m−2 which is comparable to the surface tension estimated at T = 80 °C using a group contribution method (see the ESI‡).34 However, the situation is slightly different at T = 60 °C where Fig. 1b shows that τs ≫ τexp. In other words, kinetics of association/dissociation is slower than the experimental time scale. Although under equilibrium conditions, the material is still self-healing at T = 60 °C, it is viewed as a non-self-healing material on the experimental time scale. To simplify, defects in the network (due to thermal fluctuations) exist under equilibrium conditions, but these pre-existing cracks cannot explore different crack lengths between the initial and the critical ones during the experimental time scale. Henceforth, the use of eqn (12) is questionable. We speculate that at low temperatures the mechanical pullout of chains from the ionic clusters leads to fracture but at the moment this still remains to be proven.
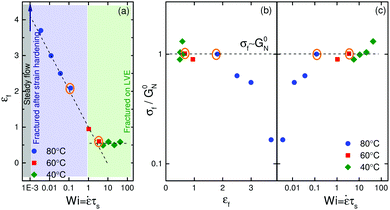
So far we have only focused on two temperatures and one strain rate in Fig. 1b. In order to probe a broader range of nonlinearity, we define a non-dimensional number called the Weissenberg number based on the average sticker lifetime as Wi = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) τs. Fig. 5a shows strain rate dependence of Hencky strain at fracture, εf. A monotonic decrease in the Hencky strain at fracture is noticed for Wi < 1. However, for Wi > 1 fracture strain is independent of Wi, and attains a constant value of ≈0.6. For Wi ≥ 1, ionic crosslinks can be thought of as permanent junctions making the material elastic like. Note that for very low Weissenberg numbers, Newtonian behavior is seen with a steady state in ηE. The filament does not fracture in this regime and the ordinate of Fig. 5a approaches infinity theoretically. Fig. 5b shows non-dimensional extensional stress at fracture, σf/G0N, vs. Hencky strain at fracture over a range of temperatures. Such a plot has been referred to as the fracture envelope.3,35 Exploring this plot is vital to understand the underlying fracture mechanisms. Two different regimes are evident. At high temperatures, the stress at fracture increases with increasing extension rate until σf ≃ G0N. At low temperatures, filaments fracture at a given critical stress σf ≃ G0N independent of the extension rate.
τs. Fig. 5a shows strain rate dependence of Hencky strain at fracture, εf. A monotonic decrease in the Hencky strain at fracture is noticed for Wi < 1. However, for Wi > 1 fracture strain is independent of Wi, and attains a constant value of ≈0.6. For Wi ≥ 1, ionic crosslinks can be thought of as permanent junctions making the material elastic like. Note that for very low Weissenberg numbers, Newtonian behavior is seen with a steady state in ηE. The filament does not fracture in this regime and the ordinate of Fig. 5a approaches infinity theoretically. Fig. 5b shows non-dimensional extensional stress at fracture, σf/G0N, vs. Hencky strain at fracture over a range of temperatures. Such a plot has been referred to as the fracture envelope.3,35 Exploring this plot is vital to understand the underlying fracture mechanisms. Two different regimes are evident. At high temperatures, the stress at fracture increases with increasing extension rate until σf ≃ G0N. At low temperatures, filaments fracture at a given critical stress σf ≃ G0N independent of the extension rate.
Finally, we recall the local shear rates that were calculated in the results section (Fig. 3a and b). These shear rates are mapped on the LVE as shown in Fig. 6. The local shear rates close to the crack surface are 3 orders of magnitude higher than the strain rate imposed during uniaxial extension. It is evident that in the frequency regime which corresponds to the local shear rates during crack propagation (grey region in Fig. 6), the storage component dominates the loss component of the complex modulus (G′ ≫ G′′). This is consistent with the finding that the crack profile follows the elastic part 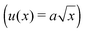 of the de Gennes trumpet model. Furthermore, from Fig. 6 it is evident that the critical stress observed in uniaxial extension is comparable to the storage modulus (107 Pa) of the sample in the LVE regime which is also the critical tensile stress of the material as discussed before.
of the de Gennes trumpet model. Furthermore, from Fig. 6 it is evident that the critical stress observed in uniaxial extension is comparable to the storage modulus (107 Pa) of the sample in the LVE regime which is also the critical tensile stress of the material as discussed before.
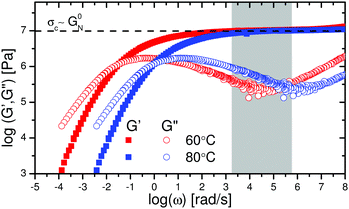 | ||
| Fig. 6 LVE master curves of the PTMO-Na ionomer at Tref = 60 °C and Tref = 80 °C.17,23 The grey region highlights the local shear rates in Fig. 3 which are in the midst of the rubbery plateau, where the material behaves like a crosslinked network. The local shear rates during fracture were obtained using eqn (6). | ||
5 Conclusions
In this study, we have demonstrated an original experimental framework to study the fracture of one class of associative polymer melts called ionomers, using a high speed camera coupled with a filament stretching rheometer under a constant strain rate deformation. The configuration allows for an excellent decoupling of extensional deformation from the fracture event.It was shown that ionomers break in a brittle fashion by edge fracture. Fracture profiles exhibit a parabolic shape which is indicative of solid like behavior. The absence of any significant bulk viscous dissipation was justified using the de Gennes viscoelastic trumpet model whereby the length of the crack was smaller than the characteristic length Vτs, beyond which the viscous effects dominate. Quantification of crack propagation velocities showed that although these were not inertia limited, they were between one and three orders of magnitude slower compared to the speed of shear waves in the material. Crack velocities were also insensitive to temperature variations. By combining fracture mechanics analysis (based on Pomeau's criterion) with constant rate uni-axial rheology, a common consensus was brought forward to understand the mechanism of fracture at different Wi values. Two regimes corresponding to different fracture mechanisms were observed. For Wi < 1, defects originating from thermal density fluctuations can explore states with different crack lengths between the initial and critical ones thus overcoming the energy barrier. Fracture energy needed to create two new air/polymer surfaces in such a scenario corresponded to the surface tension of the material. Noticeable strain hardening was observed in this regime. On the other hand for Wi ≥ 1, the pre-existing cracks due to thermal fluctuations cannot explore different crack lengths between the initial and the critical ones within the experimental time scale. Therefore, although these microcracks present the source for the crack nucleation, the driving force is not thermal energy. Classical Griffith's theory is applicable here to explain the crack propagation. No strain hardening was observed in this regime and the material fractured on the LVE envelope once the tensile stress reaches the shear modulus of the material. We have speculated the mechanical pullout of chains from the ionic clusters to be the reason for brittle fracture in this regime.
Given that the measured fracture speeds are between one and three orders of magnitude slower than the shear wave speed, we conclude that some molecular dissipation process must be involved in setting the speed. However the precise nature of this process is not clear at present. It could of course be the same process that contributes to the loss modulus in the identified frequency range of the linear viscoelastic modulus (grey area in Fig. 6). However it could also be some non-linear process near the fracture tip, where the linear analysis predicts a stress singularity and non-linear analysis will be needed ultimately. Related to this, the reason for the marked change of crack velocity by almost a factor of 100 is in our opinion also not fully resolved. We have offered a speculation in terms of crack competition, but other physical processes may be involved and more analysis will certainly be needed for a fully satisfactory explanation.
Acknowledgements
The work leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7/2007–2013), SUPOLEN under REA grant agreement no. 607937. QC and RHC thank the National Science Foundation for support from DMR-1404586.References
- J. D. Ferry, Viscoelastic Properties of Polymers, Wiley, New York, 1980 Search PubMed.
- A. Y. Malkin and C. J. S. Petrie, J. Rheol., 1997, 41, 1–25 CrossRef CAS.
- H. Kausch, Polymer Fracture, Springer-Verlag, Berlin Heidelberg, 1978 Search PubMed.
- P. Cordier, F. Tournilhac, C. Soulié-Ziakovic and L. Leibler, Nature, 2008, 451, 977–980 CrossRef CAS PubMed.
- T. Baumberger, C. Caroli and D. Martina, Nat. Mater., 2006, 5, 552–555 CrossRef CAS PubMed.
- E. Bouchbinder, J. Fineberg and M. Marder, Annu. Rev. Condens. Matter Phys., 2010, 1, 371–395 CrossRef.
- A. C. Fischer-Cripps, Introduction to Contact Mechanics, Springer, US, 2007 Search PubMed.
- A. A. Griffith, Philos. Trans. R. Soc., A, 1921, 221, 163–198 CrossRef.
- H. Tabuteau, S. Mora, G. Porte, M. Abkarian and C. Ligoure, Phys. Rev. Lett., 2009, 102, 155501 CrossRef CAS PubMed.
- P. J. Skrzeszewska, J. Sprakel, F. A. de Wolf, R. Fokkink, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2010, 43, 3542–3548 CrossRef CAS.
- A. Bhardwaj, E. Miller and J. P. Rothstein, J. Rheol., 2007, 51, 693–719 CrossRef CAS.
- A. Bhardwaj, D. Richter, M. Chellamuthu and J. Rothstein, Rheol. Acta, 2007, 46, 861–875 CrossRef CAS.
- H. Tabuteau, S. Mora, M. Ciccotti, C.-Y. Hui and C. Ligoure, Soft Matter, 2011, 7, 9474–9483 RSC.
- Q. Huang, N. J. Alvarez, A. Shabbir and O. Hassager, Phys. Rev. Lett., 2016, 117, 087801 CrossRef.
- P. Vanhoorne and R. A. Register, Macromolecules, 1996, 29, 598–604 CrossRef CAS.
- N. K. Tierney and R. A. Register, Macromolecules, 2002, 35, 2358–2364 CrossRef CAS.
- Q. Chen, G. J. Tudryn and R. H. Colby, J. Rheol., 2013, 57, 1441–1462 CrossRef CAS.
- G. H. Ling, Y. Wang and R. A. Weiss, Macromolecules, 2012, 45, 481–490 CrossRef CAS.
- F. J. Stadler, T. Still, G. Fytas and C. Bailly, Macromolecules, 2010, 43, 7771–7778 CrossRef CAS.
- M. Hara and P. Y. Jar, Macromolecules, 1988, 21, 3187–3190 CrossRef CAS.
- M. Hara, M. Bellinger and J. Sauer, Colloid Polym. Sci., 1992, 270, 652–658 CAS.
- L. Zhang, N. R. Brostowitz, K. A. Cavicchi and R. A. Weiss, Macromol. React. Eng., 2014, 8, 81–99 CrossRef CAS.
- Q. Chen, H. Masser, H.-S. Shiau, S. Liang, J. Runt, P. C. Painter and R. H. Colby, Macromolecules, 2014, 47, 3635–3644 CrossRef CAS.
- P. G. de Gennes, Langmuir, 1996, 12, 4497–4500 CrossRef CAS.
- B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Wiley, New York, 1987 Search PubMed.
- Y. Pomeau, CR Acad. Sci. Paris Ser. II, 1992, 314, 553 Search PubMed.
- J. M. Román Marn, J. K. B. Huusom, N. J. Alvarez, Q. Huang, H. K. Rasmussen, A. Bach, A. L. Skov and O. Hassager, J. Non-Newtonian Fluid Mech., 2013, 194, 14–22 CrossRef.
- A. Shabbir, I. Javakhishvili, S. Cerveny, S. Hvilsted, A. L. Skov, O. Hassager and N. J. Alvarez, Macromolecules, 2016, 49, 3899–3910 CrossRef CAS.
- O. L. Bowie, in Solutions of plane crack problems by mapping technique, ed. G. C. Sih, Springer, Netherlands, Dordrecht, 1973, pp. 1–55 Search PubMed.
- B. N. J. Persson, Phys. Rev. Lett., 1998, 81, 3439–3442 CrossRef CAS.
- P. G. de Gennes, CR Acad. Sci. Paris Ser. II, 1988, 307, 1949 CAS.
- F. Saulnier, T. Ondarçuhu, A. Aradian and E. Raphaël, Macromolecules, 2004, 37, 1067–1075 CrossRef CAS.
- C. Ligoure and S. Mora, Rheol. Acta, 2013, 52, 91–114 CrossRef CAS.
- O. R. Quayle, Chem. Rev., 1953, 53, 439–589 CrossRef CAS.
- T. L. Smith, J. Appl. Phys., 1964, 35, 27–36 CrossRef.
Footnotes |
| † Dedicated to Professor R. B. Bird on the occasion of his 92nd birthday. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm01441k |
| § Present address: State Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, China. |
| This journal is © The Royal Society of Chemistry 2016 |