Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Steady-state droplet size in montmorillonite stabilised emulsions†
William J.
Ganley
and
Jeroen S.
van Duijneveldt
School of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: William.Ganley@bristol.ac.uk; J.S.van-Duijneveldt@bristol.ac.uk
First published on 4th July 2016
Abstract
The formation of hexadecane-in-water emulsions stabilised by montmorillonite platelets was studied. In this system the platelets form a monolayer around the droplets and the droplet size decreases with increasing platelet volume fraction. However, the number of platelets present exceeds that required for monolayer coverage. The kinetics of emulsification were investigated and coalescence of droplets during turbulent mixing was found to continue even after the droplets had reached their ultimate size. Non-spherical droplets, resulting from arrested coalescence, were not observed suggesting that particles may be desorbing from the interface during the turbulent flow. A kinetic model based on a competition between droplet break-up and coalescence, mediated by particle adsorption and desorption, reproduces experimental trends in droplet diameter. The model can be used to predict the most efficient formulation to minimise droplet diameters for given materials and mixing conditions and sheds light on the processes occurring during emulsification in this system.
1 Introduction
Solid stabilised emulsions (also known as Pickering emulsions1,2) are alternatives to surfactant or polymer stabilised emulsions.3 Adsorption of nano- or microparticles to the interface between two immiscible fluids is energetically favourable when the energies of the interfaces created by adsorption of a particle are lower than those removed in the process. Typical conditions (hydrocarbon oil and particles that are wet by both phases) produce adsorption energies many times the thermal energy resulting in droplets that are very stable to coalescence under quiescent conditions. Particle stabilised emulsions therefore offer advantages over surfactant stabilised emulsions in that they can form a strongly adsorbed solid barrier to coalescence and the particles used are typically non-hazardous.Many different particles have been found to possess the correct wetting characteristics to stabilise oil/water interfaces. Silica,4 latex,5 metal oxide,6 clay7,8 and microgel9,10 particle stabilised emulsions have all been reported. Upon a simple geometric balance between the volume (V) of dispersed phase present and the total area (A) that the particles can occupy on a curved interface, after consideration of packing constraints, a typical droplet diameter of 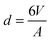 can in principle be achieved if enough interfacial area can be generated and all particles are able to adsorb. Indeed many systems have been reported to achieve this high surface area.11–13
can in principle be achieved if enough interfacial area can be generated and all particles are able to adsorb. Indeed many systems have been reported to achieve this high surface area.11–13
It is also commonplace for there to be well defined trends between droplet size and processing or compositional parameters where this idealised surface coverage is not achieved. Sturzenegger et al. reported the effect of the competition between droplet break-up and coalescence in the formation of zinc oxide nano- and microparticle stabilised water-in-toluene emulsions formed using a rotor–stator mixer.6 They showed that an increase in particle concentration resulted in a fall in average droplet diameter but there was always an excess of un-adsorbed particles in the continuous phase. The droplet size was therefore not controlled by the maximum area that the particles could cover, but rather by the speed at which the newly formed interface could be stabilised. Cui et al. reported a similar trend of size control with particle concentration for montmorillonite platelet stabilised polydecene-in-water emulsions (also using a rotor stator mixer) where a simple balance of geometry showed that the particles were in a 10× excess for the size of droplets produced.8 Ashby and Binks reported that large amounts of LAPONITE® platelets were required to stabilise toluene-in-water emulsions formed using a rotor–stator mixer.14 Similarly Lagaly et al.,15,16 Garcia et al.17 and Binks et al.18 described the use of smectite and hectorite clays as dual emulsion stabilisers and rheology modifiers due to their presence in the continuous phase after emulsification. Additionally Binks and Kirkland showed the presence of particles in the continuous phase of oil-in-water and water-in-oil emulsions after emulsification by scanning electron microscopy.19
There has been some discussion of the individual processes of break-up20 and coalescence21 of particle laden droplets and much discussion of the competition between these processes6,22,23 but little attempt to quantify the interplay between all processes occurring during turbulent mixing of particle stabilised emulsions. A model where droplets break-up and are coated by particles (and also coalesce somewhat) until the particle surface is covered implies that, given enough time, the minimum droplet size allowed by the mixing conditions would be reached. In the present system and those discussed above this is not found to be the case, therefore there may be some as yet unconsidered factor preventing full surface coverage. Previously reported factors that may affect particle adsorption at the interface include electrostatic barriers,24,25 mass transport of particles6,26 and particle aggregation.14,22 Upon consideration of experimental findings and the energies involved (see ESI,† for calculations) we find that in conditions pertaining to our experiments it is likely that particles may be forced both onto and off the interface during high shear mixing, despite desorption not occurring under quiescent conditions. In a recent paper Phipps and Gittins reach the same conclusions.27 Moreover, it has recently been shown that desorption of particles from the oil/water interface can occur in high energy environments.28
We show that montmorillonite platelet stabilised hexadecane-in-water emulsions consist of droplets covered by a monolayer of particles, that droplet size falls with increasing platelet volume fraction and decreasing oil volume fraction and that droplet coalescence continues once the droplets have reached their ultimate size. A kinetic model is constructed and it is shown that experimental trends are best reproduced when the model allows particle desorption during high shear mixing. The success of this model gives the first suggestion that a competition between particle adsorption and desorption is kinetically important for some systems and may be an indication of the position nanometric montmorillonite platelets on the continuum of emulsion stabilisers ranging from small molecule surfactants to microscopic particles.
2 Materials and methods
Wyoming montmorillonite (SWy-2) was purchased from the Clay Minerals Society source clays repository at Purdue University. The composition of SWy-2 is (Si7.94Al0.06) (Al2.88Fe0.5Mg0.62)O20(OH)4Na0.6829 and it has a cation exchange capacity of 84 mequiv./100 g.30 Berol R648 is an alkyl polyglycol ether ammonium methyl chloride and was kindly donated by Akzo Nobel. Reagent grade NaCl was purchased from Fischer, n-hexadecane (99%) was purchased from Sigma Aldrich.Montmorillonite dispersions were prepared as previously reported.31 45 g L−1 powdered clay was added to deionised water and stirred for 24 hours. The suspension was then dialysed against aqueous NaCl (1 M) for 1 week changing the solution everyday, to remove unwanted ions such as Ca2+, and then dialysed against deionised water, changing water every day, until the conductivity of the dialysate was below 5 μS cm−1. The dialysed suspension was then diluted to 1 wt% and left for 24 hours for large impurities such as sand and quartz to settle out. The supernatant was concentrated up by evaporation and used as stock. Material parameters relevant to the kinetic model are shown in Table 1.
The emulsions were prepared by first diluting stock montmorillonite suspension with appropriate NaCl and Berol solutions. NaCl concentration was fixed at 0.01 M and Berol added at 25 mg g−1 montmorillonite as this composition was previously found to produce stable Pickering emulsions.8 Hexadecane was then added to the suspensions at different oil (ϕo) and platelet (ϕp) volume fractions (calculated from densities shown in Table 1), hand-shaken to pre-emulsify and finally mixed under high shear using an Ultra Turrax IKA T18 with a S18-10G dispersing element at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 5 min. Total sample volumes were 10 mL.
000 rpm for 5 min. Total sample volumes were 10 mL.
Unadsorbed platelets were tested for their emulsifying ability by preparing a dilute emulsion, allowing the droplets to cream, isolating some of the free particles and using them to prepare another emulsion. It was found that particles could stabilise emulsions regardless of their history suggesting that all platelets present possess equal emulsifying ability.
Emulsions were imaged using an Olympus BX51 optical microscope and Pixelink PL-B62CU colour CCD camera using bright field optics with a light balancing daylight filter (BF), differential interference contrast (DIC) and polarising (POM) optics. Droplet size histograms were produced by counting a minimum of 100 droplets from each sample using Linear Intercept software (TU Darmstadt). The surface weighted droplet diameter D32 is used throughout because the relationship between average droplet diameter and population surface area is used in the analysis of results.
Small angle X-ray scattering (SAXS) measurements were carried out using a SAXSLAB Ganesha 300 XL+ with a Genix 3D Cu-source and Pilatus 300k detector running at 20 Hz. Data was reduced and water background subtracted using SAXSgui software (JJ X-Ray Systems ApS).
3 Results
3.1 Structure of a montmorillonite stabilised emulsion
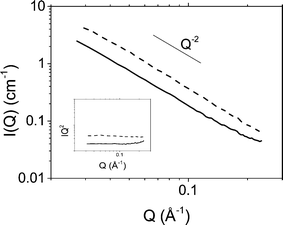
The organisation of platelets at the oil/water interface was determined by microscopy and small angle X-ray scattering. Fig. 1 shows DIC and POM images of a typical emulsion. A distinctive Maltese cross pattern is observed in POM around the droplet edge where the brightness increases from darkness at the angle of the polariser or analyser to maximum at 45° to the direction of the polariser or analyser (as has been observed before8). Such a pattern was common across all emulsions prepared. This suggests that the platelets are organised parallel to the droplet edge which is consistent with an adsorption energy argument as this configuration would lead to the maximum reduction in oil/water interfacial area per platelet. Control images for a surfactant stabilised emulsion showing no Maltese cross pattern can be found in the ESI.†The possibility of particle stacking was tested using SAXS. Fig. 2 shows scattering of a suspension of Berol R648 treated montmorillonite platelets at 0.01 M NaCl and the corresponding hexadecane-in-water emulsion. Both datasets show a scaling of I(Q) ∝ Q−2 at low Q characteristic of two dimensional plate-like objects. At high Q the emulsion signal begins to deviate from the power law. At wider angles (see ESI†) the emulsion sample shows a peak at 1.46 Å−1 which is too large to be due to platelet stacking and is, in fact, a result of hydrocarbon chain to chain separation.35 The absence of any correlations in the measured Q range in addition to the patterns observed in polarising optical microscopy show that the platelets form an adsorbed monolayer at the oil–water interface and are fully exfoliated in suspension.
3.2 Trends in droplet size
The effect of changing emulsion composition on the final droplet populations was investigated by preparing emulsions at a range of ϕo and ϕp values. Fig. 3 shows DIC images of emulsions prepared at ϕo = 0.47 as a function of ϕp and Fig. 4 shows associated droplet size histograms. These figures illustrate the effect of increasing the platelet concentration (ϕp) on the droplet populations. At lower particle volume fractions the droplet size histograms have a bimodal shape with a significant population of larger droplets resulting from coalescence. As ϕp increases, bare interface is coated with platelets more quickly, inhibiting coalescence, and the fraction of large droplets decreases, reducing the average droplet size. At lower oil volume fractions the change in this balance is even more notable, with the size distributions being dominated by the smaller diameter population associated with droplet break-up. See ESI,† for histograms of emulsions covering a wider range of emulsion compositions.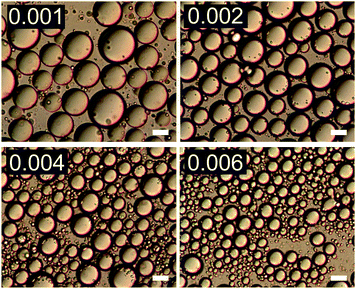 | ||
| Fig. 3 DIC images of emulsions with increasing ϕp (indicated in top left of each image) at ϕo = 0.47. Scale bars represent 20 μm. | ||
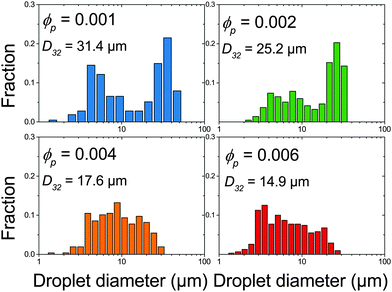 | ||
| Fig. 4 Droplet size histograms of emulsions shown in Fig. 3. | ||
Fig. 5 summarises the observed relationships between droplet size and emulsion composition for the full range of tested ϕp and ϕo (points correspond to experimental data). Clear trends in droplet size with increasing ϕp and also decreasing ϕo are observed. This can be understood as an increase in particle attachment rate as ϕp increases and a decrease in coalescence rate as ϕo decreases. This is shown in Fig. 5 by a fall in droplet size at increasing ϕp for all ϕo and also a decrease in the ϕp required to reach the smallest droplet diameter as ϕo decreases. See the Discussion section for a more quantitative treatment.
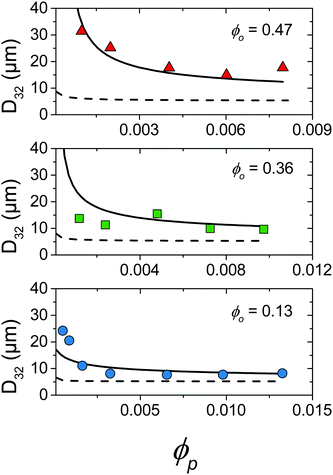 | ||
| Fig. 5 Comparison of droplet size data (points) and kinetic model detailed in Section 4.2 where kdetach = 1.7 × 105 s−1 (solid line) and kdetach = 0 (dotted line). | ||
Despite such systematic scaling of droplet size with ϕp, upon a balance of surface area between the platelets present and the droplets produced it is found that of order 10–100× the droplet surface area is required to produce drops of a given size. Taking the total surface area occupied by platelets at the interface per unit of sample volume as Ap = ϕp/t and total droplet surface area per unit of sample volume as Ao = 3ϕo/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , where t is the platelet thickness (see Table 1) and
, where t is the platelet thickness (see Table 1) and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) is the average droplet radius taken as D32/2, an area ratio Ap/Ao can be calculated. Fig. 6 shows the area ratio for all experimental data. It is shown that as ϕp is increased to push droplet sizes down the emulsification process becomes less efficient and suggests that there may be a kinetic limitation to the full utilisation of platelets in stabilisation of droplet interface.
is the average droplet radius taken as D32/2, an area ratio Ap/Ao can be calculated. Fig. 6 shows the area ratio for all experimental data. It is shown that as ϕp is increased to push droplet sizes down the emulsification process becomes less efficient and suggests that there may be a kinetic limitation to the full utilisation of platelets in stabilisation of droplet interface.
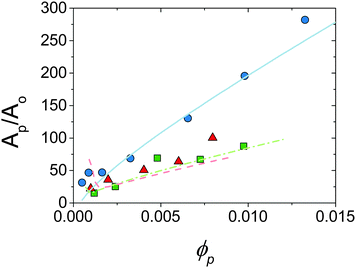 | ||
| Fig. 6 Area ratio for experimental data shown in Fig. 5 against ϕp. Points are experimental, lines are predictions of model allowing particle desorption (see Section 4.2). ϕo = 0.13 (circles, solid line), 0.36 (squares, dot-dash line) and 0.47 (triangles, dashed line). See text for calculations. | ||
3.3 Coalescence of droplets under high shear
Following the finding that a large excess of platelet surface area is required to drive droplet size down (see Fig. 5 and 6) the emulsification kinetics were investigated. Multiple phenomena that may act to impede particle adsorption at droplet interface have been reported. One is that there is a high energetic barrier to adsorption. This is unlikely to be a factor here as the main driving force for this is electrostatic repulsion and in our emulsions (following previous work8) a high electrolyte concentration was used to screen platelet–platelet and platelet–droplet electrostatic interactions. Additionally it has been reported that for non-spherical particles the adsorption barrier is reduced as particles can make contact with the interface with their smallest dimension, reducing any interaction forces greatly.36A second potential reason for the required excess of particles is that they do not adsorb as single particles. This is unlikely here as Fig. 1 and 2 show that the particles are adsorbed as a single monolayer and although the montmorillonite platelets have been reported to form particle clusters in suspension31,37 it has also been shown in high shear rotational rheometry that the particles behave hydrodynamically as single disk-like particles.38,39
Finally there is the possibility that particles may desorb during high shear mixing. Upon comparison of turbulent kinetic energy in a typical laboratory scale mixer and the adsorption energy of a montmorillonite platelet it is apparent that they may desorb as a result of such energetic hydrodynamic conditions. One consequence of this would be that the droplet size would reach a steady state, if particles are both adsorbing and desorbing then droplets should also continue to coalesce and break-up as long as mixing continues. A previously prepared emulsion that is subjected to high shear mixing again would therefore undergo further particle adsorption/desorption and droplet break-up/coalescence but the steady state droplet size would not change.
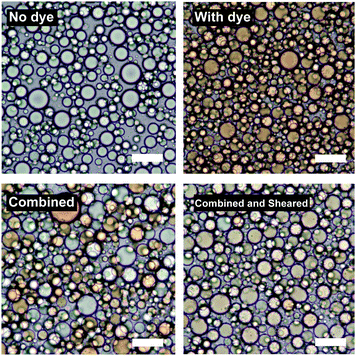
Fig. 7 shows the result of an experiment where two sets of two emulsions were prepared. Each set contained emulsions of identical composition except that in one the dispersed phase was dyed with Sudan II. These two droplet populations were first combined (bottom left of Fig. 7) and then subjected to the same high shear mixing as when they were initially emulsified (bottom right of Fig. 7).
Upon simple combination the dyed and undyed droplets do not mix. Upon high shear mixing the dye is redistributed across the two populations suggesting that further coalescence and break-up of the droplets takes place during high shear mixing resulting in mixing of the oil phases.
The D32 of the samples does not significantly change after re-shearing suggesting that further break-up also occurs. For the sample at ϕo = 0.47, D32 changes from 17.3 μm to 15.0 μm and the emulsion at ϕo = 0.13 (see ESI†) shows similar behaviour. These insignificant changes in droplet diameter (given standard deviations of around 30–40% of D32) show that there is no change in the final droplet size, despite droplets mixing at both high ϕo (∼0.5) where coalescence is thought to be dominant, and low ϕo (∼0.1) where break-up is thought to be dominant (see ESI,† for second dye experiment conducted at ϕo = 0.13).
If coalescence were to cease then it would be expected that, in the absence of any significant impediment to adsorption, droplets should either be as small as can be produced by the mixer if particles are in excess or as small as the particles can cover if they are not. Neither of these cases are observed in the present system further suggesting that there must be some kinetic limitation preventing particles remaining at the interface. The next section explores a kinetic model describing the competition between droplet break-up and coalescence being mediated by a competition between particle adsorption and desorption during turbulent flow. Predictions of this model are then compared to experimental data in an attempt to shed light on the mechanisms at play during high shear emulsification.
4 Discussion
4.1 Emulsification in turbulent flow
High shear mixers, such as the Ultra Turrax rotor–stator used in this study, produce high fluid velocities in small volumes. The type of flow can be characterised by the ratio of inertial to viscous forces quantified by the Reynolds number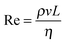 , where ρ, v and η are the density, velocity and dynamic viscosity of the fluid respectively and L is a characteristic length scale (in this case 7.5 mm which is the diameter of the rotor). In high shear mixers Re is typically >103 indicating turbulent flow where the local fluid velocity differs from the time average and turbulent eddies are present.40 If it is assumed that the turbulence is isotropic (which is valid at small length scales such as that of emulsion droplets) then the theory of Kolmogorov can be used to determine kinetic parameters.40 The key quantity in analysing a turbulent flow regime is the energy dissipation rate (ε, with units W kg−1) which has been estimated for toothed rotor–stator mixers41,42 to be of order 105 W kg−1. From this the Kolmogorov microscale λ can be defined which is the smallest size of eddies present (see ESI†). When droplets are larger than λ break-up is due to hydrodynamic interactions between the droplet and the eddies. The resulting local pressure fluctuations around a droplet, caused by variations in local flow velocity, that are larger than the Laplace pressure will cause the droplet to rupture; this is referred to as break-up in the turbulent inertial regime. When droplets are smaller than λ the local flow near the drop is likely to be laminar. The stress acting on the droplet is therefore a function of the fluid viscosity and it is this stress that causes the drops to deform and eventually rupture. This viscosity dependence is referred to as the turbulent viscous regime. Due to the inverse relationship between Laplace pressure and droplet radius a critical length scale for both regimes results where the kinetic energy of the flow is no longer sufficient to break up the droplets and this can be used as an upper limit to the lowest attainable droplet size.40 The two regimes are can be identified using a droplet Reynolds number (Red) where the droplet diameter is used in place of L; Red > 1 indicates turbulent inertial and Red < 1 indicates turbulent viscous. The parameters for the system studied here are shown in Table 2. The bulk and droplet Reynolds numbers (Re and Red) are larger than 103 and 1 respectively therefore break-up can be described by the turbulent inertial regime.40
, where ρ, v and η are the density, velocity and dynamic viscosity of the fluid respectively and L is a characteristic length scale (in this case 7.5 mm which is the diameter of the rotor). In high shear mixers Re is typically >103 indicating turbulent flow where the local fluid velocity differs from the time average and turbulent eddies are present.40 If it is assumed that the turbulence is isotropic (which is valid at small length scales such as that of emulsion droplets) then the theory of Kolmogorov can be used to determine kinetic parameters.40 The key quantity in analysing a turbulent flow regime is the energy dissipation rate (ε, with units W kg−1) which has been estimated for toothed rotor–stator mixers41,42 to be of order 105 W kg−1. From this the Kolmogorov microscale λ can be defined which is the smallest size of eddies present (see ESI†). When droplets are larger than λ break-up is due to hydrodynamic interactions between the droplet and the eddies. The resulting local pressure fluctuations around a droplet, caused by variations in local flow velocity, that are larger than the Laplace pressure will cause the droplet to rupture; this is referred to as break-up in the turbulent inertial regime. When droplets are smaller than λ the local flow near the drop is likely to be laminar. The stress acting on the droplet is therefore a function of the fluid viscosity and it is this stress that causes the drops to deform and eventually rupture. This viscosity dependence is referred to as the turbulent viscous regime. Due to the inverse relationship between Laplace pressure and droplet radius a critical length scale for both regimes results where the kinetic energy of the flow is no longer sufficient to break up the droplets and this can be used as an upper limit to the lowest attainable droplet size.40 The two regimes are can be identified using a droplet Reynolds number (Red) where the droplet diameter is used in place of L; Red > 1 indicates turbulent inertial and Red < 1 indicates turbulent viscous. The parameters for the system studied here are shown in Table 2. The bulk and droplet Reynolds numbers (Re and Red) are larger than 103 and 1 respectively therefore break-up can be described by the turbulent inertial regime.40
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. See ESI for calculations
000 rpm. See ESI for calculations
| Parameter | Value |
|---|---|
| Re | 6.45 × 104 |
| Red | 10.0 |
| ε (W kg−1) | 1.7 × 105 |
| λ (μm) | 1.1 |
4.2 Kinetics of emulsification
Understanding the emulsification in turbulent flow is key to understanding processing of these systems for industrial use and thus there have been many detailed theoretical studies into the kinetics of the processes involved and the resulting droplet size distributions.43–51 Here we take only the minimum number of arguments required to realistically represent our system and only focus on the ultimate average droplet size. Such an approach allows for the straightforward construction of models representing multiple phenomena for comparison with experimental results.Two parameters were followed; nd the droplet number density and Ac the area of droplet surface covered with particles per unit volume. The droplet number density increases upon a break-up event and decreases upon a coalescence event and can be related to the average droplet size by eqn (1):
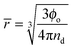 | (1) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 2nd) the probability of two regions of bare droplet interface coming into contact falls and therefore the coalescence rate drops.
2nd) the probability of two regions of bare droplet interface coming into contact falls and therefore the coalescence rate drops.
One interpretation of such quantities (when there is an excess of particles) is that the collisions between particles and droplets will occur frequently so platelets adsorb, increasing Ac and decreasing the coalescence rate, until Ac approaches Atotald, at which point coalescence will stop and the final droplet size will be reached. This suggests that the droplet size will always tend to the smallest that can be produced by the mixer and that, given sufficient emulsification time, coalescence will stop entirely. Neither of these phenomena are observed in our system. The kinetic model considered here includes particle desorption in the flow field therefore allowing Ac < Atotald even when the platelets are in excess. Upon consideration of the turbulent kinetic and platelet adsorption energies involved this would be a reasonable assumption (see ESI,† for calculations).
Combining the relevant processes and their effects on nd and Ac gives rise to the following set of equations:
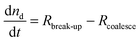 | (2) |
 | (3) |
Often Rdetach is ignored, however considering the scaling of particle desorption energy being with the square of the particle size (see calculations in ESI†) a continuum from small molecules surfactants to large solid particles is anticipated. Low molecular weight surfactants can displaced by thermal fluctuations, small particles can be displaced by the energy produced by a typical laboratory scale mixer and large particles are so strongly adsorbed that even this high power mixing cannot displace them.
Following the predictions of particle coagulation models43–45,51 we arrive at expressions for the rates Rcoalesce and Rattach given by eqn (4) and (5). The platelets are treated as single particles as SAXS data (Fig. 2) shows that there is no particle stacking and previous rheological studies of montmorillonite suspensions at high shear rates in laminar flow find that they behave hydrodynamically as single disk-like particles.38,39 Following Delichatsios and Probstein45Rcoalesce and Rattach can be expressed as:
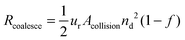 | (4) |
 | (5) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) .45 The potential for bridging (where two droplets share interfacial particles) was ignored here as due to the extremely small platelet thickness (∼1 nm) it follows that for droplets to be close enough to share a platelet the it is likely that the fluid menisci from the droplets will come into contact triggering a coalescence event.21,53
.45 The potential for bridging (where two droplets share interfacial particles) was ignored here as due to the extremely small platelet thickness (∼1 nm) it follows that for droplets to be close enough to share a platelet the it is likely that the fluid menisci from the droplets will come into contact triggering a coalescence event.21,53
The break-up of emulsion droplets has been studied for both laminar54 and turbulent flow48 and recent simulations have shown the effects of particles at the droplet surface on break-up.20 The model for droplet break-up in turbulent flow used here follows the work of Coulaloglou and Tavlarides who applied an activation energy approach to represent the transfer of kinetic energy from turbulent eddies to a droplet upon a collision and this has been shown to agree with experimental data.26,46 The break-up rate is defined as the fraction of droplets with energy high enough to break multiplied by the reciprocal of the time taken for a droplet to break:
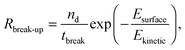 | (6) |
The individual rates are expressed in terms of known parameters as shown in Table 1. These can be substituted into eqn (2) and (3) giving a set of equations that can be solved for nd and Ac and, given ϕo and using eqn (1), the evolution of average droplet size over time can be evaluated.
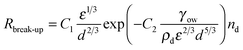 | (7) |
| Rcoalesce = 3.45πr7/3ε1/3nd2(1 − f) | (8) |
| Rattach = α1.37π(r + rp)7/3ε1/3ndnpap(1 − f) | (9) |
| Rdetach = kdetachAc | (10) |
The model was solved numerically and predicted a fall of droplet diameter to a steady state for parameters corresponding to experimental samples. kdetach, C1 and C2 were varied to fit the model to the entire ensemble of experimental droplet diameters using a least squares approach giving values of 1.7 × 105 s−1, 1.2 and 1.2 respectively. Fig. 5 shows a comparison between experimental droplet diameters (points) and the steady state droplet diameters predicted by the model (solid lines). Predictions of the model for identical conditions where kdetach = 0 are also shown (dotted lines).
In reality it is likely that kdetach would vary with system parameters such as ε and the size of the stabilising particles. Neither of these parameters vary in the present experiments, therefore kdetach is fixed for all compositions and represents the number of particles desorbing per second in the given flow conditions. At high ϕp, Rattach is initially fast which rapidly increases f and decreases Rcoalesce. This results in a droplet size that is determined by break-up processes and therefore constant with varying ϕp.
This model predicts the behaviour in the high shear region (the volume swept out by the rotor55) and not the entire sample volume. The time any given fluid element spends in the high shear region must therefore be compared to the characteristic time scales of droplet break-up, particle attachment and particle detachment. The residence time in the high shear region can be estimated as:
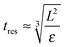 | (11) |
The typical break-up time for a single droplet can be calculated by taking the inverse of eqn (7) when applied to a single droplet which accounts for the time the droplet takes to deform and the probability that it will collide with a turbulent eddy of sufficient energy to cause rupture. Inputting values as above the break-up time scales are estimated to be of order 10 μs.
The typical time for a particle desorption event can be estimated as simply the inverse of the estimated desorption rate constant giving a time scale of 6 μs. Since all of the systems studied reach a steady state the typical steady state attachment time scale must also be approximately 6 μs.
It follows that all of the processes described by the model occur quickly enough that a fluid element entering the mixing region will remain there for sufficient time for droplets to break-up and particles to attach and detach. This means that the model should require no adjustment to account for the probability of processes occurring in the mixing volume.
At low ϕp the effects of a non-zero Rdetach become apparent. Fig. 5 shows a steep increase of droplet size with decreasing ϕp for both experimental data and the model where kdetach is non-zero. Rattach is lower at low ϕp resulting in a lower f and therefore higher Rcoalesce. This shift in the competition between break-up and coalescence results in a larger steady state droplet size at low ϕp and is in agreement with data. Interestingly it is kdetach that determines the magnitude of the deviation from the minimum droplet size. Fig. 8 shows the steady state droplet diameters predicted by the model for ϕo = 0.4 and varying ϕp at different kdetach and shows that the magnitude of the desorption rate constant determines the ϕp at which the droplet size hits the high ϕp plateau.
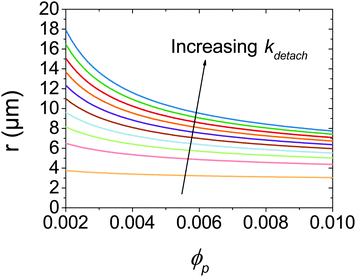 | ||
| Fig. 8 Calculated steady state droplet radii for ϕo = 0.4 as a function of ϕp for kdetach from 5 × 103 to 5 × 105 s−1. | ||
Fig. 6 shows the prediction of the model in the form of an area ratio between the platelets present in the system and steady state droplet size. There is good agreement with experimental data showing that the largest droplet surface area stabilised per total particle surface area occurs at lower ϕp. Interestingly the model area ratio appears to go through a minimum for ϕo = 0.36 and 0.47. This suggests that there exist optimum compositions for the most efficient use of stabiliser (largest droplet surface area stabilised per total surface area of particles), however given the small number of experimental data points in this region this is only a speculative conclusion.
The model reproduces the general experimental trends well (as shown in Fig. 5) however is still some quantitative discrepancy between model and data. Such agreement is still encouraging as this model combines a small number of arguments and produces a realistic representation of the experimental system and is a first step towards incorporating particle desorption during mixing into the general understanding of solid stabilised emulsions where it is appropriate. Possible advancements to the model include explicit treatment of adsorption barriers, more detailed treatment of coalescence including film thinning and particle ejection21 and study into the precise mechanisms of particle desorption under high shear mixing.
The comparison of the model and the experimental data show that to gain real insight into the mechanisms of formation of solid stabilised emulsions many factors must be considered. Here we show evidence that particle desorption during shearing may be an important factor for montmorillonite stabilised emulsions.
5 Conclusions
It has been shown that a kinetic model based on a balance between droplet break-up and coalescence mediated by particle adsorption and desorption can reproduce experimental trends in droplet diameter of emulsions formed and stabilised in turbulent flow. Under circumstances where these processes occur on similar time-scales a steady state determines the ultimate droplet size as opposed to a regime where the droplet surface area is determined by the particle surface area.11 This explains the need for a large excess of stabilising particles to drive the droplet size down and is in line with experimental work in this (Fig. 5) and previous studies.6,8,19Further work could see this model applied to other regimes such as ultrasound emulsification, which can produce higher ε,56 and emulsions with different dispersed phases. Also refinements to the model to truly capture the approach of a platelet to the interface accounting for orientation, electrostatic repulsion and an investigation into the mechanisms of particle desorption would make interesting further work.
Additionally this could be combined with previous work on rheology control using montmorillonite platelets16,18,31 to produce a system where the minority component acts as a dual emulsion stabiliser and rheology modifier. This improvement in the understanding of platelet stabilised droplets in turbulent flow can be used to optimise the design of tightly controlled and efficient emulsion-based formulations for example Fig. 5 and 6 shows that the smallest droplet sizes are produced at high ϕp or low ϕo but the lowest area ratios at low ϕp and high ϕo. It is only by combining insight gained from studies on many different systems that the intricacies of Pickering emulsification will be fully uncovered.
Acknowledgements
W. J. Ganley thanks EPSRC for funding this work (EP/L504919/1). R. M. Richardson is thanked for help with small angle X-ray scattering measurements and Ganesha X-ray scattering apparatus used for this research was purchased under EPSRC Grant “Atoms to Applications” (EP/K035746/1). Akzo Nobel are thanked for kindly donating the Berol R648.References
- W. Ramsden, Proc. R. Soc. London, 1903, 72, 156–164 CrossRef CAS.
- S. U. Pickering, J. Chem. Soc., Trans., 1907, 91, 2001–2021 RSC.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546 CrossRef CAS.
- B. P. Binks and S. O. Lumsdon, Langmuir, 2000, 16, 2539–2547 CrossRef CAS.
- B. P. Binks and S. O. Lumsdon, Langmuir, 2001, 17, 4540–4547 CrossRef CAS.
- P. N. Sturzenegger, U. T. Gonzenbach, S. Koltzenburg and L. J. Gauckler, Soft Matter, 2012, 8, 7471 RSC.
- A. Tsugita, S. Takemoto and K. Mori, J. Colloid Interface Sci., 1983, 95, 551–560 CrossRef CAS.
- Y. Cui, M. Threlfall and J. S. van Duijneveldt, J. Colloid Interface Sci., 2011, 356, 665–671 CrossRef CAS PubMed.
- T. Ngai, S. H. Behrens and H. Auweter, Chem. Commun., 2005, 331–333 RSC.
- Z. Li, D. Harbottle, E. Pensini, T. Ngai, W. Richtering and Z. Xu, Langmuir, 2015, 31, 6282–6288 CrossRef CAS PubMed.
- S. Arditty, C. P. Whitby, B. P. Binks, V. Schmitt and F. Leal-Calderon, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11, 273–281 CrossRef CAS PubMed.
- S. Arditty, V. Schmitt, J. Giermanska-Kahn and F. Leal-Calderon, J. Colloid Interface Sci., 2004, 275, 659–664 CrossRef CAS PubMed.
- K. Golemanov, S. Tcholakova, P. A. Kralchevsky, K. P. Ananthapadmanabhan and A. Lips, Langmuir, 2006, 22, 4968–4977 CrossRef CAS PubMed.
- N. Ashby and B. Binks, Phys. Chem. Chem. Phys., 2000, 2, 5640–5646 RSC.
- G. Lagaly, M. Reese and S. Abend, Appl. Clay Sci., 1999, 14, 83–103 CrossRef CAS.
- G. Lagaly, M. Reese and S. Abend, Appl. Clay Sci., 1999, 14, 279–298 CrossRef CAS.
- P. C. Garcia and C. P. Whitby, Soft Matter, 2012, 8, 1609 RSC.
- B. P. Binks, J. H. Clint and C. P. Whitby, Langmuir, 2005, 21, 5307–5316 CrossRef CAS PubMed.
- B. P. Binks and M. Kirkland, Phys. Chem. Chem. Phys., 2002, 4, 3727–3733 RSC.
- S. Frijters, F. Günther and J. Harting, Soft Matter, 2012, 8, 6542 RSC.
- E. J. Stancik, M. Kouhkan and G. G. Fuller, Langmuir, 2004, 20, 90–94 CrossRef CAS PubMed.
- J. Frelichowska, M.-A. Bolzinger and Y. Chevalier, J. Colloid Interface Sci., 2010, 351, 348–356 CrossRef CAS PubMed.
- E. Tsabet and L. Fradette, Ind. Eng. Chem. Res., 2015, 54, 2227–2236 CrossRef CAS.
- K. Larson-Smith, A. Jackson and D. C. Pozzo, Langmuir, 2012, 28, 2493–2501 CrossRef CAS PubMed.
- V. R. Dugyala, J. S. Muthukuru, E. Mani and M. G. Basavaraj, Phys. Chem. Chem. Phys., 2016, 18, 5499–5508 RSC.
- L. Nilsson and B. Bergenståhl, Langmuir, 2006, 22, 8770–8776 CrossRef CAS PubMed.
- J. S. Phipps and D. I. Gittins, Agro Food Ind. Hi-Tech, 2016, 27, 60–63 Search PubMed.
- V. Poulichet and V. Garbin, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 1–6 CrossRef PubMed.
- L. J. Michot, I. Bihannic, K. Porsch, S. Maddi, C. Baravian, J. Mougel and P. Levitz, Langmuir, 2004, 20, 10829–10837 CrossRef CAS PubMed.
- Y. Cui and J. S. van Duijneveldt, Langmuir, 2010, 26, 17210–17217 CrossRef CAS PubMed.
- W. J. Ganley and J. S. van Duijneveldt, Langmuir, 2015, 31, 4377–43785 CrossRef CAS PubMed.
- A. Goebel and K. Lunkenheimer, Langmuir, 1997, 13, 369–372 CrossRef CAS.
- Hexadecane ReagentPlus 99%, 2015, http://www.sigmaaldrich.com/catalog/product/sial/h6703 [Online; accessed 30-August-2015].
- Handbook Of Clay Science, ed. F. Bergaya and G. Lagaly, Elsevier Science, 2013, part A Search PubMed.
- G. Stewart, Phys. Rev., 1928, 31, 174–179 CrossRef CAS.
- S. Tcholakova, N. D. Denkov and A. Lips, Phys. Chem. Chem. Phys., 2008, 10, 1608–1627 RSC.
- A. Shalkevich, A. Stradner, S. K. Bhat, F. Muller and P. Schurtenberger, Langmuir, 2007, 23, 3570–3580 CrossRef CAS PubMed.
- C. Baravian, D. Vantelon and F. Thomas, Langmuir, 2003, 19, 8109–8114 CrossRef CAS.
- E. Paineau, L. J. Michot, I. Bihannic and C. Baravian, Langmuir, 2011, 27, 7806–7819 CrossRef CAS PubMed.
- P. Walstra and P. Smulders, Modern Aspects of Emulsion Science, Royal Society of Chemistry, Cambridge, 1998 Search PubMed.
- B. Brocart, P. A. Tanguy, C. Magnin and J. Bousquet, J. Dispersion Sci. Technol., 2002, 23, 45–53 CrossRef CAS.
- L. Fradette, B. Brocart and P. Tanguy, Chem. Eng. Res. Des., 2007, 85, 1553–1560 CrossRef CAS.
- P. Saffman and J. Turner, J. Fluid Mech., 1956, 1, 16–30 CrossRef.
- J. Abrahamson, Chem. Eng. Sci., 1975, 30, 1371–1379 CrossRef CAS.
- M. Delichatsios and R. Probstein, J. Colloid Interface Sci., 1975, 51, 394–405 CrossRef.
- C. Coulaloglou and L. Tavlarides, Chem. Eng. Sci., 1977, 32, 1289–1297 CrossRef CAS.
- G. Narsimhan, J. Colloid Interface Sci., 2004, 272, 197–209 CrossRef CAS PubMed.
- N. Vankova, S. Tcholakova, N. D. Denkov, I. B. Ivanov, V. D. Vulchev and T. Danner, J. Colloid Interface Sci., 2007, 312, 363–380 CrossRef CAS PubMed.
- N. Vankova, S. Tcholakova, N. D. Denkov, V. D. Vulchev and T. Danner, J. Colloid Interface Sci., 2007, 313, 612–629 CrossRef CAS PubMed.
- S. Tcholakova, N. Vankova, N. D. Denkov and T. Danner, J. Colloid Interface Sci., 2007, 310, 570–589 CrossRef CAS PubMed.
- C. Meyer and D. Deglon, Miner. Eng., 2011, 24, 719–730 CrossRef CAS.
- S. Levine, B. D. Bowen and S. J. Partridge, Colloids Surf., 1989, 38, 325–343 CrossRef CAS.
- N. Denkov and I. Ivanov, J. Colloid Interface Sci., 1992, 150, 589–593 CrossRef CAS.
- N. Grizzuti and O. Bifulco, Rheol. Acta, 1997, 36, 406–415 CrossRef CAS.
- A. T. Utomo, M. Baker and A. W. Pacek, Chem. Eng. Res. Des., 2008, 86, 1397–1409 CrossRef CAS.
- J. P. Canselier, H. Delmas, A. M. Wilhelm and B. Abismal, J. Dispersion Sci. Technol., 2002, 23, 333–349 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Calculations of flow parameters and energies used to guide construction of the kinetic models, wide angle X-ray scattering of an emulsion, POM and DIC images of a surfactant stabilised emulsion and droplet size histograms corresponding to the data points in Fig. S5 and S6. Micrographs and figure data can be found in a data repository (DOI: 10.5523/bris.fdwwgjzgv03g1ay0mkkorjc26). See DOI: 10.1039/c6sm01377e |
| This journal is © The Royal Society of Chemistry 2016 |