The nonequilibrium glassy dynamics of self-propelled particles†
Abstract
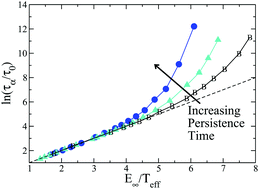
We study the glassy dynamics taking place in dense assemblies of athermal active particles that are driven solely by a nonequilibrium self-propulsion mechanism. Active forces are modeled as an Ornstein–Uhlenbeck stochastic process, characterized by a persistence time and an effective temperature, and particles interact via a Lennard-Jones potential that yields well-studied glassy behavior in the Brownian limit, which is obtained as the persistence time vanishes. By increasing the persistence time, the system departs more strongly from thermal equilibrium and we provide a comprehensive numerical analysis of the structure and dynamics of the resulting active fluid. Finite persistence times profoundly affect the static structure of the fluid and give rise to nonequilibrium velocity correlations that are absent in thermal systems. Despite these nonequilibrium features, for any value of the persistence time we observe a nonequilibrium glass transition as the effective temperature is decreased. Surprisingly, increasing departure from thermal equilibrium is found to promote (rather than suppress) the glassy dynamics. Overall, our results suggest that with increasing persistence time, microscopic properties of the active fluid change quantitatively, but the general features of the nonequilibrium glassy dynamics observed with decreasing the effective temperature remain qualitatively similar to those of thermal glass-formers.

 Please wait while we load your content...
Please wait while we load your content...