 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of surfactants in forced dynamic dewetting†
Franziska
Henrich
,
Daniela
Fell
,
Dorota
Truszkowska
,
Marcel
Weirich
,
Manos
Anyfantakis
,
Thi-Huong
Nguyen
,
Manfred
Wagner
,
Günter K.
Auernhammer
 * and
Hans-Jürgen
Butt
* and
Hans-Jürgen
Butt
Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: auhammer@mpip-mainz.mpg.de
First published on 24th August 2016
Abstract
In this work we show that the forced dynamic dewetting of surfactant solutions depends sensitively on the surfactant concentration. To measure this effect, a hydrophobic rotating cylinder was horizontally half immersed in aqueous surfactant solutions. Dynamic contact angles were measured optically by extrapolating the contour of the meniscus to the contact line. Anionic (sodium 1-decanesulfonate, S-1DeS), cationic (cetyl trimethylammonium bromide, CTAB) and nonionic surfactants (C4E1, C8E3 and C12E5) with critical micelle concentrations (CMCs) spanning four orders of magnitude were used. The receding contact angle in water decreased with increasing velocity. This decrease was strongly enhanced when adding surfactant, even at surfactant concentrations of 10% of the critical micelle concentration. Plots of the receding contact angle-versus-velocity almost superimpose when being plotted at the same relative concentration (concentration/CMC). Thus the rescaled concentration is the dominating property for dynamic dewetting. The charge of the surfactants did not play a role, thus excluding electrostatic effects. The change in contact angle can be interpreted by local surface tension gradients, i.e. Marangoni stresses, close to the three-phase contact line. The decrease of dynamic contact angles with velocity follows two regimes. Despite the existence of Marangoni stresses close to the contact line, for a dewetting velocity above 1–10 mm s−1 the hydrodynamic theory is able to describe the experimental results for all surfactant concentrations. At slower velocities an additional steep decrease of the contact angle with velocity was observed. Particle tracking velocimetry showed that the flow profiles do not differ with and without surfactant on a scales >100 μm.
Introduction
The wetting and dewetting of a solid surface by a liquid are fundamental processes of many natural phenomena and technical applications. Examples are the movement of a drop running down a window glass or being blown across a windscreen, coating, painting, printing, and the distribution of pesticides on leaf surfaces. Wetting is characterized by the contact angle formed at the three-phase contact line. In equilibrium, the contact angle (Θ) on an ideally smooth, homogeneous and nondeformable surface is determined by a balance of the interfacial tensions:1 | (1) |
When the contact angle exceeds the range between the advancing and receding contact angle, the contact line starts moving. In this case the contact angle depends on the velocity and one observes dynamic contact angles. Such a situation can arise when e.g. a drop is placed on a surface and its initial contact angle is significantly larger than the advancing contact angle. It spontaneously spreads driven by interfacial, also called capillary forces. Movement of the contact line can also be caused by external forces such as gravity. In contrast to spontaneous wetting/dewetting, in which a liquid is drawn towards its equilibrium configuration by capillary forces, in forced wetting/dewetting external forces continuously maintain a certain velocity of the contact line. One of the key questions in wetting dynamics is: how are velocity and dynamic contact angle related?
Here, we focus on forced dewetting that is, for example, essential in coating. Several techniques have been employed to measure dynamic receding contact angles. In early experiments, thin capillaries have been used to measure dynamic contact angles over a range of velocities.2,3 When plotting the dynamic contact angles versus the capillary number rather than velocity U, all results collapsed onto a single master curve.3 The capillary number Ca = ηU/γL represents the relative effect of viscous forces versus the surface tension; η is the viscosity of the liquid. A disadvantage of using a capillary is the limited accessibility of the inner surface for characterization and manipulation. In addition, optical refraction at the wall distorts the image when observing the contact angles. One of the main techniques for measuring dynamic contact angles has been to plunge or withdraw a plate,4–6 cylinder,7–11 fiber,12,13 or tape9,14–16 into or out off a liquid tank. Either the height of the meniscus is measured4,6,10 or dynamic contact angles are obtained by imaging the contour of the meniscus.8,11,13,14 A variety of materials with smooth surfaces can be used as plates or cylinders. The above techniques suffer from limitations concerning the range of realisable speeds or a limited choice of substrate materials. To circumvent these limitations we used an alternative technique: a rotating cylinder or drum.17 In this method a horizontal cylinder is half immersed in the liquid. When rotating it at a defined velocity on one side the dynamic advancing contact angle is observed, on the other side the dynamic receding contact angle can be measured. The rotating cylinder allows a continuous observation of the three-phase contact line over a wide range of wetting/dewetting speeds. One should, however, keep in mind, that the immersion time and the “dry” time (i.e., the time the surface is not immersed) are linked to the velocity and size of the cylinder. To achieve a steady state of the cylinder surface a prolonged rotation in the bath is necessary.
Several theories,18–20 such as the molecular kinetic theory,21 describe dynamic wetting. They in particular link the observed dynamic contact angles to the wetting speed. The standard description of dynamic contact angles, the hydrodynamic theory, assumes a balance of viscous and capillary forces near the contact line.22–27 Hydrodynamic theory has been successfully applied to describe forced dewetting for a wide intermediate range of capillary numbers.9,24,26,28 It often fails at very slow velocities of the order of Ca ≤ 10−4.5,6,10,29 At high velocities, of the order of Ca ≥ 10−2,10,11,30,31 typically the contact line becomes unstable and a continuous liquid film – called the Landau–Levich film – is formed.11,32–34 Often, the instability of the receding contact line occurs by formation of a V-shaped corner.15,31,35
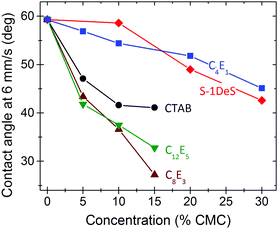
In hydrodynamic theory, a microscopic regime extending over a distance λ around the moving contact line is separated from a macroscopic flow regime. In the microscopic regime, slip between the liquid and the solid surface is allowed. For the apparent dynamic contact angle Θ the two regimes can be matched leading to:9,24,26,28
 | (2) |
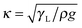 is an appropriate choice for h; ρ is the density of the liquid and g = 9.81 m s−2 is the acceleration of gravity. Eqn (2) was derived assuming low contact angles and originally for advancing contact lines. It was, however, shown that it is also valid for contact angles up to 100–150°.13,36
is an appropriate choice for h; ρ is the density of the liquid and g = 9.81 m s−2 is the acceleration of gravity. Eqn (2) was derived assuming low contact angles and originally for advancing contact lines. It was, however, shown that it is also valid for contact angles up to 100–150°.13,36
While the dynamic wetting of simple, one component liquids has been studied extensively, multi-component liquids, like surfactant solutions, are less understood. Surfactant molecules adsorbed at interfaces influence the dynamic behavior of the liquid. They change for example the hydrodynamic boundary condition at liquid–gas interfaces37–39 or the flow profile inside a liquid with a free surface.40,41 Surfactants are used to control the extent of wetting/dewetting, due to their ability to reduce liquid–solid contact angles or to allow an aqueous solution to spread on non-polar surfaces.42–47 The presence of surfactants increases the thickness of a film when withdrawing a fiber48,49 or plate40,50 from an aqueous solution. Luokkala et al. observed a decrease of the critical velocity when withdrawing a silicon wafer from aqueous solutions of nonionic surfactants poly(ethylene glycol)monododecyl ether (C12En).51 Most studies concentrate on the thickness of the Landau–Levich films40,48,52 but not directly on the velocity-dependent contact angles.
Previous studies showed that the cationic surfactant cetyl trimethylammonium bromide (CTAB) has a strong influence on the dynamic contact angle.53,54 Also the critical velocity for film formation is drastically reduced. The effect was tentatively explained by the formation of local surface tension gradients close to the three-phase contact line, and therefore Marangoni tensions. When a surface is removed from a liquid bath fresh liquid–air interface is continuously formed close to the three-phase contact line (Fig. 1). Since this freshly created interface is not immediately covered with surfactant molecules, surface tension gradients, so called Marangoni tensions, arise.48,49,55,56 These Marangoni tensions can slow down the liquid outflow of the region close to the three-phase contact line (purple arrow in Fig. 1).
The aim of the present manuscript is to demonstrate the generality of the surfactant-induced changes in the receding contact angle of surfactant solutions. Which observations are specific to CTAB and which one also hold for other surfactants? Do electrostatic effects play a role? What are the fundamental physical properties dominating forced dewetting? To answer these questions we vary the type of surfactant (anionic, cationic, nonionic) and the critical micelle concentration (CMC) of the surfactants (more than four orders of magnitude). For a set of representative surfactants we measured dynamic contact angles using a rotating cylinder setup. We demonstrate that the change in dewetting behavior is a universal phenomenon, occurring for all surfactants. We further analyze the flow profile near the receding contact line with and without surfactant. The velocities applied in this paper varied from 1 mm s−1 up to 200 mm s−1. They are faster than Langmuir–Blodgett coating but slower than Landau–Levich film formation of pure water.32 In the case of Landau–Levich film formation, added surfactants change qualitatively the flow profile.41 In our experiments, the flow profile remains qualitatively the same. Both observations support the hypothesis that a Marangoni effect close to the three-phase contact line can account for the sharp decrease of dynamic receding contact angles.
Experimental section
Materials
Anionically polymerized polystyrene (MW = 300 kg mol−1) and tetrahydrofuran (THF, Sigma-Aldrich) were used without further purification. Cetyl trimethylammonium bromide (CTAB, [(C16H33)N(CH3)3Br], cationic) was purchased from Sigma-Aldrich, sodium 1-decanesulfonate (S-1DeS, C10H21SO2OHNa, anionic) from Sigma-Aldrich and butyl glycol (C4E1, C4H9OCH2CH2OH, nonionic) from Alfa Aesar. Octyltriglycol (C8E3, C8H17(OCH2CH2)3OH, nonionic) and dodecyl pentaglycol (C12E5, C12H25(OCH2CH2)5OH nonionic) were purchased from Sigma-Aldrich. All surfactants were used without further purification. Milli-Q water was prepared by purifying water using an Arium® 611 ultrapure water system (Sartorius) or Arium® pro VF/UF&DI/UV (Sartorius) at a resistivity of 18.2 MΩ cm.Rotating cylinder setup
The rotating cylinder setup consists of an exchangeable stainless steel cylinder horizontally mounted in a bath filled with water or a surfactant solution, up to the axis (Fig. 2A).53,54 The bath has a width of 10 cm, a depth of 17 cm and a height of 15 cm. The cylinder has a diameter of 12 cm. Its spherical segment geometry allowed for a precise imaging and thus accurate measurement of the contact angle. The cylinder was coated with polystyrene by rotating it at a speed of 100 mm s−1 in a 0.8 wt% solution of polystyrene in THF (tetrahydrofuran). After 5 min the solution was quickly removed, resulting in a polystyrene film on the cylinder. This film was first dried at room temperature and then for 16 h at 60 °C. The advancing and receding contact angles of water measured with a sessile drop on the surface were 66° and 100°, respectively. Scanning force microscopy (SFM, JPK NanoWizard™, Berlin, Germany) was used to measure the roughness of the cylinder coating. The SFM measurements were performed in tapping mode (cantilever: Olympus OMCL-AC240TS, spring constant 2 N m−1, resonance frequency 70 kHz, in air at room temperature) directly on the cylinder surface. The latter was realized by building a special scaffold where the SFM head was placed. The surface roughness measured and analyzed using Gwyddion software over areas of 50 × 50 μm2 was in the order of 150 nm, mainly caused by the underlying polished steel.For measuring the contact angle brightfield microscopy with a high speed camera (Photron, Fastcam SA-1, 12× magnification, working distance about 30 cm, 250–500 frames per s) was used. The contact angle was determined by fitting straight line to the solid surface and to the liquid–air interface at the point where both meet. All experiments were carried out at a temperature of 21 °C in a closed bath with water saturated atmosphere. For cleaning the setup between the measurements the setup was first placed for several hours under flowing tap water and then rinsed for 1 h under flowing Milli-Q water. As an indication for clean conditions we took the fact that in pure water the contact angles were constant and did not change with time. The error in contact angle was ≈5° from one experiment to another and ≈3° within one series of experiments. For contact angle below 15° the error slightly increases.
For visualizing the flow profile in the rotating cylinder setup, small amounts of silica particles (0.05 wt%, Kromasil 100, diameter 10 ± 2 μm, Analysentechnik Mainz) were dispersed in the liquid. The particle movement was detected by using a macro-zoom optics (12× magnification) equipped with a fast camera (Photron, Fastcam SA-1, 1000 frames per s). The flow profile of the liquid was measured by analyzing the particle trajectories making use of the particle tracking plugin of ImageJ.
Surfactant solutions
Before surfactant was added to the bath the dynamic contact angles of pure water were measured. After adding the surfactant, the solutions were stirred for at least 20 min by rotation the cylinder at a constant speed of 100 mm s−1. Surfactant was stepwise added to achieve concentrations of up to 30% of the respective CMC. The CMCs and the surface tensions of aqueous solutions at the CMCs are summarized in Table 1. The surface tensions were measured with a Wilhelmy plate tensiometer (Dataphysics, DCAT 11EC). CMCs were extracted from a plot of surface tension versus log of concentration (Fig. S1, in ESI†). The measured CMCs agree with values reported in the literature.57,58| Surfactant | Type | CMC (mM) | γ* (mN m−1) | D (m2 s−1) | M W (g mol−1) |
|---|---|---|---|---|---|
| C4E1 | Nonionic | 1.2 × 103 | 27.9 | 9.3 × 10−10 | 118 |
| C8E3 | Nonionic | 7.5 | 27.3 | 4.6 × 10−10 | 262 |
| C12E5 | Nonionic | 7.0 × 10−2 | 30.7 | 2.9 × 10−10 | 407 |
| CTAB | Cationic | 1.0 | 35.2 | 5.4 × 10−10 | 364 |
| S-1DeS | Anionic | 38.5 | 38.7 | 7.0 × 10−10 | 244 |
NMR spectroscopy
For the 1H-NMR experiments and the diffusion measurements (DOSY)59 a 5 mm triple resonance TXI 1H/13C/15N probe equipped with a z-gradient on the 850 MHz Bruker AVANCE III system was used. For the diffusion measurements a 2D sequence (DOSY, stebpgp1s19) with a stimulated echo was used additionally with water suppression (3-9-19 pulse sequence with gradients).60 The temperature was kept at 25.1 °C and regulated by a standard 1H methanol NMR sample using the topspin 3.1 software (Bruker). The control of the temperature was realized with a VTU (variable temperature unit) and an accuracy of ±0.1 K. In this work, the gradient strength was varied in 16 steps from 2% to 100%. The diffusion time was optimised at 30 ms and the gradient length to 1.2 ms. The gradient strength was calibrated by analysis of a sample of 2H2O/1H2O and comparison with the theoretical diffusion coefficient of 2H2O/1H2O. Diffusion gradient amplitudes were varied linearly from 1 to 53 G cm−1 (10 to 470 mT m−1) over a total of 16 experiments to achieve a strong diffusion weighting. Diffusion coefficients were calculated for the integrated peak areas using an exponential decay fit function over the 16 spectra: Si = S0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Dbi). Here, the diffusion sensitivity factor b was calculated as given in the sequence description: bi = (2πgLGid)2(Δ − d/3), where gL is the gyromagnetic ratio of the observed nucleus, Gi is the gradient strength, d is the length of the gradient (1.2 ms), and Δ is the diffusion time (30 ms).
exp(−Dbi). Here, the diffusion sensitivity factor b was calculated as given in the sequence description: bi = (2πgLGid)2(Δ − d/3), where gL is the gyromagnetic ratio of the observed nucleus, Gi is the gradient strength, d is the length of the gradient (1.2 ms), and Δ is the diffusion time (30 ms).
Microtubing setup
Due to reflections from the air–liquid interface, the flow closer than ≈300 μm to the undeformed interface and in the updrawn liquid meniscus could not be visualized in the rotating cylinder experiments. To visualize the flow close to the three-phase contact line, we therefore used a different experimental setup based on a microtube (Fig. 2B).61 A glass beaker containing milli-Q water was placed on a translation stage. The beaker was connected to a capillary (inner diameter 855 μm) through a tubing system and a metering valve. The capillary, mounted in a homemade flat glass cell, was placed on the stage of an upright optical microscope (Olympus BX 51). All tubes were made from fluorinated ethylene propylene (FEP) (Bohlender, Germany). The mean surface roughness of the thin capillary was 50 nm, measured with confocal microscopy (μ-Surf, NanoFocus). To avoid light distortion due to the cylindrical geometry of the FEP capillary (refractive index n = 1.34), the glass cell was filled with water (n = 1.33).Liquid slugs containing carboxylated polystyrene microparticles (Kisker Biotech, Germany) of 4 μm diameter at a concentration 0.05% wt were introduced in the fluidic system using a syringe. The driving force for the slug motion is the pressure drop generated between the elevated beaker and the capillary outlet. Control of the flow speed was achieved by adjusting the height of the water level in the beaker as well as by regulating the metering valve. Transmission microscopy videos of the slug motion under dark field illumination conditions were captured by means of a 10× objective and a fast CMOS camera (Olympus i-speed, maximum frame rate 2000 frames per s). Before the flow visualization experiments the whole setup was carefully cleaned by flushing 150 mL acetone and 150 mL milli-Q water. Before each single measurement, the FEP capillaries were independently washed with ≈20 mL acetone and were subsequently completely dried using flowing N2. This procedure was found to provide clean surfaces, an essential requirement for reproducible results.61
Results and discussion
Pure water
To describe the dewetting behavior we plotted the apparent receding contact angles Θ (when the cylinder leaves the liquid) versus the rotation velocity at the cylinder surface. For pure water the receding contact angles decreased with increasing rotation velocity (Fig. 3, open circles). When approaching a velocity of 200 mm s−1 (Ca = 2.7 × 10−3) a triangular or V-shaped liquid film was formed spanning the whole width of the cylinder (as described in ref. 53). This change in the shape of the contact line made it difficult to measure the contact angle and we stopped at this velocity. At even higher speeds (U > 200 mm s−1) a trail of drops formed at the upper corner of the triangle and remained on the surface of the cylinder. Such V-shaped contact lines and “pearling drops” were observed before15,30,62 and their shape has been calculated.63 At even higher speeds, we observe the transition from a defined three-phase contact line to the entrainment of a liquid film, known as the Landau–Levich–Derjaguin transition.11,32–34 Above this critical velocity a continuous liquid film is drawn upwards.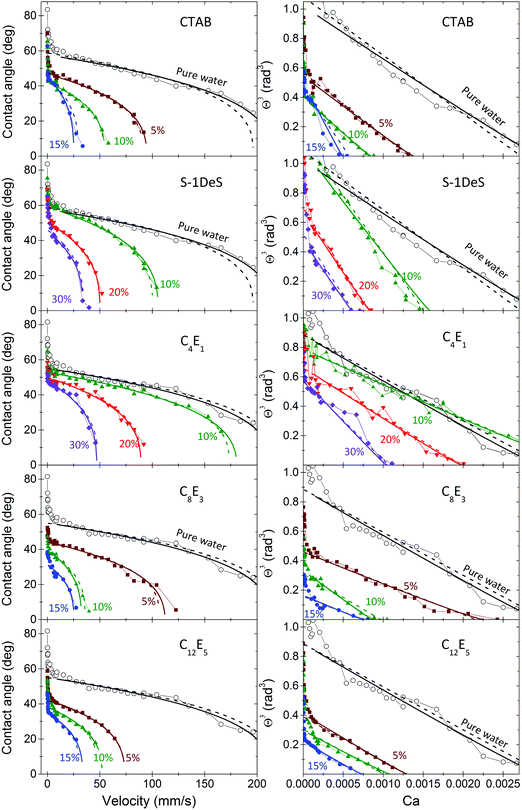 | ||
| Fig. 3 Left: Dynamic receding contact angle of aqueous solutions versus velocity for the surfactants CTAB (cationic), S-1DeS (anionic), and C4E1, C8E3, C12E5 (nonionic) on a polystyrene-coated cylinder. Right: Contact angle (in rad) cubed versus the capillary number Ca = ηU/γL. Here, η = 10−3 Pa s is the viscosity of water. Results for pure water are indicated by open black circles. The concentrations (in % of CMC) were 5% (dark red circles), 10% (green up triangles), 15% (blue circles), 20% (light red down triangles), and 30% (violet diamonds). For pure water we only show two independent measurements; the top two and the bottom three results for pure water are identical. The solid lines are fits using eqn (3), the dashed line are fits using eqn (2). | ||
Aqueous surfactant solutions
When adding surfactant, qualitatively the same phases were observed: a relatively straight, horizontal contact line at low velocity, formation of a triangular shape at intermediate velocity and formation of a continuous film at high velocity. At our optical resolution we were not able to see micrometer sized distortions as reported by Varanasi & Garoff.45Quantitatively, however, the picture changed when adding surfactant (Fig. 3):
• The slopes of the graphs Θ vs. U became steeper.
• As a result, the critical velocity for film formation decreased with increasing surfactant concentration.
• The apparent receding contact angle for zero velocity Θ(U → 0) decreased.
The described behavior was observed for all types of surfactants at roughly the same relative concentration (in %CMC). This holds even when changing the absolute surfactant concentration by more than four orders of magnitude. This similarity indicates that the reason for the decreasing dynamic contact angle effect is universal and does not depend on the specific length of the hydrocarbon chain or the specific structure of the hydrophilic head group. In particular, the charge of the surfactant does not play a role, which excludes electrostatic interactions as a major explanation for the observed decrease in contact angle.
To compare the different surfactants we looked into the dynamic contact angles at one fixed velocity (Fig. 4, velocity 6 mm s−1 and Fig. S2, 20 mm s−1 in ESI†). While the CMCs of the surfactants varied over more than four orders of magnitude (Table 1) the dynamic contact angles differed only by a factor three. The effect of scaling with the CMC is also evident, when plotting the contact angle versus the concentrations in mM, irrespective of the velocity (Fig. S3, ESI†). After scaling the concentrations with their respective CMCs, C8E3 and C12E5 are the two most effective surfactants. C4E1 and S-1DeS require a roughly three times higher concentration to reach the same dynamic contact angle.
 | ||
| Fig. 4 Dynamic receding contact angles at a velocity of 6 mm s−1versus surfactant concentration, for all surfactants used. Surfactant concentrations are given in percentages of the CMC. | ||
The fact that dynamic contact angles of all surfactant solutions are roughly the same at the same relative concentration (Fig. 4) is the most important finding. Scaling all concentrations by the CMC allows us to predict the dynamic contact angle of all surfactants. The remaining differences between different surfactants will be discussed below.
Receding contact angle for zero velocity
The receding contact angle for U → 0 decreased with increasing surfactant concentration for all surfactants (Fig. 5). That surfactants decrease the contact angle of aqueous solutions on hydrophobic surface is known.46,64–66 For a guideline in the interpretation we apply Young's eqn (1). For pure water the receding contact angle was 77°. With γL = 72.1 mN m−1 at zero surfactant concentration Young's eqn (1) leads to γS − γSL = 16.2 mN m−1. The decreasing contact angle can only be explained by assuming that surfactant adsorb at the solid–air and/or solid–liquid interface. The argument is: if there were no adsorption at the solid surface nor at the solid–liquid interfaces, γS − γSL would be constant. Keeping γS − γSL = 16.2 mN m−1 constant and inserting the measured values for γL in Young's equation leads to contact angles, which are too high, e.g. the lowest contact angle obtained within this assumption would be 61° for C8E3 at 15 %CMC. All other surfactants would have even higher contact angles between 69° and 75°. The actually observed contact angles are significantly lower and consequently in contradiction our non-adsorption assumption. Thus, γS − γSL increases. Please note, we used the measured values for γL since γL decreases when adding surfactant.Processes influencing the Marangoni effect
Surfactants adsorb to the relatively hydrophobic polystyrene surface much like they adsorb to the liquid–air interface.46,67 When the contact line recedes, the adsorbed surfactants have two possibilities: they remain on the solid surface (process 1 in Fig. 6) or they transfer to the new liquid–air interface (process 2); to directly diffuse back into the bulk is unlikely. The less surfactant transfers to the freshly created liquid–air interface, the higher the gradient in surface tension and the Marangoni stress. The more surfactants transfer to the liquid–air interface, the lower the gradient in interfacial tension.51 The fact that we observe a Marangoni effect again indicates that the transferred surface concentration is lower than the equilibrium surface concentration at the given bulk concentration.Once a fresh liquid surface has been formed at the contact line, the surface tension gradient is equilibrated by surfactants from the bulk. The transfer rate of surfactant to the liquid–air interface involves two steps: advection and diffusion from the bulk (process 3) and adsorption to the liquid–air interface (process 4). It is noteworthy that C4E1 and S-1DeS need slightly higher concentrations to achieve the same reduction in contact angle as the other surfactants (Fig. 4 and 5). They are the smallest molecules and they have the fastest diffusion coefficient (Table 1). Therefore, the faster diffusion may lead to a faster equilibration of the surface tension gradient. However, since at the same time the total concentration is much higher than for the other surfactants, one should be careful drawing conclusions. The differences remaining after scaling the dynamic receding contact angles with the CMCs could be due to any of the processes 1–4 described or a combination. At present we cannot link the remaining differences to one specific process.
Comparison of experimental results with hydrodynamic theory
For velocities above ≈10 mm s−1 (Ca ≈ 10−4) experimental results could be fitted with the Cox–Voinov law eqn (2) (dashed lines in Fig. 3). In the presence of surfactant hydrodynamic theory even fitted the results down to 1 mm s−1. This agreement is best visualized by plotting Θ3vs. Ca (Fig. 3, right), in which eqn (2) leads to straight lines. Hydrodynamic theory fitted all Θ vs. U curves up to the point, where the liquid film formed a triangular shape. Therefore, two velocity regimes could be distinguished: strongly decreasing contact angle for low velocities and a more gradual decrease of the apparent dynamic contact angle for velocities above ≈10 mm s−1. The fast part is well described by hydrodynamic theory.Snoeijer & Andreotti68 point out that eqn (2) was derived for advancing, not for receding contact angles. An approximate solution for receding contact lines was derived by Eggers27 assuming a small Θ0. To test the difference between both approaches, we also fit with the full equations valid for the receding contact lines. Eggers & Snoeijer27,69 showed that the apparent receding contact angle Θ follows
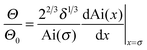 | (3) |
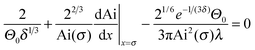 | (4) |
At this point a more detailed description of the numerical implementation of the theory is instructive. Eqn (3) and (4) were implemented in Matlab. In all investigated cases eqn (3) had only one positive root. So the root finding was found to be numerically stable when limiting the range of σ to not so large positive numbers, typically σ < 60. To perform the nonlinear fit for the unknown parameters λ and Θ0 it turned out to be more efficient to take the logarithm of λ as a fit parameter. Like for all nonlinear fits, the quality of the fit is only good, when the initial guesses of the parameters are not too far away from the final value. For the two parameters “not too far away” was not more than about ±20 for the logarithm of λ and a factor of about 1.5 for Θ0. When initial guesses are chosen within this range, the final values do not depend on the initial guesses. The fits to eqn (2) were performed with the built-in routines of Origin.
A simple interpretation of the two parameters goes as follows: Θ0 is the apparent receding contact angle when extrapolating the high velocity branch of the dynamic contact angle measurements to zero velocity: Θ0 = Θ(U → 0). This is not the equilibrium contact angle. The logarithm of the microscopic parameter αh/λ (in eqn (2)) and 1/λ (in eqn (3) and (4)) measures friction close to the contact line. The different prefactor to λ is due to the rescaling of all length in eqn (3) and (4). The higher this “friction parameter” the more energy is dissipated close to the contact line, e.g. by hydrodynamic dissipation. Note that close to the contact line surface tension gradients (due to the presence of surfactants) might alter the flow profile. Without going into the details of the changes in the flow profile, we assume that ultimately, such changes will increase the hydrodynamic dissipation close to the contact line. In our model the details of the flow profile close to the contact line are not taken into account and only summarized in changes in the friction parameter.
To identify potential differences between the simple hydrodynamic model of eqn (2) and the more developed model of eqn (3) and (4) we fitted our experimental data with both models. Despite the fact that eqn (2) should only be valid for advancing contact lines,68 our data can be fitted with eqn (2). Neither the quality of the fit nor the absolute numbers of the fit parameters showed significant differences between the two approaches (Fig. 7).
 | ||
| Fig. 7 Friction parameter λ (top) and contact angle extrapolated to zero velocity Θ0 (bottom) obtained from fitting experimental results with eqn (2) (open symbols) and with eqn (3) and (4) (solid symbols) plotted as a function of the concentration of surfactant. The concentration is scaled by dividing the actual value by the CMC of the respective surfactant. The error estimated from different experiments for pure water is of the order ≈20% and 3°, respectively. | ||
The friction coefficient is relatively constant for nonionic surfactants (Fig. 7). Up to 15% CMC we did not observe a significant change with concentration. For C4E1, which was the only nonionic surfactant studied at higher relative concentration, friction tends to increase for c > 15%. For the two charged surfactants the friction parameter increased with increasing concentration. This can also be directly seen from the linear fits of Θ3 on the left side of Fig. 3: while for CTAB and S-1Des the slope of the plots increased, for the neutral C8E3 and C12E5 curves are primarily shifted downwards. Such a downward shift is reflected in a strongly decreasing value for Θ0 (Fig. 7B). We speculate that the high friction parameter of the two ionic surfactants is due changes in the adsorption kinetics caused by electrostatic repulsion. The second step (process 4, Fig. 6), adsorption, is slowed down by electrostatic repulsion between surfactant molecules close to the surface and those already adsorbed.70
Decrease of the contact angle at slow velocity
The decrease of dynamic contact angles with contact line velocity follows two phases, a slow and a fast. Hydrodynamic theory fits well the contact angles at velocities above 5–10 mm s−1. It does not fit the slow component. As an example, Fig. 8 shows the slow change for two representative surfactants. Below a typical velocity of ≈1–5 mm s−1 (Ca ≈ 1.4–7 × 10−5), Θ vs. U decreases more steeply than at higher velocities. For pure water the slow regime even extends to U ≈ 10 mm s−1 (Ca ≈ 1.4 × 10−4), as can be seen from the fact that experimental results are still above the hydrodynamic fit up to 10 mm s−1. | ||
| Fig. 8 Dynamic receding contact angle versus velocity for S-1DeS and C12E5 measured at different surfactant concentrations. The dashed lines represent the hydrodynamic fits obtained with eqn (2) for U > 10 mm s−1. The concentration is scaled by dividing the actual value by the CMC of the respective surfactant. For pure water the results of two different experiments are shown. | ||
When comparing changes in receding contact angle for pure water and different surfactant concentrations for slow velocities (U ≤ 5 mm s−1) the curves Θ vs. U look very similar. We take this as an indication that the major reason for this decrease at slow velocity is not the Marangoni effect but that it is due to another, yet unidentified process, e.g. the small but finite roughness of the cylinder.
Flow profiles near the contact line
Tracer particles added to the rotating cylinder setup allowed to visualize the flow in pure water and CTAB solution (Fig. 9A and B). The flow observed in pure water resembles the one of pure water observed for the Landau–Levich flow and is compatible with the standard hydrodynamics of receding contact lines: close to the solid–liquid interface the water is drawn upwards. It changes direction near the three-phase contact line and flows downwards close to the liquid–air interface (Fig. 9A).In CTAB solution the overall flow profile in the bulk liquid did not change significantly. This is in contrast to the Landau–Levich flow where the presence of surfactant molecules fundamentally change the flow profile.41
The flow of water inside the capillary close to the liquid–air interface was symmetric and showed two vortices. The flow profile did not change when adding CTAB (Fig. 9C; top: water, bottom: CTAB). Also variations of the absolute value of the flow velocity did not influence the flow profiles close to the contact line, as long as the critical velocity of complete wetting was not exceeded.
Conclusions
The dynamic receding contact angle of aqueous solution changes significantly when adding surfactant. For all surfactant solutions (C4E1, C8E3, C12E5, S-1DeS, and CTAB) the receding contact angles decreased with increasing velocity as well as with increasing surfactant concentration. The Marangoni stresses seem to have the main contribution to the contact angle decrease: local surface tension gradients formed close to the three-phase contact line influencing the liquid flow along the liquid–air interface while not significantly influencing the flow profile in the bulk liquid. By comparing the results of changes in the contact angle in % of CMC we shown that the charge of the surfactant has no significant influence on the wetting behavior. The relative concentration is (in %CMC) by far the dominating parameter for the receding contact angle even for surfactants which change by more than four orders of magnitude in the CMC. The dominating scaling parameter is the CMC. This allows to give predictions of the effect for other surfactants as well. For high enough dewetting speed (>10 mm s−1), the hydrodynamic models fit the experimental data well. In the hydrodynamic model all local effects close to the contact line can be summarized in a friction parameter similar to the dewetting of simple liquids.Acknowledgements
It is a pleasure to acknowledge financial support by the ERC Advanced grant SUPRO 340391 (H. J. B.) and by the European Marie Curie Initial Training Network COWET (G. A., H. J. B.). T.-H. N. thanks the SFB 625 and IMPRS for partial financial support. We gratefully acknowledge the support of Uwe Rietzler and Rüdiger Berger for designing and building the scaffold for the SFM measurements.References
- T. Young, Philos. Trans. R. Soc. London, 1805, 95, 65–87 CrossRef.
- W. Rose and R. W. Heins, J. Colloid Sci., 1962, 17, 39–48 CrossRef CAS.
- R. L. Hoffman, J. Colloid Interface Sci., 1975, 50, 228–241 CrossRef CAS.
- J. B. Cain, D. W. Francis, R. D. Venter and A. W. Neumann, J. Colloid Interface Sci., 1983, 94, 123–130 CrossRef CAS.
- R. A. Hayes and J. Ralston, J. Colloid Interface Sci., 1993, 159, 429–438 CrossRef CAS.
- R. V. Sedev, C. J. Budziak, J. G. Petrov and A. W. Neumann, J. Colloid Interface Sci., 1993, 159, 392–399 CrossRef CAS.
- J. G. Petrov and B. P. Radoev, Colloid Polym. Sci., 1981, 259, 753–760 CAS.
- E. B. Dussan, E. Ramé and S. Garoff, J. Fluid Mech., 1991, 230, 97–116 CrossRef.
- P. G. Petrov and J. G. Petrov, Langmuir, 1992, 8, 1762–1767 CrossRef CAS.
- R. V. Sedev and J. G. Petrov, Colloids Surf., 1992, 62, 141–151 CrossRef CAS.
- M. Maleki, E. Reyssat, D. Quéré and R. Golestanian, Langmuir, 2007, 23, 10116–10122 CrossRef CAS PubMed.
- G. Inverarity, Br. Polym. J., 1969, 1, 245–251 CrossRef CAS.
- J. G. Petrov, J. Ralston, M. Schneemilch and R. A. Hayes, J. Phys. Chem. B, 2003, 107, 1634–1645 CrossRef CAS.
- R. Burley and B. S. Kennedy, Br. Polym. J., 1976, 8, 140–143 CrossRef CAS.
- T. D. Blake and K. J. Ruschak, Nature, 1979, 282, 489–491 CrossRef.
- E. B. Gutoff and C. E. Kendrick, AIChE J., 1982, 28, 459–466 CrossRef CAS.
- R. Ablett, Philos. Mag., 1923, 46, 244–256 CrossRef CAS.
- Y. D. Shikhmurzaev, Fluid Dynamics Research, 1994, 13, 45–64 CrossRef.
- J. Billingham, Eur. J. Appl. Math., 2006, 17, 347–382 CrossRef.
- A. Rednikov and P. Colinet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 010401 CrossRef PubMed.
- T. D. Blake and J. M. Haynes, J. Colloid Interface Sci., 1969, 30, 421–423 CrossRef CAS.
- G. Friz, Z. Angew. Phys., 1965, 19, 374–378 Search PubMed.
- C. Huh and L. E. Scriven, J. Colloid Interface Sci., 1971, 35, 85–101 CrossRef CAS.
- O. V. Voinov, Fluid Dyn., 1976, 11, 714–721 CrossRef.
- L. H. Tanner, J. Phys. D, 1979, 12, 1473–1484 CrossRef CAS.
- R. G. Cox, J. Fluid Mech., 1986, 168, 169–194 CrossRef CAS.
- J. Eggers, Phys. Fluids, 2005, 17, 082106 CrossRef.
- J. G. Petrov and P. G. Petrov, Colloids Surf., 1992, 64, 143–149 CrossRef.
- W. Hopf and H. Stechemesser, Colloids Surf., 1988, 33, 25–33 CrossRef CAS.
- T. Podgorski, J. M. Flesselles and L. Limat, Phys. Rev. Lett., 2001, 87, 036102 CrossRef CAS PubMed.
- I. Peters, J. H. Snoeijer, A. Daerr and L. Limat, Phys. Rev. Lett., 2009, 103, 114501 CrossRef PubMed.
- L. Landau and B. Levich, Acta Physicochim. URSS, 1942, 17, 42–54 Search PubMed.
- B. V. Derjaguin, Acta Physicochim. URSS, 1943, 20, 349–352 Search PubMed.
- J. H. Snoeijer, J. Ziegler, B. Andreotti, M. Fermigier and J. Eggers, Phys. Rev. Lett., 2008, 100, 244502 CrossRef CAS PubMed.
- K. G. Winkels, I. R. Peters, F. Evangelista, M. Riepen, A. Daerr, L. Limat and J. H. Snoeijer, Eur. Phys. J.: Spec. Top., 2011, 192, 195–205 CrossRef CAS.
- M. Fermigier and P. Jenffer, J. Colloid Interface Sci., 1991, 146, 226–241 CrossRef CAS.
- Y. Amarouchene, G. Cristobal and H. Kellay, Phys. Rev. Lett., 2001, 87, 206104 CrossRef CAS PubMed.
- O. Manor, I. U. Vakarelski, X. S. Tang, S. J. O'Shea, G. W. Stevens, F. Grieser, R. R. Dagastine and D. Y. C. Chan, Phys. Rev. Lett., 2008, 101, 024501 CrossRef PubMed.
- D. Y. C. Chan, E. Klaseboer and R. Manica, Soft Matter, 2009, 5, 2858–2861 RSC.
- R. Krechetnikov and G. M. Homsy, J. Fluid Mech., 2006, 559, 429–450 CrossRef.
- H. C. Mayer and R. Krechetnikov, Phys. Fluids, 2012, 24, 052103 CrossRef.
- M. von Bahr, F. Tiberg and V. Yaminsky, Colloids Surf., A, 2001, 193, 85–96 CrossRef CAS.
- V. Dutschk, K. G. Sabbatovskiy, M. Stolz, K. Grundke and V. M. Rudoy, J. Colloid Interface Sci., 2003, 267, 456–462 CrossRef CAS PubMed.
- V. M. Starov, M. G. Velarde and C. J. Radke, Wetting and Spreading Dynamics, CRC Press, London, 2007 Search PubMed.
- K. S. Varanasi and S. Garoff, Langmuir, 2005, 21, 9932–9937 CrossRef CAS PubMed.
- B. P. Binks, A. J. Johnson and J. A. Rodriques, Soft Matter, 2010, 6, 126–135 RSC.
- J. Venzmer, Curr. Opin. Colloid Interface Sci., 2011, 16, 335–343 CrossRef CAS.
- D. Quéré, A. de Ryck and O. O. Ramdane, Europhys. Lett., 1997, 37, 305–310 CrossRef.
- Q. Shen, B. Gleason, G. H. McKinley and H. A. Stone, Phys. Fluids, 2002, 14, 4055–4068 CrossRef.
- D. M. Campana, S. Ubal, M. D. Giavedoni and F. A. Saita, Phys. Fluids, 2010, 22, 032103 CrossRef.
- B. B. Luokkala, S. Garoff, R. D. Tilton and R. M. Suter, Langmuir, 2001, 17, 5917–5923 CrossRef CAS.
- D. Quéré, Annu. Rev. Fluid Mech., 1999, 31, 347–384 CrossRef.
- D. Fell, G. Auernhammer, E. Bonaccurso, C. J. Liu, R. Sokuler and H. J. Butt, Langmuir, 2011, 27, 2112–2117 CrossRef CAS PubMed.
- D. Fell, N. Pawanrat, E. Bonaccurso, H.-J. Butt and G. K. Auernhammer, Colloid Polym. Sci., 2013, 291, 361–366 CAS.
- L. E. Scriven and C. V. Sternling, Nature, 1960, 187, 186–188 CrossRef.
- C. W. Park, J. Colloid Interface Sci., 1991, 146, 382–394 CrossRef CAS.
- M. J. Rosen, A. W. Cohen, M. Dahanayake and X. Y. Hua, J. Phys. Chem., 1982, 86, 541–545 CrossRef CAS.
- A. Paszternák, É. Kiss and P. Jedlovszky, J. Chem. Phys., 2005, 122, 124704 CrossRef PubMed.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288 CrossRef CAS.
- A. Jerschow and N. Müller, J. Magn. Reson., 1997, 125, 372–375 CrossRef CAS.
- M. Anyfantakis, D. Fell, H.-J. Butt and G. K. Auernhammer, Chem. Lett., 2012, 41, 1232–1234 CrossRef CAS.
- G. Delon, M. Fermigier, J. H. Snoeijer and B. Andreotti, J. Fluid Mech., 2008, 604, 55–75 Search PubMed.
- J. H. Snoeijer, N. Le Grand-Piteira, L. Limat, H. A. Stone and J. Eggers, Phys. Fluids, 2007, 19, 042104 CrossRef.
- M. K. Bernett and W. A. Zisman, J. Phys. Chem., 1959, 63, 1241–1246 CrossRef.
- V. M. Starov, S. R. Kosvintsev and M. G. Velarde, J. Colloid Interface Sci., 2000, 227, 185–190 CrossRef CAS PubMed.
- K. Szymczyk, A. Zdziennicka, B. Janczuk and W. Wójcik, J. Colloid Interface Sci., 2006, 293, 172–180 CrossRef CAS PubMed.
- N. Kumar, S. Garoff and R. D. Tilton, Langmuir, 2004, 20, 4446–4451 CrossRef CAS PubMed.
- J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292 CrossRef.
- T. S. Chan, T. Gueudre and J. H. Snoeijer, Phys. Fluids, 2011, 23, 112103 CrossRef.
- T. F. Svitova, M. J. Wetherbee and C. J. Radke, J. Colloid Interface Sci., 2003, 261, 170–179 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00997b |
| This journal is © The Royal Society of Chemistry 2016 |





