Colloidal heat engines: a review
Ignacio A.
Martínez
 a,
Édgar
Roldán
a,
Édgar
Roldán
 bc,
Luis
Dinis
bc,
Luis
Dinis
 cd and
Raúl A.
Rica
cd and
Raúl A.
Rica
 *e
*e
aLaboratoire de Physique, École Normale Supérieure, CNRS UMR5672, 46 Allée d'Italie, 69364 Lyon, France
bMax Planck Institute for the Physics of Complex Systems, Nöthnitzer strasse 38, 01187 Dresden, Germany
cGISC – Grupo Interdisciplinar de Sistemas Complejos, Madrid, Spain
dDepartamento de Fisica Atómica, Molecular y Nuclear, Universidad Complutense Madrid, 28040 Madrid, Spain
eICFO – Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, 08860 Castelldefels (Barcelona), Spain. E-mail: rul@ugr.es
First published on 22nd July 2016
Abstract
Stochastic heat engines can be built using colloidal particles trapped using optical tweezers. Here we review recent experimental realizations of microscopic heat engines. We first revisit the theoretical framework of stochastic thermodynamics that allows to describe the fluctuating behavior of the energy fluxes that occur at mesoscopic scales, and then discuss recent implementations of the colloidal equivalents to the macroscopic Stirling, Carnot and steam engines. These small-scale motors exhibit unique features in terms of power and efficiency fluctuations that have no equivalent in the macroscopic world. We also consider a second pathway for work extraction from colloidal engines operating between active bacterial reservoirs at different temperatures, which could significantly boost the performance of passive heat engines at the mesoscale. Finally, we provide some guidance on how the work extracted from colloidal heat engines can be used to generate net particle or energy currents, proposing a new generation of experiments with colloidal systems.
1 Introduction: miniaturization of heat engines
Constructing efficient and powerful artificial motors at the micro- and nanoscales is currently one of the most challenging goals of physics and engineering.1–4 Mesoscopic machines operating at small scales can perform multiple tasks that are inaccessible for macroscopic engines, such as, transporting cargo inside cells or along microchannels, mixing fluids, and killing cancer cells in a selective manner.5–7 As for macroscopic engines, the working principle of artificial micro- and nano-engines is the conversion of a given fuel (such as thermal or chemical energy) into mechanical energy or work. A hallmark of mesoscopic engines is that the magnitude of the energy fluctuations is of the same order of the average energy flows that fuel or are produced by such machines. Hence the performance of a mesoscopic machine depends strongly on the properties of the surrounding environment. This motivates the study of the thermodynamics of stochastic processes and raises the question whether novel strategies can be used to optimize the performance of small engines.The idea of converting or rectifying thermal fluctuations into mechanical work using a small device dates back to the well-known Maxwell's demon.8 In the beginning of the 20th century, Lipmann introduced a thought or gedanken experiment where a mesoscopic paddle immersed in a gas performs Brownian motion due to the collisions with the gas molecules. Lippman's paddle can be set into a preferential rotation direction by attaching it to a ratchet wheel secured by a pawl and spring mechanism. Smoluchowski proved that Lippmann's device would fluctuate but not move on average at thermal equilibrium.9 Later on, Feynman showed that such a device can actually perform work (such as lifting a small weight) by immersing the wheel and the paddle in two thermal reservoirs at different temperatures.10 Feynman's ratchet cannot however reach Carnot efficiency even at zero power because the engine is constantly in contact with two different thermal baths and hence works in the nonequilibrium regime.11
The introduction of ratchets represented an important step forward in the study of Brownian motors. Ratchets are isothermal motors that can extract mechanical work in asymmetric environments. Hence, ratchets are not fuelled from the net heat flow between two different reservoirs but from the interaction with a nonequilibrium energy source, like an externally-driven potential or a chemical potential difference. In Magnasco's thermal ratchet model, a Brownian particle moving in an asymmetric potential can be drifted under isothermal conditions applying an external stochastic force with time correlations to the particle, thus breaking detailed balance.15 Ajdari and Prost introduced the flashing ratchet, where a Brownian particle is drifted in a periodic asymmetric potential that is switched on and off stochastically.16,17 The flashing ratchet mechanism is nowadays considered as the mechanism that drives the motion of many molecular motors against external forces18 such as myosin motors responsible for muscular contraction19 or RNA polymerases that are responsible for transcription of DNA into RNA.20 After the introduction of Brownian ratchets, a plethora of Brownian motors21 have been introduced from both the theoretical and experimental points of view: rocking, pulsating, gating or friction ratchets,5,22 multiparticle ratchets,23,24 mechano-chemical,25 magnetic26 and quantum ratchets.27 The working substance in these motors can be of a different nature: colloidal particles immersed in water,28,29 vortices in superconductors,30 electrons,31 Janus particles,32 and bacteria33 are just a few examples.
The first studies on ratchets focused mainly on transport properties and current analysis. Shortly after, the interest in power, energy consumption and efficiency arose. In 1998 Sekimoto introduced a theoretical framework that allows quantifying thermodynamic quantities such as heat and work for colloidal systems described by a Langevin equation.34 Following this study, stochastic thermodynamics35 has been established as a branch of statistical physics that describes the nonequilibrium fluctuations of physical systems strongly affected by thermal fluctuations.36,37 A milestone of stochastic thermodynamics has been the introduction of stochastic heat engines, where a Brownian particle acts as a working substance that is cyclically put in contact with several thermal reservoirs.38,39
The fast development of miniaturization techniques together with the aforementioned theoretical developments have led to a deep understanding of the mechanisms of work extraction in the mesoscale under isothermal conditions, as reviewed in ref. 5 and 22. Only in the last decade however, technological advances have allowed the realization of Brownian heat engines introduced in stochastic thermodynamics, which operate in asymmetric thermal environments, e.g. under temporal changes of the temperature of the environment or under active nonequilibrium thermal noise. This review focuses on the experimental realizations of colloidal heat engines that operate between different thermal reservoirs. The first Brownian heat engines have been realized using microscopic particles trapped using optical tweezers,1–4 which are the central case studies of this review. While optical tweezers have found an extraordinary application in heat engines built with micrometer sized particles, protocols to realize such processes do also exist at sub-micron,40 nano- and atomic41–43 scales.
The discussion we did so far has considered passive media, i.e., thermal baths verifying Boltzmann statistics. However, many of the envisioned scenarios where heat-to-work conversion can be of interest involve the presence of nonequilibrium fluctuations due to the presence of active media, mostly in systems of biological origin.18,44,45 Active media exhibit a very rich phenomenology,45 and some examples are bacterial baths,13 the cell cytoplasm,46 animal flocks45 or swarms of chemical catalysts.47 From a thermodynamic point of view, a distinct feature of active baths is the possibility of their components to absorb energy and transform it into useful work and dissipated heat. Notably, the statistics of the energy-fluctuations of active baths are non-Gaussian as is in general for small systems both under equilibrium and nonequilibrium conditions.48–52 Some recent experiments53 have investigated to what extent do active baths lead to deviations from the state-of-the-art theory,54,55 and very recently an implementation of a heat engine in a bacterial active bath4 has been achieved.
Recent reviews have discussed topics related to that of the present review. Seifert35 thoroughly reviewed the theoretical insights provided by the emerging field of stochastic thermodynamics, with special emphasis on the fluctuations of stochastic heat engines. Toyabe and Sano56 have discussed the nonequilibrium insights on biological machines. Bechinger et al.57 reviewed the field of active self-propelled Brownian particles in different types of environments, and in particular highlight the need to apply the framework of stochastic thermodynamics to systems coupled to active media. Finally, Reichhardt and Reichhardt58 report on ratchets that are driven by active thermal baths. Our discussion is distinct in the sense that it deals with colloidal engines that operate between different thermal baths, i.e. with cycles including non-isothermal processes, both in passive and active media, as illustrated in Fig. 1. As a genuine aspect of our review, we emphasise on the unique features found in the fluctuations of Brownian heat engines, in particular regarding their efficiency. These unique features seem counter intuitive but are at the same time very appealing as a way to inspire future developments of micro- and nanomachines.59
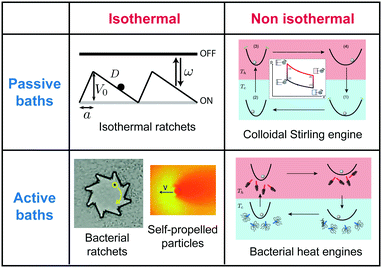 | ||
| Fig. 1 Mesoscopic heat engines. Classification of mesoscopic heat engines in terms of the thermal properties of the environment (isothermal, constant temperature; non-isothermal, time-dependent temperature) and in terms of the presence or not of active processes (non due to an external agent). This review is focused on non-isothermal passive and active colloidal engines. The figures are examples of the different types of engines.1,4,12–14 | ||
This review is organized as follows. In Section 2 we provide a brief introduction to the emerging field of stochastic thermodynamics, focusing on its formulation for colloidal systems described by a Langevin equation. In Section 3 we review experiments on stochastic thermodynamics performed with a single colloidal particle in an optical trap. Section 4 is the central part of this review, where we discuss recent designs of colloidal heat engines using optical tweezers, both in passive or an active media. In Section 5 we sketch some conclusions pointing to the most interesting achievements on this topic and provide an outlook on how the work extracted from colloidal heat engines could be used to induce net particle or energy currents.
2 Thermodynamics of Brownian engines: the meaning of fluctuating thermodynamic quantities
2.1 Stochastic energetics
A particle immersed in a fluid experiences an erratic or Brownian motion due to the continuous impacts of the molecules of the environment on the particle.60 The Langevin equation provides a coarse-grained or effective description of Einstein's theory for the dynamics of a Brownian particle in a fluid.61For simplicity we consider a particle of mass m that is immersed in a thermal bath at temperature T and moves in one dimension, with its position at time t denoted by x(t). The particle can be trapped with a conservative force generated by an attractive potential U(x;t) that may be changed arbitrarily in time following a specific protocol. Additionally, external non-conservative forces F(x,t) can be applied directly to the particle thus driving it to a nonequilibrium state. The dynamics of the particle can be described by the underdamped Langevin equation:5,22,62,63
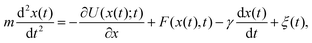 | (1) |
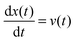 the velocity of the particle at time t and
the velocity of the particle at time t and 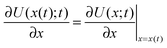 . The last two terms in (1) account for the interactions between the environment and the particle. The term −γdx(t)/dt is the friction force due to the drag of the particle in the environment with γ the friction coefficient. The last term ξ(t) is an effective stochastic force that models the random impacts of the environment molecules on the particle. This stochastic force is described as a Gaussian white noise whose average over many realizations vanishes 〈ξ(t)〉 = 0 and its correlation is 〈ξ(t)ξ(t′)〉 = σ2δ(t − t′). The fluctuation–dissipation relation imposes that the amplitude of the thermal force is
. The last two terms in (1) account for the interactions between the environment and the particle. The term −γdx(t)/dt is the friction force due to the drag of the particle in the environment with γ the friction coefficient. The last term ξ(t) is an effective stochastic force that models the random impacts of the environment molecules on the particle. This stochastic force is described as a Gaussian white noise whose average over many realizations vanishes 〈ξ(t)〉 = 0 and its correlation is 〈ξ(t)ξ(t′)〉 = σ2δ(t − t′). The fluctuation–dissipation relation imposes that the amplitude of the thermal force is 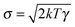 , with k Boltzmann's constant.
, with k Boltzmann's constant.
The dynamics of a Brownian heat engine that is put in contact with two thermal baths at different temperatures Th and Tc < Th can be described using eqn (1) and allowing the thermal force to change its amplitude in time between 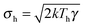 and
and 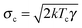 . An active heat engine can be described in the same terms but using a stochastic force with time correlations (e.g. it is described as a colored noise) or with an amplitude which does not satisfy the fluctuation–dissipation relation. The thermodynamic description of the fluctuating dynamics of both types of engines can be done using the framework of stochastic thermodynamics,35,37,64 which is revisited below.
. An active heat engine can be described in the same terms but using a stochastic force with time correlations (e.g. it is described as a colored noise) or with an amplitude which does not satisfy the fluctuation–dissipation relation. The thermodynamic description of the fluctuating dynamics of both types of engines can be done using the framework of stochastic thermodynamics,35,37,64 which is revisited below.
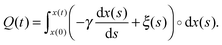 | (2) |
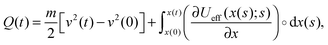 | (3) |
Analogously one can introduce a stochastic definition of the work done to the particle by the external forces. The work is here defined as the sum of conservative and non-conservative forces on the particle times its displacement:
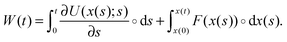 | (4) |
Notably, the above equations show explicitly that both work and heat depend on each realization and are not a state function in general. The sum of the stochastic heat (3) and the stochastic work (4) is equal to the change in the energy of the particle at time t, W(t) + Q(t) = ΔE(t) = E(t) − E(0), with 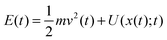 , thus recovering the first law of thermodynamics at the mesoscale.
, thus recovering the first law of thermodynamics at the mesoscale.
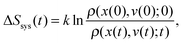 | (5) |
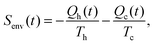 | (6) |
If additionally, local detailed balance holds, one can write a stochastic expression for the total entropy change Stot(t) = ΔSsys(t) + Senv(t) by the particle and the environment:12,67–72
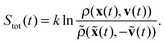 | (7) |
![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) (t) = {x(t − s)}s=0,…,t and ṽ(t) = {v(t − s)}s=0,…,t for trajectories in the time-reversed order. Eqn (7) reveals the connection between entropy and irreversibility in the mesoscopic world. Entropy production is quantified by how probable are trajectories ρ(x(t),v(t)) with respect to their time reversals
(t) = {x(t − s)}s=0,…,t and ṽ(t) = {v(t − s)}s=0,…,t for trajectories in the time-reversed order. Eqn (7) reveals the connection between entropy and irreversibility in the mesoscopic world. Entropy production is quantified by how probable are trajectories ρ(x(t),v(t)) with respect to their time reversals ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) (t),−ṽ(t)). The average over many realizations of the stochastic total entropy change is positive, 〈Stot(t)〉 ≥ 0, hence the second law of thermodynamics remains valid at the ensemble level.
(t),−ṽ(t)). The average over many realizations of the stochastic total entropy change is positive, 〈Stot(t)〉 ≥ 0, hence the second law of thermodynamics remains valid at the ensemble level.
2.2 The fluctuation theorems
The stochastic definition of the total entropy change accounts for the possibility of transient reductions of total entropy. Fluctuation theorems are universal‡ equalities of the form35,67,71,76–79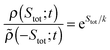 | (8) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (−Stot;t) the probability density in the time-reversed process to produce the same but negative amount of entropy. In a nonequilibrium steady state, the fluctuation relation reads simply ρ(Stot;t)/ρ(−Stot;t) = exp(Stot/k) and it expresses a symmetry relation for the same distribution ρ(Stot;t). An integral fluctuation theorem for entropy production was introduced in ref. 66, 67, 80 and 81:
(−Stot;t) the probability density in the time-reversed process to produce the same but negative amount of entropy. In a nonequilibrium steady state, the fluctuation relation reads simply ρ(Stot;t)/ρ(−Stot;t) = exp(Stot/k) and it expresses a symmetry relation for the same distribution ρ(Stot;t). An integral fluctuation theorem for entropy production was introduced in ref. 66, 67, 80 and 81:| 〈e−Stot(t)/k〉 = 1, | (9) |
The fluctuation theorems are valid for arbitrarily far from equilibrium processes, which is especially interesting for experimental purposes. For instance, both detailed and integral fluctuation theorems allow the estimation of equilibrium free energy changes from nonequilibrium protocols80 and have been widely applied to determine the free energies of biomolecules such as DNA hairpins.87,88
2.3 Fluctuations of power and efficiency in small engines
The power and the efficiency are the two fundamental magnitudes used to quantify the performance of an engine. The stochastic definitions of thermodynamic quantities can be applied to study the fluctuations of power and efficiency performed by mesoscopic engines.The power output of an mesoscopic engine is defined as the work extracted per unit of time, P(τ) = −W(τ)/τ, with τ the duration of the cycle. The power is defined positive since work is extracted in a heat engine, W(τ) < 0. For τ larger than any relaxation time of the particle the power average over many realizations is
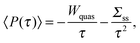 | (10) |
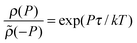 , where ρ(P) is the probability density of the power extracted by the engine and
, where ρ(P) is the probability density of the power extracted by the engine and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (−P) is the probability density of observing a negative power in the refrigerator.
(−P) is the probability density of observing a negative power in the refrigerator.
Analogously, one can consider a stochastic definition of efficiency given by the ratio of the stochastic work extracted in a cycle and the stochastic heat transferred from the hot bath to the particle in a cycle, η(τ) = −W(τ)/Qh(τ).39 The second law of thermodynamics imposes a restriction on the standard efficiency given by the ratio between the average work and the average heat influx in a cycle, which is bound by ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) (τ) = −〈W(τ)〉/〈Qh(τ)〉 ≤ ηC, with
(τ) = −〈W(τ)〉/〈Qh(τ)〉 ≤ ηC, with
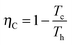 | (11) |
Another interesting regime is when the engine attains its maximum power, which was first considered by Novikov in the study of atomic power plants.92 Novikov, and later on Curzon and Ahlborn93 found that for an endoreversible engine operating at finite time, the efficiency at maximum power is
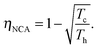 | (12) |
More recently, universal relations for the large deviation function of the distribution of the stochastic efficiency have been derived.99–105 In engines that operate following a time-symmetric protocol Carnot efficiency is the least likely efficiency.99,102 A generalization of the above result was found for time-asymmetric cycles, where the least likely efficiency was found to be greater or equal than Carnot efficiency.100 Strikingly, in a mesoscopic engine driven under a time-asymmetric protocol, two reversible efficiencies appear. The entropy production averaged over trajectories that perform with the minimum of the efficiency distribution is equal to zero, as it is for the ensemble that reaches Carnot efficiency.100 This means that there is a regime for the operation of the engine that is reversible in addition to the Carnot regime. Other hallmarks of the efficiency fluctuations at the mesoscale are the power law tails of the efficiency distributions,104,106 the bimodality of the distribution at moderate driving times101,103 and the possibility to observe super Carnot efficiencies at short observation times.100,103
3 Implementing thermodynamic processes with optically-trapped particles: the building blocks for work extraction
Thermodynamic processes connect different states of equilibrium or non-equilibrium steady states of a system. These processes are the building blocks of thermodynamic cycles and their proper concatenation make possible the extraction of work from thermal reservoirs. In order to accurately implement thermodynamic protocols with single particles in suspension, a technique giving precise control of their dynamics is needed. In particular, the control over the effective confinement or the accessible volume of the particle and of the temperature is key to the design of thermodynamic processes and engines. The many possibilities offered by optical tweezers for micromanipulation have been previously reviewed.107,108 Hence, our discussion here focuses on the latest advances in the design of thermodynamic processes at the microscale using the optical trapping technique.Optical trapping uses the radiation pressure and scattering forces exerted by a strongly focused beam of light to hold in place and move objects ranging in size from tens of nanometers to tens of micrometers.110–113 Moreover, the dynamics described by eqn (1) can be experimentally implemented with a single colloidal particle in an optical trap. Near the optical focus, the optical potential U(x,t) is parabolic U(x,t) = κ(t)(x(t) − x0(t))2/2, wherein two parameters can be controlled in time, namely the equilibrium position x0(t) and the trap stiffness κ(t). The trap stiffness depends linearly on the laser power, thus making its modulation easily implementable114 (see Fig. 2a). Remarkably, the potential landscape is nearly Gaussian even far from the focus115,116 and its shape is independent of the optical power.114 Great control of the position of the trap, stiffness and even different shapes of the potential is achievable by well-established techniques, including steering mirrors, electro-optic and acousto-optic modulators or holographic tweezers.107,108,117–119
 | ||
| Fig. 2 Expansion and compression of the accesible volume of an optically-trapped colloid. (a) The laser power is increased to produce a stronger confinement of the colloid. (b) Work done on the colloid for different effective temperatures T = (300, 610, 885, 1920, 2950) K (blue, red, green, magenta and orange, respectively) during compression (empty symbols) and expansion processes (full symbols). For each temperature, the work distributions of the forward (compression) and the backward (expansion) protocols cross at a value that equals to the free energy change in the compression (represented by a vertical line in each case). This is in agreement with Crooks fluctuation theorem [eqn (11) in ref. 67]. Figure adapted from ref. 109. | ||
Interestingly, one can draw analogies between a colloidal particle in an optical trap and an ideal gas inside a piston. In fact, it is commonly assumed that the stiffness of the trap is analogous to the inverse of an effective volume while the variance of the trajectory of the particle can be seen as an effective pressure.109,120–122 This analogy readily allows one to consider implementing thermodynamic porcesses with an optically trapped particle. The connection of the system to different thermal baths is pivotal in the design of heat engines. However, the accurate control of temperature in small systems is challenging and strongly constrained by the boundaries, typically leading to gradients and large relaxation times. In particular, standard ways to control temperature like resistances,123 Peltier units124 or recirculating water baths125 are not the best options to achieve the desired level of control. Recent approaches include the use of lasers that either match one absorption line of the medium1 or that of ITO films.126 Alternatively, one can consider creating an effective thermal bath for the trapped particle by changing its kinetic temperature using external noisy forces120,127 as discussed below.
In what follows, we first review different thermodynamic processes realized with optical potentials, distinguishing between isothermal and non-isothermal processes. We further discuss how these processes can be accurately implemented by tuning the kinetic temperature of the particle by means of external stochastic forces.
3.1 Isothermal protocols
We define as isothermal any thermodynamic process where the temperature of the environment remains constant in time. A well-studied isothermal process at the mesoscale is the transport of colloids at constant velocity or a drift-diffusion process.120,128,129 Although being very useful to test the validity of the fluctuation theorems,130 the drift-diffusion process has a purely dissipative nature that makes it unsuitable to build heat engines.An isothermal process that can be implemented to extract work is the breathing parabola, which is illustrated in Fig. 2a. In this process, the optical potential “breathes” as the stiffness of the trap is increased (decreased), so the accessible volume for the particle decreases (increases) with time. This process is analogous to an isothermal compression (expansion) of a single-molecule gas.131 Unlike for the drift-diffusion process, here the free-energy of the particle changes with time as ΔF(t) = (kT/2)log(κ(t)/κ(0)). Work distributions for expanding and compressing breathing parabolas for microscopic trapped particles are shown in Fig. 2b. Fluctuation theorems can be used in such a protocol to estimate free energy changes, which coincide with the minimal or reversible work extracted in the process. The dependency of ΔF on the temperature of the system clearly predicts that expansion and compression at different temperatures give a different amount of useful work. However, in order to be able to cyclically extract work from such protocols, an (efficient) way of connecting expansion and compression steps is still needed.
3.2 Non-isothermal protocols
For an ideal gas, the simplest non-isothermal protocol that can be imagined is the temperature change at constant volume or under isochoric conditions. During such a protocol, no work is done since no control parameter is changed with time. Note that temperature is not a control parameter since it depends on unknown degrees of freedom and temperature changes have to be considered as heat. The definition of the mesoscopic heat in the quasistatic limit can be used to find the mean value of the heat transfer, i.e. 〈Q〉 = 〈ΔE〉 = kΔT, and for quasistatic processes, equipartition allows the splitting of heat into the kinetic and potential contributions as 〈Qx〉 = 〈Qv〉 = kΔT/2.1,121 Hence changing the temperature of the bath by an isochoric process, as it is done for example in the Stirling cycle, implies an inherently irreversible heat transfer to the particle which affects the efficiency of the engine.38,132 Reaching Carnot efficiency requires to have control over the amplitude of the full Hamiltonian of the system, including both potential and kinetic contributions.105In order to extract useful work from a thermal cycle, it is fundamental to connect the system with different reservoirs.§ The precise way of transitioning from one thermal bath to another affects both the efficiency and power of the engine. In particular, protocols that disregard the role of kinetic energy may result in inefficiencies. Whether the overdamped dynamics is sufficient to describe the energetics of engines or not is one of the principal controversies regarding non-isothermal processes. Even though the overdamped limit is a very good approximation to the dynamics of a Brownian particle, it is not sufficient to describe the energetics of a Brownian heat engine where temperature (and therefore kinetic energy) changes with time. This is the basic point of the solvable model by Schmiedl and Seifert.38 However, if the whole dynamics of the system is initially studied without neglecting the kinetic term, and the overdamped limit is later adopted, the kinetic energy will give a contribution of the same order of magnitude as the potential energy.
In the so-called pseudoadiabatic protocol defined by Schmiedl and Seifert,38 a Brownian particle trapped in a harmonic potential is subject to cyclic variations of the stiffness of the trap and of the temperature of the environment. The protocol results in a net work extraction. If the temperature is changed proportionally to the stiffness of the harmonic trapping potential, T(t) ∝ κ(t), the position histogram, and in particular its variance 〈x2(t)〉 = kT(t)/κ(t), will remain constant under quasistatic driving. On the other hand, the velocity fluctuations will evolve during this protocol according to the temperature 〈v2(t)〉 = kT(t)/m. An irreversible flux of heat between the system and the environment 〈Q(t)〉 = 〈Qv(t)〉 = kΔT(t)/2 will follow from these protocols.
In order to maximize the efficiency of a heat engine, Carnot's advice must be followed and hence develop truly adiabatic protocols when connecting the system with different thermal baths. Hence, the energetics of both the positional and velocity degrees of freedom have to be taken into account.105,134 Carnot already realized that the heat transfer between the reservoir and the system at different temperatures is irreversible. Therefore, in order to avoid dissipation, the system should transition between baths adiabatically, that is, the protocol must be such that no heat flux occurs. Note that it is not possible however to isolate a Brownian particle from its environment and therefore avoid any heat transfer between the particle and the bath.
It is nevertheless possible to design a microadiabatic protocol where the total heat exchanged between the system and its environment is zero when averaged over many realizations of the same protocol. Such microadiabatic protocols were pioneered experimentally by Martínez et al.132 by controlling the full Hamiltonian of an optically-trapped Brownian particle. In the microadiabatic protocol the total average heat vanishes 〈Q(t)〉 = 0 and this condition is met following a nontrivial protocol introduced by Bo and Celani135 where the stiffness changes quadratically with the temperature κ(t) ∝ T(t)2. During a microadiabatic protocol, one increases the temperature, resulting in the increase of the fluctuations of the position of the particle. To ensure microadiabaticity, one therefore has to “squeeze” the velocity degree of freedom, by increasing the stiffness such that the conservation of the phase space volume of the particle is ensured. Note that during a microadiabatic protocol work is done (extracted) when the temperature increases (decreases).
3.3 Stochastic external forces: noise as temperature
One of the foundations of stochastic thermodynamics is the possibility to split energy transfers into two contributions, heat and work, at the mesoscopic level, as described in Section 2. In this context, heat is defined as any exchange of energy that takes place between the system, in this case the trapped particle, and the thermal bath it is in contact with.65 An equivalent definition of heat is the energy change of the system due to degrees of freedom whose dynamics is unknown. For example, the molecules of the surrounding fluid exert effectively a stochastic force on the particle that is modeled with the stochastic force term ξ(t) in the Langevin eqn (1). Determining the movement of every single molecule of the surrounding fluid is unattainable and therefore the energy changes in the colloid due to its collisions with the molecules of the environment are considered as heat.65Consider the case where an additional external noisy force F is exerted on the colloid. Suppose that this force changes with time F(t) but that it is also a random force, with similar statistical properties as the thermal force ξ(t). Namely, the force has zero average 〈F(t)〉 = 0 and it is delta correlated 〈F(t)F(t′)〉 = σnoise2δ(t − t′). An effective temperature Tnoise can be defined in terms of the friction, the noise intensity and the Boltzmann constant, 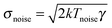 . This definition is such that if only the external force is present, the fluctuation–dissipation theorem holds at temperature Tnoise. Under the action of both the thermal ξ(t) and the external noise F(t) one can define an effective thermal bath including all the stochastic forces in the system ξeff(t) = ξ(t) + F(t), with 〈ξeff(t)〉 = 0, σeff2 = 2kTγ + 2kTnoiseγ and an effective temperature of the particle,
. This definition is such that if only the external force is present, the fluctuation–dissipation theorem holds at temperature Tnoise. Under the action of both the thermal ξ(t) and the external noise F(t) one can define an effective thermal bath including all the stochastic forces in the system ξeff(t) = ξ(t) + F(t), with 〈ξeff(t)〉 = 0, σeff2 = 2kTγ + 2kTnoiseγ and an effective temperature of the particle,
| Teff = T + Tnoise | (13) |
The idea was first applied macroscopically in the diffusion of millimetric charged balls in a circular channel.136 The first experimental attempt in a mesoscale system was carried out by Gómez-Solano and colaborators.137 They studied two systems, an optically trapped colloidal particle and an AFM cantilever, where noises of different characteristics were applied at different intensities. Both systems reach a nonequilibrium steady state where the fluctuation theorem seems to work at a temperature higher than the environmental one. This situation appears once the intensity of the non-thermal fluctuations becomes predominant.
Martínez et al.120 and Mestres et al.109 tested the consistency of mimicking a thermal bath by an externally applied noisy force to an optically trapped microparticle in water. In their experiment, a noisy voltage is applied to a pair of electrodes in a single particle electrophoresis chamber138 that exerts a noisy force on the charged microparticle. This noisy force increases the effective temperature of the particle. Since the bandwidth of the noise is limited by that of the signal generator and the polarizability of the particle,121 it is not clear a priori whether this approach should work. Two different non-equilibrium protocols were considered, namely, a “dragged trap” where the position of the optical trap varies with time, and a “breathing trap”, where the stiffness of the trap is periodically changed. A careful analysis of these two processes with the tools of stochastic thermodynamics validated the consistency of the externally tuned effective temperature of the system, provided that the sampling rate of the position of the particle was high enough, in particular, higher than the cutoff frequency of the trap. These experiments validated the technique to reliably control an effective thermal bath of the particle, which has later been demonstrated to be very useful in the study of stochastic thermodynamics, as we will discuss below in Section 4.
The technique has been shown to be also reliable in more complex scenarios, like a situation where a gradient of temperature is present. Berut et al.127,139 tackled this problem considering two colloidal particles held in two independent optical traps at a certain distance. If the distance is only of a few particle radius, the hydrodynamic interactions cannot be neglected and both particles will be coupled by a viscous interaction. They increased the kinetic temperature of one of the particles by adding a white noise to the equilibrium position of the trap, while the temperature of the other one was determined by its interaction with the thermal bath. It was shown that the transfer of energy as heat between the two particles is proportional to the temperature difference between the two particles, since the cold particle reacts like in the presence of a real heat flux.
The examples given above and other more sophisticated situations that have been already envisioned prove the consistency of the use of effective temperatures controlled by non-equilibrium random forces.140,141 As we discuss in the next section, this concept will be a powerful tool for the implementation of heat engines with colloidal particles.
4 Mesoscopic heat engines: experimental construction
We now review experimental realizations of heat engines operating between different thermal baths that can fit within the realm of soft matter. We try to put the emphasis on the peculiarities found in the statistics of these engines, in particular regarding their efficiency, which typically run against intuition.4.1 Colloidal heat engines
The first experimental realization of a microscopic heat engine using optical tweezers was done by Blickle and Bechinger.1 In their experiment, a microscopic melamine particle of diameter ∼3 μm is immersed in an aqueous solution and confined in a microfluidic chamber. The microparticle is trapped using optical tweezers created by a highly focused infrared laser. Using an acousto-optic modulator, an accurate time-dependent control of the trap stiffness was achieved, which allows the accurate control of the effective volume accessible for the microparticle. Using a second coaxially-aligned laser tuned to an absorption peak of water, the authors succeeded in controlling the temperature of water in a range between ∼20 °C and ∼90 °C. Following a cyclic series of laser intensity changes and temperature changes, an effective Stirling engine was constructed from the concatenation of isothermal and isochoric processes, as illustrated in Fig. 3. Additionally, the authors measured the average stochastic work extracted by the engine in each cycle, which was of the order of −0.1kT, reaching a maximum power of around ∼0.02kT s−1. Interestingly, their experiment shows excellent agreement of the mean power with the Sekimoto–Sasa law (10) and experimental evidence of the validity of the Novikov–Curzon–Ahlborn equation on the mesoscopic scale. | ||
| Fig. 3 Colloidal Stirling engine. (a) A Stirling engine is designed within a parabolic potential which holds a microsphere while the temperature of the fluid is controlled with the intensity of a coaxial laser. (b) Extracted work (right) and power (left) of the stochastic heat engine as a function of the duration of the cycle. When the engine is run fast, there is no work extraction and therefore the power is negative. At slow driving, the extracted work is maximum but the power decays to zero. Adapted with permission from ref. 1. | ||
Recently a microscopic Carnot engine has been realized by Martínez, Roldán et al.2 The low efficiency developed by a Stirling engine stems from the isochoric steps, where heat is transferred between the system and the heat baths that are at different temperatures, making the cycle inherently irreversible.39,142 As found by Carnot and discussed above, the maximum efficiency can be achieved when the two isothermal states are connected by adiabatic processes, where no heat is exchanged between the system and the environment.91 In the Brownian Carnot engine, a polystyrene sphere of 1 μm diameter is immersed in water and trapped using optical tweezers of tuneable stiffness. The amplitude of the fluctuations of the particle is externally controlled by means of a random electrostatic field that can modulate the effective temperature of the particle up to 3000 K, that is, one order of magnitude above the vaporisation temperature of water.109,120 Using a synchronous control of the trap stiffness and the amplitude of the electrostatic random force, the authors achieve microadiabatic protocols where the phase space volume of the particle and therefore its entropy defined by eqn (5) are conserved with time.132 When the protocol is done quasistatically, the stochastic heat exchanged between the particle and the environment is equal to zero when averaged over many realizations of the protocol (see Fig. 4a).
 | ||
| Fig. 4 Brownian Carnot engine. (a) Carnot's diagram (temperature of the engine as a function of the system entropy change). Filled symbols are obtained from ensemble averages over cycles of duration τ = 200 ms and open symbols are obtained for τ = 30 ms. The lines correspond to the values of temperature and entropy for an equivalent endoreversible Carnot engine. The black arrow indicates the direction of the operation of the engine. (b) Power output (black diamonds, left axis) and average efficiency (yellow hexagons, right axis) as a function of the inverse of the cycle time. The black curve is a fit to eqn (10). The solid yellow line is a fit to an analogous expression for the efficiency. The yellow dash-dot line is set at the Novikov–Curzon–Ahlborn efficiency given by eqn (12), which agrees with the experimental value of the efficiency at the maximum power (vertical black dashed line). Adapted with permission from ref. 2. | ||
Following a series of isothermal and microadiabatic protocols, the authors built a microscopic engine that achieves Carnot efficiency for cycle times of the order of ∼0.1 s (see Fig. 4b), which exceed by several orders of magnitude the characteristic relaxation times of the particle (∼0.1 ms). The Brownian Carnot engine behaves as an endoreversible engine as confirmed by the value of efficiency at maximum power, which coincides with Novikov–Curzon–Ahlborn efficiency.93,94,143
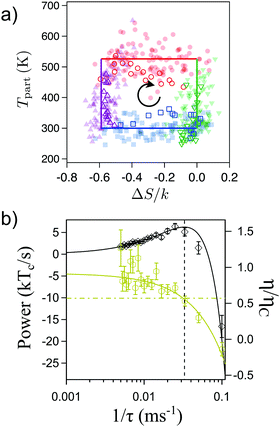
When driven out of equilibrium, the stochastic efficiency of the Brownian Carnot engine can even surpass Carnot efficiency, as predicted in ref. 101, 103 and 104. This is shown in Fig. 5(a), where one can see that efficiencies above ηC are observed for a small number of realizations of the cycle. The authors also tested for the first time the universal large deviation properties of the stochastic efficiency99,102 showing that the least likely efficiency is above Carnot efficiency, as predicted before for time-asymmetric cycles.100Fig. 5(b) shows the entropy production averaged over the cycles that perform with a given mean efficiency. Interestingly, two reversible operation regimes are observed, one at the Carnot efficiency and a second at the least likely efficiency, in agreement with recent theoretical predictions.99,100 Two other major theoretical predictions of the efficiency distributions, namely the bimodality of the distributions near the maximum power output101,103 and the power-law tails104,106 at short observation times, were also tested in the Brownian Carnot engine. This experiment confirms that despite the unattainability of an actual isolation of microparticles, protocols that behave effectively as adiabatic can be used to reach maximal bounds of efficiency at small scales.
 | ||
| Fig. 5 Efficiency fluctuations of the Brownian Carnot engine. (a) Contour map of the efficiency distribution at all times. Super Carnot efficiencies are highlighted in red shaded areas. At short times (bottom) the efficiency distribution has long tails and it can even surpass Carnot efficiency. At long times (top), the efficiency distribution is peaked below the Carnot limit. (b) Mean entropy production as a function of the mean efficiency for different realizations of the Brownian Carnot engine run at its maximum power where τ = 40 ms. The stochastic values of entropy production and the efficiency are calculated summing over 30 consecutive realizations of the engine. The mean entropy production vanishes for trajectories with mean efficiency equal to Carnot's efficiency 〈η〉 = ηC and also for non-reversible trajectories with mean efficiency equal to the least likely efficiency ηmin, whose value is measured independently and shown with a vertical pink line. Adapted with permission from ref. 2. | ||
Another point of view in the construction of heat engines was given by Quinto-Su.3 In his work, Quinto-Su was able to build a steam engine using magnetic microparticles of different sizes (1–3 μm) trapped using optical tweezers. In the microscopic steam engine, the particle is driven by explosive vaporization of the surrounding fluid and the cavitation bubbles exert forces on the particle that are of the order of 10−9–10−7 N, that is, three to five orders of magnitude larger than the usual piconewton trapping forces. As a result, the power output of this engine exceeds by several orders of magnitude the power developed by the microscopic Stirling and Carnot engine, thus overcoming the hurdle of kT of sub−kT work extraction per cycle in the mesoscale. The heat dissipation in the explosive vaporization results however in a lower efficiency of the engine with respect to the Carnot machine (Fig. 6).
 | ||
| Fig. 6 Microscopic steam engine. (a) A microscopic particle (orange) immersed in water (blue) is trapped using an optical tweezer (red). The particle approaches the trap focus from below (1-2) and heats the surrounding water when located near the trap focus (2-3), resulting in an explosive vaporization which forms cavitation bubbles that exert work on the particle (3-4-1).3 (b and c) Work done by the microparticle of 1 μm (b) and 3 μm (c) diameter as a function of time. Adapted with permission from ref. 3. | ||
4.2 Bioenergy: a colloidal heat engine pumped by biological activity
A colloid immersed in a pool of swimming bacteria is a paradigmatic model of an actively-pumped mesoscopic system.144–146 The runner-tumbler dynamics of the bacteria147 impose non-Gaussian fluctuations to a passive tracer, returning valuable information about the properties of the bath. With this scheme, research on anomalous diffusion,148–150 and generalizations of the equipartition theorem151 have been developed. The framework of stochastic thermodynamics discussed in Section 2 is in general not applicable to actively pumped engines and alternative robust frameworks on the thermodynamics of anomalous diffusion have not been developed yet. Here, we discuss a new experiment that investigates the performance of a heat engine in an active bath composed of swimming bacteria. In our discussion, we deliberately exclude active particles in either passive or active media, since some recent reviews are already available,6,57 but rather focus on passive particles in active media.Krishnamurthy et al. have recently fabricated the first colloidal heat engine working in an active medium.4 In a pioneering experiment, an optically-trapped colloid is immersed in a broth suspension with a high density of live bacteria. The motility of the bacteria depends strongly on the temperature of the medium, which can be controlled externally. Therefore, even small variations in the room temperature induce significant changes in bacterial activity, leading to a strong increase of non-equilibrium fluctuations of the microparticle due to collisions with bacteria. Such fluctuations can be accounted for as an effective temperature that exceeds the actual temperature of the bath. However, as already discussed, the fluctuations induced by active media do not have Gaussian statistics, and therefore cannot be considered simply as an additional thermal bath.52,55,109,120,141,152 Krishnamurthy et al. quantify the bacterial activity introducing an active temperature Tact, that is, the temperature that an equilibrium bath leading to the same variance of the position would have. Note that this new parameter is different from the effective temperature discussed earlier, and in fact there is not a single choice for the effective temperature of an active bath.151,153 It is also important to point out the influence of the correlation time on these kinds of active baths, since its value will affect the engine when we run it at different velocities.
With this tool at hand, Krishnamurthy et al. implemented a Stirling engine by cyclically varying the stiffness of the trap, as well as the thermal temperature, which further increases the active temperature of the trapped particle. Fig. 7 is a schematic description of the Stirling cycle in the active Brownian heat engine, composed of two isochores connected by two isotherms. Experimentally, the stiffness is controlled via tuning of the optical power like in the previously discussed engines, while the temperature of the liquid is modified using water as exchange liquid in a channel adjacent to the trapping chamber.
 | ||
| Fig. 7 Bacterial heat engine. Bacteria swim in a liquid media where a colloid is optically trapped with an optical tweezer. A Stirling cycle analogous to the one in Fig. 3 is here executed in an active bath. The dynamics of the microsphere is governed by a combination of the Gaussian thermal fluctuations with an active source of non-Gaussian fluctuations due to the interaction of the colloid with the swarm of bacteria. Adapted from ref. 4. | ||
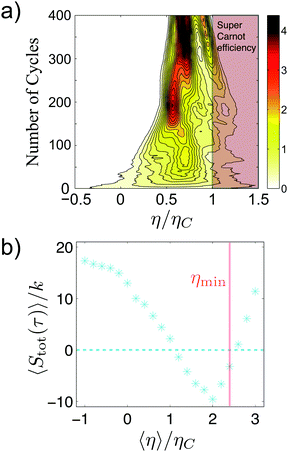
The performance of this active engine strongly depends on the activity of the bacteria, increasing in more than two orders of magnitude the work extraction of the same engine operated in a passive medium (the broth without bacteria), and reaching per cycle values of the extracted work of even tens of kT, see Fig. 8(a). The efficiency of the active engine can reach almost one order of magnitude improvement with respect to the passive one, as shown in Fig. 8(b).
 | ||
| Fig. 8 Performance of the bacterial heat engine. (a) The cumulative work done by active (closed symbols) and passive (open symbols) engine. The labels indicate the active temperatures of the hot bacterial reservoir. The inset is a zoom on the curve for the passive engine. (b) Fluctuations of the efficiency ε as a function of time when the engine is continuously executed for the active engine at Teff = 5455 K (filled squares) and the passive engine (open diamonds). The horizontal dotted lines represent the mean efficiency in each case. Adapted from ref. 4. | ||
The positional non-Gaussian fluctuations of the engine sketched in Fig. 7 are originated by the memory of the bacterial bath. Moreover, the experiment shows that the non-Gaussian tails of the fluctuations of the position of the colloid account for up to 50% of the efficiency of the active engine, in agreement with studies of super-diffusive behaviour of colloids in active media.149,154 Consequently, it is shown that active media are able to boost work extraction and efficiency by the additional energy input that comes from the conversion of chemical energy into heat executed by the bacteria.
5 Conclusions and outlook
Mesoscopic heat engines cannot be understood as a simple miniaturization of their classical counterparts. The fluctuating nature of the mesoscopic world results in genuine features that only occur in small engines and have no correspondence in the macroscopic world. The experiments presented here are colloidal revivals of the engines that were milestones in the foundation of classical thermodynamics (steam engines, Stirling engine, Carnot engine, see Section 4). These experiments exhibited unique features unattainable by macroscopic engines. For instance, Carnot efficiency can be transiently surpassed under nonequilibrium driving and a Brownian Carnot engine can operate reversibly at super-Carnot efficiencies.2 Stochastic thermodynamics, which inspired the experimental construction of the first colloidal heat engines, allows describing consistently the dynamics and energetics of these small-scale heat engines. Moreover, stochastic thermodynamics provides the suitable framework to design optimal protocols that minimize dissipation or operation times.38,97,98,155 The feasibility of such optimal protocols has been recently demonstrated experimentally also with optically-trapped microparticles.156An unsolved enigma in mesoscopic physics is whether the existing mesoscopic heat engines are only excellent toy models to test theoretical advances or if it is possible to use the extracted work for mesoscopic tasks, such as transferring energy to other parts of the system or transporting particles. We now offer fresh experimental perspectives to shed some light on this question, see Fig. 9 for illustrations. These proposals are aimed to inspire future developments in the field, since they are supported by recent theoretical proposals and experimental results in similar systems. Remarkably, a recent experiment with a single ion in a Paul trap has shown that work can be used to drive harmonic oscillation.43 Although different optical traps and Paul traps have similar dynamics,157,158 Paul traps have also been implemented with colloidal particles,159,160 which may open a future path for new investigations in the field.
A simple strategy is to build an engine in a micro-cage designed by lithography where one of the walls is free to move, very much like the piston in a classical engine (see Fig. 9a). This kind of geometry can also been built by optical potentials. Then, one or several colloids are placed within the cage, thus exerting work on the free wall. Similarly, one can envision a more sophisticated device where a nano-spring, such as a single DNA molecule, is anchored between two beads, one of which performs a Carnot cycle. With this construction, the second bead acts as a passive tracer that receives work cyclically.
Particularly intriguing are the theoretical predictions that point to the possibility to transfer heat between two colloids immersed in non-Gaussian baths at the same temperature.54Fig. 9b is an experimental proposal where two microscopic particles are immersed in two thermal baths at different temperatures Tc<Th. The cold bath is filled with bacteria that act as a source of non-Gaussian noise on one of the particles. If the two separate particles are attached by a spring, a net flow of heat from the cold active bath to the hot passive bath can occur, following ref. 54.
Other microscopic devices where work can be extracted systematically are the nonisothermal ratchets, where a current of Brownian particles is induced against external forces. A paradigmatic example is the Buttiker–Landauer ratchet.161,162Fig. 9c shows an illustration of this ratchet, where a Brownian particle is immersed in a thermal environment with periodic local temperature gradients. The broken spatial symmetry of the temperature can induce a net flow of particles against an applied external force thus performing work. Such a gedanken experiment could be in principle realized confining microscopic particles in optical periodic potentials in thermally asymmetric reservoirs.
Still also unexplored is the application of the temperature control used in colloidal heat engines in the so-called information engines.133,163 A classical example of an information engine is the one-particle Maxwell demon or Szilard engine. A colloidal Szilard engine was recently constructed using optical tweezers164 and with a single electron box.165 Until now, information engines have been realized only under isothermal conditions.164–170 New clever strategies for the design of autonomous minimal engines have also been recently proposed171–173 but few experimental autunomous engines have been reported.174,175 These kinds of engines are expected to play a crucial role in the uprising era of nanorobots.176 Nanomachines able to convert thermal fluctuations into mechanical energy will be of paramount interest for non-invasive therapies in nanomedicine in the near future.177,178
Acknowledgements
I. A. M. acknowledges financial support from the European Research Council Grant OUTEFLUCOP. E. R. and L. D. acknowledge funding from Spanish Government through grant TerMic (FIS2014-52486-R). R. A. R. acknowledges financial support from Fundació Privada Cellex Barcelona and the Severo Ochoa program. I. A. M. acknowledges useful discussions with Artyom Petrosyan. E. R. acknowledges fruitful discussions with Izaak Neri. R. A. R. thanks Pau Mestres for comments on the manuscript. All the authors acknowledge enlightening discussions with Juan M. R. Parrondo.References
- V. Blickle and C. Bechinger, Nat. Phys., 2012, 8, 143–146 CrossRef CAS.
- I. A. Martínez, É. Roldán, L. Dinis, D. Petrov, J. M. R. Parrondo and R. A. Rica, Nat. Phys., 2016, 12, 67–70 CrossRef PubMed.
- P. A. Quinto-Su, Nat. Commun., 2014, 5, 5889 CrossRef CAS PubMed.
- S. Krishnamurthy, S. Ghosh, D. Chatterji, R. Ganapathy and A. Sood, 2016, arXiv preprint arXiv:1601.03130.
- P. Hänggi, Rev. Mod. Phys., 2009, 81, 387–442 CrossRef.
- S. Sanchez, L. Soler and J. Katuri, Angew. Chem., Int. Ed., 2015, 54, 1414–1444 CrossRef CAS PubMed.
- G. Ozin, I. Manners, S. Fournier-Bidoz and A. Arsenault, Adv. Mater., 2005, 17, 3011–3018 CrossRef CAS.
- H. S. Leff and A. F. Rex, Maxwell's demon: entropy, information, computing, Princeton University Press, 2014 Search PubMed.
- M. Smoluchowski, Phys. Z., 1912, 13, 1069–1080 Search PubMed.
- R. P. Feynman, R. B. Leighton, M. Sands and S. Treiman, Phys. Today, 1964, 17, 45 CrossRef.
- J. M. R. Parrondo and P. Español, Am. J. Phys., 1996, 64, 1125–1129 CrossRef.
- É. Roldán, I. Neri, M. Dörpinghaus, H. Meyr and F. Jülicher, Phys. Rev. Lett., 2015, 115, 250602 CrossRef PubMed.
- R. Di Leonardo, L. Angelani, D. DellArciprete, G. Ruocco, V. Iebba, S. Schippa, M. Conte, F. Mecarini, F. De Angelis and E. Di Fabrizio, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9541–9545 CrossRef CAS PubMed.
- I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed.
- M. O. Magnasco, Phys. Rev. Lett., 1993, 71, 1477 CrossRef PubMed.
- A. Ajdari and J. Prost, C. R. Acad. Sci., Ser. II: Mec., Phys., Chim., Sci. Terre Univers, 1992, 315, 1635–1639 Search PubMed.
- J. Prost, J.-F. Chauwin, L. Peliti and A. Ajdari, Phys. Rev. Lett., 1994, 72, 2652 CrossRef CAS PubMed.
- F. Jülicher, A. Ajdari and J. Prost, Rev. Mod. Phys., 1997, 69, 1269 CrossRef.
- R. Ait-Haddou and W. Herzog, J. Electromyogr. Kinesiol., 2002, 12, 435–445 CrossRef CAS PubMed.
- M. Dangkulwanich, T. Ishibashi, S. Liu, M. L. Kireeva, L. Lubkowska, M. Kashlev and C. J. Bustamante, eLife, 2013, 2, e00971 Search PubMed.
- J. M. R. Parrondo and B. J. de Cisneros, Appl. Phys. A: Mater. Sci. Process., 2002, 75, 179–191 CrossRef CAS.
- P. Reimann, Phys. Rep., 2002, 361, 57–265 CrossRef CAS.
- C. J. Olson, C. Reichhardt, B. Jankó and F. Nori, Phys. Rev. Lett., 2001, 87, 177002 CrossRef CAS PubMed.
- F. J. Cao, L. Dinis and J. M. R. Parrondo, Phys. Rev. Lett., 2004, 93, 040603 CrossRef PubMed.
- V. Serreli, C.-F. Lee, E. R. Kay and D. A. Leigh, Nature, 2007, 445, 523–527 CrossRef CAS PubMed.
- A. Auge, A. Weddemann, F. Wittbracht and A. Hütten, Appl. Phys. Lett., 2009, 94, 183507 CrossRef.
- P. Reimann, M. Grifoni and P. Hänggi, Phys. Rev. Lett., 1997, 79, 10 CrossRef CAS.
- J. Rousselet, L. Salome, A. Ajdari and J. Prostt, Nature, 1994, 370, 446–447 CrossRef CAS PubMed.
- R. Schmitt, J. M. R. Parrondo, H. Linke and J. Johansson, New J. Phys., 2015, 17, 065011 CrossRef.
- J. E. Villegas, S. Savel'ev, F. Nori, E. M. Gonzalez, J. V. Anguita, R. Garcia and J. L. Vicent, Science, 2003, 302, 1188 CrossRef CAS PubMed.
- A. Song, Appl. Phys. A: Mater. Sci. Process., 2002, 75, 229–235 CrossRef CAS.
- P. K. Ghosh, V. R. Misko, F. Marchesoni and F. Nori, Phys. Rev. Lett., 2013, 110, 268301 CrossRef PubMed.
- C. S. Peskin, G. M. Odell and G. F. Oster, Biophys. J., 1993, 65, 316 CrossRef CAS PubMed.
- K. Sekimoto, Prog. Theor. Phys. Suppl., 1998, 130, 17–27 CrossRef CAS.
- U. Seifert, Rep. Prog. Phys., 2012, 75, 126001 CrossRef PubMed.
- C. Bustamante, J. Liphardt and F. Ritort, Phys. Today, 2005, 58, 43–48 CrossRef CAS.
- C. Jarzynski, Annu. Rev. Condens. Matter Phys., 2011, 2, 329–351 CrossRef CAS.
- T. Schmiedl and U. Seifert, EPL, 2007, 81, 20003 CrossRef.
- K. Sekimoto, F. Takagi and T. Hondou, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 7759 CrossRef CAS.
- A. Dechant, N. Kiesel and E. Lutz, Phys. Rev. Lett., 2015, 114, 183602 CrossRef PubMed.
- O. Abah, J. Rossnagel, G. Jacob, S. Deffner, F. Schmidt-Kaler, K. Singer and E. Lutz, Phys. Rev. Lett., 2012, 109, 203006 CrossRef CAS PubMed.
- J. Roßnagel, O. Abah, F. Schmidt-Kaler, K. Singer and E. Lutz, Phys. Rev. Lett., 2014, 112, 030602 CrossRef PubMed.
- J. Roßnagel, S. T. Dawkins, K. N. Tolazzi, O. Abah, E. Lutz, F. Schmidt-Kaler and K. Singer, Science, 2016, 352, 325–329 CrossRef PubMed.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- M. Marchetti, J. Joanny, S. Ramaswamy, T. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- E. Barkai, Y. Garini and R. Metzler, Phys. Today, 2012, 65, 29 CrossRef CAS.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. S. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424–13431 CrossRef CAS PubMed.
- U. Seifert, Eur. Phys. J. B, 2008, 64, 423–431 CrossRef CAS.
- E. Ben-Isaac, Y. Park, G. Popescu, F. L. H. Brown, N. S. Gov and Y. Shokef, Phys. Rev. Lett., 2011, 106, 238103 CrossRef PubMed.
- J. Gomez-Solano, A. Petrosyan and S. Ciliberto, Phys. Rev. Lett., 2011, 106, 200602 CrossRef CAS PubMed.
- V. Blickle, T. Speck, L. Helden, U. Seifert and C. Bechinger, Phys. Rev. Lett., 2006, 96, 070603 CrossRef CAS PubMed.
- K. Kanazawa, T. Sagawa and H. Hayakawa, Phys. Rev. Lett., 2012, 108, 210601 CrossRef PubMed.
- A. Argun, A.-R. Moradi, E. Pince, G. B. Bagci and G. Volpe, 2016, arXiv preprint arXiv:1601.01123.
- K. Kanazawa, T. Sagawa and H. Hayakawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052124 CrossRef PubMed.
- E. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. van Wijland, Phys. Rev. Lett., 2016, 117, 038103 CrossRef PubMed.
- S. Toyabe and M. Sano, J. Phys. Soc. Jpn., 2015, 84, 102001 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, 2016, arXiv preprint arXiv:1602.00081.
- C. Reichhardt and C. Reichhardt, 2016, arXiv preprint arXiv:1604.01072.
- S. J. Ebbens and J. R. Howse, Soft Matter, 2010, 6, 726–738 RSC.
- R. Brown, The Philosophical Magazine, or Annals of Chemistry, Mathematics, Astronomy, Natural History and General Science, 1828, 4, 161–173 Search PubMed.
- A. Einstein, Ann. Phys., 1905, 17, 549 CrossRef CAS.
- P. Langevin, C. R. Acad. Sci., 1908, 146, 530 CAS.
- E. Frey and K. Kroy, Ann. Phys., 2005, 517, 20–50 CrossRef.
- C. Van den Broeck and M. Esposito, Phys. A, 2015, 418, 6–16 CrossRef.
- K. Sekimoto, Stochastic energetics, Springer, 2010, vol. 799 Search PubMed.
- U. Seifert, Phys. Rev. Lett., 2005, 95, 040602 CrossRef PubMed.
- G. E. Crooks, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 2721 CrossRef CAS.
- C. Maes, J. Stat. Phys., 1999, 95, 367–392 CrossRef.
- P. Gaspard, J. Stat. Phys., 2004, 117, 599–615 CrossRef.
- R. Kawai, J. M. R. Parrondo and C. Van den Broeck, Phys. Rev. Lett., 2007, 98, 080602 CrossRef CAS PubMed.
- J. M. R. Parrondo, C. Van den Broeck and R. Kawai, New J. Phys., 2009, 11, 073008 CrossRef.
- É. Roldán, Irreversibility and dissipation in microscopic systems, Springer, 2014 Search PubMed.
- J. L. Lebowitz and H. Spohn, J. Stat. Phys., 1999, 95, 333–365 CrossRef.
- C. Aron, G. Biroli and L. F. Cugliandolo, J. Stat. Mech.: Theory Exp., 2010, 2010, P11018 CrossRef.
- S. Gupta, T. Dauxois and S. Ruffo, EPL, 2016, 113, 60008 CrossRef.
- G. Gallavotti and E. Cohen, Phys. Rev. Lett., 1995, 74, 2694 CrossRef CAS PubMed.
- J. Kurchan, J. Phys. A: Math. Gen., 1998, 31, 3719 CrossRef.
- D. J. Evans and D. J. Searles, Adv. Phys., 2002, 51, 1529–1585 CrossRef.
- P. I. Hurtado, C. Pérez-Espigares, J. J. del Pozo and P. L. Garrido, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7704–7709 CrossRef CAS PubMed.
- C. Jarzynski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5018 CrossRef CAS.
- H. Tasaki, 2000, arXiv preprint cond-mat/0009244.
- R. Chetrite and S. Gupta, J. Stat. Phys., 2011, 143, 543–584 CrossRef.
- P. Pietzonka, A. C. Barato and U. Seifert, Phys. Rev. E, 2016, 93, 052145 CrossRef PubMed.
- T. R. Gingrich, J. M. Horowitz, N. Perunov and J. L. England, Phys. Rev. Lett., 2016, 116, 120601 CrossRef PubMed.
- I. Neri, É. Roldán and F. Jülicher, 2016, arXiv preprint arXiv:1604.04159.
- K. Saito and A. Dhar, 2015, arXiv preprint arXiv:1504.02187.
- D. Collin, F. Ritort, C. Jarzynski, S. B. Smith, I. Tinoco and C. Bustamante, Nature, 2005, 437, 231–234 CrossRef CAS PubMed.
- J. Liphardt, S. Dumont, S. B. Smith, I. Tinoco and C. Bustamante, Science, 2002, 296, 1832–1835 CrossRef CAS PubMed.
- K. Sekimoto and S.-i. Sasa, J. Phys. Soc. Jpn., 1997, 66, 3326–3328 CrossRef CAS.
- M. V. Bonança and S. Deffner, J. Chem. Phys., 2014, 140, 244119 CrossRef PubMed.
- S. Carnot, Réflexions sur la puissance motrice du feu, Vrin, 1978 Search PubMed.
- I. Novikov, J. Nucl. Energy, 1958, 7, 125–128 Search PubMed.
- F. Curzon and B. Ahlborn, Am. J. Phys., 1975, 43, 22–24 CrossRef.
- M. Esposito, R. Kawai, K. Lindenberg and C. Van den Broeck, Phys. Rev. Lett., 2010, 105, 150603 CrossRef PubMed.
- M. Moreau, B. Gaveau and L. Schulman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021129 CrossRef CAS PubMed.
- A. Emmanouilidou, X.-G. Zhao, P. Ao and Q. Niu, Phys. Rev. Lett., 2000, 85, 1626 CrossRef CAS PubMed.
- T. Schmiedl and U. Seifert, Phys. Rev. Lett., 2007, 98, 108301 CrossRef PubMed.
- T. R. Gingrich, G. M. Rotskoff, G. E. Crooks and P. L. Geissler, 2016, arXiv preprint arXiv:1602.01459.
- G. Verley, M. Esposito, T. Willaert and C. Van den Broeck, Nat. Commun., 2014, 5, 4721 CrossRef CAS PubMed.
- T. R. Gingrich, G. M. Rotskoff, S. Vaikuntanathan and P. L. Geissler, New J. Phys., 2014, 16, 102003 CrossRef.
- S. Rana, P. Pal, A. Saha and A. Jayannavar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042146 CrossRef PubMed.
- G. Verley, T. Willaert, C. Van den Broeck and M. Esposito, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 052145 CrossRef PubMed.
- M. Polettini, G. Verley and M. Esposito, Phys. Rev. Lett., 2015, 114, 050601 CrossRef CAS PubMed.
- K. Proesmans, B. Cleuren and C. Van den Broeck, EPL, 2015, 109, 20004 CrossRef.
- M. Bauer, K. Brandner and U. Seifert, Phys. Rev. E, 2016, 93, 042112 CrossRef PubMed.
- S. Rana, P. Pal, A. Saha and A. Jayannavar, Phys. A, 2016, 444, 783–798 CrossRef.
- D. G. Grier, Nature, 2003, 424, 810–816 CrossRef CAS PubMed.
- D. McGloin, Philos. Trans. R. Soc. London, Ser. A, 2006, 364, 3521–3537 CrossRef CAS PubMed.
- P. Mestres, I. A. Martínez, A. Ortiz-Ambriz, R. A. Rica and E. Roldan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032116 CrossRef PubMed.
- A. Ashkin, Phys. Rev. Lett., 1970, 24, 156 CrossRef CAS.
- A. Ashkin, J. Dziedzic, J. Bjorkholm and S. Chu, Opt. Lett., 1986, 11, 288–290 CrossRef CAS PubMed.
- A. Ashkin, J. Dziedzic and T. Yamane, Nature, 1987, 330, 769–771 CrossRef CAS PubMed.
- A. Ashkin and J. Dziedzic, Science, 1987, 235, 1517–1520 CAS.
- A. Mazolli, P. M. Neto and H. Nussenzveig, Philos. Trans. R. Soc. London, Ser. A, 2003, 3021–3041 CrossRef.
- M. Jahnel, M. Behrndt, A. Jannasch, E. Schäffer and S. W. Grill, Opt. Lett., 2011, 36, 1260–1262 CrossRef PubMed.
- I. A. Martínez and D. Petrov, Appl. Opt., 2012, 51, 5522–5526 CrossRef PubMed.
- K. Visscher, S. P. Gross and S. M. Block, IEEE J. Sel. Top. Quantum Electron., 1996, 2, 1066–1076 CrossRef CAS.
- K. Dholakia, P. Reece and M. Gu, Chem. Soc. Rev., 2008, 37, 42–55 RSC.
- G. C. Spalding, J. Courtial and R. Di Leonardo, Holographic optical tweezers, Academic Press, 2008 Search PubMed.
- I. A. Martínez, É. Roldán, J. M. R. Parrondo and D. Petrov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032159 CrossRef.
- É. Roldán, I. A. Martínez, L. Dinis and R. A. Rica, Appl. Phys. Lett., 2014, 104, 234103 CrossRef.
- L. Dinis, I. A. Martínez, É. Roldán, J. M. R. Parrondo and R. A. Rica, J. Stat. Mech.: Theory Exp., 2016, 2016, 054003 CrossRef.
- H. Mao, J. R. Arias-Gonzalez, S. B. Smith, I. Tinoco and C. Bustamante, Biophys. J., 2005, 89, 1308–1316 CrossRef CAS PubMed.
- M. C. Leake, D. Wilson, M. Gautel and R. M. Simmons, Biophys. J., 2004, 87, 1112–1135 CrossRef CAS PubMed.
- K. Svoboda, C. Schmidt, D. Branton and S. Block, Biophys. J., 1992, 63, 784 CrossRef CAS PubMed.
- A. Bérut, A. Petrosyan, J. R. Gomez-Solano and S. Ciliberto, J. Stat. Mech.: Theory Exp., 2015, 2015, P10020 CrossRef.
- A. Bérut, A. Petrosyan and S. Ciliberto, EPL, 2014, 107, 60004 CrossRef.
- G. Wang, E. M. Sevick, E. Mittag, D. J. Searles and D. J. Evans, Phys. Rev. Lett., 2002, 89, 050601 CrossRef CAS PubMed.
- W. Wang, T.-Y. Chiang, D. Velegol and T. E. Mallouk, J. Am. Chem. Soc., 2013, 135, 10557–10565 CrossRef CAS PubMed.
- D. Andrieux, P. Gaspard, S. Ciliberto, N. Garnier, S. Joubaud and A. Petrosyan, Phys. Rev. Lett., 2007, 98, 150601 CrossRef CAS PubMed.
- G. E. Crooks and C. Jarzynski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021116 CrossRef PubMed.
- I. A. Martínez, É. Roldán, L. Dinis, D. Petrov and R. A. Rica, Phys. Rev. Lett., 2015, 114, 120601 CrossRef PubMed.
- C. H. Bennett, Int. J. Theor. Phys., 1982, 21, 905–940 CrossRef CAS.
- A. Celani, S. Bo, R. Eichhorn and E. Aurell, Phys. Rev. Lett., 2012, 109, 260603 CrossRef PubMed.
- S. Bo and A. Celani, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 050102 CrossRef PubMed.
- G. Coupier, M. Saint Jean and C. Guthmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 031112 CrossRef PubMed.
- J. R. Gomez-Solano, L. Bellon, A. Petrosyan and S. Ciliberto, EPL, 2010, 89, 60003 CrossRef.
- O. Otto, C. Gutsche, F. Kremer and U. Keyser, Rev. Sci. Instrum., 2008, 79, 023710 CrossRef PubMed.
- A. Bérut, A. Imparato, A. Petrosyan and S. Ciliberto, Phys. Rev. Lett., 2016, 116, 068301 CrossRef PubMed.
- J. R. Gomez-Solano, C. July, J. Mehl and C. Bechinger, New J. Phys., 2015, 17, 045026 CrossRef.
- E. Dieterich, J. Camunas-Soler, M. Ribezzi-Crivellari, U. Seifert and F. Ritort, Nat. Phys., 2015, 11, 971–977 CrossRef CAS.
- Z. Tu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 052148 CrossRef CAS PubMed.
- Z. Tu, J. Phys. A: Math. Theor., 2008, 41, 312003 CrossRef.
- C. Valeriani, M. Li, J. Novosel, J. Arlt and D. Marenduzzo, Soft Matter, 2011, 7, 5228–5238 RSC.
- T. Pedley and J. Kessler, Annu. Rev. Fluid Mech., 1992, 24, 313–358 CrossRef.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489–1499 RSC.
- I. A. Martínez, S. Campoy, M. Tort, M. Llagostera and D. Petrov, PLoS One, 2013, 8, e61630 Search PubMed.
- V. Zaburdaev, S. Denisov and J. Klafter, Rev. Mod. Phys., 2015, 87, 483 CrossRef.
- X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017 CrossRef CAS PubMed.
- D. T. Chen, A. Lau, L. A. Hough, M. F. Islam, M. Goulian, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 2007, 99, 148302 CrossRef CAS PubMed.
- C. Maggi, M. Paoluzzi, N. Pellicciotta, A. Lepore, L. Angelani and R. Di Leonardo, Phys. Rev. Lett., 2014, 113, 238303 CrossRef CAS PubMed.
- S. K. Nandi, 2016, arXiv preprint arXiv:1607.04478.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 088304 CrossRef PubMed.
- Y. Hatwalne, S. Ramaswamy, M. Rao and R. A. Simha, Phys. Rev. Lett., 2004, 92, 118101 CrossRef PubMed.
- S. Vaikuntanathan and C. Jarzynski, Phys. Rev. Lett., 2008, 100, 190601 CrossRef PubMed.
- I. A. Martínez, A. Petrosyan, D. Guéry-Odelin, E. Trizac and S. Ciliberto, Nat. Phys., 2016 DOI:10.1038/nphys3758.
- A. F. Izmailov, S. Arnold, S. Holler and A. S. Myerson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 1325–1332 CrossRef CAS.
- I. Alda, J. Berthelot, R. A. Rica and R. Quidant, 2016, arXiv preprint arXiv:1606.04829.
- W. Guan, S. Joseph, J. H. Park, P. S. Krstić and M. A. Reed, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9326–9330 CrossRef CAS PubMed.
- J. H. Park and P. S. Krstić, Nanoscale Res. Lett., 2012, 7, 1 CrossRef PubMed.
- R. Landauer, J. Stat. Phys., 1988, 53, 233–248 CrossRef.
- M. Büttiker, Z. Phys. B: Condens. Matter, 1987, 68, 161–167 CrossRef.
- J. M. R. Parrondo, J. M. Horowitz and T. Sagawa, Nat. Phys., 2015, 11, 131–139 CrossRef CAS.
- É. Roldán, I. A. Martínez, J. M. R. Parrondo and D. Petrov, Nat. Phys., 2014, 10, 457–461 CrossRef.
- J. V. Koski, V. F. Maisi, J. P. Pekola and D. V. Averin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13786–13789 CrossRef CAS PubMed.
- B. J. Lopez, N. J. Kuwada, E. M. Craig, B. R. Long and H. Linke, Phys. Rev. Lett., 2008, 101, 220601 CrossRef PubMed.
- S. Toyabe, T. Sagawa, M. Ueda, E. Muneyuki and M. Sano, Nat. Phys., 2010, 6, 988–992 CrossRef CAS.
- A. Bérut, A. Arakelyan, A. Petrosyan, S. Ciliberto, R. Dillenschneider and E. Lutz, Nature, 2012, 483, 187–189 CrossRef PubMed.
- Y. Jun, M. Gavrilov and J. Bechhoefer, Phys. Rev. Lett., 2014, 113, 190601 CrossRef PubMed.
- M. Gavrilov and J. Bechhoefer, 2016, arXiv preprint arXiv:1603.07814.
- D. Mandal and C. Jarzynski, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11641–11645 CrossRef CAS PubMed.
- A. C. Barato and U. Seifert, EPL, 2013, 101, 60001 CrossRef CAS.
- Z. Lu, D. Mandal and C. Jarzynski, Phys. Today, 2014, 67, 60 CrossRef.
- A. Kutvonen, J. Koski and T. Ala-Nissila, Sci. Rep., 2016, 6, 21126 CrossRef CAS PubMed.
- M. Serra-Garcia, A. Foehr, M. Molerón, J. Lydon, C. Chong and C. Daraio, Phys. Rev. Lett., 2016, 117, 010602 CrossRef PubMed.
- S. M. Douglas, I. Bachelet and G. M. Church, Science, 2012, 335, 831–834 CrossRef CAS PubMed.
- G. M. Patel, G. C. Patel, R. B. Patel, J. K. Patel and M. Patel, J. Drug Targeting, 2006, 14, 63–67 CrossRef CAS PubMed.
- A. Cavalcanti, B. Shirinzadeh, R. A. Freitas Jr and T. Hogg, Nanotechnology, 2007, 19, 015103 CrossRef.
Footnotes |
† The symbol ∘ denotes that the integral is taken in Stratonovich sense, i.e. with a mid-point rule in the discretization scheme 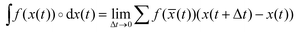 , with , with ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (t) = (x(t) + x(t + Δt))/2. This prescription is essential for an appropriate definition of the first law of thermodynamics in the mesoscale. (t) = (x(t) + x(t + Δt))/2. This prescription is essential for an appropriate definition of the first law of thermodynamics in the mesoscale. |
| ‡ The universal character of the fluctuation theorems means that they are valid for general nonequilibrium processes even far from the linear response regime, such as, for Markovian processes described by the Langevin or Master equation,66,73 for non-Markovian processes74 and even for systems with long-range interactions.75 This includes the cases of heat engines where the total entropy contains contributions from the interactions between the engines and the two thermal baths. |
| § Work can also be extracted from a single thermal bath by performing measurements, but the discussion of information engines133 is out of the scope of this review. |
| This journal is © The Royal Society of Chemistry 2017 |





