Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics of formation of bile salt micelles from coarse-grained Langevin dynamics simulations†
Ana
Vila Verde‡
 *a and
Daan
Frenkel‡
b
*a and
Daan
Frenkel‡
b
aTheory and Bio-Systems Department, Max Planck Institute of Colloids and Interfaces, Wissenschaftspark Golm, 14424 Potsdam, Germany. E-mail: ana.vilaverde@mpikg.mpg.de; Fax: +49 331 567 9602; Tel: +49 331 567 9608
bDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK. E-mail: df246@cam.ac.uk; Tel: +44 1223 336377
First published on 10th May 2016
Abstract
We examine the mechanism of formation of micelles of dihydroxy bile salts using a coarse-grained, implicit solvent model and Langevin dynamics simulations. We find that bile salt micelles primarily form via addition and removal of monomers, similarly to surfactants with typical head–tail molecular structures, and not via a two-stage mechanism – involving formation of oligomers and their subsequent aggregation to form larger micelles – originally proposed for bile salts. The free energy barrier to removal of single bile monomers from micelles is ≈2kBT, much less than what has been observed for head–tail surfactants. Such a low barrier may be biologically relevant: it allows for rapid release of bile monomers into the intestine, possibly enabling the coverage of fat droplets by bile salt monomers and subsequent release of micelles containing fats and bile salts – a mechanism that is not possible for ionic head–tail surfactants of similar critical micellar concentrations.
1 Introduction
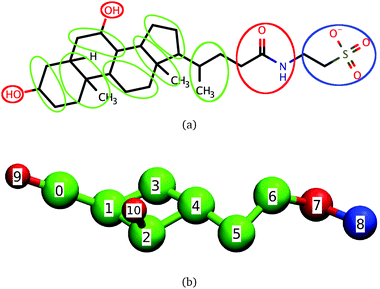
Bile salts and bile acids are surfactants that play a key role in the digestion of fats by humans. Together with phospholipids and cholesterol at physiological concentrations, bile salts form dietary mixed micelles (DMMs) responsible for displacing the proteins coating lipid droplets and for solubilizing fats and fat-soluble nutrients or drugs.1–8 After solubilization takes place, DMMs carry nutrients to the intestinal wall where they are released and absorbed by intestinal cells.2,3 Bile salts are also used in the formulation of both hydrophilic and hydrophobic drugs, because of their ability to enhance drug transport across tissues.7,9 The ability of bile salts and other steroidal surfactants to solubilize hydrophobic molecules is not limited to biological systems: for example, bile salts solubilize single-walled nanotubes more effectively than surfactants like sodium dodecyl sulfate (SDS);10,11 steroidal surfactants can even encapsulate charged molecules12 and are commonly used during protein purification and crystallization.13–16The molecular structure of bile salts differs from those of well-studied surfactants like SDS or the DMM component phosphatidylcholine. Instead of the hydrophilic head–hydrophobic tail (head–tail) structure that leads to a prolate shape typically associated with surfactants, bile salts have a rigid steroid group with four rings attached to a short and flexible tail, as shown in Fig. 1(a) for the bile salt taurochenodeoxycholate. The hydrophilic character of one of the steroid faces results from the presence of two or three hydroxyl groups, which are absent from the hydrophobic face. In the upper intestinal tract, the bile salt tail predominantly ends in a hydrophilic glycine or taurine group which, depending on pH, may be charged. Further down in the intestinal tract the taurine or glycine conjugation is removed and the bile salts become more hydrophobic.
Despite the molecular scale differences between the various bile salts that exist in the human body – they may differ in the presence or absence of conjugation to taurine or glycine, in the number and position of the hydroxyl groups – they share similar static and thermodynamic properties at physiological NaCl concentration (0.15 M) and temperature: the concentration at which micelles begin to predominate in the system, called the critical micellar concentration or CMC, is high (CMC = 1–10 mM) and the average number of molecules composing micelles, called the average aggregation number, near the CMC ranges between 2 and 30, i.e., it is low.2,17–27 The low average aggregation numbers of pure bile micelles compared to those of canonical surfactants like SDS stem from the bile salts' unusual molecular structure. This structure enables them to form oligomers (with aggregation numbers, n = 2, 3, 4…10), which are almost non-existent for other surfactants.21,22,24–26,28–32 Molecular dynamics simulations using all-atom28–30 and coarse-grained31 models, indicate that both oligomers and micelles are primarily stabilized by hydrophobic interactions, in agreement with experimental data that indicates that micellization is entropy-driven because of the release of water molecules from the hydrophobic face of the bile salts.32–34
While the static properties of pure bile micelles are reasonably well characterized as summarized above, considerably less is known about their mechanism of formation. Understanding this mechanism is important because the rate and extent to which lipophilic nutrients are solubilized in DMMs are directly related to the rate and extent of uptake by the body.35 Empiric knowledge about the role of DMMs in nutrient uptake has been used for several years to influence the solubilization of particular nutrients or drugs by DMMs for nutritional or health benefits, with only partial success.2,3,5 Further progress has been hampered in part by our lack of detailed knowledge of the molecular scale mechanism of formation of DMMs. To gain such knowledge, we must first understand the solution behavior of the individual components of DMMs. Bile salts are the least understood of all DMM components, so here we focus on them.
The size of micelles of any surfactant may change in two ways: via the stepwise addition or removal of monomers, or the fission and fusion of larger groups of molecules.36–41 For ionic surfactants with the typical head–tail geometry like SDS, theory and simulation38,40–42 suggest that micelle size changes occur primarily via the addition and removal of monomers, and that addition and removal of dimers, trimers and other small fragments should play a very small role, consistent with the expected very low concentration of these fragments in solution. Only at high counterion concentrations should fission and fusion of fragments become frequent. In contrast with this canonical picture, Ekwall and Small propose a two-step mechanism of micelle formation for bile salts, made possible by the abundance of bile salt oligomers in solution even at relatively low counterion concentrations: above the CMC, bile salts initially form smaller micelles (containing between 2 and 9 molecules) by stepwise addition;17,43 larger (called secondary) micelles are then assumed to form by fusion of the primary ones via intramicellar hydrogen bonds. Subsequent reports of experiments and simulations indicating that intramicellar hydrogen bonds are frequent in larger bile micelles were interpreted as supporting such a mechanism.29,44–46 At present, direct molecular scale information on the mechanism of formation of pure bile micelles is unavailable, so it remains controversial whether bile micelles form primarily via addition and removal of monomers or of oligomers.
In this paper we address this on-going controversy by performing Langevin dynamics simulations of conjugated dihydroxy bile salts using a coarse-grained model developed by us.31 The model satisfactorily reproduces the average aggregation number of bile salts determined from experiment as a function of concentration and the molecular scale structure of bile micelles determined from simulations using all-atom models. The modest computational cost of this model allows for the indispensable long simulations at concentrations close to the CMC, where fission and fusion of both monomers and oligomers can be well-sampled. We identify the dominant mechanisms involved in size change of pure bile micelles, calculate their rate constants, relate this kinetic information to free energy profiles along an appropriate reaction coordinate and relate our observations to the biological role of bile salts.
2 Methods
2.1 Approach
Using Langevin dynamics simulations, we investigate the formation of micelles of conjugated dihydroxy bile salts at physiological temperature and NaCl concentration for bile salt concentrations 1.8, 8.9 and 18 times larger than the CMC (0.000442 molecules/σ2); these concentrations are denoted as 1.8 CMC, 8.9 CMC and 18 CMC. These concentrations are reported as a multiple of the CMC because different experimental methods lead to CMCs differing by a factor as large as 3 for the same bile system;31 expressing concentrations as a multiple of the CMC thus facilitates comparisons with experiment. The concentration range used in this study is sufficiently broad to examine the dependence of micelle formation mechanisms on this variable47 and is physiologically relevant. We define the CMC as the concentration at which 50% of all molecules exist as monomers, a definition which is commonly employed in simulations.42,48,49 Monomers are distinguished from aggregates using a distance criterion:31 two molecules are considered part of the same aggregate if the distance between their centers of mass is <3σ, where σ is the unit of length in our simulations and is defined in more detail below. Full details of the model used in this study are given in a prior publication31 so below we offer only a brief description.2.2 Coarse-grained model of bile salts
The coarse-grained model of dihydroxy taurine- or glycine-substituted bile salts used here is shown in Fig. 1. In the same figure we show the correspondence between the coarse-grained model and the molecular structure of taurochenodeoxycholate; we emphasize, however, that the model is also representative of other conjugated dihydroxy bile salts.Significant overlap between any two beads is prevented through a Weeks–Chandler–Andersen potential. The water and the salt ions present in aqueous solutions of bile salts are modeled through effective interactions. To mimic the effective attraction experienced by hydrophobic groups in water we use a cosine square potential. This potential has a finite range and has been shown to capture the characteristic short-range attraction of hydrophobic interactions necessary for self-assembly of micelles and bilayers.50,51 We specify no net attraction or repulsion between any two hydrophilic beads or between a hydrophilic and a hydrophobic bead beyond volume exclusion because these interactions are comparable to the interactions of these groups with water, and are much weaker than hydrophobic interactions.31 The only exceptions are the charged beads, which interact with other charged beads through a Debye–Hückel potential. This potential accounts for the screening effect brought by the dielectric constant of water and the presence of NaCl on the electrostatic interactions. The model is parameterized to reproduce the critical micellar concentration and average aggregation number of conjugated dihydroxy bile salts near the CMC at physiological temperature and concentration of NaCl but it can easily be adapted to represent bile salts under other conditions, or even molecules similar to bile salts like the triterpenoids asiatic acid and madecassic acid.52,53
2.3 Simulation details
The model is implemented in the ESPResSo molecular dynamics simulation package.54 For computational convenience the implementation is done using reduced units, i.e. we chose suitable units of length, mass and energy and express all quantities as multiples of these units. The unit of mass is m ≈ 8 × 10−26 kg, of energy is ε = 8.6 × 10−21J = 1.2 kcal mol−1 = 2kBT and of length is σ ≈ 4.0 Å as described elsewhere.31 It follows that our unit of temperature is ε/kB, where kB is the Boltzmann constant. The unit of time τ is estimated by equating the diffusion coefficient of cholate ions (5 × 10−10 m2 s−1)55 to the diffusion coefficient of monomers (0.04σ2/τ) from our simulation at the lowest concentration here tested. We find τ ≈ 12 ps. We note that this value represents only a coarse estimate of the unit of time, so in this work we focus on understanding the relative dynamics of the various processes involved in changes of micelle size and the sequence of events involved in such processes. The trends seen in the simulations are thus directly comparable to experiment despite the uncertainty in our estimate of τ.We investigate micellization using Langevin dynamics simulations at constant volume, temperature and number of particles. The initial configuration for each simulation is obtained from a prior simulation (described in ref. 31) performed with Grand Canonical Langevin Dynamics (GCLD). The initial configuration thus already has a micelle size distribution characteristic of equilibrium, and further equilibration is not necessary. Cubic boxes with periodic boundary conditions are used for all simulations. The dimensions of the simulation boxes and the number of molecules used at each concentration are given in Table 1. All simulations are performed at a temperature of 0.5ε/kB, enforced through a Langevin thermostat. The equations of motion are integrated using a velocity Verlet algorithm with a time step of 0.01τ. Production runs last 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, with configurations saved every 100 steps. Saved configurations are visualized using VMD-Visual Molecular Dynamics.56
000 steps, with configurations saved every 100 steps. Saved configurations are visualized using VMD-Visual Molecular Dynamics.56
| Concentration (×CMC) | N mol | L (σ) |
|---|---|---|
| 1.8 | 43 | 37.5 |
| 8.9 | 207 | 37.5 |
| 18 | 64 | 20 |
3 Results and discussion
3.1 Simulations properly sample the system configuration space
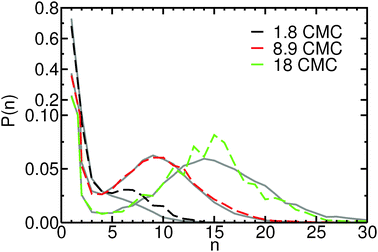
Investigating the mechanism(s) of micelle formation requires simulations where the number of fission and fusion events is sufficiently high to allow proper sampling of the system configuration space. We demonstrate that our NVT simulations meet this condition by: (i) verifying that the NVT simulations sample the correct micelle size distribution at each concentration by comparison to simulations using grand canonical Langevin dynamics; (ii) confirming that individual molecules sample a wide range of micellar environments by calculating the mean square displacement in micelle size space and comparing its saturation value with predictions from diffusion theory57 (see ESI†); and (iii) for the most frequent events – the addition and removal of monomers, dimers or trimers to/from micelles, as shown below – by showing that the rates calculated from the micelle size distribution are identical to those directly calculated in the simulation (see ESI†).The micelle size distribution is quantified here through the probability, P(n), of finding micelles with n molecules (i.e., with aggregation number n):
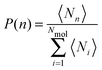 | (1) |
3.2 Micelle size changes occur primarily via monomer removal and addition at all concentrations
To evaluate which processes contribute most to changes in micellar size we calculate the reaction rates, λ, for addition and removal of monomers and larger fragments. Fission and fusion events are described by quasichemical reactions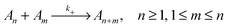 | (2) |
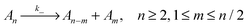 | (3) |
| λ+ = k+CnCm | (4) |
| λ− = k−Cn | (5) |
We calculate the reaction rates as the number of fission or fusion events occurring per unit time and per unit volume. Fission and fusion events are identified by detecting a change in aggregate size between two consecutive saved configurations. The reaction rates calculated this way necessarily depend on the time interval between saved configurations but we expect this dependence to be small because the rate constants are sufficiently low (e.g., the fission rate constant k−, is O(10−2τ−1)), that there is only a negligible chance that the same micelle has been involved in more than one fission or fusion event between two saved configurations (separated by 1τ).
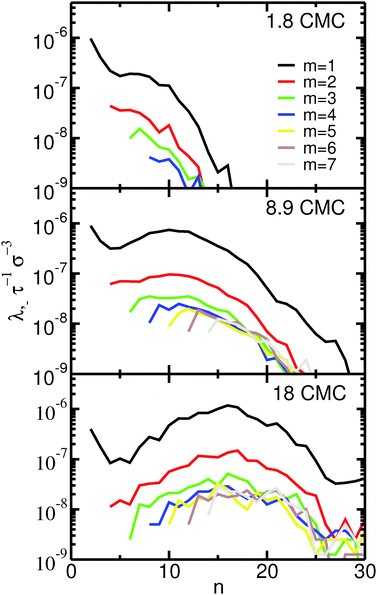
The fission reaction rates, λ−, as a function of the aggregation number of the initial micelle, n, are shown in Fig. 3. Almost identical curves (not shown) are obtained for the fusion reaction rates, λ+, as expected for a system in equilibrium. Inspection of Fig. 3 indicates that the fission reaction rates depend strongly on concentration. This dependence follows that expected from eqn (5) assuming a rate constant, k−, that is independent of the concentration. In the ESI† we show that this assumption indeed holds for our systems. Fig. 3 clearly shows that fusion and fission of monomers are by far the most frequent events even at concentrations far from the CMC: the reaction rates for fission and fusion of dimers, trimers etc. are at least one order of magnitude lower than for monomers. Events involving fission or fusion of larger aggregates are nevertheless still frequent. At the lowest concentration investigated (1.8 CMC) these events represent 10% of all fission and fusion events; at the highest concentration (18 CMC) they represent 25%. Most of the events with m > 1 are restricted to fission and fusion of dimers or trimers (m = 2, 3): even at the highest concentration, fission and fusion events with m > 3 represent only 13% of the total number of events.
These results indicate that the dominant mechanism for changes of micellar size is monomer fission and fusion for both large and small micelles, even at concentrations much higher than the CMC. This observation is supported by recent ultrasonic relaxation measurements of micellar kinetics in bile salt solutions.58 In that work, the experimental results were well-fitted by analytical models of micelle kinetics relying solely on monomer addition and removal, indicating that fission and fusion of larger micelles should play a secondary role. The observed importance of monomer addition and removal is in line with simulations of model coarse-grained ionic head–tail surfactants42 and, more generally, with the expected behavior of ionic surfactants at concentrations near the CMC and for low to moderate counterion concentration.40 Our results thus do not support the mechanism initially proposed by Small and Ekwall,17,43 that larger micelles form primarily by fusion of smaller ones. In apparent contradiction with our observations and the ultrasonic relaxation measurements58 we mentioned above, recent conductivity measurements34 have been interpreted to support the two-stage mechanism proposed by Small and Ekwall.17,43 It is our opinion, however, that such a conclusion may not be reached from those measurements. In conductivity measurements, the CMC is estimated from the position of a break point in a graph of conductivity vs. concentration. In the study by Kumar et al., that break point is not sharp, which was interpreted to suggest the presence of oligomers as well as micelles near the CMC. We agree with that interpretation; however, we point out that the mere presence of oligomers does not constitute evidence that larger micelles form via the fusion of small oligomers, as suggested by Kumar et al.
3.3 Models of micellar kinetics developed for head–tail surfactants apply for bile salts
Experimentally determined chemical relaxation times in micellar systems are often interpreted resorting to models of micellar kinetics that assume that micelle size changes take place only by monomer fission and fusion.36–38 Our results confirm that relaxation times in bile salt solutions at physiologically relevant concentrations may be interpreted using those models, as was recently successfully done by Ravichandran et al.,58 as discussed above. For improved quantitative agreement, however, fission and fusion of dimers and trimers should be included in the models at high concentrations, where these events become more frequent. These theoretical models of micellar kinetics also often assume that the rate constants of fission and fusion are independent of total micelle concentration and, in the region of proper micelles, are independent of micelle size.36–38 In the ESI† we show that rate constants depend weakly on the total bile salt concentration, that the fusion rates are indeed independent of micelle size for all but the smallest aggregates, but that the fission rates depend on micelle size, and we discuss the implications of these findings in the context of the theoretical models used to interpret chemical relaxation times in micellar systems.3.4 Rate constants and free energy landscapes
For head–tail surfactants, simulations47,59 suggest that addition and removal of a monomer from a micelle is well-described via a single reaction coordinate, the distance, r, between monomer and micelle. The removal process is activated, being associated with large free energy barriers (8kBT, including the contribution of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(r) term47). In contrast, monomer addition is essentially barrierless: the rate constants for monomer fusion directly measured in simulations are large compared to the fusion rate for barrierless attachment estimated from the Smoluchowsky model (k+ = 4π(Rn + R1)(Dn + D1), where R are the radii and D are translational diffusion coefficients of a monomer or of a micelle of aggregation number n).59
ln(r) term47). In contrast, monomer addition is essentially barrierless: the rate constants for monomer fusion directly measured in simulations are large compared to the fusion rate for barrierless attachment estimated from the Smoluchowsky model (k+ = 4π(Rn + R1)(Dn + D1), where R are the radii and D are translational diffusion coefficients of a monomer or of a micelle of aggregation number n).59
To assess whether r is a reasonable reaction coordinate for bile salts as well, we compute the free energy, A(r), as a function of the distance between two aggregates, and relate this landscape with the fission and fusion rate constants, shown in the ESI.† We first calculate the probability, Pn,m(r), of finding monomers, dimers or trimers (m = 1, 2, 3) around aggregates of size n and then obtain A(r) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Pn,m(r)). We make the assumption that the free energy profile is not significantly affected by small changes in n, and calculate Pn,m(r) averaged over a narrow range of micelle sizes (n = 9–13). To obtain a free energy landscape that gives insight into fission and fusion, the function Pn,m(r) must include not only pairs of distinct aggregates with sizes m and n but also pairs of subaggregates of sizes m and n that are a part of a micelle of size n + m; therefore, Pn,m(r) is defined as
ln(Pn,m(r)). We make the assumption that the free energy profile is not significantly affected by small changes in n, and calculate Pn,m(r) averaged over a narrow range of micelle sizes (n = 9–13). To obtain a free energy landscape that gives insight into fission and fusion, the function Pn,m(r) must include not only pairs of distinct aggregates with sizes m and n but also pairs of subaggregates of sizes m and n that are a part of a micelle of size n + m; therefore, Pn,m(r) is defined as
 | (6) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) n,m(r) is the number of pairs of subaggregates of size m and n separated by distance r and belonging the same micelle (with size n + m); Nn,m and
n,m(r) is the number of pairs of subaggregates of size m and n separated by distance r and belonging the same micelle (with size n + m); Nn,m and ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) n,m are the analogous quantities summed over all r. Each micelle with size n + m is arbitrarily divided into a single pair of subaggregates of sizes m and n, so
n,m are the analogous quantities summed over all r. Each micelle with size n + m is arbitrarily divided into a single pair of subaggregates of sizes m and n, so ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) n,m is equal to the number of micelles of size n + m in the simulation box. We note that, because Pn,m(r) does not include a 1/(4πr2) term, A(r) includes the ideal gas contribution to the free energy, i.e., the entropic term 2
n,m is equal to the number of micelles of size n + m in the simulation box. We note that, because Pn,m(r) does not include a 1/(4πr2) term, A(r) includes the ideal gas contribution to the free energy, i.e., the entropic term 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(r).
ln(r).
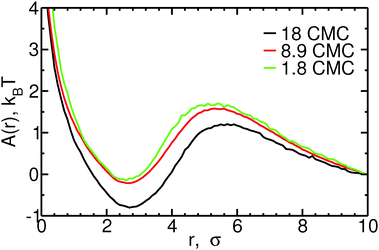
Fig. 4 shows the free energy profiles as a function of the distance r between micelles and monomers, for different bile salt concentrations. Both fusion and fission of monomers to/from micelles are associated with low free energy barriers. For monomer fusion, the free energy difference between r = 10σ and the maximum in A(r) (at r = 5–6σ, depending on the concentration) is of order 1–2kBT in all cases. This low barrier is consistent with the fact that the rates we measure are large compared to the fusion rate for barrierless attachment estimated from the Smoluchowsky model. The fission of monomers from micelles is also associated with low free energy barriers: e.g., at 8.9 CMC, A(r = 5.5σ) − A(r = 2.5σ) ≈ 2kBT. For both fission and fusion events, the free energy barriers have large contributions from the ideal gas term (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(r)). The free energy barrier associated with fission of monomers from micelles increases slightly with increasing concentration – less than 0.5kBT between 1.8 and 18 CMC – an increase which is quantitatively consistent with the observed decrease in monomer fission rates shown in the ESI;† the opposite trend is seen for the free energy barrier of fusion of monomers to micelles, consistent with the larger monomer fusion rates observed at higher concentrations. The reasonable agreement between the trends in fission and fusion rate constants and those in the one dimensional free energy profiles shown in Fig. 4 thus suggests that to understand addition or removal of monomers to/from micelles, it is sufficient to consider only the reaction coordinate r. In the ESI,† we show that this coordinate is also sufficient to describe addition and removal of oligomers to/from micelles.
ln(r)). The free energy barrier associated with fission of monomers from micelles increases slightly with increasing concentration – less than 0.5kBT between 1.8 and 18 CMC – an increase which is quantitatively consistent with the observed decrease in monomer fission rates shown in the ESI;† the opposite trend is seen for the free energy barrier of fusion of monomers to micelles, consistent with the larger monomer fusion rates observed at higher concentrations. The reasonable agreement between the trends in fission and fusion rate constants and those in the one dimensional free energy profiles shown in Fig. 4 thus suggests that to understand addition or removal of monomers to/from micelles, it is sufficient to consider only the reaction coordinate r. In the ESI,† we show that this coordinate is also sufficient to describe addition and removal of oligomers to/from micelles.
4 Concluding remarks
The coarse-grained model of bile salts used in this work has modest computational cost, enabling the investigation of the mechanisms by which pure bile micelles change aggregation number at concentrations near and far the critical micellar concentration via straightforward Langevin dynamics simulations. The model used in this study may be easily modified to represent head–tail surfactants typical of dietary mixed micelles, other nutrients or drugs, allowing the investigation of unanswered questions important to understand the physical chemistry of digestion: e.g., the mechanisms of nutrient or drug uptake and release by dietary mixed micelles, the role of association of phospholipids with bile salts on the protection of cellular membranes against solubilization, the mechanism of destruction of mitochondrial membranes in cholestatic patients and, more generally, the interpretation of experimental data reporting on the structure and dynamics of mixed micelles, which currently cannot be unambiguously interpreted.60–62 These models may also be used to understand the general trends leading to improved solubilization of drugs and nutraceuticals in artificial DMM-like micelles for oral drug delivery, and the subsequent interaction of these carrier vehicles with DMMs.7,63 Detailed studies of micelle formation using models with explicit solvent, either all-atom or coarse-grained, are currently only possible at concentrations much higher than the physiologically relevant range;6,64,65 only with implicit solvent, coarse-grained models do the physiologically relevant length- and time-scales become accessible.31,66–68Our results indicate that the dominant mechanism of micelle size change in bile salt solutions is monomer addition or removal, even at concentrations 18 times higher than the critical micellar concentration, in agreement with recent ultrasonic studies of the kinetics of bile salt micelles.58 The simulations do not support the popular assumption that bile micelles predominantly form in a two-stage process, by formation of oligomers and subsequent oligomer fusion to produce larger micelles. Addition of monomers to micelles is nearly barrierless, similarly to head–tail surfactants, and the free energy barrier to monomer removal is of order 2kBT, i.e., much lower than the 8kBT found for head–tail surfactants.47
We propose that the low free energy barrier associated with removal of monomers from bile micelles plays a role during digestion. Solubilization of fats by surfactant micelles occurs typically via two mechanisms:69,70 (i) for fats with sizable solubility in water, micelles can capture fat molecules dissolved in the solution; (ii) when fats are poorly soluble, the surfactant must first adsorb at the surface of the fat droplet, and subsequently a micelle containing both surfactant and fat is formed and desorbs from the fat droplet. This second mechanism, however, is only effective for non-ionic surfactants or ionic surfactants at high ionic strength; when ionic surfactants are present in solutions with low ionic strength, the electrostatic repulsion between surfactant micelles and partially covered fat droplets prevents further adsorption of the micelles. We speculate that the low free energy barrier associated with fission of bile monomers combined with the high CMC of bile salts may increase the effectiveness of solubilization of fats via mechanism (ii): these two properties of bile salts enable them to more rapidly cover the surface of fat droplets, because the electrostatic repulsion between single bile monomers and a fat droplet partially covered with bile salts is much smaller than that between the fat droplet and a micelle. A recent simulation study of the solubilization of a phospholipid vesicle by sodium cholate using a coarse-grained model similar to ours suggests that adsorption of monomeric bile salts to a phospholipid vesicle is indeed fast.66
Acknowledgements
The work of the FOM Institute is part of the research program of FOM and is made possible by financial support from the Netherlands organization for Scientific Research (NWO). DF acknowledges financial support from the Royal Society of London (Wolfson Merit Award), from Senter-Novem and the Dutch Ministry of Economic Affairs through the Food & Nutrition Delta 2 Program (grant DFN0642300) for a joint FOM-Unilever project, and from the ERC (Advanced Grant agreement 227758). We thank SARA Computing and Networking Services (http://www.sara.nl) for their support in using the Lisa and Huygens Compute Clusters. AVV thanks Mr Francesco Bonazzi, Mr Sadra Kashef Ol Gheta and Dr Krassimir Velikov (UNILEVER) for helpful discussions in the course of the project.References
- A. F. Hofmann, Biochem. J., 1963, 89, 57–68 CrossRef CAS PubMed.
- The Bile Acids: Chemistry, Physiology, and Metabolism, ed. P. Nair and D. Kritchevsky, Plenum Press, New York, London, 1971, vol. 1: Chemistry Search PubMed.
- The Bile Acids – Chemistry, Physiology, and Metabolism, ed. P. Nair and D. Kritchevski, Plenum Press, New York, London, 1973, vol. 2: Physiology and Metabolism Search PubMed.
- T. S. Wiedmann and L. Kamel, J. Pharm. Sci., 2002, 91, 1743–1764 CrossRef CAS PubMed.
- J. Maldonado-Valderrama, P. Wilde, A. Macierzanka and A. Mackie, Adv. Colloid Interface Sci., 2011, 165, 36–46 CrossRef CAS PubMed.
- P. Prakash, A. Sayyed-Ahmad, Y. Zhou, D. E. Volk, D. G. Gorenstein, E. Dial, L. M. Lichtenberger and A. A. Gorfe, Biochim. Biophys. Acta, 2012, 1818, 3040–3047 CrossRef CAS PubMed.
- Y. S. R. Elnaggar, Int. J. Nanomed., 2015, 10, 3955–3971 CrossRef CAS PubMed.
- S. R. Euston, W. G. Baird, L. Campbell and M. Kuhns, Biomacromolecules, 2013, 14, 1850–1858 CrossRef CAS PubMed.
- L. Galantini, M. C. di Gregorio, M. Gubitosi, L. Travaglini, J. Vazquez Tato, A. Jover, F. Meijide, V. H. Soto Tellini and N. V. Pavel, Curr. Opin. Colloid Interface Sci., 2015, 20, 170–182 CrossRef CAS.
- S. Lin and D. Blankschtein, J. Phys. Chem. B, 2010, 114, 15616–15625 CrossRef CAS PubMed.
- D. Kiriya, K. Chen, H. Ota, Y. Lin, P. Zhao, Z. Yu, T.-J. Ha and A. Javey, J. Am. Chem. Soc., 2014, 136, 11188–11194 CrossRef CAS PubMed.
- R. Barnadas-Rodriguez and J. Cladera, Langmuir, 2015, 31, 8980–8988 CrossRef CAS PubMed.
- T. Odahara, Biochim. Biophys. Acta, 2004, 1660, 80–92 CrossRef CAS.
- M. le Maire, P. Champeil, J. V. Møller and V. Jesper, Biochim. Biophys. Acta, 2000, 1508, 86–111 CrossRef CAS.
- G. G. Privé, Methods, 2007, 41, 388–397 CrossRef PubMed.
- A. M. Seddon, P. Curnow and P. J. Booth, Biochim. Biophys. Acta, 2004, 1666, 105–117 CrossRef CAS PubMed.
- D. M. Small, Adv. Chem. Ser., 1968, 84, 31–51 CrossRef.
- N. A. Mazer, M. C. Carey, R. F. Kwasnick and G. B. Benedek, Biochemistry, 1979, 18, 3064–3075 CrossRef CAS PubMed.
- A. Roda, A. F. Hofmann and K. J. Mysels, J. Biol. Chem., 1983, 258, 6362–6370 CAS.
- W. Spivak, C. Morrison, D. Devinuto and W. Yuey, Biochem. J., 1988, 252, 275–281 CrossRef CAS PubMed.
- N. Funasaki, R. Ueshiba, S. Hada and S. Neya, J. Phys. Chem., 1994, 98, 11541–11548 CrossRef CAS.
- N. Funasaki, S. Hada and S. Neya, J. Phys. Chem. B, 1999, 103, 169–172 CrossRef CAS.
- P. Garidel, A. Hildebrand, R. Neubert and A. Blume, Langmuir, 2000, 16, 5267–5275 CrossRef.
- N. Funasaki, M. Nomura, S. Ishikawa and S. Neya, J. Phys. Chem. B, 2000, 104, 7745–7751 CrossRef CAS.
- N. Funasaki, M. Fukuba, T. Kitagawa, M. Nomura, S. Ishikawa, S. Hirota and S. Neya, J. Phys. Chem. B, 2004, 108, 438–443 CrossRef CAS.
- N. Funasaki, M. Fukuba, T. Hattori, S. Ishikawa, T. Okuno and S. Hirota, Chem. Phys. Lipids, 2006, 142, 43–57 CrossRef CAS PubMed.
- D. Madenci and S. U. Egelhaaf, Curr. Opin. Colloid Interface Sci., 2010, 15, 109–115 CrossRef CAS.
- L. Partay, M. Sega and P. Jedlovszky, Langmuir, 2008, 24, 10729–10736 CrossRef CAS PubMed.
- L. B. Partay, P. Jedlovszky and M. Sega, J. Phys. Chem. B, 2007, 111, 9886–9896 CrossRef CAS PubMed.
- L. Partay, M. Sega and P. Jedlovszky, Langmuir, 2007, 23, 12322–12328 CrossRef CAS PubMed.
- A. Vila Verde and D. Frenkel, Soft Matter, 2010, 6, 3815–3825 RSC.
- A. Maestre, P. Guardado and M. Luisa Moya, J. Chem. Eng. Data, 2014, 59, 433–438 CrossRef CAS.
- N. E. Olesen, P. Westh and R. Holm, J. Colloid Interface Sci., 2015, 453, 79–89 CrossRef CAS PubMed.
- K. Kumar, B. S. Patial and S. Chauhan, J. Chem. Thermodyn., 2015, 82, 25–33 CrossRef CAS.
- Y. Yang and D. J. McClements, J. Colloid Interface Sci., 2013, 405, 312–321 CrossRef CAS PubMed.
- E. A. G. Aniansson and S. N. Wall, J. Phys. Chem., 1974, 78, 1024–1030 CrossRef CAS.
- E. A. G. Aniansson and S. N. Wall, J. Phys. Chem., 1975, 79, 857–858 CrossRef CAS.
- E. A. G. Aniansson, S. N. Wall, M. Almgren, H. Hoffmann, I. Kielmann, W. Ulbricht, R. Zana, J. Lang and C. Tondre, J. Phys. Chem., 1976, 80, 905–922 CrossRef CAS.
- G. C. Kresheck, E. Hamori, G. Davenport and H. A. Scheraga, J. Am. Chem. Soc., 1966, 88, 246–253 CrossRef CAS.
- M. Kahlweit, J. Colloid Interface Sci., 1982, 90, 92–99 CrossRef CAS.
- A. Patist, J. R. Kanicky, P. K. Shukla and D. O. Shah, J. Colloid Interface Sci., 2002, 245, 1–15 CrossRef CAS PubMed.
- S. V. Burov, A. A. Vanin and E. N. Brodskaya, J. Phys. Chem. B, 2009, 113, 10715–10720 CrossRef CAS PubMed.
- P. Ekwall, K. Fontell and A. Sten, Proceedings of Second International Congress of Surface Activity, London, 1957, pp. 357–373 Search PubMed.
- D. G. Oakenfull and L. R. Fisher, J. Phys. Chem., 1977, 81, 1838–1841 CrossRef CAS.
- D. G. Oakenfull and L. R. Fisher, J. Phys. Chem., 1978, 82, 2243–2245 CrossRef.
- L. R. Fisher and D. G. Oakenfull, J. Phys. Chem., 1980, 84, 936–937 CrossRef CAS.
- R. Pool and P. G. Bolhuis, Phys. Rev. Lett., 2006, 97, 018302 CrossRef PubMed.
- P. G. Bolhuis and D. Frenkel, Phys. A, 1997, 244, 45–58 CrossRef CAS.
- R. Pool and P. G. Bolhuis, J. Phys. Chem. B, 2005, 109, 6650–6657 CrossRef CAS PubMed.
- I. R. Cooke and M. Deserno, Biophys. J., 2006, 91, 487–495 CrossRef CAS PubMed.
- I. R. Cooke, K. Kremer and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011506 CrossRef PubMed.
- B. C. Stephenson, K. A. Stafford, K. J. Beers and D. Blankschtein, J. Phys. Chem. B, 2008, 112, 1634–1640 CrossRef CAS PubMed.
- J. T. James and I. A. Dubery, Molecules, 2009, 14, 3922–3941 CrossRef CAS PubMed.
- H. J. Limbach, A. Arnold, B. A. Mann and C. Holm, Comput. Phys. Commun., 2006, 174, 704–727 CrossRef CAS.
- B. Lindman, Hepatology, 1984, 4, 103S–109S CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- T. Bickel, Phys. A, 2007, 377, 24–32 CrossRef.
- G. Ravichandran and D. Gopinath, J. Mol. Liq., 2014, 198, 122–127 CrossRef CAS.
- G. Mohan and D. I. Kopelevich, J. Chem. Phys., 2008, 128, 044905 CrossRef PubMed.
- G. Mangiapia, G. D'Errico, F. Capuano, O. Ortona, R. K. Heenan, L. Paduano and R. Sartorio, Phys. Chem. Chem. Phys., 2011, 13, 15906–15917 RSC.
- W. A. Birru, D. B. Warren, A. Ibrahim, H. D. Williams, H. Benameur, C. J. H. Porter, D. K. Chalmers and C. W. Pouton, Mol. Pharmaceutics, 2014, 11, 2825–2834 CrossRef CAS PubMed.
- S. Schulz, S. Schmitt, R. Wimmer, M. Aichler, S. Eisenhofer, J. Lichtmannegger, C. Eberhagen, R. Artmann, F. Tookos, D. Walch, A. Krappmann, C. Brenner, C. Rust and H. Zischka, Biochim. Biophys. Acta, 2013, 1828, 2121–2133 CrossRef CAS PubMed.
- R. Vashishat, R. Sanan and R. K. Mahajan, RSC Adv., 2015, 5, 72132–72141 RSC.
- D. B. Warren, D. K. Chalmers, K. Hutchison, W. B. Dang and C. W. Pouton, Colloids Surf., A, 2006, 280, 182–193 CrossRef CAS.
- P. Prakash and A. A. Gorfe, Biochemistry, 2013, 52, 7461–7469 CrossRef CAS PubMed.
- H.-J. Mögel, M. Wahab, R. Schmidt and P. Schiller, Chem. Lett., 2012, 41, 1066–1068 CrossRef.
- M. Haustein, P. Schiller, M. Wahab and H.-J. Mögel, J. Solution Chem., 2014, 43, 1755–1770 CrossRef CAS.
- M. Haustein, M. Wahab, H.-J. Mögel and P. Schiller, Langmuir, 2015, 31, 4078–4086 CrossRef CAS PubMed.
- P. D. Todorov, P. A. Kralchevsky, N. D. Denkov, G. Broze and A. Mehreteab, J. Colloid Interface Sci., 2002, 245, 371–382 CrossRef CAS PubMed.
- S. Ariyaprakai and S. R. Dungan, Langmuir, 2008, 24, 3061–3069 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00763e |
| ‡ Previously at the FOM institute AMOLF, Science Park 102, 1098 XG Amsterdam, The Netherlands. |
| This journal is © The Royal Society of Chemistry 2016 |