Open Access Article
Open Access ArticleStatic and dynamic behaviour of responsive graphene oxide–poly(N-isopropyl acrylamide) composite gels
B.
Berke
ab,
O.
Czakkel
*a,
L.
Porcar
a,
E.
Geissler
c and
K.
László
b
aInstitut Laue Langevin, CS 20156, F – 38042 Grenoble Cedex 9, France. E-mail: czakkel@ill.eu; Tel: +33 476207182
bDepartment of Physical Chemistry and Materials Science, Budapest University of Technology and Economics, 1521, Budapest, Hungary
cLaboratoire Interdisciplinaire de Physique, CNRS and Université Grenoble Alpes, 38000 Grenoble, France
First published on 28th July 2016
Abstract
Thermoresponsive hydrogels have enormous potential e.g., as sensors, actuators, and pollution control remedies or in drug delivery systems. Nevertheless, their application is often restricted by physical limitations (poor mechanical strength and uncontrolled thermal response). Composite systems may offer a means of overcoming these limitations. This paper presents a systematic study of the structure and dynamics of graphene oxide–poly-(N-isopropylacrylamide) composite systems, and investigates the effect of the nanoparticle filler content on the mechanical and swelling properties of the systems. A combination of macroscopic (swelling and elastic modulus) and microscopic (differential scanning microcalorimetry, small angle neutron scattering and neutron spin-echo spectroscopy) investigations reveals that the architecture of the polymer network is modified by chain nucleation at the surface of the GO platelets, and these form a percolating network inside the gel. Our results show that the elastic modulus of the gels is reinforced by the filler, but the mobility of the polymer chains in the swollen state is practically unaffected. The macroscopic deswelling of the composites, however, is slowed by the kinetics of ordering in the GO network.
Introduction
Responsive hydrogels are three-dimensional polymer networks with high water content.1,2 They exhibit a reversible volume phase transition (VPT) under certain conditions.3,4 This response can be induced by changing the environment, such as the nature of the swelling medium (composition,5 pH6), temperature,7 electromagnetic field,8etc. Among temperature sensitive responsive hydrogels those based on poly-(N-isopropylacrylamide) (PNIPA) are distinguished by their peculiar volume phase transition temperature (TVPT) around 34 °C, close to the temperature of the human body.9,10 In the VPT of PNIPA, the swelling medium of the polymer, along with its dissolved ions, molecules, or drugs, is released into the surroundings. This property opens the route to various applications that require targeted delivery of drugs. The gels are relatively deformable and – owing to their high water content and the physiochemical similarity of the network to the native extracellular matrix – are potentially biocompatible.Although their properties make them excellent candidates for applications in drug delivery,10,11 sensors,12 actuators,13,14 microvalves15 and pollution control, they have certain drawbacks. Their poor mechanical strength for example bars their use in load-bearing applications. Limited drug uptake and its non-uniform distribution within the system, particularly in the case of hydrophobic drugs, could also compromise certain applications. Furthermore, high water content combined with very wide pores often results in uncontrolled and/or undesirably rapid drug release,16,17 which can be detrimental in targeted drug delivery systems.
These challenges may conceivably be overcome by composite hydrogels. Carbon nanoparticles are widely used as polymer fillers, with a positive impact both on the physical and the chemical properties of composites. Moreover, their density is low and they are easily recycled. Carbon black, consisting of almost pure elemental carbon, has been the most commonly used carbon filler for many years.18 Graphite has also been used for a long time, mainly to enhance the thermal and electrical conductivity of polymers.19 Recent developments in nanotechnology have raised interest in polymer composites containing carbon nanofibers and nanotubes. The carbon nanoparticles that have been the most intensely studied in the past few years are graphene and its derivatives.19–22 Nanocomposites containing members of the graphene family, especially graphene oxide (GO),23–25 have become the focus of interest. GO is considered to be non-toxic and highly biocompatible,26 which favours its use in biomedical applications. Moreover, incorporation of GO gives visible27 or near infrared light sensitivity to the composite systems,28–30 which extends their potential, for example, as NIR controlled microvalves, artificial muscles or actuators. Potential applications are numerous, but the detailed properties of graphene-based composites remain to be explored. In recent years several groups have reported on GO containing PNIPA gels [e.g. see ref. 23–25, 28 and 31–35], but direct comparison of the results is difficult, as the preparation methods differ significantly. The majority of the studies have addressed PNIPA systems of relatively high cross-link density ([monomer]/[cross-linker] ≤ 100), and functionalised GO nanoparticles are often used to ensure first order bond formation.23,24 Studies using as-prepared GO as a filler have also been made.
In addition to the structural characteristics and direct information about drug release efficiency,10,36 knowledge of the dynamics of nanocomposite systems is of crucial importance for sensing and controlled release applications. Such investigations could, however, prove difficult at the nanoscale level, owing to the limited number of appropriate methods. Dynamic light scattering (DLS) is a widely used technique for investigating dynamics in gels,37,38 but it is inapplicable to non-transparent systems, such as those containing carbon nanoparticles. Neutron spin-echo (NSE) spectroscopy39 can overcome these difficulties. The NSE technique is well suited for measuring slow (nanosecond timescale) dynamics in soft matter systems, with the highest energy resolution among all types of neutron spectrometers. It has proved to be an excellent tool for investigating dynamics in polymer gels.40–45 It has been a fertile source of important new insights into polymer melt–silica nanocomposite systems,46,47 but to our knowledge, no investigation of PNIPA hydrogel composite systems using NSE has yet been reported in the literature.
Here we present a systematic study of the structural and dynamical properties of GO containing PNIPA hydrogels in which results from macroscopic [elastic modulus measurements and differential scanning microcalorimetry (MicroDSC)] and microscopic [small angle neutron scattering (SANS) and NSE] length scales are compared.
Experimental
Graphene oxide (GO)
Graphene oxide (GO) was obtained by the improved Hummers' method48 from natural graphite (Graphite Tyn, GK, China). The GO suspension was purified and mildly exfoliated by centrifuging 5 times (7000g) from 1 M HCl and 6–9 times (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100g) from doubly distilled water, in order to remove unreacted graphite and inorganic salts. After the final washing and centrifugation step a light brown suspension with a GO nanoparticle content of ∼1 w/w% was obtained. Its C/O ratio, determined by XPS, was 2.2.
100g) from doubly distilled water, in order to remove unreacted graphite and inorganic salts. After the final washing and centrifugation step a light brown suspension with a GO nanoparticle content of ∼1 w/w% was obtained. Its C/O ratio, determined by XPS, was 2.2.
Gel synthesis
The PNIPA polymer gel was synthesised from the N-isopropylacrylamide (NIPA) monomer (Tokyo Chemical Industry, Japan) and the N,N′-methylenebisacrylamide (BA) cross-linker (Sigma Aldrich) in aqueous medium at 20 °C by free radical polymerization. The reaction was initiated by ammonium persulphate (APS, Sigma Aldrich) and N,N,N′,N′-tetramethylethylenediamine (TEMED, Fluka). For the synthesis of a pure PNIPA gel with a cross-linking ratio [NIPA]/[BA] = 150, 18.75 ml of a 1 M aqueous solution of NIPA and 1.225 ml of a 0.1 M solution of BA were mixed with 4.9 ml of water and 25 μl of TEMED. Finally, 1.25 ml of a 10 w/w% solution of APS was added to the mixture, and polymerization took place at 20 °C. Films of thickness 2 and 4 mm and 10 × 10 mm isometric cylinders were prepared. All chemicals were used as received, except NIPA, which was recrystallized from a toluene–hexane mixture. Doubly distilled water was used for the synthesis, purification and measurements.38 To obtain hybrid gels with <20 mg of GO/g NIPA content the aqueous GO suspension of the required concentration was mixed with the precursor solution of the gel. The total volume of the precursor solution, including the GO suspension, was kept constant by adding the appropriate complement of water. Gels with the highest filler content (21 mg GO/g NIPA) were prepared by adding solid NIPA and BA directly to the GO suspension. The reaction medium was stirred in an ice-bath for 15 min after addition of each component. GO filled samples were polymerised and purified in the same way as the nanoparticle-free system. The nomenclature of the samples is listed in Table 1.| Sample name | GO content (mg GO/g NIPA) |
|---|---|
| PNIPA | 0 |
| 5GO@PNIPA | 5.25 |
| 10GO@PNIPA | 10.50 |
| 15GO@PNIPA | 15.75 |
| 20GO@PNIPA | 21.00 |
Macroscopic characterisation
For the swelling experiments gel disks of diameter of 7 mm were cut from a 2 mm thick film. Prior to the experiment the disks were dried in order to determine their dry mass (m0), and then reswollen in excess doubly distilled water thermostated at 20.0 ± 0.2 °C for one week. The equilibrium swelling degree was defined as m/m0, where m is the mass of the swollen samples.The elastic modulus was measured on fully swollen isometric gel cylinders using an INSTRON 5543 mechanical testing instrument at ambient temperature. Samples were compressed by 10% of their initial height in steps of 0.1 mm with a relaxation time of 4 × 4 s and a force threshold of 300 N. No barrel distortion was observed.
The macroscopic thermal response of the systems was tested by placing the samples (30 mm × 40 mm, 4 mm thick, fully swollen in D2O at 25 °C) in closed quartz containers in an incubation oven at 41 °C for 3 weeks.
Differential scanning microcalorimetry (MicroDSC)
Scanning microcalorimetry measurements were made on ground samples using a MicroDSCIII apparatus (SETARAM, France). About 10 mg of dry gel sample were placed in contact with 500 μl of Millipore water and kept at 20 °C for 2 h to allow the gels to equilibrate in the swollen state and to obtain a stable baseline. The samples were heated to 50 °C at 0.03 °C per min scanning rate. Determination of the peak position and calculation of the specific enthalpy of the volume phase transition (ΔHVPT) were performed using instrument software.Neutron spin-echo (NSE) measurements
NSE measurements49 were made on a IN11 spectrometer at the Institut Laue-Langevin (Grenoble, France) in the IN11A high-resolution set-up. For these experiments gel films of 4 mm nominal thickness and 3 × 4 cm cross-section were used. Prior to the measurements, the gel samples were dried, and then reswollen in excess D2O for at least 3 days at 25.0 ± 0.1 °C. Previous measurements50 had shown that the swelling properties of the PNIPA gel are not affected by the H2O/D2O isotopic substitution. The swollen samples were placed in 5 mm thick sandwich-type cells with quartz windows. To exclude air and avoid deswelling, the remaining space in the sample holder was filled with D2O. Measurements were performed at 25.0 ± 0.1 °C in the transfer vector Q-range 0.042 Å−1 ≤ Q ≤ 0.209 Å−1, where Q = (4π/λ)sin(θ/2), λ being the incident wavelength of the neutrons (7.83 Å) and θ the scattering angle. The Fourier-time range covered was 0.1–30 ns. The resolution functions of the instrument were determined for the different experimental conditions using the elastic scattering of graphite. The NSE method measures directly the intermediate scattering function I(Q,τ) as a function of Q and the Fourier time τ, i.e., it yields directly the time dependence of the density–density autocorrelation function.51 The resulting intermediate scattering functions were corrected for the D2O background dynamics.Small angle neutron scattering (SANS)
SANS measurements were performed on the D22 small angle instrument at the Institut Laue-Langevin. The gels were swollen in D2O in order to enhance the scattering contrast between the polymer and the matrix, and to minimize the incoherent background scattering. The incident neutron wavelength was 6 Å. Two sample-detector distances (17 m and 2 m) were used to cover the Q-range 0.004–0.5 Å−1. Raw SANS data were corrected for the empty cell, dark counts, sample thickness and detector efficiency. The corrected scattering data were normalized by the incident beam flux to obtain the scattered intensity in absolute units. Data reduction was done using the GRASansP v.7.04 program.Results and discussion
Composite systems with various GO/polymer ratios were studied systematically. The influence of the nanoparticle content on the swelling ratio in pure water and on the elastic modulus of the composites is shown in Fig. 1.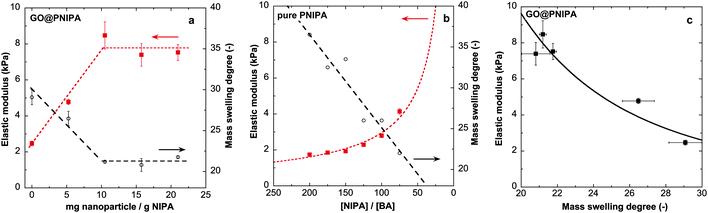 | ||
| Fig. 1 Equilibrium mass swelling degree in pure water at 20 °C and the elastic modulus of (a) GO@PNIPA hybrid gels and (b) the pure PIPA gel from ref. 52. Note that a high [NIPA]/[BA] molar ratio means low cross-link density. Broken lines are guides for the eye. (c) Correlation between the elastic modulus and the observed equilibrium swelling degree in GO@PNIPA systems. Solid line is a power law fit with an exponent of 3.2. | ||
Increasing the GO content drastically decreases the swelling degree and increases the elastic modulus (Fig. 1a). A similar trend is observed in pure PNIPA gels on increasing the cross-link density,52 but the shapes of the responses are different (Fig. 1a and b). Increasing the cross-link density of the PNIPA network (i.e., decreasing the molar ratio of [NIPA]/[BA]) monotonically changes the swelling degree and the elastic modulus, whereas when the GO loading is increased a plateau is observed in both quantities. Li also reported an increase in modulus when chemically modified GO is used as a co-monomer.23 In gels with higher cross-link density (molar ratio of [NIPA]/[BA] = 35 instead of 150), addition of unmodified GO to the precursor solution results in an opposite tendency in both the swelling ratio and elastic modulus.24,25 In the present systems the elastic modulus and the observed swelling ratio are strongly correlated (Fig. 1c). In pure PNIPA gels with different cross-link densities, the dependence of the modulus on the equilibrium polymer volume fraction ϕ (ϕ ≈ 1/(ρ × swelling ratio), taking ρ = 1.115 g cm−3 as the density of the dry polymer38) could be described by an apparent power law with an exponent of ∼2.07, as expected under good solvent conditions.52–54 In the GO@PNIPA systems the exponent is ∼3.2 (Fig. 1c), which could perhaps be interpreted as a sign of the theta solvent condition.55 This interpretation, however, is inconsistent with the rest of the observations. During the polymerisation the GO particles not only contribute to nucleating the reaction at their surfaces but also act as a filler in the network. With increasing GO content, the gel is reinforced by the filler and the architecture of the network is increasingly dominated by cross-link hypernodes, at the expense of the simple tetrafunctional cross-link structure that prevails with N,N′-methylenebisacrylamide alone. At the percolation threshold, the GO particles establish an interpenetrating network inside that of the polymer. Fig. 1a suggests that the percolation threshold of the GO occurs at a concentration of 10 mg g−1 dry PNIPA, i.e., roughly cp ≈ 0.5 mg g−1 of the swollen gel.
The MicroDSC measurements show that TVPT (33.8 °C) is unaffected by the presence of GO (Fig. 2), which implies that, while part of the polymer chains are tightly bound to the GO surface, the rest remain freely surrounded by solvent and subject to excluded volume conditions. This picture is corroborated by the fact that in the pure PNIPA gel the enthalpy of the phase transition is unaffected by changes in cross-link density,52 whereas when the GO content is increased ΔHVPT decreases monotonically (Table 2). The observed decrease in enthalpy by 18.9 J g−1 in the 20GO@PNIPA sample implies that 21 mg of GO reduce the number of free chains by 27%. This means that GO immobilises more than 10 times its own mass of PNIPA.
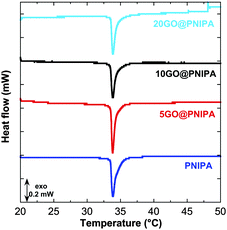 | ||
| Fig. 2 Differential scanning calorimetry results of PNIPA and GO@PNIPA gels. Curves are shifted vertically for clarity. | ||
| Sample | T VPT (°C) | ΔHVPT (J g−1 dry sample) |
|---|---|---|
| PNIPA | 33.8 | 70.4 |
| 5GO@PNIPA | 33.8 | 65.3 |
| 10GO@PNIPA | 33.8 | 54.6 |
| 20GO@PNIPA | 33.8 | 51.5 |
On the macroscopic scale the thermal responses of the two systems are substantially different (Fig. 3). Whereas the pure PNIPA gel reaches its fully deswollen state after less than 2 h of incubation at 41 °C, almost no size change is observed in the GO@PNIPA systems within this timescale. By contrast, at longer times the highest GO content sample responds most strongly to the temperature increase, with a final size smaller than that of pure PNIPA. This is an unexpected result, since it is known that pure PNIPA gels in their high temperature deswollen state contain a significant fraction of trapped microscopic water droplets.56 The present finding implies that the GO, by matching the hydrophobic/hydrophilic character of PNIPA, mediates the expulsion of the trapped water. However, the timescales are different in the two cases. In the pure PNIPA gel deswelling is governed by simple mechanical expulsion of the solvent,57 whereas deswelling in the filled system is slowed by the kinetics of the collapse and stacking of the GO filler network. It should nevertheless be emphasized that the smaller final swelling ratio of the filled gels is the consequence not of the cross-linking by the GO but rather of the improved evacuation of water from the network. This implies that, in the collapsed state, the PNIPA chains are oriented by the GO surfaces.
 | ||
| Fig. 3 Images of PNIPA and GO@PNIPA samples below (25 °C) and above (41 °C) the volume phase transition temperature at different incubation times. | ||
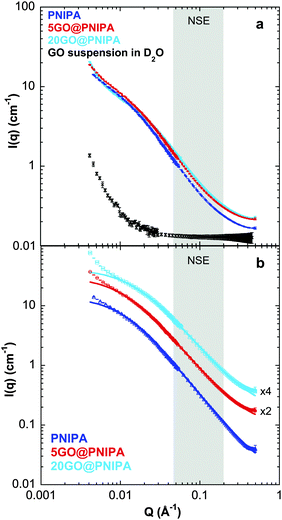
To explore the structural differences caused by incorporating GO into the polymer matrix, small angle neutron scattering (SANS) measurements were performed on selected samples. In scattering experiments the detected signal depends on the contrast between the particle and the solvent. In the case of neutron scattering this contrast is defined by the difference in scattering length density (ρ) between the components. The value of ρ of the PNIPA matrix is significantly different from that of the swelling medium, namely D2O (Table 3), resulting in a strong scattering signal. In the composite samples, which are ternary systems, the signal is still dominated by the PNIPA signal. As seen in Table 3 and Fig. 4a the neutron scattering contrast between GO and D2O is weak, and the overall signal therefore originates almost exclusively from the polymer, even in the composite systems.
| Component | ρ (10−6/Å2) |
|---|---|
| PNIPA (C6H11NO)n | 0.825 |
| GO C65O35 | 5.993 |
| D2O | 6.364 |
Small differences are visible in the shapes of the SANS response curves of the three investigated systems (Fig. 4a). The continuous lines through the background-subtracted data (Fig. 4b) are the modified Ornstein–Zernike (OZ) expression (eqn (1)),55,58 which yields a good fit to all three curves in the range Q > 0.01 Å−1. The deviation in the lowest Q region (Q < 0.01 Å−1) stems from the well-known concentration inhomogeneities due to cross-linking in gel networks.59 In the OZ model the scattered intensity can be described by
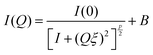 | (1) |
| Sample | D diff × 1011 (m2 s−1) | ξ H (Å) | ξ (Å) | Power law exponent |
|---|---|---|---|---|
| PNIPA | 7.03 ± 0.14 | 28.4 ± 0.01 | 92.0 ± 1.09 | 1.6 |
| 5GO@PNIPA | 7.41 ± 0.24 | 26.9 ± 0.08 | 90.0 ± 1.11 | 1.7 |
| 20GO@PNIPA | 8.10 ± 0.30 | 24.6 ± 0.9 | 66.7 ± 0.67 | 1.6 |
The exponent p = 5/3 in eqn (1) is also consistent with the excluded volume interaction for polymer chains in good solvent.54,55 In summary, the concentration dependence of the correlation length ξ and the excluded volume character of the exponent p imply that the network chain statistics of the gel on a length scale of 1/Q < 100 Å are not affected by the GO.
The dynamic behaviour of the PNIPA matrix was explored by neutron spin-echo (NSE) spectroscopy. The NSE method measures the energy transfer of neutrons at extremely high energy resolution as a phase shift in the Larmor precession of the neutron spins in a magnetic field.51 The intermediate scattering function I(Q,τ) is defined by eqn (2), as a function of Q and the Fourier time τ:
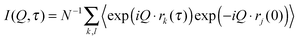 | (2) |
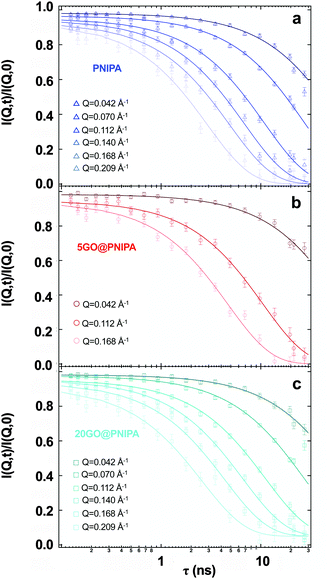 | ||
| Fig. 5 Experimental intermediate scattering functions from NSE with the corresponding single exponential fits for the pure PNIPA hydrogel, 5GO@PNIPA and 20GO@PNIPA composites, measured at 25 °C. | ||
In all three cases the curves I(Q,τ)/I(Q,0) can be fit by a single exponential function
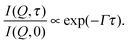 | (3) |
In the pure PNIPA gel (Fig. 5a) the curves decay to zero, indicative of practically ergodic behaviour, i.e., there is no frozen-in component.59Fig. 1 shows that GO affects the elastic properties of the composite systems on the macroscopic scale. At the microscopic level, by contrast, the NSE results indicate that the motion of the polymer chains is only partially affected. For 20GO@PNIPA, the intermediate scattering functions (Fig. 5c) decay to a baseline value of 0.05, which corresponds to 5% immobile fraction. The GO content of this sample is about 2 w/w% of the dry content, i.e., 0.1 w/w% of the swollen gel. Comparison of these findings with the microcalorimetry results of Table 1 suggests that the GO hypernodes may also partly immobilize the gel network immediately surrounding them. In the case of 5GO@PNIPA the NSE curves appear to decay to zero (Fig. 5b), as in the pure PNIPA gel. The GO content of this gel is about 0.5 w/w%. This implies a baseline of 0.005, which is beyond the accuracy of the measurements.
The measured relaxation rates (Γ = 1/τ) are proportional to Q2 (Fig. 6), characteristic of diffusive motion. The diffusion coefficient (Ddiff) is obtained directly from the linear fit
| Γ = Ddiff·Q2. | (4) |
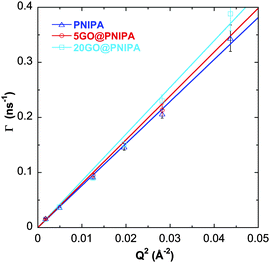 | ||
| Fig. 6 Relaxation rates (Γ) vs. Q2 for pure PNIPA, 5GO@PNIPA and 20GO@PNIPA. Solid lines are linear fits. | ||
With increasing GO content, owing to the lower degree of swelling, Ddiff increases slightly (Table 4). The hydrodynamic correlation length of the samples (ξH) is determined from the Stokes–Einstein relation
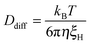 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60). Like the static correlation length, ξH decreases with increasing GO content (Table 4), albeit with a smaller exponent (ξH ∝ c−0.43) than predicted by scaling theory (Fig. 7), but consistent with dynamic light scattering measurements on pure PNIPA gels.52 This suggests that the dynamics of the polymer chains is hindered only marginally by the GO sheets.
60). Like the static correlation length, ξH decreases with increasing GO content (Table 4), albeit with a smaller exponent (ξH ∝ c−0.43) than predicted by scaling theory (Fig. 7), but consistent with dynamic light scattering measurements on pure PNIPA gels.52 This suggests that the dynamics of the polymer chains is hindered only marginally by the GO sheets.
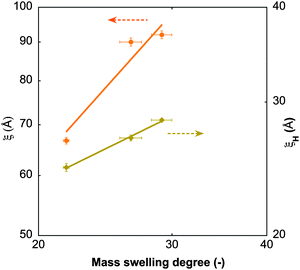 | ||
| Fig. 7 Static (ξ) and hydrodynamic (ξH) correlation lengths from SANS and NSE measurements at 25 °C, as a function of the mass swelling degree of the gels. Solid lines are power-law fits to the data. | ||
On combining these observations with macroscopic results we can conclude that GO forms a strong bonding with the PNIPA chains. As the GO concentration is low even at the highest loading, it does not affect the overall movement of the polymer chains. However, it does hinder their motion in the immediate surroundings. The reason for this may be that some of the PNIPA chains remain linked to the GO surface, even in the swollen state (Fig. 8).
Conclusions
Graphene oxide (GO) containing composite PNIPA gels were prepared and characterized both on the macro- and the nanoscale size range. Increasing the GO content reduces the swelling capacity and increases the elastic modulus of the gels. The relationship between the two properties can be described approximately by a power law with exponent ∼3.2. This unusual behaviour is attributed to changes in the architecture of the polymer gel with the build up of an interpenetrating GO network in which the polymer matrix develops through chain nucleation at the surface of the GO. This picture is consistent with MicroDSC measurements, which show that the volume phase transition temperature of the mobile PNIPA segments is unaffected by the presence of GO, while, conversely, as the amount of bound polymer increases with increasing GO content, the enthalpy of the volume phase transition decreases. The fraction of hindered chains that are prevented from participating in the VPT amounts to more than ten times the mass of the GO filler. In the composite gels, the GO mediates the evacuation of water in the high temperature collapsed state, which, in pure PNIPA, would otherwise remain trapped in the network in the form of microscopic droplets. This implies that the collapsed PNIPA chains are oriented by the GO surfaces. The neutron scattering observations in the swollen state show that, as the gel deswells with increasing GO content, the static polymer–polymer correlation length ξ decreases according to scaling theory. The shape of the neutron scattering response is also fully consistent with scaling predictions for excluded volume interactions. The hydrodynamic properties of the network chains measured by neutron spin-echo spectroscopy are also consistent with those of the unfilled polymer gels. The correlation functions obtained from this technique also display a static component that corresponds to about 5% of the network chains in the gel that are immobilised on the GO surface. It may be speculated that the platelet structure of the GO filler modifies the hydrodynamic flow field in the vicinity of the polymer chains. Numerical comparison between the neutron spin-echo measurements and the MicroDSC measurements suggests that not all the hindered PNIPA chains are necessarily immobilized on the surface of the GO. Crowding of the chains near the surface could give rise to partial associations, which would contribute to the reduction in enthalpy at the transition.Acknowledgements
The authors are grateful to the Institut Laue-Langevin for providing beamtime on the IN11 and D22 instruments. We thank Mr D. Renzy and Mr M. Jacques for technical assistance. The work was supported by the Hungarian grant OTKA K101861 (Hungarian Scientific Research Fund). This work is part of the scientific program “Development of quality-oriented and harmonized R+D+I strategy and functional model at BME” project supported by the New Széchenyi Plan (Project ID: TÁMOP-4.2.1/B-09/1/KMR-2010-0002).Notes and references
- N. K. Singh and D. S. Lee, J. Controlled Release, 2014, 193, 214 CrossRef CAS PubMed.
- J. Kopecek, Biomaterials, 2007, 28, 5185 CrossRef CAS PubMed.
- J. H. Bradbury, M. D. Fenn and I. Gosney, J. Mol. Biol., 1965, 11, 137 CrossRef CAS PubMed.
- M. Heskins and J. E. Guillet, J. Macromol. Sci., Part A: Pure Appl.Chem., 1968, 2, 1441 CrossRef CAS.
- T. Tanaka, Phys. Rev. Lett., 1978, 40, 820 CrossRef CAS.
- J. Ricka and T. Tanaka, Macromolecules, 1984, 17, 2916 CrossRef CAS.
- Y. H. Bae, T. Okano and S. Wan Kim, J. Polym. Sci., Part B: Polym. Phys., 1990, 28, 923 CrossRef CAS.
- S. Reinicke, S. Döhler, S. Tea, M. Krekhova, R. Messing, A. M. Schmidt and H. Schmalz, Soft Matter, 2010, 6, 2760 RSC.
- K. Depa, A. Strachota, M. Šlouf and J. Hromádková, Eur. Polym. J., 2012, 48, 1997 CrossRef CAS.
- D. C. Coughlan and O. I. Corrigan, Int. J. Pharm., 2006, 313, 163 CrossRef CAS PubMed.
- A. K. Bajpai, S. K. Shukla, S. Bhanu and S. Kankane, Prog. Polym. Sci., 2008, 33, 1088 CrossRef CAS.
- A. Kumar, A. Srivastava, I. Y. Galaev and B. Mattiasson, Prog. Polym. Sci., 2007, 32, 1205 CrossRef CAS.
- L. Ionov, Mater. Today, 2014, 17, 494 CrossRef.
- P. Kim, L. D. Zarzar, X. He, A. Grinthal and J. Aizenberg, Curr. Opin. Solid State Mater. Sci., 2011, 15, 236 CrossRef CAS.
- S. Sugiura, K. Sumaru, K. Ohi, K. Hiroki, T. Takagi and T. Kanamori, Sens. Actuators, A, 2007, 140, 176 CrossRef CAS.
- T. R. Hoare and D. S. Kohane, Polymer, 2008, 49, 1993 CrossRef CAS.
- S. B. Campbell and T. Hoare, Curr. Opin. Chem. Eng., 2014, 4, 1 CrossRef.
- M. Biron, Thermosets and Composites, Material Selection, Applications, Manufacturing and Cost Analysis, Elsevier, 2nd edn, 2013 Search PubMed.
- U. Szeluga, B. Kumanek and B. Trzebicka, Composites, Part A, 2015, 73, 204 CrossRef CAS.
- H. Kim, A. A. Abdala and C. W. Macosko, Macromolecules, 2010, 43, 6515 CrossRef CAS.
- K. K. Sadasivuni, D. Ponnamma, S. Thomas and Y. Grohens, Prog. Polym. Sci., 2014, 39, 749 CrossRef CAS.
- T. Kuilla, S. Bhadra, D. Yao, N. H. Kim, S. Bose and J. H. Lee, Prog. Polym. Sci., 2010, 35, 1350 CrossRef CAS.
- Z. Li, J. Shen, H. Ma, X. Lu, M. Shi, N. Li and M. Ye, Soft Matter, 2012, 8, 3139 RSC.
- C.-W. Lo, D. Zhu and H. Jiang, Soft Matter, 2011, 7, 5604 RSC.
- X. Ma, Y. Li, W. Wang, Q. Ji and Y. Xia, Eur. Polym. J., 2013, 49, 389 CrossRef CAS.
- G. Cirillo, S. Hampel, U. G. Spizzirri, O. I. Parisi, N. Picci and F. Iemma, BioMed Res. Int., 2014, 2014, 825017 Search PubMed.
- D. Kim, H. S. Leeb and J. Yoon, RSC Adv., 2014, 4, 25379 RSC.
- K. Shi, Z. Liu, Y. Y. Wei, W. Wang, X. J. Ju, R. Xie and L. Y. Chu, ACS Appl. Mater. Interfaces, 2015, 7, 27289 CAS.
- E. Manek, B. Berke, N. Miklósi, M. Sajbán, A. Domán, T. Fukuda, O. Czakkel and K. László, eXPRESS Polym. Lett., 2016, 10, 710–720 CrossRef.
- C.-H. Zhu, Y. Lu, J. Peng, J.-F. Chen and J.-H. Yu, Adv. Funct. Mater., 2012, 22, 4017 CrossRef CAS.
- Y. Wu, M. Cai, X. Pei, Y. Liang and F. Zhou, Macromol. Rapid Commun., 2013, 34, 1785–1790 CrossRef CAS PubMed.
- D. Kim, H. S. Lee and J. Yoon, Sci. Rep., 2016, 6, 20921 CrossRef CAS PubMed.
- V. Alzari, D. Nuvoli, S. Scognamillo, M. Piccinini, E. Gioffredi, G. Malucelli, S. Marceddu, M. Sechi, V. Sanna and A. Mariani, J. Mater. Chem., 2011, 21, 8727 RSC.
- L. Breuer, M. Raue, M. Kirschbaum, T. Mang, M. J. Schöning, R. Thoelen and T. Wagner, Phys. Status Solidi A, 2015, 212, 1368–1374 CrossRef CAS.
- D. Kim, H. S. Lee and J. Yoon, RSC Adv., 2014, 4, 25379 RSC.
- J. Kost and R. Langer, Adv. Drug Delivery Rev., 2012, 64, 327 CrossRef.
- E. Geissler, Dynamic Light Scattering from Polymer Gels, in Dynamic Light Scattering, ed. W. Brown, Clarendon Press, Oxford, 1993 Search PubMed.
- K. László, K. Kosik, C. Rochas and E. Geissler, Macromolecules, 2003, 36, 7771 CrossRef.
- F. Mezei, Neutron Spin Echo, in Lect. Notes Phys., ed. F. Mezei, vol. 128, 1980 Search PubMed.
- Y. Hertle, M. Zeiser, P. Fouquet, M. Maccarini and T. Hellweg, Z. Phys. Chem., 2014, 228, 1053 CrossRef CAS.
- T. Kanaya, N. Takahashi, K. Nishida, H. Seto, M. Nagao and T. Takeda, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 1 CrossRef PubMed.
- M. Shibayama, K. Nishi and T. Hiroi, Macromol. Symp., 2015, 348, 9 CrossRef CAS.
- T. Hellweg, K. Kratz, S. Pouget and W. Eimer, Colloids Surf., A, 2002, 202, 223 CrossRef CAS.
- S. Koizumi, M. Monkenbusch, D. Richter, D. Schwahn, B. Farago and M. Annaka, Appl. Phys. A: Mater. Sci. Process., 2002, 74, 399 CrossRef.
- C. Scherzinger, O. Holderer, D. Richter and W. Richtering, Phys. Chem. Chem. Phys., 2012, 14, 2762 RSC.
- G. J. Schneider, K. Nusser, L. Willner, P. Falus and D. Richter, Macromolecules, 2011, 44, 5857–5860 CrossRef CAS.
- K. Nusser, G. J. Schneider and D. Richter, Soft Matter, 2011, 7, 7988 RSC.
- D. C. Marcano, D. V. Kosynkin, J. M. Berlin, A. Sinitskii, Z. Sun, A. Slesarev, L. B. Alemany, W. Lu and J. M. Tour, ACS Nano, 2010, 4, 4806 CrossRef CAS PubMed.
- O. Czakkel, B. Berke, E. Geissler and K. László, Study of the internal dynamics of soft gel – carbon nanoparticle composite systems, Institut Laue-Langevin (ILL), DOI: 10.5291/ILL-DATA.9-12-374 Search PubMed.
- K. László, DSc dissertation, Hugarian Academy of Science, Budapest, 2005.
- Neutron Spin Echo Spectroscopy – Basics, Trends and Applications, ed. F. Mezei, C. Pappas and T. Gutberlet, Springer, Heidelberg, 2003 Search PubMed.
- K. László, K. Kosik and E. Geissler, Macromolecules, 2004, 37, 10067 CrossRef.
- F. Horkay and M. Zrínyi, Macromolecules, 1982, 15, 1306 CrossRef CAS.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, 1979 Search PubMed.
- L. S. Ornstein and F. Zernike, KNAW, Proceedings, 1914, 17(II), 793.
- K. László, A. Guillermo, A. Fluerasu, A. Moussaïd and E. Geissler, Langmuir, 2010, 26, 4415 CrossRef PubMed.
- K. László, A. Fluerasu, A. Moussaïd and E. Geissler, Soft Matter, 2010, 6, 4335 RSC.
- P. Pusey and W. van Meegen, Physica A, 1989, 157, 705 CrossRef CAS.
- E. Geissler, F. Horkay and A. M. Hecht, Phys. Rev. Lett., 1993, 71, 645 CrossRef CAS PubMed.
- A. Vértes, S. Nagy, Z. Kulcsár, R. G. Lovas and F. Rösch, Handbook of Nuclear Chemistry, Springer, Dordrecht, Heidelberg, London, New York, 2011 Search PubMed.
| This journal is © The Royal Society of Chemistry 2016 |