Open Access Article
Open Access ArticleUpper bound on the Edwards entropy in frictional monodisperse hard-sphere packings
Vasili
Baranau
a,
Song-Chuan
Zhao
b,
Mario
Scheel
cd,
Ulrich
Tallarek
*a and
Matthias
Schröter
 *ef
*ef
aDepartment of Chemistry, Philipps-Universität Marburg, Hans-Meerwein-Strasse 4, D-35032 Marburg, Germany. E-mail: tallarek@staff.uni-marburg.de; Fax: +49-6421-28-27065; Tel: +49-6421-28-25727
bPhysics of Fluids, MESA + Institute for Nanotechnology, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
cESRF, The European Synchrotron, 71 Rue des Martyrs, 38000 Grenoble, France
dSynchrotron Soleil, L'Orme des Merisiers, 91190 Saint-Aubin, France
eMax Planck Institute for Dynamics and Self-Organization (MPIDS), 37077 Goettingen, Germany. E-mail: matthias.schroeter@ds.mpg.de
fInstitute for Multiscale Simulation, Friedrich-Alexander-Universität, 91052 Erlangen, Germany
First published on 15th March 2016
Abstract
We extend the Widom particle insertion method [B. Widom, J. Chem. Phys., 1963, 39, 2808–2812] to determine an upper bound sub on the Edwards entropy in frictional hard-sphere packings. sub corresponds to the logarithm of the number of mechanically stable configurations for a given volume fraction and boundary conditions. To accomplish this, we extend the method for estimating the particle insertion probability through the pore-size distribution in frictionless packings [V. Baranau, et al., Soft Matter, 2013, 9, 3361–3372] to the case of frictional particles. We use computer-generated and experimentally obtained three-dimensional sphere packings with volume fractions φ in the range 0.551–0.65. We find that sub has a maximum in the vicinity of the Random Loose Packing Limit φRLP = 0.55 and decreases then monotonically with increasing φ to reach a minimum at φ = 0.65. Further on, sub does not distinguish between real mechanical stability and packings in close proximity to mechanical stable configurations. The probability to find a given number of contacts for a particle inserted in a large enough pore does not depend on φ, but it decreases strongly with the contact number.
1 A statistical mechanics approach to granular media
While granular materials are ubiquitous in our daily lives, we still lack a comprehensive theory describing their behaviour. The underlying problem stems from their mesoscopic size (typically several hundred micrometers). In consequence, granular systems are athermal, i.e. thermal fluctuations are orders of magnitudes smaller than the potential energy of the particles in a gravitational field. Also, they are dissipative as collisions and sliding contacts excite internal degrees of freedom which irreversibly convert the kinetic energy of the particles into heat. Finally, all contacts between particles are frictional, i.e. the contact forces between particles have tangential components.Still, if granular materials are dilute, which means that their volume fraction φ is smaller than a few percent, their dynamics can be well described by an appropriately extended kinetic theory, which has by now reached the maturity level of text books.1
But the question if dense systems with φ ≥ 0.55 can also be described with the toolkit of statistical mechanics is still open to debate. One of the first suggestions that this might be the case was made by Sam Edwards and coworkers in two seminal papers.2,3 They suggested that due to the dissipative nature of granular systems the role of the conserved quantity should be played by the volume of the system. Assuming that there exists some type of dynamics which samples all mechanically stable states of the system equiprobably, they defined a configurational entropy S which is proportional to the logarithm of the number of mechanically stable states at a given volume V. Finally, they introduce a configurational temperature X, named compactivity, in analogy to classical statistical mechanics as 1/X = ∂S(V)/∂V.
The following almost three decades have seen an increasing number of work building on these ideas.4–39 Specifically, it has been realized that for each spatial configuration of frictional hard spheres there can be a multitude of contact force configurations, all of which fulfill the same boundary stress conditions.23 This leads to a second temperature-like variable named angoricity ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) .12,16,33 Moreover, there exist a number of open questions regarding the feasibility of such an approach. For example, there exist four different approaches how to build a “thermometer” to determine compactivity and angoricity from the experimental data.5,10,15–18,20,25,32,33 It turns out that only two of them agree quantitatively while the other two have problems to account for certain aspects of loose packings.34 Other open questions include the existence of a zeroth law for X and
.12,16,33 Moreover, there exist a number of open questions regarding the feasibility of such an approach. For example, there exist four different approaches how to build a “thermometer” to determine compactivity and angoricity from the experimental data.5,10,15–18,20,25,32,33 It turns out that only two of them agree quantitatively while the other two have problems to account for certain aspects of loose packings.34 Other open questions include the existence of a zeroth law for X and ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) 33 and the possibility or even necessity of an equiprobable sampling protocol.21,24,27,30,36,37 For recent reviews on this field see ref. 40 and 41.
33 and the possibility or even necessity of an equiprobable sampling protocol.21,24,27,30,36,37 For recent reviews on this field see ref. 40 and 41.
1.1 Defining mechanical stability
A core idea of Edwards' approach is to consider only mechanically stable packings. For an experimentalist on earth, such packings are the most generic state of granular matter: due to gravity and the dissipative nature of contacts and collisions, eventually all grains in a not permanently driven sample will come to a complete rest. And the resulting packings will have a small but finite bulk and the shear modulus as they have to withstand the anisotropic pressure p created by gravity. This pressure can only be reduced to zero by microgravity42 or embedding the particles in a density matched fluid.43Comparing with thermal hard sphere model systems, such as colloids, the condition of mechanical stability significantly reduces the number of valid configurations in the phase space. While the former only requires non-overlap between all particles, the latter additionally requires that the particles have a least in average Ziso contacts, to exhibit a finite shear and a bulk modulus. This isostatic contact number Ziso can be computed by equating the number ndof of degrees of freedom each particle possesses with the number of constraints fixed by its contacts 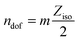 . The factor two in the number of constraints mZiso/2 follows from the fact that each contact is shared by two particles; the multitude m of blocked forces depends on the dimension, the shape of the contact area and the friction coefficient μ. For spheres in three dimensions m = 1 in the frictionless case (each contact blocks only one normal force) and m = 3 for frictional contacts (one normal and two tangential forces). ndof does also depend on μ: for μ = 0 we only need to consider the three translations, for μ > 0 additionally the three rotations become relevant.†
. The factor two in the number of constraints mZiso/2 follows from the fact that each contact is shared by two particles; the multitude m of blocked forces depends on the dimension, the shape of the contact area and the friction coefficient μ. For spheres in three dimensions m = 1 in the frictionless case (each contact blocks only one normal force) and m = 3 for frictional contacts (one normal and two tangential forces). ndof does also depend on μ: for μ = 0 we only need to consider the three translations, for μ > 0 additionally the three rotations become relevant.†
This results in Ziso = 4 for frictional spheres (granular matter) and Ziso = 6 for frictionless spheres (such as foams and emulsions). One consequence of the lower Ziso for frictional spheres is that most granular packings are hyperstatic (Z > Ziso) as shown in simulations and experiments.45–49
The intuitive connection between Z and φ seems obvious: the more dilute the packing, the fewer the contacts should be on average. However, for frictional hard spheres, where Z is controlled by the packing geometry and not compression, there exists presently only a mean field theory.19 The predicted Z(φ) is in good agreement with experiments49,50 and the ansatz has recently been expanded to more shapes,51,52 however only for the frictionless case.
1.2 The range of mechanically stable packings
As the Edwards entropy is only defined for mechanically stable, yet amorphous states, we are interested here in the upper and lower bounds of φ between which these packings exist in the thermodynamic limit.‡The upper boundary is often referred to as Random Close Packing (RCP). Although both its exact value of φ and its physical interpretation are still a matter of debate54–56 there is a growing consensus that φ ≈ 0.65 corresponds to the onset of crystallization in monodisperse sphere packings.56–63 An alternative, a more precise name would be the Glass Close Packing (GCP) limit as it is the highest achievable density for packings with suppressed crystallization, which is the ideal glass density for monodisperse spheres.64–67 The onset of crystallization at GCP has to be distinguished from the spontaneous crystallization occurring in equilibrating thermal systems such as colloids at φ ≈ 0.494–0.61.64,68–74 The latter is driven by the entropy increase due to newly gained vibrational degrees of freedom which implies that these hard sphere crystals are not mechanically stable. In contrast, in crystallization occurring above the GCP limit all particles are completely arrested by their contacts with their neighbors. Because the contact number at GCP is larger or equal to 6 and therefore above Ziso of both the frictionless and frictional cases, this upper boundary is unaffected by μ.
The lower bound on the mechanical stability of granular, frictional packings is commonly referred to as Random Loose Packing (RLP). It does depend on pressure43,75 and the friction coefficient:43,76 the higher the μ the smaller the φRLP. For experimentally relevant values of μ ≈ 0.5 and vanishing pressure φRLP approaches 0.55.19,43,75–79 While the existence of RLP is an experimental fact, the physics behind this threshold is still an open question. However, numerical studies47,48 of the μ dependence of Ziso lead to the conjecture that at least in the zero pressure limit RLP does correspond to the isostatic point.
In summary, the configurational entropy of sphere packings can only be nonzero for volume fractions between the Random Loose Packing limit (depends on friction, but for most materials φ ≈ 0.55) and the Glass Close Packing limit (independent of friction, φ ≈ 0.65).
1.3 Measuring the configurational entropy
Except for simplified model systems4,26 the configurational entropy cannot be directly computed from first principles. And a direct enumeration of the distinct mechanical states can only be achieved for systems composed of a relatively small number (less than 20) of frictionless disks.21,24,30,80Under certain additional assumptions, S(φ) can be computed from the volume fluctuations of a repeatedly driven granular packing.18,20,34 However, the results obtained this way do not agree: while in ref. 18 and 34S(φ) decreases monotonously from RLP to RCP, in ref. 20 an intermediate maximum of S(φ) was reported.
Finally, S can be determined for soft frictionless disks by dividing the total accessible phase space volume by that of an average basin of attraction.24,30,36,81 Due to its limitation to frictionless systems these results have however been limited to the rather narrow range of volume fractions around GCP.
1.4 Outline
In this paper, we present a method to compute an upper bound on the Edwards entropy of frictional hard-sphere packings. This method is an extension of the Widom particle insertion method,82–84 which for frictionless hard spheres link the excess chemical potential of packing to the probability of particle insertion in this packing. For this paper, we need the probability of inserting a particle into a mechanically stable packing so that the inserted particle is mechanically stable itself. To determine this probability, we extend a method for estimating the particle insertion probability in frictionless packings65 onto the case of frictional packings.The paper is structured as follows: in Section 2 we discuss the preparation protocols utilized for creating the packings used in the paper, Section 3 introduces the method to estimate the Edwards entropy of the packings, and in Section 4 we present and discuss our results. Finally, Section 5 concludes our paper and Appendix 6 provides additional experimental details.
2 Packing preparation
In this section, we describe the computational protocols and experimental methods used to create mechanically stable packings of spheres. Additionally, we introduce a method for the numerical generation of mechanically unstable packings, which are used for comparison. A summary of different preparation protocols can be found in Table 1, two examples of packings are depicted in Fig. 1.| Protocol | Mechanical stability | Friction | Gravity | Periodic b.c. | No. of particles | No. of packings | Density range |
|---|---|---|---|---|---|---|---|
| a In the bulk region. | |||||||
| Lubachevsky–Stillinger | Approximately stable | − | − | + | 104 | 71 | 0.560–0.650 |
| Makse | Stable | + | − | + | 104 | 13 | 0.551–0.637 |
| Diluted | Unstable | − | − | + | 104 | 36 | 0.550–0.650 |
| Fluidized bed | Stable | + | + | − | 1903–2053a | 503 | 0.570–0.592 |
2.1 Lubachevsky–Stillinger packings
The Lubachevsky–Stillinger (LS) algorithm85,86 simulates Newtonian dynamics and elastic collisions of hard spheres under a vacuum with zero gravity, while at the same time the spheres grow (or, equivalently, the box is contracted). The algorithm terminates when the non-equilibrium reduced pressure (compressibility factor)68,87 reaches a certain threshold (1012). After termination, the final configuration of the particles, i.e. their coordinates and radii are stored as one packing. The volume fraction of this packing can be controlled by the compression rate of the box; for low enough compression rates the packings become crystalline.The packings generated by the LS algorithm contain 104 monodisperse frictionless spheres, residing in a cubic box under periodic boundary conditions. Using the code by Skoge et al.68 we created packings in a density range φ = [0.565–0.65],§ corresponding to compression rates between 0.2 and 4.6 × 10−4.
The mechanical stability of the resulting packings is not automatically enforced by the Lubachevsky–Stillinger algorithm. An infinite equilibrium pressure would be equivalent to mechanical stability even for frictionless particles,88 but (i) the pressure that is tracked during the algorithm operation is inherently non-equilibrium and (ii) the dynamics is stopped at a finite pressure threshold where the particles are still moving.
However, as our analysis later will show that the properties of these packing are close to the properties of fully arrested packings. This can also be seen by expanding all particles with a single linear strain step of 10−4 and counting particle intersections as contacts.19 The average contact number Z determined in such a way is larger than the isostatic, frictional limit of 4 in all our simulations. This is not a generic feature of numerically produced packings and other protocols produce packings with φ < 0.65 only with Z ≈ 0.65
2.2 Makse packings
The next set of packings corresponds to the mechanically stable packings used in the paper by Briscoe et al.,18 which can be downloaded from ref. 89. This protocol takes Lubachevsky–Stillinger packings and stabilizes them using a discrete element method (cf. Section VI from Supplementary material in ref. 19). During the operation of the discrete element method, the particles are enhanced with Hertzian normal forces and tangential friction. Like Lubachevsky–Stillinger packings, these packings are three-dimensional and reside in cubic boxes with periodic boundary conditions in all directions.The lowest value of φ = 0.5513 for Makse packings was reached by Briscoe et al. for spheres with a friction coefficient of μ = 104. To avoid mixing of packings created with different parameters, we use in this paper only the subset of their packings created with this value of μ.
2.3 Fluidized bed packings
This experimental dataset addresses the question of mechanical stability by preparing loose packings of glass spheres which are (a) completely at rest and (b) stable under a finite pressure, i.e. their own weight.The sample consists of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 monodisperse quartz glass spheres with a diameter of 351 ± 0.5 μm from Sandoz Fils S.A. Individual packings are created by fluidizing the particles with flow pulses of water in a fluidized bed.10 Then X-ray tomographies of the samples were obtained at the European synchrotron radiation facility (ESRF) in Grenoble at beamline ID15A. The high X-ray flux allowed us to take a full tomogram with up to 1500 projections in less than 20 seconds in the monochromatic X-ray beam. This enabled us to gather several hundred tomograms (cf.Table 2), each representing a separate packing configuration.
000 monodisperse quartz glass spheres with a diameter of 351 ± 0.5 μm from Sandoz Fils S.A. Individual packings are created by fluidizing the particles with flow pulses of water in a fluidized bed.10 Then X-ray tomographies of the samples were obtained at the European synchrotron radiation facility (ESRF) in Grenoble at beamline ID15A. The high X-ray flux allowed us to take a full tomogram with up to 1500 projections in less than 20 seconds in the monochromatic X-ray beam. This enabled us to gather several hundred tomograms (cf.Table 2), each representing a separate packing configuration.
| Flow rate, Q (μl s−1) | Flow duration (s) | Resolution (μm per voxel) | No. of particles | No. of packings | Average bulk density, φ | Density range |
|---|---|---|---|---|---|---|
| a For this set of packings, we were slightly varying the radius of the bulk region to ensure an equal amount of spheres in the latter. | ||||||
| 250 | 10 | 12 | 1909–1962 | 263 | 0.574 | 0.570–0.579 |
| 167 | 10 | 12 | 1903–1968 | 173 | 0.575 | 0.571–0.580 |
| 150 | 15 | 18 | 2053a | 67 | 0.588 | 0.581–0.592 |
The fluidized bed consists of a cylindrical tube with an inner diameter of 8 mm or 22.7 particle diameters. The inner surface of the tube was roughened manually to prevent crystallization near the boundary. During preparation, the bed is expanded by a short water pulse (10 or 15 s), then it sediments for 10 seconds. After sedimentation, while the bed is in a stationary state, a tomogram is taken. Then the cycle “water pulse–sedimentation–reconstruction” is repeated.
The fluidization parameters used in three different experiments are listed in Table 2. We will subsequently refer to the three experiments according to their flow rate Q, i.e. Q_250, Q_167, and Q_150. Table 2 lists also the average φ of all packings, as well as the φ interval in each set.¶ In agreement with previous work10 we find that lower flow rates create denser packings. By comparing successive tomograms, we validated that even the lowest Q used in the experiments was sufficient to create a new packing configuration with each pulse. To ensure that beds are not disturbed by rotation during tomography scans, we took two tomograms without issuing a water pulse in-between. The resulting difference in particle positions is smaller than our overall accuracy of approximately 0.1 voxel.
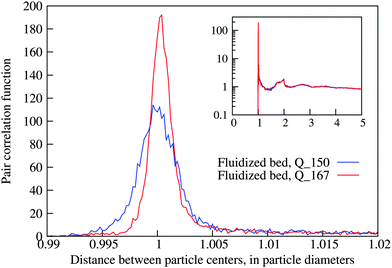
The sphere positions were first detected as the centers of mass of the binarized images; this estimate was then improved by finding the cross correlation maximum with a set of grey-scale template shifted in 0.1 voxel steps along all axes.|| Together with the good monodispersity of the quartz spheres this method results in the, to our knowledge, the best published accuracy of experimental particle positions. This claim is made quantitatively in Appendix 6.1, where we demonstrate the first peak of the pair correlation function.
We restrict our subsequent analysis to the bulk regions of fluidized bed packings, i.e. we analyse only particles whose centers are at least 2 mm (respectively, 5.6 particle diameters) away from the cylinder boundary. In addition, we exclude a layer of two particle diameters at the top and bottom of every reconstructed packing.
We find that we still have to exclude 34% of the packings from our analysis because their pore-size distributions show features which both differ from theoretical predictions and are not seen in any of the computer-generated packings. We attribute these unexpected features to image processing artefacts which distort the positions of a small number of spheres. Details on how experiments with untypical pore-size distribution are identified can be found in Appendix 6.2.
2.4 Diluted packings
These types of packings are intended to illustrate the effect of missing mechanical stability. They are created by first taking a reference Lubachevsky–Stillinger packing at a density φ = 0.65. Then, particle positions and box size are proportionally scaled to obtain densities in a desired range φ = 0.55–0.65. The resulting packings have contact numbers Z equal to zero and are therefore not mechanically stable.3 Computing an upper bound on the Edwards entropy
3.1 Theoretical approach
In this subsection, we discuss our modified version of the Widom particle insertion method82–84 which allows us to compute an upper bound on the Edwards entropy per particle. The main idea here is that we enforce the condition of mechanical stability by (a) starting from packings which already possess these properties and (b) by inserting particles in such a way that they will have enough contacts to be mechanically stable themselves.Packing preparation protocols can be described in two equivalent ways: either the volume of the box is decreased, or the particle diameter is increased. The former is more equivalent to experimental methods where fixed-size particles “settle” from an expanded state into a final volume. The latter is normally used in numerical protocols.
We will assume in the following discussion monodisperse packings** that are prepared by increasing the particle diameters: starting from an arbitrary low density configuration in the phase space, the protocol changes the particle positions (moving the configurational point in the phase space) and at the same time increases the particle diameter until they reach a configuration that is mechanically stable for a given friction coefficient.
Then configurations with the same final particle diameter can be grouped into equivalence classes if these configurations can be obtained from one another by (i) continuous symmetry operations (translational or—in the case of cylindrical or spherical boundaries—rotational symmetries);88 (ii) rattler displacements.
Thus, the entire phase space can be divided into (protocol-dependent) countable81 basins of attraction of equivalence classes of mechanically stable configurations with different particle volume fractions (densities). For frictionless particles, basins of attraction can be produced, among other protocols, by “Stillinger quenches” (quenches that try to increase particle diameters as fast as possible).90,91
In order to investigate the “number of mechanically stable states” at a given particle diameter D or equivalently volume fraction φ, we need to operate with the density of states. It will be more convenient to investigate the number of states in a small interval of final particle diameters D.
If N is the number of particles, V is the box volume, Ωi is the volume of the phase space of a basin of attraction, and Di is its final particle diameter, we can write the total volume of the basins of attraction with Di ∈ [D;D + dD) as
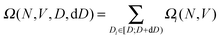 | (1) |
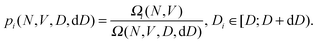 | (2) |
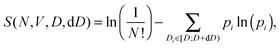 | (3) |
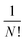 accounts for indistinguishability of particles.36,81
accounts for indistinguishability of particles.36,81
If we assume equiprobability of stable states,36,41i.e. the equality of all Ωi, the Edwards entropy becomes S = ln(C/N!) where C(N,V,D,dD) is the number of mechanically stable configurations with Di ∈ [D;D + dD).
Switching back to a more experimental view we assume now that the final particle diameter is equal to the initial one but the box is rescaled to match the final density. This leads to a range of accepted box linear dimensions [L,L + h) instead of a range for accepted particle diameters, where h can be termed a “granular Planck length”.
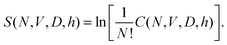 | (4) |
It will be convenient for the discussion below to allow particle centers to move inside the Planck volumes of size h3. That is the entire phase space will be split into hypercubes of volume h3N and a hypercube is considered mechanically stable if it contains at least one mechanically stable configuration. The number of mechanically stable hypercubes will be equal to C(N,V,D,h) for a sufficiently small h (if h is too big, one hypercube may contain several mechanically stable configurations). Again, hypercubes shall be merged into equivalence classes. From now on D and h are considered fixed and we omit them from the list of parameters.
We can also define a probability to sample a correct (mechanically stable) configuration among all possible configurations as
| pcorrect(N,V) = C(N,V)h3N/VN. | (5) |
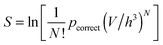 .
.
The number of all correct configurations C(N + 1,V) can thus be estimated as
| C(N + 1,V) ≥ K1 + K2 + ⋯ + KC(N,V) = C(N,V)〈K〉, | (6) |
We can now introduce the average insertion probability (into an already stable packing):
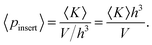 | (7) |
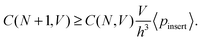 | (8) |
By combining eqn (4) and (8) we obtain
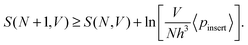 | (9) |
By combining eqn (5) and (8), we could also derive an equivalent expression for pcorrect(N,V):
| pcorrect(N + 1,V) ≥ pcorrect(N,V)〈pinsert〉. | (10) |
We immediately derive from eqn (9)
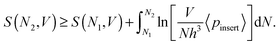 | (11) |
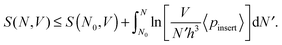 | (12) |
An important step in the Widom method is to assume that the 〈pinsert〉 can be represented by pinsert from a single system:
| 〈pinsert〉 = pinsert. | (13) |
A sufficient condition for eqn (13) in classical systems is that an examined single packing is in equilibrium. But the discussion above does not necessarily require packings to be equilibrated and does not imply ergodicity. The only requirement is that packings produced by a given protocol at given (N,V) possess similar properties and are in this sense “typical”, so that we can apply eqn (13).††
It will be more natural to switch in eqn (12) to the entropy per particle, s = S/N. This quantity shall depend only on the particle volume fraction φ and h. We also replace N with φ in the integration in eqn (12) through φ = NVsp/V, where Vsp is the sphere volume. We thus arrive at the master equation (where we use the subscript “ub” to denote the upper bound)
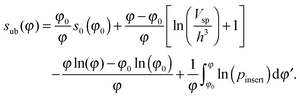 | (14) |
A natural choice for φ0 in eqn (14) is the point where s0 is zero: the entire term  will then vanish. As discussed in the introduction, the highest possible value of φ for packings with suppressed crystallization is the Glass Close Packing limit φGCP. At this endpoint of the amorphous branch of the hard sphere phase diagram55 there will be only one densest configuration (up to particle permutations, symmetry operations, and possibly up to rattler displacement). All configurations equivalent up to continuous symmetry operations, such as translations, and rattler displacements are already combined by design into equivalence classes. The number of discrete symmetry operations is the same for any N, it is 48 for a fully periodic cubic box (symmetry order of the octahedral symmetry Oh).94 The density φGCP can be expressed through the box size LGCP with
will then vanish. As discussed in the introduction, the highest possible value of φ for packings with suppressed crystallization is the Glass Close Packing limit φGCP. At this endpoint of the amorphous branch of the hard sphere phase diagram55 there will be only one densest configuration (up to particle permutations, symmetry operations, and possibly up to rattler displacement). All configurations equivalent up to continuous symmetry operations, such as translations, and rattler displacements are already combined by design into equivalence classes. The number of discrete symmetry operations is the same for any N, it is 48 for a fully periodic cubic box (symmetry order of the octahedral symmetry Oh).94 The density φGCP can be expressed through the box size LGCP with 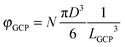 . If we select h so that the last interval of box volumes (LGCP − h,LGCP] in eqn (4) contains only the GCP configuration, then we can compute s0 as s0 = ln(48N!/N!)/N = 48/N, which in the thermodynamic limit will go to zero. We note that this selection of the reference point leaves h hidden in sub (cf.eqn (4)), and the value of h is essentially unknown.
. If we select h so that the last interval of box volumes (LGCP − h,LGCP] in eqn (4) contains only the GCP configuration, then we can compute s0 as s0 = ln(48N!/N!)/N = 48/N, which in the thermodynamic limit will go to zero. We note that this selection of the reference point leaves h hidden in sub (cf.eqn (4)), and the value of h is essentially unknown.
A more detailed mathematical discussion of the Widom method can be found in our accompanying paper.96 We validate there our procedure65 for estimating pinsert for the hard-sphere fluid. The same procedure, extended for granular systems, is presented in the next section.
For classical systems, all the equations in the previous section are exact. For such systems one also measures the volume of valid configurations, not their number. The phase space for classical systems contains additional kinetic degrees of freedom, but switching to excess quantities eliminates them from equations. Thus, it is more common to express eqn (10) through the excess chemical potential Δμ, Δμ/kT = −ln(〈pinsert〉).82,84,92,95Eqn (14) looks even simpler in excess quantities, 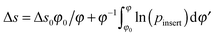 . We validate this form of equation in the accompanying paper.96Eqn (10) requires minimal changes to switch to classical systems, we only have to replace inequality with equality:
. We validate this form of equation in the accompanying paper.96Eqn (10) requires minimal changes to switch to classical systems, we only have to replace inequality with equality:
| pcorrect(N + 1,V) = pcorrect(N,V)〈pinsert〉. | (15) |
We illustrate eqn (15) in Fig. 2 for the case of a one-dimensional hard-sphere fluid with N = 2 (i.e. ignoring the requirement of mechanical stability). In this case the N + 1 phase space is only three-dimensional and can therefore be still visualized.
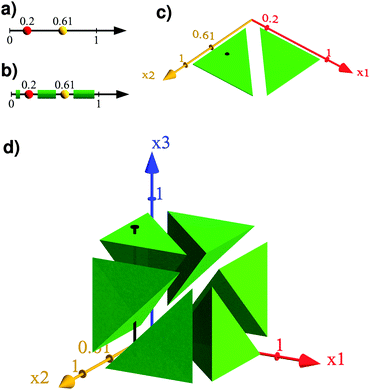 | ||
| Fig. 2 Visualization of the Widom method (eqn (15)) using a one-dimensional hard-sphere system, and ignoring the condition of mechanical stability. Panel (a) shows a specific two-particle system in a one-dimensional box extending from 0 to 1. Panel (c) displays the available phase space pcorrect(2,V), for arbitrary positions of the two particles, as a green area. The specific system of panel (a) is here indicated as a black dot. Panel (b) visualizes in green the available space for the insertion of a third particle in this specific system without overlap with the first two particles. The green area in panel (d) shows the available phase space of the generic three-particle system. Panel (b) coresponds to an one-dimensional hyperslice of this phase space, it is indicated by the black vertical line. The Widom insertion method now corresponds to the statement that one can compute pcorrect(3,V) (the fraction of the green volume in 3D in panel (d)) by multiplying pcorrect(2,V) (the fractiton of the green area in panel (c)) with pinsert (the fraction of the green length in panel (b)). | ||
Both s and s0 in eqn (14) contain h (cf.eqn (4)). Thus, the presence of additional h3 there, as well as of Vsp, can be daunting. We note though that Vsp and h3 in eqn (14) are also both hidden in pinsert and are cancelled out. The presence of h3 follows directly from eqn (7). To understand the dependence of pinsert on Vsp, we notice that K from eqn (7) shall be extensive, i.e. K = Nα(φ), and thus 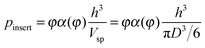 , where D is the particle diameter. We will discuss the implications
, where D is the particle diameter. We will discuss the implications
| pinsert ∼ h3(if h → 0), pinsert ∼ D−3 | (16) |
In classical systems the Widom insertion method is normally used in conjunction with the canonical ensemble.82–84 This is in principle also possible for the granular case: the ratio C(N,V)/h from eqn (4) represents the density of states, which can also be written as 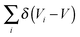 ,2,41 where the summation of delta-functions is over all mechanically stable states. Switching to the canonical ensemble would remove the delta-functions and the unknown hidden h from eqn (14). In the canonical ensemble the partition function ZN looks like
,2,41 where the summation of delta-functions is over all mechanically stable states. Switching to the canonical ensemble would remove the delta-functions and the unknown hidden h from eqn (14). In the canonical ensemble the partition function ZN looks like 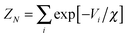 , where χ is the compactivity. Here the compactivity controls the average volume that the small subsystem gains when it is generated (along with a large “bath” of particles) with a certain packing preparation protocol. However, as the correct method to measure compactivities is still an active area of research,34 we abstain here from switching to the canonical ensemble.
, where χ is the compactivity. Here the compactivity controls the average volume that the small subsystem gains when it is generated (along with a large “bath” of particles) with a certain packing preparation protocol. However, as the correct method to measure compactivities is still an active area of research,34 we abstain here from switching to the canonical ensemble.
We also mention that for particles with soft shells, when mechanically stable states are defined by local elastic energy minima and shells are wide enough to avoid zero energy plateaus at any relevant φ, entropy can be defined as the number of states at every φ even in the microcanonical ensemble.36,81 It would also remove the delta-functions and unknown hidden h from eqn (14). We do not consider such particles in this paper.
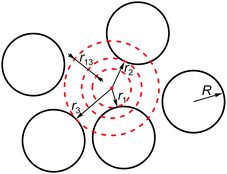 | ||
| Fig. 3 Schematic illustration of distances from a random point to the closest particle surfaces in two dimensions. | ||
The idea is now to estimate the correct insertion probability of a “virtual” particle with a given number of contacts by giving conditions on these distances. We assume two particles to be in contact if the closest distance between their surfaces does not exceed some small arbitrary constant δ. To insert a virtual particle with an arbitrary radius r0 having ≥z contacts, we require two conditions: (a) the particle has to fit in, i.e. r1 = r0, (b) it has to touch at least z particles, i.e. rz ≤ r1 + δ.
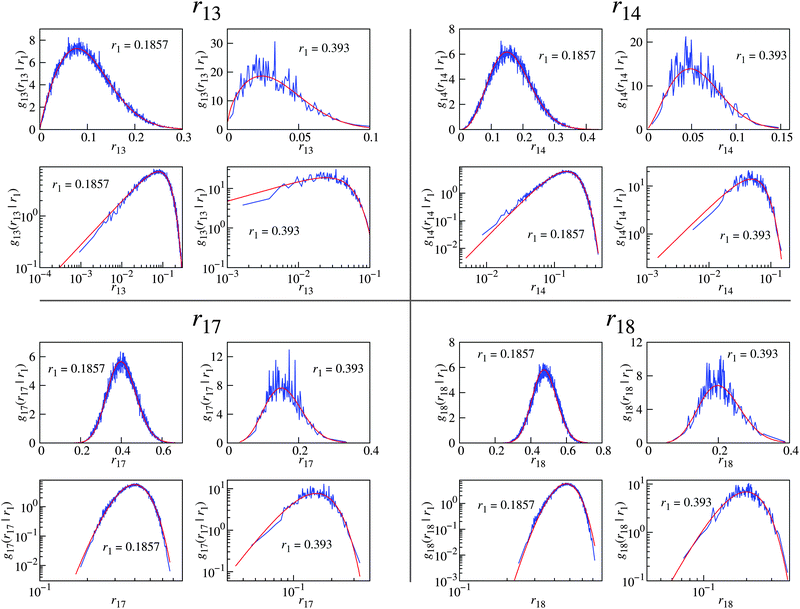
The last condition will be easier to discuss if we operate with relative distances r1z = rz − r1 for z > 1 (cf.Fig. 3). By inserting a large number of virtual particles we then measure the probability density functions for the distributions of r1 and r1z, which we denote as f(r1) and g1z(r1,r1z), respectively (note that g1z depends on r1 as well). f(r1) is described in many papers as pore-size distribution.97–105 We also operate with the conditional probability density g1z(r1z|r1) to find a given value r1z when the distance to the first closest sphere is r1: g1z(r1z|r1) = g1z(r1,r1z)/f(r1). We denote the corresponding cumulative distributions as G1z(r1,r1z) and G1z(r1z|r1).
The probability density hz(r0) to insert a particle with radius r0 and at least z contacts can be computed using the two conditions named above as
| hz(r0)dr0 = Pr{r1 ∈ [r0,r0 + dr0), r1z ∈ [0,δ)} = f(r0)dr0 × Pr{r1z ∈ [0,δ)|r1 = r0}. | (17) |
| Pr{r1z ∈ [0,δ)|r1 = r0} = G1z(δ|r0). | (18) |
| hz(r0) = f(r0)·G1z(δ|r0). | (19) |
If R is the radius of “real” particles, then hz(R)dR is the probability for an inserted particle to have at least z contacts and the radius in the range [R,R + dR).
To enforce mechanical stability for inserted virtual particles, we have to choose a relevant z. The two immediate choices are z = 3 and z = 4. It is known that 4 is the minimal possible average coordination number in mechanically stable packings (realized in packings with infinite friction). The contact number distribution is never a “delta-function”,19 so non-rattler particles with three contacts are inevitable, though not every configuration of three contacts will be mechanically stable. We will denote the correct minimal z as zmin, but will discuss the choice between zmin = 330,106,107 and zmin = 4108,109 in the Results Section 4.
At this point, we can estimate the probability pinsert from eqn (14) to correctly insert a particle in a packing:
| pinsert = dR·f(R)·G1zmin(δ|R). | (20) |
| dR = δ = h = 2 × 10−7. | (21) |
Eqn (16) implies that pinsert scales as h3 and D−3. Because h is present as dR in eqn (20) explicitly, G1zmin(h|R) shall conform to
| G1zmin(h|R) ∼ h2 (if h → 0). | (22) |
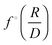 and
and 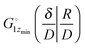 , respectively. From the elementary probability theory it follows that
, respectively. From the elementary probability theory it follows that 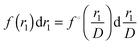 and thus
and thus 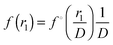 . Through rewriting g1z(r1,r1z) in the same way (applied to both arguments) and dividing by f(R), we can write
. Through rewriting g1z(r1,r1z) in the same way (applied to both arguments) and dividing by f(R), we can write  . Thus,
. Thus, 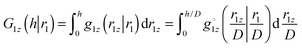 . Note that we had to change the limits of integration. It means that whenever we require that G1z(h|r1) ∼ h2 (i.e. G1z(h|r1) = A(D)h2), it implies that
. Note that we had to change the limits of integration. It means that whenever we require that G1z(h|r1) ∼ h2 (i.e. G1z(h|r1) = A(D)h2), it implies that 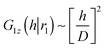
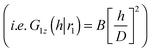 . Thus,
. Thus, 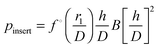 , and scaling with both h and D is correct, if eqn (22) indeed holds as expected. We will imply D = 1 a.u. from now on.
, and scaling with both h and D is correct, if eqn (22) indeed holds as expected. We will imply D = 1 a.u. from now on.
3.2 Overview of data analysis steps
In finite size packings, such as our experiments and simulations, neither f(R) nor G1z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min(h|R) can be measured directly. The maximum observed value for r1 (radius of inserted particle) is ∼0.4R. Moreover, the minimum values of r1zmin (and generally of all r1z) are much larger than h even for r1 < 0.4R. To fix this issue, we fit the obtained values of f(r1) and extrapolate r1 → R. Additionally, we need to fit G1z(r1z|r1) for z = zmin and extrapolate r1z → h and r1 → R. To make our results more general, we will present a method applicable for all z from 3 at least to 11.
min(h|R) can be measured directly. The maximum observed value for r1 (radius of inserted particle) is ∼0.4R. Moreover, the minimum values of r1zmin (and generally of all r1z) are much larger than h even for r1 < 0.4R. To fix this issue, we fit the obtained values of f(r1) and extrapolate r1 → R. Additionally, we need to fit G1z(r1z|r1) for z = zmin and extrapolate r1z → h and r1 → R. To make our results more general, we will present a method applicable for all z from 3 at least to 11.
The entire procedure to estimate the upper bound of the Edwards entropy according to eqn (14) contains therefore the following steps:
(1) We uniformly generate 107 random points in all packings. For each point, we measure distances to the closest particles, with indices z from 3 to 11 (though in principle we will need only z = zmin).
(2) We fit f(r1) and extrapolate it to r1 = R (cf. the next section for the fitting procedures).
(3) We distribute values of r1 into bins. Initially we use 100 bins of equal size, then merge some of them to ensure that the minimum number of points in each bin is 80. For each bin (i.e. for each r1), we fit g1z(r1z|r1) as a function of r1z. Then we extrapolate it to r1z = 0, and estimate G1z(h|r1).
(4) For each value of z, we fit G1z(h|r1) as a function of r1 and extrapolate it to r1 = R.
(5) Finally, we insert f(R) and G1zmin(h|R) into eqn (20) to obtain pinsert at each φ and insert pinsert into eqn (14) to obtain the upper bound of the Edwards entropy per particle sub.
3.3 Details of the fitting and extrapolation steps
In this subsection we will justify our choice of fit functions used for the extrapolation steps. In order to demonstrate better statistics we present in the figures in this section the combined distributions g1z(r1z|r1) from 39 fluidized bed packings with φ = 0.587 ± 0.003.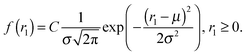 | (23) |
Theoretical results97–99 predict that f(r1) is of the form A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ar13 + br12 + cr1 + d), of which eqn (23) is a special case. The validity of the function from eqn (23) was already demonstrated in our previous paper65 (see Fig. 2 in that reference).
exp(ar13 + br12 + cr1 + d), of which eqn (23) is a special case. The validity of the function from eqn (23) was already demonstrated in our previous paper65 (see Fig. 2 in that reference).
The normalization constant C in eqn (23) corresponds to the fact that the probability for a pore to appear in the interparticle void space is 1 − φ. It can be computed using 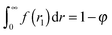 . Fits were performed using the maximum likelihood method for a truncated Gaussian distribution.110
. Fits were performed using the maximum likelihood method for a truncated Gaussian distribution.110
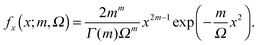 | (24) |
As there is no first-principle based theory supporting our choice of the Nakagami distribution, we have tried to fit other distributions with support x ∈ [0,+∞) and fx → 0 at x → 0. The result is that one-parameter distributions do not have enough degrees of freedom to fit all the different g1z(r1z|r1) curves, while three-parameter distributions are too flexible and fits are not robust. Among the examined two-parameter distributions, the gamma and Rice distributions possess shapes similar to the observed g1z(r1z|r1), but the quality of fit is inferior to the Nakagami distribution. For example, the gamma distribution decays at large x with exp(−x) which is too slow.
From the parameters m and Ω from the Nakagami fit we compute the zero distance probability G1z(h|r1), which is the cumulative density function of the Nakagami distribution Fx at x = h. The latter has the following analytical expression
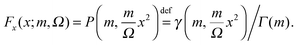 | (25) |
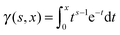 is the lower incomplete gamma function, and Γ(m) is the gamma function. Thus, we can express G1z(h|r1) as
is the lower incomplete gamma function, and Γ(m) is the gamma function. Thus, we can express G1z(h|r1) as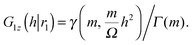 | (26) |
| ln[G1z(h|r1)] = d − exp[ar12 + br1 + c] | (27) |
 | ||
| Fig. 5 Extrapolating the zero distance probability G1z(h|r1) (blue lines) using eqn (27) (red lines). G1z(h|r1) ≡ Pr(r1z < h|r1) is the probability that a pore with radius r1 will have exactly z contacts with real particles in a shell of width h. The data represent 39 combined fluidized bed packings (Q_150) with an average φ of 0.585. The particle diameter is normalized to unity, the extrapolation is therefore to r1 = 0.5. | ||
We confirm that the estimates of pinsert do not change qualitatively if G1zmin(h|R) is determined by averaging the three G1zmin(h|r1) values with the highest available r1.
4 Results and discussion
4.1 Scaling of zero-distance probabilities G1z(h|R) with h
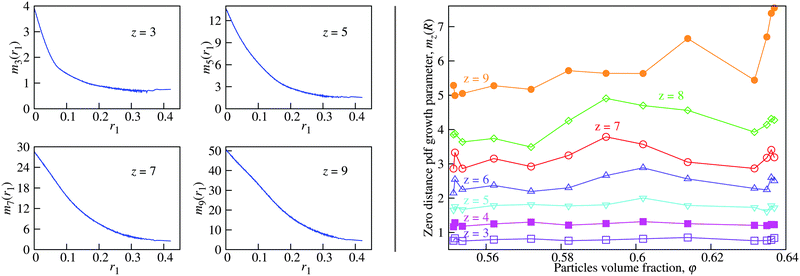
Eqn (22) requires that G1zmin(h|R) ∼ h2 for sufficiently small h. It follows from the form of the Nakagami distribution (eqn (24)) that for small x the cumulative Nakagami distribution Fx(x;m,Ω) scales as x2m. For a given protocol, m is a function of z, φ, and r1. Thus, eqn (22) implies that mzmin(r1 = R) = 1 at all φ (the Nakagami distribution is then transformed into the Rayleigh distribution).To test the behaviour of mz, we build mz(r1) from the Nakagami fits for the combined g1z(r1z|r1) distributions for the 39 Q_150 packings used in Section 3.3 (with φ = 0.587 ± 0.003). The results are presented in the left panel of Fig. 6.
As before, to estimate mz(R) we have to extrapolate r1 to R. For z ≤ 6, the mz(r1) plots visually reach asymptotes for the largest values of r1 for all the packings that we used. Thus, to estimate mz(R) we simply take an average of the last three values of mz(r1). The plots mz(R) vs. φ for the Makse packings are presented in the right panel of Fig. 6.
The values with z ≤ 8 show no systematic dependence on φ in Fig. 6. Thus, we can compute their averages. The estimates 〈mz(R)〉φ for the Makse packings are (z = 3…11): 0.792, 1.238, 1.761, 2.424, 3.185, 4.128, 5.883, 8.412, and 11.923. The values with z > 6 are very crude estimates.
Both m3(R) and m4(R) are around unity, which is in line with the requirement mzmin = 1. None of them is equal to unity though. One possible explanation is that our estimates for m4(R) are still too high and the plot m4(r1) continues to decrease with r1 (like plots mz(r1) do, cf.Fig. 6), so that it eventually reaches the value m4(r1) = 1 at r1 = R. This effect will be incorporated into the extrapolation of G1z(h|r1) with r1 → R (cf.Fig. 5), if this extrapolation is correct. At the same time, m3(R) does not seem to reach the value 1. Thus, we will prefer zmin = 4 to zmin = 3.
The proximity of m3(R) and m4(R) to unity and their independence from φ, as expected from general scaling considerations, demonstrate the validity of our approach and the correctness of fits, though we never incorporated these requirements during the fitting procedure.
4.2 Zero-distance probabilities G1z(h|R)
Fig. 7 shows that the zero distance probabilities G1z(h|R) have no systematic dependence on φ for z ≥ 3. The data shown here represent the Makse packings, but the Lubachevsky–Stillinger packings are qualitatively similar. This result corresponds to the statement that the local structure of large pores in a packing remains unchanged over the entire density range of random monodisperse packings.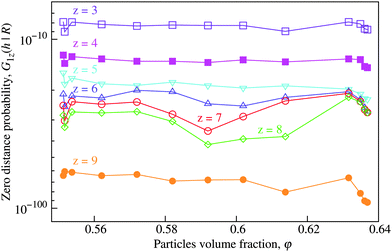 | ||
| Fig. 7 The zero-distance probabilities G1z(h|R) for the different contact numbers z show no systematic dependence on the volume fraction φ. Presented are the data from the Makse packings. | ||
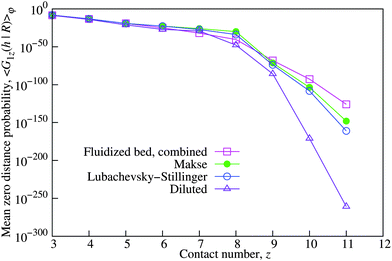
Because the values of G1z(h|R) do not change systematically with φ, we can compute an average 〈G1z(h|R)〉φ by averaging over the whole volume fraction range. The corresponding results for all the protocols are shown in Fig. 8. For the fluidized bed packings, we combined the data for all the values of flow rate Q prior to averaging.
Differences between the protocols become only apparent for z > 5. Among the numerical protocols, the Makse packings have the highest zero distance probabilities, followed by the Lubachevsky–Stillinger packings. Zero distance probabilities for the diluted packings are significantly low, especially for z > 7. This sequence corresponds to the “degree of mechanical stability” of the packings: the Makse packings are mechanically stable, the Lubachevsky–Stillinger packings are close to being stable, while the diluted packings have large interparticle gaps by design. Fluidized bed packings demonstrate even higher “degree of mechanical stability” than the Makse packings for z > 9, but there is a crossover in the order of lines between z = 8 and z = 9. Fig. 8 demonstrates that G1z(h|R) might therefore be an interesting tool to quantify the proximity to mechanical stability.
4.3 Insertion probabilities pinsert
Fig. 9 shows the results for pinsert computed with zmin = 4. We have excluded here the diluted packings, because their average coordination number is zero.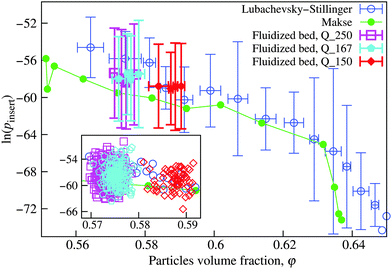 | ||
| Fig. 9 All the estimates of pinsert(φ) decrease monotonously with the volume fraction φ. Results are computed using eqn (20) with zmin = 4. LS and fluidized bed data points were binned in the main plot. Vertical error bars represent 95% prediction intervals in bins, horizontal error bars represent minimum and maximum densities in bins. Data were grouped to ensure 5, 66, 43, and 17 packings in the bins for the LS, Q_250, Q_167, and Q_150 lines, respectively. The inset shows all the individual experiments. | ||
Two main results are shown in Fig. 9. First, within error bars the Makse, LS, and fluidized bed packing agree quantitatively in their pinsert, without any fit parameter. Interestingly, the agreement between the only approximately stable LS and fully stable fluidized bed packings is better than with the also fully mechanically stable Makse packings. We will come back to this point in Section 4.4. Second, pinsert exhibits a maximum at RLP and then decays monotonously with increasing φ.
4.4 Upper bound on the Edwards entropy per particle
With pinsert(φ) at hand, we can compute the estimates of the Edwards entropy per particle sub according to eqn (14). As discussed in Section 3.1.2, we assume here that s0 becomes zero at the Glass Close Packing limit φGCP = 0.65. Because the Makse packings are only defined up to a maximum φ of 0.637 and because the pinsert(φ) of the Lubachevsky–Stillinger packings agrees better with the experimental data in Fig. 9, we will use the Lubachevsky–Stillinger packings to compute the upper bound on the Edwards entropy displayed in Fig. 10. At least in the range 0.570 < φ < 0.592, sub can also be computed from the fluidized bed data, using a corresponding Lubachevsky–Stillinger value of s at φ0 = 0.592 as a reference value s0 in eqn (14). These results are also shown in Fig. 10, it is within our accuracy indistguishable from the Lubachevsky–Stillinger derived values.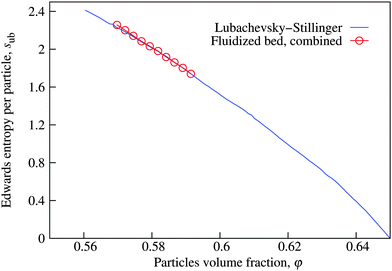 | ||
| Fig. 10 The upper bounds on the Edwards entropy per particle sub(φ) decrease monotonously with the volume fraction φ. Results are computed using eqn (14) with zmin = 4, pinsert is taken from Fig. 9. | ||
The values of sub exhibit a maximum at RLP and decay monotonously with increasing φ. This behaviour supports previous numerical19,112 and experimental34 analyses. It also agrees with the idea that s drops sharply to zero (in the canonical ensemble) for φ below RLP.
More generally, this method to compute sub will allow for the first time to test the different protocols that have been suggested to measure the configurational temperature X.5,10,15–18,20,25,32–34 Moreover, our approach should be extendable to bidisperse systems, which will allow us to test the idea that segregation in dense bidisperse systems is controlled by configurational entropy.7,31,113–116
The origin of the difference between s(φ) and sub(φ) is configurations which gain stability only due to insertion of an additional particle. To account for such configurations, we can formally rewrite eqn (6) as
| C(N + 1,V) = C(N,V)〈K〉α(N,V), | (28) |
If we keep the definition for the average insertion probability into an already stable packing (eqn (7)) the same, eqn (12) will then be replaced by
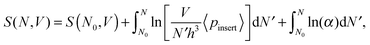 | (29) |
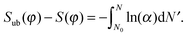 | (30) |
A qualitative estimate for α might be obtained by investigating the case of removing a particle from the packing under consideration. The likelihood that any of the neighbors of this particle becomes unstable will decrease with increasing distance to isostaticity, z − ziso, which corresponds to the statement that packings close to RLP are the most “fragile”. By analogy, configuration close to RLP should therefore also be the most likely to gain mechanical stability by adding another particle. Thus, we conclude that α will be maximum at the RLP limit. This argument should also allow us to measure α numerically and therefore turn the upper bound into a direct estimate of the Edwards entropy. To do so one needs to measure the probability that removing single particles from given mechanically stable packings will make them lose their stability.
Our analysis does not consider the effects of a finite boundary pressure and by design we have no access to the degeneracy that hyperstatic packings have in the phase space spanned by the contact forces. However, all our packings were comprised from hard particles so that particle positions and contact forces decouple. The numerical packings do so by design, and the fluidized bed experiments were done under a constant pressure small enough that the glass spheres can be considered as perfectly hard: the pressure between two glass spheres at the bottom of a 1 m high column will deform them by approximately 10 nm, which is an orders of magnitude smaller than the vertical surface roughness of typical glass spheres.117 And the grain column in our fluidized bed experiment was only 0.03 m high.
However, the value of RLP, measured with glass spheres, does depend on pressure.43 This means that at least close to the isostatic point also s will show some pressure dependence. This effect originates in the reduced degeneracy in the contact force space; the closer to isostaticity a packing is, the fewer configurations will exist to fulfil certain pressure boundary conditions. An analysis of loose packing created at different pressure levels should provide interesting insights.
Finally, we would like to point out that a generalization of our method to other particles shapes, such as ellipsoids or Platonic bodies, seems feasible.
5 Summary
In this paper, we present a method to compute an upper bound on the Edwards entropy per particle of three-dimensional, mechanically stable hard-sphere packings within a microcanonical ensemble. We modify the Widom insertion method to be applicable for granular systems and also extend our method to estimate particle insertion probabilities for hard-sphere systems using their pore-size distribution to account for the requirement of mechanical stability of the packing. Then we supply these insertion probabilities into the master equation from the Widom method.We apply this procedure to experimentally obtained and computer-generated packings covering the volume fraction range from 0.551 to φGCP ≈ 0.65 (the Glass Close Packing density, according to some estimates). The experimental packings are created with flow pulses in a water-fluidized bed, the numerical packings are prepared using the Lubachevsky–Stillinger algorithm. One subset, taken from the publication of Briscoe et al.,18 adds an additional discrete element simulation step to obtain fully jammed configurations.
Starting from a minimum at the Glass Close Packing density the upper bound on the Edwards entropy grows monotonically with decreasing volume fraction to reach a maximum around the Random Loose Packing density φRLP ≈ 0.55. Because there are by definition no mechanically stable packings below Random Loose Packing, the Edwards entropy shall drop there to zero (in the canonical ensemble).
Additionally, we find that the local structure around pores large enough to fit in another particle does not depend on the volume fraction. This volume fraction independence was quantified by computing the probabilities of the inserted particles to have a given number of contacts.
6 Appendix
6.1 Pair correlation functions for fluidized bed packings
The monodispersity of the particles and the high quality of the particle detection of fluidized bed experiments are demonstrated by the pair correlation functions shown in Fig. 11. The data correspond to individual fluidized bed packings where we have discarded a layer of one diameter thickness along the cylinder walls. While the absolute height of the first peak, which corresponds to particles in contact, depends on the bin size, its width is a testimonial to the quality of the data.6.2 Selecting fluidized bed packings
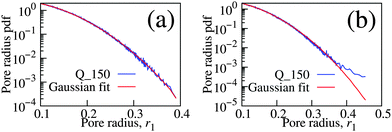
Approximately 34% of the fluidized bed packings were discarded due to the atypical pore-size distributions. Fig. 12 shows two examples. The experiment in panel (b) behaves atypically as the tail deviates from the expected Gaussian curve (eqn (23)) towards higher probability densities. Such a behaviour was neither observed in the computer-generated Makse, Lubachevsky–Stillinger, and diluted packings nor was it observed for the force-biased and Jodrey–Tory packings studied in our previous paper65 and by Schenker et al.103 Thus, we assume that this atypical behaviour stems from reconstruction artefacts and discards such packings from the calculation of entropies.Fig. 12 demonstrates also that the pore-size distribution may serve as an additional indicator of packing reconstruction quality, besides the pair-correlation function discussed in Section 6.1.
Acknowledgements
We thank Sibylle Nägle for creating Fig. 2 and Udo Krafft and Wolf Keiderling for building the fluidized bed setup. X-ray tomographies were performed on the ID15A beamline at the European Synchrotron Radiation Facility (ESRF), Grenoble, France. Computational resources were provided by FZJ (Forschungszentrum Jülich, Germany). The authors would like to acknowledge the funding of the Deutsche Forschungsgemeinschaft (DFG) through the Cluster of Excellence Engineering of Advanced Materials. The French National Research Agency (ANR) is acknowledged for support via EQUIPEX grant ANR-11-EQPX-0031 (project NanoimagesX). We are grateful to the John von Neumann Institute for Computing (NIC) and the Jülich Supercomputing Center (JSC) for the allocation of a special CPU-time grant (NIC project number: 8214, JSC project ID: HMR10).References
- N. V. Brilliantov and T. Pöschel, Kinetic Theory of Granular Gases, Oxford University Press, 2004 Search PubMed.
- S. F. Edwards and R. B. S. Oakeshott, Physica A, 1989, 157, 1080–1090 CrossRef.
- A. Mehta and S. F. Edwards, Physica A, 1989, 157, 1091–1100 CrossRef.
- R. Monasson and O. Pouliquen, Physica A, 1997, 236, 395–410 CrossRef.
- E. R. Nowak, J. B. Knight, E. Ben-Naim, H. M. Jaeger and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 57, 1971–1982 CrossRef CAS.
- H. A. Makse and J. Kurchan, Nature, 2002, 415, 614–617 CrossRef CAS PubMed.
- M. Nicodemi, A. Fierro and A. Coniglio, Europhys. Lett., 2002, 60, 684–690 CrossRef CAS.
- R. Blumenfeld and S. F. Edwards, Phys. Rev. Lett., 2003, 90, 114303 CrossRef PubMed.
- H. A. Makse, J. Brujić and S. F. Edwards, in The Physics of Granular Media, ed. H. Hinrichsen and D. E. Wolf, Wiley-VCH, Weinheim, 2004, pp. 45–85 Search PubMed.
- M. Schröter, D. I. Goldman and H. L. Swinney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 030301 CrossRef PubMed.
- P. T. Metzger and C. M. Donahue, Phys. Rev. Lett., 2005, 94, 148001 CrossRef PubMed.
- S. F. Edwards, Physica A, 2005, 353, 114–118 CrossRef.
- M. Pica Ciamarra, A. Coniglio and M. Nicodemi, Phys. Rev. Lett., 2006, 97, 158001 CrossRef PubMed.
- F. Lechenault, F. da Cruz, O. Dauchot and E. Bertin, J. Stat. Mech.: Theory Exp., 2006, 2006, P07009 Search PubMed.
- P. Ribiére, P. Richard, P. Philippe, D. Bideau and R. Delannay, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 22, 249–253 CrossRef PubMed.
- S. Henkes, C. S. O'Hern and B. Chakraborty, Phys. Rev. Lett., 2007, 99, 038002 CrossRef PubMed.
- T. Aste and T. Di Matteo, Eur. Phys. J. B, 2008, 64, 511–517 CrossRef CAS.
- C. Briscoe, C. Song, P. Wang and H. A. Makse, Phys. Rev. Lett., 2008, 101, 188001 CrossRef PubMed.
- C. Song, P. Wang and H. A. Makse, Nature, 2008, 453, 629–632 CrossRef CAS PubMed.
- S. McNamara, P. Richard, S. K. de Richter, G. Le Caer and R. Delannay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031301 CrossRef PubMed.
- G.-J. Gao, J. Blawzdziewicz, C. S. O'Hern and M. Shattuck, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061304 CrossRef PubMed.
- S. Henkes and B. Chakraborty, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 061301 CrossRef PubMed.
- B. P. Tighe, J. H. Snoeijer, T. J. H. Vlugt and M. van Hecke, Soft Matter, 2010, 6, 2908–2917 RSC.
- N. Xu, D. Frenkel and A. J. Liu, Phys. Rev. Lett., 2011, 106, 245502 CrossRef PubMed.
- L. A. Pugnaloni, J. Damas, I. Zuriguel and D. Maza, Pap. Phys., 2011, 3, 030004 Search PubMed.
- R. K. Bowles and S. S. Ashwin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031302 CrossRef PubMed.
- F. Paillusson and D. Frenkel, Phys. Rev. Lett., 2012, 109, 208001 CrossRef PubMed.
- K. Wang, C. Song, P. Wang and H. A. Makse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 011305 CrossRef PubMed.
- S.-C. Zhao, S. Sidle, H. L. Swinney and M. Schröter, EPL, 2012, 97, 34004 CrossRef.
- S. S. Ashwin, J. Blawzdziewicz, C. S. O'Hern and M. D. Shattuck, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061307 CrossRef CAS PubMed.
- M. Schröter and K. E. Daniels, 2012, arXiv:1206.4101.
- R. Blumenfeld, J. F. Jordan and S. F. Edwards, Phys. Rev. Lett., 2012, 109, 238001 CrossRef PubMed.
- J. G. Puckett and K. E. Daniels, Phys. Rev. Lett., 2013, 110, 058001 CrossRef PubMed.
- S.-C. Zhao and M. Schröter, Soft Matter, 2014, 10, 4208–4216 RSC.
- I. G. Tejada, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 1–8 CrossRef CAS PubMed.
- D. Asenjo, F. Paillusson and D. Frenkel, Phys. Rev. Lett., 2014, 112, 098002 CrossRef PubMed.
- F. Paillusson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 012204 CrossRef PubMed.
- Y. Wu and S. Teitel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022207 CrossRef PubMed.
- V. Becker and K. Kassner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052201 CrossRef PubMed.
- M. Pica Ciamarra, P. Richard, M. Schröter and B. P. Tighe, Soft Matter, 2012, 8, 9731–9737 RSC.
- D. Bi, S. Henkes, K. E. Daniels and B. Chakraborty, Annu. Rev. Condens. Matter Phys., 2015, 6, 63–83 CrossRef CAS.
- P. Yu, S. Frank-Richter, A. Börngen and M. Sperl, Granular Matter, 2014, 16, 165–173 CrossRef.
- M. Jerkins, M. Schröter, H. L. Swinney, T. J. Senden, M. Saadatfar and T. Aste, Phys. Rev. Lett., 2008, 101, 018301 CrossRef PubMed.
- M. van Hecke, J. Phys.: Condens. Matter, 2010, 22, 033101 CrossRef CAS PubMed.
- L. E. Silbert, D. Ertas, G. S. Grest, T. C. Halsey and D. Levine, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031304 CrossRef PubMed.
- H. P. Zhang and H. A. Makse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011301 CrossRef CAS PubMed.
- K. Shundyak, M. van Hecke and W. van Saarloos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 010301 CrossRef PubMed.
- S. Henkes, M. van Hecke and W. van Saarloos, EPL, 2010, 90, 14003 CrossRef.
- F. M. Schaller, M. Neudecker, M. Saadatfar, G. W. Delaney, G. E. Schröder-Turk and M. Schröter, Phys. Rev. Lett., 2015, 114, 158001 CrossRef PubMed.
- T. Aste, M. Saadatfar and T. J. Senden, J. Stat. Mech.: Theory Exp., 2006, 2006, P07010 Search PubMed.
- A. Baule, R. Mari, L. Bo, L. Portal and H. A. Makse, Nat. Commun., 2013, 4, 2194 Search PubMed.
- A. Baule and H. A. Makse, Soft Matter, 2014, 10, 4423–4429 RSC.
- S. Torquato and F. H. Stillinger, J. Appl. Phys., 2007, 102, 093511 CrossRef.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, Phys. Rev. Lett., 2000, 84, 2064 CrossRef CAS PubMed.
- R. D. Kamien and A. J. Liu, Phys. Rev. Lett., 2007, 99, 155501 CrossRef PubMed.
- A. V. Anikeenko and N. N. Medvedev, Phys. Rev. Lett., 2007, 98, 235504 CrossRef CAS PubMed.
- M. Bargieł and E. M. Tory, Adv. Powder Technol., 2001, 12, 533–557 CrossRef.
- K. Lochmann, L. Oger and D. Stoyan, Solid State Sci., 2006, 8, 1397–1413 CrossRef CAS.
- C. Radin, J. Stat. Phys., 2008, 131, 567–573 CrossRef.
- Y. Jin and H. A. Makse, Physica A, 2010, 389, 5362–5379 CrossRef CAS.
- B. A. Klumov, S. A. Khrapak and G. E. Morfill, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 184105 CrossRef.
- S. C. Kapfer, W. Mickel, K. Mecke and G. E. Schroder-Turk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 030301 CrossRef PubMed.
- N. Francois, M. Saadatfar, R. Cruikshank and A. Sheppard, Phys. Rev. Lett., 2013, 111, 148001 CrossRef CAS PubMed.
- G. Parisi and F. Zamponi, Rev. Mod. Phys., 2010, 82, 789–845 CrossRef.
- V. Baranau, D. Hlushkou, S. Khirevich and U. Tallarek, Soft Matter, 2013, 9, 3361–3372 RSC.
- V. Baranau and U. Tallarek, Soft Matter, 2014, 10, 3826–3841 RSC.
- V. Baranau and U. Tallarek, Soft Matter, 2014, 10, 7838–7848 RSC.
- M. Skoge, A. Donev, F. H. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041127 CrossRef PubMed.
- W. G. Hoover and F. H. Ree, J. Chem. Phys., 1968, 49, 3609–3617 CrossRef CAS.
- E. Sanz, C. Valeriani, E. Zaccarelli, W. C. K. Poon, P. N. Pusey and M. E. Cates, Phys. Rev. Lett., 2011, 106, 215701 CrossRef PubMed.
- E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon, M. E. Cates and P. N. Pusey, Phys. Rev. Lett., 2009, 103, 135704 CrossRef CAS PubMed.
- C. Valeriani, E. Sanz, E. Zaccarelli, W. C. K. Poon, M. E. Cates and P. N. Pusey, J. Phys.: Condens. Matter, 2011, 23, 194117 CrossRef CAS PubMed.
- L. Filion, M. Hermes, R. Ni and M. Dijkstra, J. Chem. Phys., 2010, 133, 4115 CrossRef PubMed.
- P. N. Pusey, E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon and M. E. Cates, Philos. Trans. R. Soc., A, 2009, 367, 4993–5011 CrossRef CAS PubMed.
- G. Y. Onoda and E. G. Liniger, Phys. Rev. Lett., 1990, 64, 2727–2730 CrossRef CAS PubMed.
- G. R. Farrell, K. M. Martini and N. Menon, Soft Matter, 2010, 6, 2925–2930 RSC.
- J. M. Valverde and A. Castellanos, EPL, 2006, 75, 985 CrossRef CAS.
- L. E. Silbert, Soft Matter, 2010, 6, 2918–2924 RSC.
- G. W. Delaney, J. E. Hilton and P. W. Cleary, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 051305 CrossRef PubMed.
- M. Pica Ciamarra and A. Coniglio, Phys. Rev. Lett., 2008, 101, 128001 CrossRef PubMed.
- S. Martiniani, K. J. Schrenk, J. D. Stevenson, D. J. Wales and D. Frenkel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2016, 93, 012906 CrossRef PubMed.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, San Diego, 2nd edn, 2002 Search PubMed.
- D. J. Adams, Mol. Phys., 1974, 28, 1241–1252 CrossRef CAS.
- B. D. Lubachevsky and F. H. Stillinger, J. Stat. Phys., 1990, 60, 561–583 CrossRef.
- B. D. Lubachevsky, J. Comput. Phys., 1991, 94, 255–283 CrossRef.
- G. A. Mansoori, N. F. Carnahan, K. E. Starling and T. W. Leland, J. Chem. Phys., 1971, 54, 1523–1525 CrossRef CAS.
- Z. W. Salsburg and W. W. Wood, J. Chem. Phys., 1962, 37, 798–804 CrossRef CAS.
- H. Makse, Software and Data|Hernan Makse, http://www-levich.engr.ccny.cuny.edu/webpage/hmakse/software-and-data/.
- F. H. Stillinger and T. A. Weber, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 25, 978–989 CrossRef CAS.
- F. H. Stillinger, Science, 1995, 267, 1935–1939 CAS.
- R. J. Speedy, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 329–335 RSC.
- W. G. Hoover, W. T. Ashurst and R. Grover, J. Chem. Phys., 1972, 57, 1259–1262 CrossRef CAS.
- D. M. Bishop, Group Theory and Chemistry, Dover Publications, New York, Revised edn., 1993 Search PubMed.
- R. J. Speedy and H. Reiss, Mol. Phys., 1991, 72, 999–1014 CrossRef CAS.
- V. Baranau and U. Tallarek, J. Chem. Phys., 2016 Search PubMed , submitted.
- S. Torquato, B. Lu and J. Rubinstein, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 2059–2075 CrossRef CAS.
- B. Lu and S. Torquato, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 5530–5544 CrossRef CAS.
- S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 51, 3170–3182 CrossRef CAS.
- M. Alonso, M. Satoh and K. Miyanami, Can. J. Chem. Eng., 1992, 70, 28–32 CrossRef CAS.
- M. Alonso, E. Sainz, F. Lopez and K. Shinohara, Chem. Eng. Sci., 1995, 50, 1983–1988 CrossRef CAS.
- I. Schenker, F. Filser, M. Hutter and L. Gauckler, Granular Matter, 2012, 14, 333–340 CrossRef CAS.
- I. Schenker, F. T. Filser, L. J. Gauckler, T. Aste and H. J. Herrmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021302 CrossRef PubMed.
- S. Torquato, Annu. Rev. Mater. Res., 2002, 32, 77–111 CrossRef CAS.
- D. Stoyan, A. Wagner, H. Hermann and A. Elsner, J. Non-Cryst. Solids, 2011, 357, 1508–1515 CrossRef CAS.
- C. B. O'Donovan and M. E. Möbius, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 020302 CrossRef PubMed.
- C. F. Schreck, T. Bertrand, C. S. O'Hern and M. D. Shattuck, Phys. Rev. Lett., 2011, 107, 078301 CrossRef PubMed.
- M. Clusel, E. I. Corwin, A. O. N. Siemens and J. Brujic, Nature, 2009, 460, 611–615 CrossRef CAS.
- L. Berthier, H. Jacquin and F. Zamponi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 051103 CrossRef PubMed.
- A. C. Cohen, Ann. Math. Stat., 1950, 21, 557–569 CrossRef.
- M. Nakagami, in Statistical Methods in Radio Wave Propagation, ed. W. C. Hoffman, Pergamon Press, Oxford, 1960, pp. 3–36 Search PubMed.
- M. Pica Ciamarra, M. Nicodemi and A. Coniglio, Soft Matter, 2010, 6, 2871–2874 RSC.
- Y. Srebro and D. Levine, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 061301 CrossRef PubMed.
- A. Coniglio, A. Fierro and M. Nicodemi, Phys. D, 2004, 193, 292–302 CrossRef.
- M. Tarzia, A. Fierro, M. Nicodemi, M. Pica Ciamarra and A. Coniglio, Phys. Rev. Lett., 2005, 95, 078001 CrossRef CAS PubMed.
- T. Finger, M. Schröter and R. Stannarius, New J. Phys., 2015, 17, 093023 CrossRef.
- S. Utermann, P. Aurin, M. Benderoth, C. Fischer and M. Schröter, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031306 CrossRef PubMed.
Footnotes |
| † This calculation is strictly valid only for infinite friction. For a more detailed discussion see ref. 44. |
| ‡ A counter example is the “tunnelled crystals” described in ref. 53. Here the number of configurations does not grow exponentially with the number of particles in the system, which means that in the thermodynamic limit their entropy is zero. |
| § Some of the packings with φ > 0.6 were already used in Fig. 3 and 4 of Baranau et al.65 |
| ¶ The fluidized bed volume fraction was measured by uniformly generating 107 points in the bulk regions and counting the number of points that were inside the particles. |
| || This method proved itself superior to an interpolation from a set of cross correlations based on a voxel-distance grid. |
| ** These ideas can be generalized to polydisperse packings by assigning a nominal diameter to each particle before multiplying with the growth factor. |
| †† The replacement of 〈pinsert〉 with pinsert is often used implicitly, e.g. in eqn (3) in ref. 92 and eqn (4) in ref. 93. |
| This journal is © The Royal Society of Chemistry 2016 |