Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
From soft to hard rod behavior in liquid crystalline suspensions of sterically stabilized colloidal filamentous particles†
Eric
Grelet
* and
Richa
Rana
Université de Bordeaux & CNRS, Centre de Recherche Paul-Pascal, 115 Avenue Schweitzer, 33600 Pessac, France. E-mail: grelet@crpp-bordeaux.cnrs.fr
First published on 8th April 2016
Abstract
The liquid crystalline phase behavior of a colloidal system of sterically stabilized rods is reported. Our colloidal suspensions consist of highly monodisperse, semi-flexible filamentous viruses which have been coated with neutral hydrophilic polymers by irreversibly binding poly(ethylene glycol) (PEG) to the surface of the virus particles. Depending on the size of the grafted polymer, up to three different phase transitions are observed (isotropic-to-chiral nematic, chiral nematic-to-smectic, and smectic-to-columnar). Each phase transition is shown to be independent of ionic strength, confirming the steric stabilization of the viral colloids. A direct, i.e. without any free parameters, comparison with theory and computer simulations of the volume fraction associated with the phase transition can be performed, showing a quantitative agreement with hard rod behavior at a low polymer chain size, and some deviation stemming from soft repulsion by increasing the polymer thickness coating of the rod. Specifically, we demonstrate that the columnar mesophase is not stabilized by electrostatic repulsion, and we discuss the conditions of its existence.
I. Introduction
Entropy-driven transitions in systems of rod-shaped particles have attracted considerable interest both from theoretical and experimental research since decades. Onsager was the first to propose a theory accounting for the transition from the isotropic liquid state to an orientationally ordered nematic phase based only on excluded-volume arguments.1 Later, numerical simulations showed that the transition from the nematic to smectic phase, which exhibits additionally quasi-long ranged translational order, can be driven by entropy alone.2 From an experimental point of view, colloidal suspensions represent paradigms in soft condensed matter physics for their ability to both mimic molecular systems and to provide new insights into the structure and the dynamics of self-assembly phenomena. Moreover, they can be directly compared with theoretical and computer simulation results because colloidal interactions are mainly based on steric and electrostatic effects. Among dispersions formed by non-spherical colloids, rod-like particles such as silica rods3 or filamentous fd viruses4 are appealing because of their model system features like size monodispersity. The renormalization of the charged fd virus suspension phase diagram has been reported lately demonstrating the hard-rod behavior of such a system in the dense ordered states.5 This has been achieved by accounting for the electrostatic repulsion between highly charged viral rods thanks to the introduction of effective particle sizes and charges (with counterion condensation). However, beyond the electrostatic interaction which can be tricky to handle, steric repulsion using grafted polymeric molecules represents a convenient approach in colloidal science for creating stable particle suspensions. Following this idea, we investigate in the current work the whole liquid crystalline phase behavior of filamentous bacteriophages, which have been preliminarily functionalized by a poly(ethylene glycol) (PEG) layer.6–8 Depending on the grafted polymer size, these PEGylated virus suspensions display up to three mesophases, chiral nematic, smectic and columnar phases, with the noteworthy feature that all the associated phase transitions are independent of the ionic strength, with the system being not driven by electrostatic effects. Thanks to the PEG coating, completely sterically stabilized system of rods shown to be controlled by hard-core interaction has been prepared, which can then be directly (i.e. with no free parameters) compared over the whole range of rod densities to theoretical predictions and computer simulations.II. Materials and methods
Our experimental system of rods is the filamentous M13KE virus, a longer mutant compared to wild-type M13 bacteriophage. M13KE is a one micron-length (L = 1 μm) semiflexible charged rod-like particle with a diameter of D = 7 nm and a persistence length of about P = 2.8 μm.9 Its molecular weight (Mw) of 1.86 × 107 g mol−1 is proportional to its contour length.10 Viruses were grown using the ER2738 strain as E. coli host bacteria and purified following standard biological protocols.4The PEGylation of the M13KE viruses was performed by covalent binding between coat protein amino groups and N-hydroxysuccinimide ester activated poly(ethylene glycol) (PEG-NHS). Two average molecular weights MPEGw of NHS-PEG were used: 5.5 and 21 kg mol−1 (referred to as PEG5k and PEG20k, respectively) which were purchased from NOF Corporation (Japan) under the name Sunbright ME-050HS and ME-200HS, respectively. The chemical reaction was carried out in a 1 mg mL−1 virus solution in PBS buffer (100 mM, pH 7.8) for 2 hours. Taking into account around 3000 proteins per virus, a three times molar equivalent amount of PEG-NHS polymer has been added to the virus suspension. The excess of non-grafted PEG-NHS was removed by at least two purification steps of ultracentrifugation (244![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g for 3 hours) and redispersion, followed by extensive dialysis against a TBS buffer (20 mM, pH 8.2) adjusted with NaCl to get an added salt ionic strength Is of 10, 50 or 110 mM. After dialysis the virus suspensions were concentrated again by ultracentrifugation, and a series of samples in quartz cylindrical capillaries (purchased from W. Müller, Germany) of 1 mm diameter was prepared at different dilutions from the most concentrated sample and reaching the I–N transition. The capillaries were sealed with flame and UV glue (NOA81) was applied at the sealed end and polymerized under UV (for 5 minutes) to ensure that there is no drying with time of the liquid crystalline suspensions. The virus concentration C of each dilution was measured using spectrophotometry with an absorption coefficient of 3.84 cm2 mg−1 at 269 nm which is only sensitive to the presence of viruses, the PEG polymer being almost transparent at this wavelength.
000g for 3 hours) and redispersion, followed by extensive dialysis against a TBS buffer (20 mM, pH 8.2) adjusted with NaCl to get an added salt ionic strength Is of 10, 50 or 110 mM. After dialysis the virus suspensions were concentrated again by ultracentrifugation, and a series of samples in quartz cylindrical capillaries (purchased from W. Müller, Germany) of 1 mm diameter was prepared at different dilutions from the most concentrated sample and reaching the I–N transition. The capillaries were sealed with flame and UV glue (NOA81) was applied at the sealed end and polymerized under UV (for 5 minutes) to ensure that there is no drying with time of the liquid crystalline suspensions. The virus concentration C of each dilution was measured using spectrophotometry with an absorption coefficient of 3.84 cm2 mg−1 at 269 nm which is only sensitive to the presence of viruses, the PEG polymer being almost transparent at this wavelength.
The amount of PEG-NHS grafted per virus was measured by refractive index increment experiments (dn/dc) performed on PEG-NHS polymers, bare M13KE viruses and PEGylated viruses.7 Since dn/dc is proportional to the mass density, the difference in dn/dc values between the bare viruses and the PEGylated ones is directly proportional to the number of polymers grafted per virus, Nexp. The determination of dn/dc values for the three samples in the same buffer was done by injecting aliquots of known concentration into an Optilab rEX refractive index detector (Wyatt technology, USA) working at a wavelength of 658 nm and a temperature of 30 °C. All the measurements are detailed in Fig. S1 of the ESI.†
The signature of the columnar mesophase was given by the hexagonal positional order probed by small angle X-ray scattering (SAXS).11 SAXS experiments were performed using a NanoStar-Bruker AXS setup, working at a wavelength of 1.54 Å (Cu Kα emission) and with a sample-to-detector distance of 1.06 m. Typical exposure time was 6 hours. The smectic phase was mainly identified by its optical iridescence stemming from the diffraction by visible light of about 1 μm-thick smectic layers.5 It has to be emphasized that kinetics strongly matters in order to get samples at equilibrium. For instance, in the case of the M13-PEG20k system which is very viscous at high rod concentration, a few weeks were necessary before evidencing any smectic organization. Similar kinetic effects were observed for the chiral nematic phase; a few days of equilibration were necessary before the typical fingerprint texture was observed by polarizing microscopy.7 The isotropic liquid phase was determined by its lack of birefringence between crossed polarizers.
III. Results
A. Polymer conformation and PEG number per virus
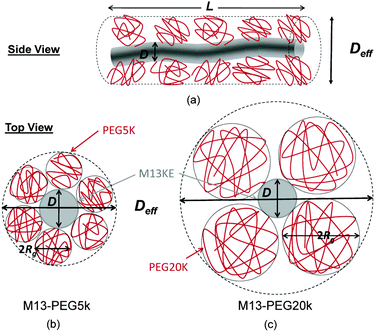
The number Nexp of PEG-NHS polymers grafted per virus has been determined from the refractive index increment experiments, and is reported in Table 1. Depending on the grafting density, the polymer chains can adopt different conformations, from coil-like (so-called mushroom) conformation at low density to a brush regime with stretched chains at high grafting density.12 The transition between the two regimes is given by the comparison of the average distance dPEG between the grafting terminals of the PEG chains on the virus surface and the Flory radius, RF. The latter one is related to the radius of gyration, Rg by: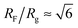 .13 In contrast to a “grafting-from” method where polymers are usually synthesized in situ from the particle surface and which can then lead to high grafting density, a “grafting-to” approach has been used here for the PEGylation of the virus.8,14 Because of the weak polymer molar excess, we can then reasonably assume a low grafting density and therefore a mushroom conformation of the polymers, which is usually described as a hemisphere of radius RF when grafted on a flat substrate. In order to account for the high curvature of the virus surface (for which D ∼ Rg), allowing therefore for an increase of the free volume accessible to the polymer chains compared to a flat surface, we approximate the shape of the polymer coil by a sphere of radius Rg. This description of the PEG conformation as a spherical coil relies also on the assumption that the PEG-virus interaction is repulsive, which is expected due to the well-known antifouling properties exhibited by PEG coating.15 Considering the effective surface available, we estimate by simple geometrical arguments (Fig. 1) the highest number NCP of hard spheres of radius Rg that can be packed around a long cylinder of length L and diameter D (L ≫ D) by the following relation:
.13 In contrast to a “grafting-from” method where polymers are usually synthesized in situ from the particle surface and which can then lead to high grafting density, a “grafting-to” approach has been used here for the PEGylation of the virus.8,14 Because of the weak polymer molar excess, we can then reasonably assume a low grafting density and therefore a mushroom conformation of the polymers, which is usually described as a hemisphere of radius RF when grafted on a flat substrate. In order to account for the high curvature of the virus surface (for which D ∼ Rg), allowing therefore for an increase of the free volume accessible to the polymer chains compared to a flat surface, we approximate the shape of the polymer coil by a sphere of radius Rg. This description of the PEG conformation as a spherical coil relies also on the assumption that the PEG-virus interaction is repulsive, which is expected due to the well-known antifouling properties exhibited by PEG coating.15 Considering the effective surface available, we estimate by simple geometrical arguments (Fig. 1) the highest number NCP of hard spheres of radius Rg that can be packed around a long cylinder of length L and diameter D (L ≫ D) by the following relation: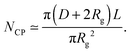 | (1) |
| PEG/virus, N | Measured, Nexp | Modeled, NCP |
|---|---|---|
| M13-PEG5k | 596 | 1440 |
| M13-PEG20k | 329 | 430 |
B. SAXS data and the 2D swelling law
X-ray scattering spectra have been recorded for the whole series of dilution in both systems of M13-PEG5k and M13-PEG20k; an example is provided for a given added salt molarity in Fig. 2. In the range of wavevectors studied in our experiments, only the radial ordering (i.e. normal to the long-rod axis) can be probed, and two distinct orders are evidenced: liquid-like order at low virus concentration, and 2D positional hexagonal order for the dense regime (Fig. 2).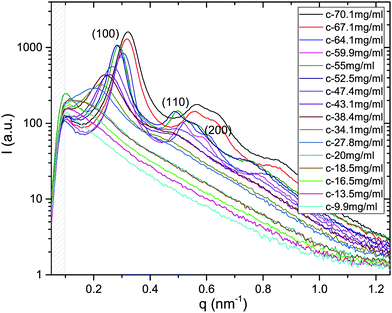 | ||
| Fig. 2 X-ray scattering spectra plotted for the whole range of studied concentrations in the case of M13-PEG5k at Is = 10 mM. For the dense rod packings (from C = 70.1 to 52.5 mg mL−1), the (100), (110) and (200) Bragg reflections are the hallmark of a 2D positional hexagonal ordering. At intermediate virus concentrations (between C = 47.4 and C = 20 mg mL−1), a broad (100) peak is evidenced, characteristic of liquid-like order.11 Because at too low wavevector q, this structure factor peak is out of our accessible range for concentration C below 18.5 mg mL−1. The gray dashed area indicates the unphysical region of the spectra near the beam stop. | ||
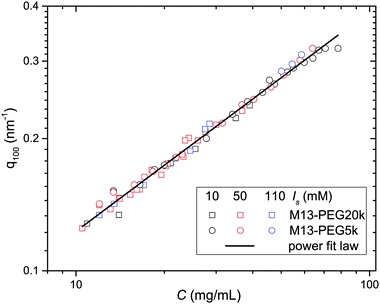
From the associated spectra, the position of the (100) reflection has been extracted and plotted as a function of virus concentration C as shown in Fig. 3. These data have been numerically fitted using a power law q100 ∝ C1/2.17,18 The power law exponent 1/2 is the signature of a 2D swelling, which is expected in our system because of the high aspect ratio (L/D ≫ 1) of the rod-like viruses.
Assuming a local hexagonal ordering around viruses, we have calculated the prefactor η corresponding to the 2D swelling law of infinitely long rods:
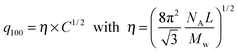 | (2) |
C. Experimental phase diagrams
The phase diagram of M13-PEG5k and M13-PEG20k suspensions has been established for three different added salt molarities, as depicted in Fig. 4. The main result is that all the phase transitions are independent of ionic strength within the studied range from Is = 10 mM to 110 mM. This shows that our PEGylated systems are not stabilized by electrostatic effects anymore but by the steric repulsion between the polymers in a good solvent. If the isotropic-to-(chiral) nematic (I–N) phase transition has been investigated in previous studies,6–8 we report herein that both the (chiral) nematic-to-smectic (N–Sm) and the smectic-to-columnar (Sm–Col) phase transitions can be driven only by the steric repulsion between colloidal rods. It is apparent that the electrical double layer associated with the charged rod-like viruses is confined within the grafted polymer layer whatever the ionic strength and the virus concentration. For the two systems studied here, the I–N transition occurs at virus concentrations slightly smaller than the ones previously reported for similar systems.6,7 We assign this result both to an increase of polymer grating density by about 50% (see Table 1) compared to these initial studies7 and to a larger virus contour length L. Another consequence is that for the range of studied ionic strengths Is ≥ 10 mM, no crossover is observed for which the rod phase behavior would be driven by weakly screened electrostatic interaction. This is consistent with the isotropic concentration at the I–N transition Ciso = 10.2 mg mL−1 and Ciso = 5.7 mg mL−1 found for M13-PEG5k and M13-PEG20k, respectively (Fig. 4(a) and (b)), which are both lower than the one found for purely charged systems, Ciso = 13.5 mg mL−1 at Is = 10 mM.10 A quantitative description of the I–N transition is presented in the next section of this paper.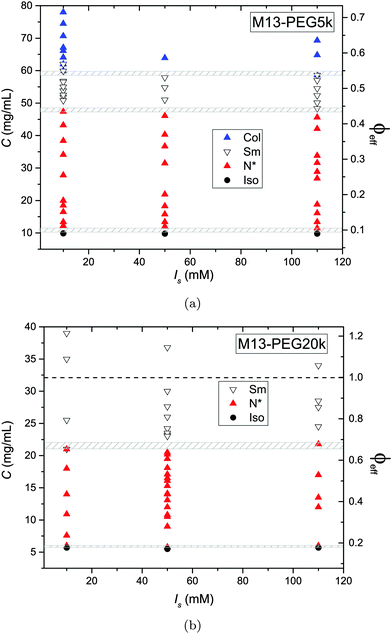 | ||
| Fig. 4 Liquid crystal phase diagram of PEGylated filamentous virus suspensions as a function of the added salt molarities Is for two molecular weights of coated polymer (a) PEG5k corresponding to L/Deff ≈ 50, and (b) PEG20k corresponding to L/Deff ≈ 30, respectively. The gray dashed area indicate the phase coexistence associated with the different first order phase transitions, including also experimental uncertainties. The effective rod volume fraction ϕeff is obtained using the effective rod diameter Deff = D + 4Rg according to eqn (3) and (4). | ||
In contrast to a recent study,5 the nature of the smectic order has not been systematically investigated. Nevertheless, if the lamellar ordering corresponds mainly to a smectic-B organization, a small range of smectic-A phases in which liquid-like order is evidenced within the layers has been found in both systems of different PEG sizes.5,11 It is noteworthy that no columnar phase exists for M13-PEG20k suspensions in which only a smectic organization has been found up to the highest rod density accessible after sample concentration by ultracentrifugation. In the case of M13-PEG5k, the existence of a columnar phase in a sterically stabilized system proves that the columnar state cannot be assigned to generic charge-induced stabilization as suggested by different theoretical studies.19–21
D. Effective diameter and effective volume fractions
In order to account for the steric repulsion between our rod-like colloids, the bare diameter D has to be replaced by a thicker effective one Deff which can be estimated by the virus bare diameter D = 7 nm plus twice the diameter of PEG, as represented in Fig. 1:| Deff = D + 4Rg | (3) |
This gives Deff = 19 nm with Rg = 3 nm and Deff = 35 nm with Rg = 7 nm for M13-PEG5k and M13-PEG20k, respectively.7,16 Note that because L ≫ Rg, we approximate Leff ≈ L. It has to be emphasized that the physical origin of the effective diameter Deff stemming from steric repulsion between PEG polymers in good solvent allows for its straightforward determination based on purely geometrical arguments. This makes PEGylated viruses much simpler for quantitative comparison with hard rods than the charged ones, for which a detailed description of the electric double layer surrounding each charged particle including counterion condensation has to be provided through complex models.5 In this case, Delectrostaticeff has been found to reach its highest value of about 16 nm at Is = 10 mM,5 confirming that Delectrostaticeff < Deff and therefore that the steric repulsion dominates the phase behavior of PEGylated rods for the range of ionic strengths studied here. The effective volume fraction related to the rod number density ρ = N/V via ϕeff = ρveff where 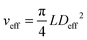 is the effective volume of one rod, can then be calculated without any free parameter according to:
is the effective volume of one rod, can then be calculated without any free parameter according to:
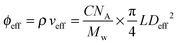 | (4) |
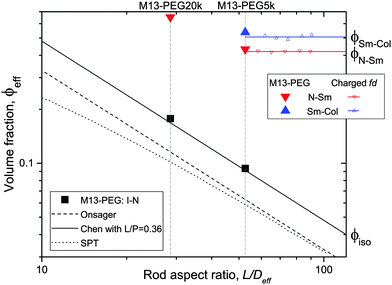 | ||
| Fig. 5 Effective volume fraction at the different phase transitions as a function of the rod aspect ratio. The full symbols represent the experimental data corresponding to PEGylated viruses as shown in Fig. 4, and the open ones are the renormalized values for charged viruses reported recently in ref. 5. The color code is black for the I–N transition, red for the N–Sm and blue for the Sm–Col. For each first order phase transition, the data indicate the lowest volume fraction at the coexistence. Different predictions of the I–N transition are provided for comparison: Onsager theory described using eqn (5) (black dashed line),1 scaled particle theory (SPT) for rigid rods (black dotted line),4,22 and the Chen model for semi-flexible rods (full black line).24 | ||
IV. Discussion
The I–N transition for a system of hard rods has been first theoretically described by Onsager.1 In the limit of infinitely long rigid rods (L ≫ D), the volume fraction ϕ is given for the coexisting isotropic and nematic phases by ref. 4: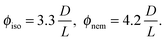 | (5) |
To go beyond the needle-like limit and account for rod-like particles with finite aspect ratio L/D, the scaled particle theory (SPT) as first proposed by Cotter22 includes in an approximate way higher virial coefficients and therefore better describes the phase behavior at higher rod density or equivalently rods with lower L/D.4 However, because of the relative high aspect ratio of our PEGylated viruses having L/Deff ≳ 30, no significant deviation is expected from the long rod limit as quantitatively shown in Fig. 5. A major physical feature of our rod-like viruses is their semi-flexibility with P ∼ 3L, which affects their phase behavior by destabilizing the location of the phase transitions to higher volume fractions. Khokhlov and Semenov extended Onsager theory to semi-flexible rods,23 for which Chen was able to determine an accurate numerical solution,24 as described in detail in Fig. S2 of the ESI.† By increasing rod flexibility L/P, the I–N transition takes place at higher rod densities: ϕiso = 4.8 D/L for L/P = 0.36,24 which corresponds to an increase of about 45% compared to the Onsager limit of infinitely long and rigid (L/P → 0) rods (eqn (5)). As can be observed in Fig. 5, Chen prediction is in excellent agreement with both systems of PEGylated rods of different aspect ratios. Moreover, the width w = (Cnem − Ciso)/Ciso of the coexistence region at I–N transition is expected to decrease by increasing rod flexibility from w = 0.27 for rigid rods as predicted by Onsager (eqn (5)) to w ≈ 0.1 for L/P ≈ 0.4.24 This is consistent with the experimental results including error bars, which give w ≃ 0.12 ± 0.05 and w ≃ 0.07 ± 0.03 for M13-PEG5k and M13-PEG20k, respectively (Fig. 4). Our results show therefore that the phase behavior of our sterically stabilized rods at I–N transition is accurately described at the level of the second virial coefficient for the rod aspect ratio down to L/D ≈ 30, as long as the rod flexibility is appropriately accounted for. It is worth mentioning again that this agreement between theory and experiments is obtained without any free parameter thanks to the steric definition of the effective diameter Deff.
While the I–N transition of M13-PEG particles matches the hard rod behavior, some deviation starts to appear in the concentrated regime. The N–Sm transition is expected to be universal in the long-rod limit, i.e. independent of the rod aspect ratio. Considering infinitely long freely rotating rods, the volume fraction at the N–Sm transition is found in the literature to be in the range from ϕN–Sm = 0.39 to 0.42.19,25–28 Introducing rod flexibility affects the phase behavior by destabilizing the smectic phase to higher densities, as shown experimentally on charged filamentous particles5,29 by a shift of ϕN–Sm of about 10% when rod stiffness decreases from P ∼ 10L to P ∼ 3L, and by theoretical approaches or computer simulations.27,28,30–32 However, numerical predictions remain limited to rather short semi-flexible rods (L/D ≲ 10) because of the computational cost.31–33 Therefore, a quantitative comparison of the location of the N–Sm and a fortiori of the Sm–Col phase transitions found in our experiments is currently not possible by the lack of theoretical and numerical descriptions of the phase behavior of both long and semi-flexible rods self-organized in dense states. Because we recently succeeded in renormalizing the phase diagram of semi-flexible charged rod-like viruses, we can then compare our present results on PEGlyated viral rods with the charged viruses. Specifically, the N–Sm and Sm–Col transitions have been found to occur for charged filamentous particles of P ∼ 3L at ϕchargedN–Sm = 0.42 and ϕchargedSm–Col = 0.51, respectively (see open triangle symbols in Fig. 5). These renormalized values are in very good agreement with the ones obtained for the M13-PEG5k system for which ϕstericN–Sm = 0.43 and ϕstericSm–Col = 0.53 by using the steric effective diameter defined in eqn (3). This result demonstrates the self-consistency of our approach and confirms the hard rod behavior of the filamentous particles sterically stabilized with a low polymer chain size (M13-PEG5k) for the whole range of rod densities.
The existence of a columnar phase in a system of hard rods has been a subject of intense discussion, and the last results obtained by theoretical studies and computer simulations indicate that both parallel and freely rotating hard spherocylinders only exhibit a metastable columnar phase.34–36 Nevertheless, other physical parameters such as polydispersity in rod size37,38 or surface charge19–21 have been predicted to stabilize the columnar ordering with respect to the smectic and the crystalline phases. In this context in which filamentous viruses combine both monodispersity, flexibility, chirality and steric repulsion thanks to their PEGylation, the conditions of existence of the columnar mesophase in virus suspensions is discussed. Here, we show the presence of a columnar mesophase beyond the smectic range for the thinnest PEGylated viruses: this proves that the existence of the columnar state driven by electrostatic interactions as suggested by many theoretical studies has to be ruled out.19–21 The other main explanation of the stabilization of columnar ordering invokes the polydispersity in the size of the particles.37,38 Because our bacterioviruses are intrinsically monodisperse,39 rod flexibility mimicking rod polydispersity can be postulated, as first suggested by van der Schoot.27 However, this assumption did not receive to date a formal demonstration in terms of phase diagram determination. Because the virus chirality is not screened by the presence of a grafted polymer layer,7 the influence of a helical twist induced by chirality has been recently hypothesized for the stabilization of the columnar phase.11 As displayed in Fig. 4(b), it is worth mentioning that no columnar phase exists for the M13-PEG20k system. This could suggest that the columnar structure only appears for a high enough rod aspect ratio, but such an assumption should be still confirmed. Therefore, our result on rod-like particles exhibiting steric repulsion should stimulate new investigation by computer simulations for studying the stabilization of the columnar phase in assemblies of long, semi-flexible and/or chiral rods. In M13-PEG20k rod suspensions, the effective volume fractions calculated according to eqn (3) and (4) reach unphysical values larger than 1. This shows that the definitions of both the effective diameter Deff as depicted in Fig. 1 and of ϕeff assuming a cylinder-shaped particle with a volume veff are not valid anymore for high rod concentration, even if it properly accounts for the I–N transition in the dilute regime. Moreover, the N–Sm phase transition is not expected to significantly depend on the rod aspect-ratio in the needle-like limit,34 so the strong increase of the volume fraction ϕN–Sm = 0.65 for M13-PEG20k compared to M13-PEG5k with ϕN–Sm = 0.43 suggests some interaction or inter-penetration between the PEG layers of close viruses. This interaction could originate in some deviation from the cylindrical shape of the rod-like particle (Fig. 1) which could matter at high densities, or in some partial compressibility of the PEG layer adding softness of the inter-particle potential.40
V. Conclusions
In this work, the quantitative liquid crystalline phase behavior of monodisperse colloidal semi-flexible rods stabilized by a hydrophilic polymer layer of tunable size has been reported. Thanks to the steric repulsion between the rod-like particles, the effective diameter and the effective volume fractions at different phase transitions have been determined in a straightforward way allowing for a quantitative comparison with hard rod predictions. If the I–N transition is appropriately described by an extension of the Onsager theory to semi-rigid rods, the soft interaction between polymers affects the dense states of the system grafted with the largest PEG coat (M13-PEG20k). Conversely, the rod-like particles having the lowest PEG molecular weight (M13-PEG5k) match the hard rod behavior in the whole range of rod densities. In this case, the effective volume fractions at both the N–Sm and Sm–Col phase transitions are shown to be in very good agreement with the renormalized phase diagrams of charged viral rods. These results confirm the feature of a model system of our sterically stabilized semi-flexible viral rods. We provide herein a new set of data that should stimulate further research in theory and computer simulations for establishing the detailed phase diagram of long and semi-flexible rods, focusing especially on the dense states with the relative stability of the smectic and the columnar mesophases.Acknowledgements
This research was supported by CNRS and Région Aquitaine. We would like to thank Nicolas Guidolin for his help in dn/dc measurements.References
- L. Onsager, The effects of shape on the interaction of colloidal particles, Ann. N. Y. Acad. Sci., 1949, 51, 627 CrossRef CAS.
- D. Frenkel, H. N. W. Lekkerkerker and A. Stroobants, Thermodynamic stability of a smectic phase in a system of hard rods, Nature, 1988, 332, 822 CrossRef CAS.
- A. Kuijk, D. V. Byelov, A. V. Petukhov, A. van Blaaderen and A. Imhof, Phase behavior of colloidal silica rods, Faraday Discuss., 2012, 159, 181 RSC.
- Z. Dogic and S. Fraden, in Soft Matter, ed. G. Gompper and M. Schick, Wiley-VCH, Weinheim, 2006, vol. 2, pp. 1–86 Search PubMed.
- E. Grelet, Hard-Rod Behavior in Dense Mesophases of Semiflexible and Rigid Charged Viruses, Phys. Rev. X, 2014, 4, 021053 Search PubMed.
- Z. Dogic and S. Fraden, Development of model colloidal liquid crystals and the kinetics of the isotropic smectic transition, Philos. Trans. R. Soc., A, 2001, 359, 997 CrossRef CAS.
- E. Grelet and S. Fraden, What Is the Origin of Chirality in the Cholesteric Phase of Virus Suspensions?, Phys. Rev. Lett., 2003, 90, 198302 CrossRef PubMed.
- T. Zan, F. Wu, X. Pei, S. Jia, R. Zhang, S. Wu, Z. Niu and Z. Zhang, Into the polymer brush regime through the “grafting-to” method: Densely polymer-grafted rodlike viruses with an unusual nematic liquid crystal behavior, Soft Matter, 2016, 12, 798 RSC.
- E. Barry, D. Beller and Z. Dogic, A model liquid crystalline system based on rodlike viruses with variable chirality and persistence length, Soft Matter, 2009, 5, 2563 CAS.
- K. R. Purdy and S. Fraden, Isotropic-cholesteric phase transition of filamentous virus suspensions as a function of rod length and charge, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061703 CrossRef PubMed.
- E. Grelet, Hexagonal Order in Crystalline and Columnar Phases of Hard Rods, Phys. Rev. Lett., 2008, 100, 168301 CrossRef PubMed.
- P. G. de Gennes, Poymers at an interface; a simplified view, Adv. Colloid Interface Sci., 1987, 27, 189 CrossRef CAS.
- I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley & Sons, Inc., New York, 2002 Search PubMed.
- M. P. Lettinga, J. K. G. Dhont, Z. Zhang, S. Messlinger and G. Gompper, Hydrodynamic interactions in rod suspensions with orientational ordering, Soft Matter, 2010, 6, 4556 RSC.
- E. Ostuni, R. G. Chapman, R. E. Holmlin, S. Takayama and G. M. Whitesides, A Survey of Structure-Property Relationships of Surfaces that Resist the Adsorption of Protein, Langmuir, 2001, 17, 5605 CrossRef CAS.
- K. Devanand and J. C. Selser, Asymptotic Behavior and Long-Range Interactions in Aqueous Solutions of Poly(ethylene oxide), Macromolecules, 1991, 24, 5943 CrossRef CAS.
- K. R. Purdy, Z. Dogic, S. Fraden, A. Rühm, L. Lurio and S. G. J. Mochrie, Measuring the nematic order of suspensions of colloidal fd virus by x-ray diffraction and optical birefringence, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 031708 CrossRef PubMed.
- E. E. Maier, R. Krause, M. Deggelmann, M. Hagenbüchle, R. Weber and S. Fraden, Liquidlike Order of Charged Rodlike Particle Solutions, Macromolecules, 1992, 25, 1125 CrossRef CAS.
- H. H. Wensink, Columnar versus smectic order in systems of charged colloidal rods, J. Chem. Phys., 2007, 126, 194901 CrossRef CAS PubMed.
- H. Graf and H. Löwen, Phase diagram of tobacco mosaic virus solutions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 1932 CrossRef CAS.
- E. M. Kramer and J. Herzfeld, Avoidance model for soft particles. II. Positional ordering of charged rods, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 6872 CrossRef CAS.
- M. A. Cotter, in The Molecular Physics of Liquid Crystals, ed. G. R. Luckhurst and G. W. Gray, Academic Press, London, 1979, pp. 169–189 Search PubMed.
- A. R. Khokhlov and A. N. Semenov, Liquid-crystalline ordering in the solution of partially flexible macromolecules, Physica A, 1982, 112, 605 CrossRef.
- Z. Y. Chen, Nematic Ordering in Semiflexible Polymer Chains, Macromolecules, 1993, 26, 3419 CrossRef CAS.
- A. Poniewierski, Nematic to smectic-A transition in the asymptotic limit of very long hard spherocylinders, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 5605 CrossRef.
- A. M. Somoza and P. Tarazona, Nematic and smectic liquid crystals of hard spherocylinders, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 965 CrossRef.
- P. van der Schoot, The Nematic-Smectic Transition in Suspensions of Slightly Flexible Hard Rods, J. Phys. II, 1996, 6, 1557 CrossRef CAS.
- J. M. Polson and D. Frenkel, First-order nematic-smectic phase transition for hard spherocylinders in the limit of infinite aspect ratio, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, R6260 CrossRef CAS.
- E. Pouget, E. Grelet and M. P. Lettinga, Dynamics in the smectic phase of stiff viral rods, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041704 CrossRef PubMed.
- A. V. Tkachenko, Nematic-Smectic Transition of Semiflexible Chains, Phys. Rev. Lett., 1996, 77, 4218 CrossRef CAS PubMed.
- P. Bladon and D. Frenkel, Simulating polymer liquid crystals, J. Phys.: Condens. Matter, 1996, 8, 9445 CrossRef CAS.
- S. Naderi and P. van der Schoot, Effect of bending flexibility on the phase behavior and dynamics of rods, J. Chem. Phys., 2014, 141, 124901 CrossRef PubMed.
- G. Cinacchi and L. de Gaetani, Phase behavior of wormlike rods, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051705 CrossRef PubMed.
- P. Bolhuis and D. Frenkel, Tracing the phase boundaries of hard spherocylinders, J. Chem. Phys., 1997, 106, 666 CrossRef CAS.
- J. A. C. Veerman and D. Frenkel, Relative stability of columnar and crystalline phases in a system of parallel hard spherocylinders, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 4334 CrossRef.
- J. A. Capitan, Y. Martinez-Raton and J. A. Cuesta, Phase behavior of parallel hard cylinders, J. Chem. Phys., 2008, 128, 194901 CrossRef PubMed.
- M. A. Bates and D. Frenkel, Influence of polydispersity on the phase behavior of colloidal liquid crystals: A Monte Carlo simulation study, J. Chem. Phys., 1998, 109, 6193 CrossRef CAS.
- Y. Martinez-Raton and J. A. Cuesta, Smectic and columnar ordering in length-polydisperse fluids of parallel hard cylinders, Mol. Phys., 2009, 107, 415 CrossRef CAS.
- Filamentous bacteriophages are considered as a monodisperse system of rods despite their presence in a small amount of a few polyphages (dimers, trimers, etc.) which do not affect the smectic phase stability because of their commensurability in length with the layer spacing29.
- K. Shundyak, R. van Roij and P. van der Schoot, Theory of the isotropic-nematic transition in dispersions of compressible rods, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021710 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00527f |
| This journal is © The Royal Society of Chemistry 2016 |