Hydrophilic nanoparticles stabilising mesophase curvature at low concentration but disrupting mesophase order at higher concentrations

Abstract

Using high pressure small angle X-ray scattering (HP-SAXS), we have studied monoolein (MO) mesophases at 18 wt% hydration in the presence of 10 nm silica nanoparticles (NPs) at NP–lipid number ratios (ν) of 1 × 10⁻⁶, 1 × 10⁻⁵ and 1 × 10⁻⁴ over the pressure range 1–2700 bar and temperature range 20–60 °C. In the absence of the silica NPs, the pressure–temperature (p–T) phase diagram of monoolein exhibited inverse bicontinuous cubic gyroid (Q^G_II), lamellar alpha (L_α), and lamellar crystalline (L_c) phases. The addition of the NPs significantly altered the p–T phase diagram, changing the pressure (p) and the temperature (T) at which the transitions between these mesophases occurred. In particular, a strong NP concentration effect on the mesophase behaviour was observed. At low NP concentration, the p–T region pervaded by the Q^G_II phase and the L_α–Q^G_II mixture increased, and we attribute this behaviour to the NPs forming clusters at the mesophase domain boundaries, encouraging transition to the mesophase with a higher curvature. At high NP concentrations, the Q^G_II phase was no longer observed in the p–T phase diagram. Instead, it was dominated by the lamellar (L) phases until the transition to a fluid isotropic (FI) phase at 60 °C at low pressure. We speculate that NPs formed aggregates with a “chain of pearls” structure at the mesophase domain boundaries, hindering transitions to the mesophases with higher curvatures. These observations were supported by small angle neutron scattering (SANS) and scanning electron microscopy (SEM). Our results have implications to nanocomposite materials and nanoparticle cellular entry where the interactions between NPs and organised lipid structures are an important consideration.

---

1. Introduction

Understanding the structure of lipid mesophases is important to their applications in biosensing,^1,2 gene therapy,^3–5 protein crystallisation,^6–8 and drug delivery.⁹ The mesophase structure can be tailored by the lipid molecular architecture (as characterised by their packing parameter) and by controlling intermolecular forces mediated via the hydrophilic headgroup and the hydrophobic tail. Changes in the external environment (e.g. temperature, pressure, pH, water content, and additives) can also affect mesophase stability and induce mesophase transitions.^10–14

Depending on their architecture and solution conditions, lipids can self-assemble into a range of different mesophases. The lamellar phase (L), consisting of domains of bilayer stacks, experiences the lowest degree of curvature (Fig. 1a), which can be further sub-divided (Fig. 1b): such as the alpha phase (L_α), also known as the fluid phase with splayed flexible tails; the ripple phase (P_β) with an undulated surface; and the crystalline phase (L_c) with compact and rigid hydrocarbon tails. Lipids can form both positive and negative curvature structures. The inverse mesophase structures with a negative curvature are typically denoted with a subscript “II”, and these include e.g. the inverted hexagonal phase (H_II), with tubular lipid aggregates packed into a hexagonal lattice. Other phases include the bicontinuous cubic phase with triply periodic minimal surfaces enclosing two interconnected water channels, and the fluid isotropic phase with no long range order. A homogenised mesophase sample (such as the ones we have studied here) typically consists of randomly oriented domains packed with a particular mesophase (Fig. 1c). The size of the domains (characterised by the coherence length) and the d-spacing fluctuations can both contribute to the broadening of the intensity peaks at different diffraction orders obtained in scattering experiments;^15–17 the larger the domain size and the smaller the d-spacing fluctuations, the smaller the full width at half maximum (FWHM) of the peaks, thus the bigger the coherence length, and the more highly ordered the mesophase sample is.¹⁸ Another factor is the thermal fluctuations in the bilayers, which can have a damping effect on the intensity of the higher order reflections.

Fig. 1 (a) Lipids may self-assemble to form the lamellar, cubic, hexagonal and fluid isotropic phases, with different curvatures in the constituent monolayers. (b) The fluid (L_α), ripple (P_β) and crystalline (L_c) lamellar phases. (c) Schematic of domains of L_c stacks at low hydration.

Knowledge of mesophase transitions is essential to tailoring desired mesoscopic structures for applications, such as light-activated release mechanism for drug delivery,¹⁹ catalysis,^20,21 photovoltaics,²² and nanowire production,²³ as well as being important on a fundamental level to understanding the energetic process of lipid molecular deformations. This process is also relevant to membrane fusion and cellular entrance by nanoparticles (NPs).²⁴ To form different mesophase structures, lipids must facilitate molecular deformations by tilting, stretching or bending, to accommodate different mesoscopic curvatures which deviate from the energetically optimal lipid configurations.²⁵ In addition, the unfavourable exposure of the hydrophobic tails to water typically occurs during the phase transition. This amounts to an energetic barrier for the phase transition,^26,27 which can be overcome by exerting stress to the lipids imparted by various stimuli such as hydration/dehydration, temperature, pressure, or an external mechanical force (e.g. shear).^10,13,28

Of particular interest to this work, mesophase transitions may also be induced by the presence of certain additives (such as NPs) with curvatures that mismatch the spontaneous curvature of the lipid monolayers, or with a surface chemistry that would preferentially interact with the lipid head or tail. In the case of 5 nm hydrophobic silver NPs, when exposed to a lamellar structure made of the double-chained surfactant dioctyl sulfosuccinate sodium (AOT), the NPs could penetrate and reside in the hydrophobic region. The silver NPs encouraged curvature by assisting the formation of stalk structures between the two separating bilayers.²⁹ In a number of simulation studies, the fluid model biomembrane was found to wrap around NPs of size smaller than 10 nm including dendrimers,³⁰ charged NPs³¹ and thiol-coated gold NPs.³² Other computer simulation studies have concluded that NP–lipid bilayer interactions are affected by the NP physical properties such as the size,^33,34 geometry,^35,36 surface charge density,^32,37 hydrophobicity,^38,39 and surface ligand distribution.^40–42 For more information on nanoparticle adsorption on membranes, we refer the reader to the review by Saric et al.⁴³

In previous studies, mesophase transitions have been commonly induced by varying temperature or hydration levels, and characterised by scattering methods,⁴⁴ nuclear magnetic resonance,²³ differential scanning calorimetry⁴⁵ and polarised light microscopy.⁴⁶ Mesophase transitions may also be induced by varying the pressure applied on the hydrated lipid system, as implemented in high pressure small angle X-ray scattering (HP-SAXS) measurements.^13,47–51 The covalent structure of biological materials such as lipids, proteins and polysaccharides are not perturbed by pressures below 20 kbar; instead, the pressure affects the configuration of these molecules.⁴⁸ Increasing the pressure leads to a decrease in the lipid tail volume that lipids pervade, shifting the curvature to more positive values, reducing the magnitude of the curvature of inverse mesophase structures while increasing the curvature of mesophases with initially a zero or positive curvature.

There are a number of advantages of using pressure to induce phase transitions. Pressure can propagate through a sample volume rapidly, greatly reducing the required equilibrium time, hence enabling time limited experiments. Large pressure-jumps are also possible, allowing for detailed kinetic studies on mesophase transitions. In addition, pressure change has smaller effects on the solvent properties compared to thermal stimuli. HP-SAXS has been used to study mesophase transitions and their kinetics on a range of pure phospholipid systems, including dipalmitoylphosphatidylcholine (DPPC), dieurucoylphosphocholine (DEPC), and dioleoylphosphocholine (DOPC), and mixed systems; egg-phosphatidylethanolamine (egg-PE), dipalmitoylphosphatidylcholine (DMPC)–distearoylphosphocholine (DSPC), DMPC–myristic acid dihexanoylphosphocholine (DHPC)–DMPC, DMPC–gramicidin D and palmitoyloleoylphosphatidylcholine (POPC)–sphingomyelin (SM)–cholesterol bilayers.^49,50,52,53

Using HP-SAXS, Bulpett et al.⁵¹ have recently observed that 14 nm hydrophobic silica NPs promoted L to H_II transitions in dioleoylphosphoethanolamine (DOPE) mesophases, shifting the H_II/L_α boundaries in the DOPE pressure–temperature (p–T) phase diagram. The addition of the hydrophobic NPs enlarged the H_II phase region and encouraged the highly curved H_II phase to occur at lower temperatures. It would be interesting to study the effect of NPs on transitions between the L phase and a bicontinuous phase. Motivated by this, here we have studied the monoolein (MO) mesophase transition behaviour in the absence and presence of hydrophilic silica NPs.

Monoolein (MO) is among the most widely studied lipids,⁹ with six different mesophases identified at hydration levels <60 wt% and temperatures up to 120 °C.¹⁰ Further MO mesophases can also form in the presence of additives. For instance, the lamellar sponge phase (L₃) has been reported with the addition of 1,4-butanediol.²⁸ Such a rich mesophase behaviour makes MO systems well suited for mesophase transition studies.^52,54,55 In the reported p–T diagram for MO in excess water, the inverse cubic double diamond phase (Q^DD_II) persisted over a large temperature and pressure range, with the H_II only observed at the high temperature and low pressure region and the L_c further at lower temperatures and higher pressures.^48,56 Monoelaidin (ME), a monoglyceride with a similar structure to MO but a saturated bond in the trans- rather than cis-position, expresses an even more diverse phase behaviour in the p–T diagram, with the additional inverse cubic primitive (Q^P_II) and L_α phases observed.⁵⁶ In an HP-SAXS kinetics study, a 2 : 1 lauric acid : dilauroylphosphatidylcholine (DLPC) lipid system hydrated to 50 wt% showed a rapid Q^DD_II–Q^G_II transition, with an H_II phase implicated as the transient structure.⁵⁷ However, no such H_II intermediate phases were observed in the Q^DD_II–Q^G_II transition for MO.⁵⁴ To our knowledge, kinetic studies on the MO Q^DD_II–Q^G_II phase transition in the presence of NPs have not been previously reported.

In the current work, we have studied the effect of NPs on the MO mesophase behaviour using the HP-SAXS technique. Spherical hydrophilic silica NPs of 10 nm in diameter were added to MO hydrated to 18 wt% at NP–lipid number ratio (ν) of 1 × 10⁻⁶, 1 × 10⁻⁵ and 1 × 10⁻⁴. This corresponded to NP–lipid volume ratios (ϕ) of 8.7 × 10⁻², 8.7 × 10⁻³ and 8.7 × 10⁻⁴, respectively. The mesophase behaviour was investigated at a pressure range of 1–2700 bar and a temperature range of 20–60 °C. We have observed that the mesophase transition temperature (T) and pressure (p) were affected by the NP addition and the extent of this effect also depended on the NP concentration. We have also attempted to examine the NP distribution in the mesophases using contrast matched small angle neutron scattering (SANS) and scanning electron microscopy (SEM).

2. Materials and methods

2.1. Sample preparation

1-(cis-9-Octadecenoyl)-rac-glycerol (1-monoolein (MO), >99% purity) was purchased from Nu-Chek, US, and stored at −30 °C. Before use the MO was freeze dried (SciQuip alpha 1–2 LDplus) and then its purity was checked by electrospray ionisation mass spectrometry (ESI-MS). The NPs in the form of bare hydrophilic silica nanopowder (>99.8%, 10.6 ± 3.6 nm, PlasmaChem, Germany) were characterised by transmission electron microscopy (TEM). Once suspended in ethanol by sonication, the NPs were added to the MO at NP–lipid volume ratios (ϕ) of 8.7 × 10⁻², 8.7 × 10⁻³ and 8.7 × 10⁻⁴, which could be related to the ν as:With the use of MO molecular weight (M_w = 356.54 g mol⁻¹), density (ρ_l = 0.94 g cm⁻³), and the NP diameter (D ∼ 10 nm), the ν values were estimated to be 1 × 10⁻⁶, 1 × 10⁻⁵ and 1 × 10⁻⁴. After adding the NPs in ethanol to the dried MO, the sample containing NP–lipid–ethanol was shaken in a Stuart SI505 shaker at 40 °C for a minimum of 3 h until thoroughly mixed, and ethanol was then removed by evaporation in a vacuum oven (Heraeus vacutherm VT6025) until a constant weight was reached. The dried sample with the designated MO-NPs composition was then immediately hydrated to 18 wt% by adding appropriate amounts of water (Milli-Q; resistivity 18.2 MΩ cm and total organic content (ToC) <3–4 ppb) for the HP-SAXS measurements. For the SANS measurements, H₂O : D₂O (Sigma-Aldrich) was added at an 89 : 11 volume ratio to 30 wt% to contrast match the scattering by MO and the solvent. The sample vial was then sealed and centrifuged until all the materials were collected at the bottom of the vial before being shaken at 40 °C at 750 rpm overnight. The sample was centrifuged again for 10–20 s before being freeze thawed for 54 cycles to assist mixing. After every 10 cycles the sample was centrifuged again for ∼10–20 s. The sample obtained was then stored at −30 °C before scattering measurements were carried out within 2 and ½ weeks.

2.2. SAXS measurements

SAXS was performed at I22 beamline at the Diamond Light Source synchrotron (Oxfordshire, UK) using a high-pressure cell, designed by Brooks et al.⁵⁸ X-ray energy was set to 18 keV (wavelength λ = 0.689 Å) at a camera length of 3 m giving a scattering vector (q) range of 0.015–0.66 Å⁻¹ using a Pilatus P3-2M detector (Dectris, Baden-Daetwill, Switzerland), calibrated with silver behenate and glassy carbon. Here, q = 4π sin(2θ/2)/λ, with 2θ being the scattering angle. Within the pressure cell, polycarbonate KI-Beam capillary tubes were used as the sample holder (Enki Microtubes, Italy). The capillary tube was prepared by coating one end with Araldite® instant clear epoxy resin and cured at 40 °C for 30 min. The sample was loaded and compressed with the supplied cap to remove air bubbles and sealed with the epoxy resin. The resin was cured under the same conditions as above, then the sample was frozen to remove possible mesophase hysteresis. Samples were inserted into the pressure cell and cycled between 1 and 2700 bar, holding for 30 s each time before a pressure change and this was repeated six times to check for any possible leakage in the capillary and also to ensure homogeneity within the sample. Samples were measured at 20, 40, 50 and 60 °C between 1–2700 bar at 300 bar steps, allowing an equilibrium time of 2 min per pressure step and 20 min per temperature step. At the end of the experiment samples were returned back to ambient pressure and temperature and scanned again to ensure that no sample damage or composition change had occurred during the measurements. The collected scattering intensity was normalised by the incident beam intensity and radially integrated to obtain 1D scans using DAWN 1.1 beta⁵⁹ (a data analysis package developed at Diamond) and analysed with Igor pro 6.2 and YAX 2.0.⁶⁰ The peak positions from the 1D scans can be used to identify the mesophase, as shown in Fig. S1 in the ESI.† The FWHM of the peaks was calculated by first subtracting either a linear or cubic background around the peak and then fitting with a Gaussian function.

2.3. SANS measurements

SANS was performed at the Sans2d diffractometer at the ISIS neutron facility (Rutherford Appleton Laboratory, UK) using a water tight sample cell with its design based on the sample cells available on the D22 beamline at the ILL facility (Grenoble). Possible residual shear effect during sample loading was removed by heating the sample to 60 °C then freezing at −16 °C. Neutron wavelengths of 1.75–16.5 Å were used simultaneously by time of flight. Incident collimation and sample-detector distances were both 4 m for a q range of 0.005–0.591 Å⁻¹, and the sample aperture was 8 mm. The samples were measured at 12, 31, 39, 45, 50 and 73 °C, allowing 40 min equilibrium time for each temperature step. Similar to the SAXS measurements, at the end of the experiment, samples were returned to ambient temperature and scanned again to check if any sample damage had occurred during the measurements. The data was reduced and the solvent background scattering was subtracted by MantidPlot 2.6.0 and analysed with the Igor script Irena.⁶¹

3. Results and discussions

3.1. p–T phase diagram of MO mesophases without NPs

As a control, the p–T phase diagram was determined for MO hydrated at 18 wt% (Fig. 2). At ambient pressure, Q^G_II, L_α and L_c, as well as two mixed phases were observed. With increasing pressure the Q^G_II phase was structurally unfavourable due to the drive towards zero interfacial curvature (as described above). The phase transition to a flat L_α phase is accompanied by a significant reduction in the lattice parameter from 101–105 Å to 40–43 Å (Fig. S3 in ESI†). Our observation is consistent with those previously reported in other mesophase systems.^13,47,54,62 In the p–T diagram a region co-existence between L_α and L_c was observed at the low temperature range; when the pressure was increased, L_α stability decreased and only L_c remained at the high pressure low temperature region of the p–T phase diagram. The Q^G_II phase was present at the top left corner of the p–T phase diagram (high T and low p), and increasing pressure destabilised the Q^G_II phase which transformed into L_α, through a limited p–T range in which the Q^G_II and L_α phases co-existed. Fig. S2 in the ESI,† shows all the 1D scans measured for the NPs free control system at all temperatures and pressures measured.

Fig. 2 p–T phase diagram of MO hydrated to 18 wt%. In the range 20–60 °C and 1–2700 bar the MO formed Q^G_II and L phases with L_α–Q^G_II co-existence and L_α–L_c co-existence regions also observed.

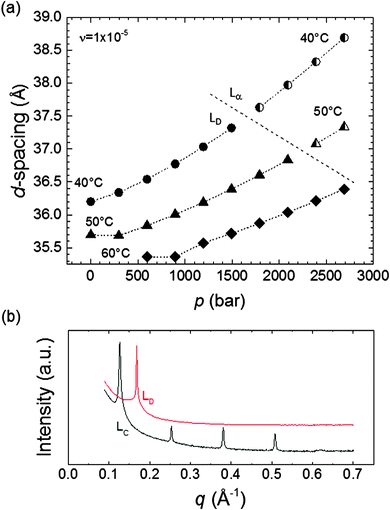
An L_α to L_c transition was observed upon a p increase or a T decrease. The d-spacing (d = 2nπ/q_n, where n is the order of the diffraction peak and q_n its position) for the L_α phase ranged between 40.3–44.1 Å, ∼6 Å smaller than that for the L_c phase at 20 °C (d = 49.0–49.8 Å) due to the increased L_c tail order, which increased the bilayer thickness slightly (Fig. 3). The error in the d-spacing is estimated to be σ_d = 0.02 Å (ESI,† 4). The L_c and L_α phases can be distinguished by the pressure dependence of their d-spacing. Whilst the L_αd-spacing increased mildly with the pressure due to enhanced tail ordering resulting in lateral compression of the bilayer, the hydrophobic tails in the L_α phase were already highly ordered, and thus the d-spacing remained largely constant with the pressure increase. Fig. 3 also shows that the L_cd-spacing slightly decreased as p increased, and this could be attributed to the increased pressure providing a more uniform compression of the lipids in the bilayer that is already highly ordered, resulting in the observed slight bilayer thinning.

Fig. 3 d-spacing vs. p for the MO L_α (filled symbols) and L_c (partially filled circles) mesophases. The d-spacing for the L_α phase increased slightly with pressure, whereas that for the L_c phase remained largely constant. The uncertainty in the d-spacing is estimated as δd = 0.02 Å. The stability of the pressure within the sample cell was ±5 bar.⁵⁸

3.2. p–T diagrams in the presence of NPs

The p–T diagrams in Fig. 4 show the MO mesophase behaviour with the addition of 10 nm silica NPs, where an NP concentration (i.e. NP/lipid number ratio (ν)) dependence was observed. We note that the hydrophilic surface of the silica NPs would complete with the MO head groups for the limited amount of water molecules. This would result in a dehydrating effect, and this effect could be considered as shifting the phase boundaries in the phase diagrams to the left. In fact, one could consider the NP/MO/water system a ternary mixture. However, the effect of NPs is more complex and cannot be accounted for by considering them as a molecular additive. Their surface chemistry, aggregation structure, distribution of the aggregates, as well as their shape, will all contribute the mesophase behaviour of the NP/MO/water mixture.

Fig. 4 p–T diagrams of MO mesophases containing silica NPs at ν of (a) 1 × 10⁻⁶, (b) 1 × 10⁻⁵, and (c) 1 × 10⁻⁴ between 20–60 °C and 1–2700 bar. At lower ν, the NPs stabilised the Q^G_II phase so that its phase region persisted to higher pressures and lower temperatures. However, at higher NP ν, the Q^G_II phase was suppressed and the lamellar phases were retained until the fluid isotropic (FI) phase formed.

At ν = 1 × 10⁻⁶ (Fig. 4a), the Q^G_II structure was more prominent compared to the pure MO system in Fig. 2, with an enlarged Q^G_II region, as well as an enlarged L_α/Q^G_II coexistence region and the emergence of a Q^G_II/L_α/L_c triply mixed phase region. In contrast at higher ν (1 × 10⁻⁴ and 1 × 10⁻⁵, Fig. 4b and c) the Q^G_II phase did not form in the p–T range investigated; instead, the lamellar phases were retained throughout until the fluid isotropic (FI) phase formed.

At higher ν values, a lamellar phase (termed L_D phase; see Fig. 5b) was prominent, at the expense of the Q^G_II phase. Compared to the L_c phase, the L_D phase had similar d-spacing values; however, the L_D phase did not have the same short range order, evident by the absence of higher order Bragg peaks at high q in SAXS 1D scan Fig. 5b). If a transition to a different mesophase, other than an alternative lamellar phase, had occurred, then a jump in the d-spacing value (similar to that shown in Fig. 3) would have been expected. However, this was not observed during the L_D–L_α transition, and instead the d-spacing followed a steady increase, suggesting that the bilayer structure was retained. The 1D scattering curve of the L_D phase showed a single sharp peak (Fig. 5b), distinguishing it from that for L_c, which possessed multiple peaks with evenly spaced q values. This scattering pattern has been previously observed and attributed to the L phase.^63,64 These considerations taken together, the L_D phase is likely to be a bilayer structure with a higher degree of disorder compared to the L_α phase.

Fig. 5 (a) Comparison of the d-spacing values for L_D and L_α phases at 40, 50 and 60 °C at ν of 1 × 10⁻⁵. The d-spacing for both L_α and L_D followed the same increasing trend with pressure (dotted lines as a guide for the eye). (b) 1D SAXS curves showing the appearance of higher order Bragg peaks after the L_D–L_c transition, suggest an enhanced order in the lamellar structure rather than a complete mesophase transition. The vertical scale of the curves has been displaced for clarity.

At ν = 1 × 10⁻⁴ and 1 × 10⁻⁵ the FI phase formed, which was not observed in the NP free p–T diagram. According to the MO phase diagram produced by Qiu and Caffrey with MO hydrated at 18 wt%, the FI phase was not expected until 90–95 °C.¹⁰ Thus, our observation indicates that, due to the presence of silica NPs, the FI phase had formed at a temperature 30–35 °C lower than expected. In contrast, at ν = 1 × 10⁻⁶, the FI and L_D phases were not observed, and instead the Q^G_II phase was formed, which appeared at a lower temperature and was retained at higher pressures when compared to the NP free p–T diagram.

The differences in the p–T diagrams in the absence (Fig. 2) and presence (Fig. 4) of NPs reflect the effects of NP–membrane interactions. An important question to address is the distribution and location of the NPs in the mesophases. To this end, contrast matched SANS experiments were performed (Fig. 6). The idea is that the scattering would be predominantly due to the NPs, from which one could deduce the size and shape of the NPs by fitting the SANS curve in the low q range; whereas MO would be made “invisible” to neutrons by matching its scattering length density with that of the H₂O/D₂O mixture (i.e. instead of using pure H₂O for preparing the MO mesophase as in the HP-SAXS experiment) by tuning the H₂O/D₂O mixing ratio. Fig. 6 shows the SANS curves of the contrast matched MO mesophase samples at 30 wt% composition at 15 °C, at ν of 1 × 10⁻⁴, 1 × 10⁻⁵ and 1 × 10⁻⁶. Fig. S4 (ESI†) presents the scans of each concentration at all temperatures measured, which are all very similar in their scattering patterns. In all scans a small peak is observed between 0.1–0.2 Å⁻¹ (as indicated by a downward arrow in Fig. 6), which concurs with the first Bragg peak observed in the HP-SAXS (cf.Fig. 5b). This small amount of scattering was due to the imperfect contrast matching ratio between MO and the D₂O and H₂O mixture. However, this would not mask the details at the lower q. When compared to the modelled SANS curve for NPs 10.6 ± 3.6 nm (Fig. 6 inset), the absence of the Guinier regime at low q indicates that the NPs did not exist as individually dispersed particles, and must have formed aggregates (possibly including some water and MO molecules). The absence of the Guinier region plateau at low q (which is evident in the model SANS curve in the Fig. 6 inset) suggests that the aggregate size had exceeded the upper limit of the particle size (∼126 nm, corresponding to the minimum q, q_min = 0.005 Å⁻¹). The initial decay in SANS intensity at low q varies with the NP concentration, suggesting different NP arrangements in the samples with different NP concentrations. However, the contrast matched SANS curves did not change with temperature (Fig. S4 in ESI†), even at temperatures where a mesophase transition was expected, as shown in the HP-SAXS p–T phase diagrams in Fig. 2 and 4. The fact that the d-spacing of the mesophases was not affected by the NPs also suggests that the NPs were not intercalated within the mesophase structure. Rather, clustered around the periphery of the mesophase domains.

Fig. 6 Contrast matched SANS curves on a log–log scale of silica NPs in 30% hydrated MO at ν of 1 × 10⁻⁴, 1 × 10⁻⁵ and 1 × 10⁻⁶, measured at 15 °C. The solvent was a mixture of H₂O : D₂O at a volume ratio of 89 : 11, to match the scattering length density of MO. The SANS curves showed little temperature dependence, with the curves at all the temperatures shown in Fig. S4 (ESI†). The inset shows a model SANS curve for 10 ± 3.4 nm spherical nanoparticles (modelled using SansView), with the polydispersity modelled as a Gaussian distribution. The SLD of the contrast matched solvent was 2.1 × 10⁻⁵ Å⁻², and that for the silica sphere was 3.475 × 10⁻⁶ Å⁻². The vertical scale of the curves has been displaced for clarity.

SEM was used to further elucidate the distribution of the NPs in the sample. For this, the lipid and water molecules of a sample containing 10 nm NPs at ν = 1 × 10⁻⁴ were burnt off by heating at a rate of 10 °C min⁻¹ from RT to 600 °C, and then the sample was held isothermally for 1 h before cooling. The obtained SEM images revealed that the residual structure of the silica NPs was a highly porous network (Fig. S5 in ESI†). Previous dissipative particle dynamics simulation studies have shown that NPs could reside at a lipid bilayer interface as either aggregated clusters, a chain of pearls or as non-aggregated individual particles depending on the NP size.^34,65 Surface charge distribution has also been reported to affect the aggregated structure including dense ordered crystal-like aggregates, dendritic structures, clusters and linear chain of pearls.^41,42 The properties of the bilayer are also known to affect the NP aggregation. Šarić and Cacciuto reported that spherical NPs aggregated together either as hexagonal arrays or a linear chain of pearls depending on the bilayers bending rigidity.⁶⁶ For bilayers with bending rigidity values comparable to that of a biological membrane (10–100k_BT), the NPs formed a chain of pearls structure, while when the bilayer bending rigidity exceeded outside of this range, the hexagonal aggregated structure was preferred.

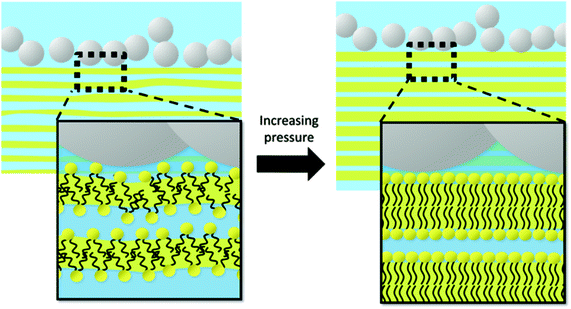
Whilst the contrast matched SANS and SEM results could not ascertain the exact distribution of the NPs, the results suggest the NPs formed clusters. We suggest that, at higher NP concentrations, the NPs could aggregate into a chain of pearls structure (Fig. 7) as Šarić and Cacciuto suggested,⁶⁶ which was sintered together to form the porous structure revealed by the SEM image (Fig. S5, ESI†). It is conceivable that the corrugated NP chains of pearls have a large hydrophilic surface area. The affinity, and thus preferred contact, between the NP clusters and the hydrated lipid domain boundaries would stabilise the lamellar structure, as a phase transition to Q^G_II would involve detaching the lamellar phase domain from the NP clusters or deforming the conformation of the chains of pearls, both energetically costly. As such, the NP clusters at high NP concentrations would suppress the increase in curvature from the L_α to the Q^G_II phase. However, we would like to emphasize caution in drawing this conclusion, and such a hypothesis on the structure of the nanoparticle aggregates is at this stage a speculation. It remains challenging to ascertain the structure and location of the nanoparticles and their aggregates in the mesophase, which will be the focus of our continuing experimental effort. The lamellar domain size can be estimated from an analysis using the Scherrer equation and using the FWHM of the first Bragg peak.^16,67,68 At 40 °C, the L_D and L_α domain sizes were similar (124.3 ± 61.9 and 140.8 ± 15 nm respectively, for ν = 1 × 10⁻⁵), which suggests that the number of bilayers stacked to form the domains did not change significantly. As the pressure is increased, the suppression of the transition to the Q^G_II phase means that alternative pathways must be adopted to reduce the volume pervaded by the lipids, leading to the more densely packed L_c phase, whilst the NPs remained in their chain of pearls structure at the domain boundaries (Fig. 7).

Fig. 7 At higher NP ν, the NPs may form chain of pearl-like aggregates. These aggregates reside at the domain interface. Upon increasing the pressure, the L_α phase to the Q^G_II phase transition is suppressed. To seek smaller volumes, the lipids would adopt denser packing. As a result, the L_D phase would rearrange, eventually forming the L_α and then the L_c domains, with the NPs retaining the chain of pearls structure at the domain boundaries.

As discussed above, NPs have been shown to affect the structure of lipid packing in mesophases. For instance, Wang et al.⁶⁹ found that, upon exposure of DLPC, DOPC and DPPC unilamellar vesicles to 20 nm polystyrene NPs modified with carboxyl and amidine surface groups, the NPs reconstructed the vesicle surface locally. The cationic amidine NPs increased the order of the lipid packing, which transformed to a more gel-like phase, within a fluid bilayer; whereas the anionic carboxyl NPs increased the fluidity in the bilayer. The NP size has also been observed to be sensitive to the membrane stiffness, with smaller polystyrene NPs (≤200 nm) concentrated at stiffer, ordered phases of a mixed DOPC/DPPC/Cholesterol bilayer, while larger NPs preferred the more disordered bilayer regions.⁷⁰ In a dissipative particle dynamics simulation, uncharged NPs were observed to alter the morphology of the H₁T₃ modelled lipid vesicles via membrane-curvature-mediated NP clustering at the interior and exterior of the vesicle, enhancing bending rigidity and enabling the observed morphology alterations.⁶⁵ Another molecular dynamics study showed that 2–5 nm cadmium selenide quantum dots increased the fluidly of the bilayer of mixed DOPC/DMPC/DSPC vesicles.⁷¹ However, a clear explanation as to why the NPs aggregate into a range of structures remained elusive.

A possible explanation for the absence of the Q^G_II phase at NP ν = 1 × 10⁻⁴ and 1 × 10⁻⁵ at elevated temperatures may lie in the consideration of the stress that the NP aggregates could impose on the bilayer. As the temperature increases, the lipid bilayer becomes more fluid, and thus more susceptible to curvature. This would continue with increasing temperature until the Q^G_II phase forms. However, the interactions between the bilayers and the NP clusters in the configuration of the linear chain of pearls would physically constrain the lipids, preventing curvature formation. As the temperature continues to rise, the lipid bilayer would become increasingly fluid until forming the more disordered L_D. Further temperature increase would see the bilayer structure unable to relieve the increasing stress within the structure, resulting in the formation of the disordered fluid isotropic phase at a lower temperature than expected in the absence of NPs.

In contrast, at the lower ν of 1 × 10⁻⁶, the stability of the Q^G_II phase was enhanced (Fig. 4). We speculate that this could be explained by the formation of a different NP aggregate structure. Due to the scarcity of the NPs, rather than the chain of pearls structure, the NPs could form isolated clusters, i.e. without the extended chain structure. These discrete clusters would accumulate at the water–Q^G_II mesophase interface. The corrugated surfaces of the aggregate clusters would be better accommodated by the curved Q^G_II surface, probably due to the optimal contact area with the lipid surface. This in effect would hinder the transition to the L phase as the pressure is increased, leading to a higher Q^G_II/L transition pressure and the observed enlarged Q^G_II phase region. Further pressure increase would ultimately negate such stabilising effects of the NP clusters, leading to Q^G_II/L transition occurring progressively spatially, thus explaining the observed enlargement in the L/Q^G_II co-existence region in Fig. 4a.

4. Conclusions

The p–T diagrams for monoolein (MO) mesophases at 18 wt% hydration have been obtained, in the presence of 10 nm silica nanoparticles (NPs) at lipid–NP number ratios (ν) of 1 × 10⁻⁶, 1 × 10⁻⁵ and 1 × 10⁻⁴ over the pressure range 1–2700 bar and temperature range 20–60 °C, using high pressure small angle X-ray scattering (HP-SAXS). The presence of the NPs significantly altered the p–T phase diagram, changing the pressure (p) and the temperature (T) at which the transitions between different mesophases occurred. In particular, a strong and nonlinear NP concentration effect on the mesophase behaviour was observed. At high concentrations, NPs suppressed the Q^G_II phase; instead, the lamellar phases were retained, bypassing the curved Q^G_II phase and transforming into the fluid isotropic phase at 60 °C at low pressure. This transition temperature was lower by 30–35 °C as compared to that in the control sample (without NPs). We attribute this to NPs forming aggregates with a chain of pearls structure at the mesophase domain boundaries, hindering transitions to the mesophases with higher curvatures. These observations were supported by small angle neutron scattering (SANS) and scanning electron microscope (SEM) imaging.

In contrast, the NPs at the lowest ν studied (1 × 10⁻⁶) encouraged curvature and the formation of the Q^G_II phase. We suggest that this could be attributed to a different structure that NPs formed at the mesophase domain boundaries. Instead of the continuous chains of pearls, insufficient numbers of NPs would form isolated smaller clusters, which could be accommodated at the Q^G_II domain surface. In addition, the absence of the continuous chain-like clusters as in the case of high NP concentrations would mean that the L–Q^G_II transition would not require disruption of these structures, which is energetically costly. As such, the NPs would in effect act as a curvature catalyst, promoting the Q^G_II phase, leading to the enlarged the Q^G_II phase region in the p–T phase diagram (Fig. 4a).

Our results show the complex effects of the nanoparticle concentration on their interactions with model membrane systems. Previously, we have observed that hydrophobic nanoparticles promoted inverted hexagonal phases, as compared to the hydrophilic counterparts,⁵¹ pointing to the importance of the NP surface chemistry. Our results here show that the NP concentration also plays an important role, and the effects may be interpreted in terms of the NP aggregation, the structure of the aggregates, and the effect of these structures have on the mesophase transitions. The molecular deformations the lipids undergo during mesophase transitions are analogous to those experienced by the lipids during endocytosis in the cell membrane,^24,72 a process that can be induced and exploited by NPs for cellular entry. As such, we have suggested that studying the effects of NPs on lipid mesophase transitions using physicochemical methods, in this case HP-SAXS, could contribute to understanding, on a fundamental level, NP induced membrane fusion, relevant to the topical nanotoxicity field, where gaining cellular entry is one of the important mechanisms for NPs to impart toxicity.

Acknowledgements

W. H. B. acknowledges funding from the Engineering and Physical Science Research Council (EPSRC), the Royal Society, Taiho Kogyo Tribology Research Foundation (TTRF), the European for Cooperation in Science and Technology (CMST COST) Action CM1101, and the Marie Curie Initial Training Network (MC-ITN) NanoS3. C. M. B. thanks the Bristol Centre for Functional Nanomaterials for funding (EP/G036780/1). We acknowledge Diamond Light Source for beamtime on I22 under proposal SM8319-1. Experiments at the ISIS Pulsed Neutron and Muon Source were supported by a beamtime allocation from the Science and Technology Facilities Council under proposal RB1120306. Dr A. Perriman is thanked for his advice on high pressure SAXS capillary preparation, and Dr D. Tang for her advice on the HP-SAXS experiment. Dr A. Seddon is acknowledged for a useful discussion on monoolein, with whom manuscripts on anisotropic scattering due to nanoparticle-containing mesophases are under preparation.

Notes and references

1. B. A. Cornell, V. L. B. Braach-Maksvytis, L. G. King, P. D. J. Osman, B. Raguse, L. Wieczorek and R. J. Pace, Nature, 1997, 387, 580–583.
2. A. Angelova, M. Ollivon, A. Campitelli and C. Bourgaux, Langmuir, 2003, 19, 6928–6935.
3. S. R. Cyrus, Curr. Opin. Struct. Biol., 2001, 11, 440–448.
4. L. Wasungu and D. Hoekstra, J. Controlled Release, 2006, 116, 255–264.
5. D. Costa, W. H. Briscoe and J. Queiroz, Colloids Surf., B, 2015, 133, 156–163.
6. M. Caffrey and V. Cherezov, Nat. Protoc., 2009, 4, 706–731.
7. M. Caffrey and C. Porter, J. Visualized Exp., 2010, 45, e1712.
8. V. Cherezov, J. Clogston, Y. Misquitta, W. Abdel-Gawad and M. Caffrey, Biophys. J., 2002, 83, 3393–3407.
9. C. V. Kulkarni, W. Wachter, G. Iglesias-Salto, S. Engelskirchen and S. Ahualli, Phys. Chem. Chem. Phys., 2011, 13, 3004–3021.
10. H. Qiu and M. Caffrey, Biomaterials, 2000, 21, 223–234.
11. C. Grabielle-Madelmont and R. Perron, J. Colloid Interface Sci., 1983, 95, 471–482.
12. P. Alexandridis, U. Olsson and B. Lindman, Langmuir, 1998, 14, 2627–2638.
13. T. Y. D. Tang, N. J. Brooks, C. Jeworrek, O. Ces, N. J. Terrill, R. Winter, R. H. Templer and J. M. Seddon, Langmuir, 2012, 28, 13018–13024.
14. H. Chang and R. M. Epand, Biochim. Biophys. Acta, Biomembr., 1983, 728, 319–324.
15. A. L. Patterson, Phys. Rev., 1939, 56, 978–982.
16. T. G. Dane, P. T. Cresswell, O. Bikondoa, G. E. Newby, T. Arnold, C. F. J. Faul and W. H. Briscoe, Soft Matter, 2012, 8, 2824–2832.
17. J. M. Bulpett, A. M. Collins, N. H. M. Kaus, P. T. Cresswell, O. Bikondoa, D. Walsh, S. Mann, S. A. Davis and W. H. Briscoe, J. Mater. Chem., 2012, 22, 15635–15643.
18. B. Sironi, T. Snow, C. Redeker, A. Slastanova, O. Bikondoa, T. Arnold, J. Klein and W. H. Briscoe, Soft Matter, 2016, 12, 3877–3887.
19. J. D. Du, W.-K. Fong, S. Salentinig, S. M. Caliph, A. Hawley and B. J. Boyd, Phys. Chem. Chem. Phys., 2015, 17, 14021–14027.
20. S. A. Miller, E. Kim, D. H. Gray and D. L. Gin, Angew. Chem., Int. Ed., 1999, 38, 3021–3026.
21. T.-T.-T. Nguyen, F.-X. Simon, N. S. Khelfallah, M. Schmutz and P. J. Mesini, J. Mater. Chem., 2010, 20, 3831–3833.
22. D. Adam, P. Schuhmacher, J. Simmerer, L. Haussling, K. Siemensmeyer, K. H. Etzbachi, H. Ringsdorf and D. Haarer, Nature, 1994, 371, 141–143.
23. L. Liu, G. Tan, G. McPherson, V. T. John, K. Maskos and A. Bose, Langmuir, 2008, 24, 9286–9294.
24. C. M. Beddoes, C. P. Case and W. H. Briscoe, Adv. Colloid Interface Sci., 2015, 218, 48–68.
25. V. A. Frolov, A. V. Shnyrova and J. Zimmerberg, Cold Spring Harbor Perspect. Biol., 2011, 3, a004747.
26. P. I. Kuzmin, J. Zimmerberg, Y. A. Chizmadzhev and F. S. Cohen, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 7235–7240.
27. S. M. Gruner, V. A. Parsegian and R. P. Rand, Faraday Discuss., 1986, 81, 29–37.
28. A. M. Seddon, G. Lotze, T. S. Plivelic and A. M. Squires, J. Am. Chem. Soc., 2011, 133, 13860–13863.
29. X. Chen, E. Shlomo, R. Oren, W. Wang, L. Niu, Z. Sui, B. Zhu, X. Yuan and K. Yang, Sci. China, Ser. B: Chem., 2001, 44, 492–499.
30. R. Guo, J. Mao and L.-T. Yan, ACS Nano, 2013, 7, 10646–10653.
31. Y. Li and N. Gu, J. Phys. Chem. B, 2010, 114, 2749–2754.
32. E. L. d. Rocha, G. F. Caramori and C. R. Rambo, Phys. Chem. Chem. Phys., 2013, 15, 2282–2290.
33. J. Lin and A. Alexander-Katz, ACS Nano, 2013, 7, 10799–10808.
34. T. Yue and X. Zhang, ACS Nano, 2012, 6, 3196–3205.
35. K. Yang and Y.-Q. Ma, Nat. Nanotechnol., 2010, 5, 579–583.
36. R. Vácha, F. J. Martinez-Veracoechea and D. Frenkel, Nano Lett., 2011, 11, 5391–5395.
37. J. Lin, H. Zhang, Z. Chen and Y. Zheng, ACS Nano, 2010, 4, 5421–5429.
38. B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Muller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464.
39. A. K. Sachan and H.-J. Galla, Small, 2013, 10, 1069–1075.
40. H.-M. Ding, W.-D. Tian and Y.-Q. Ma, ACS Nano, 2012, 6, 1230–1238.
41. Y. Li, X. Zhang and D. Cao, J. Phys. Chem. B, 2013, 117, 6733–6740.
42. Y. Li, X. Zhang and D. Cao, Soft Matter, 2014, 10, 6844–6856.
43. A. Saric and A. Cacciuto, Soft Matter, 2013, 9, 6677–6695.
44. X. Gong, M. J. Moghaddam, S. M. Sagnella, C. E. Conn, X. Mulet, S. J. Danon, L. J. Waddington and C. J. Drummond, Soft Matter, 2011, 7, 5764–5776.
45. C. Demetzos, J. Liposome Res., 2008, 18, 159–173.
46. J. Clogston, J. Rathman, D. Tomasko, H. Walker and M. Caffrey, Chem. Phys. Lipids, 2000, 107, 191–220.
47. C. Czeslik, R. Winter, G. Rapp and K. Bartels, Biophys. J., 1995, 68, 1423–1429.
48. R. Winter, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 2002, 1595, 160–184.
49. J. Eisenblätter and R. Winter, Biophys. J., 2006, 90, 956–966.
50. C. Jeworrek, S. Uelner and R. Winter, Soft Matter, 2011, 7, 2709–2719.
51. J. M. Bulpett, T. Snow, B. Quignon, C. M. Beddoes, T. Y. D. Tang, S. Mann, O. Shebanova, C. L. Pizzey, N. J. Terrill, S. A. Davis and W. H. Briscoe, Soft Matter, 2015, 11, 8789–8800.
52. J. Erbes, A. Gabke, G. Rapp and R. Winter, Phys. Chem. Chem. Phys., 2000, 2, 151–162.
53. C. Nicolini, J. Kraineva, M. Khurana, N. Periasamy, S. S. Funari and R. Winter, Biochim. Biophys. Acta, Biomembr., 2006, 1758, 248–258.
54. C. E. Conn, O. Ces, A. M. Squires, X. Mulet, R. Winter, S. M. Finet, R. H. Templer and J. M. Seddon, Langmuir, 2008, 24, 2331–2340.
55. A. M. Squires, C. E. Conn, J. M. Seddon and R. H. Templer, Soft Matter, 2009, 5, 4773–4779.
56. R. Winter and R. Köhling, J. Phys.: Condens. Matter, 2004, 16, S327.
57. A. M. Squires, R. Templer, J. Seddon, J. Woenkhaus, R. Winter, T. Narayanan and S. Finet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011502.
58. N. J. Brooks, B. L. Gauthe, N. J. Terrill, S. E. Rogers, R. H. Templer, O. Ces and J. M. Seddon, Rev. Sci. Instrum., 2010, 81, 064103.
59. M. Basham, J. Filik, M. T. Wharmby, P. C. Y. Chang, B. El Kassaby, M. Gerring, J. Aishima, K. Levik, B. C. A. Pulford, I. Sikharulidze, D. Sneddon, M. Webber, S. S. Dhesi, F. Maccherozzi, O. Svensson, S. Brockhauser, G. Naray and A. W. Ashton, J. Synchrotron Radiat., 2015, 22, 853–858.
60. S. L. Gras and A. M. Squires, Methods Mol. Biol., 2011, 752, 147–163.
61. J. Ilavsky and P. R. Jemian, J. Appl. Crystallogr., 2009, 42, 347–353.
62. A. M. Squires, R. H. Templer, J. M. Seddon, J. Woenckhaus, R. Winter, S. Finet and N. Theyencheri, Langmuir, 2002, 18, 7384–7392.
63. C. E. Conn, C. Darmanin, X. Mulet, A. Hawley and C. J. Drummond, Soft Matter, 2012, 8, 6884–6896.
64. P. W. Zhu and J. W. White, J. Chem. Phys., 1996, 104, 9169–9173.
65. X. Chen, F. Tian, X. Zhang and W. Wang, Soft Matter, 2013, 9, 7592–7600.
66. A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 108, 118101.
67. T. G. Dane, P. T. Cresswell, G. A. Pilkington, S. Lilliu, J. E. Macdonald, S. W. Prescott, O. Bikondoa, C. F. J. Faul and W. H. Briscoe, Soft Matter, 2013, 9, 10501–10511.
68. R. Hosemann and A. Hindeleh, J. Macromol. Sci., Phys., 1995, 34, 327–356.
69. B. Wang, L. Zhang, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18171–18175.
70. T. Hamada, M. Morita, M. Miyakawa, R. Sugimoto, A. Hatanaka, M. d. C. Vestergaard and M. Takagi, J. Am. Chem. Soc., 2012, 134, 13990–13996.
71. W. Zheng, Y. Liu, A. West, E. E. Schuler, K. Yehl, R. B. Dyer, J. T. Kindt and K. Salaita, J. Am. Chem. Soc., 2014, 136, 1992–1999.
72. D. P. Siegel, Biophys. J., 1993, 65, 2124–2140.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00393a

---