Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conformational changes of polyelectrolyte chains in solvent mixtures†
Takeaki
Araki
Department of Physics, Kyoto University, Sakyo-ku, Kyoto 606-8505, Japan. E-mail: araki@scphys.kyoto-u.ac.jp
First published on 28th June 2016
Abstract
We numerically investigate the behaviors of polyelectrolyte chains in solvent mixtures, taking into account the effects of the concentration inhomogeneity and the degree of the ionization. When changing the interaction parameters between the solvent components, we found a first order transition of the polymer conformation. In the mixing state far from the coexistence curve, the polymers behave as semi-flexible chains. In the phase-separated state, on the other hand, they show compact conformations included in the droplets. As the interaction parameters of the mixture are increased, an inhomogeneous concentration field develops around the polymer and induces critical Casimir attractive interactions among the monomers. The competition between the electrostatic interactions and the critical Casimir ones gives rise to drastic changes in the conformation.
1 Introduction
Polyelectrolytes play important roles in many systems from biology to industry. Since the conformations of polyelectrolytes affect their physical and biological properties, they have been intensively studied.1–6 In comparison to electrically neutral polymers, polyelectrolytes are more rigid because of long-range electrostatic interactions among the monomers.7,8 They tend to behave like rod or semi-flexible polymers in good or theta solvents. In poor solvent conditions, on the other hand, effective attractive interactions work among the monomers. These interactions lead to a variety of conformations such as sausage, toroid and necklace-like structures.9–12One easily accessible way to control the interactions is to add salts. When salt is added to a polyelectrolyte solution, the electrostatic interactions among the monomers are screened and weakened. Then, the polyelectrolytes adopt compact conformations, if the molecular attractive interactions work among the monomers. In particular, multivalent ions show drastic effects on the polyelectrolyte conformation.13–17 They are strongly attached to the polymers, and some of them bridge the polymers, so that a small amount of the multivalent salt induces large conformational changes, compared to monovalent salts.
To control the interactions, solvent mixtures are also often useful.13,14 The electrostatic interaction is inversely proportional to the dielectric constant, dependent on the mixing fraction. The electrostatic interactions become stronger when a solvent with a small dielectric constant is mixed. The solvent mixtures also change the electrostatic interactions in a different way. In weak polyelectrolytes, the degree of ionization, or the electric charge, depends on the solvent.18–23 Usually, polyelectrolytes are highly charged in water-like solutions, while they are poorly charged in less polar liquids. In solvent mixtures, the ionization degree is changed with the mixing fraction.13,24–29 It is not so simple to use solvent mixtures to control the interactions in polyelectrolytes, even if the mixtures are homogeneously mixed.
The behaviors of neutral polymers in solvent mixtures have also been studied.30–34 The dimensions of the polymer are changed when the solvent mixture approaches its critical point. There, the concentration inhomogeneity in the solvent mixture induces effective attractive interactions among the monomers. On the other hand, there are only a few studies which consider the effects of the concentration inhomogeneity on the polyelectrolytes.27,35 To our knowledge, there is no study which considers both the contributions from the electrostatic interactions and the concentration inhomogeneity to the polymer conformation, in spite of their importance. Solvent mixtures have been importantly utilized in applications of polyelectrolytes in biology. For example, ethanol is added to aqueous solutions of polyelectrolytes, such as DNA and proteins, in order to purify and concentrate them.14 DNA collapses into a compact state in aqueous solutions of poly(ethylene glycol).13,14,24,27,36 So, it is very important to understand the behaviors of polyelectrolytes in solvent mixtures.
In this article, we study the behaviors of polyelectrolytes in solvent mixtures by means of fluid particle dynamics simulation with a bead-spring model.37–39 In particular, we focus on the effects of the ionization degree and the attractive interactions, caused by the concentration inhomogeneity, on the conformation of the polymer chain. Here, we follow previous studies on charged colloids in binary mixtures.40 It was indicated that the inhomogeneous concentration profiles near the colloidal surfaces induce attractive interactions among the particles. The ionization degree and the affinity between the colloid and the solvent depend on the interaction parameters between the solvent components.
2 Model and simulation
2.1 Free energy
We consider polyelectrolyte chains immersed in a mixture of water-like (W) and organic (O) solvents, which are both good solvents for the polymer. The W-solvent is more polar than the O-solvent. Salt was added to the mixture and was dissociated into monovalent ions. We describe the system with five coarse-grained variables. The polymers are described with θ (see below), and the compositions of the W- and O-solvents are (1 − θ)ϕ and (1 − θ)(1 − ϕ), respectively, where 0 ≤ ϕ ≤ 1. The cation and anion fractions are given by cc and ca, respectively.Polyelectrolyte chains are described by a particle-based model, namely, the bead-spring model. Each chain consists of N beads and the i-th bead is expressed by a shape function with a smooth profile θi(r) in a lattice space as37,41
 | (1) |
 is the effective volume of the i-th bead. The distribution of the beads is defined as
is the effective volume of the i-th bead. The distribution of the beads is defined as  , where Np is the number of chains in the simulation boxes.
, where Np is the number of chains in the simulation boxes.
The free energy functional consists of the following five terms,
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pol + pol + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) dis + dis + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ion + ion + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ele + ele + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sol. sol. | (2) |
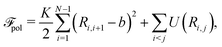 | (3) |
 | (4) |
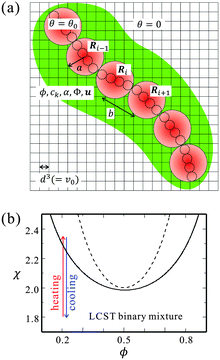
Fig. 1(a) shows a schematic picture of our bead-spring model. The circles with solid lines indicate the beads, which correspond to the Kuhn monomers. The small circles with broken lines represent the repeat units. In Fig. 1(a), ν = 4 repeat units compose a bead. We note that the kinetics of each repeat unit is not considered in our simulations. The size of a cell grid corresponds to those of the solvent molecules and the repeat units (d).
Since each bead contains ν ionizable groups, we treat the ionization degree with a continuous variable α, ranging from zero to unity. Depending on the local environment, it obeys the free energy of the ion dissociation given by23,40
 | (5) |
Upon the ionization, the polymer is dissociated into a negatively charged polymer and mobile cations. We assume that the counterions and the cations from the salt are the same species, so that they are described by a single variable cc. On the other hand, the small anions originate only from the salt. The conservation of the ions and the charge neutrality conditions give
 | (6) |
We assume the free energy of the ions as40,42–44
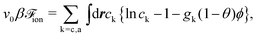 | (7) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ele is the electrostatic energy given by
ele is the electrostatic energy given by
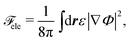 | (8) |
ε = ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) + (εϕ − + (εϕ − ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) )(ϕ − )(ϕ − ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) )(1 − θ) + (εθ − )(1 − θ) + (εθ − ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) )θ/θ0 )θ/θ0 | (9) |
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) being the average of the permittivity. εϕ and εθ correspond to the dielectric constants of the W-solvent and the polymer. The electrostatic potential is obtained by solving the Poisson equation,
being the average of the permittivity. εϕ and εθ correspond to the dielectric constants of the W-solvent and the polymer. The electrostatic potential is obtained by solving the Poisson equation, | (10) |
The solvent free energy is given in terms of ϕ by48
 | (11) |
f(ϕ) = ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ϕ + (1 − ϕ)ln(1 − ϕ) + χϕ(1 − ϕ), ϕ + (1 − ϕ)ln(1 − ϕ) + χϕ(1 − ϕ), | (12) |
2.2 Kinetics
We treat only ϕ(r) and {Ri} (or θ(r)) as slow variables. In other words, the ion distributions and the ionization degree are calculated by minimizing![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) with respect to ck and α at any time t.
with respect to ck and α at any time t.
We readily obtained
 | (13) |
For the ionization degree, we also obtained
| α = [1 + exp{Δ0 − Δ1ϕ − βeΦ + λc}]−1. | (14) |
The concentration field obeys48
 | (15) |
 | (16) |
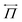 is the mechanical stress tensor and is given by
is the mechanical stress tensor and is given by  , where η(r) is the viscosity. In fluid particle dynamics, it depends on the polymer distribution as
, where η(r) is the viscosity. In fluid particle dynamics, it depends on the polymer distribution as 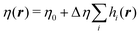 .37,38η0 is the solvent viscosity and η0 + Δη is the viscosity of the polymer bead. p is the pressure, which imposes the incompressible condition ∇·u = 0.
.37,38η0 is the solvent viscosity and η0 + Δη is the viscosity of the polymer bead. p is the pressure, which imposes the incompressible condition ∇·u = 0.  represents the random stress noise, which satisfies the fluctuation–dissipation relation at T.49 The first term is due to the concentration inhomogeneity and includes the effect of the interface tension.48 The second term of eqn (16) represents the force acting on the beads. Fi is given by Fi = −∂
represents the random stress noise, which satisfies the fluctuation–dissipation relation at T.49 The first term is due to the concentration inhomogeneity and includes the effect of the interface tension.48 The second term of eqn (16) represents the force acting on the beads. Fi is given by Fi = −∂![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /∂Ri.41,50
/∂Ri.41,50
The kinetics of the beads are solved in the off-lattice space by means of a fluid particle dynamics method. The bead is transported by the hydrodynamic flow averaged inside the bead as37
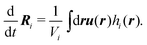 | (17) |
Here we note the roles of the random noises in our simulation. Our model is a hybrid one, employing the field theoretic and particle-based descriptions. The ion distributions and the ionization degree are determined by minimizing the free energy adiabatically. Also, we do not impose the random noises to ϕ, ck and α. Thus, our model is not beyond the mean-field description when we concern the resulting interactions among the beads. Although the correlations among the electric charges would lead to interactions in the polymers,2,51 such charge correlation effects are not considered in this work.
On the other hand, we consider the conformation of the polymer chains with the particle-based description and we introduce the random noises for the chain motions via hydrodynamic flow in eqn (16). Then, the kinetics of the polymer conformations are given by a Langevin-type equation. As we will see below, the conformational change occurs like a first-order transition, so the random noises for the particle motions play important roles. Such explicit conformational changes cannot be treated in the field theoretic description of the polymer chains.52,53
2.3 Simulation parameters
In numerical simulations, we assume the molecular size d(=v01/3) = 3 Å and the bead radius a = 2d. Thus, each bead contains ν(=2a/d) = 4 repeat units and the repeat unit density is set to θ0(≅νv0/Vi) = 0.12. In![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pol, we set βKd2 = 10 and βU0 = 1, with which we ensured |Ri,i+1 − b| ≪ d. The average Bjerrum length is
pol, we set βKd2 = 10 and βU0 = 1, with which we ensured |Ri,i+1 − b| ≪ d. The average Bjerrum length is ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) B = e2/(4π
B = e2/(4π![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) kBT) = 3d, which corresponds to
kBT) = 3d, which corresponds to ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ≅ 62 at T = 300 K. The ionization parameters are set Δ0 = 2 and Δ1 = 10, which give α0 ≅ 0.999 and α0 ≅ 0.119 for ϕ = 1 and ϕ = 0, respectively. Here, α0 is obtained from δ
≅ 62 at T = 300 K. The ionization parameters are set Δ0 = 2 and Δ1 = 10, which give α0 ≅ 0.999 and α0 ≅ 0.119 for ϕ = 1 and ϕ = 0, respectively. Here, α0 is obtained from δ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) dis/δα = 0 as α0 = {1 + eΔ0−Δ1ϕ}−1. In
dis/δα = 0 as α0 = {1 + eΔ0−Δ1ϕ}−1. In ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sol, we use C = d2. A mean field theory gives the interface tension as γ = kBT|χ − 2|3/2/(2d2),48 which estimates γ = 4.76 mN m−1 at χ = 2.35. The ion interaction parameters are gc = ga = 2, both of which correspond to the Gibbs energy of transfer of 4.99 kJ mol−1. The ions prefer the W-solvent (hydrophilic). For simplicity, we also set gp = 0, with which the polymer backbone is neutral in the affinity to the solvent components. The permittivity parameters are set to εϕ = 1.4
sol, we use C = d2. A mean field theory gives the interface tension as γ = kBT|χ − 2|3/2/(2d2),48 which estimates γ = 4.76 mN m−1 at χ = 2.35. The ion interaction parameters are gc = ga = 2, both of which correspond to the Gibbs energy of transfer of 4.99 kJ mol−1. The ions prefer the W-solvent (hydrophilic). For simplicity, we also set gp = 0, with which the polymer backbone is neutral in the affinity to the solvent components. The permittivity parameters are set to εϕ = 1.4![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) and εθ =
and εθ = ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) . The viscosity parameters are η0 = 0.1kBT/(Dϕd) and Δη = 10η0. Our results presented below are essentially insensitive to our choices of η parameters.
. The viscosity parameters are η0 = 0.1kBT/(Dϕd) and Δη = 10η0. Our results presented below are essentially insensitive to our choices of η parameters.
In this article, we fix the spatial average of the W-solvent composition at ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.2. This choice of
= 0.2. This choice of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) is because we expect that attractive interactions caused by the inhomogeneous concentration field are strengthened when the fraction of the W-solvent is small, as in colloidal systems.54,55 The binodal and spinodal points for
is because we expect that attractive interactions caused by the inhomogeneous concentration field are strengthened when the fraction of the W-solvent is small, as in colloidal systems.54,55 The binodal and spinodal points for ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.2 are χt = 2.31 and χs = 3.125, respectively. We add the salts, the concentrations of which are set to cs = 1 × 10−5 and 4 × 10−5. They correspond to the Debye parameter κa = (8π
= 0.2 are χt = 2.31 and χs = 3.125, respectively. We add the salts, the concentrations of which are set to cs = 1 × 10−5 and 4 × 10−5. They correspond to the Debye parameter κa = (8π![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) Bcs/v0)1/2a ≈ 0.055 and 0.11, respectively.
Bcs/v0)1/2a ≈ 0.055 and 0.11, respectively.
It is known that the coexistence curve of the binary mixture shifts when impurities such as salts are dissolved. The degree of the change depends on the affinity of the impurity and the concentration.43 For our parameters of cs and gk, the shift of the phase separation point is negligibly small, so that we do not consider the change of the phase separation point in this study. Assuming a lower critical solution temperature (LCST)-type mixture, we consider two quenching processes; heating from a mixing state with increasing χ and cooling from a phase-separated state with decreasing χ as shown in Fig. 1(b).
3 Results and discussion
3.1 Polymer conformations
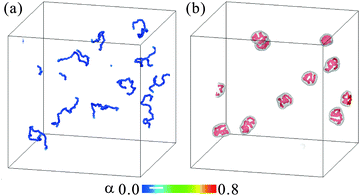
Fig. 2(a) and (b) show the snapshots of the polyelectrolyte chains in the solvent mixtures at χ = 1.8 and 2.35, respectively (ESI†). We solve Np = 10 chains, each of which consists of N = 40 beads, in a cubic box of Vt = (256d).3 The volume fraction of the polymer beads is 7.9 × 10−5. We set the salt concentration to cs = 4 × 10−5. The colors of the beads represent the degree of ionization. The interfaces between the phase-separated domains are also drawn with isosurfaces of ϕ = 0.5. In the mixed state, far from the coexistence curve at χ = 1.8 as in Fig. 1(b), the polymers behave as flexible chains. Here sharp interfaces are not formed. At χ = 2.35, on the other hand, they are compartmented in the droplets of the phase-separated domains. Here, the relative fraction of the W-solvent rich phase is 0.022 and this minority phase forms the droplets. Since the droplet size is smaller than the contour length of the polymers, the polymer chains are strongly distorted by the interface tension in the droplets.Since the polymer volume fraction is small and the relative fraction of the W-solvent rich phase is also small, each droplet contains a single chain and the droplets are dispersed well. But, some of the polymer chains can occasionally be contained in the same droplet. In order to see detailed behaviors of the conformational changes, it is better to avoid many body effects. Then, we consider a single polyelectrolyte chain in a cuboid box, the size of which is Vt = 256d × (128d).2 The polymer is composed of Np = 40 beads and its volume fraction is 3.2 × 10−4. Since the periodic boundary conditions are employed, the simulated polymer corresponds to one of the chains in a dilute polymer solution, not an isolated one in an infinite cell.
Fig. 3(a) and (b) show their snapshots, for which χ is changed between 2.1 and 2.35 (ESI†). The salt concentration is cs = 1 × 10−5. Assuming a lower critical solution temperature (LCST)-type mixture, we consider two quenching processes; heating from a mixed state with increasing χ in Fig. 3(a) and cooling from a phase-separated state with decreasing χ in Fig. 3(b). In Fig. 4, we plot their gyration radii Rg with respect to χ. This is calculated as
 | (18) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0 estimates its gyration radius as Rg ≈ 4.85b. Rg of a neutral polymer is indicated by the broken line in Fig. 4. The gyration radii in the solvent mixture with cs = 4 × 10−5 are also plotted.
= 0 estimates its gyration radius as Rg ≈ 4.85b. Rg of a neutral polymer is indicated by the broken line in Fig. 4. The gyration radii in the solvent mixture with cs = 4 × 10−5 are also plotted.
In Fig. 3(a) and (b), we observe drastic changes in the polymer conformations. As χ is increased, an expanded chain collapses into a compact state and vice versa. In both cases, the polymer behaves as a flexible chain at χ = 2.1(<χt). As indicated in Fig. 4, it swells larger than the neutral polymer of the same N because of the electrostatic interactions. At χ = 2.35(>χt), on the other hand, the bulk mixture phase-separates and then the polyelectrolyte is covered by the minority W-rich droplet. Since the droplet radius is smaller than the gyration radius, the contributions of the electrostatic interactions and the interface tension compete in determining the droplet shape and the polymer conformation. In the cases of χ = 2.35 in Fig. 3(a) and (b), the interface tension is so large that the droplet remains spherical. In the intermediate range of χ (2.2 ≤ χ ≤ 2.25), the structures depend on the quenching path. This difference of the conformations is also seen in the hysteresis loop of Rg in Fig. 4, suggesting the nature of a first order transition.27,28 It is interesting that the drastic conformational changes occur in the one-phase state of the bulk mixture (χ < χt).
In the case of cs = 4 × 10−5, the polymer chains tend to collapse at smaller χ, in comparison with that of cs = 1 × 10−5. This is because the salt not only weakens the electrostatic repulsions, but also enhances the affinity of the charged polymers to the W-solvent.44 As we will see below, the affinity to one of the solvent components gives rise to the attractive interactions among the Kuhn monomers.
3.2 Ionization and adsorption
Fig. 5(a) plots the degrees of ionization as functions of χ in the two processes of Fig. 3(a) and (b). They are averaged inside the beads as . At low χ, the ionization degrees are small and then they increase with χ. The increase of
. At low χ, the ionization degrees are small and then they increase with χ. The increase of ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) accompanies that of the electric charges. The slight increase of Rg for χ ≤ 2.25 in the heating process (see Fig. 4) reflects the resultant enhancement of the electrostatic repulsions. We attribute the change of
accompanies that of the electric charges. The slight increase of Rg for χ ≤ 2.25 in the heating process (see Fig. 4) reflects the resultant enhancement of the electrostatic repulsions. We attribute the change of ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) to that of the concentration field. The effective affinity between the polymer and the W-solvent is given by
to that of the concentration field. The effective affinity between the polymer and the W-solvent is given by![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) p = gp +Δ1 p = gp +Δ1![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) . . | (19) |
![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) in
in ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) p. In Fig. 5(b), we plot the adsorption amount Γ, which is defined as
p. In Fig. 5(b), we plot the adsorption amount Γ, which is defined as  , with χ. As χ is increased, the polymer beads adsorb the W-solvent more, since the susceptibility of the concentration field to the external field (here
, with χ. As χ is increased, the polymer beads adsorb the W-solvent more, since the susceptibility of the concentration field to the external field (here ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) p) is increased. Since the local composition of the W-solvent is enriched around the beads, the ionizations of the beads occur more widely. Furthermore, the progress of the ionization makes the polymer more preferred to the W-solvent.23 Thus, the ionization and adsorption proceed with χ cooperatively. Fig. 5(b) also shows that the adsorption amount in the cooling process is larger than that in the heating one. It indicates that the compact conformations can adsorb the W-solvent more than the expanded conformations. The ionization degree in the cooling process is large compared to that in the heating process, too. This is because the larger amount of the W-solvent wets the chain in the cooling process.
p) is increased. Since the local composition of the W-solvent is enriched around the beads, the ionizations of the beads occur more widely. Furthermore, the progress of the ionization makes the polymer more preferred to the W-solvent.23 Thus, the ionization and adsorption proceed with χ cooperatively. Fig. 5(b) also shows that the adsorption amount in the cooling process is larger than that in the heating one. It indicates that the compact conformations can adsorb the W-solvent more than the expanded conformations. The ionization degree in the cooling process is large compared to that in the heating process, too. This is because the larger amount of the W-solvent wets the chain in the cooling process.
3.3 Pairwise interaction between two beads
The inhomogeneous concentration field induces attractive interactions among the beads. For colloidal systems, they are sometimes called critical Casimir interactions in mixed solvents, or capillary ones in phase-separated solvents. Here, we consider a bead pair (N = 2) to see the pairwise interaction more clearly. In Fig. 6, we plot the force F1,2 acting on the bead pair with respect to the particle separation R1,2. It is estimated by the spring force F1,2 = K(R1,2 − b) by changing the natural spring length b. In Fig. 6, we set . In the equilibrium states, this force balances with the sum of the other interactions, such that this spring force gives an estimation of the force between the non-connected beads. Its positive and negative values mean repulsive and attractive interactions, respectively. The salt concentration is set to cs = 1 × 10−5. Fig. 6 shows that the force consists of short-ranged attraction and a long-ranged repulsion as reported for colloidal systems.40 The former attraction is due to the inhomogeneous concentration field and the latter repulsion comes from the electrostatic interaction. As χ is increased, the repulsive interaction becomes strong for large R1,2. This is because the ionization degree is increased with χ as in Fig. 5(a). Also, the range showing the attractive force expands, and the corresponding force becomes negatively large with increasing χ. The critical Casimir interaction (or the capillary interaction) works between the beads when the enriched profiles of the W-solvent around the beads overlap each other. As in Fig. 5(b), the adsorption layer of the W-solvent develops with χ, so that the inhomogeneous concentration profiles can overlap easily when χ is large, even for large separations. The changes of the force curves leading to the conformational changes seen in Fig. 3. However, the force curves themselves cannot explain the hysteresis behaviors of Rg in Fig. 4. The combination of the total interactions among the beads and the conformation entropy would give rise to the first order transition suggested in Fig. 3 and 4.27,28
. In the equilibrium states, this force balances with the sum of the other interactions, such that this spring force gives an estimation of the force between the non-connected beads. Its positive and negative values mean repulsive and attractive interactions, respectively. The salt concentration is set to cs = 1 × 10−5. Fig. 6 shows that the force consists of short-ranged attraction and a long-ranged repulsion as reported for colloidal systems.40 The former attraction is due to the inhomogeneous concentration field and the latter repulsion comes from the electrostatic interaction. As χ is increased, the repulsive interaction becomes strong for large R1,2. This is because the ionization degree is increased with χ as in Fig. 5(a). Also, the range showing the attractive force expands, and the corresponding force becomes negatively large with increasing χ. The critical Casimir interaction (or the capillary interaction) works between the beads when the enriched profiles of the W-solvent around the beads overlap each other. As in Fig. 5(b), the adsorption layer of the W-solvent develops with χ, so that the inhomogeneous concentration profiles can overlap easily when χ is large, even for large separations. The changes of the force curves leading to the conformational changes seen in Fig. 3. However, the force curves themselves cannot explain the hysteresis behaviors of Rg in Fig. 4. The combination of the total interactions among the beads and the conformation entropy would give rise to the first order transition suggested in Fig. 3 and 4.27,28
4 Conclusions and future works
In this article, we numerically studied the conformations of polyelectrolytes in solvent mixtures. We take into account the electrostatic interaction, the effective interaction induced by the concentration inhomogeneity and the ionization degree, simultaneously. We observed drastic changes in the conformation and a hysteresis loop of Rg when changing the interaction parameters between the solvent components. Approaching the phase separation point, the inhomogeneous concentration field develops around the beads and it induces attractive interactions among the beads. With these attractive interactions, the polymer collapses into a compact conformation against the electrostatic repulsions. We also found the ionization degree and the inhomogeneous concentration field develop with the interaction parameters in a cooperative way.Our simulations demonstrate the collapsed state of polyelectrolytes in the mixed state of a solvent mixture. They may suggest an aggregation and precipitation of polyelectrolyte chains in solvent mixtures, which do not show phase separation, as observed in the so-called ethanol precipitation of DNA. Addition of an organic liquid reduces the dielectric constant of the solvent and strengthens the electrostatic interactions among the ions and polymers. The stable ionic bonds between the polymers and the counterions are formed, and then the polymers become uncharged. The uncharged chains will aggregate and precipitate. Usually, the solvent mixture is considered to be well mixed, since it does not show the phase separation at any accessible temperature.
Addition of salt into a mixed solvent sometimes leads to phase separation, that is, salting out. We consider that the phase separation might be induced locally around the polyelectrolytes and the interface tensions work to aggregate them, even if the mixture appears to be mixed macroscopically. In order to confirm this mechanism in actual polyelectrolyte solutions, some experimental observations are desired. However, it would not be easy to measure the interface tension of such droplets of a molecular scale size. If we can measure the local contents of the W-solvent and the ions in the aggregates, and they are larger than those in the supernatant, they would support our mechanism.
We have many parameters in our model. The results we presented here were limited in the choice of the parameters so we could not discuss the behaviors in a wide range of the parameters. Other choices of parameters, such as ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) , cs and gk, would give richer and more interesting behaviors of polyelectrolytes in solvent mixtures. We will enumerate what we should do below and we hope to report some results about them in the near future.
, cs and gk, would give richer and more interesting behaviors of polyelectrolytes in solvent mixtures. We will enumerate what we should do below and we hope to report some results about them in the near future.
(i) The composition of the mixture can be controlled easily. In this study, we consider only an asymmetric mixture (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.2), with which we expect the interaction caused by the inhomogeneous concentration field is strengthened as in colloidal systems. However, other conformations will be observed when the mixing fraction is changed. When approaching the critical point in a symmetric mixture (
= 0.2), with which we expect the interaction caused by the inhomogeneous concentration field is strengthened as in colloidal systems. However, other conformations will be observed when the mixing fraction is changed. When approaching the critical point in a symmetric mixture (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5), the interface tension is reduced48 and the effective attractive interaction would also be weakened. Our preliminary simulations indicate that non-spherical domains containing semi-flexible chains, which are expanded by the electrostatic repulsion, are formed (not shown here).
= 0.5), the interface tension is reduced48 and the effective attractive interaction would also be weakened. Our preliminary simulations indicate that non-spherical domains containing semi-flexible chains, which are expanded by the electrostatic repulsion, are formed (not shown here).
In the present simulations, both of the relative fractions of the W-solvent rich phase and the polymer fractions are small even in the two phase region (χ > χt). Then, we observed in Fig. 2 that each polymer chain is compartmented in a droplet of the W-solvent rich phase. If we increase them, we will see that some polyelectrolytes are confined in a same droplet. With changing the interaction parameter χ, aggregates of the polymer chains will also be observed. The aggregation process of the polyelectrolytes via the mechanisms discussed above is an interesting problem.
In Fig. 2 and 3, the polymer forms a compact conformation in the phase-separated state (χ > χt). This is because the diameters of the droplets are shorter than the polymer contour length. Since the periodic boundary conditions are employed, the maximum droplet size is uniquely determined by the relative fraction of the phase-separated domain and the simulation box size. If we consider an isolated chain in a larger cell or an infinite one, the droplet of the minority phase will grow larger than the polymer size and the polymer will adopt a more relaxed conformation in the droplet. In this sense, the gyration radius of the polyelectrolyte will depend on the system size. Also, we fix the total amount of salt as constant in the simulations. If we are interested in the infinite cell, we had better control its chemical potential of the ions, not their total amounts. This difference may lead to some quantitatively different results.
(ii) The salt concentration is also an important parameter, which is easy to change. Although only two salt concentrations are employed and the difference between them is not large, a quantitatively large difference in the conformational changes is observed (Fig. 4). If we change the salt concentration in a wider range, more drastic conformational changes will be observed. In particular, it is expected that the polyelectrolyte chain will behave as a neutral polymer when a sufficiently large amount of salt is added. However, our present simulation scheme does not apply to such a high salinity limit as noted in Appendix A. It is desired to improve the simulation method.
Also, we treat the ions by means of a coarse-grained model, namely, the Poisson–Boltzmann equation. Then, we do not consider the multivalent ions15–17 and the correlation effect of the fluctuating ions.2,51 We have to treat the ions by a particle-based model, in order to see these effects.
(iii) Although the dependence of the conformation on the chain length is quite important,4 our polymer chains consist only of N = 40 beads. Our simulations with shorter chains (N = 10 and 20) (not presented here) give essentially the same behaviors that we reported in this article. But, some qualitatively different behaviors may be observed when longer chains are used. For example, when a long charged polymer collapses into a compact conformation, the electrostatic repulsions among the monomers become enlarged. When the droplet of a finite interface tension no longer confines the polymer, Coulomb explosion locally occurs and some complex structure may be formed as a necklace.4 In the solvent mixtures, the ions are strongly confined in the W-solvent rich domain because of the solvation energy. Then, the entropic gain of the counterions is possibly different from that in a one-component solvent. To consider it, another scaling theory should be developed.
Also from the viewpoint of phase separation, the usage of long polymer chains will be interesting. As shown in Fig. 2 and 3, the polyelectrolyte chains behave as nuclei for the phase separation near χ = χt. It is known that the interface tension suppresses the formation of the small droplets of the minority phase. So, when long polyelectrolytes are dissolved, they may induce phase separation more efficiently. Although the usage of long polymers is important and interesting, it is not easy to simulate them. When we use longer chains, we have to carry out simulations with much longer annealing times to equilibrate the system. Simulation improvements are desired.
(vi) In this work, we do not change the material parameters, such as gk, Δ0 and Δ1. In particular, the simulated solvation energy gk is rather small, in comparison with actual ions and solvents. Not only does the addition of a salt with large gk change the phase diagram largely, but it will also enhance the interaction between the charged polymer and the solvent.44 Although our present simulation cannot adopt large gk, we have to consider its influence seriously. Also, Δ1 plays an important role in our mechanism. It is also needed to consider the dependence of the conformation on it.
Appendix
A Simulation scheme
Our simulation model deals with lattice and off-lattice spaces. The solvent composition ϕ, the ion concentration ck, the local ionization degree α, the electrostatic potential Φ and the hydrodynamic flow u are solved in the lattice space. The grid size of the lattice space is set to d as shown in Fig. 1(a), and the periodic boundary conditions are employed. Here we describe our simulation scheme.(i) First, we determined ck, Φ and α recursively, since they are coupled in a complicated manner. At this stage, we fixed θ(t) and ϕ(t). The electrostatic potential Φ(p) was obtained from eqn (10) with ck = c(p)k and α = α(p) by means of the Crank–Nikolson method. Here, the suffix p(=0, 1, 2,…) indicates the iteration index. (As the initial conditions for the iterations at t = 0, we set c(0)k = cs and α(0) = {1 + eΔ0−Δ1![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) }−1. Otherwise, we set c(0)k = ck(t) and α(0) = α(t).) We calculated the Lagrange multipliers as
}−1. Otherwise, we set c(0)k = ck(t) and α(0) = α(t).) We calculated the Lagrange multipliers as
 | (20) |
 | (21) |
We should note that the range of the salt concentration is limited in our scheme. To solve the electrostatic potential in the lattice space, the Debye screening length should be longer than the simulation grid length d. Since the ions prefer to be dissolved in the W-solvent, their concentrations in the droplets of the W-solvent rich phase becomes much larger than their spatial averages. Then, we have to keep the salt concentration so small that the Debye screening length remains longer than the grid size even in the W-solvent rich phase. On the other hand, the concentration of the counterions in the simulation box is about 2 × 10−5 when the polyelectrolyte chain is highly charged, so that the solution of cs = 1 × 10−5 corresponds to a low salinity solution.
(ii) We calculated the hydrodynamic flow u by means of the Maker and cell method.56 The flow vector field was defined in a staggered lattice. Since the Reynolds number is considered negligibly small, we iterated to develop eqn (16) without updating ϕ and θ until  . The fluid particle dynamics method was originally developed to consider colloidal suspensions in a simple liquid. In the limits of Δη/η0 → ∞ and d/a → 0, this method is able to describe solid spherical particles with hydrodynamic interactions with high accuracy. Since we do not need to consider the boundary conditions at the colloidal surfaces, we can calculate the hydrodynamic flow efficiently, and then apply this method to some systems. The details of this numerical scheme are given elsewhere.38 In this study, the beads do not represent colloid particles, so we use a moderate value of Δη/η0.
. The fluid particle dynamics method was originally developed to consider colloidal suspensions in a simple liquid. In the limits of Δη/η0 → ∞ and d/a → 0, this method is able to describe solid spherical particles with hydrodynamic interactions with high accuracy. Since we do not need to consider the boundary conditions at the colloidal surfaces, we can calculate the hydrodynamic flow efficiently, and then apply this method to some systems. The details of this numerical scheme are given elsewhere.38 In this study, the beads do not represent colloid particles, so we use a moderate value of Δη/η0.
(iii) Now we knew u, ck and α. We updated the bead positions Ri and the concentration field by means of the explicit Euler scheme with the same time increment Δt = 10−2d2/Dϕ. The new polymer field θ is given by eqn (1). Then we returned to (i) using θ(t + Δt) and ϕ(t + Δt), instead of θ(t) and ϕ(t).
Acknowledgements
We acknowledge valuable discussions with A. Onuki, H. Tanaka and Y. Uematsu. This work was supported by KAKENHI (no. 25000002 and 25610122). Computation was done using the facilities of the Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo. This research was also partly supported by CREST, JST.References
- F. Oosawa, Polyelectrolyte, Mercel Dekker, New York, 1971 Search PubMed.
- J.-L. Barrat and J.-F. Joanny, Adv. Chem. Phys., 1996, 94, 1–66 CAS.
- C. Holm, J.-F. Joanny, K. Kremer, R. R. Netz, P. Reineker, T. A. Seidel, C. Vilgis and R. G. Winkler, Adv. Polym. Sci., 2004, 166, 67–111 CrossRef CAS.
- A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 CrossRef CAS.
- M. Rubinstein and G. A. Papoian, Soft Matter, 2012, 8, 9265–9267 RSC.
- Y. Uematsu and T. Araki, J. Chem. Phys., 2013, 139, 094901 CrossRef PubMed.
- T. Odijk, J. Polym. Sci., Part B: Polym. Phys., 1977, 15, 477–483 CAS.
- J. Skolnick and M. Fixman, Macromolecules, 1977, 10, 944–948 CrossRef CAS.
- A. R. Khokhlov, J. Phys. A: Math. Gen., 1980, 13, 979–987 CrossRef CAS.
- G. E. Plum, P. G. Arscott and V. A. Bloomfield, Biopolymers, 1990, 30, 631–643 CrossRef CAS PubMed.
- A. V. Dobrynin, M. Rubinstein and S. P. Obukhov, Macromolecules, 1996, 29, 2974–2979 CrossRef CAS.
- H. J. Limbach and C. Holm, Comput. Phys. Commun., 2002, 147, 321–324 CrossRef.
- V. A. Bloomfield, Biopolymers, 1991, 31, 1471–1481 CrossRef CAS PubMed.
- V. A. Bloomfield, Curr. Opin. Struct. Biol., 1996, 6, 334–341 CrossRef CAS PubMed.
- E. Raspaud, M. Olvera de la Cruz, J.-L. Sikorav and F. Livolant, Biophys. J., 1998, 74, 381–393 CrossRef CAS PubMed.
- B. I. Shklovskii, Phys. Rev. Lett., 1999, 82, 3268–3271 CrossRef CAS.
- P.-Y. Hsiao and E. Luijten, Phys. Rev. Lett., 2006, 97, 148301 CrossRef PubMed.
- E. Raphael and J.-F. Joanny, Europhys. Lett., 1990, 13, 623–628 CrossRef CAS.
- I. Borukhov, D. Andelman and H. Orland, Europhys. Lett., 1995, 32, 499–504 CrossRef CAS.
- I. Borukhov, D. Andelman, R. Borrega, M. Cloitre, L. Leibler and H. Orland, J. Phys. Chem. B, 2000, 104, 11027–11034 CrossRef CAS.
- Y. Burak and R. R. Netz, J. Phys. Chem. B, 2004, 108, 4840–4849 CrossRef CAS.
- R. Okamoto and A. Onuki, J. Chem. Phys., 2009, 131, 094905 CrossRef PubMed.
- A. Onuki and R. Okamoto, J. Phys. Chem. B, 2009, 113, 3988–3996 CrossRef CAS PubMed.
- L. S. Lerman, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 1886–1890 CrossRef CAS.
- H. L. Frisch and S. J. Fesciyan, J. Polym. Sci., Polym. Lett. Ed., 1979, 17, 309–315 CrossRef CAS.
- P. G. Arscott, C. Ma, J. R. Wenner and V. A. Bloomfield, Biopolymers, 1995, 36, 345–364 CrossRef CAS PubMed.
- V. V. Vasilevskaya, A. R. Khokhlov, Y. Matsuzawa and K. Yoshikawa, J. Chem. Phys., 1995, 102, 6595–6602 CrossRef CAS.
- M. Ueda and K. Yoshikawa, Phys. Rev. Lett., 1996, 77, 2133–2136 CrossRef CAS PubMed.
- S. M. Mel'nikov, M. O. Khan, B. Lindman and B. Jönsson, J. Am. Chem. Soc., 1999, 121, 1130–1136 CrossRef.
- A. R. Shultz and P. J. Flory, J. Polym. Sci., 1955, 15, 231–242 CrossRef CAS.
- F. Brochard and P. G. de Gennes, Ferroelectrics, 1980, 30, 33–47 CrossRef CAS.
- J. J. Magda, G. H. Fredrickson, R. G. Larson and E. Helfand, Macromolecules, 1988, 21, 726–732 CrossRef CAS.
- K. To and H. J. Choi, Phys. Rev. Lett., 1998, 80, 536–539 CrossRef CAS.
- C. A. Grabowski and A. Mukhopadhyay, Phys. Rev. Lett., 2007, 98, 207801 CrossRef PubMed.
- D. Baigl and K. Yoshikawa, Biophys. J., 2005, 88, 3486–3493 CrossRef CAS PubMed.
- D. Ben-Yaakov, D. Andelman, D. Harries and R. Podgornik, J. Phys. Chem. B, 2009, 113, 6001–6011 CrossRef CAS PubMed.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS PubMed.
- H. Tanaka and T. Araki, Chem. Eng. Sci., 2006, 61, 2108–2141 CrossRef CAS.
- K. Kamata, T. Araki and H. Tanaka, Phys. Rev. Lett., 2009, 102, 108303 CrossRef PubMed.
- R. Okamoto and A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 051401 CrossRef PubMed.
- T. Araki and H. Tanaka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061506 CrossRef PubMed.
- A. Onuki, R. Okamoto and T. Araki, Bull. Chem. Soc. Jpn., 2011, 84, 569–587 CrossRef CAS.
- A. Onuki and R. Okamoto, Curr. Opin. Colloid Interface Sci., 2011, 16, 525–533 CrossRef CAS.
- S. Samin and Y. Tsori, J. Chem. Phys., 2012, 136, 154908 CrossRef PubMed.
- D. Ben-Yaakov, D. Andelman, D. Harries and R. Podgornik, J. Phys.: Condens. Matter, 2009, 21, 424106 CrossRef PubMed.
- Z.-G. Wang, J. Phys. Chem. B, 2008, 112, 16205 CrossRef CAS PubMed.
- Z.-G. Wang, Phys. Rev. Lett., 2010, 81, 021501 Search PubMed.
- A. Onuki, Phase Transition Dynamics, Cambridge Univ. Press, Cambridge, 2002 Search PubMed.
- A. Furukawa and H. Tanaka, Phys. Rev. Lett., 2010, 104, 245702 CrossRef PubMed.
- T. Araki and H. Tanaka, J. Phys.: Condens. Matter, 2008, 20, 072101 CrossRef.
- B.-Y. Ha and A. J. Liu, Phys. Rev. Lett., 1997, 79, 1289–1929 CrossRef CAS.
- Y. O. Popov, J. Lee and G. H. Fredrickson, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 3223–3230 CrossRef CAS.
- R. A. Riggleman and G. H. Fredrickson, J. Chem. Phys., 2010, 132, 024104 CrossRef PubMed.
- D. Beysense and D. Estève, Phys. Rev. Lett., 1985, 54, 2123–2126 CrossRef PubMed.
- R. Okamoto and A. Onuki, J. Chem. Phys., 2012, 136, 114704 CrossRef PubMed.
- F. H. Harlow and H. E. Welch, Phys. Fluids, 1965, 8, 2182–2189 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00352d |
| This journal is © The Royal Society of Chemistry 2016 |