Open Access Article
Open Access ArticleRupture and recoil of bent-core liquid crystal filaments†
S. M.
Salili
a,
T.
Ostapenko‡
b,
O.
Kress‡
a,
C.
Bailey
c,
W.
Weissflog
d,
K.
Harth
b,
A.
Eremin
b,
R.
Stannarius
*b and
A.
Jákli
*a
aChemical Physics Interdisciplinary Program and Liquid Crystal Institute, Kent State University, Kent, OH 44242, USA. E-mail: ajakli@kent.edu
bInstitute of Experimental Physics, Otto von Guericke University, Universitätsplatz 2, 39106 Magdeburg, Germany. E-mail: ralf.stannarius@ovgu.de
cLeidos, 3745 Pentagon Blvd., Beavercreek, OH 45431, USA
dMartin Luther University Halle-Wittenberg, Department of Chemistry, Physical Chemistry, von-Danckelmann-Platz 4, 06120 Halle, Germany
First published on 8th April 2016
Abstract
The recoil process of free-standing liquid crystal filaments is investigated experimentally and theoretically. We focus on two aspects, the contraction speed of the filament and a spontaneously formed undulation instability. At the moment of rupture, the filaments buckle similarly to the classical Euler buckling of elastic rods. The tip velocity decays with decreasing filament length. The wavelength of buckling affinely decreases with the retracting filament tip. The energy gain related to the decrease of the total length and surface area of the filaments is mainly dissipated by layer rearrangements during thickening of the fibre. A flow back into the meniscus is relevant only in the final stage of the recoil process. We introduce a model for the quantitative description of the filament retraction speed. The dynamics of this recoil behaviour may find relevance as a model for biology-related filaments.
Introduction
Filamentous materials hold promise for an entirely new class of artificial muscles and/or strain sensors due to their fascinating mechanical, electro-mechanical, optical and electro-optical properties. Dynamic buckling and recoil mechanisms of elastic materials have been studied in materials ranging from solids1 to rubbers2 and even to non-Newtonian fluids.3–8 When the axial compression of a straight beam exceeds a critical value, a dynamic buckling instability initiates – as noted first by Euler9 – with a characteristic wavelength.1,10,11 The threshold character of this phenomenon may be the first practical example of a critical bifurcation of the solution of a differential equation. Apart from that, interesting dynamic properties are found when the critical stress is exceeded.12 Dynamic instabilities can also be triggered in rotationally forced filament rubbers13,14 and in an elastic rubber band submerged in a viscous fluid,2 or during the extrusion of a rod into a viscous fluid.15Some viscoelastic materials can easily form free-standing filaments and can be stabilized by hardening induced by cooling, solvent evaporation (as in spider silk16), or polymerization. The dynamic buckling instability of filaments of non-Newtonian fluids is a phenomenon replete with complexity. The degree of this complexity increases when a dynamic buckling instability becomes responsible for the recoil of a fluid filament when one end is broken free from its structural support. Such processes have tremendous importance in diverse biophysical phenomena, such as the viscoelastic properties of muscle fibres in the physiologically relevant regime, which have been studied only recently.13,14,17–19
Newtonian fluids show elastic responses only at free surfaces due to surface tension. In the filament form, they experience a Plateau–Rayleigh instability when their length L is larger than their perimeter, 2πR.20,21 Fluids with one- or two-dimensional internal molecular order, such as columnar and some smectic liquid crystals, may overcome the P–R instability to form stable, free-standing liquid filaments.22 In particular, stable filaments can be formed by achiral bent-core liquid crystals with nanoscale modulated smectic and columnar (B7) phases. They can be considered as 1-D fluid structures exhibiting high slenderness ratios greater than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.23–28 These bent-core filaments have a fascinating structure. Recently, we described the formation of chiral nanostructures observed in these filaments,27 which are believed to contribute to their viscoelastic behaviour.22
000.23–28 These bent-core filaments have a fascinating structure. Recently, we described the formation of chiral nanostructures observed in these filaments,27 which are believed to contribute to their viscoelastic behaviour.22
Here, we present our experimental methods, results and analysis of the rupture and recoil properties of several bent-core liquid crystal filaments, anticipating that they may serve as a model system for complex biological fibres.
Experimental
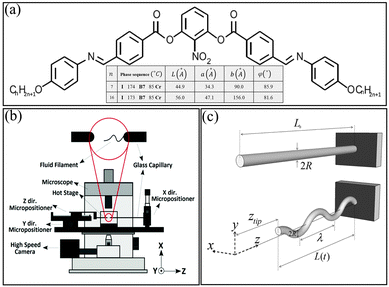
For our studies, we chose the n = 7 and n = 16 homologues of 2-nitro-1,3-phenylene bis[4-(4-n alkyloxy phenylimino methyl)benzoates], which are the prototypical B7 materials where the peculiar chiral superstructures were first observed29 [see Fig. 1(a)] because they form the most stable bent-core filaments discovered so far. Both the n = 7 (N7) and n = 16 (N16) materials have a B7 phase with a broad temperature range between TI-B7 = 174 °C and TB7-Cr = 85 °C. In this phase, the materials have a monoclinic, 2-D lattice with parameters a, b and ϕ, where a is the smectic layer spacing, b is the periodicity of the layer undulation and ϕ is the angle between a and b. These parameters are nearly temperature independent in the bulk. For example, at 150 °C, they are a = 3.43 nm, b = 9.0 nm, and ϕ = 85° for N7, and a = 4.7 nm, b = 15.6 nm, and ϕ = 81.6° for N16. Recent cryo-TEM experiments show that these materials have a strongly modulated layer structure, where there are half layer step discontinuities at the boundaries of the splay domains,30 which resemble columnar structures.31,32A motorized and temperature-controlled setup [Fig. 1(b)], in which 1 mm diameter glass capillaries with fused tips were used to manipulate the filaments, was built in our lab. This apparatus provides motion in three orthogonal directions so that the positions of the two tips can be adjusted with respect to each other and moved apart to initially draw and later stretch the filaments. The filaments were formed a few degrees below the isotropic-B7 phase transition, with diameters between 4 μm and 7 μm. A high-speed CCD camera (Phantom v211) was used to record video at frame rates between 1900 and 6000 frames per second. It was mounted onto a Nikon inverted optical microscope on which the pulling device was placed for observation.
Filament ruptures were initiated both mechanically and thermally. In order to induce a mechanical rupture, the fibre length was suddenly increased. This was repeated at different shear rates for several fibres. Thermal rupture was initiated by heating the air surrounding the fibre at 20 K min−1 until one end reached the clearing temperature. Typically, the same end ruptured each time due to one of the glass capillaries being closer to the heating element than the other. Before the ruptures were triggered, the filaments were pulled to a length not longer than 2 mm at constant temperature.
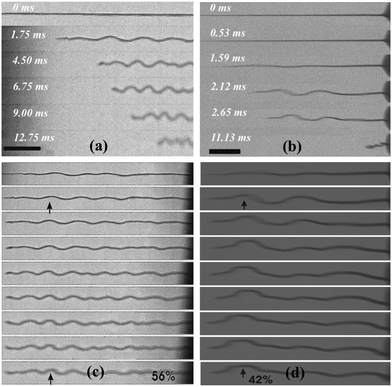
After rupture, the filaments retract by forming a buckling structure as illustrated schematically in Fig. 1(c) and by snapshots taken at short time intervals using the fast camera in Fig. 2(a) and (b) for thermal and mechanical ruptures, respectively. The images show only part of the filaments while the video in the ESI† shows the entire filaments. It should be noted that in Fig. 2(b), the filament ruptured in the middle. Although the still frames only allow a two-dimensional analysis as illustrated in Fig. 1(c), a close observation of details of the video footage (out of focus displacements) reveals three-dimensional recoiling.
One immediately observes a relation between the undulation structure and the filament material displacement: does the undulation travel like an elastic wave along the filament or are the undulations fixed to the material?
In Fig. 2(c) and (d), the images were stretched to adjust for the filament tip displacement after each time step. The images show that the undulations stay in essentially the same positions, with only a slight shift towards the tip of the filament. In addition, new, smaller wavelength undulations appear at later stages. This leads to the conclusion that the undulations remain essentially fixed to the material, i.e. the contraction is nearly uniform along the filament. While the tip collects some filament material during rupture, the main influence on filament retraction comes from a global, uniform shortening of the filament requiring the local radius to increase. This is accompanied by a growth of the undulation amplitudes and the formation of additional undulations. The retraction of the material into the meniscus seems to be of minor importance; otherwise, the wave structures would move to the right, approaching the fixed edge (meniscus) in the images of Fig. 2(c) and (d).
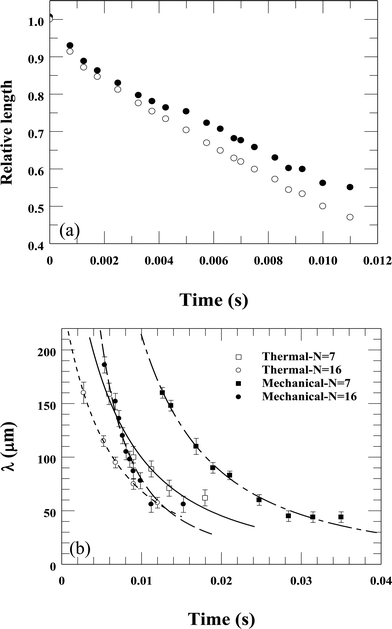
To understand the quantitative relation between the tip movement and the length of the filament, we normalized the arc length of the projected filament shown in Fig. 2(c) and plotted it versus time in Fig. 3(a). The open circles show the straight relative distance from the filament's tip to its base (L(t)/L0), while the filled circles represent the filament's total (arc) relative length. The reduction of the total length is smaller than the reduction of the end-to-end length by approximately 10%. Of course, the video shows only a 2D projection of the buckled and coiled filament, thus underestimating the remaining filament length. Assuming a three-dimensional undulation, one can estimate that the actual length reduction amounts to about 80% of the observed tip motion.
The initial wavelength of the buckling pattern was observed to be about 150–200 μm for both materials, decreasing with time proportional to the length L(t) of the filament. For this reason (and based on our analysis described below in Discussion), we have fitted the data to the equation 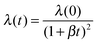 , where β is given in eqn (7). The best fits to this function are shown in Fig. 3(b). This holds for both rupture methods and is a direct consequence of the observed affine filament deformation seen in Fig. 2(c) and (d).
, where β is given in eqn (7). The best fits to this function are shown in Fig. 3(b). This holds for both rupture methods and is a direct consequence of the observed affine filament deformation seen in Fig. 2(c) and (d).
The time dependence of the displacement, ztip(t) = L0 − L(t), of the endpoints of recoiling filaments is shown in Fig. 4. Fig. 4(a) and (b) show the time dependence for several temperatures when the rupture was initiated thermally. Fig. 4(a) shows ztip(t) of two L0 ∼ 1.9 mm length N7 filaments ruptured at 165 °C and 170 °C. Fig. 4(b) depicts ztip(t) of two N16 filaments ruptured at 160 °C (L0 = 1.1 mm) and 165 °C (L0 = 1.5 mm). One sees that the relative displacement increases quickly at the beginning, then slows down as ztip/L0 ∼ 1 is approached. The speed of recoil depends on the temperature of the filament at the moment of rupture.
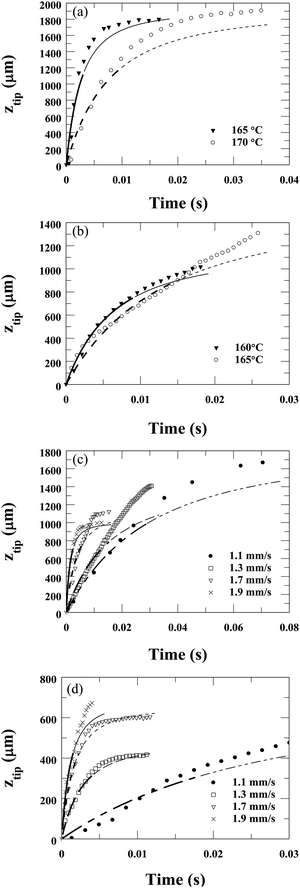 | ||
| Fig. 4 Time dependences of ztip of filaments after ruptures. (a and b) Thermally initiated ruptures at several temperatures for N7 (a) and N16 (b). (c and d) Mechanically initiated ruptures by fast pulling at various speeds at 165 °C for N7 (c) and N16 (d). Lines are best fits to equation ztip = L0[1 − 1/(1 + βt)2], based on eqn (8) derived in Discussion. In this equation L0 is the initial length of the filament. Thick lines correspond to the range where the fit was obtained, thin lines show how they deviate from the data outside the fit range. For all fits, the lengths of the fibres were constant corresponding to the measured values. The fitted relaxation rate β values are the following: (a) β(165 °C) = 185 s−1, β(170 °C) = 66 s−1; (b) β(160 °C) = 78 s−1, β(165 °C) = 39 s−1; (c) β(1.1 mm s−1) = 17 s−1; β(1.3 mm s−1) = 33 s−1; β(1.7 mm s−1) = 131 s−1; β(1.9 mm s−1) = 351 s−1; (d) β(1.1 mm s−1) = 19 s−1; β(1.3 mm s−1) = 182 s−1; β(1.7 mm s−1) = 306 s−1; β(1.9 mm s−1) = 418 s−1. | ||
Since the temperature of the filament during the thermally induced rupture process is not uniform, we also tested the mechanical rupture at constant temperatures. The time dependences of the relative displacements at pulling speeds of 1.1, 1.3, 1.7 and 1.9 mm s−1 are shown in Fig. 4(c) for N7, and Fig. 4(d) for N16. One sees qualitatively similar behaviour in the thermally and mechanically initiated rupture processes, indicating that the temperature inhomogeneity might be negligible. The rate of recoil correlates to the pulling speed (faster speed–quicker retraction).
Discussion
The above experiments show that the ruptures start with a visually observable buckling, similarly to the classic Euler buckling of a rod due to axial load.9 In order to quantify this rupture behaviour, we consider the dynamic equation of lateral displacement ξ(z,t) of a straight elastic beam under an applied longitudinal force T, which is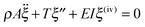 | (1) |
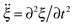 , ξ′′ = ∂2ξ/∂z2, ρ is the mass density; A = R2π is the cross-sectional area of the filament with radius R; E is the Young's modulus, and I = πR4/4 is the moment of inertia of the area. As shown for elastic rods,1 the stability analysis of eqn (1) for a constant force T reveals the wavelength λ0 and the growth rate τ−1 of the fastest growing mode to be:
, ξ′′ = ∂2ξ/∂z2, ρ is the mass density; A = R2π is the cross-sectional area of the filament with radius R; E is the Young's modulus, and I = πR4/4 is the moment of inertia of the area. As shown for elastic rods,1 the stability analysis of eqn (1) for a constant force T reveals the wavelength λ0 and the growth rate τ−1 of the fastest growing mode to be: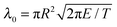 | (2) |
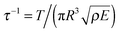 | (3) |
The snapshots of the recoil (Fig. 2) show that once buckling occurred, the number of waves nw remained constant during the recoil process (in examples of Fig. 2, nw ≅ 4 for N16 and 3 for N7). This is consistent with the observation that the wavelength decreases during recoil as λ(t) = L(t)/nw (Fig. 3(b)).
The dynamics of the shape transformation is driven by the reduction of surface energy. Thus, it is insightful to estimate the amount of surface energy that is converted into kinetic energy. We start with an analysis similar to that developed to describe the propagation of the rim of bursting thin fluid films. The model of Taylor33 and Culick34 is based on the assumption that the moving edge of bursting films collects all the retracting material. This is fulfilled in good approximation for low viscosity (soap) films. For viscous sheets, a global thickening as in our experiments is a common feature.35 For the filaments, we assume (and our observations support) that they contract uniformly, and only a small portion of the material of the retracting structure is collected in the tip.
The local velocity v(z) along the filament axis is in good approximation proportional to the distance z from the filament base (meniscus). This yields v(z) = vtipz/L and a kinetic energy Ekin = mvtip2/6, where m is the filament mass. If we neglect the small frontal area of the filament, the surface area is
| A = 2πRL = 2(πVL)1/2 = 2(πV(L0 − ztip))1/2. | (4) |
| vtip = (12σ/m)1/2(πV)1/4(L01/2 − (L0 − ztip)1/2)1/2. | (5) |
We assume that this difference is related to the more complex inner structure of the filaments,36,37 which requires a greater level of reorganization of the internal layer arrangement than in more commonly studied soap films or smectic films.
In the experiment, we find that the filament tip initially moves with nearly constant speed (see Fig. 4), and the above estimation shows that the kinetic energy is in first approximation negligible with respect to the released surface energy. Thus, we can make the approximating assumption that after a short transient, all surface energy is dissipated. The dissipation term can be sought for an energy necessary to form new layers on the filament surface. This energy cannot be retrieved again when the filament thins. Thickening of the filament requires permeation flow across the smectic layers. To describe it, it is reasonable to introduce a viscous term that relates the layer formation process with a viscous coefficient γ. The relation between the growth rate ṅ of new layers and the pressure in the corresponding filament segment is 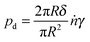 , where δ is the thickness of a single layer, n is the number of smectic layers, A0 = πR2 is the filament cross-section, and γ is a new material parameter, which has the unit of a viscosity. With ṅδ = Ṙ, one obtains pd = 2γṘ/R. This is the lateral pressure on a filament segment necessary to compress it axially and to create new smectic layers at the surface to conserve the volume. On the other hand, the pressure resulting from the surface tension can be approximated by
, where δ is the thickness of a single layer, n is the number of smectic layers, A0 = πR2 is the filament cross-section, and γ is a new material parameter, which has the unit of a viscosity. With ṅδ = Ṙ, one obtains pd = 2γṘ/R. This is the lateral pressure on a filament segment necessary to compress it axially and to create new smectic layers at the surface to conserve the volume. On the other hand, the pressure resulting from the surface tension can be approximated by  .
.
The outer filament surface (neglecting the tip front area Af for L ≫ R) is A = 2(πVL)1/2 as given above, thus 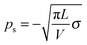 , and using
, and using 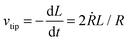 , one obtains
, one obtains 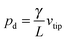 .
.
Setting pd + ps = 0, one finds
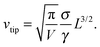 | (6) |
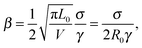 | (7) |
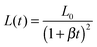 | (8) |
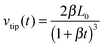 | (9) |
 , so
, so 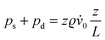 , where z is a material-fixed coordinate which moves with the local filament. This yields a second order differential equation for L, which presumably can be solved only numerically. However, an order of magnitude analysis shows that ps is of the order of σ/R ≈ 4000 Pa, the term pd is of the same order of magnitude. The deceleration adds a term of the order of ϱ
, where z is a material-fixed coordinate which moves with the local filament. This yields a second order differential equation for L, which presumably can be solved only numerically. However, an order of magnitude analysis shows that ps is of the order of σ/R ≈ 4000 Pa, the term pd is of the same order of magnitude. The deceleration adds a term of the order of ϱ![[v with combining dot above]](https://www.rsc.org/images/entities/i_char_0076_0307.gif) 0L, which hardly exceeds 100 Pa. Accordingly, it is appropriate to neglect the inertial term and use eqn (8) to fit our experimental data. Indeed, we found that this function is well suited to fit all experimental data shown above. Since the number of waves was constant during retraction, λ(t) has the same time dependence as L(t) and we could well fit λ(t) in Fig. 3(b) with an equation proportional to eqn (8). In Fig. 4, the measured ztip was fitted by L0–L(t) with only one fit parameter β, while the initial length L0 was set to the measured value. Good fits were obtained only in the initial phase of recoil, where eqn (8) is valid (thick lines). Thin lines correspond to the same fit equations and show how they deviate from the data outside the fit range. There, corrections due to flow into the meniscus etc. become essential.
0L, which hardly exceeds 100 Pa. Accordingly, it is appropriate to neglect the inertial term and use eqn (8) to fit our experimental data. Indeed, we found that this function is well suited to fit all experimental data shown above. Since the number of waves was constant during retraction, λ(t) has the same time dependence as L(t) and we could well fit λ(t) in Fig. 3(b) with an equation proportional to eqn (8). In Fig. 4, the measured ztip was fitted by L0–L(t) with only one fit parameter β, while the initial length L0 was set to the measured value. Good fits were obtained only in the initial phase of recoil, where eqn (8) is valid (thick lines). Thin lines correspond to the same fit equations and show how they deviate from the data outside the fit range. There, corrections due to flow into the meniscus etc. become essential.
The values of the relaxation rate β obtained by the fit are the following: Fig. 4(a)β(165 °C) = 185 s−1, β(170 °C) = 66 s−1; (b) β(160 °C) = 78 s−1, β(165 °C) = 39 s−1; (c) β(1.1 mm s−1) = 17 s−1; β(1.3 mm s−1) = 33 s−1; β(1.7 mm s−1) = 131 s−1; β(1.9 mm s−1) = 351 s−1; (d) β(1.1 mm s−1) = 19 s−1; β(1.3 mm s−1) = 182 s−1; β(1.7 mm s−1) = 306 s−1; β(1.9 mm s−1) = 418 s−1. The viscosity γ related to the permeation flow normal to the layers was calculated from the fit values of β as defined in eqn (7) by assuming a surface tension40σ = 25 mN m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and an average initial radius of the filaments R0 = 3 μm (although R0 may vary by a factor 2). The viscosity values obtained are the following: Fig. 4(a)γ(165 °C) = 23 Pa s, γ(170 °C) = 63 Pa s; Fig. 4(b)γ(160 °C) = 53 Pa s, γ(165 °C) = 107 Pa s; Fig. 4(c)γ(1.1 mm s−1) = 245 Pa s; γ(1.3 mm s−1) = 126 Pa s; γ(1.7 mm s−1) = 31 Pa s; γ(1.9 mm s−1) = 12 s−1; Fig. 4(d)γ(1.1 mm s−1) = 219 Pa s; γ(1.3 mm s−1) = 23 Pa s; γ(1.7 mm s−1) = 14 Pa s; γ(1.9 mm s−1) = 10 Pa s. The lower range of viscosity values of 10–20 Pa s are in the same range as shear viscosity values measured previously on these and similar liquid crystals in the B7 phase during shear flow.38
and an average initial radius of the filaments R0 = 3 μm (although R0 may vary by a factor 2). The viscosity values obtained are the following: Fig. 4(a)γ(165 °C) = 23 Pa s, γ(170 °C) = 63 Pa s; Fig. 4(b)γ(160 °C) = 53 Pa s, γ(165 °C) = 107 Pa s; Fig. 4(c)γ(1.1 mm s−1) = 245 Pa s; γ(1.3 mm s−1) = 126 Pa s; γ(1.7 mm s−1) = 31 Pa s; γ(1.9 mm s−1) = 12 s−1; Fig. 4(d)γ(1.1 mm s−1) = 219 Pa s; γ(1.3 mm s−1) = 23 Pa s; γ(1.7 mm s−1) = 14 Pa s; γ(1.9 mm s−1) = 10 Pa s. The lower range of viscosity values of 10–20 Pa s are in the same range as shear viscosity values measured previously on these and similar liquid crystals in the B7 phase during shear flow.38
There are several interesting trends we can see on these viscosity values: (i) the viscosity values under the same conditions are larger for N16 (Fig. 4(b) and (d)) than for N7 (Fig. 4(a) and (c)). This is consistent with the smaller b values of N7 (b ∼ 9 nm for N7 and b ∼ 16 nm for N16 as seen in Fig. 1(a)), meaning more areas with lower packing densities30 where the molecules can be pushed between layers. (ii) The viscosities at higher temperatures appear to be lower. For N7 it is consistent with the slightly increasing b values toward higher temperatures, however, for N16 it is not the case indicating the role of other factors in determining the viscosity for permeation flows. (iii) The apparent viscosities are larger when the rupture occurred at higher pulling speeds. This indicates the annihilation of defects at higher pulling speeds leading to a decrease of the permeation sites, thus an increase of the apparent viscosity at higher pulling speeds.
Looking at Fig. 4, we can see that the fits consistently give up to 20–30% lower than measured recoil rates at the last stage of the recoil. This is related to the flow back to the meniscus that results in shorter L(t), which was not considered in our model. Such a deviation is consistent with Fig. 3(a).
To summarize, the recoil processes of viscoelastic free-standing liquid crystal filaments are investigated experimentally and theoretically. The rupture starts with a buckling instability. During recoil the initial buckling pattern is affinely compressed with the retracting filament tip, and the total length of the filament slowly decreases. The shrinkage of the filament length is mainly compensated by its thickening, which dissipates the energy gain related to the decrease of the surface energy. A flow back into the meniscus is relevant only in the final stage of rupture. We introduced a theoretical model that takes into account the dissipation related to the thickening and explains the measured retraction speed quantitatively. The model opens new insights into the dynamics of smectic materials. It will be interesting to compare the results with filaments of simple smectic (A or C) phases to test how the permeation coefficient γ depends upon the phase structure. The problem is that such filaments are not stable, they can only be created during pinch-off processes or rupture of smectic films.39
Acknowledgements
This work was supported by the National Science Foundation under grants DMR No. 1307674, OISE 1259419 and DFG within grant STA 425/28.References
- J. Gladden, N. Handzy, A. Belmonte and E. Villermaux, Phys. Rev. Lett., 2005, 94, 035503 CrossRef CAS PubMed.
- R. Vermorel, N. Vandenberghe and E. Villermaux, Proc. R. Soc. A, 2007, 463, 641–658 CrossRef.
- C. Dombrowski, B. Lewellyn, A. I. Pesci, J. M. Restrepo, J. O. Kessler and R. E. Goldstein, Phys. Rev. Lett., 2005, 95, 184501 CrossRef.
- M. Le Merrer, D. Quéré and C. Clanet, Phys. Rev. Lett., 2012, 109, 064502 CrossRef.
- S. I. Nagahiro and Y. Hayakawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 8–11 CrossRef.
- Y. Rahmani, M. Habibi, A. Javadi and D. Bonn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 1–4 CrossRef.
- N. M. Ribe, M. Habibi and D. Bonn, Annu. Rev. Fluid Mech., 2012, 44, 249–266 CrossRef.
- W. S. Ryu and A. D. T. Samuel, Nature, 1998, 392, 140 Search PubMed.
- L. Euler, Opera Omnia I, 1744, vol. 34, pp. 231–297 Search PubMed.
- H. E. Lindberg, J. Appl. Mech., 1965, 32, 315–322 CrossRef.
- S. Alexander, Phys. Rep., 1998, 65, 236 Search PubMed.
- L. Golubovic, D. Moldovan and A. Peredera, Phys. Rev. Lett., 1998, 81, 3387 CrossRef CAS.
- C. W. Wolgemuth, T. R. Powers and R. E. Goldstein, Phys. Rev. Lett., 2000, 84, 1623–1626 CrossRef CAS PubMed.
- H. Fu, T. Powers and C. Wolgemuth, Phys. Rev. Lett., 2007, 99, 258101 CrossRef PubMed.
- F. P. Gosselin, P. Neetzow and M. Paak, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 052718 CrossRef.
- F. Vollrath and D. P. Knight, Nature, 2001, 410, 541–548 CrossRef CAS PubMed.
- D. K. Vig and C. W. Wolgemuth, Phys. Rev. Lett., 2012, 109, 218104 CrossRef PubMed.
- A. A. Evans, S. E. Spagnolie, D. Bartolo and E. Lauga, Soft Matter, 2013, 9, 1711 RSC.
- M. R. Rehorn, A. K. Schroer and S. S. Blemker, J. Biomech., 2014, 47, 687–693 CrossRef PubMed.
- L. Rayleigh, Proc. London Math. Soc., 1879, 10, 4–13 Search PubMed.
- L. Rayleigh, Proc. London Math. Soc., 1878, XI, 50–57 Search PubMed.
- A. Jákli and A. Saupe, One and Two Dimensional Fluids – Physical Properties of Smectic Lamellar and Columnar Liquid Crystals, Taylor & Francis, Boca Raton, 2006 Search PubMed.
- C. A. Bailey, M. Murphy, A. Eremin, W. Weissflog and A. Jákli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031708 CrossRef CAS.
- J. Petzold, A. Nemeş, A. Eremin, C. Bailey, N. Diorio, A. Jákli, R. Stannarius and A. Nemes, Soft Matter, 2009, 5, 3120–3126 RSC.
- R. Stannarius, A. Nemeş and A. Eremin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 020702 CrossRef.
- A. Nemeş, A. Eremin, R. Stannarius, M. Schulz, H. Nádasi and W. Weissflog, Phys. Chem. Chem. Phys., 2006, 8, 469–476 RSC.
- T. Ostapenko, S. M. Salili, A. Eremin, A. Jákli and R. Stannarius, Ferroelectrics, 2014, 468, 101–113 CrossRef CAS.
- A. Jákli, D. Krüerke and G. G. Nair, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 051702 CrossRef.
- G. Pelzl, S. Diele, A. Jákli, C. H. Lischka, I. Wirth and W. Weissflog, Liq. Cryst., 1999, 26, 135–139 CrossRef CAS.
- C. Zhang, S. M. Salili, N. Diorio, W. Weissflog and A. Jákli, Liq. Cryst., 2015, 42, 1621–1626 CAS.
- N. Vaupotič, M. Čopič, E. Gorecka and D. Pociecha, Phys. Rev. Lett., 2007, 98, 247802 CrossRef PubMed.
- C. Folcia, J. Etxebarria, J. Ortega and M. B. Ros, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 041709 CrossRef CAS PubMed.
- S. G. Taylor, Proc. R. Soc. A, 1959, 253, 313–321 CrossRef.
- F. E. C. Culick, J. Appl. Phys., 1960, 31, 1128–1129 CrossRef.
- G. Debrégeas, P. Martin and F. Brochart-Wyart, Phys. Rev. Lett., 1995, 75, 3886 CrossRef PubMed.
- A. Eremin, et al. , Phys. Rev. Lett., 2012, 109, 017801 CrossRef PubMed.
- D. A. Coleman, et al. , Science, 2003, 301, 1204 CrossRef CAS PubMed.
- C. A. Bailey, K. Fodor-Csorba, J. T. Gleeson, S. N. Sprunt and A. Jákli, Soft Matter, 2009, 5, 3618 RSC.
- K. May, K. Harth, T. Trittel and R. Stannarius, ChemPhysChem, 2014, 15, 1508 CrossRef CAS PubMed.
- See, e.g. H. Schüring, C. Thieme and R. Stannarius, Liq. Cryst., 2001, 28, 241 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00290k |
| ‡ Current affiliation: Max Planck Institute for Dynamics and Self-Organization (MPIDS), Am Faßberg 17, 37077 Göttingen, Germany. |
| This journal is © The Royal Society of Chemistry 2016 |