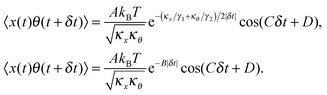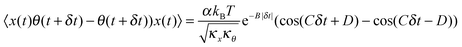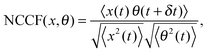DOI:
10.1039/C6SM00264A
(Communication)
Soft Matter, 2016,
12, 5077-5080
Using Brownian motion to measure shape asymmetry in mesoscopic matter using optical tweezers†
Received
31st January 2016
, Accepted 10th May 2016
First published on 11th May 2016
Abstract
We propose a new method for quantifying shape asymmetry on the mesoscopic scale. The method takes advantage of the intrinsic coupling between rotational and translational Brownian motion (RBM and TBM, respectively) which happens in the case of asymmetric particles. We determine the coupling by measuring different correlation functions of the RBM and TBM for single, morphologically different, weakly trapped red blood cells in optical tweezers. The cells have different degrees of asymmetry that are controllably produced by varying the hypertonicity of their aqueous environment. We demonstrate a clear difference in the nature of the correlation functions both qualitatively and quantitatively for three types of cells having a varying degree of asymmetry. This method can have a variety of applications ranging from early stage disease diagnosis to quality control in microfabrication.
Measuring shape asymmetry can be almost trivial as long as the object is visualized easily and can be measured using standard length scales. However, as the size of the system reduces, visualization is rendered more and more difficult, and becomes extremely challenging once the size of the object is less than the diffraction limit of the wavelength of light used for imaging. Therefore, non-visual yet simpler techniques to study asymmetry need to be explored in this regime. This is even more so since asymmetry on the microscopic scales has far-reaching consequences, especially in the context of biological entities such as motor proteins or cells, where any biochemical process often results in morphological changes to the cell shape1 or the nuclear structure.2 Changes in the shapes of the cells are also observed at the onset of diseases – as in the case of red blood cells (RBCs) due to malaria,3 or sickle cell anaemia.4 Thus, the sensitive detection of small changes in asymmetry may lead to early stage disease detection, which is presently a major technological challenge. Similarly, such methods may be useful for quality control in microfabrication processes, in order to check for small deviations from a preferred structure.
A mesoscopic particle suspended in a fluid undergoes both translational and rotational Brownian motion due to random collisions with solvent particles surrounding it.5 While translational Brownian motion dominates for symmetric particles, for asymmetric ones – there is a strong rotational component. For the latter, the two types of motion also get coupled,6 and the coupling can be expected to be stronger with increasing asymmetry. Optical tweezers are a very useful tool to study the Brownian motion of microparticles since they confine the particle spatially, and the trapped particle then executes the Brownian motion with amplitude and frequency determined by the trap stiffness. In fact, the Brownian motion can be used to characterize the trap itself, as is very often done by measuring its power spectral density.7 However, an important aspect of Brownian dynamics that remains largely ignored is the coupling between the translational and rotational Brownian motion (ESI†) for asymmetric particles inside an optical trap, except in occasional studies.6 It is this coupling that we exploit in this communication to study asymmetry, and we go on to show both theoretically and experimentally that the amount of coupling increases with the degree of asymmetry. As test particles, we use RBCs due to the fact that shape of such cells can be controllably modified by varying the hypertonicity of a hypertonic aqueous solution – with healthy RBCs in normal aqueous solutions being quite symmetric in shape.3 Note that asymmetric particles also exhibit rotational motion (spin) inside an optical trap due to torque generated by asymmetric scattering.8,9 This rotation rate depends linearly on the light intensity. We avoid such motion in our work by maintaining a weak trap so that the light intensity is not enough to observe such motion. Rotation is also observed for birefringent particles with incident circularly polarized light, but this can be avoided by using linearly polarized light.
We first develop the theoretical premise for observing the effects of the coupling between rotational and translational Brownian motion. It is well known that Brownian motion – both rotational and translational – can be described by the Langevin equation.7 In our theoretical approach, we add two coupling terms to cross-couple the rotation and the translation equations. Therefore, the final equation becomes:
| | 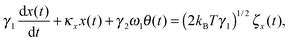 | (1) |
| | 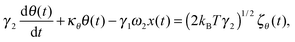 | (2) |
where
κx denotes the force constant of the optical trap for the translational motion, while
κθ is that for rotational motion that is polarization-dependent (
i.e. it tries to orient an object with the optic axis along the polarization of the input laser beam for both birefringence-driven rotation and that due to asymmetric scattering). (2
kBTγ1)
1/2ζx(
t) and (2
kBTγ2)
1/2ζθ(
t) are two independent Gaussian random noises (
kB being the Boltzmann constant), which represent the Brownian forces at the absolute temperature
T for both
x and
θ coordinate systems. In the above equations
γ2ω1θ(
t), and
γ1ω2x(
t) denote the coupling between
x and
θ.
After solving (ESI†) for x and θ,10 we compute the auto-correlation functions (ESI†) for the translational and rotational Brownian motions as:11
| | 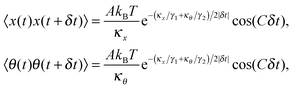 | (3) |
where
A is the coupling amplitude whose exact form is not known to us, but which is strongly manifested in the experimental data, as we show later.
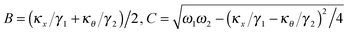
, and characterizes the coupling strength. Here,
κx/
γ1 is the translational corner frequency while the
κθ/
γ2 is the rotational corner frequency. We then go on to define the well known cross-correlation function (CCF) between the translational and rotational Brownian motions
11 that is given by:
| | 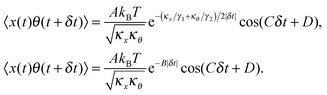 | (4) |
Here, tan(
D) =
B/
C. The CCF differs from the ACF by the phase factor
D, which has two consequences: (i) it renders the CCF asymmetric, (note that the ACF is necessarily symmetric due to causality), and (ii) it introduces another parameter that may be used to quantify asymmetry, which is obviously advantageous to us. The form of the CCF is thus similar to a coupled harmonic oscillator system, and has been used in diverse areas of physics such as quantum optics,
10 cavity quantum electrodynamics,
12 and torque calibration in Brownian motion.
11 Thus, our task is to measure
A,
B,
C, and
D for different levels of asymmetry in microparticles executing Brownian motion in optical tweezers with high precision so that small changes in asymmetry may be detected with enough signal to noise (S/N). For this reason, we proceed to introduce the differential cross-correlation, DCCF, the difference of two CCFs,
13 to yield better precision:
| | 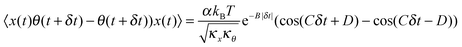 | (5) |
The nature of the DCCF is anti-symmetric since the functional form is similar to the derivative of the CCF. Now, for dielectric particles with only form birefringence (or even for birefringent particles at low laser intensities), the translational corner frequency is much larger than the rotational one.
14 Thus, the product of coupling coefficients
ω1ω2 can be written as (ESI
†)
The individual values of
ω1 and
ω2 cannot be ascertained from here since that would require exact information about the asymmetry causing the cross-coupling. However, even the value of the product indicates how well the rotational Brownian motion and the translational Brownian motion are coupled. A very crucial point to note is that these equations work when the translational and rotational corner frequencies are lower than the coupling frequencies, so that one requires rather weak optical traps in order to probe the value of the coupling constants. Note that weak traps are also required to stop asymmetric particles from spinning, as has been described earlier. For our optical tweezers experiments (ESI
†), we extracted RBCs from healthy donors, and typically started individual experiments after up to 1 hour from preparing the diluted solution in the hypertonic solvent (ESI
†), allowing time for the RBCs to get deformed. The RBCs were also visually monitored continuously and experiments were started after the RBC reached the required degree of deformity.
Fig. 1 shows RBCs at various degrees of deformation, starting with a normal RBC in aqueous solution (
Fig. 1(a)), a moderately deformed RBC (
Fig. 1(b)), and a maximally deformed RBC (
Fig. 1(c)). With maximally deformed RBCs, we regularly obtained rotation (spin) at constant rates depending on the trapping laser power, which demonstrated that the RBCs maintained a definite shape in the trap. However, at laser powers of around 15 mW after the microscope objective, the maximally deformed RBCs were stably trapped but did not spin even though they were typically aligned with the polarization direction of the linearly polarized laser beam. We used the same laser power for all RBCs during the experiments. The normal RBCs almost never showed rotation, while moderately deformed RBCs rarely showed rotation at high laser powers (less than 5% cases).
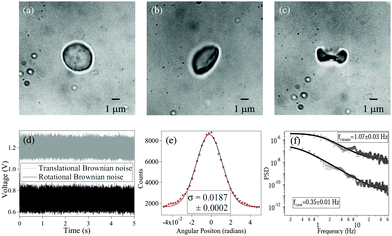 |
| | Fig. 1 (a) Normal RBC. (b) Moderately deformed RBC (hypertonic solution). (c) Maximally deformed RBC (hypertonic solution). (d) Typical measured time series for and translational (grey) and rotational (black) Brownian motion in RBC. The original data have been offset in voltage for visualization. (e) Histogram of time series data for rotational Brownian motion of normal RBC. (f) Power spectral density of translational (upper) and rotational (lower) motion of normal RBC. | |
The measurements of Brownian motion are performed using a quadrant photodiode (ESI†), and we use the technique we recently developed to detect rotational and translational motion simultaneously by measuring the sum and difference of the signals from the diagonal quadrants of the QPD.14 The rotational and translational data are acquired at a sampling frequency of 40 KHz taken for 5 seconds. Typical time series for translational and rotational Brownian motion for normal RBC are given in Fig. 1(d). The histograms of the time series data fit well with Gaussian distributions – a sample of which is shown in Fig. 1(e). Corresponding power spectral densities (PSD) for both translational and rotational motion are obtained by averaging over 25 individual spectra. We also check that our signal PSD for RBCs is substantially higher than that of the noise floor of the setup (ESI†). The measured PSDs are shown in Fig. 1(f), with the translational corner frequency (1.07 Hz) being 3 times higher than the rotational one (0.35 Hz). Before computing the CCF, we first find out the ACF for all types of RBCs and find that these are symmetric around t = 0, as is expected (ESI†). We now compute the CCF and DCCF for the different types of RBCs. Before proceeding with that, we normalize the functions in the following representative manner:
| | 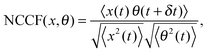 | (7) |
where NCCF (NDCCF) is the normalized CCF (DCCF). We first proceed to measure the NCCF. As a control, we use a spherical polystyrene bead of diameter 3 μm and determine the NCCF as shown in
Fig. 2(a). As expected, the signal has very small amplitude, since the rotational Brownian motion of the sphere is negligible. On the other hand, the NCCF from the least asymmetric NRBC has a clear structure. We can fit it well to
eqn (4) with an additional offset term
y0. It is also asymmetric in nature as seen from the non-zero values of
D. The fit values of
y0,
A,
B,
C, and
D with their respective error bars are given in the box inside
Fig. 3(b). Similarly, the fit parameters for moderately and maximally deformed RBCs are given in
Fig. 3(c) and (d). Using these, we calculate the coupling coefficient products
ω1ω2 from
eqn (6), the values of which are given in
Table 1. We observe that the amplitude
A for the NCCF increases with increasing asymmetry, and is the most robust parameter in differentiating between the RBCs, even at the 3
σ level of error bars. The errors in the fit parameters
B and
C (indicated in parentheses) lead to the errors in
ω1ω2, and it is clear that we are not able to differentiate between normal RBC (
ω1ω2 = 6.7 ± 3.0), and moderately deformed RBC (
ω1ω2 = 9.3 ± 3.5) even at the 1
σ level of error. Maximally deformed RBC (
ω1ω2 = 17.1 ± 5.1), however, is different from the other types of RBCs at the 1
σ level. Also, the value of
D increases with increasing asymmetry, being the highest for a single maximally deformed RBC. Thus, even this could serve as a parameter that could be used to quantify asymmetry. Note that the value of
D also acts as a consistency check for the values of
B and
C, since tan(
D) =
B/
C, and the fit values of
D can thus be compared independently to that obtained from this relation. We obtained matches for all three types of RBCs considering the overlaps of error bars at the 3
σ level (ESI
†). Interestingly, the signs of
C and
D change for maximally deformed RBCs, and this needs further careful investigation at various levels of asymmetry. In addition, we check the value of
B from the fit with that obtained by adding the translational and rotational corner frequencies, and as shown in the case of a normal RBC – the value of
B from
Fig. 1 comes out to be 1.15(15) Hz, matches well with the value 1.20(15) in
Table 1. We check this for all other cases and obtain similar results. The value of
B increases for a maximally deformed RBC even for the same trapping powers as the other types of RBCs, and we believe that the reason may be the increase of both
kx and
kθ due to the asymmetry of the cell. Note that such an increase of
kx has been reported earlier in
ref. 15, where malaria-affected RBCs whose shape is distinctly different from normal RBCs (and similar to the maximally deformed RBCs in our case) showed a 25% increase in corner frequency over normal ones. The enhanced coupling of the two types of motion resultantly leads to an increase in
kθ, which leads to a higher value of
B.
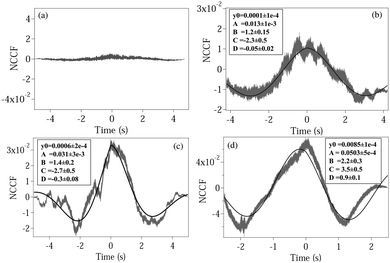 |
| | Fig. 2 Plots of the normalized CCF (NCCF) for (a) a spherical polystyrene bead, (b) normal RBC, (c) moderately deformed RBC, (d) maximally deformed RBC. (b–d) Are fit (bold line) using eqn (4). The fit values of different parameters are given in boxes inside each plot, with the respective 1σ errors in parentheses. | |
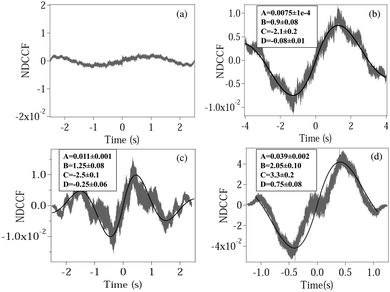 |
| | Fig. 3 Plots of the normalized DCCF (NDCCF) for (a) a spherical polystyrene bead, (b) normal RBC, (c) moderately deformed RBC, (d) maximally deformed RBC. (b–d) Are fit (bold line) using eqn (5). The fit values of different parameters (except y0, which is not of significance) are given in boxes inside each plot. | |
Table 1 Table showing the values of different parameters obtained from fitting experimentally measured NCCF and NDCCF for normal (NRBC), moderately deformed (MoRBC), and maximally deformed (MaRBC) RBC
| RBC type |
NCCF |
NDCCF |
|
A
|
B (Hz) |
C (Hz) |
D (rad) |
ω
1
ω
2 (Hz2) |
A
|
B (Hz) |
C (Hz) |
D (rad) |
ω
1
ω
2 (Hz2) |
| NRBC |
0.013(3) |
1.20(15) |
−2.3(5) |
−0.05(02) |
6.7(3.0) |
0.0075(1) |
0.90(08) |
−2.1(3) |
−0.08(2) |
5.2(1.0) |
| MoRBC |
0.031(3) |
1.4(2) |
−2.7(5) |
−0.30(08) |
9.3(3.5) |
0.011(1) |
1.25(08) |
−2.5(1) |
−0.25(06) |
7.8(7) |
| MaRBC |
0.0503(4) |
2.2(3) |
3.5(5) |
0.9(1) |
17.1(5.1) |
0.039(2) |
2.05(10) |
3.3(2) |
0.75(06) |
15.1(1.6) |
We now calculate the NDCCF to check whether error bars are reduced, and whether we can statistically differentiate the RBCs in terms of values of ω1ω2. Fig. 3(a)–(d) shows the plots of NDCCF for all four cases as in Fig. 2. While that for a sphere is very small in amplitude, we obtain good signals (anti-symmetric as expected) for RBCs, and much better fits to the function for NDCCF defined in eqn (5) compared to the NCCF. While A still remains the most robust parameter for differentiation between RBCs, we now have lower error bars for ω1ω2. Thus, as we observe from Table 1, we can differentiate normal RBC (ω1ω2 = 5.2 ± 1.0) from moderately deformed RBC (ω1ω2 = 7.8 ± 0.7) at the 1σ level and maximally deformed RBC (ω1ω2 = 15.1 ± 1.6) from the other RBCs at the 3σ level. Thus, it is clear that the NDCCF is a much better tool to quantify shape asymmetry using our technique. Finally, we repeat these measurements for other RBCs having similar relative asymmetries, and obtain similar results. While it is not possible to control the shape asymmetry quantitatively for RBCs by varying the hypertonicity of the aqueous solution, we observe that single maximally deformed RBCs can be statistically differentiated from other RBCs using the NDCCF. Finally, we would like to point out that RBCs often exhibit membrane fluctuations due to thermal effects,16 but such motional modes are mostly radially symmetric and would not be detected by our rotation measurement technique using the QPD (ESI†) so that we may safely conclude that our technique for measuring the CCF is immune to membrane fluctuations.
In conclusion, we have developed a new technique for quantifying shape asymmetry by determining the cross-correlation between translational and rotational Brownian motion. The values of the coupling amplitude increase with increasing asymmetry, while other parameters also change appreciably. We have used RBCs as test particles, and our technique can differentiate between RBCs that have different morphological states, which we control by changing the hypertonicity of the aqueous environment of the RBCs. This is a proof of concept, and we believe that the technique can be improved further by fabricating particles with controlled asymmetry using the various advanced lithography tools8 presently available, and could thus be useful in diverse applications in biology (early disease detection, etc.) and microfabrication (in terms of checking the symmetry of fabricated microparticles).
The authors acknowledge Dr Giovanni Volpe for useful discussions. This work was supported by the Indian Institute of Science Education and Research, Kolkata, an autonomous institute funded by the Ministry of Human Resource Development, Govt. of India.
References
- S. J. Morrison and J. Kimble, Nature, 2006, 441, 1068–1074 CrossRef CAS PubMed.
- A. Adjuk, S. B. Shivhare and M. Zernicka-Goetz, Dev. Biol., 2014, 392, 133–140 CrossRef PubMed.
- A. K. Dharmadhikari, H. Basu, J. A. Dharmadhikari, S. Sharma and D. Mathur, J. Biomed. Opt., 2013, 18, 125001 CrossRef PubMed.
- H. A. Pearson, J. Infect. Dis., 1977, 136, S25–S30 CrossRef PubMed.
- R. Brown, Philos. Mag., 1828, 4, 161–173 Search PubMed.
- Y. Han, A. M. Alsayed, M. Nobili, J. Zhang, T. C. Lubensky and A. G. Yodh, Science, 2006, 314, 626–630 CrossRef CAS PubMed.
- S. F. Norrelykke and H. Flyvberg, Rev. Sci. Instrum., 2010, 81, 075103 CrossRef PubMed.
- P. Galajda and P. Ormos, Appl. Phys. Lett., 2001, 78, 249 CrossRef CAS.
- S. K. Mohanty, K. S. Mohanty and P. K. Gupta, Opt. Express, 2005, 13, 4745 CrossRef PubMed.
- H. J. Carmichael, R. J. Brecha and P. Rice, Opt. Commun., 1991, 82, 73–79 CrossRef CAS.
- G. Volpe and D. Petrov, Phys. Rev. Lett., 2006, 97, 210603 CrossRef PubMed.
- G. T. Foster, S. L. Mielke and L. A. Orozco, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 61, 053821 CrossRef.
- G. Volpe, G. Volpe and D. Petrov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 037301 CrossRef PubMed.
- B. Roy, S. K. Bera and A. Banerjee, Opt. Lett., 2014, 39, 3316–3319 CrossRef PubMed.
- V. Saraogi, P. Padmapriya, A. Paul, U. S. Tatu and V. Natarajan, J. Biomed. Opt., 2010, 15, 037003 CrossRef PubMed.
- J. Evans, W. Gratzer, N. Mohandas, K. Parker and J. Sleep, Biophys. J., 2008, 94, 4134 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00264a |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article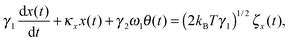
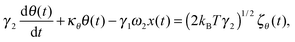
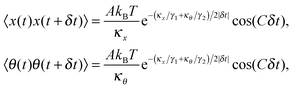
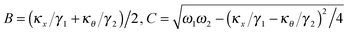 , and characterizes the coupling strength. Here, κx/γ1 is the translational corner frequency while the κθ/γ2 is the rotational corner frequency. We then go on to define the well known cross-correlation function (CCF) between the translational and rotational Brownian motions11 that is given by:
, and characterizes the coupling strength. Here, κx/γ1 is the translational corner frequency while the κθ/γ2 is the rotational corner frequency. We then go on to define the well known cross-correlation function (CCF) between the translational and rotational Brownian motions11 that is given by: