Open Access Article
Open Access ArticleInteractions between charged surfaces mediated by stiff, multivalent zwitterionic polymers
Klemen
Bohinc
*a,
Jurij
Reščič
b and
Leo
Lue
c
aFaculty of Health Sciences, University of Ljubljana, SI-1000 Ljubljana, Slovenia. E-mail: klemen.bohinc@zf.uni-lj.si; Fax: +386 1 300 1170; Tel: +386 1 300 1119
bFaculty of Chemistry and Chemical Technology, University of Ljubljana, SI-1000 Ljubljana, Slovenia. E-mail: jurij.rescic@fkkt.uni-lj.si; Fax: +386 1 241 9144; Tel: +386 1 479 8517
cDepartment of Chemical and Process Engineering, University of Strathclyde, James Weir Building, 75 Montrose Street, Glasgow G1 1XJ, UK. E-mail: leo.lue@strath.ac.uk; Fax: +44 141 548 2837; Tel: +44 141 548 2470
First published on 18th April 2016
Abstract
The interaction between like-charged objects in electrolyte solutions can be heavily altered by the presence of multivalent ions which possess a spatially distributed charge. In this work, we examine the influence of stiff, multivalent zwitterionic polymers on the interaction between charged surfaces using a splitting field theory previously shown to be accurate for the weak to the intermediate to the strong electrostatic coupling regimes. The theory is compared to Monte Carlo simulations and good agreement is found between both approaches. For surface separations shorter than the polymer length, the polymers are mainly oriented parallel to the surfaces, and the surface–surface interaction is repulsive. When the surface separation is comparable to the length of polymers, the polymers have two main orientations. The first corresponds to the polymers adsorbed onto the surface with their centers located near to or in contact with the surface; the second corresponds to polymers which are perpendicular to the charged surfaces, bridging both surfaces and leading to an attractive force between them. Increasing the surface charge density leads to more pronounced attraction via bridging. At surface separations greater than the polymer length, the polymers in the center of the system are still mainly perpendicular to the surfaces, due to “chaining” between zwitterions that enable them to bridge the surfaces at larger separations. This leads to an attractive interaction between the surfaces with a range significantly longer than the length of the polymers.
1 Introduction
Aqueous solutions containing charged macroions and small mobile ions appear in nearly all biological systems and biotechnological applications. Typical examples of macroions include proteins, viruses, cells, micelles, DNA molecules, actin molecules, mica, colloids, lipid membranes and silica particles. Understanding the interactions between macroions in electrolyte solutions is of fundamental importance, because they play a major role in determining the properties and behaviour of these systems. These interactions can be attractive or repulsive, depending on the surface charge density of the macroions, the structure and the valence of the mobile ions in solution.Replacing monovalent ions with multivalent ions can lead to an effective attractive force between colloidal particles.1,2 These attractions can cause the system to undergo phase separation.3–5 One example is the network formation in actin solutions;6 this is the consequence of the attractive interactions between cytoskeletal filamentous actin molecules mediated by small multivalent ions. Another example is the condensation of negatively charged DNA molecules on zwitterionic lipid layers,7,8 which requires the presence of divalent calcium ions. This effect has been exploited in practical applications. Divalent calcium ions are used to coagulate cement paste. Divalent diamine ions induce the aggregation of rod-like M13 viruses,9 and divalent calcium or magnesium counterions are able to induce condensation of DNA.10–12 Multivalent ions that are spatially extended usually show a strong tendency to induce aggregation of like-charged macroions. This is observed for positively charged colloids that condense DNA13 or for DNA that induces attraction between cationic lipid membranes.14
In many colloidal solutions, the macroions are significantly larger than the coions and counterions which surround them. Consequently, the interaction between a pair of macroions can be modeled as two like-charged planar surfaces with an intervening solution. DLVO theory15,16 has been extremely successful in describing the interaction between charged surfaces in different electrolyte solutions composed of point-like ions.
Modeling the interactions between surfaces immersed in polyelectrolyte solutions is less well developed than for the case of point charges. Wiegel17 treated the conformational properties of a polyelectrolyte chain interacting with only one surface. He found a structural transition between surface bound and extended configurations of the polyelectrolytes as the surface charge density changes. Miklavic and Mar![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) elja18 proposed a self-consistent field theory for grafted polyelectrolytes immersed in an electrolyte solution and confined between two charged walls. Åkesson, Woodward, and Jönsson19 used a combination of Monte Carlo simulations and the Poisson–Boltzmann (PB) approach to study two charged walls embedded in a solution of oppositely charged polyelectrolytes. Their results showed that the connectivity of the chains can cause additional attractive interactions between the charged surfaces, due to the bridging of the polyelectrolytes between the walls. Podgornik investigated the forces between two charged macroscopic surfaces where the intervening medium is composed of ions and infinitely long polyelectrolytes. He demonstrated that an additional attractive force appears, even in the mean-field approximation.20 Forsman21 introduced a simple correlation-corrected PB theory which semi-quantitatively, and in some cases quantitatively, reproduces the net attraction between like-charged surfaces and charge reversal in electrical double layers. Also, the effect of added salt on the adsorption of polyelectrolytes onto oppositely charged surfaces and their influence on the interaction between charged surfaces have been investigated.22
elja18 proposed a self-consistent field theory for grafted polyelectrolytes immersed in an electrolyte solution and confined between two charged walls. Åkesson, Woodward, and Jönsson19 used a combination of Monte Carlo simulations and the Poisson–Boltzmann (PB) approach to study two charged walls embedded in a solution of oppositely charged polyelectrolytes. Their results showed that the connectivity of the chains can cause additional attractive interactions between the charged surfaces, due to the bridging of the polyelectrolytes between the walls. Podgornik investigated the forces between two charged macroscopic surfaces where the intervening medium is composed of ions and infinitely long polyelectrolytes. He demonstrated that an additional attractive force appears, even in the mean-field approximation.20 Forsman21 introduced a simple correlation-corrected PB theory which semi-quantitatively, and in some cases quantitatively, reproduces the net attraction between like-charged surfaces and charge reversal in electrical double layers. Also, the effect of added salt on the adsorption of polyelectrolytes onto oppositely charged surfaces and their influence on the interaction between charged surfaces have been investigated.22
The presence of oligomeric multivalent ions additionally enhances the magnitude of the attractive interaction between like charged colloidal particles. The bridging mechanism is responsible for the aggregation of colloidal particles by oppositely charged short polyions.23 The forces between charged spherical aggregates conferred by oppositely charged polymeric chains have also been studied.24 Two types of polymer mediated attractions, entropic and energetic bridging, were found.
Traditional mean-field theories, such as Poisson–Boltzmann (PB) theory, are not able to describe such systems adequately.25 Specifically, within PB theory, the force between equally charged surfaces with intervening point ions is always repulsive. However, mean-field theories are able to describe the attraction between like-charged plates mediated by extended charge distributions, such as the polyelectrolytes with large separations between monovalent charges. In this case, the attraction arises due to intra-ionic charge correlations. These mean-field theories breakdown when the charge–charge correlations between different counterions become important. This occurs as the charge densities of the plates increase or in the limiting case of very short rod-like counterions (which approach point-like multivalent ions). Mean field theories are not able to describe such situations. These interionic correlations alone can give rise to an attraction between the like-charged surfaces.26–29
Complex multivalent ions with spatially separated charges are common in biological systems. Rod-like polyelectrolytes are relevant in biological applications, such as gene therapy14,30 and biotechnology.31 Examples of rod-like polyelectrolytes include the short polyamines, spermine and spermidine, which play an important role in DNA packaging.11 Recently, we modeled rod-like ions between like-charged walls and demonstrated that intra-ionic correlations induced by the fixed distance between charges within a particular rod-like ion can be sufficient to change repulsive into attractive interactions between like-charged surfaces.32,33 It was shown that a minimum interaction energy is observed when the rod-like counterions are oriented perpendicularly to the like-charged surfaces, thus connecting surfaces via bridging.11,34,35 The theory was validated by Monte Carlo (MC) simulations.36–38 It was also shown that the addition of monovalent point-like salt ions causes screening that can turn the attractive interaction to repulsive.34 The theory was extended to ions with arbitrary charge distributions along rods and within spheres.30,39,40
Zwitterions are molecules with both cationic and anionic groups. Depending on the solution conditions, molecules can become zwitterionic. Amino acids are the best known examples of zwitterions. Usually, membrane-forming phospholipids are zwitterions, where the polar head groups consist of anionic phosphates and cationic quaternary ammonium centers. Another simple example of a zwitterionic polymer is a uranyl ion, which was described in our previous work41 as a rod-like ion with a spatially distributed charge. The uranium in the middle of the ion has a charge of +2.5e0 (where e0 is the fundamental unit of charge), while the oxygens at both ends of the ion have a charge of −0.25e0. In this work, we investigate systems composed of multivalent zwitterionic polymers confined between two like-charged surfaces. Multiple positive and negative charges are located along the length of the zwitterionic polymers.
The remainder of this paper is organized as follows. In the next section, we describe an approximate field theory for systems of stiff, zwitterionic polymers, composed of point charges distributed along an infinitely thin rod. In this theoretical approach, the correlations between different ions, as well as the correlations within a particular ion, are taken into account. We then apply this theory to analyze the behavior of zwitterionic polymers confined between two like-charged, planar surfaces. To gain insight into this system, their properties are examined, including the electrostatic potential, the ion density distributions, the orientational order parameter of the stiff zwitterions, and, in particular, the pressure between the charged surfaces. The details of Monte Carlo simulations for this system are described in the following section. In the final section, the main findings of this paper are summarized, and directions for the future work are presented.
2 Theory
In this work, we examine a system composed of two plates, one located at position z = 0 and the other located at position z = D, and each with a uniform surface charge density Σ. Between the plates is an aqueous solution of stiff, multivalent, zwitterionic polymers. This is shown schematically in Fig. 1. Each zwitterionic polymer consists of c point charges of magnitude q that are evenly spaced along its total length l. The charge density Q(r,![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ) due to one of these rods, with its center located at the origin and its axis parallel to the unit vector
) due to one of these rods, with its center located at the origin and its axis parallel to the unit vector ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) , is given by
, is given by | (1) |
 | ||
| Fig. 1 Schematic illustration of the system: stiff zwitterionic polymers are embedded between two like-charged planar surfaces. | ||
The total charge density ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) (r) in the system is
(r) in the system is
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) k is the orientation of polymer k.
k is the orientation of polymer k.
The only interactions that we consider between the stiff polymers are electrostatic interactions; excluded volume and other interactions are neglected. For a system where the polymers are immersed in a solvent with a uniform dielectric constant ε, the electrostatic interaction energy E is given by
 | (2) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ) is the self energy of a polymer:
) is the self energy of a polymer: | (3) |
In order to obtain an approximate theory for this system that is accurate in the limits when the electrostatic interactions in the system are both weak and strong, as well as for intermediate strengths, we divide the Green's function of the electrostatic interactions into short-wavelength Gs and long-wavelength Gl contributions:29,42
| G(r,r′) = Gs(r,r′) + Gl(r,r′) | (4) |
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) G, and Gs = (1 −
G, and Gs = (1 − ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) )G, and
)G, and ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) is an operator that “filters” out the short-wavelength fluctuations. The choice of this operator is fairly arbitrary, and in this work, we use
is an operator that “filters” out the short-wavelength fluctuations. The choice of this operator is fairly arbitrary, and in this work, we use ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) = [1 − σ2∇2 + σ4∇4]−1. The parameter σ is a length scale which distinguishes between short-wavelength and long-wavelength phenomena. Physically, this “splitting” parameter corresponds to the size of the correlation hole around each of the charges.
= [1 − σ2∇2 + σ4∇4]−1. The parameter σ is a length scale which distinguishes between short-wavelength and long-wavelength phenomena. Physically, this “splitting” parameter corresponds to the size of the correlation hole around each of the charges.
Using the Hubbard–Stratonovich transformation43,44 for both the short-wavelength and long-wavelength electrostatic interactions in the system, the grand partition function of the system can be re-expressed as a functional integral over two fields, ψs and ψl, respectively. The resulting functional integration over ψs is evaluated by a first-order cumulant expansion, while the functional integration over ψl is evaluated using the mean-field approximation. Details of the derivation can be found in ref. 29 and 42 for systems of point ions and in ref. 45 and 46 for ions with extended charge distributions.
This procedure results directly in the following approximate expression for the Helmholtz free energy F of the system
 | (5) |
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) −1
−1![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l is the mean electrostatic potential of the system, and ρ(R,
l is the mean electrostatic potential of the system, and ρ(R,![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ) is the number density of polymers at position R and orientation
) is the number density of polymers at position R and orientation ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) .
.
The first term in eqn (5) is the entropic contribution of the zwitterionic polymers to the system free energy. The second and third terms account for the (long-wavelength) energy of the electrostatic field. The fourth term is the contribution of one-body interactions u(R,![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ) of the polymers, which is given by
) of the polymers, which is given by
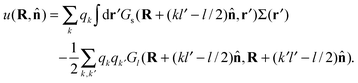 | (6) |
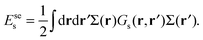 | (7) |
The expression for the free energy given in eqn (5) is similar to that given by Poisson–Boltzmann theory, as modified to account for rod-like counterions. The main differences are the presence of the long wavelength field ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l, rather than the electrostatic potential ϕ, and the appearance of the two final terms, which are not present in the Poisson–Boltzmann. As mentioned previously, the second and third terms in the free energy functional account only for the long-wavelength contributions to the energy of the electrostatic field, which is represented by
l, rather than the electrostatic potential ϕ, and the appearance of the two final terms, which are not present in the Poisson–Boltzmann. As mentioned previously, the second and third terms in the free energy functional account only for the long-wavelength contributions to the energy of the electrostatic field, which is represented by ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l. In the limit σ → 0,
l. In the limit σ → 0, ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l → βϕ; in this case, the splitting theory reduces to the Poisson–Boltzmann equation. The short-wavelength contribution to the electrostatic energy is contained in the final two terms in the free energy; both these terms vanish when the splitting parameter approaches zero.
l → βϕ; in this case, the splitting theory reduces to the Poisson–Boltzmann equation. The short-wavelength contribution to the electrostatic energy is contained in the final two terms in the free energy; both these terms vanish when the splitting parameter approaches zero.
Given the free energy functional, all the equilibrium static properties of the system can be determined. For example, the density of the polymers is
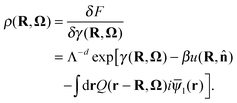 | (8) |
In order to complete the theory, we need to specify ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l and σ. The value of the slowly varying field
l and σ. The value of the slowly varying field ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l is determined by minimizing the free energy functional
l is determined by minimizing the free energy functional
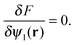 | (9) |
 | (10) |
![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) is the total charge density of the system (due to the fixed charge and that of the mobile polymers), which is given by
is the total charge density of the system (due to the fixed charge and that of the mobile polymers), which is given by | (11) |
 | (12) |
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) l is computed from the mean electrostatic potential ϕ using a fast Fourier transform. In Section 4, we present the results of these calculations.
l is computed from the mean electrostatic potential ϕ using a fast Fourier transform. In Section 4, we present the results of these calculations.
3 MC simulations
The zwitterionic polymer system was examined by NVT Monte Carlo (MC) simulations, using the integrated MC/molecular dynamics/Brownian dynamics simulation package Molsim,47 following the standard Metropolis scheme.The simulation box was a rectangular parallelepiped with periodic boundary conditions applied in the x- and y-directions. The dimensions of the box were 40.026 × 40.026 × 2.0 nm and 40.026 × 40.026 × 4.0 nm for a plate surface charge density of Σ = 0.05 C m−2 and 28.303 × 28.303 × 2.0 nm, and 28.303 × 28.303 × 4.0 nm for Σ = 0.1 C m−2. The number of zwitterionic polymers was always equal to 1000, making the simulation box electrically neutral. In order to avoid the collapse of the point charges, in the MC simulations, all the point charges were surrounded by a hard sphere with a radius of 0.1 nm.
Inter-particle interactions were calculated as suggested by Jönsson et al.,48 including the contribution to the excess internal energy caused by charges outside the simulation cell. Instead via the lattice sum technique the contribution is preferably calculated using the average charge distribution.49
Each trial move consists of both a random displacement and a random rotation of zwitterionic polymers. The magnitude of the displacement parameters was chosen so that the acceptance rate was approximately 50%. The simulations were started with the zwitterionic polymers randomly placed in the simulation box. 105 attempted moves per particle were used for equilibration runs, followed by 2 × 105 attempted moves during the production runs.
To obtain the density profiles of positive and negative charges within the zwitterionic polymers, as well as the distribution of their centers-of-mass in the direction perpendicular to the x–y plane, the z-axis was divided into 200 bins. The standard deviation of the values for each separate bin of the histograms was less than 0.5% in all cases.
4 Results and discussion
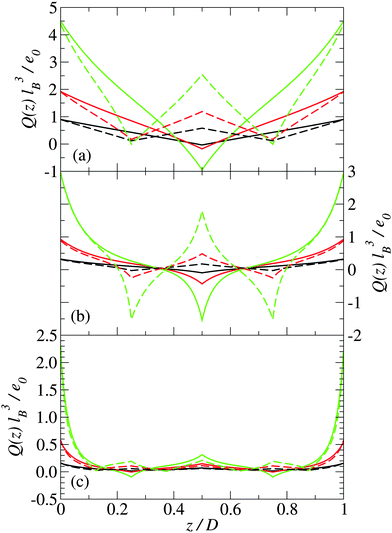
In this section, we present predictions of the field theory described previously for a system of zwitterions that are confined between two uniform negatively charged planar surfaces with the same surface charge density Σ. Two types of zwitterionic polymers are considered. The first are polymers with a total length of l = 2 nm that are composed of three uniformly spaced point charges: +e0, −e0 and +e0 (where e0 is the fundamental unit of charge). The second are polymers with a total length of l = 2 nm that consist of five uniformly spaced point charges: +e0, −e0, +e0, −e0, and +e0.The density profile of the polymer centers is shown in Fig. 2 for three different plate separations and three different surface charge densities. Similarly, in Fig. 3, the charge distribution is shown. The solid lines are for systems with 3-mer polymers, whereas the dashed lines are for 5-mer polymers. The distances between the charged surfaces are D = 0.5 nm, 2 nm and 4 nm.
For narrow plate separations (i.e. smaller than the length of the polymers), the density distribution of polymer centers shows a pronounced peak in the middle of the system (see Fig. 2(a)). Most of the centers are located in the middle of the system. Here the orientations of the polymers are highly restricted and forced to be nearly parallel to the surface of the plates. The charge distribution in the system reflects the charge distribution on the polymers (see Fig. 3), which indicates that the polymers near the center of the system tend to be angled so that their ends are on opposite plates. This tilting is stronger at higher plate surface charge densities.
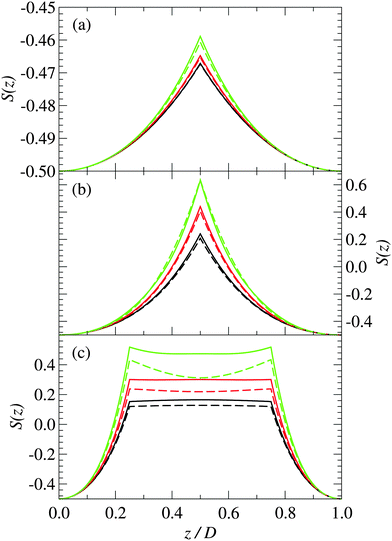
The orientation of the rod-like polymers in the system is characterized by the parameter S, which is defined as
 | (13) |
From Fig. 4(a), we can see that at short plate separations the orientational order parameter becomes less negative as the plate surface charge density increases, which indicates a decrease in orientational ordering. This provides further evidence that the polymers increase their tilt as Σ increases.
As the spacing between the plates increases, the density peak gradually decreases in height, however, it still remains up to the point where the separation between the plates is approximately equal to the length of the polymer. At a plate spacing equal to the length of the polymer, the polymers in the center of the system are aligned more perpendicularly to the plates, as can be deduced from Fig. 4(b). The polymer density and orientational order parameter profiles are nearly identical for both the 3-mer and 5-mer polymers. For both the 3-mer and 5-mer polymer systems, the charge distribution (see Fig. 3(b)) indicates that the positive charges are located near the surface of the plates. However, for the 3-mer polymers, the negative charges are located in the middle of the system, whereas for the 5-mer polymers, there is a positive charge at the center of the system, with negatively charged regions on either side of it. The difference in the charge density is primarily due to the difference in the charge distribution within the 3-mer and 5-mer zwitterionic polymers.
At larger separations between the plates (much larger than the length of the polymers), the distribution of the polymer centers has pronounced peaks close to the charged surfaces. The polymers are predominately near plates and oriented parallel to the charged surfaces. The charge distribution exhibits a sharp peak of positive charge at the charged plate and a small peak in the middle of the system (Fig. 3(c)).
For both the 3-mer and 5-mer zwitterions, the charge density profiles imply that the polymers are oriented perpendicularly to the charged surfaces. This suggests a bridging mechanism of the polymers, when D ≈ l, which holds the two planar, charged surfaces together—an effect that has been previously predicted for polyelectrolytes interacting with macroions.50,51 This result is consistent with the often rod-like structure of common condensing agents, such as polyamines and certain linear peptides that are able to condense DNA11,52 and other macroions.53
Note that this bridging mechanism appears to occur for plate separations greater than the length of the polymer. From Fig. 2(c), we can see that there are four peaks in the polymer density profile. The peaks closest to the plate surfaces correspond to polymers that are adsorbed parallel to the surfaces. The peaks farther from the surface, which occur at a distance about half of the length of the polymers, correspond to polymers that are perpendicular to the surface with one end interacting with a surface. The polymers in the interior of the system (see Fig. 4(c)) are oriented mainly perpendicularly to the plates. This seems to be facilitated through the “chaining” of the zwitterionic polymers, with the positive charges on one polymer interacting strongly with the negative charges on another polymer. This “chaining” effect appears to be stronger in the 3-mer polymers, as they are more strongly orientated than the 5-mer polymers (see Fig. 4(c)).
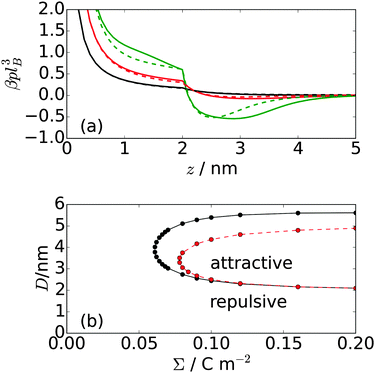
Finally, we analyzed the pressure between the two charged surfaces. The pressure is calculated by taking the derivative of the free energy functional with respect to the plate separation D of the system, which leads to the expression
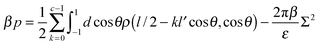 | (14) |
For the lowest surface charge density, the interaction between the plates remains repulsive; however, for the higher charge densities, there is a region of attraction that extends from a separation slightly greater than the length of the polymers and to a separation roughly twice the polymer length. At larger separations, the interaction again becomes repulsive. The strength of the attraction, as well as its range, increases with increasing plate charge density. The size of the attractive region is greater for the 3-mer than for the 5-mer zwitterionic polymer. This is attributed to the stronger “chaining” effect in the 3-mer polymers, in comparison to the 5-mer polymers. The regions of attraction and repulsion for the zwitterionic polymer system are shown in Fig. 5(b). The number of polymers between the plates is fixed by the surface charge density on the plates (i.e. the system must be neutral overall). There are no polymers or other particles outside the plates; therefore, there are no entropic depletion forces acting on the plates. In fact, the exclusion of the polymers from the interior of the plates causes an effective repulsive force. Consequently, the regions of net attraction in the system are entirely driven by electrostatic interactions, in particular, due to correlations in the fluctuations of the charge density.
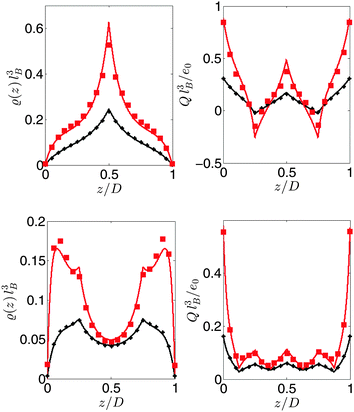
In order to assess the accuracy of the theory, we compare its predictions of the density distribution of the polymers with MC simulation results in Fig. 6 for 3-mers and those in Fig. 7 for 5-mers. The curves correspond to the theoretical predictions, and the symbols represent the MC simulation data. We find fairly good agreement between the theory and MC simulations. The deviations are due to the slight difference in the treatment of the zwitterions: the charges in the theory are point-like, while in the MC simulations, the charges are surrounded by a hard sphere of radius of 0.1 nm. Similar agreement was previously found for similar systems.35,41,54
5 Conclusions
In this work, we have applied an approximate field theory for zwitterionic stiff polymers confined between two parallel like-charged surfaces. The predictions of the theory were validated against MC simulations for these systems, and good agreement was found for both the polymer density and charge distributions.When separation between the surfaces becomes comparable to the length of polymers, they are in two main orientations. The first corresponds to the polymers adsorbed onto the surface with their centers located near to or in contact with the surface. The second orientation corresponds to polymers which are oriented perpendicularly to the charged surfaces, “bridging” them. Case (b) shows a schematic illustration of the bridging mechanism, where the polymers are oriented perpendicularly to the charged surfaces.
Fig. 8 schematically summarizes the predictions of the field theory for this system. Case (a) shows a short separation between the surfaces. The polymers lie more or less parallel to the surfaces, although they are tilted such that their ends are near opposite surfaces. The entropic penalty of restricting the orientation of the polymers causes the force between the surfaces to be repulsive.
 | ||
| Fig. 8 Schematic illustration of three situations with different plate separations: (a) D < l, (b) l = D, and (c) D > l, where l is the length of rod-like zwitterionic polymers. | ||
Case (c) shows a large separation between the surfaces. Polymers are adsorbed onto the left and right surfaces, and polymers in the midplane tend to be orientated perpendicularly to the surfaces. This seems to be driven by the “chaining” of zwitterionic polymers to each other, with the positive ions of one polymer interacting strongly with the negative ions of another. As a result, the attractive region between the plates extends to a range significantly longer than the length of the zwitterionic polymers.
This behavior differs from that observed for dimer-charges connected by infinite thin lines46 and linear rod-like counterions composed of evenly spaced point charges.45,55,56 For these systems, the polymers are randomly oriented in the center of the system at large plate separations, and the region of attraction does not extend too far beyond the length of the polymers.
In future, we plan to perform AFM measurements to verify these theoretical predictions with experimental systems. In real macromolecular systems, typically salt is present. Although we have not included the presence of added electrolytes in this work, the splitting theory used here is capable of accounting for this. In fact, it has already been applied to systems with multivalent point counterions with added salts and found to yield predictions in good agreement with MC simulation results.29 In future, we plan to investigate the influence of added monovalent salts on the behavior of the charged rod systems. We expect that the salt will screen the charge on the macroions (charged plates), leading to a decreased interaction range and shrinking of the attractive regime.34,57
References
- L. Guldbrand, B. Jönsson, H. Wennerström and P. Linse, J. Chem. Phys., 1984, 80, 2221–2228 CrossRef CAS.
- J. P. Valleau, R. Ivkov and G. M. Torrie, J. Chem. Phys., 1991, 95, 520 CrossRef CAS.
- V. Lobaskin and P. Linse, Phys. Rev. Lett., 1999, 83, 4208 CrossRef.
- J. Reš
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) and P. Linse, J. Chem. Phys., 2001, 114, 10131 CrossRef.
and P. Linse, J. Chem. Phys., 2001, 114, 10131 CrossRef. - L. B. Bhuiyan and C. W. Outhwaite, J. Chem. Phys., 2002, 116, 2650 CrossRef CAS.
- T. E. Angelini, H. Liang, W. Wriggers and G. C. L. Wong, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8634–8637 CrossRef CAS PubMed.
- D. H. Mengistu, K. Bohinc and S. May, J. Phys. Chem. B, 2009, 113, 12277–12282 CrossRef CAS PubMed.
- K. Bohinc, G. Brezesinski and S. May, Phys. Chem. Chem. Phys., 2012, 40, 10613–10621 RSC.
- J. C. Butler, T. Angelini, J. X. Tang and G. C. L. Wong, Phys. Rev. Lett., 2003, 91, 028301 CrossRef PubMed.
- V. A. Bloomfield, Curr. Opin. Struct. Biol., 1996, 6, 334–341 CrossRef CAS PubMed.
- V. B. Teif and K. Bohinc, Prog. Biophys. Mol. Biol., 2011, 105, 208–222 CrossRef CAS PubMed.
- K. Bohinc and L. Lue, AIMS Biophysics, 2016, 3, 75–87 CrossRef.
- W. M. Gelbart, R. F. Bruinsma, P. A. Pincus and V. A. Parsegian, Phys. Today, 2000, 53, 38–44 CrossRef CAS.
- J. O. Radler, I. Koltover, T. Salditt and C. R. Safinya, Science, 1997, 275, 810–814 CrossRef CAS PubMed.
- B. V. Derjaguin and L. D. Landau, Acta Physicochim. URSS, 1941, 14, 633 Search PubMed.
- E. J. Vervey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948 Search PubMed.
- F. Wiegel, J. Phys. A: Math. Gen., 1977, 10, 299–303 CrossRef.
- S. Miklavic and S. Mar
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) elja, J. Phys. Chem., 1988, 92, 6718–6722 CrossRef CAS.
elja, J. Phys. Chem., 1988, 92, 6718–6722 CrossRef CAS. - T. Åkesson, C. Woodward and B. Jönsson, J. Chem. Phys., 1989, 91, 2461–2469 CrossRef.
- R. Podgornik, Chem. Phys. Lett., 1990, 174, 191–198 CrossRef CAS.
- J. Forsman, J. Phys. Chem. B, 2004, 108, 9236–9245 CrossRef CAS.
- M. Dahlgren, A. Waltermo, E. Blomberg, P. Claesson, L. Sjostrom, T. Åkesson and B. Jönsson, J. Phys. Chem., 1993, 97, 11769–11775 CrossRef CAS.
- R. J. Hunter, Foundations of Colloid Science, Oxford Science Publications, Oxford, 1987, vol. 1 Search PubMed.
- R. Podgornik, T. Åkesson and B. Jönsson, J. Chem. Phys., 1995, 102, 9423–9434 CrossRef CAS.
- G. Cevc, Biochim. Biophys. Acta, 1990, 1031, 311–382 CrossRef CAS.
- J. G. Kirkwood and J. B. Shumaker, Proc. Natl. Acad. Sci. U. S. A., 1953, 38, 863–871 CrossRef.
- R. Kjellander, S. Mar
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) elja, R. M. Pashley and J. P. Quirk, J. Phys. Chem., 1988, 92, 6489–6492 CrossRef CAS.
elja, R. M. Pashley and J. P. Quirk, J. Phys. Chem., 1988, 92, 6489–6492 CrossRef CAS. - Y. Levin, Rep. Prog. Phys., 2002, 65, 1577–1632 CrossRef CAS.
- M. M. Hatlo and L. Lue, Soft Matter, 2009, 5, 125–133 RSC.
- K. Bohinc, J. M. A. Grime and L. Lue, Soft Matter, 2012, 8, 5679–5686 RSC.
- S. Fodor, Science, 1997, 17, 393 CrossRef.
- K. Bohinc, A. Igli
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) and S. May, Europhys. Lett., 2004, 68, 494–500 CrossRef CAS.
and S. May, Europhys. Lett., 2004, 68, 494–500 CrossRef CAS. - S. May, A. Igli
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) , J. Reš
, J. Reš![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) , S. Maset and K. Bohinc, J. Phys. Chem. B, 2008, 112, 1685–1692 CrossRef CAS PubMed.
, S. Maset and K. Bohinc, J. Phys. Chem. B, 2008, 112, 1685–1692 CrossRef CAS PubMed. - S. Maset, J. Reš
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) , S. May, J. I. Pavli
, S. May, J. I. Pavli![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) and K. Bohinc, J. Phys. A: Math. Theor., 2009, 42, 105401 CrossRef.
and K. Bohinc, J. Phys. A: Math. Theor., 2009, 42, 105401 CrossRef. - J. Reš
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) and K. Bohinc, Acta Chim. Slov., 2015, 62, 582–587 CrossRef.
and K. Bohinc, Acta Chim. Slov., 2015, 62, 582–587 CrossRef. - K. B. M. A. Grime and M. O. Khan, Langmuir, 2010, 26, 6343 CrossRef PubMed.
- Y. W. Kim, J. Yi and P. A. Pincus, Phys. Rev. Lett., 2008, 101, 208305 CrossRef PubMed.
- K. Bohinc, J. Reš
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) , S. Maset and S. May, J. Chem. Phys., 2011, 134, 074111 CrossRef PubMed.
, S. Maset and S. May, J. Chem. Phys., 2011, 134, 074111 CrossRef PubMed. - S. May and K. Bohinc, Croat. Chem. Acta, 2011, 84, 251–257 CrossRef CAS.
- J. G. Ibarra-Armenta, A. Martín-Molina, K. Bohinc and M. Quesada-Pérez, J. Chem. Phys., 2012, 137, 224701 CrossRef PubMed.
- K. Bohinc, J. Reš
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) , J.-F. Dufreche and L. Lue, J. Phys. Chem. B, 2013, 117(37), 10846–10851 CrossRef CAS PubMed.
, J.-F. Dufreche and L. Lue, J. Phys. Chem. B, 2013, 117(37), 10846–10851 CrossRef CAS PubMed. - M. M. Hatlo and L. Lue, Europhys. Lett., 2010, 89, 25002 CrossRef.
- R. L. Stratonovich, Dokl. Akad. Nauk SSSR, 1957, 115, 1097–1100 Search PubMed.
- J. Hubbard, Phys. Rev. Lett., 1959, 3, 77–78 CrossRef.
- M. M. Hatlo, A. Karatrantos and L. Lue, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061107 CrossRef PubMed.
- M. M. Hatlo, K. Bohinc and L. Lue, J. Chem. Phys., 2010, 132, 114102 CrossRef PubMed.
- J. Reš
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) and P. Linse, J. Comput. Chem., 2015, 36, 1259–1274 CrossRef PubMed.
and P. Linse, J. Comput. Chem., 2015, 36, 1259–1274 CrossRef PubMed. - B. Jönsson, H. Wennerström and B. Halle, J. Phys. Chem., 1980, 84, 2179–2185 CrossRef.
- G. Torrie and J. Valleau, Chem. Phys. Lett., 1979, 65, 343–346 CrossRef CAS.
- H. Huang and E. Ruckenstein, Adv. Colloid Interface Sci., 2004, 112, 37–47 CrossRef CAS PubMed.
- R. Podgornik and M. Li
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) er, Curr. Opin. Colloid Interface Sci., 2006, 11, 273–279 CrossRef CAS.
er, Curr. Opin. Colloid Interface Sci., 2006, 11, 273–279 CrossRef CAS. - V. A. Bloomfield, Biopolymers, 1997, 44, 269–282 CrossRef CAS PubMed.
- B. Hribar and V. Vlachy, J. Phys. Chem. B, 1997, 101, 3457–3459 CrossRef CAS.
- J. Reš
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) and K. Bohinc, Acta Chim. Slov., 2012, 59, 601–608 Search PubMed.
and K. Bohinc, Acta Chim. Slov., 2012, 59, 601–608 Search PubMed. - K. Bohinc and L. Lue, Chin. J. Polym. Sci., 2011, 29, 414–420 CrossRef CAS.
- K. Bohinc, J. M. A. Grime and L. Lue, Soft Matter, 2012, 8, 5679–5686 RSC.
- K. Bohinc and L. Lue, Mod. Phys. Lett. B, 2015, 29, 1550202 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |