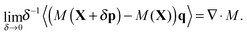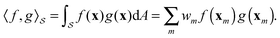DOI:
10.1039/C6SM00194G
(Paper)
Soft Matter, 2016,
12, 6685-6707
Hydrodynamic coupling of particle inclusions embedded in curved lipid bilayer membranes
Received
25th January 2016
, Accepted 24th June 2016
First published on 27th June 2016
Abstract
We develop theory and computational methods to investigate particle inclusions embedded within curved lipid bilayer membranes. We consider the case of spherical lipid vesicles where inclusion particles are coupled through (i) intramembrane hydrodynamics, (ii) traction stresses with the external and trapped solvent fluid, and (iii) intermonolayer slip between the two leaflets of the bilayer. We investigate relative to flat membranes how the membrane curvature and topology augment hydrodynamic responses. We show how both the translational and rotational mobility of protein inclusions are effected by the membrane curvature, ratio of intramembrane viscosity to solvent viscosity, and intermonolayer slip. For general investigations of many-particle dynamics, we also discuss how our approaches can be used to treat the collective diffusion and hydrodynamic coupling within spherical bilayers.
1. Introduction
Cellular membranes are complex heterogeneous materials consisting of mixtures of lipids, proteins, and other small molecules.3 The individual and collective dynamics of these species are fine-tuned to carry out complex cellular processes ranging from cell signalling to shape regulation of organelles.3,20,44,62,65,87 The effective two dimensional fluid-elastic nature of cell membranes results in interfacial phenomena and interesting geometric shapes effecting both molecular interactions and dynamics that can be very distinct from their bulk counter-parts. To gain a deeper understanding of cellular processes requires insights into the fundamental mechanics of such heterogeneous fluid bilayer membranes. We present here results for investigating protein motions within curved membranes.
Early theoretical investigations of the hydrodynamics of flat lipid bilayer membranes include the work by Saffman and Delbrück75,76 and more recently the related works.13,14,44,49,57,61,65,72,73 In the now classic papers of Saffman and Delbrück,75,76 the bilayer is treated as a two dimensional fluid. The two dimensional fluid is coupled to a bulk three dimensional fluid accounting for the solvent surrounding the membrane on both sides. This description of the hydrodynamics is used to model a protein inclusion within a flat infinite membrane to derive the self-mobility MSD = (1/4πμm)(log(2LSD/a) − γ). This asymptotic result assumes a ≪ LSD, where a is the protein size, γ ∼ 0.577 is the Euler–Mascheroni constant. The LSD = μm/2μf is the Saffman–Delbrück length associated with how dissipation within the entrained bulk solvent fluid of viscosity μf regularizes the long-range two dimensional flow of viscosity μm. These results highlight the importance of dissipation in the bulk solvent fluid that if neglected would otherwise lead to the well-known Stokes paradox.35,45,75 This shows that particle motions even within a flat interface has a very different character than its counter-part in a bulk fluid. From Stokes theory the bulk self-mobility of a particle scales like M ∼ 1/6πμfa.2,35 For curved membranes the topology and geometry can result in even more significant differences. This includes providing a finite closed membrane surface and trapped solvent fluid in a bounded interior domain augmenting the hydrodynamics and coupling.
Early work on formulating conservation laws and constitutive laws for general interfaces and Newtoninan and non-Newtonian fluids include.52,53,79,82,84,88 More recent works explore the mechanics of membranes both through coarse-grained molecular models10,11,18,19,23,24,29,74 and through the many continuum mechanics approaches.4,10,13,15,16,24,27,30,34,36,37,42,44,48,49,52,55,59,61,64,65,68–70,77,78,80–84,86 The particular works20,36,49,55,58,65,69,77,79,81,86 introduce continuum mechanics descriptions for the hydrodynamics of spherical vesicles and tubules. In ref. 39 and 49 self-mobility of an embedded particle is computed as the curvature is varied using a truncation of the series representation of the hydrodynamic flow. The works of ref. 55, 77, 81 and 86 formulate models and develop asymptotic results for the responses of vesicles subject to changes in shape and external shear flow. In ref. 4 and 69 an exterior calculus description of the continuum mechanics of a fluid-elastic membrane sheet is introduced and used to investigate lipid flow during processes such as membrane bending and budding with asymptotic results for the contributions of the ambient fluid. The prior work in this area primarily has focused on single particle mobility and transport by hydrodynamics averaged over the two bilayer leaflets.
We introduce here further approaches to investigate the collective hydrodynamic coupling of multiple particle inclusions within leaflets of curved fluid lipid bilayer membranes. We consider the case of spherical bilayer membranes where inclusion particles are coupled through (i) intramembrane hydrodynamics, (ii) traction stresses with the external and trapped solvent fluid, and (iii) intermonolayer slip between the two leaflets of the bilayer. We formulate tractable descriptions of the continuum mechanics of curved fluid bilayers drawing on results from the exterior calculus of differential geometry. We formulate a tractable description for the collective hydrodynamic coupling of the inclusion particles on curved manifolds building on our prior work on immersed boundary approximations.6,8,9,83 We compute the translational and rotational mobilities of inclusion particles. Relative to infinite flat membranes, we show that spherical vesicles exhibit significant differences arising from the curvature and finite domain size. We remark that our approaches may also be useful for other fluid interfaces arising in applications to capture particle dynamics and interface-mediated interactions, such as self-assembly at fluid–fluid interfaces.17,47,56
In Section 2 we introduce our continuum mechanics description of the bilayer hydrodynamics expressed in terms of the operators of exterior calculus of differential geometry. We use exterior calculus to help take a less coordinate-centric approach in our derivations and to obtain more concise expressions that often have a more clear geometric interpretation. We also show how the exterior calculus can be used to generalize many of the techniques used in fluid mechanics to the context of curved surfaces. In Section 2.2, we use Lamb's solution for the fluid flow exterior and interior to a spherical shell to obtain the traction stresses arising from the surrounding solvent fluid and the trapped solvent fluid. In Section 2.5, we consider the hydrodynamic flow within the lipid bilayer membrane. We use a spherical harmonics representation to derive analytic results for the solutions of the coupled hydrodynamic equations. In Section 2.7, we discuss some roles played by curvature in hydrodynamic flows within surfaces. We discuss flows on surfaces with constant Gaussian curvature comparing for the sphere and pseudo-sphere how curvature contributes to shearing motions of transported material.
In Section 3, we introduce immersed boundary approximations on manifolds to account for the coupling between the lipid flow and inclusion particles. We discuss some particular properties of this type of approximation. We then derive mobility tensors for the translational and rotational motions of inclusion particles within curved membranes.
In Section 4, we investigate the self mobility and the collective mobility of inclusion particles when varying (i) vesicle curvature, (ii) membrane viscosity vs. solvent viscosity, and (iii) intermonolayer slip. In Section 4.3, we consider approaches for the collective dynamics of many coupled inclusion particles within spherical vesicles. We consider the collective mobility associated with an attracting cluster of particles and briefly discuss some of the interesting dynamics that can arise from the collective hydrodynamic coupling. We then discuss the collective drift-diffusion of inclusion particles subject to particle–particle interactions, hydrodynamic coupling, and thermal fluctuations. We investigate the diffusive motions of inclusion particles in a crowded environment and explore the contributions of the hydrodynamics to the correlated diffusive motions. We find significant differences in the diffusivity when compared to the standard Langevin dynamics which neglects lateral hydrodynamic coupling. These results highlight the important roles played by hydrodynamics in the collective drift-diffusion dynamics of inclusion particles within curved bilayers.
Finally, in Appendix A we discuss briefly how we have addressed some of the numerical issues that arise for spherical surfaces in practical computations to obtain our results. In summary, the work presented here is meant as a starting point for understanding the basic features of the collective mobility of inclusion particles within curved bilayers.
2. Continuum mechanics of the vesicle
We formulate a continuum mechanics description of (i) the hydrodynamic flow of lipids within the two bilayer leaflets, (ii) intermonolayer slip, and (iii) coupling to the surrounding solvent fluid, see Fig. 1. We derive a set of conservation laws on manifolds using tensor calculus and results from differential geometry similar to Marsden.51 We then use identities as in Arroyo and DeSimone4 to express our equations in a convenient covariant form that is geometrically invariant. To obtain analytic results for hydrodynamic flows on the curved surface, we use exterior calculus to generalize techniques often employed in fluid mechanics to 2-manifolds. We summarize here our results and present a detailed discussion of these derivations in Appendix B. We then use these exterior calculus approaches to perform numerical calculations. While our approaches provide methods for working with hydrodynamics within general manifolds, we focus in this paper on the spherical case which is relevant to flow within the lipid bilayers of vesicles.
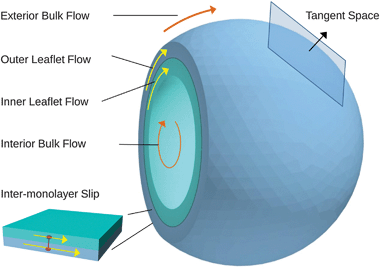 |
| | Fig. 1 Vesicle hydrodynamics. We take into account the hydrodynamics within each leaflet of the bilayer, the intermonolayer slip between leaflets, and the traction stresses for both the solvent fluid trapped interior to the vesicle and the solvent fluid exterior to the vesicle. We use a covariant formulation of the continuum mechanics. | |
2.1. Hydrodynamics of bilayer leaflets
We first consider the hydrodynamics within a single bilayer leaflet of the membrane. We treat the membrane as a two-dimensional embedded continuum in the case that the surface velocity V = v + vnn has zero velocity in the direction of the surface normal vn = 0. The conservation of momentum and mass of such a deforming two-dimensional continuum is given by ref. 51| | 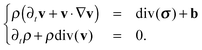 | (1) |
The ∇ denotes the covariant derivative which when expressed in terms of tensor components is (∇v)ab = va|b = ∂xbva + Γabcvc, where Γabc denotes the Christoffel symbols.1,67 In the notation div(·) and grad(·) the corresponding covariant operations for divergence div(w) = wa|a and gradient grad(w)ab = wa|b. The ρ denotes the mass density per unit surface area, the v the velocity components tangent to the surface, b the body force per unit surface area, and σ the surface stress tensor. We remark that while these equations look superficially similar to the Euclidean case owing to the convenient covariant derivative notation, as we shall discuss, the curved geometry introduces important differences and additional terms.
The constitutive law for an incompressible Newtonian fluid can be expressed in terms of the rate of deformation tensor of the surface
which in terms of tensor components is
Dab =
va|b +
vb|a. The Newtonian stress is given by
| | 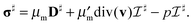 | (3) |
The
μm and
μm′ are the first and second viscosities of the membrane. The
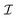
is the (1,1)-identity tensor with
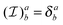
where
δab denotes the Kronecker delta-function. This has
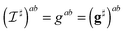
, where
g is the metric tensor for the surface.
51
We remark that we have adopted the notation for raising and lowering indices corresponding to the isomorphisms between the tangent and co-tangent spaces of the surface given by ♭: vj∂xj → vidxi and ♯: vidxi → vj∂xj as in ref. 1. Additional details on this notation and operators can be found in Appendix B.
For an incompressible Newtonian fluid, the steady-state Stokes equations corresponding to eqn (1) can be expressed in tensor components as
| | 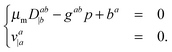 | (4) |
We can express this in a more geometrically transparent manner by using exterior calculus.
1 For the steady-state Stokes problem on the curved surface, this takes on the form
| | 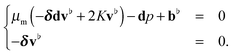 | (5) |
The
d denotes the exterior derivative,
δ = ⋆
d⋆ denotes the codifferential, ⋆ denotes the Hodge star, and
K denotes the Gaussian curvature of the surface.
1,67 In this case for the curved surface, the
d plays a role similar to the gradient operator and
δ the divergence operator.
1 The divergence of the shear stress is div(
D) = −
δdv♭ + 2
Kv♭.
As we shall discuss further, this form of the equations provides a convenient approach for analytic and numerical calculations. We can see already from this formulation that the differential operator of the Stokes equations for curved manifolds is self-adjoint.50,71 This has the important consequence of yielding results for hydrodynamics on curved manifolds related to Lorentz reciprocity66 and as we shall discuss symmetric mobility tensors for inclusion particle responses. We also remark that the hydrodynamic eqn (83) are consistent with the results of ref. 69 and 86 in the limit of a non-deforming surface for in-plane hydrodynamics. For a more detailed discussion of the exterior calculus formulation of the Stokes equations and further discussion of the operators see Appendix B.
2.2. Coupling to external solvent fluid
The solvent fluid surrounding the lipid bilayer membrane also exerts a traction stress on the inner and outer leaflets. We account for this using the Stokes equationsThe Ω = Ω± denotes either the outside region Ω+ of fluid surrounding the vesicle or the domain Ω− of fluid trapped inside the vesicle.
For the solvent fluid velocity u− in the domain Ω− interior to the vesicle and the membrane velocity V = v + vnn with vn = 0, Lamb showed results that allow for the solution to be expressed as35,45
| | 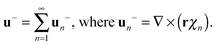 | (10) |
The
χn are a combination of the spherical harmonics of degree
n| | 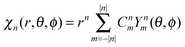 | (11) |
| | | Ynm(θ,ϕ) = eimϕPmn(cos(θ)). | (12) |
The
Pmn denote the associated Legendre polynomials.
85 The membrane surface flow
V =
v determines the external solvent flow through the solid spherical harmonic functions
χn by
| | 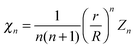 | (13) |
| | 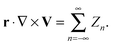 | (14) |
The
Zn denotes the combination of the surface spherical harmonics of degree
n in the expansion of the scalar field
r·∇ ×
V. The
R denotes the radius of the spherical surface. As we shall discuss, this provides a convenient way to compute the surface traction stress exerted by the solvent fluid on the membrane.
Similarly, for the solvent fluid velocity u+ in the domain Ω+ exterior to the vesicle, Lamb's solution gives35,45
| | 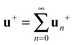 | (15) |
| | 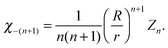 | (17) |
The membrane surface fluid velocity
V =
v again determines the solution through the expansion with
Zn in
eqn (14).
Using these results, the traction stress of the external solvent fluid on the lipid bilayer membrane is
| | 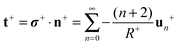 | (18) |
| | 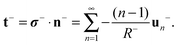 | (19) |
The
n± denotes the unit normal on the surface ∂
Ω± in the direction pointing into the solvent domain. We remark that similar expressions for the traction stress have been obtained in
ref. 38, 55, 81 and 86. For a more detailed discussion of our derivation of the traction stress exerted on the membrane from the bulk solvent fluid, see Appendix B.
2.3. Intermonolayer slip
We account for the two bilayer leaflets of the membrane by considering two surface velocity fields v+ and v−. We model the intermonolayer slip between these two leaflets by the traction term proportional to the difference in lipid velocityIn practice depending on the type of lipid and conditions the intermonolayer slip between leaflets of the bilayer have been reported over a wide range 104–109 N s m−3.22,28,54,77
2.4. Full membrane hydrodynamics
Putting these results together and using an approach similar to Section 2.1, we obtain for a two-leaflet membrane the following hydrodynamic equations.| | 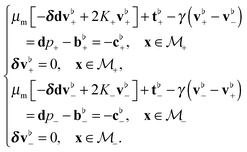 | (21) |
The 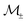 denotes the two surfaces representing the inner and outer bilayer leaflets. These equations take into account the internal membrane hydrodynamics of each leaflet of viscosity μm, the intermonolayer slip γ, and the traction stresses with the bulk solvent fluids of viscosity μ± trapped within and external to the vesicle. To obtain the coupling in the collective dynamics of inclusions embedded in such bilayer membranes, we must solve these equations for the hydrodynamic flow.
denotes the two surfaces representing the inner and outer bilayer leaflets. These equations take into account the internal membrane hydrodynamics of each leaflet of viscosity μm, the intermonolayer slip γ, and the traction stresses with the bulk solvent fluids of viscosity μ± trapped within and external to the vesicle. To obtain the coupling in the collective dynamics of inclusions embedded in such bilayer membranes, we must solve these equations for the hydrodynamic flow.
2.5. Membrane hydrodynamics and modal responses
We use exterior calculus methods to derive solutions to the membrane hydrodynamic eqn (21). For analytic and numerical calculations of flow within surfaces, the exterior calculus provides a number of advantages over more coordinate-centric approaches such as tensor calculus.1 As already seen in our expressions of the hydrodynamic equations, there are fewer explicit references to the metric tensor with instead more geometrically intrinsic operations appearing such as the exterior derivative and Hodge star.1 In analytic calculations, we take advantage of this to develop succinct methods for curved manifolds that generalize many of the vector calculus based techniques often employed in fluid mechanics.
From the exterior calculus formulation of the Stokes equations we can readily show that the incompressible surface flow can be expressed in terms of a scalar velocity potential Φ as
This provides a generalization for the surface geometry of the usual velocity potential used in fluid mechanics. The
eqn (22) generalizes to surfaces the operation in Euclidean space of taking the curl to obtain an incompressible flow.
2,35 The exterior calculus allows us to readily verify that the generated velocity field on the surface is incompressible
| | | −δv♭ = (⋆d⋆)(⋆dΦ) = −⋆d2Φ = 0. | (23) |
This follows since ⋆⋆ = −1 on a surface (2-manifold) and
d2 = 0 holds.
1
2.5.1. Modal response for intramembrane hydrodynamics.
To obtain equations for Φ, we use the exterior calculus to determine the eigenfunctions of the operator in the Stokes equations. This can then be used to rigorously derive expressions for the modal responses of the hydrodynamics when acted upon by an applied force in a manner similar to ref. 39. For this purpose, we consider the eigenproblem| | | μ[−δdv♭s + 2Kv♭s] = λsv♭s. | (24) |
Let Φs be a function such that v♭s = −⋆dΦs. The operator −⋆d commutes with −δd since −δdv♭s = −δd(−⋆d)Φs = ⋆d ⋆ d ⋆ dΦs = −⋆d(−δd)Φs. The eigenproblem becomes| | | (−⋆d)μ[−δdΦs + 2KΦs] = (−⋆d)(λsΦs). | (25) |
This can be satisfied if Φs is a solution of| | | μ[−δdΦs + 2KΦs] = λsΦs. | (26) |
This can also be expressed aswhere γs = (λs/μ − 2K). For scalar fields, the operator −δd is the Laplace–Beltrami operator of the surface. In the special case of the sphere, the solutions are surface spherical harmonics of the form| | Φs = Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(θ,ϕ) = eimϕPm m(θ,ϕ) = eimϕPm![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (cos(θ)) (cos(θ)) | (28) |
where s = (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m) subject to the restriction |m| ≤
,m) subject to the restriction |m| ≤ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The eigenvalues are γs = −
. The eigenvalues are γs = −![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1)/R2 and λs = μ(−
+ 1)/R2 and λs = μ(−![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1)/R2 + 2K).
+ 1)/R2 + 2K).
We can express the solution of the Stokes eqn (83) by expanding the velocity field as
| | 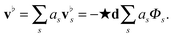 | (29) |
We can also represent the solution with
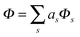
. In a similar manner, the applied surface force can be expanded with coefficients
cs as
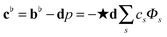
. The problem now becomes to find the coefficients
as for the flow when given an applied force with coefficients
cs.
As a demonstration of the utility of this exterior calculus approach, consider the Stokes eqn (83) for the surface flow on a sphere associated with a single leaflet, without yet the intermonolayer slip or traction stress. We treat the Stokes problem in eqn (83) by taking −⋆d of both sides to eliminate the pressure term. This yields
| | | −⋆dμ[−δdv♭ + 2Kv♭] − ⋆ddp = −⋆db♭. | (30) |
Using the expansion for
v♭ in terms of
v♭s = −⋆
dΦs and that
Φs was chosen to solve the eigenproblem in
eqn (24), we have
| | 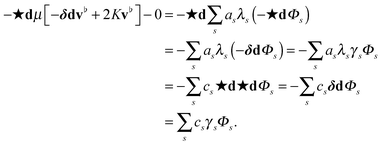 | (31) |
We remark that we use
c♭ as opposed to
b♭ throughout our calculations to emphasize that only the solenoidal component of the applied force effects the flow. This is further exhibited in the identity −⋆
dc♭ = −⋆
db♭. For mode
s, we have
λsas =
cs and
K = 1/
R2 which gives
| | 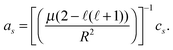 | (32) |
This applies for
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
≥ 2. For the Stokes flow on the membrane surface this gives the modal response to an applied force.
We have assumed for this solution that the applied force has net-zero torque. The mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 does not introduce an internal shear stress within the membrane since this mode corresponds to a rigid-body motion of the spherical shell. Since we have not yet included the intermonolayer slip or the external fluid traction stress there would be no stresses to balance a force having non-zero net torque.
= 1 does not introduce an internal shear stress within the membrane since this mode corresponds to a rigid-body motion of the spherical shell. Since we have not yet included the intermonolayer slip or the external fluid traction stress there would be no stresses to balance a force having non-zero net torque.
2.5.2. Modal response when coupled to external solvent fluid and with intermonolayer slip.
Using this approach, we can also incorporate for a two leaflet lipid bilayer membrane the additional contributions of the traction stress with the external solvent fluid and the intermonolayer slip. We consider the case when the outer bilayer leaflet of the membrane vesicle has radius R+ and the inner bilayer leaflet has radius R−. We remark that R+ and R− each refer to the midplane of the respective leaflet. The traction stress requires us to derive the modal response to the induced bulk external solvent flow. The solvent flow satisfies the Stokes eqn (84)–(87) with no-slip with respect to the flow within the membrane surface. These Stokes equations must be solved twice, once in the domain Ω+ exterior to 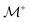 and once in the domain Ω− interior to
and once in the domain Ω− interior to 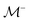 . We obtain a representation for these solutions using Lamb's solution,35 see Section 2.2.
. We obtain a representation for these solutions using Lamb's solution,35 see Section 2.2.
We represent the fluid velocity v± within each leaflet of the membrane using the velocity potential Φ±. As in Section 2.5.1, we expand the velocity potential in spherical harmonics Φs as 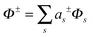 . This allows us to express the membrane velocity as
. This allows us to express the membrane velocity as
| | 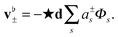 | (33) |
From this representation and
eqn (18), we can express the traction stress from the external solvent fluid on the membrane leaflet as
| | 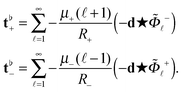 | (34) |
The
![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ±
± denotes the linear combination of modes of degree
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
. In particular,
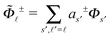
where
s′ = (
m′,
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
′).
By applying −⋆d we have
| | 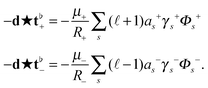 | (35) |
We use that −⋆
d(−⋆
d) = −
δd is the Laplace–Beltrami operator and that −
δdΦs± =
γs±Φs±, see
eqn (24) and (27).
Now we apply the operator −⋆d to eqn (21). By using eqn (24) and (35), we obtain for the coefficients as± of the velocity fields of the leaflets
| | 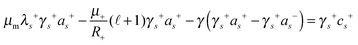 | (36) |
| | 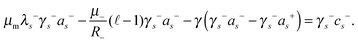 | (37) |
The solution coefficients for
v♭+ and
v♭− for the full two-leaflet membrane hydrodynamics in
eqn (21) can be expressed as
| | 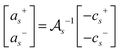 | (38) |
where
| | 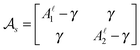 | (39) |
with
| | 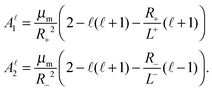 | (40) |
Associated with the inner and outer external fluids, we define the length-scales
L− =
μm/
μ− and
L+ =
μm/
μ+. The Saffman–Delbrück length-scale
75,76 associated with each leaflet is
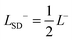
and
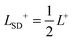
and on average
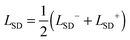
.
In summary, the eqn (38)–(40) provide the modal responses for the hydrodynamic flow satisfying the two leaflet Stokes problem in eqn (21). The model captures the hydrodynamic flow of lipids within the two curved bilayer leaflets that are coupled to one another by intermonolayer slip and that are coupled to the flow of the external solvent fluid. The key parameters are given in Table 1.
Table 1 Description of notation and parameters
| Notation |
Description |
|
μ
m
|
Intramembrane viscosity |
|
γ
|
Intermonolayer slip |
|
μ
±
|
External bulk solvent viscosity |
|
R
+
|
Radius of the outer leaflet |
|
R
−
|
Radius of the inner leaflet |
|
R
|
Average radius of the vesicle |
We remark that the membrane fluid velocity fields are obtained from these calculations for specific coordinates by
| | 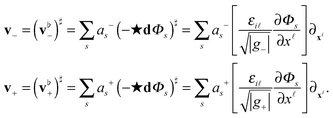 | (41) |
The |
g±| denotes the determinant of each of the metric tensors
g± associated with the leaflet surfaces
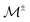
and the
εi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
denotes the Levi-Civita tensor. We remark that given coordinate singularities on the sphere to use robustly this velocity representation for numerical calculations, we need to use different coordinate charts. For details see our discussion in Appendix A.
2.6. Characteristic physical scales
To characterize the hydrodynamic responses, we discuss a few useful non-dimensional groups. We first consider how the bulk solvent fluid regularizes the two dimensional membrane hydrodynamics. This can be characterized by considering a disk-shaped patch of a flat membrane of radius r. An interesting length-scale is the radius r where the bulk three dimensional traction stress acting on the patch of area A = πr is comparable in magnitude to the intramembrane stresses acting on the perimeter of the patch of length 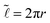 . This occurs for the inner and outer leaflets on length-scales scaling respectively like L− = μm/μ− and L+ = μm/μ+. The Saffman–Delbrück length-scale75,76 associated with each leaflet is
. This occurs for the inner and outer leaflets on length-scales scaling respectively like L− = μm/μ− and L+ = μm/μ+. The Saffman–Delbrück length-scale75,76 associated with each leaflet is 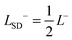 and
and 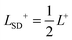 with average
with average 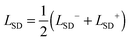 . For a vesicle, it is natural to consider these length-scales relative to the radius of the vesicle R. We introduce the non-dimensional groups Π1+ = L+/R+ and Π1− = L−/R−.
. For a vesicle, it is natural to consider these length-scales relative to the radius of the vesicle R. We introduce the non-dimensional groups Π1+ = L+/R+ and Π1− = L−/R−.
For the intermonolayer slip, we consider for the flow the response of the leading order modes with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1. These correspond to the rigid rotations of the spherical shell. For a velocity difference between the layers, the drag is given by γ. For the leading order modes with
= 1. These correspond to the rigid rotations of the spherical shell. For a velocity difference between the layers, the drag is given by γ. For the leading order modes with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, the traction stresses arising from the entrained surrounding bulk solvent fluid give an effective drag μ+/R+, see eqn (39) and (40). To characterize for a lealfet the strength of the intermonolayer slip relative to the traction stress exerted by the surrounding solvent fluid, we introduce the non-dimensional groups Π2+ = γR+/μ+ and Π2− = γR−/μ−. For convenience, we also introduce the notation γ0± = μ±/R±, so that we can express Π2± = γ/γ0±.
= 1, the traction stresses arising from the entrained surrounding bulk solvent fluid give an effective drag μ+/R+, see eqn (39) and (40). To characterize for a lealfet the strength of the intermonolayer slip relative to the traction stress exerted by the surrounding solvent fluid, we introduce the non-dimensional groups Π2+ = γR+/μ+ and Π2− = γR−/μ−. For convenience, we also introduce the notation γ0± = μ±/R±, so that we can express Π2± = γ/γ0±.
We remark that Π2± can be expressed in the more familiar terms of a ratio of rotational drag coefficients. We have Π2+ = [8π(γR+)R+3]/[8πμ+R+3]. For a rigid spherical particle subject to torque τ in a fluid with viscosity ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) , the angular velocity ω is given by ω = [8π
, the angular velocity ω is given by ω = [8π![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) R+3]−1τ.35 This shows that the intermonolayer slip contributes similarly to leading order as a bulk solvent fluid of viscosity γR+. We can express similarly Π2−. Other dimensional analyses and non-dimensional groups for slip have been reported in ref. 40 and 77.
R+3]−1τ.35 This shows that the intermonolayer slip contributes similarly to leading order as a bulk solvent fluid of viscosity γR+. We can express similarly Π2−. Other dimensional analyses and non-dimensional groups for slip have been reported in ref. 40 and 77.
These four non-dimensional groups Π1+, Π1−, Π2+, Π2− serve to characterize the relative contributions of the vesicle geometry, shear viscosity within the bilayer leaflets, the shear viscosity of the bulk solvent fluid, and the intermonolayer slip. To simplify our notation, we drop the ± when the same values are used for each leaflet and denote Π1 = Π1+ = Π1− and Π2 = Π2+ = Π2−. For the non-dimensionalization of the hydrodynamic eqn (114)–(116) using these characteristic scales see Appendix C.
2.7. Curvature and shear
In contrast to a flat membrane, material transported on a curved membrane can undergo shear even by a flow having an effectively constant velocity field on the surface. To investigate the role of intrinsic curvature of the surface, we consider flow on the sphere which has constant positive Gaussian curvature K > 0 and the pseudosphere which has constant negative Gaussian curvature K < 0,67 see Fig. 2.
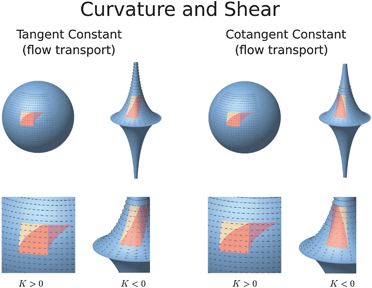 |
| | Fig. 2 Curvature and shear. In contrast to a flat membrane, material transported on a curved membrane can exhibit shear even by a flow having an effectively constant surface velocity. We consider two surfaces (i) the sphere with constant Gaussian curvature K > 0 and (ii) the pseudosphere with constant Gaussian curvature K < 0. For a rectangular patch of material on the surface (beige), we show how transport changes its shape over time (red). On the left we show the transport for a velocity field with zero co-variant derivative ∇v = 0 (tangent vectors are constant). On the right we show transport for a velocity field with zero dual exterior derivative dv♭ = 0 (co-tangent vectors are constant). For either type of velocity field on the surface, in contrast to a flat surface, we see that the intrinsic curvature can result in shearing of the transported material. This effect is captured in our hydrodynamic model by the Gaussian curvature term and exterior calculus in eqn (83). | |
For concreteness, we parametrize the sphere having Gaussian curvature K = 1 with the coordinates (θ,ϕ) with x = ψ(θ,ϕ) = [sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ), sin(θ)
cos(ϕ), sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ), cos(θ)]. We parametrize the pseudosphere having Gaussian curvature K = −1 with the coordinates (θ,ϕ) with x = ψ(θ,ϕ) = [sech(θ)
sin(ϕ), cos(θ)]. We parametrize the pseudosphere having Gaussian curvature K = −1 with the coordinates (θ,ϕ) with x = ψ(θ,ϕ) = [sech(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ), sech(θ)
cos(ϕ), sech(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ), θ − tanh(θ)].
sin(ϕ), θ − tanh(θ)].
We first consider a flow having a velocity field v with zero co-variant derivative ∇v = 0 on the surface (constant tangent vector). On both the sphere and pseudo-sphere a velocity having this property is given by v = [−sin(ϕ), cos(ϕ), 0]. We remark that it is convenient here to express the velocity in terms of the xyz-components in ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 given by the embedding from the parametrization above. For a curved surface, this provides the analogue to a flat surface of having a flow with constant velocity. We find that the curvature results in shearing of the transported material. Intuitively, this arises relative to the flat surface by the way intrinsic curvature requires distortion of the distance relationships between points on the surface. More precisely, consider two points located at (θ1,ϕ0) and (θ2,ϕ0) with θ2 > θ1 ≥ 0 in the upper hemisphere. While both points travel at exactly the same speed, the point (θ2,ϕ0) which starts closer to the north pole will take less time to traverse fully around the xy-circular cross-section of the surface. This curvature associated distortion of the distances results in shearing of the transported material. This is illustrated in the panel on the left in Fig. 2.
3 given by the embedding from the parametrization above. For a curved surface, this provides the analogue to a flat surface of having a flow with constant velocity. We find that the curvature results in shearing of the transported material. Intuitively, this arises relative to the flat surface by the way intrinsic curvature requires distortion of the distance relationships between points on the surface. More precisely, consider two points located at (θ1,ϕ0) and (θ2,ϕ0) with θ2 > θ1 ≥ 0 in the upper hemisphere. While both points travel at exactly the same speed, the point (θ2,ϕ0) which starts closer to the north pole will take less time to traverse fully around the xy-circular cross-section of the surface. This curvature associated distortion of the distances results in shearing of the transported material. This is illustrated in the panel on the left in Fig. 2.
We can also consider a flow having a velocity field v with dual field v♭ having zero exterior derivative dv♭ = 0 (constant co-tangent vector field). The constant co-tangent case is motivated by the exterior calculus formulation of the fluid equations where for such an incompressible field the flow is determined only from the Gaussian curvature term, see eqn (83). We remark that while the co-tangent vector field v♭ = vbdxb is constant on both the sphere and pseudosphere, the velocity field v = va∂xa on each surface is modulated by the local components of the inverse metric factor as va = gabvb. For any incompressible velocity field with zero exterior derivative dv♭ = 0, according to eqn (83) on any constant Gaussian curvature surface the force density b♭ must also have zero exterior derivative db♭ = 0.
To construct such a flow, we consider for the sphere v♭ = −b♭/2K = +dϕ and for the pseudosphere v♭ = −b♭/2K = −dϕ. The sign change in the fluid velocity arises from the way in which the Gaussian curvature effects the flow response to the force density, see eqn (83). For the velocity field on the sphere, the inverse metric term gϕϕ = 1/cos2(θ) yields v = [−sin(ϕ)/cos(θ), cos(ϕ)/cos(θ), 0]. For the pseudosphere, the inverse metric term gϕϕ = 1/sech2(θ) yields the velocity v = [sin(ϕ)/sech(θ), −cos(ϕ)/sech(θ), 0].
We see that for both the sphere and pseudosphere the material transported under such a flow is sheared. For the sphere and pseudosphere the shear is expected to be in the opposite direction arising from the difference in sign of the Gaussian curvature K of the surface. This is illustrated in the panel on the right in Fig. 2. We remark that similar types of geometry and shear effects can be used for performing rheological experiments as was done in ref. 12.
3. Particle-bilayer coupling: immersed boundary methods for manifolds
To model the motions of particles within the membrane, we compute a mobility tensor using approximations closely related to the Immersed Boundary Method (IB).5–9,63 In IB the fluid-structure interactions are approximated by coupling operators that perform operations on the surrounding flow field to determine the particle velocity and perform operations yielding a force density field to account for particle forces.9,63 We introduce IB approaches for manifolds to capture both the translational and rotational responses of inclusion particles to applied forces and torques when subject to coupling through the membranes hydrodynamics. We show how our IB approaches can be used to compute an effective mobility tensor for these responses.
3.1. Mobility tensor
We express the mobility tensor M for the velocity response of a collection of particles asThe V is the collective vector of velocities and angular velocities of the particles and F is the collective vector of forces and torques applied to the particles. For particle i, the velocity is given by Vi = [V]i and the particle force by Fi = [F]i. It is also convenient to decompose the mobility tensor into the components Mij where| | 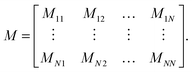 | (43) |
The response of a single particle to a force applied directly to that particle is given by the diagonal block components Mii. The two-particle response associated with the velocity of particle i in response to a force applied to particle j is given by the off-diagonal block component Mij.
3.2. Coupling operators Γ and Λ for curved surfaces
The mobility tensor for the interactions between the ith and jth particle is given by| | 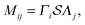 | (44) |
where we have the operators Γi = Γ[Xi] and Λj = Λ[Xj]. In the notation, we denote by the solution operator for the hydrodynamic eqn (21). The velocity field for the hydrodynamics v(x) under the applied force density f(x) is given by 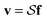 . The operators Γ, Λ approximate the fluid-structure interaction by modelling the velocity response and forces of the particles. The force density generated by an applied force F on particle j is given by f = ΛjF. In response, the velocity V of particle i is given by V = Γiv.
. The operators Γ, Λ approximate the fluid-structure interaction by modelling the velocity response and forces of the particles. The force density generated by an applied force F on particle j is given by f = ΛjF. In response, the velocity V of particle i is given by V = Γiv.
Many choices can be made for the operators Γ and Λ. This can be used for both translational and rotational responses.9 To ensure that the approximate fluid-structure coupling is non-dissipative, it has been shown the operators must be adjoints.5,9,63 We require for any choice of field v and vector F that the operators satisfy the adjoint condition
The inner-products are defined as
| | 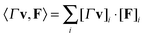 | (46) |
| | 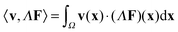 | (47) |
where·denotes the dot-product in the embedding space
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3
3. We use the notation
ΓT =
Λ to denote succinctly the adjoint condition
(45). An important consequence of the adjoint condition is that it preserves the symmetry of the mechanical responses. This is particularly desirable since as discussed in Section 2.1 the solution operator
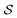
is symmetric and the adjoint condition ensures that the mobility tensor
M will be symmetric.
To obtain the translation and rotational responses of the particles, we introduce the operators
| | 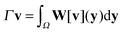 | (48) |
The
X denotes the collective vector of particle locations. The
ith particle is at location [
X]
i.
To obtain the particle velocity in response to the hydrodynamic flow, the tensor W serves to average by sampling and weighing the velocity values on the surface. For a particle force the adjoint tensor W* serves to produce a force density field.
For a curved surface, W must be chosen carefully. A simple form which is widely used in IB is to use a scalar weight W*[F] = η(y − X)F where η is the Peskin δ-function.9,63 However, for a curved surface this is not a good choice since the force density field produced by ΛF = η(y − X)F is not in the tangent space of a curved surface. Similarly, the averaging procedure Γ may produce a particle velocity which is not in the tangent space.
For curved surfaces, we use a more geometrically motivated operator of the form
| | 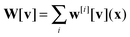 | (50) |
| | 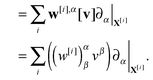 | (51) |
The sum
i runs over the particle indices and the
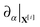
denotes the tangent basis vector in direction
α at location
X[i]. The square brackets [
i] are used to help distinguish entries not involved in the Einstein conventions of summation. This can be interpreted as the procedure of obtaining the average velocity for particle
i by using for each coordinate direction
α the inner-product of the velocity field
v with the reference vector field
qα = (
w[i],α)
♯ = (
w[i],α)
γ∂
γ. The adjoint tensor yielding the local force density is given by
| | 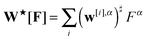 | (52) |
| | 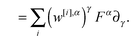 | (53) |
For translational motions we use the reference vector fields of the form
qθ =
ψ(
x −
X[i])∂
θ and
qϕ =
ψ(
x −
X[i])/cos(
θ)∂
ϕ, where
ψ(
r) =
C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp(−
r2/2
σ2). For rotational responses we use the reference vector field on the surface
qn =
ψ(
x −
X[i])(
n × (
x −
X[i])). We emphasize that we only use these expressions for a coordinate chart chosen so that the particle location
X[i] is away from a polar singularity, see Appendix A. The reference velocity fields are illustrated in
Fig. 3.
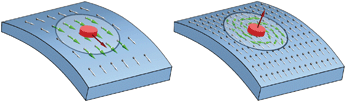 |
| | Fig. 3 For curved surfaces the coupling operators Γ and Λ must be consistent with the tangent bundle of the surface. We use reference vector fields on the surface to construct the coupling operators Λ and Γ. We derive operators Γ and Λ for translational and rotational motions using the adjoint conditions in eqn (45) and (57). On the left we show the reference vector field for translational responses (green). On the right we show the reference vector field for rotational responses (green). | |
We remark that σ is related to the approximate size of the modeled inclusion particle. One should think about the force balance in the immersed boundary model as capturing the motion both of the inclusion particle and the entrained lipids in the immediate viscinity of the particle. A relationship can be established in principle between σ and the particle size by considering the hydrodynamic radius obtained by comparing self-mobility results from the immersed boundary model to other more detailed hydrodynamic calculations that explicitly account for the fluid–solid boundary of the particle.
In practice for the spatially discretized system, the operators and the associated fields they generate can be expressed conveniently as
The index
m corresponds to the discrete degrees of freedom, such as the index of a lattice point or harmonic mode, and the
i and
j index the components of the vector. We have
| | | VkFk = ΓkmvmFk = vmΛmkFk = vmfm. | (56) |
The adjoint condition can be expressed as
In practice, we define the operator
Λ in numerical calculations using the specified reference velocity fields
qα above to generate the force density at lattice sites on the sphere surface. Using the sparse matrix representation of this operation for
Λ,
eqn (57) provides the adjoint velocity averaging operator
Γ. This approach for developing consistent operators
Λ and
Γ on the sphere also extends straight-forwardly to immersed boundary approximations on more general curved surfaces and manifolds.
4. Dynamics of inclusion particles embedded in spherical bilayers
For particle inclusions embedded within spherical lipid bilayer membranes, we investigate their translational and rotational motions in response to applied forces and torques. We consider the case when each embedded inclusion particle only spans one of the fluid bilayer leaflets, see Fig. 4. We investigate the mobility of these inclusions when varying the (i) vesicle radius, (ii) membrane viscosity, (iii) solvent viscosity, and (iv) intermonolayer slip. We investigate the four interaction cases (i) outer–outer, (ii) outer–inner, (iii) inner–outer, and (iv) inner–inner. We also investigate the coupled motions for the four cases (i) translation–translation, (ii) translation–rotation, (iii) rotation–translation, and (iv) rotation–rotation.
 |
| | Fig. 4 We consider the case when each embedded inclusion particle only spans one of the bilayer leaflets. We consider the interaction cases when particles are both in the same leaflet or are in different leaflets. | |
We express the translational and rotational responses as
| | 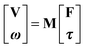 | (58) |
where we decompose the mobility tensor into the blocks
| |  | (59) |
In the notation, the
V denotes the collective translational velocities and
ω the collective rotational angular velocities. The
F denotes the collective forces applied to particles within the inner and outer leaflets. The
τ denotes the collective torques applied to particles within the inner and outer leaflets.
We denote the different ways in which the forces F and torques τ couple to the particle translational motions V and rotational motions ω using the notation MXY. The X denotes the response as either translation (t) or rotational (r). The Y denotes the type of applied force as either standard force (t) or torque (r). The mobility components can be further decomposed into MXY,i1,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1,i2,
1,i2,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 where ik denotes the location of the ikth particle. The leaflets in which the inclusions are embedded is denoted by
2 where ik denotes the location of the ikth particle. The leaflets in which the inclusions are embedded is denoted by ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) k ∈ {inner, outer}.
k ∈ {inner, outer}.
There are a few notable differences between spherical fluid membranes and flat fluid membranes. In the flat case, the membrane domain is often treated as effectively infinite and for theoretical convenience often as having periodic boundary conditions. In the spherical case, the membrane is intrinsically of finite area. Also for a sphere, as consequence of the topology, any in-plane hydrodynamic flow must have a singularity.43 For the solvent fluid, flat membranes have fluid extending over an infinite domain symmetrically on both sides. In the spherical case, this symmetric is broken with solvent fluid trapped within the interior in a region of finite volume and with solvent fluid extending exterior over an infinite domain. The curvature of the membrane surface can also play an important role in the hydrodynamics. This is particularly apparent from the Gaussian term that appears in eqn (21) and the effects we discussed in Section 2.7.
We investigate the mobility of inclusion particles within spherical bilayers in a few different regimes. We consider the characteristic scales introduced in Section 2.6. The regime with Π1 = L/R ≫ 1 and for Π2 = γR/μf with Π2−1Π1 = 1 corresponds to the case when the hydrodynamic flow is dominated by the intramembrane viscosity and intermonolayer slip. In this regime, for a force density having a non-zero net torque, the flow is approximated well by the leading order spherical harmonic modes with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, see eqn (116). The intramembrane viscosity strongly couples the surface fluid resulting in a flow that is a rigid body rotation of the entire spherical shell, see Fig. 5. Parameter values are given in Table 2.
= 1, see eqn (116). The intramembrane viscosity strongly couples the surface fluid resulting in a flow that is a rigid body rotation of the entire spherical shell, see Fig. 5. Parameter values are given in Table 2.
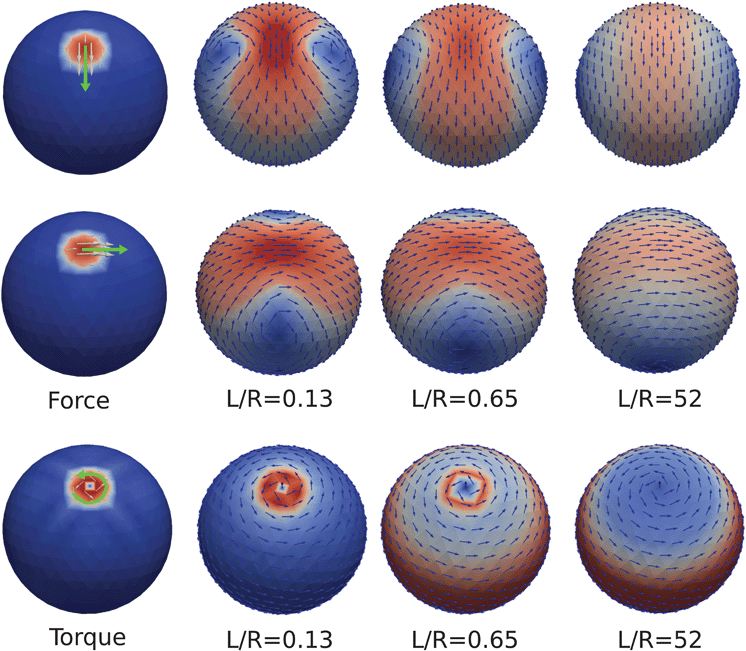 |
| | Fig. 5 Hydrodynamic flow in response to force acting on an inclusion particle. The L/R = Π1 is the relative Saffman–Delbrück length-scale scaled by the vesicle radius. For small intramembrane viscosity the force produces a localized hydrodynamic flow on the surface. As the membrane viscosity increases the hydrodynamic flow becomes less localized and eventually approaches the velocity field of a rigid body rotation of the sphere. The flow exhibits two vortices with locations that migrate toward the equatorial poles as the viscosity increases. Parameter values in Table 2. | |
Table 2 Vesicle parameters. We use these default parameters throughout our discussions unless specified otherwise. These parameters correspond to the non-dimensional regime with Π1 = L/R = 0.65 and Π2 = γR/μf = 4.0
| Parameter |
Value |
Parameter |
Value |
|
R
−
|
14 nm |
μ
± = μf |
598.44 amu ps−1 nm−1 |
|
R
+
|
16.6 nm |
μ
m
|
5984.4 amu ps−1 |
|
R
|
15.3 nm |
γ
|
156.25 amu ps−1 nm−2 |
|
σ
|
1 nm |
m
0
|
1 amu |
|
τ
|
0.64 ps |
ε
|
2.5 amu nm2 ps−2 |
Mathematically, this arises from the dominant spherical harmonic modes with degree index ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and order index m = −1, 0, 1. Using the exterior calculus formation we apply the generalized curl = −⋆d on the surface to the vector potential Φ given by a linear combination of the harmonic modes of degree
= 1 and order index m = −1, 0, 1. Using the exterior calculus formation we apply the generalized curl = −⋆d on the surface to the vector potential Φ given by a linear combination of the harmonic modes of degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1. This yields for the velocity field on the surface that of a rigid body rotation, see eqn (41). In the case when the surface force has zero net torque in the regime Π1 ≫ 1, Π2−1Π1 = 1, the leading order flow is determined by the intramembrane viscosity and intermonolayer slip and depends on the higher-order moments of the torque of degree
= 1. This yields for the velocity field on the surface that of a rigid body rotation, see eqn (41). In the case when the surface force has zero net torque in the regime Π1 ≫ 1, Π2−1Π1 = 1, the leading order flow is determined by the intramembrane viscosity and intermonolayer slip and depends on the higher-order moments of the torque of degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1.
> 1.
The regime with Π1 ≪ 1 and Π2 ≪ 1 corresponds to the case when the traction stress from the entrained external solvent fluid dominates the hydrodynamic response relative to the intramembrane viscosity and intermonolayer slip. This results in more localized flow within the surface, see Fig. 5.
We remark that the regime when Π2 ≫ 1 corresponds to the case when the intermonolayer slip strongly couples the hydrodynamic flow between the two leaflets to make them nearly identical. This effectively doubles the intramembrane viscosity.
We have presented a few regimes indicating the contributing factors in the hydrodynamic responses and the interplay between the entrained solvent fluid, intramembrane viscosity, and intermonolayer slip. We now discuss some features of the hydrodynamic response that arise from the geometry of the spherical membrane.
4.1. Vortices and membrane viscosity
As a consequence of the spherical topology of the membrane, any hydrodynamic flow within the surface must contain a singularity.43 We consider the case of an inclusion particle located at the north pole of the sphere and subjected to a force. These singularities manifest in the flow as two vortices of opposite sign, see Fig. 5. The location of these vortices depends on Π1 = L/R characterizing the relative strength of the intermembrane shear viscosity vs. the solvent traction stress. For small Π1 the vortices start near the north pole and as Π1 increases they migrate toward the equator, see Fig. 5. For a force applied to a particle in either the outer leaflet or inner leaflet we consider how the vortex location changes as the viscosity of the membrane is varied. We show the vortex locations in the outer and inner leaflets in Fig. 6. In this case we vary Π1 = L/R and keep fixed Π2 = γ/γ0 where γ0 = μf/R with parameters in Table 2. We remark that these results can be used as a reference to estimate the membrane shear viscosity by making observations of the vortex locations of the fluid flow within the leaflets. Some recent experimental work to estimate the membrane viscosity of vesicles using vortex locations can be found in ref. 25, 41 and 89.
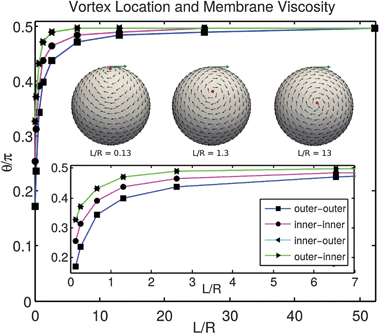 |
| | Fig. 6 Vortex location and membrane viscosity. For a force applied to a particle in the outer leaflet located at the north pole, we show as the shear viscosity is varied how the vortex location changes in the outer and inner leaflets. In the nomenclature X–Y in the figure caption, X refers to the leaflet of the applied force and Y the leaflet of the flow response. For low viscosity the vortices are near the north pole θ = 0. As viscosity increases the vortices migrate toward the equator θ = π/2. The inset left to right shows typical progression in flows of the vortex location. The intermonolayer slip Π2 = γ/γ0 = 4 moderately couples the inner leaflet to the outer leaflet. We find this results in a flow within the inner leaflet with a vortex location closer toward the equator. Parameter values in Table 2. | |
4.2. Self-mobility and coupled-mobility
We next consider the hydrodynamic responses when a force or torque is applied to an inclusion particle embedded in the outer leaflet when the center of the sphere is held fixed. We take as our convention that this particle is embedded at a pole where we parametrize this position on the sphere with (θ,ϕ) = 0. We then consider how the resulting hydrodynamic flows within the inner or outer leaflets within the spherical bilayer couple the translational motions and rotational motions of inclusion particles at other locations. Throughout, we use the base-line parameters given in Table 2. These parameters correspond to the non-dimensional regime with Π1 = 0.65 and Π2 = 4.0.
We investigate the roles played by the bulk solvent fluid, the intramembrane viscosity, and the intermonolayer slip. We use our methods to compute profiles of the mobility responses at different locations when varying the intramembrane viscosity and intermonolayer slip in Fig. 7 and 8. We show how the mobility varies when changing the intermonolayer slip and membrane viscosity in Fig. 9 and 10. For comparison we also compute the mobility responses within a flat membrane shown in Fig. 11.
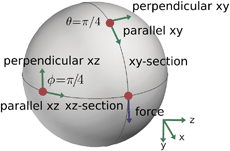 |
| | Fig. 7 Cross Sections of the sphere and conventions. We consider the hydrodynamic responses when a force or torque is applied to an inclusion particle. For convenience in our calculations, we use by convention the coordinates for the inclusion particle X = (x, y, z) = (1, 0, 0) and we apply force to the inclusion particle in the direction F = (fx, fy, fz) = (0, 1, 0). To characterize the hydrodynamic responses, we consider the cross-sections of the sphere in the xy-plane and the xz-plane. This gives two great circles of the sphere. We consider the velocity in the directions parallel and perpendicular to the tangents of each of the respective great circles. | |
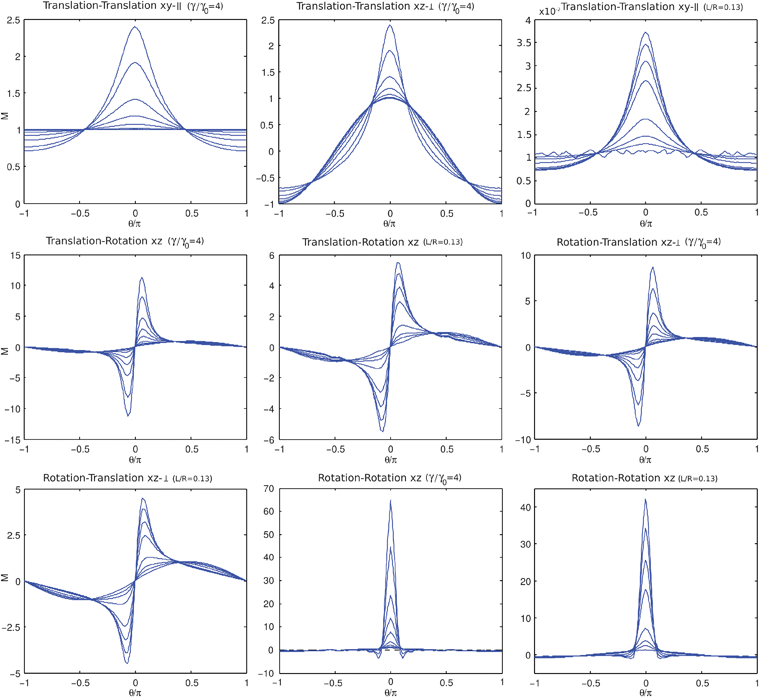 |
| | Fig. 8 Mobility profiles of inclusion particles when varying the membrane viscosity and intermonolayer slip. In each case a force or a torque is applied to a single inclusion particle within the outer leaflet located at (θ,ϕ) = 0. The resulting inclusion particle hydrodynamic response within the outer leaflet or inner leaflet is shown in terms of the mobility M defined in Section 3.1. We use in the nomenclature in the titles of X–Y to indicate a forcing of type X and a response of type Y. We normalize the mobility by the self-mobility response obtained in the case when Π1 = L/R = 48 and Π2 = γR/μf = γ/γ0 = 32. The intramembrane viscosity or intermonolayer slip is held fixed in panels displaying respectively Π1 = L/R = 0.13 or Π2 = γ/γ0 = 4. All figures show the outer leaflet response with the exception of the figure on the upper-right for the translation–translation response which shows how the inner leaflet responds to increasing intermonolayer slip. The other panels show the dependence of the mobility response of inclusion particles embedded within the outer-leaflet when increasing the membrane viscosity as Π1 = L/R = 0.13, 0.26, 0.65, 1.3, 2.6, 6.5, 13, 26, 52. The curve with largest amplitude at θ = 0 corresponds to the largest local mobility response which occurs for the smallest membrane viscosity. The panels show the dependence of the mobility response of inclusion particles embedded within the inner-leaflet when increasing the intermonolayer slip as Π2 = γ/γ0 = 0.040, 0.10, 0.40, 1.0, 4.0, 8.0, 16, 32. The curve with smallest amplitude at θ = 0 shows the smallest mobility response corresponds in each case to the smallest intermonolayer slip. | |
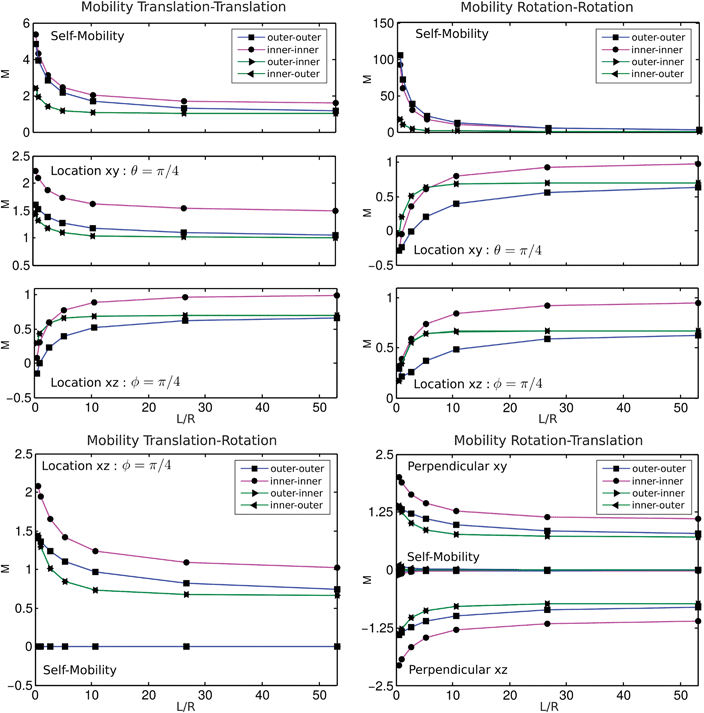 |
| | Fig. 9 Membrane viscosity and particle mobility. For a torque applied to a particle embedded within either the inner or outer leaflet, we show as the membrane viscosity is varied the translational and rotational responses of inclusion particles embedded within the inner or outer leaflet. The intermonolayer slip is kept fixed at Π2 = γ/γ0 = 4. This is discussed in more detail in Section 4.2. | |
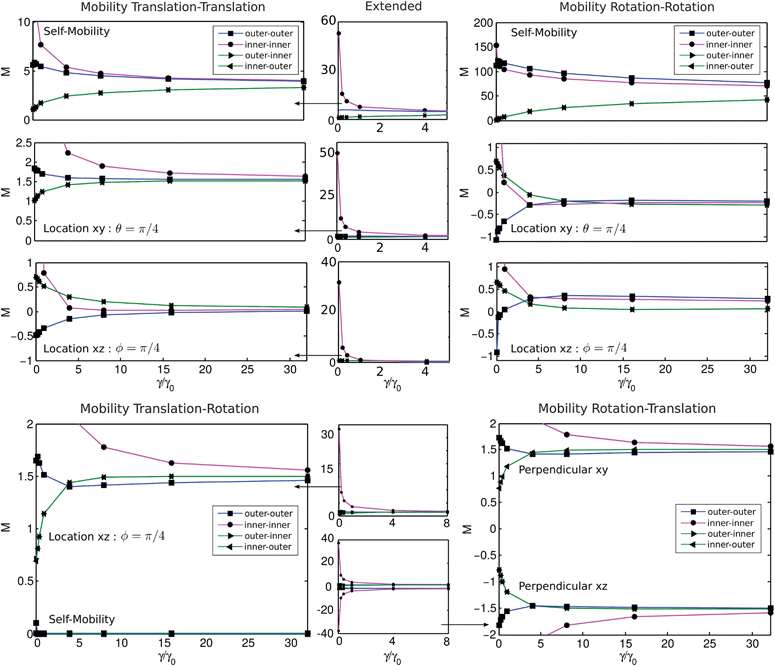 |
| | Fig. 10 Intermonolayer slip and particle mobility. For a torque applied to a particle embedded within either the inner or outer leaflet, we show as the intermonolayer slip is varied the translational and rotational responses of inclusion particles embedded within the inner or outer leaflet. The membrane viscosity is kept fixed at Π1 = L/R = 0.13. This is discussed in more detail in Section 4.2. | |
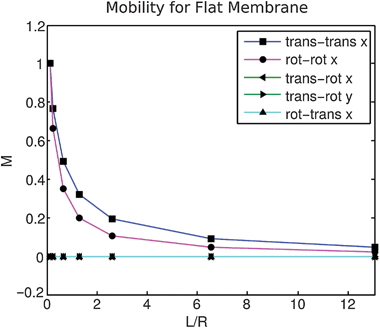 |
| | Fig. 11 Mobility for flat membranes. For a force or torque applied to a particle embedded within a large flat membrane, we show as the intramembrane viscosity is varied the translational and rotational responses of inclusion particles. Normalized by the mobility response when Π1 = L/R = 0.13. These results were obtained from solving in Fourier space the hydrodynamic flow in response to an applied force density following closely the analytic approach presented in ref. 61 and 75 and our method for computing the mobility tensor discussed in Section 3.2. | |
Before discussing in more detail these results, we make a few remarks concerning how the mobility results are reported. The responses are shown along the two great circles on the sphere corresponding to the intersection with the xy-plane and the xz-plane.
We consider the velocity responses in the parallel ∥ and perpendicular ⊥ directions along each of these curves. We normalize all of the mobility results by comparing to the case of large intramembrane viscosity Π1 = L/R = 48 for the leaflet or large intermonolayer slip corresponding to Π2 = γR/μf = 32. This regime provides a reference case corresponding to the situation when the large intramembrane viscosity yields an effective rigid body rotation of the spherical shell within the bulk solvent fluid or when the two leaflets are tightly coupled.
We remark that this is in contrast to the flat membrane case where the mobility tends to zero as Π1 = L/R becomes large. In the flat membrane case, we normalize instead our reported results by the self-mobility when Π1 = L/R = 0.1. Given the mobility model for the hydrodynamic responses discussed in Section 3.1, the self-mobility on the sphere for each type of coupling is given in our model by the results reported at location (θ,ϕ) = 0.
The mobility profiles reveal a number of interesting aspects of the hydrodynamic coupling between inclusion particles and leaflets. We find that the intermonolayer slip and curvature yield coupling for particles embedded in the inner leaflet significantly different than for particles embedded in the outer leaflet. For a force or torque applied to a particle embedded in the outer leaflet, the intermonolayer slip yields a flow for the inner leaflet with recirculation over a larger scale. This is seen when looking at the vortex locations when applying force at the north pole, where the intermonolayer slip plays a role pushing the vortex location of the inner leaflet closer to the equatorial poles, see Fig. 6.
We see this can result in both the translational motions and rotational motions of a particle within the inner leaflet moving in the opposite direction of an inclusion particle within the outer leaflet at the same location. This is seen for the smallest viscosities and intermonolayer slips for the translation–translation responses at location xz with ϕ = π/4 and for the rotation–rotation responses at location xy with θ = π/4, see Fig. 9 and 10.
For the translational and rotational response to forces in the outer leaflet, we find that the intermonolayer coupling smoothes the flow over a larger scale within the inner leaflet.
We next consider for fixed intramembrane viscosity how the intermonolayer slip effects the flow. We see for a force acting on the outer leaflet as the intermonolayer slip becomes small the flow within the inner leaflet approaches a rigid body rotation, see the bottom curve in the upper-right panel of Fig. 5.
From an analysis of the hydrodynamic response eqn (40), we have two interesting cases for the modes of the inner leaflet: (i) ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and (ii)
= 1 and (ii) ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1. In the first case, the inner-leaflet rotates as a rigid spherical shell and entrains the fluid trapped within to a rigid body motion. As a consequence there is no traction stress with the external solvent fluid for the inner leaflet and no intramembrane shear stress. This means there are no other stresses acting against the intermonolayer drag so −γ(a
> 1. In the first case, the inner-leaflet rotates as a rigid spherical shell and entrains the fluid trapped within to a rigid body motion. As a consequence there is no traction stress with the external solvent fluid for the inner leaflet and no intramembrane shear stress. This means there are no other stresses acting against the intermonolayer drag so −γ(a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − − a
− − a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +) = 0 and the inner leaflet matches the outer leaflets rotation with a
+) = 0 and the inner leaflet matches the outer leaflets rotation with a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − = a
− = a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + for
+ for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1.
= 1.
In the second case with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1, the intramembrane stress and traction stress balance the intermonolayer drag. In this case, the hydrodynamic modes of the inner leaflet scale in proportion to the intermonolayer slip and the modes of the outer leaflet. As the intermonolayer slip decreases, the modes a
> 1, the intramembrane stress and traction stress balance the intermonolayer drag. In this case, the hydrodynamic modes of the inner leaflet scale in proportion to the intermonolayer slip and the modes of the outer leaflet. As the intermonolayer slip decreases, the modes a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − of the inner leaflet become small for
− of the inner leaflet become small for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1.
> 1.
This can be seen mathematically from eqn (40) where the inner leaflet modes satisfy a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − = −((A
− = −((A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/γ) − 1)−1a
2/γ) − 1)−1a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +. This can be expressed as
+. This can be expressed as
a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − = −Π3(2 − − = −Π3(2 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ( (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1) − Π1−1( + 1) − Π1−1(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − 1) − Π3)−1a − 1) − Π3)−1a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + + |
where for convenience we denote
Π3 =
Π2−/
Π1−. For
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
= 1 this shows
a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −
− =
a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +
+ independent of the magnitude of
Π3 ≠ 0. For
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
> 1, we have as the intermonolayer slip becomes small
Π3 ≪ 1 the hydrodynamic response for the mode of the inner leaflet with
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
> 1 become small
a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −
− ≪ 1. This shows that the resulting hydrodynamic responses in the inner leaflet become dominated by the rigid rotation mode
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
= 1 for small intermonolayer slip. This can be seen in the upper-right panel of
Fig. 8.
This has a number of interesting consequences for the motions of inclusion particles embedded within leaflets of spherical bilayers. From the different hydrodynamics of the two spherical shells, we have that for small intermonolayer slip the self-mobility and coupled-mobilities can result in large motions when forces or torques act on an inclusion particle within the inner leaflet. For small intermonolayer slip this arises since the rigid body mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 of the hydrodynamic response for the inner leaflet is not damped by the trapped solvent fluid but only by the weak intermonolayer coupling. This manifests in a near rigid rotation of the inner leaflet and a large self-mobility and coupled-mobility in response to an applied force or torque, see Fig. 10.
= 1 of the hydrodynamic response for the inner leaflet is not damped by the trapped solvent fluid but only by the weak intermonolayer coupling. This manifests in a near rigid rotation of the inner leaflet and a large self-mobility and coupled-mobility in response to an applied force or torque, see Fig. 10.
We remark that it is important to keep in mind this behaviour arises when forces applied to inclusion particles result for the inner leaflet in a force moment with non-zero net torque. This is what drives a significant hydrodynamic response for the rotation mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1. In contrast, for the case of a collection of inclusion particles with total force acting on the inner leaflet that yields a zero net torque, super-position of the particle hydrodynamic responses cancel for the
= 1. In contrast, for the case of a collection of inclusion particles with total force acting on the inner leaflet that yields a zero net torque, super-position of the particle hydrodynamic responses cancel for the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 mode and the behaviour of large motions for inclusions from the rigid shell rotation is suppressed. This means for inclusion particles embedded within spherical bilayers it is important to consider carefully the different ways forces and net torque act on the leaflets.
= 1 mode and the behaviour of large motions for inclusions from the rigid shell rotation is suppressed. This means for inclusion particles embedded within spherical bilayers it is important to consider carefully the different ways forces and net torque act on the leaflets.
As the intermonolayer slip becomes large, the hydrodynamic flows within each of the two leaflets approach a common velocity. The self-mobility of inclusion particles embedded in the inner and outer leaflet also approach a common value. It is interesting to note that the common value is not simply 1/2 of the self-mobility for the uncoupled leaflets, see Fig. 10. This arises from the asymmetric way in which the leaflets couple to the external solvent. For the outer leaflet the solvent is within an unbounded domain exterior to the spherical shell. For the inner leaflet the solvent is within a bounded domain trapped interior to the spherical shell. As a consequence, we see there are different tractions acting on the inner and outer leaflet, see eqn (40). As we saw for the rigid rotation mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, there is no traction stress on the inner leaflet since the solvent fluid rigidly rotates within the spherical shell but there is traction stress from the solvent on the outer leaflet. For the other modes
= 1, there is no traction stress on the inner leaflet since the solvent fluid rigidly rotates within the spherical shell but there is traction stress from the solvent on the outer leaflet. For the other modes ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1 there continue to be asymmetries in the strength of the traction stress. As a result, the mobility of inclusion particles depend on the particular leaflet in which they are embedded. In the large intermonolayer slip limit, the mobility is determined by a combination of these different solvent tractions from each of the leaflets.
> 1 there continue to be asymmetries in the strength of the traction stress. As a result, the mobility of inclusion particles depend on the particular leaflet in which they are embedded. In the large intermonolayer slip limit, the mobility is determined by a combination of these different solvent tractions from each of the leaflets.
When investigating the mobility of membrane inclusion particles, the finite spatial extent and curved geometry of the bilayer can result in important hydrodynamic effects not captured when treating the membrane as an infinite flat sheet. We remark that the key consideration is how large the spatial extent or curvature is relative to the Saffman–Delbrück length LSD. For a very large vesicle radius or small curvatures, we do expect of course to recover similar behaviours as in the case of an infinite flat sheet. The interesting case is when the vesicle radius or membrane curvature yields a scale comparable or smaller than the Saffman–Delbrück length LSD.
We show the self-mobility of an inclusion particle embedded in a membrane treated as an infinite flat sheet in Fig. 11. These results were obtained by solving in Fourier space the hydrodynamic flow in response to an applied force density following closely the analytic approach presented in ref. 61 and 75 and our method for computing the mobility tensor discussed in Section 3.2. We see significant differences compared to the mobility responses in spherical bilayers.
In the regime of a vesicle radius comparable to the Saffman–Delbrück length LSD, the finite spatial extent of the membrane and topology can play an important role. For spherical leaflets, it is required that mobility responses result in recirculation flows of the material within the finite leaflet. As we have seen, this can yield non-trivial behaviours in the coupling and provide possibly useful flow features for estimating viscosity as discussed in Section 4.1.
In contrast when treating the membrane as an infinite flat sheet, no vortex arises in the flows generated from single particle responses. The infinite flat sheet also no longer results in trapped fluid within an interior domain. The bulk solvent fluid is treated as occupying an effectively infinite domain on both sides of the bilayer. This results in more traction stress acting on the infinite flat sheet relative to the spherical shell which as a result reduces the self-mobility and strength of the coupled mobilities. In particular, as the intramembrane viscosity increases the rotational mode of the spherical case is no longer available and the self-mobility decays to zero, see Fig. 11. Our results show that significant differences can arise with treatment of the bilayer as an infinite flat sheet requiring treatment of the finite domain size and curved geometry of the bilayer when these length scales are comparable to the Saffman–Delbrück length LSD.
4.3. Many-particle dynamics: hydrodynamic coupling and diffusion
We also consider how our results can be used to investigate the collective dynamics of multiple particles within a spherical membrane. The drift-diffusion of a collection of inclusion particles subject to force interactions and hydrodynamic coupling can be modelled as| | 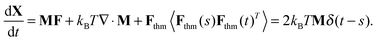 | (60) |
The X denotes the collective particle configuration and F the collective forces acting on the particles. The mobility M is obtained for the spherical membrane from the hydrodynamic-coupling methods we introduced in Section 3.1. The thermal fluctuations driving diffusion are accounted for by the drift term kBT∇·M and the Gaussian random force Fthm(t). The Fthm(t) is δ-correlated in time with mean zero and covariance 〈Fthm(s)Fthm(t)T〉 = 2kBTMδ(t − s).5,9,33 The equations for the inclusion particles are to be interpreted in the sense of Ito Calculus.33,60 The thermal drift term kBT∇·M arises from the configuration-dependent correlations of the thermal fluctuations.5,9
We first discuss some results that illustrate features of the collective hydrodynamic coupling of inclusion particles when embedded in a spherical membrane of finite extent. We then discuss results related to the collective drift-diffusion dynamics of inclusion particles when there are crowding effects and direct interactions between particles.
4.3.1. Hydrodynamic coupling and collective dynamics.
The collective dynamics of inclusion particles on the sphere can exhibit interesting coordinated motions arising from the hydrodynamic coupling. We consider the specific case of 4 particles that are attracted to a central particle located on the positive x-axis at the east pole. We consider the hydrodynamic flow and particle dynamics within the outer-leaflet of the curved spherical bilayer. In addition to the 4 attracting particles, we consider the motions of 195 passive tracer particles that are advected by the flow, see Fig. 12.
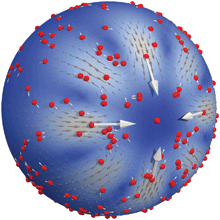 |
| | Fig. 12 Many-particle dynamics within a spherical lipid bilayer membrane. The inclusion particles are coupled through hydrodynamic flow both within the membrane bilayers and through the external solvent fluid. We show the hydrodynamic response in the case of a group of four inclusion particles attracted to a central particle. We show the velocity of the other particles passively advected by the flow that either move in the opposite direction or are swept along depending on their relative location to the attracted particles. | |
We see that the hydrodynamic coupling can result in interesting dynamics with the passive particles either moving in the opposite direction of the attracting particles or swept along depending on their relative location. This can be characterized by looking at the coupled mobility M of the passively advected particles defined by M = V/FT. The V is the passive particle velocity, FT the total force acting on the attracted particles. We consider the responses in the circular section in the yz-plane of radius r0 = 0.5R centred about the x-axis near the east pole and in the circular section in the xz-plane of radius r0 = R about the center of the sphere, see Fig. 12 and 13. The parameters in these calculations are taken to be the same as in Table 2.
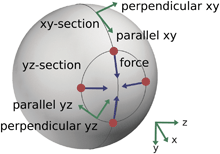 |
| | Fig. 13 Cross sections of the sphere and conventions. We consider the hydrodynamic responses of the inclusion particles on two cross-sections of the sphere. The first is the great circle of the sphere when intersected with the xy-plane. The second is the circle of radius r0 on the sphere surface parallel to the xz-plane. For forces applied to the four attracting inclusion particles, we consider for the motions of the other inclusion particles as characterized by the mobility components parallel and perpendicular to the tangent of the respective cross-section curves. We parametrise the xz-section using angle θ with 0 corresponding to the location (x, y, z) = (1, 0, 0) and the xy-section using angle θ with 0 for location (x, y, z) = (0, 0, r0). | |
We see from the yz-responses Mx that for locations half-way between the attracted particles, the passive particle move in the opposite direction to the attracted particles. This change in direction is a consequence of the incompressibility of the fluid which results in an out-flow to compensate for the in-flow toward the east pole generated by the attracted particles, see Fig. 14.
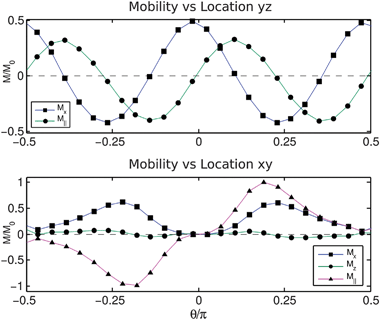 |
| | Fig. 14 Multi-particle mobility. We show the location dependent mobility of the passively advected particles in response to the hydrodynamic coupling to the four attracting particles. We show M = V/FT where V is the particle velocity, FT the total force, M∥ is the mobility tangent along the circular section. The yz indicates the circular section in the yz-plane of radius r0 = 0.5R about the east pole and xz indicates the circular section in the xz-plane of radius r0 = R about the sphere center, see Fig. 13. In the response, depending on the position, the passive particles either move in the opposite direction or are swept along with the attracting particles. The maximum response M0 corresponds to the self-mobility of each of the attracting particles. | |
We also see this manifest in the yz-responses M∥ which are out of phase with Mx reflecting that the passive particles move laterally toward the out-flow half-way between the attracted particles. The xz-responses correspond to passive particle motions when located on the same great circle in the xz-plane as two of the attracted particles. We see in these responses that the passive particles always move toward the attracting particle at the east pole, see bottom panel of Fig. 14.
4.3.2. Diffusion and collective dynamics.
The collective drift-diffusion of inclusion particles subject to direct force interactions when embedded in spherical membranes can be captured using our introduced methods. This is given by the Brownian-hydrodynamic model in eqn (60). To integrate the stochastic dynamics of the inclusion particles, we use a stochastic predictor–corrector numerical method related to the work of Fixman31 proposed in ref. 21. We update the configuration of the inclusion particles using| | 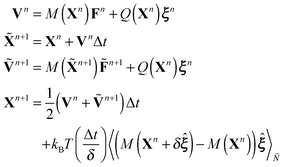 | (61) |
The thermal fluctuations have correlations Qn such that QnQn,T = 2kBTM(Xn)/Δt with ξ standard Gaussian random variates with independent components having mean zero and covariance one. The ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) n+1 gives the predictor part of the update of the configuration that is used to evaluate the force
n+1 gives the predictor part of the update of the configuration that is used to evaluate the force ![[F with combining tilde]](https://www.rsc.org/images/entities/b_char_0046_0303.gif) n+1 and mobility M(
n+1 and mobility M(![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) n+1). The Xn+1 gives the corrector part for the update of the configuration which makes use of the predictor data and an additional thermal drift term.
n+1). The Xn+1 gives the corrector part for the update of the configuration which makes use of the predictor data and an additional thermal drift term.
The thermal drift term captures on average the contribution of kBT∇·M in eqn (60). The 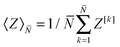 denotes a partial average of a random variable Z where the Z[k] denote the
denotes a partial average of a random variable Z where the Z[k] denote the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) independent samples. The thermal drift term is motivated by the result that for the random variables p and q satisfying 〈piqj〉 = δij we have
independent samples. The thermal drift term is motivated by the result that for the random variables p and q satisfying 〈piqj〉 = δij we have
This provides a probabilistic method for approximating the divergence of the mobility tensor. For an individual time-step of the dynamics, we use 〈·〉
Nδ with
Nδ samples to obtain a controlled estimate of the thermal drift contribution. Over the duration of the simulation this term yields the average required to account for the contributions of the thermal drift in the stochastic dynamics.
Using these methods, we consider the collective dynamics of a pair of particles that are bonded together by a harmonic spring with non-zero rest-length having the energy
| | 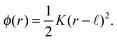 | (62) |
where the distance between the two inclusion particles is given by
r = ∥
X1 −
X2∥ and the rest-length
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
. For a pair of bonded inclusion particles diffusing over the surface the Boltzmann equilibrium distribution of their separation is given by
| | 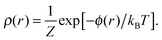 | (63) |
The
Z denotes the partition function.
We take throughout the thermal energy kBT = 2.48 amu nm2 ps−2 and the harmonic spring stiffness K = 72kBT/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2. We take the vesicle to have membrane viscosity corresponding to L/R = 0.65 and intermonolayer slip corresponding to γ/γ0 = 0.03. The mobility is obtained using the immersed boundary coupling for the hydrodynamics discussed in Section 3. We performed simulations with the stochastic integrator in eqn (61) using time-steps Δt = 1.3 × 105 ps, δ = 10−1,
2. We take the vesicle to have membrane viscosity corresponding to L/R = 0.65 and intermonolayer slip corresponding to γ/γ0 = 0.03. The mobility is obtained using the immersed boundary coupling for the hydrodynamics discussed in Section 3. We performed simulations with the stochastic integrator in eqn (61) using time-steps Δt = 1.3 × 105 ps, δ = 10−1, ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) = 10.
= 10.
We consider the equilibrium fluctuations for the particle configurations over 105 time-steps. We perform three studies where we vary the spring rest-length and compare our results with the distribution in eqn (63), see Fig. 15. We find in each case that the stochastic methods yield good agreement with theory which indicates the validity of the equilibrium properties of our methods for incorporating hydrodynamic coupling and thermal fluctuations.
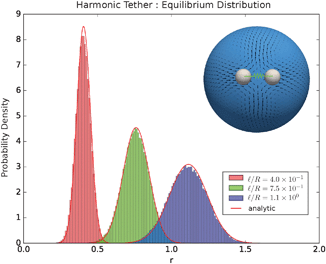 |
| | Fig. 15 Harmonic tether equilibrium distributions. For two particles coupled by a harmonic tether with non-zero rest-length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) we consider the equilibrium distribution of their spontaneous configurations driven by thermal fluctuations. We consider the cases with the rest-lengths we consider the equilibrium distribution of their spontaneous configurations driven by thermal fluctuations. We consider the cases with the rest-lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /R = 4.0 × 10−1, 7.5 × 10−1, 1.1 × 100. We find very good agreement between the spontaneous configurations during the stochastic simulations using the integrator (61) and the analytic predictions given in eqn (63). These results indicate that the introduced stochastic methods yield correct equilibrium properties for the system. /R = 4.0 × 10−1, 7.5 × 10−1, 1.1 × 100. We find very good agreement between the spontaneous configurations during the stochastic simulations using the integrator (61) and the analytic predictions given in eqn (63). These results indicate that the introduced stochastic methods yield correct equilibrium properties for the system. | |
We next consider the collective diffusion of inclusion particles within the surface when subject to hydrodynamic coupling and crowding effects. We consider the mean-squared displacement (MSD) over time of an inclusion particle when varying the concentration of particles subject to the repulsive potential
We take
C = 0.75
RkBT with parameters
R = 15.3 nm and thermal energy
kBT = 2.48 amu nm
2 ps
−2. We compare the case without hydrodynamic coupling obtained from simulations using conventional Langevin dynamics
32 corresponding to
with the case with hydrodynamic coupling
M obtained from simulations using our methods in Section 3. These are shown in
Fig. 16. We find that the hydrodynamics results in significant differences with the Langevin simulations. One notable difference is that the hydrodynamic coupling case allows for collective movements through rotation of the vesicle whereas the Langevin dynamics has a constant drag force that references a zero constant ambient velocity field.
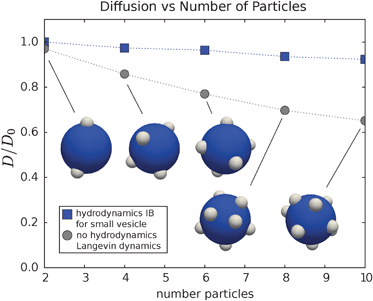 |
| | Fig. 16 Collective diffusivity of particles and crowding. We consider a collection of diffusing inclusion particles subject to mutual repulsive forces having the energy given in eqn (64). We consider one of the diffusing particles and its mean-squared displacement over the time-scale [0, 0.1τD] where τD = R2/D0 when the number of mutually repelling particles is 2, 4, 6, 8, 10. The D0 is the diffusivity given by the self-mobility of a single particle. We compare the case using the methods for hydrodynamic coupling in Section 3 for a small vesicle with the case without hydrodynamics using standard Langevin dynamics.32 The collective dynamics arising from the hydrodynamic coupling results in a significantly enhanced diffusivity relative to Langevin dynamics. For a small vesicle, this arises since the hydrodynamics allows for a collective rotational mode in the collective diffusivity of the cluster. | |
In summary, these results indicate some of the rich dynamics that can arise from hydrodynamic coupling even for relatively simple configurations of particles and force laws. The analytic approaches and computational methods we have introduced for the collective mobility tensor M allow for incorporating such effects into simulations of many-particle dynamics within spherical lipid bilayers. Many of the approaches we have introduced can also be extended for more general curved bilayers.
5. Conclusions
The hydrodynamics of inclusion particles embedded within curved lipid bilayer membranes can differ significantly from the case when a membrane is treated as a flat infinite sheet. We have shown how analytic approaches can be developed for analysis of the hydrodynamic flows that occur within such curved geometries. For spherical vesicles we have found that the interplay between curvature and topology can yield interesting effects resulting in induced shears and recirculation in the hydrodynamics. We further showed how the translational and rotational mobility responses of particle inclusions embedded within the different bilayer leaflets can be taken into account. For this purpose, we introduced an immersed boundary model for the hydrodynamic coupling within curved surfaces. In contrast to widely used treatments of membranes as flat infinite sheets, we have shown for spherical vesicles that the dissipation from the solvent fluid plays an interesting asymmetric role yielding significantly different inclusion responses depending on the bilayer leaflet (inner vs. outer). We further showed how these effects contribute in the collective drift-diffusion dynamics of inclusion particles. We introduced for inclusion particles a general stochastic model for such investigations incorporating particle–particle interactions, hydrodynamic coupling, and collective diffusion. When inclusion particles are subject to crowding effects we showed that the hydrodynamics contributes important correlations to the collective dynamics enhancing diffusion relative to non-hydrodynamic motions like those modelled by Langevin dynamics. The results we present show the rich individual and collective dynamics that can arise for inclusions embedded within spherical bilayers. Many of our analytic approaches and computational methods also can be used to study inclusions embedded within more general curved lipid bilayer membranes.
Appendix
A. Spherical harmonic methods: Lebedev quadratures, SPH transform, and polar singularities
We make a few brief remarks on our methods for numerical computations and the issues that arise when performing calculations on spherical surfaces. We have developed our methods using high-order Lebedev quadratures which integrate exactly spherical harmonics up to large degree.46 We evaluate inner-products using
The wm are the weights and xm the nodes. We use this to compute spherical harmonic coefficients by the inner-product ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) s = 〈f,Φs〉, where Φs is the spherical harmonic with index s = (m,
s = 〈f,Φs〉, where Φs is the spherical harmonic with index s = (m,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). While computationally more expensive than Fast Spherical Harmonic Transforms (FSHT),26 a distinct of advantage of our Lebedev-based methods over the latitude–longitude sampling of FSHT is the more uniform and symmetric sampling of Lebedev nodes which have octahedral symmetry,46 see Fig. 17.
). While computationally more expensive than Fast Spherical Harmonic Transforms (FSHT),26 a distinct of advantage of our Lebedev-based methods over the latitude–longitude sampling of FSHT is the more uniform and symmetric sampling of Lebedev nodes which have octahedral symmetry,46 see Fig. 17.
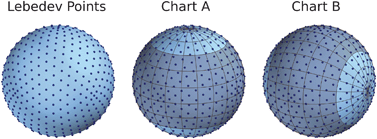 |
| | Fig. 17 Locations of the 590 Lebedev quadrature points and the two charts A and B used to deal with singularities at the poles. | |
On a spherical surface, coordinate singularities arise, such as exhibited by spherical coordinates at the north–south pole. We handle this issue by using two alternative coordinate charts A or B depending on the location. Chart A corresponds to the spherical coordinates with singularities at the north and south poles. Chart B corresponds to the spherical coordinates with singularities at the west and east poles. A notable feature of the Lebedev sampling is that its symmetry allows us to make use of the same quadrature nodes in the two coordinate charts, see Fig. 17.
To perform numerical calculations for operations on field values at the Lebedev points, such as divergence, gradient, and curl, we make use whenever possible of the intrinsic geometric meaning of such operations (as opposed to the coordinate-centric formulas). When coordinate-centric formulas are used, we express the operations in one of the two different coordinate charts A or B. The particular chart is chosen to yield significant distance to the coordinate-system singularities. This allows for robust numerical calculations at all points on the sphere surface. This further highlights one of the advantages of our less coordinate-centric exterior calculus approach to the hydrodynamics.
We obtain the membrane velocity field in our calculations by
| | 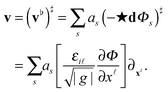 | (65) |
The |
g| = det(
g) is the determinant of the metric tensor and
εi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
is the Levi-Civita tensor (slight abuse of notation). The
x![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
denotes the coordinates. For spherical coordinates in chart A,
x1 =
θA,
x2 =
ϕA and in chart B,
x1 =
θB,
x2 =
ϕB. To obtain the velocity, we express in each of the charts the coordinate derivatives of the spherical harmonic modes ∂
Φ/∂
x![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
and the basis vectors ∂
xi in terms of the embedding space
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3
3. We then choose at each given location the expression for the chart that has a significant distance to the coordinate-system singularities. In this manner, we compute robustly the velocity field over the entire surface.
B. Formulation of the hydrodynamics equations using exterior calculus
B.1. Hydrodynamic equations.
The steady-state Stokes equations corresponding to eqn (1) can be expressed in tensor components as| | | μmDab|b − gabp + ba = 0 | (66) |
We can express this in a more geometrically transparent manner by considering further the divergence of the rate of deformation tensor| | | Dab|b = gacgbdvc|d|b + gacgbdvd|c|b. | (68) |
We have that| | | gacgbdvc|d|b = (ΔRv)a + Kva | (69) |
where ΔRv := rough-laplacian(v) = div(grad(v)) and K is the Gaussian curvature of the surface. We have that
| gacgbdvd|c|b = grad(div(v)) + Kva |
This follows since div(v) = 0.
It is convenient to express the equations and differential operators in terms of the exterior calculus as follows. Let d denote the usual exterior derivative for a k-form α as
| | 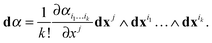 | (71) |
The
δ denotes the co-differential operator given by
δ = ⋆
d⋆, where for a
k-form
α = (1/
k!)
αi1…ikdxi1 ∧…∧
dxik the ⋆ denotes the Hodge star given by
| | 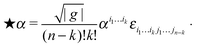 | (72) |
where
αi1…ik =
gi1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1
1·
gik![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) kα
kα![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1…
1…![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) k
k,
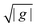
is the square-root of the determinant of the metric tensor, and
εi1…ikj1…jn−k denotes the Levi-Civita tensor.
51
The generalization of the common differential operators of vector calculus to manifolds can be expressed in terms of exterior calculus as
| | | div(F) = −(⋆d⋆F♭) = −δF♭ | (75) |
The
f is a smooth scalar function and the
F is a smooth vector field.
We have adopted the notation for raising and lowering indices corresponding to the isomorphisms between the tangent and co-tangent spaces of the surface given by
The ∂
xj denotes the coordinate associated basis vectors of the tangent space and
dxj the one-form coordinate associated basis of the co-tangent space. The isomorphisms can also be expressed directly in terms of the components as
vi =
gijvj and
vi =
gijvj, where we denote the metric tensor as
gij and its inverse as
gij.
1 This extends naturally to tensors.
There are different types of Laplacians that can be defined for manifolds
| | | ΔH(F) = −[(δd + dδ)F♭]♯ | (79) |
| | | ΔHf = ΔRf = −(⋆d⋆)df = −δdf. | (81) |
The Δ
R = div(grad(·)) denotes the rough-Laplacian given by the usual divergence of the gradient. For vector fields, Δ
H(
F) denotes the Hodge-de Rham Laplacian, which has similarities to taking the curl of the curl.
1 In fact, in the case that div(
F) = −
δF♭ = 0 we have Δ
H(
F) = Δ
S(
F) = −[
δdF♭]
♯.
Using these conventions, we have
| | | div(D) = −δdv♭ + 2Kv♭ | (82) |
where we used that div(
v) = −
δv♭ = 0. This allows for the steady-state Stokes problem on the surface to be expressed using exterior calculus in the convenient form
| | 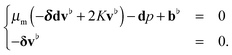 | (83) |
As we discuss, this form only involves the operators ⋆ and
d (note
δ = ⋆
d⋆) providing a very convenient approach for analytic and numerical calculations.
B.2. Derivation of the traction stress from the external solvent fluid.
The solvent fluid surrounding the lipid bilayer membrane also exerts a traction stress on the inner and outer leaflets. We account for this using the Stokes equationsThe Ω = Ω± denotes either the outside region Ω+ of fluid surrounding the vesicle or the domain Ω− of fluid trapped inside the vesicle.
The solution to the Stokes equations and traction stress can be conveniently expressed in terms of harmonic functions. This is most immediately seen for the pressure, which when taking the divergence of eqn (84), yields
For the spherical geometry, the pressure can be expanded as
| | 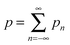 | (89) |
where
pn is the solid spherical harmonic of order
n| | 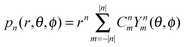 | (90) |
where
| | | Ynm(θ,ϕ) = eimϕPmn(cos(θ)). | (91) |
We remark to avoid any confusion that the spherical harmonics expansions will be used here to give an exact represention of the pressure and velocity fields over the surface.
For the solvent fluid velocity u− in the domain Ω− interior to the vesicle, Lamb showed that the solution can be expressed as35,45
| | 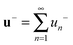 | (92) |
where
| | | un− = ∇ × (rχn) + ∇Φn | (93) |
| | 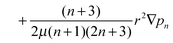 | (94) |
| | 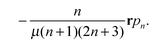 | (95) |
We shall refer to this as the Lamb's solution. The surface flow
v determines the solid spherical harmonic functions
χn,
Φn,
pn by the following relations
| | 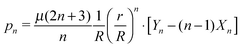 | (96) |
| | 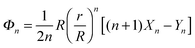 | (97) |
| | 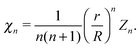 | (98) |
The
R is the radius of the spherical surface. For the surface fluid velocity
V =
v +
vnn of the membrane, the
Xn,
Yn,
Zn are combined surface spherical harmonics of degree
n obtained by expanding the following scalar fields on the surface
| | 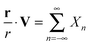 | (99) |
| | 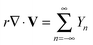 | (100) |
| | 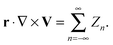 | (101) |
For the solvent fluid velocity
u+ in the domain
Ω+ exterior to the vesicle, Lamb's solution is
ref. 35 and 45| | 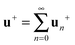 | (102) |
where
| | | un+ = ∇ × (rχ−(n+1)) + ∇Φ−(n+1) | (103) |
| | 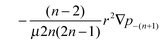 | (104) |
| | 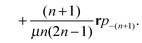 | (105) |
The surface fluid velocity
V =
v +
vnn of the membrane, determines the harmonic functions
χ−(n+1),
Φ−(n+1),
p−(n+1) giving
| | 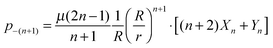 | (106) |
| | 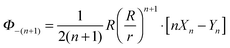 | (107) |
| | 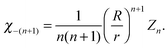 | (108) |
In the special case of
vn = 0 and div(
v) = 0 we have that
Xn =
Yn = 0 and that only the
Zn term is non-trivial. The Lamb's solution simplifies to
| | | un+ = ∇ × (rχ−(n+1)) | (109) |
In this case, the traction stress of the external fluid on the lipid bilayer membrane is
| | 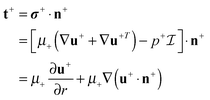 | (111) |
| | 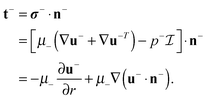 | (112) |
The
n± denotes the unit normal on the surface ∂
Ω± in the direction pointing into the domain. In these expressions, we emphasize that
n± is to be held fixed during differentiation. From
eqn (111) and (112) and the properties of solid spherical harmonics, we have that the traction stress on the membrane leaflets can be expressed as
| | 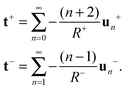 | (113) |
C. Non-dimensional hydrodynamic equations
We can non-dimensionalize eqn (114)–(116) by introducing a characteristic velocity v0± and force density f0±. We find it convenient to consider the rigid rotation at angular velocity ω0 of the spherical shell in the solvent fluid. This motivates the choice of characteristic force density f0± = μfω0 and velocity v0± = Rω0. For simplicity, we consider only the case with μ± = μf and R± = R. The non-dimensional velocity is ṽ♭± = v♭±/v0 and force density ![[c with combining tilde]](https://www.rsc.org/images/entities/b_char_0063_0303.gif) ♭± = c♭±/f0 with coefficients ã and
♭± = c♭±/f0 with coefficients ã and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . With this choice, we can express the non-dimensional problem for the full two-leaflet membrane hydrodynamics in eqn (21) as
. With this choice, we can express the non-dimensional problem for the full two-leaflet membrane hydrodynamics in eqn (21) as| | 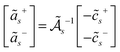 | (114) |
where| | 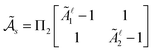 | (115) |
with
Ã![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 = Π2−1Π1(2 − 1 = Π2−1Π1(2 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ( (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1) − Π1−1( + 1) − Π1−1(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1)) + 1)) |
| | Ã![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 = Π2−1Π1(2 − 2 = Π2−1Π1(2 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ( (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1) − Π1−1( + 1) − Π1−1(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − 1)). − 1)). | (116) |
As we shall discuss, this analysis will be useful when considering the relative contributions of the solvent traction stress, intramembrane viscosity, and the intermonolayer slip. Other non-dimensional scalings can also be considered using a similar approach.
Acknowledgements
The authors P. J. A., J. K. S. acknowledge support from research grant NSF DMS-1616353, NSF CAREER DMS-0956210, and DOE ASCR CM4 DE-SC0009254.
References
-
R. Abraham, J. E. Marsden and T. S. Ratiu, Manifolds, Tensor Analysis, and Applications, Springer, New York, 1988, vol. 75 Search PubMed.
-
D. J. Acheson, Elementary Fluid Dynamics, Oxford Applied Mathematics and Computing Science Series, 1990 Search PubMed.
-
B. Alberts, A. Johnson, P. Walter, J. Lewis, M. Raff and K. Roberts, Molecular Cell Biology of the Cell, Garland Publishing Inc., New York, 5th edn, 2007 Search PubMed.
- M. Arroyo and A. DeSimone, Relaxation dynamics of fluid membranes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79(3), 031915 CrossRef PubMed.
- G. Tabak and P. J. Atzberger, Stochastic reductions for inertial fluid-structure interactions subject to thermal fluctuations, SIAM J. Appl. Math., 2015, 75(4), 1884–1914 CrossRef.
- P. J. Atzberger, Velocity correlations of a thermally fluctuating brownian particle: A novel model of the hydrodynamic coupling, Phys. Lett. A, 2006, 351(4–5), 225–230 CrossRef CAS.
- P. J. Atzberger, A note on the correspondence of an immersed boundary method incorporating thermal fluctuations with stokesian-brownian dynamics, Phys. D, 2007, 226(2), 144–150 CrossRef.
- P. J. Atzberger, P. R. Kramer and C. S. Peskin, A stochastic immersed boundary method for fluid-structure dynamics at microscopic length scales, J. Comput. Phys., 2007, 224(2), 1255–1292 CrossRef.
- P. J. Atzberger, Stochastic eulerian lagrangian methods for fluid-structure interactions with thermal fluctuations, J. Comput. Phys., 2011, 230(8), 2821–2837 CrossRef CAS.
- G. S. Ayton, J. Liam McWhirter and G. A. Voth, A second generation mesoscopic lipid bilayer model: Connections to field-theory descriptions of membranes and nonlocal hydrodynamics, J. Chem. Phys., 2006, 124(6), 064906 CrossRef PubMed.
- W. F. Drew Bennett and D. Peter Tieleman, Computer simulations of lipid membrane domains, Biochim. Biophys. Acta, Biomembr., 2013, 1828(8), 1765–1776 CrossRef PubMed.
- N. Calvo and O. H. Campanella, A novel geometry for rheological characterization of viscoelastic materials, Rheol. Acta, 1990, 29(4), 323–331 CrossRef CAS.
- B. A. Camley and F. L. H. Brown, Contributions to membrane-embedded-protein diffusion beyond hydrodynamic theories, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061921 CrossRef PubMed.
- B. A. Camley and F. L. H. Brown, Diffusion of complex objects embedded in free and supported lipid bilayer membranes: role of shape anisotropy and leaflet structure, Soft Matter, 2013, 9, 4767–4779 RSC.
- R. Capovilla and J. Guven, Stresses in lipid membranes, J. Phys. A: Math. Gen., 2002, 35(30), 6233 CrossRef CAS.
- R. Capovilla and J. Guven, Stress and geometry of lipid vesicles, J. Phys.: Condens. Matter, 2004, 16(22), S2187 CrossRef CAS.
- M. Cavallaro, L. Botto, E. P. Lewandowski, M. Wang and K. J. Stebe, Curvature-driven capillary migration and assembly of rod-like particles, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(52), 20923–20928 CrossRef CAS PubMed.
- I. R. Cooke, K. Kremer and M. Deserno, Tunable generic model for fluid bilayer membranes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72(1), 011506 CrossRef PubMed.
- S. J. Marrink, D. P. Tieleman and H. J. C. Berendsen, A computer perspective of membranes: molecular dynamics studies of lipid bilayer systems, Biochim. Biophys. Acta, Rev. Biomembr., 1997, 1331, 235–270 CrossRef.
-
T. Piran, D. Nelson and S. Weinberg, Statistical Mechanics of Membranes and Surfaces, World Scientific Publishing, 2004 Search PubMed.
- S. Delong, Y. Sun, B. E. Griffith, E. Vanden-Eijnden and A. Donev, Multiscale temporal integrators for fluctuating hydrodynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90(6), 063312 CrossRef PubMed.
- W. K. den Otter and S. A. Shkulipa, Intermonolayer friction and surface shear viscosity of lipid bilayer membranes, Biophys. J., 2007, 93(2), 423–433 CrossRef CAS PubMed.
- M. Deserno, Mesoscopic membrane physics: Concepts, simulations,
and selected applications, Macromol. Rapid Commun., 2009, 30(9–10), 752–771 CrossRef CAS PubMed.
-
M. Deserno, Fluid lipid membranes: From differential geometry to curvature stresses, Membrane mechanochemistry: From the molecular to the cellular scale, 2015, 185, 11-45.
- R. Dimova, C. Dietrich, A. Hadjiisky, K. Danov and B. Pouligny, Falling ball viscosimetry of giant vesicle membranes: Finite-size effects, Eur. Phys. J. B, 1999, 12(4), 589–598 CrossRef CAS.
- J. R. Driscoll and D. M. Healy, Computing fourier transforms and convolutions on the 2-sphere, Advances in Applied Mathematics, 1994, 15(2), 202–250 CrossRef.
- Q. Du, C. Liu and X. Wang, A phase field approach in the numerical study of the elastic bending energy for vesicle membranes, J. Comput. Phys., 2004, 198(2), 450–468 CrossRef.
- K. Falk, N. Fillot, A.-M. Sfarghiu, Y. Berthier and C. Loison, Interleaflet sliding in lipidic bilayers under shear flow: comparison of the gel and fluid phases using reversed non-equilibrium molecular dynamics simulations, Phys. Chem. Chem. Phys., 2014, 16(5), 2154–2166 RSC.
- O. Farago, “Water-free” computer model for fluid bilayer membranes, J. Chem. Phys., 2003, 119(1), 596–605 CrossRef CAS.
- F. Feng and W. S. Klug, Finite element modeling of lipid bilayer membranes, J. Comput. Phys., 2006, 220(1), 394–408 CrossRef CAS.
- M. Fixman, Simulation of polymer dynamics. I. General theory, J. Chem. Phys., 1978, 69(4), 1527–1537 CrossRef CAS.
-
D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, San Diego, 2nd edn, 2002, pp. 25–532 Search PubMed.
-
C. W. Gardiner, Handbook of stochastic methods, Series in Synergetics, Springer, 1985 Search PubMed.
- J. Guven, Membrane geometry with auxiliary variables and quadratic constraints, J. Phys. A: Math. Gen., 2004, 37(28), L313 CrossRef.
-
J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, Springer, Netherlands, 1983 Search PubMed.
- M. L. Henle, R. McGorty, A. B. Schofield, A. D. Dinsmore and A. J. Levine, The effect of curvature and topology on membrane hydrodynamics, EPL, 2008, 84(4), 48001 CrossRef.
- M. L. Henle, R. McGorty, A. B. Schofield, A. D. Dinsmore and A. J. Levine, The effect of curvature and topology on membrane hydrodynamics, EPL, 2008, 84(4), 48001 CrossRef.
- M. L. Henle and A. J. Levine, Effective viscosity of a dilute suspension of membrane-bound inclusions, Phys. Fluids, 2009, 21(3), 033106 CrossRef.
- M. L. Henle and A. J. Levine, Hydrodynamics in curved membranes: The effect of geometry on particulate mobility, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81(1), 011905 CrossRef PubMed.
- R. J. Hill and C.-Y. Wang, Diffusion in phospholipid bilayer membranes: dual-leaflet dynamics and the roles of tracer-leaflet and inter-leaflet coupling, Proc. R. Soc. A, 2014, 470(2167), 20130843 CrossRef PubMed.
- A. R. Honerkamp-Smith, F. G. Woodhouse, V. Kantsler and R. E. Goldstein, Membrane viscosity determined from shear-driven flow in giant vesicles, Phys. Rev. Lett., 2013, 111(3), 038103 CrossRef PubMed.
- J.-J. Xu, J. Lowengrub and A. Voigt, Surface phase separation and flow in a simple model of multicomponent drops and vesicles, Fluid Dyn. Mater. Process., 2007, 3, 1–19 Search PubMed.
- T. Jarvis and J. Tanton, The hairy ball theorem via sperner’s lemma, The American Mathematical Monthly, 2004, 111(7), 599–603 CrossRef.
- O. Kahraman, N. Stoop and M. M. Müller, Fluid membrane vesicles in confinement, New J. Phys., 2012, 14(9), 095021 CrossRef.
-
H. Lamb, Hydrodynamics, University Press, 1895 Search PubMed.
- V. I. Lebedev and D. N. Laikov, A quadrature formula for the sphere of the 131st algebraic order of accuracy, Dokl. Math., 1999, 59, 477–481 Search PubMed.
- M. Lee, M. Xia and B. Park, Transition behaviors of configurations of colloidal particles at a curved oil–water interface, Materials, 2016, 9(3), 138 CrossRef.
- A. J. Levine and F. C. MacKintosh, Dynamics of viscoelastic membranes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061606 CrossRef PubMed.
- A. J. Levine, T. B. Liverpool and F. C. MacKintosh, Mobility of extended bodies in viscous films and membranes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69(2), 021503 CrossRef PubMed.
-
E. H. Lieb and M. Loss, Analysis, American Mathematical Society, 2001 Search PubMed.
-
J. E. Marsden and T. J. R. Hughes, Mathematical Foundations of Elasticity, Dover, 1994 Search PubMed.
- G. M. Mavrovouniotis and H. Brenner, A micromechanical investigation of interfacial transport processes. i. interfacial conservation equations, Philos. Trans. R. Soc., A, 1993, 345(1675), 165–207 CrossRef CAS.
- G. M. Mavrovouniotis, H. Brenner, D. A. Edwards and L. Ting, A micromechanical investigation of interfacial transport processes. ii. interfacial constitutive equations, Philos. Trans. R. Soc., A, 1993, 345(1675), 209–228 CrossRef CAS.
- R. Merkel, E. Sackmann and E. Evans, Molecular friction and epitactic coupling between monolayers in supported bilayers, J. Phys., 1989, 50(12), 1535–1555 CAS.
- L. Miao, M. A. Lomholt and J. Kleis, Dynamics of shape fluctuations of quasi-spherical vesicles revisited, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9(2), 143–160 CrossRef CAS PubMed.
- M. M. Müller, M. Deserno and J. Guven, Interface-mediated interactions between particles: A geometrical approach, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72(6), 061407 CrossRef PubMed.
- A. Naji, A. J. Levine and P. A. Pincus, Corrections to the saffman-delbrück mobility for membrane bound proteins, Biophys. J., 2007, 93, L49–L51 CrossRef CAS PubMed.
- H. Noguchi and G. Gompper, Fluid vesicles with viscous membranes in shear flow, Phys. Rev. Lett., 2004, 93(25), 258102 CrossRef PubMed.
- S. A. Nowak and T. Chou, Membrane lipid segregation in endocytosis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78(2), 021908 CrossRef PubMed.
-
B. Oksendal, Stochastic Differential Equations: An Introduction, Springer, 2000 Search PubMed.
- N. Oppenheimer and H. Diamant, Correlated diffusion of membrane proteins and their effect on membrane viscosity, Biophys. J., 2009, 96(8), 3041–3049 CrossRef CAS PubMed.
- R. Parthasarathy and J. T. Groves, Curvature and spatial organization in biological membranes, Soft Matter, 2007, 3(1), 24–33 RSC.
- C. S. Peskin, The immersed boundary method, Acta Numerica, 2002, 11, 1–39 CrossRef.
- T. R. Powers, Dynamics of filaments and membranes in a viscous fluid, Rev. Mod. Phys., 2010, 82(2), 1607–1631 CrossRef.
- T. R. Powers, G. Huber and R. E. Goldstein, Fluid-membrane tethers: Minimal surfaces and elastic boundary layers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65(4), 041901 CrossRef PubMed.
-
C. Pozrikidis, Boundary Integral and Singularity Methods for Linearized Viscous Flow, Cambridge University Press, 1992http://dx.doi.org/10.1017/CBO9780511624124 Search PubMed.
-
A. Pressley, Elementary Differential Geometry, Springer, 2001 Search PubMed.
- F. Quemeneur, J. K. Sigurdsson, M. Renner, P. J. Atzberger, P. Bassereau and D. Lacoste, Shape matters in protein mobility within membranes, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(14), 5083–5087 CrossRef CAS PubMed.
- M. Rahimi, A. De Simone and M. Arroyo, Curved fluid membranes behave laterally as effective viscoelastic media, Soft Matter, 2013, 9, 11033–11045 RSC.
- P. Rangamani, A. Agrawal, K. K. Mandadapu, G. Oster and D. J. Steigmann, Interaction between surface shape and intra-surface viscous flow on lipid membranes, Biomech. Model. Mechanobiol., 2013, 12(4), 833–845 CrossRef PubMed.
-
M. Reed and B. Simon, Functional Analysis, Elsevier, 1980 Search PubMed.
- E. Reister and U. Seifert, Lateral diffusion of a protein on a fluctuating membrane, Europhys. Lett., 2005, 71, 859–865 CrossRef CAS.
- E. Reister-Gottfried, S. M. Leitenberger and U. Seifert, Diffusing proteins on a fluctuating membrane: Analytical theory and simulations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031903 CrossRef PubMed.
- B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Muller, K. Kremer and M. Deserno, Aggregation and vesiculation of membrane proteins by curvature-mediated interactions, Nature, 2007, 447(7143), 461–464 CrossRef CAS PubMed.
- P. G. Saffman, Brownian motion in thin sheets of viscous fluid, J. Fluid Mech., 1976, 73, 593–602 CrossRef.
- P. G. Saffman and M. Delbrück, Brownian motion in biological membranes, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113 CrossRef CAS.
- J. T. Schwalbe, P. M. Vlahovska and M. J. Miksis, Monolayer slip effects on the dynamics of a lipid bilayer vesicle in a viscous flow, J. Fluid Mech., 2010, 647, 403–419 CrossRef.
- J. T. Schwalbe, P. M. Vlahovska and M. J. Miksis, Vesicle electrohydrodynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046309 CrossRef PubMed.
- L. E. Scriven, Dynamics of a fluid interface equation of motion for newtonian surface fluids, Chem. Eng. Sci., 1960, 12(2), 98–108 CrossRef CAS.
- U. Seifert, Configurations of fluid membranes and vesicles, Adv. Phys., 1997, 46(1), 13–137 CrossRef CAS.
- U. Seifert, Fluid membranes in hydrodynamic flow fields: Formalism and an application to fluctuating quasispherical vesicles in shear flow, Eur. Phys. J. B, 1999, 8(3), 405–415 CrossRef CAS.
- U. Seifert and S. A. Langer, Viscous modes of fluid bilayer membranes, Europhys. Lett., 1993, 23, 71–76 CrossRef.
- J. K. Sigurdsson, F. L. H. Brown and P. J. Atzberger, Hybrid continuum-particle method for fluctuating lipid bilayer membranes with diffusing protein inclusions, J. Comput. Phys., 2013, 252, 65–85 CrossRef CAS.
- J. D. Steigmann, Fluid films with curvature elasticity, Arch. Ration. Mech. Anal., 1999, 150(2), 127–152 CrossRef.
-
W. Strauss, Partial Differential Equations: An Introduction, John Wiley and Sons, 2008 Search PubMed.
- P. M. Vlahovska and R. S. Gracia, Dynamics of a viscous vesicle in linear flows, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75(1), 016313 CrossRef PubMed.
- G. K. Voeltz and W. A. Prinz, Sheets, ribbons and tubules [mdash] how organelles get their shape, Nat. Rev. Mol. Cell Biol., 2007, 8(3), 258–264 CrossRef CAS PubMed.
- A. M. Waxman, Dynamics of a couple-stress fluid membrane, Stud. Appl. Math., 1984, 70(1), 63–86 CrossRef.
- F. G. Woodhouse and R. E. Goldstein, Shear-driven circulation patterns in lipid membrane vesicles, J. Fluid Mech., 2012, 705, 165–175 CrossRef.
Footnote |
| † Work supported by DOE ASCR CM4 DE-SC0009254, NSF DMS-1616353, and NSF CAREER Grant DMS-0956210. |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
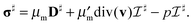
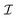 is the (1,1)-identity tensor with
is the (1,1)-identity tensor with 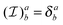 where δab denotes the Kronecker delta-function. This has
where δab denotes the Kronecker delta-function. This has 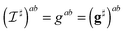 , where g is the metric tensor for the surface.51
, where g is the metric tensor for the surface.51
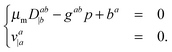
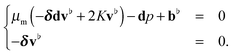
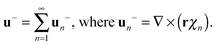
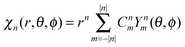
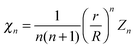
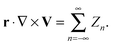
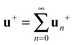
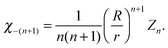
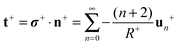
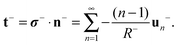
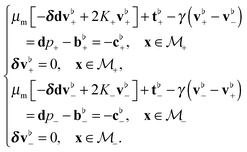
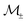 denotes the two surfaces representing the inner and outer bilayer leaflets. These equations take into account the internal membrane hydrodynamics of each leaflet of viscosity μm, the intermonolayer slip γ, and the traction stresses with the bulk solvent fluids of viscosity μ± trapped within and external to the vesicle. To obtain the coupling in the collective dynamics of inclusions embedded in such bilayer membranes, we must solve these equations for the hydrodynamic flow.
denotes the two surfaces representing the inner and outer bilayer leaflets. These equations take into account the internal membrane hydrodynamics of each leaflet of viscosity μm, the intermonolayer slip γ, and the traction stresses with the bulk solvent fluids of viscosity μ± trapped within and external to the vesicle. To obtain the coupling in the collective dynamics of inclusions embedded in such bilayer membranes, we must solve these equations for the hydrodynamic flow.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(θ,ϕ) = eimϕPm
m(θ,ϕ) = eimϕPm![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (cos(θ))
(cos(θ))![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m) subject to the restriction |m| ≤
,m) subject to the restriction |m| ≤ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The eigenvalues are γs = −
. The eigenvalues are γs = −![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1)/R2 and λs = μ(−
+ 1)/R2 and λs = μ(−![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1)/R2 + 2K).
+ 1)/R2 + 2K).
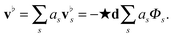
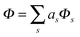 . In a similar manner, the applied surface force can be expanded with coefficients cs as
. In a similar manner, the applied surface force can be expanded with coefficients cs as 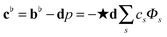 . The problem now becomes to find the coefficients as for the flow when given an applied force with coefficients cs.
. The problem now becomes to find the coefficients as for the flow when given an applied force with coefficients cs.
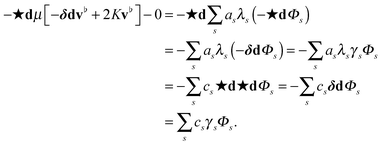
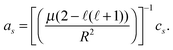
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≥ 2. For the Stokes flow on the membrane surface this gives the modal response to an applied force.
≥ 2. For the Stokes flow on the membrane surface this gives the modal response to an applied force.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 does not introduce an internal shear stress within the membrane since this mode corresponds to a rigid-body motion of the spherical shell. Since we have not yet included the intermonolayer slip or the external fluid traction stress there would be no stresses to balance a force having non-zero net torque.
= 1 does not introduce an internal shear stress within the membrane since this mode corresponds to a rigid-body motion of the spherical shell. Since we have not yet included the intermonolayer slip or the external fluid traction stress there would be no stresses to balance a force having non-zero net torque. and once in the domain Ω− interior to
and once in the domain Ω− interior to  . We obtain a representation for these solutions using Lamb's solution,35 see Section 2.2.
. We obtain a representation for these solutions using Lamb's solution,35 see Section 2.2.
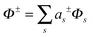 . This allows us to express the membrane velocity as
. This allows us to express the membrane velocity as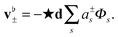
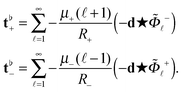
![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ± denotes the linear combination of modes of degree
± denotes the linear combination of modes of degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . In particular,
. In particular, 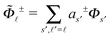 where s′ = (m′,
where s′ = (m′,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ′).
′).
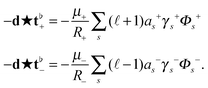
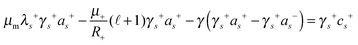
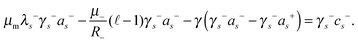
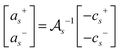
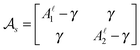
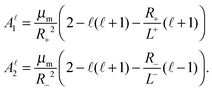
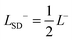 and
and 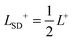 and on average
and on average 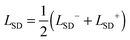 .
.
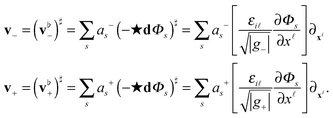
 and the εi
and the εi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) denotes the Levi-Civita tensor. We remark that given coordinate singularities on the sphere to use robustly this velocity representation for numerical calculations, we need to use different coordinate charts. For details see our discussion in Appendix A.
denotes the Levi-Civita tensor. We remark that given coordinate singularities on the sphere to use robustly this velocity representation for numerical calculations, we need to use different coordinate charts. For details see our discussion in Appendix A.
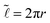 . This occurs for the inner and outer leaflets on length-scales scaling respectively like L− = μm/μ− and L+ = μm/μ+. The Saffman–Delbrück length-scale75,76 associated with each leaflet is
. This occurs for the inner and outer leaflets on length-scales scaling respectively like L− = μm/μ− and L+ = μm/μ+. The Saffman–Delbrück length-scale75,76 associated with each leaflet is 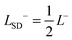 and
and 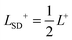 with average
with average 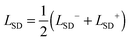 . For a vesicle, it is natural to consider these length-scales relative to the radius of the vesicle R. We introduce the non-dimensional groups Π1+ = L+/R+ and Π1− = L−/R−.
. For a vesicle, it is natural to consider these length-scales relative to the radius of the vesicle R. We introduce the non-dimensional groups Π1+ = L+/R+ and Π1− = L−/R−.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1. These correspond to the rigid rotations of the spherical shell. For a velocity difference between the layers, the drag is given by γ. For the leading order modes with
= 1. These correspond to the rigid rotations of the spherical shell. For a velocity difference between the layers, the drag is given by γ. For the leading order modes with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, the traction stresses arising from the entrained surrounding bulk solvent fluid give an effective drag μ+/R+, see eqn (39) and (40). To characterize for a lealfet the strength of the intermonolayer slip relative to the traction stress exerted by the surrounding solvent fluid, we introduce the non-dimensional groups Π2+ = γR+/μ+ and Π2− = γR−/μ−. For convenience, we also introduce the notation γ0± = μ±/R±, so that we can express Π2± = γ/γ0±.
= 1, the traction stresses arising from the entrained surrounding bulk solvent fluid give an effective drag μ+/R+, see eqn (39) and (40). To characterize for a lealfet the strength of the intermonolayer slip relative to the traction stress exerted by the surrounding solvent fluid, we introduce the non-dimensional groups Π2+ = γR+/μ+ and Π2− = γR−/μ−. For convenience, we also introduce the notation γ0± = μ±/R±, so that we can express Π2± = γ/γ0±.![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) , the angular velocity ω is given by ω = [8π
, the angular velocity ω is given by ω = [8π![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) R+3]−1τ.35 This shows that the intermonolayer slip contributes similarly to leading order as a bulk solvent fluid of viscosity γR+. We can express similarly Π2−. Other dimensional analyses and non-dimensional groups for slip have been reported in ref. 40 and 77.
R+3]−1τ.35 This shows that the intermonolayer slip contributes similarly to leading order as a bulk solvent fluid of viscosity γR+. We can express similarly Π2−. Other dimensional analyses and non-dimensional groups for slip have been reported in ref. 40 and 77.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ), sin(θ)
cos(ϕ), sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ), cos(θ)]. We parametrize the pseudosphere having Gaussian curvature K = −1 with the coordinates (θ,ϕ) with x = ψ(θ,ϕ) = [sech(θ)
sin(ϕ), cos(θ)]. We parametrize the pseudosphere having Gaussian curvature K = −1 with the coordinates (θ,ϕ) with x = ψ(θ,ϕ) = [sech(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ), sech(θ)
cos(ϕ), sech(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ), θ − tanh(θ)].
sin(ϕ), θ − tanh(θ)].![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 given by the embedding from the parametrization above. For a curved surface, this provides the analogue to a flat surface of having a flow with constant velocity. We find that the curvature results in shearing of the transported material. Intuitively, this arises relative to the flat surface by the way intrinsic curvature requires distortion of the distance relationships between points on the surface. More precisely, consider two points located at (θ1,ϕ0) and (θ2,ϕ0) with θ2 > θ1 ≥ 0 in the upper hemisphere. While both points travel at exactly the same speed, the point (θ2,ϕ0) which starts closer to the north pole will take less time to traverse fully around the xy-circular cross-section of the surface. This curvature associated distortion of the distances results in shearing of the transported material. This is illustrated in the panel on the left in Fig. 2.
3 given by the embedding from the parametrization above. For a curved surface, this provides the analogue to a flat surface of having a flow with constant velocity. We find that the curvature results in shearing of the transported material. Intuitively, this arises relative to the flat surface by the way intrinsic curvature requires distortion of the distance relationships between points on the surface. More precisely, consider two points located at (θ1,ϕ0) and (θ2,ϕ0) with θ2 > θ1 ≥ 0 in the upper hemisphere. While both points travel at exactly the same speed, the point (θ2,ϕ0) which starts closer to the north pole will take less time to traverse fully around the xy-circular cross-section of the surface. This curvature associated distortion of the distances results in shearing of the transported material. This is illustrated in the panel on the left in Fig. 2.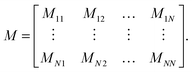
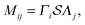
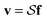 . The operators Γ, Λ approximate the fluid-structure interaction by modelling the velocity response and forces of the particles. The force density generated by an applied force F on particle j is given by f = ΛjF. In response, the velocity V of particle i is given by V = Γiv.
. The operators Γ, Λ approximate the fluid-structure interaction by modelling the velocity response and forces of the particles. The force density generated by an applied force F on particle j is given by f = ΛjF. In response, the velocity V of particle i is given by V = Γiv.
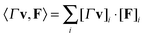
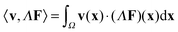
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3. We use the notation ΓT = Λ to denote succinctly the adjoint condition (45). An important consequence of the adjoint condition is that it preserves the symmetry of the mechanical responses. This is particularly desirable since as discussed in Section 2.1 the solution operator
3. We use the notation ΓT = Λ to denote succinctly the adjoint condition (45). An important consequence of the adjoint condition is that it preserves the symmetry of the mechanical responses. This is particularly desirable since as discussed in Section 2.1 the solution operator 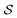 is symmetric and the adjoint condition ensures that the mobility tensor M will be symmetric.
is symmetric and the adjoint condition ensures that the mobility tensor M will be symmetric.
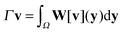
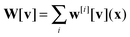
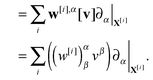
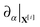 denotes the tangent basis vector in direction α at location X[i]. The square brackets [i] are used to help distinguish entries not involved in the Einstein conventions of summation. This can be interpreted as the procedure of obtaining the average velocity for particle i by using for each coordinate direction α the inner-product of the velocity field v with the reference vector field qα = (w[i],α)♯ = (w[i],α)γ∂γ. The adjoint tensor yielding the local force density is given by
denotes the tangent basis vector in direction α at location X[i]. The square brackets [i] are used to help distinguish entries not involved in the Einstein conventions of summation. This can be interpreted as the procedure of obtaining the average velocity for particle i by using for each coordinate direction α the inner-product of the velocity field v with the reference vector field qα = (w[i],α)♯ = (w[i],α)γ∂γ. The adjoint tensor yielding the local force density is given by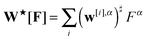
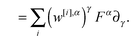
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−r2/2σ2). For rotational responses we use the reference vector field on the surface qn = ψ(x − X[i])(n × (x − X[i])). We emphasize that we only use these expressions for a coordinate chart chosen so that the particle location X[i] is away from a polar singularity, see Appendix A. The reference velocity fields are illustrated in Fig. 3.
exp(−r2/2σ2). For rotational responses we use the reference vector field on the surface qn = ψ(x − X[i])(n × (x − X[i])). We emphasize that we only use these expressions for a coordinate chart chosen so that the particle location X[i] is away from a polar singularity, see Appendix A. The reference velocity fields are illustrated in Fig. 3.

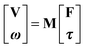
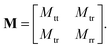
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1,i2,
1,i2,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 where ik denotes the location of the ikth particle. The leaflets in which the inclusions are embedded is denoted by
2 where ik denotes the location of the ikth particle. The leaflets in which the inclusions are embedded is denoted by ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) k ∈ {inner, outer}.
k ∈ {inner, outer}.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, see eqn (116). The intramembrane viscosity strongly couples the surface fluid resulting in a flow that is a rigid body rotation of the entire spherical shell, see Fig. 5. Parameter values are given in Table 2.
= 1, see eqn (116). The intramembrane viscosity strongly couples the surface fluid resulting in a flow that is a rigid body rotation of the entire spherical shell, see Fig. 5. Parameter values are given in Table 2.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and order index m = −1, 0, 1. Using the exterior calculus formation we apply the generalized curl = −⋆d on the surface to the vector potential Φ given by a linear combination of the harmonic modes of degree
= 1 and order index m = −1, 0, 1. Using the exterior calculus formation we apply the generalized curl = −⋆d on the surface to the vector potential Φ given by a linear combination of the harmonic modes of degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1. This yields for the velocity field on the surface that of a rigid body rotation, see eqn (41). In the case when the surface force has zero net torque in the regime Π1 ≫ 1, Π2−1Π1 = 1, the leading order flow is determined by the intramembrane viscosity and intermonolayer slip and depends on the higher-order moments of the torque of degree
= 1. This yields for the velocity field on the surface that of a rigid body rotation, see eqn (41). In the case when the surface force has zero net torque in the regime Π1 ≫ 1, Π2−1Π1 = 1, the leading order flow is determined by the intramembrane viscosity and intermonolayer slip and depends on the higher-order moments of the torque of degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1.
> 1.

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 and (ii)
= 1 and (ii) ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1. In the first case, the inner-leaflet rotates as a rigid spherical shell and entrains the fluid trapped within to a rigid body motion. As a consequence there is no traction stress with the external solvent fluid for the inner leaflet and no intramembrane shear stress. This means there are no other stresses acting against the intermonolayer drag so −γ(a
> 1. In the first case, the inner-leaflet rotates as a rigid spherical shell and entrains the fluid trapped within to a rigid body motion. As a consequence there is no traction stress with the external solvent fluid for the inner leaflet and no intramembrane shear stress. This means there are no other stresses acting against the intermonolayer drag so −γ(a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − − a
− − a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +) = 0 and the inner leaflet matches the outer leaflets rotation with a
+) = 0 and the inner leaflet matches the outer leaflets rotation with a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − = a
− = a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + for
+ for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1.
= 1.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1, the intramembrane stress and traction stress balance the intermonolayer drag. In this case, the hydrodynamic modes of the inner leaflet scale in proportion to the intermonolayer slip and the modes of the outer leaflet. As the intermonolayer slip decreases, the modes a
> 1, the intramembrane stress and traction stress balance the intermonolayer drag. In this case, the hydrodynamic modes of the inner leaflet scale in proportion to the intermonolayer slip and the modes of the outer leaflet. As the intermonolayer slip decreases, the modes a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − of the inner leaflet become small for
− of the inner leaflet become small for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1.
> 1.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − = −((A
− = −((A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/γ) − 1)−1a
2/γ) − 1)−1a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +. This can be expressed as
+. This can be expressed as![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − = −Π3(2 −
− = −Π3(2 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1) − Π1−1(
+ 1) − Π1−1(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − 1) − Π3)−1a
− 1) − Π3)−1a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +
+![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 this shows a
= 1 this shows a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − = a
− = a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + independent of the magnitude of Π3 ≠ 0. For
+ independent of the magnitude of Π3 ≠ 0. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1, we have as the intermonolayer slip becomes small Π3 ≪ 1 the hydrodynamic response for the mode of the inner leaflet with
> 1, we have as the intermonolayer slip becomes small Π3 ≪ 1 the hydrodynamic response for the mode of the inner leaflet with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1 become small a
> 1 become small a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − ≪ 1. This shows that the resulting hydrodynamic responses in the inner leaflet become dominated by the rigid rotation mode
− ≪ 1. This shows that the resulting hydrodynamic responses in the inner leaflet become dominated by the rigid rotation mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 for small intermonolayer slip. This can be seen in the upper-right panel of Fig. 8.
= 1 for small intermonolayer slip. This can be seen in the upper-right panel of Fig. 8.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 of the hydrodynamic response for the inner leaflet is not damped by the trapped solvent fluid but only by the weak intermonolayer coupling. This manifests in a near rigid rotation of the inner leaflet and a large self-mobility and coupled-mobility in response to an applied force or torque, see Fig. 10.
= 1 of the hydrodynamic response for the inner leaflet is not damped by the trapped solvent fluid but only by the weak intermonolayer coupling. This manifests in a near rigid rotation of the inner leaflet and a large self-mobility and coupled-mobility in response to an applied force or torque, see Fig. 10.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1. In contrast, for the case of a collection of inclusion particles with total force acting on the inner leaflet that yields a zero net torque, super-position of the particle hydrodynamic responses cancel for the
= 1. In contrast, for the case of a collection of inclusion particles with total force acting on the inner leaflet that yields a zero net torque, super-position of the particle hydrodynamic responses cancel for the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 mode and the behaviour of large motions for inclusions from the rigid shell rotation is suppressed. This means for inclusion particles embedded within spherical bilayers it is important to consider carefully the different ways forces and net torque act on the leaflets.
= 1 mode and the behaviour of large motions for inclusions from the rigid shell rotation is suppressed. This means for inclusion particles embedded within spherical bilayers it is important to consider carefully the different ways forces and net torque act on the leaflets.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, there is no traction stress on the inner leaflet since the solvent fluid rigidly rotates within the spherical shell but there is traction stress from the solvent on the outer leaflet. For the other modes
= 1, there is no traction stress on the inner leaflet since the solvent fluid rigidly rotates within the spherical shell but there is traction stress from the solvent on the outer leaflet. For the other modes ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1 there continue to be asymmetries in the strength of the traction stress. As a result, the mobility of inclusion particles depend on the particular leaflet in which they are embedded. In the large intermonolayer slip limit, the mobility is determined by a combination of these different solvent tractions from each of the leaflets.
> 1 there continue to be asymmetries in the strength of the traction stress. As a result, the mobility of inclusion particles depend on the particular leaflet in which they are embedded. In the large intermonolayer slip limit, the mobility is determined by a combination of these different solvent tractions from each of the leaflets.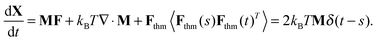

![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) n+1 gives the predictor part of the update of the configuration that is used to evaluate the force
n+1 gives the predictor part of the update of the configuration that is used to evaluate the force ![[F with combining tilde]](https://www.rsc.org/images/entities/b_char_0046_0303.gif) n+1 and mobility M(
n+1 and mobility M(![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) n+1). The Xn+1 gives the corrector part for the update of the configuration which makes use of the predictor data and an additional thermal drift term.
n+1). The Xn+1 gives the corrector part for the update of the configuration which makes use of the predictor data and an additional thermal drift term.
 denotes a partial average of a random variable Z where the Z[k] denote the
denotes a partial average of a random variable Z where the Z[k] denote the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) independent samples. The thermal drift term is motivated by the result that for the random variables p and q satisfying 〈piqj〉 = δij we have
independent samples. The thermal drift term is motivated by the result that for the random variables p and q satisfying 〈piqj〉 = δij we have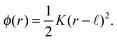
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . For a pair of bonded inclusion particles diffusing over the surface the Boltzmann equilibrium distribution of their separation is given by
. For a pair of bonded inclusion particles diffusing over the surface the Boltzmann equilibrium distribution of their separation is given by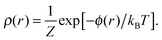
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2. We take the vesicle to have membrane viscosity corresponding to L/R = 0.65 and intermonolayer slip corresponding to γ/γ0 = 0.03. The mobility is obtained using the immersed boundary coupling for the hydrodynamics discussed in Section 3. We performed simulations with the stochastic integrator in eqn (61) using time-steps Δt = 1.3 × 105 ps, δ = 10−1,
2. We take the vesicle to have membrane viscosity corresponding to L/R = 0.65 and intermonolayer slip corresponding to γ/γ0 = 0.03. The mobility is obtained using the immersed boundary coupling for the hydrodynamics discussed in Section 3. We performed simulations with the stochastic integrator in eqn (61) using time-steps Δt = 1.3 × 105 ps, δ = 10−1, ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) = 10.
= 10.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) we consider the equilibrium distribution of their spontaneous configurations driven by thermal fluctuations. We consider the cases with the rest-lengths
we consider the equilibrium distribution of their spontaneous configurations driven by thermal fluctuations. We consider the cases with the rest-lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /R = 4.0 × 10−1, 7.5 × 10−1, 1.1 × 100. We find very good agreement between the spontaneous configurations during the stochastic simulations using the integrator (61) and the analytic predictions given in eqn (63). These results indicate that the introduced stochastic methods yield correct equilibrium properties for the system.
/R = 4.0 × 10−1, 7.5 × 10−1, 1.1 × 100. We find very good agreement between the spontaneous configurations during the stochastic simulations using the integrator (61) and the analytic predictions given in eqn (63). These results indicate that the introduced stochastic methods yield correct equilibrium properties for the system. with the case with hydrodynamic coupling M obtained from simulations using our methods in Section 3. These are shown in Fig. 16. We find that the hydrodynamics results in significant differences with the Langevin simulations. One notable difference is that the hydrodynamic coupling case allows for collective movements through rotation of the vesicle whereas the Langevin dynamics has a constant drag force that references a zero constant ambient velocity field.
with the case with hydrodynamic coupling M obtained from simulations using our methods in Section 3. These are shown in Fig. 16. We find that the hydrodynamics results in significant differences with the Langevin simulations. One notable difference is that the hydrodynamic coupling case allows for collective movements through rotation of the vesicle whereas the Langevin dynamics has a constant drag force that references a zero constant ambient velocity field.

![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) s = 〈f,Φs〉, where Φs is the spherical harmonic with index s = (m,
s = 〈f,Φs〉, where Φs is the spherical harmonic with index s = (m,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). While computationally more expensive than Fast Spherical Harmonic Transforms (FSHT),26 a distinct of advantage of our Lebedev-based methods over the latitude–longitude sampling of FSHT is the more uniform and symmetric sampling of Lebedev nodes which have octahedral symmetry,46 see Fig. 17.
). While computationally more expensive than Fast Spherical Harmonic Transforms (FSHT),26 a distinct of advantage of our Lebedev-based methods over the latitude–longitude sampling of FSHT is the more uniform and symmetric sampling of Lebedev nodes which have octahedral symmetry,46 see Fig. 17.

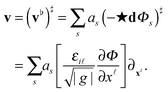
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the Levi-Civita tensor (slight abuse of notation). The x
is the Levi-Civita tensor (slight abuse of notation). The x![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) denotes the coordinates. For spherical coordinates in chart A, x1 = θA, x2 = ϕA and in chart B, x1 = θB, x2 = ϕB. To obtain the velocity, we express in each of the charts the coordinate derivatives of the spherical harmonic modes ∂Φ/∂x
denotes the coordinates. For spherical coordinates in chart A, x1 = θA, x2 = ϕA and in chart B, x1 = θB, x2 = ϕB. To obtain the velocity, we express in each of the charts the coordinate derivatives of the spherical harmonic modes ∂Φ/∂x![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and the basis vectors ∂xi in terms of the embedding space
and the basis vectors ∂xi in terms of the embedding space ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3. We then choose at each given location the expression for the chart that has a significant distance to the coordinate-system singularities. In this manner, we compute robustly the velocity field over the entire surface.
3. We then choose at each given location the expression for the chart that has a significant distance to the coordinate-system singularities. In this manner, we compute robustly the velocity field over the entire surface.
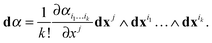
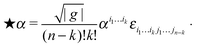
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1·gik
1·gik![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) kα
kα![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1…
1…![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) k,
k,  is the square-root of the determinant of the metric tensor, and εi1…ikj1…jn−k denotes the Levi-Civita tensor.51
is the square-root of the determinant of the metric tensor, and εi1…ikj1…jn−k denotes the Levi-Civita tensor.51
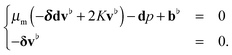
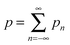
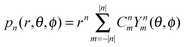
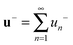
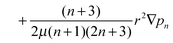
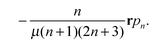
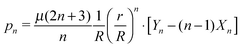
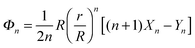
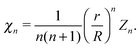
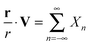
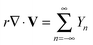
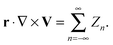
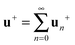
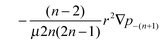
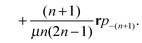
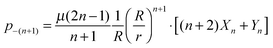
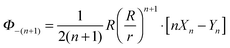
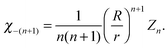
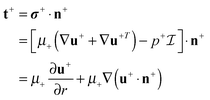
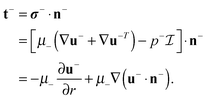
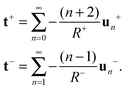
![[c with combining tilde]](https://www.rsc.org/images/entities/b_char_0063_0303.gif) ♭± = c♭±/f0 with coefficients ã and
♭± = c♭±/f0 with coefficients ã and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) . With this choice, we can express the non-dimensional problem for the full two-leaflet membrane hydrodynamics in eqn (21) as
. With this choice, we can express the non-dimensional problem for the full two-leaflet membrane hydrodynamics in eqn (21) as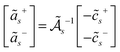
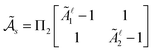
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 = Π2−1Π1(2 −
1 = Π2−1Π1(2 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1) − Π1−1(
+ 1) − Π1−1(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1))
+ 1))![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 = Π2−1Π1(2 −
2 = Π2−1Π1(2 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1) − Π1−1(
+ 1) − Π1−1(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − 1)).
− 1)).