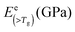Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Glass transitions in native silk fibres studied by dynamic mechanical thermal analysis
Juan
Guan
*a,
Yu
Wang†
b,
Beth
Mortimer
c,
Chris
Holland
d,
Zhengzhong
Shao
b,
David
Porter
c and
Fritz
Vollrath
*c
aSchool of Materials Science and Engineering, International Research Center for Advanced Structural and Biomaterials, Beihang University, Beijing, 100191, China. E-mail: juan.guan@buaa.edu.cn
bState Key Laboratory of Molecular Engineering of Polymers, Laboratory of Advanced Materials and Department of Macromolecular Science, Fudan University, Shanghai, 200433, China
cDepartment of Zoology, University of Oxford, Oxford, OX1 3PS, UK. E-mail: fritz.vollrath@zoo.ox.ac.uk
dDepartment of Materials Science and Engineering, University of Sheffield, Sheffield, S1 3JD, UK
First published on 9th June 2016
Abstract
Silks are a family of semi-crystalline structural materials, spun naturally by insects, spiders and even crustaceans. Compared to the characteristic β-sheet crystalline structure in silks, the non-crystalline structure and its composition deserves more attention as it is equally critical to the filaments' high toughness and strength. Here we further unravel the structure–property relationship in silks using Dynamic Mechanical Thermal Analysis (DMTA). This technique allows us to examine the most important structural relaxation event of the disordered structure the disordered structure, the glass transition (GT), in native silk fibres of the lepidopteran Bombyx mori and Antheraea pernyi and the spider Nephila edulis. The measured glass transition temperature Tg, loss tangent tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and dynamic storage modulus are quantitatively modelled based on Group Interaction Modelling (GIM). The “variability” issue in native silks can be conveniently explained by the different degrees of structural disorder as revealed by DMTA. The new insights will facilitate a more comprehensive understanding of the structure–property relations for a wide range of biopolymers.
δ and dynamic storage modulus are quantitatively modelled based on Group Interaction Modelling (GIM). The “variability” issue in native silks can be conveniently explained by the different degrees of structural disorder as revealed by DMTA. The new insights will facilitate a more comprehensive understanding of the structure–property relations for a wide range of biopolymers.
Introduction
The glass transition (GT) is the reversible process occurring in a material when its amorphous components convert between hard (glassy) and soft (rubbery) states. This paper primarily focuses on the structural changes during this process, hence we use the term GT instead of the commonly known Tg, which specifically refers to changes in temperature. GT is among the most important structural relaxation events of materials, even though aspects of its physical basis are still under discussion and conventional thermodynamics does not consider the glassy state of polymers an equilibrium state.1–3 Yet it is important to understand GT for any successful application of such amorphous materials simply because during this transition the engineering modulus experiences a dramatic drop by two orders of magnitude (from GPa to MPa) while viscosity decreases by up to 1012 Pa. For any vitreous (glassy) polymer, GT causes the characteristic relaxation time of the backbone segments to become short enough for increased molecular mobility (minutes/seconds) to be captured under ordinary experimental conditions. Porter, using the framework of Group Interaction Modelling (GIM), fundamentally assigned this increased molecular mobility, along with the change in stiffness, to the activation of polymer backbone freedoms.4Volumetric, entropic and enthalpic property changes occur during GT, which allows its detection using techniques such as dilatometry and Differential Scanning Calorimetry (DSC). Additionally, Dynamic Mechanical Thermal Analysis (DMTA) is a standard technique used by industry (and less so in academia) to measure the change in viscoelasticity of polymeric materials during structural relaxation events.5–7 Since DMTA principally measures the stiffness (energy storage) and molecular mobility (energy dissipation), it provides arguably the most sensitive technique for GT measurements. However, to date extensive DMTA studies are still rare in the examination of biopolymer structural transitions at levels of sufficient detail to truly elucidate underlying structure–property relations. Principally this is due to practical difficulties such as the handling and control of biological samples. Nevertheless, the term GT has long been introduced to the field of biomaterials, and importantly protein–water GT has been experimentally and theoretically demonstrated for various types of globular proteins.8–10
Silks are biopolymers that bridge biology and physics and have for centuries provided great utility for both commerce and science communities.11 Nature's silks are spun by a wide range of invertebrate animals and consist mostly of fibrous proteins.12 Silks have independently evolved numerous times to perform a wide range of functions from providing a lifeline for spiders to protecting pupae during metamorphosis for silkmoth caterpillars.13,14 The two ‘model’ silks are the commercial textile Bombyx mori (B. mori) mulberry silk and high performance spider dragline spider silk (often of Nephila spp.), however recently other ‘wild’ silks such as from the silkmoth Antheraea pernyi have offered key comparative insights concerning variation in both mechanical and structural properties.
Silk structural variability is a result of numerous intrinsic and extrinsic factors such as genetic differences, as well as variable processing conditions (e.g. diet, spinning speed) and environmental effects (e.g. temperature and humidity) during production and storage.15–18 Importantly the micro- and nano-scale structural variability in silk is reflected in highly sensitive macroscopic properties such as tensile mechanical properties and super-contraction capacities of spider dragline silks.19,20 Furthermore, associated spectroscopic evidence21,22 suggests that water content and changing microstructure contributes to the variability in mechanical properties of silk.
Many silks possess a semi-crystalline, hierarchical structure and morphology. A simplified perception of a silk consists of sub-micron sized fibrils and nano-structural domains within the fibril.23 At the nano-scale, β-sheets, the characteristic crystalline structure of many silks, are believed to contribute directly to stiffness and strength24–26 whereas the non-crystalline/amorphous phase contributes significantly to fibre extensibility and toughness.27–32
The distribution of these structures has been identified to some extent, i.e. native B. mori silk possesses 49–57% β-sheets33–35 and native Nephila spider dragline silk possesses 36–46%.33,36 Details of the composition of the non-crystalline structure is still under debate due to silks' high degree of structural heterogeneity shown by techniques such as Nuclear Magnetic Resonance (NMR)37,38 where silks demonstrate highly oriented molecular structures but lack well-defined β-sheet or α-helix structures (long-range order). Therefore the concept of the non-periodic lattice structure, proposed by Guinier and others,39–41 could be an alternative solution for the complex conformational structures of silks, plus an orientation effect in the conformation complexity.42 Clearly it is important to acknowledge different conformational forms in silks as they differentiate energetically on the nano-scale.
In response to the issues surrounding the categorisation of the semi-crystalline morphology in silk, Vollrath and Porter43–45 proposed the case for a distinction between ordered and disordered regions (as opposed to crystalline/non-crystalline fractions). This approach has the benefit that complex structural morphology can be reduced to a few fundamental structural parameters that reflect quantitative relationships and allow useful predictions via an established methodology developed from traditional polymer physics.
The order–disorder approach seeks to explain the molecular scale structural origins of macroscopic properties in silks and enables prediction of changes in properties induced by environmental conditions. GT in silk has been studied previously46–48 and the effect of different environmental conditions on GT has also been evaluated.49 To date DMTA has been applied to reconstituted silk fibroin (RSF) and its derived products to examine the GT behaviours, thermo-mechanical property and Tg.50 For native spider silks, the GT phenomenon has been shown to occur in a thermo-hydro cycle, and humidity-induced GT directly contributes to the property changes in spider silks.49 Finally a recent study has shown that the GT temperature (Tg) is 200 °C for N. edulis spider silks and 220 °C for B. mori silkworm silks.51
However, despite many specific studies, the generic GT behaviour, its structural origin, and the induced property changes in silk are yet to see a comprehensive analysis. Importantly, the high degree of order and the high density of hydrogen-bonding in silks (which sets them apart from conventional polymers) makes the quantitative analysis of GT behaviours technically and theoretically challenging and calls for new approaches in order to understand the non-crystalline structures in silks.
In this paper we provide experimental evidence of GT patterns in native silks using DMTA on single fibres. This data leads to the development of a structural model based on the Vollrath/Porter order–disorder proposition and Group Interaction Modelling (GIM). The main results will be presented in two sections: firstly the major GT behaviour of three native silks (B. mori, A. pernyi and N. edulis) and secondly the effect of intra- and inter-individual variability, commercial silk quality and processing conditions on the GT behaviour of silk.
Results and discussion
The major glass transition in silk
We use a temperature-ramp DMTA experiment to dynamically deform the fibre samples as a function of temperature at a frequency of 1 Hz. The recorded raw signals of stress and strain wave forms allow the calculation of the storage modulus E′ (energy storage) and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (energy dissipation). At GT the storage modulus experiences a steeper decrease as tan
δ (energy dissipation). At GT the storage modulus experiences a steeper decrease as tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increases and forms a Gaussian-shape peak. The transition temperature Tg, defined by the peak temperature of tan
δ increases and forms a Gaussian-shape peak. The transition temperature Tg, defined by the peak temperature of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, the mathematical integrated peak area of tan
δ, the mathematical integrated peak area of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (cumulative peak tan
δ (cumulative peak tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) and the storage modulus are the three quantities for our quantitative analysis and the subsequent modelling of the structure–property relations of native silk fibres.
δ) and the storage modulus are the three quantities for our quantitative analysis and the subsequent modelling of the structure–property relations of native silk fibres.
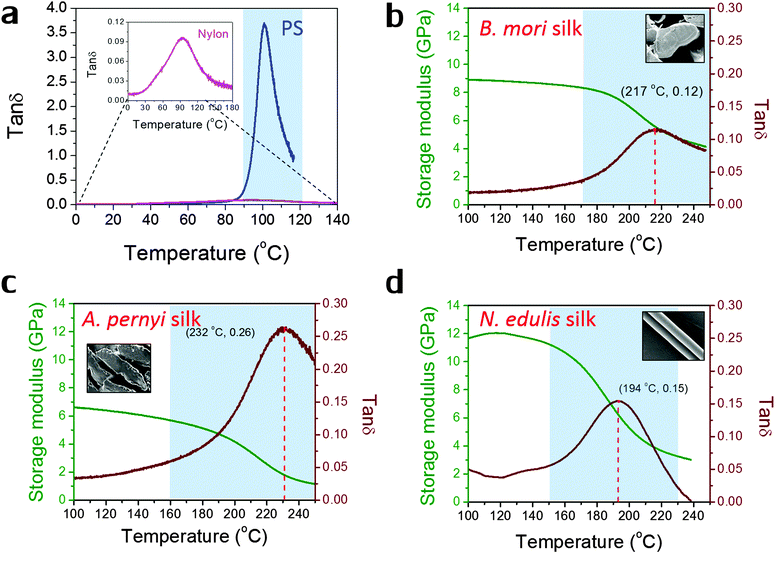
Fig. 1 shows the profiles of both storage modulus and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ during GT for two synthetic polymers and three types of silks in a DMTA temperature-ramp experiment. The data in Fig. 1(a) demonstrate that the amorphous polystyrene film displays a large Gaussian-shape tan
δ during GT for two synthetic polymers and three types of silks in a DMTA temperature-ramp experiment. The data in Fig. 1(a) demonstrate that the amorphous polystyrene film displays a large Gaussian-shape tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak (peak value = 3.6) in a narrow temperature range (from 90 °C to 120 °C). This stands in contrast to a nylon 6,6 fibre shown in the enlarged inserted graph whose tan
δ peak (peak value = 3.6) in a narrow temperature range (from 90 °C to 120 °C). This stands in contrast to a nylon 6,6 fibre shown in the enlarged inserted graph whose tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak shows a low peak value of 0.10 and a very broad temperature range (from 60 °C to 150 °C). This much broader span and lower peak in tan
δ peak shows a low peak value of 0.10 and a very broad temperature range (from 60 °C to 150 °C). This much broader span and lower peak in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ may imply that the amorphous structure in semi-crystalline nylons has more diffused and less intense molecular motions during GT. In Fig. 1(b)–(d), the three silks show GT behaviours similar to that of nylon 6,6 in terms of tan
δ may imply that the amorphous structure in semi-crystalline nylons has more diffused and less intense molecular motions during GT. In Fig. 1(b)–(d), the three silks show GT behaviours similar to that of nylon 6,6 in terms of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ magnitude and temperature range. Comparing the three silks, A. pernyi silk has a much greater tan
δ magnitude and temperature range. Comparing the three silks, A. pernyi silk has a much greater tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak than silk of B. mori, which indicates a larger fraction of molecular motions in this wild silkworm silk. N. edulis spider dragline silk shows the tan
δ peak than silk of B. mori, which indicates a larger fraction of molecular motions in this wild silkworm silk. N. edulis spider dragline silk shows the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak at a lower temperature (194 °C) than both silkworm silks. Common to other semi-crystalline polymers, low peak-value and broad span of the tan
δ peak at a lower temperature (194 °C) than both silkworm silks. Common to other semi-crystalline polymers, low peak-value and broad span of the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak are the two features of GT behaviour patterns that suggest less intense and more diffused motions of the segmental molecular structures in the silks. The data in Fig. 1 allow us to calculate the fractional changes of E′ before and after GT for the three silks, which are 40% loss for B. mori; 66% loss for A. pernyi and 58% loss for N. edulis.
δ peak are the two features of GT behaviour patterns that suggest less intense and more diffused motions of the segmental molecular structures in the silks. The data in Fig. 1 allow us to calculate the fractional changes of E′ before and after GT for the three silks, which are 40% loss for B. mori; 66% loss for A. pernyi and 58% loss for N. edulis.
T g: observations and predictions
The physical nature of the thermally induced glass transition of silk fibroin is proposed to derive from the cooperative or non-cooperative motions of backbone segments in the non-crystalline or disordered regions of silk when the intermolecular forces go through a maximum, or the intermolecular stiffness tends to zero.52 The transition condition is known as Born's elastic instability criterion, which concentrates on bond stiffness/mobility (perpendicular to the interaction axis) instead of bond strength (along the interaction axis). Quantitatively, Porter's Group Interaction Modelling (GIM) theory offers a satisfying relationship between the structure and properties of polymers, and the expression between Tg and the structural parameters is shown in eqn (1).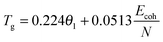 | (1) |
| Peptide | Structure | E coh (kJ mol−1) (without H-bond) | Degrees of freedom N | Molar fraction as counted in AA sequence | ||
|---|---|---|---|---|---|---|
| B. mori | A. pernyi | N. edulis | ||||
| Peptide base | –C–CO–NH– | 24.3 | 6 | |||
| (–R group) | ||||||
| Glycine (G) | –H | 0 | 0 | 47.5% | 33% | 47% |
| Alanine (A) | –CH3 | 4.5 | 2 | 31.7% | 53% | 29% |
| Serine (S) | –CH2–OH | 10.8 | 3 | 15.8% | 14% | 3% |
| Glutamine (Q) | –CH2–CH2–CO–NH2 | 28.8 | 5 | 0 | 0 | 9% |
| Tyrosine (Y) | –CH2–Ph–OH | 35.8 | 4 | 5% | 0 | 3% |
| Leucine (L) | –CH2–C(CH3)2 | 18 | 4 | 0 | 0 | 6% |
| Arginine (R) | –CH2–CH2–CH2–NH–C(NH2)2 | 45 | 7 | 0 | 0 | 3% |
| Average | B. mori | 29.2 | 6 | |||
| A. pernyi | 28.2 | 6 | ||||
| N. edulis | 32.0 | 7 | ||||
The experimental Teg is defined as the peak temperature of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ Gaussian peak through GT, as indicated in Fig. 1 and shown in Table 2. Using the GIM methods and the structural parameters (Ecoh = 125 kJ mol−1, N = 28, θ1 = 241 °C), the Tg of nylon 6,6 is modelled to be 71 °C without considering the contribution from hydrogen-bonding, which is lower than our DMTA observation. If an average of 6 hydrogen bonds is added to the group cohesive energy, the resultant Tg becomes 82 °C, closer to the temperature at peak tan
δ Gaussian peak through GT, as indicated in Fig. 1 and shown in Table 2. Using the GIM methods and the structural parameters (Ecoh = 125 kJ mol−1, N = 28, θ1 = 241 °C), the Tg of nylon 6,6 is modelled to be 71 °C without considering the contribution from hydrogen-bonding, which is lower than our DMTA observation. If an average of 6 hydrogen bonds is added to the group cohesive energy, the resultant Tg becomes 82 °C, closer to the temperature at peak tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. In silks, the hydrogen-bonds among amide groups are easier to form from the highly oriented molecular structure and the number of hydrogen bonds directly impact the cohesive energy, as shown in Table 2. Hydrogen bond energy takes 10 kJ mol−1 as an average of N–H⋯O and N–H⋯N forms. For example, in B. mori silks, if two hydrogen bonds per peptide are added, an additional energy of 20 kJ mol−1 will be added to the peptide base value of 29.2 kJ mol−1 to give the final average Ecoh of 49.2 kJ mol−1 for each characteristic segment. As a result, the Tg for B. mori silk is 243.1 °C from eqn (1). If only one hydrogen bond is taken, the result would become 157.6 °C, which sets a lower bound for Tg of B. mori silk. Borrowing the non-periodic lattice concept, we argue that the molecular structures responsible for GT in silk do not have a singular form, but a probability spectrum with several favoured forms, e.g. of one or two hydrogen bonds per peptide. The experimental Tg of 217 °C in Fig. 1(b) thus is the result of the averaged hydrogen-bonding density contributed by hydrogen-bonding forms with different probabilities. If one or two hydrogen bonds are adopted, the molecular structure in native B. mori silk would have a 70% chance of 2 hydrogen bonds (H-bonds). In comparison, the hydrogen-bonding density in the reconstituted silk films (Tg = 177 °C50) would have 23% of probable structures possessing 2 H-bonds per peptide.
δ. In silks, the hydrogen-bonds among amide groups are easier to form from the highly oriented molecular structure and the number of hydrogen bonds directly impact the cohesive energy, as shown in Table 2. Hydrogen bond energy takes 10 kJ mol−1 as an average of N–H⋯O and N–H⋯N forms. For example, in B. mori silks, if two hydrogen bonds per peptide are added, an additional energy of 20 kJ mol−1 will be added to the peptide base value of 29.2 kJ mol−1 to give the final average Ecoh of 49.2 kJ mol−1 for each characteristic segment. As a result, the Tg for B. mori silk is 243.1 °C from eqn (1). If only one hydrogen bond is taken, the result would become 157.6 °C, which sets a lower bound for Tg of B. mori silk. Borrowing the non-periodic lattice concept, we argue that the molecular structures responsible for GT in silk do not have a singular form, but a probability spectrum with several favoured forms, e.g. of one or two hydrogen bonds per peptide. The experimental Tg of 217 °C in Fig. 1(b) thus is the result of the averaged hydrogen-bonding density contributed by hydrogen-bonding forms with different probabilities. If one or two hydrogen bonds are adopted, the molecular structure in native B. mori silk would have a 70% chance of 2 hydrogen bonds (H-bonds). In comparison, the hydrogen-bonding density in the reconstituted silk films (Tg = 177 °C50) would have 23% of probable structures possessing 2 H-bonds per peptide.
| Silk name | Group | H-bonds | E coh (kJ mol−1) | N | T g (°C) | T eg (°C) | tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δg Δg |
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg Δeg |
f dis |
|---|---|---|---|---|---|---|---|---|---|
Note: the number of H-bonds per peptide group is 1 or 2; cohesive energy Ecoh is the sum of that from hydrogen bonds and the peptide base; N is the degrees of freedom; tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δg and tan Δg and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg are respectively the theoretical and experimental cumulative tan Δeg are respectively the theoretical and experimental cumulative tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ through GT; and fdis is the predicted degree of structural disorder by GIM. Theta temperature θ1 is taken to be 153 °C for all cases. δ through GT; and fdis is the predicted degree of structural disorder by GIM. Theta temperature θ1 is taken to be 153 °C for all cases. |
|||||||||
| B. mori | G0.475A0.317S0.158Y0.05 | 1 | 39.2 | 6 | 157.6 | 217 | 56 | 7.6 | 0.21 |
| 2 | 49.2 | 6 | 243.1 | 70 | 7.6 | 0.16 | |||
| A. pernyi | G0.33A0.53S0.14 | 1 | 38.2 | 6 | 149.0 | 232 | 54 | 20.4 | 0.56 |
| 2 | 48.2 | 6 | 234.5 | 68 | 20.4 | 0.45 | |||
| N. edulis | G0.47A0.29S0.03X0.21 | 1 | 42 | 7 | 130.0 | 194 | 51 | 7.9 | 0.23 |
| 2 | 52 | 7 | 203.5 | 63 | 7.9 | 0.19 | |||
For A. pernyi silks, the representative group is taken as G0.33A0.53S0.14, whose total molar fraction accounts for 82% of the whole fibroin sequence. The average cohesive energy per peptide is 48.2 kJ mol−1 if 2 H-bonds are taken into account, and the predicted high-bound Tg for A. pernyi silk is 234.5 °C. The observed Tg of 232 °C for A. pernyi silk implies the great majority of the non-crystalline molecular structures is highly hydrogen-bonded (close to 2 H-bonds per peptide).
For N. edulis spider silk, detailed modelling parameterisation based on N. edulis dragline Spidroin I can be found in reference.43 Different from the two silkworm silks, spider dragline silk sequence has a number of peptides with bulky side groups (e.g. glutamine), the motions of which are restricted until the backbone chain segments become free to move. The increase in the degrees of freedom of the side –R groups needs to be taken into account together with that of the backbone to infer the overall degrees of freedom, which brings N from 6 to 7. The two bounds for Tg values for N. edulis silk are 203.5 °C (Ecoh = 52 kJ mol−1, 2 H-bonds and N = 7) and 130.4 °C (Ecoh = 42 kJ mol−1, 1 H-bond and N = 7). The observed Tg of 194 °C corresponds to 87% of 2 H-bonds and 13% of 1 H-bond.
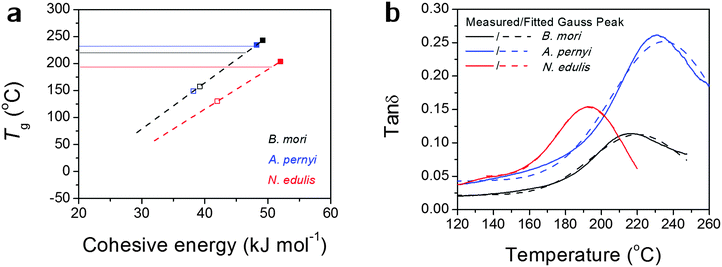
Alternatively, the observed Tg might, as we believe, be contributed by an average number of hydrogen bonds in the structure. Fig. 2(a) more directly translates eqn (1) into a linear relationship between Tg and Ecoh. This calculation suggests the spider silk possesses an average of 1.87 hydrogen bonds per peptide group in the non-crystalline region, in comparison to 1.70 for B. mori and 1.97 for A. pernyi. Additionally, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profiles for the three silks are fitted by single Gaussian peaks as found in Fig. 2(b), which confirms the segmental motions of native silks through GT are in a Gaussian probability form.
δ profiles for the three silks are fitted by single Gaussian peaks as found in Fig. 2(b), which confirms the segmental motions of native silks through GT are in a Gaussian probability form.
So far the broad temperature span of GT seems sufficiently explained as the predicted Tg has a limited number of “favoured” values whereas the observed Tg is a probability function of different predicted Tgs according to the variations in hydrogen-bonding and degrees of freedom. The higher the observed Tg is, the more tightly hydrogen bonded the non-crystalline structure in the silk molecular structure is. We note that the structural model of two hydrogen bonds per peptide group for an “amorphous” disordered phase may be confused with the crystalline β-sheet phase as both possess similar density of hydrogen-bonding on average. According to the most recent series of NMR studies,53 the liquid silk I structure prior to the native solid silk formation has been identified to be type II β-turns with both inter- and intra-molecular hydrogen-bonding, which is a form with a high energy density. Our results further suggest that the non-crystalline structure in native solid silks is highly hydrogen-bonded, although this structural form (e.g. β-turns) is different from long-range order of β-sheet. This will add evidence to the understanding of the non-crystalline structural regions of native silks from the perspective of macroscopic property measurements.
Cumulative tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) δ and the degree of structural disorder
δ and the degree of structural disorder
How can the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profiles through GT in the DMTA measurement be interpreted for structural analysis of native silks? As previously introduced, the order–disorder proposition avoids the complicated assignments of secondary structures and yet still can be correlated effectively with the macroscopic properties of silks. Firstly, a structural parameter is defined as the degree of structural disorder, fdis, which is the molar fraction of the non-crystalline structures that are responsible for GT. Arguably the degree of structural disorder approximates an averaged structural parameter of heterogeneous nano-structures in a mean-field homogeneous micro- and macroscopic morphology. For the three silks, the following fdis values are referenced from amino acid sequence analysis54 and FTIR analysis: 0.23 for B. mori silk; 0.43 for A. pernyi silk and 0.30 for N. edulis dragline silk.
δ profiles through GT in the DMTA measurement be interpreted for structural analysis of native silks? As previously introduced, the order–disorder proposition avoids the complicated assignments of secondary structures and yet still can be correlated effectively with the macroscopic properties of silks. Firstly, a structural parameter is defined as the degree of structural disorder, fdis, which is the molar fraction of the non-crystalline structures that are responsible for GT. Arguably the degree of structural disorder approximates an averaged structural parameter of heterogeneous nano-structures in a mean-field homogeneous micro- and macroscopic morphology. For the three silks, the following fdis values are referenced from amino acid sequence analysis54 and FTIR analysis: 0.23 for B. mori silk; 0.43 for A. pernyi silk and 0.30 for N. edulis dragline silk.
Eqn (2) from GIM55 describes the quantitative relationship of cumulative tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (tan
δ (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δg) over the transition temperature range with the structural parameters of the interactive group, Ecoh and N. This relation is derived fundamentally and validated with a database of over 250 polymers.4 A quick calculation using eqn (2) for silk shows that tan
Δg) over the transition temperature range with the structural parameters of the interactive group, Ecoh and N. This relation is derived fundamentally and validated with a database of over 250 polymers.4 A quick calculation using eqn (2) for silk shows that tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δg is in the numerical range of 51–70 (shown in Table 2), which appears much greater than the experimental values. For semi-crystalline native silks, it is straightforward to introduce the degree of structural disorder fdis to the equation, and adapt a new form, as presented in eqn (3). The factor fdis is easy to understand as only the motions of the disordered structure can be activated in GT and contribute to the experimentally measured tan
Δg is in the numerical range of 51–70 (shown in Table 2), which appears much greater than the experimental values. For semi-crystalline native silks, it is straightforward to introduce the degree of structural disorder fdis to the equation, and adapt a new form, as presented in eqn (3). The factor fdis is easy to understand as only the motions of the disordered structure can be activated in GT and contribute to the experimentally measured tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ.
δ.
Regarding the other coefficient (2/3) in eqn (3), it is introduced to correct for the experimental effect of the uni-axial tensile mode in DMTA measurement because the molecular structures subjected to the static stress of the tensile direction cannot be relaxed as the motions along this direction are restrained. As a result, the probability of molecular motions of the overall disordered structure through GT is reduced by one dimention, or a factor of 2/3.
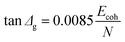 | (2) |
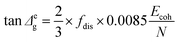 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg. The integration temperature limits are taken as 100 °C and 250 °C as shown in Fig. 1, and the integration curves are shown in the later Fig. 3 for a variety of silks. As shown in Table 3, from referenced fdis we have succeeded to explain the apparent discrepancy of the experimental cumulative tan
Δeg. The integration temperature limits are taken as 100 °C and 250 °C as shown in Fig. 1, and the integration curves are shown in the later Fig. 3 for a variety of silks. As shown in Table 3, from referenced fdis we have succeeded to explain the apparent discrepancy of the experimental cumulative tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg and the theoretical tan
Δeg and the theoretical tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δg (100% disorder) through GT in native silks using the GIM framework and an order–disorder structural model without bringing in detailed effects. Moreover, by using the experimentally measured tan
Δg (100% disorder) through GT in native silks using the GIM framework and an order–disorder structural model without bringing in detailed effects. Moreover, by using the experimentally measured tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg, the resultant fdis for the three silks lie in the frame of the reported values from other techniques,55e.g. FTIR measurements report 0.40–0.61 for A. pernyi silk.15
Δeg, the resultant fdis for the three silks lie in the frame of the reported values from other techniques,55e.g. FTIR measurements report 0.40–0.61 for A. pernyi silk.15
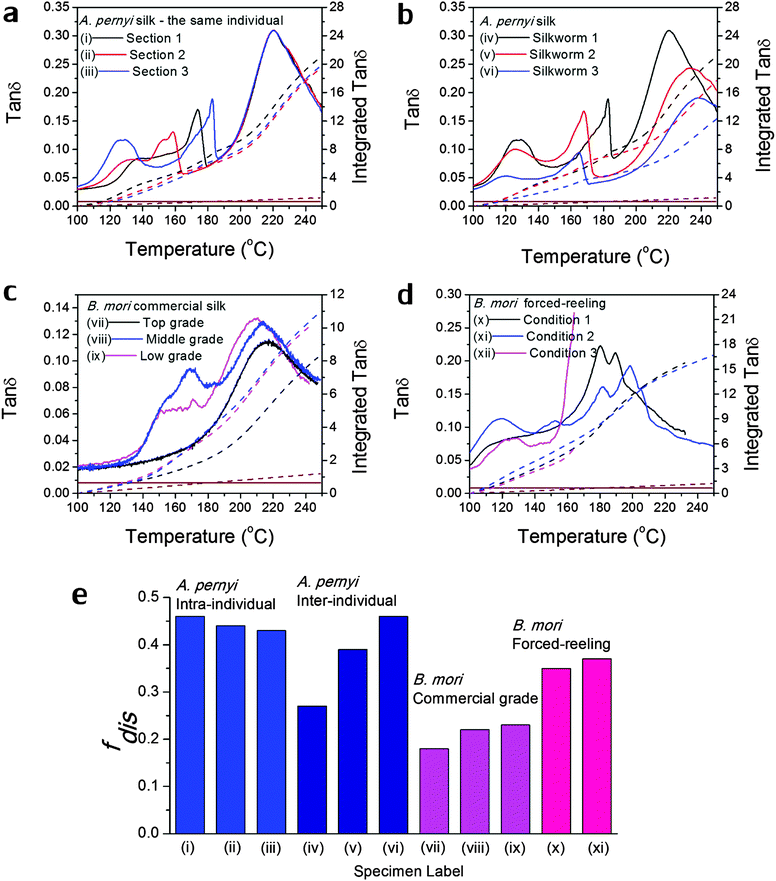 | ||
Fig. 3 Variability in GT of silks as seen in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profiles of various silks: (a) A. pernyi silk from different sections of the same reel from one individual silkworm; (b) A. pernyi silk from three individual silkworms; (c) B. mori silk from three cocoons of graded quality (G1 is commercially better priced than G2 and G3); (d) B. mori silk through forced-reeling under varied conditions.58 The brown coloured lines denote the baseline tan δ profiles of various silks: (a) A. pernyi silk from different sections of the same reel from one individual silkworm; (b) A. pernyi silk from three individual silkworms; (c) B. mori silk from three cocoons of graded quality (G1 is commercially better priced than G2 and G3); (d) B. mori silk through forced-reeling under varied conditions.58 The brown coloured lines denote the baseline tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, which equates a constant 0.008 for most polymers. The right axis corresponds to the mathematical integration (in dashed lines) of each tan δ, which equates a constant 0.008 for most polymers. The right axis corresponds to the mathematical integration (in dashed lines) of each tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profile in the temperature range. (e) compares the calculated structural disorder fdis for the above listed silk varieties. Note that the fdis for (xii) silk cannot be determined as the tan δ profile in the temperature range. (e) compares the calculated structural disorder fdis for the above listed silk varieties. Note that the fdis for (xii) silk cannot be determined as the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profile is not complete for comparison. δ profile is not complete for comparison. | ||
| Silk type | E coh (kJ mol−1) | V w* (cc mol−1) | B of 3 ideal states (GPa) | f dis | B (<Tg) | B (>Tg) | tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg Δeg |
E (>Tg) (GPa) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | G | R | |||||||||
Note: van der Waal's volume Vw of the peptide group can be found in ref. 43 and the average Vw for each silk is calculated from molar fractions listed in Table 1; bulk modulus B is presented in the three states of polymer which are abbreviated as (C) for crystalline, (G) for glassy amorphous and (R) for rubbery amorphous; fdis is the structural disorder and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg is the experimental cumulative tan Δeg is the experimental cumulative tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. δ. |
|||||||||||
| B. mori | 49.2 | 34.93 | 19.2 | 9.0 | 4.2 | 0.21 | 15.5 | 11.0 | 7.6 | 6.9 | 4.1 |
| A. pernyi | 48.2 | 36.53 | 17.9 | 8.4 | 4.0 | 0.45 | 11.9 | 6.9 | 20.4 | 1.0 | 1.5 |
| N. edulis | 52.0 | 41.45 | 17.1 | 8.0 | 3.8 | 0.19 | 14.1 | 10.2 | 7.9 | 6.1 | 3.3 |
The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profile through GT enabled us to conveniently obtain the degree of structural disorder, or the fraction of the disordered structure that is responsible for GT. Nevertheless, without understanding the forms of “order” and “disorder”, a simple order–disorder structural model cannot sufficiently explain the properties of certain silks, for example the supercontraction in spider silks. As discussed previously,56N. edulis silk contains some inter-phase structural components, meta-order and meta-disorder. The complete resolution of the structural composition requires extra information on the structural relaxations of the intermediate structures between crystalline order and the GT-responsible disorder, e.g. from thermal analysis (DSC) or mechanical property analysis (tensile testing), which cannot be acquired using DMTA.
δ profile through GT enabled us to conveniently obtain the degree of structural disorder, or the fraction of the disordered structure that is responsible for GT. Nevertheless, without understanding the forms of “order” and “disorder”, a simple order–disorder structural model cannot sufficiently explain the properties of certain silks, for example the supercontraction in spider silks. As discussed previously,56N. edulis silk contains some inter-phase structural components, meta-order and meta-disorder. The complete resolution of the structural composition requires extra information on the structural relaxations of the intermediate structures between crystalline order and the GT-responsible disorder, e.g. from thermal analysis (DSC) or mechanical property analysis (tensile testing), which cannot be acquired using DMTA.
Understanding storage modulus changes through GT
Experimentally measured tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profiles and tan
δ profiles and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg through GT can reveal the structural disorder for the three native silk examples using GIM. Nevertheless, correlations between the loss events and the changes in mechanical properties are also fundamentally useful and have practical importance. Since GIM combines a cell or lattice model and the mean-field theory, we first introduce the fundamentally important “elastic” parameter of bulk modulus, B, which is a ratio of pressure to volumetric strain in a ‘material’ cell. The B expression from GIM55 considers the contributions from the cohesive energy, the van der Waals volume of the unit group and the relative interaction distance between groups. B changes as the relative interaction distance r/r0 changes over temperature or pressure especially through a change in “state” (crystalline, glassy or rubbery amorphous). Here we conveniently extract the expressions of B for the three “states” or phases of polymer from GIM as shown in eqn (4). For silks, we could thus establish the correlation between the state theory and the order–disorder structural model: the crystalline phase corresponds to the ordered structure, the glassy amorphous to the disordered structure below Tg, and the rubbery amorphous to the disordered structure above Tg. We assume that silks transit from a “(amorphous glass) + (crystal)” state to a “(amorphous rubber) + (crystal)” state through GT.
Δeg through GT can reveal the structural disorder for the three native silk examples using GIM. Nevertheless, correlations between the loss events and the changes in mechanical properties are also fundamentally useful and have practical importance. Since GIM combines a cell or lattice model and the mean-field theory, we first introduce the fundamentally important “elastic” parameter of bulk modulus, B, which is a ratio of pressure to volumetric strain in a ‘material’ cell. The B expression from GIM55 considers the contributions from the cohesive energy, the van der Waals volume of the unit group and the relative interaction distance between groups. B changes as the relative interaction distance r/r0 changes over temperature or pressure especially through a change in “state” (crystalline, glassy or rubbery amorphous). Here we conveniently extract the expressions of B for the three “states” or phases of polymer from GIM as shown in eqn (4). For silks, we could thus establish the correlation between the state theory and the order–disorder structural model: the crystalline phase corresponds to the ordered structure, the glassy amorphous to the disordered structure below Tg, and the rubbery amorphous to the disordered structure above Tg. We assume that silks transit from a “(amorphous glass) + (crystal)” state to a “(amorphous rubber) + (crystal)” state through GT.
To solve the problem of structure–property relations of multi-phase polymer systems, the B of the system ensemble can be approximated using a simple additivity rule (see eqn (5)) if homogeneous volumetric distributions of the different phases can be assumed. It is important to mention that each phase is responding to thermal energy independently and energy sharing between phases is excluded when the additivity rule is applied. Using this rule and the previously modelled fdis, the average B of the two “states” of silk below Tg and above Tg can be estimated. As shown in Table 3, the predicted B after GT for the three silks is: 15.5 GPa for B. mori (fdis = 0.21); 11.9 GPa for A. pernyi (fdis = 0.45) and 14.1 GPa for N. edulis (fdis = 0.19).
 | (4) |
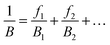 | (5) |
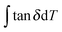 uses experimental tan
uses experimental tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg, contributed by the molecular mobility of the disordered fraction in the tensile experimental mode. The proportionality constant A is determined by structural parameters of the characteristic group unit, and most polymers have A in the range 1–2 GPa−1. Here a generic A for all silks takes 1.5 GPa−1 in line with the literature.43
Δeg, contributed by the molecular mobility of the disordered fraction in the tensile experimental mode. The proportionality constant A is determined by structural parameters of the characteristic group unit, and most polymers have A in the range 1–2 GPa−1. Here a generic A for all silks takes 1.5 GPa−1 in line with the literature.43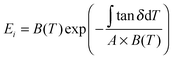 | (6) |
Variability in GT of silks
As discussed in the introduction, variability is an important issue when studying natural materials such as silk. Silk structures can vary highly between species and even individuals, and for this reason it is not surprising to observe a variety of GT behaviours in silk materials. The library of silk fibres is expanded in this section to include some of the “unnaturally” manipulated silks from the native dope by forced-reeling. Hence the goal of this section is to give clear visions of the structural origin of the variability of properties in silks.Previous work showed that A. pernyi silks had an inherent, relatively large variability among individuals in the tensile mechanical properties and DMTA profiles.57 As shown in Fig. 3(a) and (b), DMTA results show that silks from different representative individuals have more variability in Tg (at major peak tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) and tan
δ) and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg through GT than that from the same individual. The shift in Tg suggests the average cohesive energy varies due to different hydrogen-bonding densities; and the difference in tan
Δeg through GT than that from the same individual. The shift in Tg suggests the average cohesive energy varies due to different hydrogen-bonding densities; and the difference in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ suggests varying degrees of structural disorder changing from 0.40 to 0.65, as calculated by Porter and confirmed by FTIR.15 The structural differences in this particular case of A. pernyi silks may originate from the forced-reeling process, which has been shown to have a dramatic impact on the structure of B. mori silks.58 It is also noticed that silks from the same individual show a consistent major GT peak with several minor peaks, which may be the relaxation of the locked-in low-ordered structures due to the coagulation during spinning.
δ suggests varying degrees of structural disorder changing from 0.40 to 0.65, as calculated by Porter and confirmed by FTIR.15 The structural differences in this particular case of A. pernyi silks may originate from the forced-reeling process, which has been shown to have a dramatic impact on the structure of B. mori silks.58 It is also noticed that silks from the same individual show a consistent major GT peak with several minor peaks, which may be the relaxation of the locked-in low-ordered structures due to the coagulation during spinning.
B. mori silks from commercially graded cocoons show traits comparable to the inter-individual A. pernyi silks in Fig. 3(c). Shifts in major Tg and changes in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg are apparent between different grades. This has implications for the commercial value of silks as poor grade cocoons of small size and defects consist of poor silks with a high degree of structural disorder, which could directly impact performance (reeling, weaving and so on) in the industrial processing.
Δeg are apparent between different grades. This has implications for the commercial value of silks as poor grade cocoons of small size and defects consist of poor silks with a high degree of structural disorder, which could directly impact performance (reeling, weaving and so on) in the industrial processing.
The introduction of forced-reeling could induce more variability and undesirable structural disorder as discussed for A. pernyi silks and shown for B. mori silks in Fig. 3(d). The manipulation of the natural spinning process – including forced-reeling w/wo post-drawing treatment – perturbs the formation of native structures under natural conditions and may lock in more disorder during the liquid–solid transformation.58
Fig. 3(e) summarises the variability issue in silks and compares the structural disorder, fdis (modelled from eqn (3) using the experimental integrated tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and the two structural parameters Ecoh and N from Table 1), among silks of intra- and inter-individual differences, of various commercial grades and of conditioned forced-reeling. It infers that the intrinsic reason for silk variability is the different forms of hydrogen-bonding in the non-crystalline structure. Note that there is a tan
δ and the two structural parameters Ecoh and N from Table 1), among silks of intra- and inter-individual differences, of various commercial grades and of conditioned forced-reeling. It infers that the intrinsic reason for silk variability is the different forms of hydrogen-bonding in the non-crystalline structure. Note that there is a tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ baseline of 0.008 through our temperature range (brown lines in Fig. 3a–d) and the integration is subtracted. Importantly, this quantitative analysis of tan
δ baseline of 0.008 through our temperature range (brown lines in Fig. 3a–d) and the integration is subtracted. Importantly, this quantitative analysis of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δeg can be used to compare the delicate structural differences in silks, and to develop quality control methods for silk processing.
Δeg can be used to compare the delicate structural differences in silks, and to develop quality control methods for silk processing.
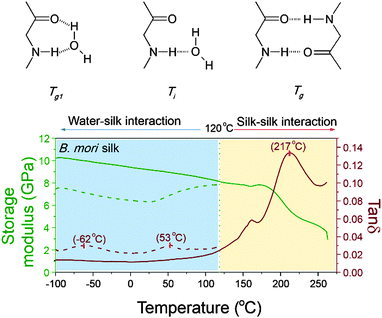
Protein–water GT and denaturation in silk
As mentioned earlier, peptide–water glass transition and denaturation are the two structural change mechanisms at temperatures below the major GT. Peptide–water glass transition is a relaxation process of the peptide–water complex, whereas denaturation involves both evaporation of volatile water and reformation of hydrogen-bonding from water–amide to amide–amide. Fig. 4 shows the three structure change mechanisms and the contributing group interactions in the representative tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profile of B. mori silk from −100 °C to 250 °C. The water–amide (in “wet” silk) and amide–amide (in “dry” silk) interactions are separated at T = 120 °C. The first lower relaxation temperature lies in a temperature range from −80 °C to −30 °C with tan
δ profile of B. mori silk from −100 °C to 250 °C. The water–amide (in “wet” silk) and amide–amide (in “dry” silk) interactions are separated at T = 120 °C. The first lower relaxation temperature lies in a temperature range from −80 °C to −30 °C with tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peaks at −60 °C; and the second relaxation lies in a temperature range from 30 °C to 90 °C with tan
δ peaks at −60 °C; and the second relaxation lies in a temperature range from 30 °C to 90 °C with tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peaks at about 60 °C. Different from the major GT, both lower relaxations disappear when the silk has gone through thermal annealing up to 120 °C, which confirms that the presence of water is the prerequisite of these two mechanisms. For the native silk fibres studied, the water content is about 6%, as reported previously.48
δ peaks at about 60 °C. Different from the major GT, both lower relaxations disappear when the silk has gone through thermal annealing up to 120 °C, which confirms that the presence of water is the prerequisite of these two mechanisms. For the native silk fibres studied, the water content is about 6%, as reported previously.48
Porter59 emphasised the importance of the two lower-temperature structure change mechanisms in understanding the properties and functions of proteins that perform in vivo (although it is noted that our silk model material has long evolved to perform ex vivo). For proteins such as enzymes, which have a key-and-lock structure–property-function relationship, the molecular structure and the peptide–water interactions are expected to be more sensitive to external stimuli. Therefore the question arises: can we follow the protocol of detecting GT in silks to study the structure–property relationships, especially peptide–water interactions, of more functionalised proteins in living organisms? Here the standard approaches for property measurements in polymer science such as thermal analysis and dielectric analysis, complemented by other means, may help to get the complete picture of protein structure–property–function relations.
Experimental
Materials
B. mori cocoon fibres were first unravelled carefully with as minimal force possible from the cocoon middle layer, and then single fibres were mounted loosely onto paper frames that are specifically designed to fit in the tension clamps of the DMTA Q800 (TA Instruments, Delaware). Furthermore, graded B. mori cocoon fibres were also prepared from the commercially graded B. mori cocoons in the silk production region (Jiangsu Province) in China, for more details refer to ref. 48 and 60.N. edulis spider dragline major ampullate silk was collected directly from live spiders under ambient conditions at a reeling speed of 10 mm s−1 as previously described.61 Synthetic polymer examples include highly amorphous polystyrene thin film and nylon 6,6 fibre. Polystyrene thin sheet was prepared using a simple hot-press technique. Medium tenacity nylon 6,6 fibres were purchased from GoodFellows UK and the diameter of the fibres was supplied as 25 μm and verified using SEM (JEOL Neoscope) in the lab.
The presence of minerals and sericin makes A. pernyi silk fibres very difficult to be unravelled directly from the cocoon, and during unravelling it was inevitable that the fibres may be taken under tension. Therefore A. pernyi fibres were mostly obtained through forced-reeling of A. pernyi silkworms, and fibres from three different individuals were characterised for the variability of the GT behaviour (for more information refer to57). Similarly, B. mori fibres were also obtained through forced-reeling under varied conditions: without post-stretch treatment and with post-stretch treatment (for more details refer to58).
Methods
A. pernyi and B. mori silk fibres have irregular cross-sections. For A. pernyi and B. mori cocoon silk fibres, a bundle of silk fibres were held tightly together through a thin tube, and then short tubular sections were cut (see examples inset to Fig. 1). An average cross-sectional area was calculated from over 30 measurements of the individual cross-sectional areas. For A. pernyi and B. mori forced-reeled silk fibres, the cross-sectional area of the adjacent section of silk to that being used for DMTA was applied. The adjacent silk fibre was embedded in epoxy resin and sectioned to expose cross-sections. The measurement of the cross-sectional area was taken through the software ImageJ after the SEM micrographs were taken.
Conclusions
We have shown that the disordered phase in native silks is a critical structural component that affects the mechanical properties of silks and is of equal importance to the ordered phase. Here we deployed Dynamic Mechanical Thermal Analysis (DMTA) to examine the structural relaxation of the disordered phase of native silks and focus on the Glass Transition (GT). The observed high Tg of the disordered structure of three native silks suggests a hydrogen-bonding density of nearly 2 hydrogen bonds per peptide group. Based on GIM and the order–disorder argument, the key structural parameter of silk, fdis, can be successfully deduced from the model parameters and the experimental cumulative tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ during GT. We were also able to provide a quantitative analysis on the observed dynamic storage modulus and to make predictions of the modulus changes through GT, which would be useful for engineering applications and practical uses of silk materials.
δ during GT. We were also able to provide a quantitative analysis on the observed dynamic storage modulus and to make predictions of the modulus changes through GT, which would be useful for engineering applications and practical uses of silk materials.
The developed theory and methods is intended to explain observed variability in a variety of native and manipulated silks. In addition to protein structure, processing and post-treatments also contribute to the final structure and properties of silk fibres.
Moreover, two lower-temperature structural relaxations of native silks, namely peptide–water GT at −60 °C and “denaturation” (water evaporation and change of amide–water interaction to amide–amide interaction) at 60 °C, are briefly introduced to complete the overall thermo-mechanical property graph for native silks.
The experimental data and theoretical modelling presented in this paper provide not only new insights on the microstructural picture of native silks, but also new possibilities on understanding the molecular interactions and structure–property–function relationships for other biological polymers.
Notes
This paper is written in the spirit of Dr David Porter, who could not see this paper published. He will be remembered by all the authors as a great friend as well as for his development of GIM and many contributions to silk research.Acknowledgements
GJ thanks the National Natural Science Foundation of China (51503009), the State Key Laboratory of Molecular Engineering of Polymer (Fudan University) (K2016-05), and Beihang University for financial support. Funding for the research in Oxford was provided by the US Air Force Office of Scientific Research (FA9550-12-1-0294) and the European Research Council (SP2-GA-2008-233409). BM thanks The Leverhulme Trust (F/08705/D) and Jesus College, Oxford for funding, and CH thanks the EPSRC (EP/K005693/1).References
- J. Mattsson, H. M. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. B. Hu, D. R. Reichman and D. A. Weitz, Nature, 2009, 462, 83–86 CrossRef CAS PubMed.
- Z. Yang, Y. Fujii, F. K. Lee, C.-H. Lam and O. K. C. Tsui, Science, 2010, 328, 1676–1679 CrossRef CAS PubMed.
- E. Flenner and G. Szamel, Nat. Commun., 2015, 6, 7392 CrossRef CAS PubMed.
- D. Porter, Group Interaction Modelling of Polymer Properties, Marcel Dekker, New York, 1995 Search PubMed.
- D. M. Crawford and J. A. Escarsega, Thermochim. Acta, 2000, 357–358, 161–168 CrossRef CAS.
- W. Schlesing, M. Buhk and M. Osterhold, Prog. Org. Coat., 2004, 49, 197–208 CrossRef CAS.
- P. G. Royall, C.-Y. Huang, S.-W. J. Tang, J. Duncan, G. Van-de-Velde and M. B. Brown, Int. J. Pharm., 2005, 301, 181–191 CrossRef CAS PubMed.
- W. Doster, Eur. Biophys. J., 2008, 37, 591–602 CrossRef CAS PubMed.
- P. Chen and L. Zhang, Macromol. Biosci., 2005, 5, 237–245 CrossRef CAS PubMed.
- S. Khodadadi, A. Malkovskiy, A. Kisliuk and A. P. Sokolov, Biochim. Biophys. Acta, Proteins Proteomics, 2010, 1804, 15–19 CrossRef CAS PubMed.
- F. G. Omenetto and D. L. Kaplan, Science, 2010, 329, 528–531 CrossRef CAS PubMed.
- C. Craig, Annu. Rev. Entomol., 1997, 42, 231–267 CrossRef CAS PubMed.
- F. J. Chen, D. Porter and F. Vollrath, J. R. Soc., Interface, 2012, 9, 2299–2308 CrossRef CAS PubMed.
- F. Vollrath, D. Porter and C. Holland, Soft Matter, 2011, 7, 9595–9600 RSC.
- Y. Wang, J. Guan, N. Hawkins, D. Porter and Z. Z. Shao, Soft Matter, 2014, 10, 6321–6331 RSC.
- G. V. Guinea, M. Elices, J. I. Real, S. Gutierrez and J. Perez-Rigueiro, J. Exp. Zool., Part A, 2005, 303, 37–44 CrossRef PubMed.
- J. Perez-Rigueiro, M. Elices, G. Plaza, J. I. Real and G. V. Guinea, J. Exp. Biol., 2005, 208, 2633–2639 CrossRef CAS PubMed.
- C. J. Fu, D. Porter and Z. Z. Shao, Macromolecules, 2009, 42, 7877–7880 CrossRef CAS.
- Y. Liu, Z. Z. Shao and F. Vollrath, Nat. Mater., 2005, 4, 901–905 CrossRef CAS PubMed.
- J. Perez-Rigueiro, M. Elices and G. Guinea, Polymer, 2003, 44, 3733–3736 CrossRef CAS.
- M. Wojcieszak, A. Percot, S. Noinville, G. Gouadec, B. Mauchamp and P. Colomban, J. Raman Spectrosc., 2014, 45, 895–902 CrossRef CAS.
- A. Percot, P. Colomban, C. Paris, H. M. Dinh, M. Wojcieszak and B. Mauchamp, Vib. Spectrosc., 2014, 73, 79–89 CrossRef CAS.
- A. Sponner, W. Vater, S. Monajembashi, E. Unger, F. Grosse and K. Weisshart, PLoS One, 2007, e998 CrossRef PubMed.
- S. Keten, Z. Xu, B. Ihle and M. J. Buehler, Nat. Mater., 2010, 9, 359–367 CrossRef CAS PubMed.
- S. Xiao, W. Stacklies, M. Cetinkaya, B. Markert and F. Gräter, Biophys. J., 2009, 96, 3997–4005 CrossRef CAS PubMed.
- G. Q. Xu, L. Gong, Z. Yang and X. Y. Liu, Soft Matter, 2014, 10, 2116–2123 RSC.
- J. E. Trancik, J. T. Czernuszka, F. I. Bell and C. Viney, Polymer, 2006, 47, 5633–5642 CrossRef CAS.
- Z. Yang, D. T. Grubb and L. W. Jelinski, Macromolecules, 1997, 30, 8254–8261 CrossRef CAS.
- T. Seydel, W. Knoll, I. Greving, C. Dicko, M. M. Koza, I. Krasnov and M. Muller, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83 Search PubMed.
- P. Colomban, H. M. Dinh, J. Riand, L. C. Prinsloo and B. Mauchamp, J. Raman Spectrosc., 2008, 39, 1749–1764 CrossRef CAS.
- S. P. Patil, S. Xiao, K. Gkagkas, B. Markert and F. Grater, PLoS One, 2014, 9, e104832 CrossRef PubMed.
- P. Colomban, J. M. H. Ramirez, R. Paquin, A. Marcellan and A. Bunsell, Eng. Fract. Mech., 2006, 73, 2463–2475 CrossRef.
- T. Lefevre, M. E. Rousseau and M. Pezolet, Biophys. J., 2007, 92, 2885–2895 CrossRef CAS PubMed.
- M. Boulet-Audet, T. Lefèvre, T. Buffeteau and M. Pézolet, Appl. Spectrosc., 2008, 62, 956–962 CrossRef CAS PubMed.
- T. Asakura, J. M. Yao, T. Yamane, K. Umemura and A. S. Ultrich, J. Am. Chem. Soc., 2002, 124, 8794–8795 CrossRef CAS PubMed.
- F. Paquet-Mercier, T. Lefevre, M. Auger and M. Pezolet, Soft Matter, 2013, 9, 208–215 RSC.
- T. Asakura, Y. Suzuki, Y. Nakazawa, K. Yazawa, G. P. Holland and J. L. Yarger, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 69, 23–68 CrossRef CAS PubMed.
- J. D. van Beek, S. Hess, F. Vollrath and B. H. Meier, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10266–10271 CrossRef CAS PubMed.
- A. Guinier, Solid State Physics, ed. S. Frederick and T. David, Academic Press, 1959, vol. 9, pp. 293–398 Search PubMed.
- R. Bonart, R. Hosemann and R. L. McCullough, Polymer, 1963, 4, 199–211 CrossRef CAS.
- B. L. Thiel, K. B. Guess and C. Viney, Biopolymers, 1997, 41, 703–719 CrossRef CAS PubMed.
- T. Lefevre, S. Boudreault, C. Cloutier and M. Pezolet, J. Mol. Biol., 2011, 405, 238–253 CrossRef CAS PubMed.
- D. Porter, F. Vollrath and Z. Shao, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 16, 199–206 CrossRef CAS PubMed.
- F. Vollrath and D. Porter, Soft Matter, 2006, 2, 377–385 RSC.
- C. Dicko, D. Porter, J. Bond, J. M. Kenney and F. Vollratht, Biomacromolecules, 2008, 9, 216–221 CrossRef CAS PubMed.
- P. M. Cunniff, S. A. Fossey, M. A. Auerbach, J. W. Song, D. L. Kaplan, W. W. Adams, R. K. Eby, D. Mahoney and D. L. Vezie, Polym. Adv. Technol., 1994, 5, 401–410 CrossRef CAS.
- J. Magoshi, Y. Magoshi and S. Nakamura, J. Appl. Polym. Sci., 1977, 21, 2405–2407 CrossRef CAS.
- J. Guan, D. Porter and F. Vollrath, Biomacromolecules, 2013, 14, 930–937 CrossRef CAS PubMed.
- G. R. Plaza, G. V. Guinea, J. Perez-Rigueiro and M. Elices, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 994–999 CrossRef CAS.
- Q. Q. Yuan, J. R. Yao, L. Huang, X. Chen and Z. Z. Shao, Polymer, 2010, 51, 6278–6283 CrossRef CAS.
- Y. Yang, X. Chen, Z. Z. Shao, P. Zhou, D. Porter, D. P. Knight and F. Vollrath, Adv. Mater., 2005, 17, 84–88 CrossRef CAS.
- M. Born, J. Chem. Phys., 1939, 591–603 CrossRef CAS.
- T. Asakura, K. Okushita and M. P. Williamson, Macromolecules, 2015, 48, 2345–2357 CrossRef CAS.
- C. Fu, D. Porter, X. Chen, F. Vollrath and Z. Shao, Adv. Funct. Mater., 2011, 21, 729–737 CrossRef CAS.
- D. Porter and P. J. Gould, Int. J. Solids Struct., 2009, 46, 1981–1993 CrossRef CAS.
- J. Guan, F. Vollrath and D. Porter, Biomacromolecules, 2011, 12, 4030–4035 CrossRef CAS PubMed.
- Y. Wang, D. Porter and Z. Z. Shao, Biomacromolecules, 2013, 14, 3936–3942 CrossRef CAS PubMed.
- B. Mortimer, J. Guan, C. Holland, D. Porter and F. Vollrath, Acta Biomater., 2015, 11, 247–255 CrossRef CAS PubMed.
- D. Porter and F. Vollrath, Biochim. Biophys. Acta, Proteins Proteomics, 2012, 1824, 785–791 CrossRef CAS PubMed.
- J. Guan, F. Vollrath and D. Porter, Presented in part at the 6th BACSA International Conference: Building Value Chains in Sericulture, Padua, Italy, 2013 Search PubMed.
- B. Madsen, Z. Z. Shao and F. Vollrath, Int. J. Biol. Macromol., 1999, 24, 301–306 CrossRef CAS PubMed.
Footnote |
| † Present address: Tufts University, Medford, US. |
| This journal is © The Royal Society of Chemistry 2016 |