Linking micellar structures to hydrogelation for salt-triggered dipeptide gelators

Abstract

Some functionalised dipeptides can form hydrogels when salts are added to solutions at high pH. We have used surface tension, conductivity, rheology, optical, confocal and scanning electron microscopy, ¹H NMR and UV-Vis spectroscopy measurements to characterise fully the phase behaviour of solutions of one specific gelator, 2NapFF, at 25 °C at pH 10.5. We show that this specific naphthalene–dipeptide undergoes structural transformations as the concentration is increased, initially forming spherical micelles, then worm-like micelles, followed by association of these worm-like micelles. On addition of a calcium salt, gels are generally formed as long as worm-like micelles are initially present in solution, although there are structural re-organisations that occur at lower concentrations, allowing gelation at lower than expected concentration. Using IR and SANS, we show the differences between the structures present in the solution and hydrogel phases.

---

Introduction

There have been recent significant efforts to develop a range of new materials utilising the self-assembly of oligopeptides.^1–3 Using oligopeptides to form hydrogels is a specific target,⁴ with the resulting gels having applications in areas such as cell culturing,⁵ tissue engineering,⁶ drug delivery, as antimicrobial coatings,⁷ as well as non-biological applications.^8–10 The gels are generally prepared by exploiting non-covalent interactions to self-assemble the oligopeptides into one-dimensional structures that then entangle. The resulting materials are often kinetically trapped and hence the mechanical properties of the gels can be heavily influenced by the process used to form the gels.¹¹ Hence, there is a real need to better understand the assembly process to be able to better control the final gel properties.

Functionalised dipeptides can be effective low molecular weight gelators.^12–14 Hydrogels can be formed using concentrations of the dipeptide of around 0.5 wt%. Gels are typically formed in a number of ways, most commonly by a temperature change,¹⁵ adding water to an organic solution of the dipeptide,¹⁶ changing the pH of a solution,^5,17 adding a suitable salt¹⁸ or by an enzymatic reaction on a precursor to the gelator.¹⁹

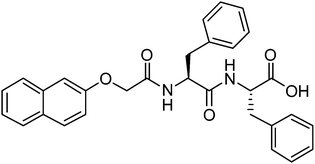
For salt-triggered or pH-triggered gelation, it is typical to initially have the dipeptide as a solution at an alkaline pH, most often above pH 9.^18,20 For most of these gelators, the C-terminus of the dipeptide is unprotected (the structure of an example gelator is shown in Fig. 1). At high pH, the carboxylate is formed, which is sufficient to allow apparent dissolution of the gelator. Although not often discussed, at high pH these dipeptides are therefore surfactants,^21–23 having a significant hydrophobic domain and a charged head group. We showed previously for a range of naphthalene–dipeptides that critical micelle concentrations (cmc's) could be determined.²⁴

Fig. 1 Structure of 2NapFF. At high pH, the carboxylic acid will be deprotonated.

We have also shown that a number of functionalised dipeptides form free-flowing solutions with low viscosity at high pH at concentrations of 0.5 wt%, whilst others form viscous solutions under these conditions.^18,25 We assigned these behaviours to the formation of spherical aggregates and worm-like micelles respectively.^18,25 Solutions of the dipeptides that formed worm-like micelles (for example 2NapFF, Fig. 1) most often resulted in the formation of gels when a calcium salt was added.^18,25 We have also found that it is possible to magnetically align these worm-like micelles, which can then be gelled.²⁶ 2NapFF also forms gels at low pH, below the pK_a of the carboxylic acid. However, we do not discuss this further here.²⁴

In many ways, these observations are similar to those for another class of low molecular weight gelator, peptide-amphiphiles (PAs).²⁷ PAs are oligopeptides conjugated to an alkyl tail. There is a significant body of work on these gelators, but again it has been shown that worm-like micelles are formed,²⁸ which then cross-link when calcium salts are added.²⁹

A key question for this type of system is therefore: do the micellar aggregates that are formed at high pH pre-determine the properties of the gels? In our initial work on calcium triggered gels, we hypothesised that the addition of calcium simply ‘locks-in’ the worm-like micellar structure.¹⁸ However, we later showed using NMR measurements that the mesh size in a solution of the worm-like micelles at 1.0 wt% was smaller than that at 0.5 wt%.³⁰ This is expected assuming that there are simply more of the micellar structures at the higher concentration. However, on adding a solution of calcium chloride, the mesh size at 1.0 wt% was greater than that of the corresponding gel at 0.5 wt%. This implies that the addition of the calcium salt does not simply ‘lock-in’ the structure. Hence, here we fully investigate the micellar aggregates that are formed over a range of concentrations as well and the resulting structures that form on addition of calcium salts.

Results and discussion

Characterisation of the micellar structures

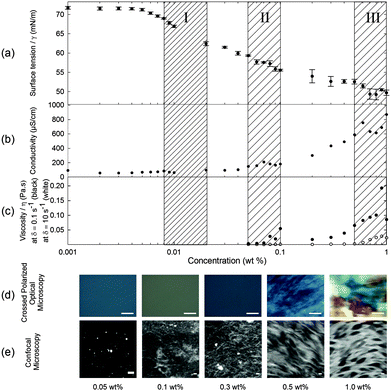
When 2NapFF is dissolved in water at high pH, transparent or translucent solutions are formed at concentrations up to 1.0 wt% (the maximum investigated here; higher concentrations are difficult to prepare due the high hydrophobicity of 2NapFF). We used surface tension, conductivity, rheology, optical, confocal and scanning electron microscopy, ¹H NMR and UV-Vis spectroscopy measurements to characterise fully the phase behaviour of the 2NapFF solutions at 25 °C at pH 10.5 ± 0.5 (Fig. 1 and Fig. S1, ESI†). These techniques can be used to identify the cmc of surfactant solutions. At concentrations above the cmc, it is expected that amphiphilic molecules in a polar solvent such as water pass through a series of micellar transitions, from spherical micelles to worm-like micelles and further to vesicles.

An ideal surfactant solution has a concentration-dependent surface tension in which a clear plateau is observed once the air/water interface is saturated with molecules. Any further added surfactant should not change the surface tension because micellar structures are formed in solution. However, for 2NapFF, there is no clear transition to a defined plateau region, which would allow us to identify unambiguously the cmc (Fig. 2a). However, we obtained an air–water partitioning coefficient (K_aw) of 0.005 ± 0.0005 wt% for 2NapFF through a Gibbs adsorption model.³¹ This coefficient measures the molecular affinity of the air/water interface and it is proportional to the ratio between the number of molecules found in the bulk and the interface.

Fig. 2 2NapFF solution characterisation of micellar states at pH 10.5 ± 0.5 by (a) surface tensiometry; (b) conductivity; (c) viscosity at shear rate of 0.1 s⁻¹ (closed symbols) and 10 s⁻¹ (open symbols); (d) cross-polarised optical microscopy (scale bar: 500 μm) and (e) confocal microscopy measurements, collected in the presence of Nile blue as a stain (scale bar: 20 μm). The concentration is plotted in a logarithmic scale. Each hatched region represents one of three different micellar transitions of the peptide solutions at high pH identified by the changes in the measured properties (see text). The error bars represent the standard deviation of three measurements.

In contrast to surface tensiometry data, conductivity measurements probe the bulk. Changes in conductivity can be used to evaluate the cmc of surfactants. In Fig. 2b, the conductivity of 2NapFF solutions is shown as a function of concentration. A detailed analysis of this measurement shows a significant reduction in the rate of increase in conductivity in the concentration range from 0.008 to 0.04 wt% (Fig. 3a), suggesting that there is a cmc transition in this concentration range. These data are typical for the conductivity measurements of a surfactant's cmc. As the micellar structures become the dominant species in solution, they decrease the exchange rate of OH⁻ with the electrode surfaces and slow down the diffusion of OH⁻, thus decreasing the rate of increase in conductivity. These results agree with the surface tensiometry data, which suggest that the micellar structures start to form above 0.005 wt% (from K_aw).

Fig. 3 Detailed analysis of the conductivity data as a function of concentration for 2NapFF at a pH 10.6 ± 0.2 and a temperature of 22.4 ± 0.7 °C. (a) Analysis of the first change in the rate of increase in conductivity, with linear regression fits to the regions between 0.002 and 0.007 wt% (solid line), 0.008 to 0.04 wt% (short dashed line) and 0.008 and 0.04 wt%, excluding 0.009 and 0.01 wt% (long dashed line). The first (solid line) and last (long dashed line) interval were used for cmc approximation. (b) Analysis of the second change in the rate of increase in conductivity with linear regression fits to the regions 0.04 to 0.07 wt% (solid line) and 0.07 to 0.09 wt% (dashed line). All blue curves are delimiting the 95% confidence intervals used for evaluating both cmc's. The error bars represent the standard deviation of three measurements.

Typical surfactants, such as sodium dodecyl sulphate (SDS), go through micellar transitions with increasing concentration.^32,33 A first transition occurs from free surfactants in solution to micellar structures, at the cmc, typically forming spherical micelles. In some surfactants this is followed by a second transition from spherical micelles to worm-like micelles, cmc₂. The concentrations at which these transitions occur are highly dependent on the chemical structure of the surfactant with a lowering of the cmc with increasing tail length in traditional surfactants, i.e. those based on a hydrophobic alkyl tail and hydrophilic head group.³⁴ Further transitions can occur at higher concentrations to form other liquid crystalline phases such as the lamellar, cubic and hexagonal phases.³³ Our conductivity data suggest that for 2NapFF, there is a first cmc (cmc₁) in the region from 0.008 to 0.02 wt% (region I shown in Fig. 2). From 0.05 to 0.1 wt%, there is a significant increase in the conductivity with a peak in the data at 0.07 wt% (Fig. 3b), suggesting a second transition within this concentration range (region II, shown in Fig. 2). We assign the second transition to a second cmc (cmc₂). Linear fits to the conductivity data (Fig. 3) result in an accurate quantification of the critical micellar concentrations.

These transitions in conductivity are consistent with a first aggregation into spherical micelles, followed by the formation of elongated worm-like micelles. The second transition was further investigated using rheological measurements. These measurements show that there is a gradual change in viscosity of the solution (Fig. 2c). We attribute the increase in viscosity between 0.08 to 0.1 wt% for low shear rates (see Fig. 2c, closed symbols) to the initial formation of worm-like micelles. For higher shear rates (10 s⁻¹), the viscosity increases significantly only above 0.5 wt% (Fig. 2c, open symbols). This can be attributed to the structures elongating to a persistence length capable of jamming the solution for concentrations above 0.5 wt%. In particular, these data suggest that there is a mechanical response (possibly shear alignment³⁵), caused by the worm-like micellar entanglements, causing a gradual increase in viscosity from 0.1 wt% and 0.5 wt% for low and high shear rates, respectively. These rheological features concur with the conductivity increase up to 0.5 wt% and plateau reached in the concentration range from 0.5 to 1.0 wt% (region III, Fig. 2c).

Through the analysis of the viscosity data in the dominant worm-like phase region (Fig. S2, ESI†), relaxation times of the micellar network can be extrapolated (Fig. S3, ESI†). The relaxation time increases with concentration above 0.5 wt%, with a significant increase to over 3 seconds between 0.8 and 1.0 wt%. This suggests a rapid decrease in mesh size in this region leading to more entanglement points. Frequency and strain sweeps were carried out at different concentrations to completely characterise the mechanical properties of each phase (Fig. S4–S9, ESI†). Analysis of the plateau values of storage (G′), loss (G′′) and complex (G*) modulus from the frequency and strain-sweep measurements, fully agree with two transitions suggested from the conductivity data, shown in Fig. 3.

Samples observed under cross-polarized light are birefringent for concentrations from 0.5 to 1.0 wt% (Fig. 2d). This agrees with the formation of a hierarchical structure, possibly bundles of worm-like micelles, at these higher concentrations. These birefringent domains have a size in the order of 100 μm to over 1 mm and increase in size with concentration. We were also able to identify a network of worm-like structures using confocal microscopy with a Nile blue staining technique for concentrations above 0.1 wt% (Fig. 2e). There is an apparent increase in the microstructural packing of the network of worm-like micellar structures at 1.0 wt% as compared to lower concentrations. This is visible by the high contrast in the raw images obtained for 1.0 wt% as compared with 0.3 and 0.5 wt%. Bundling has also been observed in longer peptide amphiphile systems,^36,37 often driven by hydrophobic interactions of particular residues such as leucine.³⁸ Since the phenomenon of bundling is part of the microstructure formation, in turn it contributes to the mechanical properties of the solution and hydrogel networks.^11,39 However at lower concentrations, in the 0.05 and 0.1 wt% samples, it is possible to observe what appear to be spherical aggregates (the bright spots in Fig. 2e at 0.05 wt%), but the resolution of the images is not sufficient to clarify the nature of these structures. We hypothesise that these are Nile blue aggregates, which have no suitable hydrophobic regions to associate with at these concentrations of 2NapFF.

¹H NMR spectroscopy was also used to further identify the micellar phases. Despite the detection limits of the technique, it is still possible to determine the phases at higher concentrations because of the sensitivity to the molecular environment. Under optimised measurement conditions, we can identify the change in the chemical shift of the protons of 2NapFF as a function of concentration (Fig. S1a, ESI†) and quantify the amount detectable by solution state NMR spectroscopy (Fig. S1b, ESI†). The chemical shifts of the naphthalene protons start to move upfield at 0.1 wt%, implying that aggregation is occurring. Above 0.5 wt% the chemical shift becomes constant. These data indicate a phase change at each of these concentrations, in agreement with our other data.

Putting all of the data together from these techniques, we can see that there are distinct solution phases and transition regions. First, the 2NapFF molecules start to associate at the liquid–air interface at a concentration of 0.005 wt% ± 0.0005 wt% (0.101 ± 0.010 mM). Secondly, transient spherical micellar structures form and become the dominant phase after the first cmc at 0.011 ± 0.004 wt% (0.222 ± 0.075 mM). This value is amongst the lowest reported in the surfactant literature.⁴⁰ The first transition (cmc₁) is difficult to pinpoint exactly because of limited sensitivity of the available techniques at these concentrations. As the concentration is increased, the spherical micellar structures aggregate to form elongated worm-like micellar structures. This transition can be associated with a second cmc (cmc₂) at 0.069 ± 0.015 wt% (1.39 ± 0.302 mM). These two cmc values were estimated based on a detailed analysis of conductivity measurements above (Fig. 3a and b). At approximately 0.08 wt%, the viscoelastic nature of the solution phase observed in the frequency- and strain-sweep rheological data suggests the initial formation of elongated worm-like micellar structures (after the second cmc), possibly coexisting with the previous micellar phase. At 0.5 wt% (10.1 mM), the worm-like micellar structures become dominant in the solution and entangle as the concentration is increased further. These entanglements form micellar networks with increasing relaxation time (Fig. S3, ESI†). This is consistent with the conductivity data above and the assignment of a critical aggregation concentration (cac) at 0.5 wt%. As the concentration increases further, not only are there more worm-like micellar structures, but also they form more compact assemblies. Hence, the data are consistent with three transitions: (1) free molecule to spherical micellar phase (cmc₁), (2) spherical micellar phase to worm-like micellar phase (cmc₂); and (3) worm-like micellar phase to a compact micellar phase (cac).

Correlations between 2NapFF solutions and the corresponding hydrogels

Having assigned the phase diagram for 2NapFF up to a concentration of 1.0 wt%, we next attempt to correlate the micellar phases with the behaviour of the solutions when calcium salts are added. We have previously shown that hydrogels are formed at 2NapFF concentrations of 0.5 wt% when divalent cations such as Ca²⁺ are added.^18,25 For all of the following data, the ratio of Ca²⁺ to 2NapFF was kept constant for all solutions (the ratio was chosen on the basis of our previous work¹⁸). Interestingly, the inversion vial test shows that self-supporting hydrogels are formed between 0.03 and 1.0 wt% (Fig. 4a). Between 0.001 and 0.01 wt%, the solutions do not pass the inversion vial test after the addition of a calcium salt. At 0.02 wt%, the sample has typical behaviour for a weak low molecular weight hydrogel when probed by rheology with G′ (16 Pa) an order of magnitude above G′′ (1.6 Pa) and the sample partially passes the inversion vial test (Fig. 4a). We therefore assign a concentration of 0.02 wt% as the 2NapFF minimum gelation concentration (mgc). This value is just above the corresponding solution phase cmc₁ (0.011 ± 0.0037 wt%).

Fig. 4 Inversion vial test and mechanical correlation for 2NapFF solutions and hydrogels formed on addition of calcium nitrate. (a) Inversion vial test for 2NapFF solutions on addition of calcium nitrate at a molar ratio of 2 : 1 calcium to 2NapFF; the samples are 2NapFF concentrations of, from left to right, 0.001, 0.002, 0.003, 0.004, 0.005, 0.006, 0.007, 0.008, 0.009, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0 wt%. In the top row, the samples are standing in the upright position and in the bottom row, the samples are inverted. (b) Correlation between the complex modulus (G*) of 2NapFF solutions and the concentration of the corresponding hydrogels, all obtained from frequency sweeps in the strain-independent region. The region from 0.1 to 1.0 wt% is fitted to an exponential function of the concentration. An exponent of 2.2 was found in this interval. (c) Correlation between G*s of the solution and the hydrogel phase. Axes are all plotted in logarithmic scale.

Hence, in general gels are formed where a worm-like micelle phase is present. However, gels are also formed at concentrations just below cmc₂, i.e. where we first detect worm-like micelle formation in the solution phase. This implies that there are structural transformations when the calcium salt is added and the gelation is not simply a result of ‘locking in’ the micellar structures as we first suggested.¹⁸ Sphere-to-worm micellar transitions have been observed previously, for example in aqueous solutions of cetyltrimethylammonium bromide (CTAB).⁴¹

The complex modulus (G*) is an indicator of mechanical strength. In Fig. 4c, the G* of the solution phase is plotted against G* of the corresponding hydrogel phase (frequency sweeps, strain sweeps and recovery tests for the hydrogel phase are shown in Fig. S10–S18, ESI†). The samples can be grouped into three regions (Fig. 4b and c). In the first region, the micellar solutions have a G* below 17 mPa. No hydrogel is formed on addition of calcium nitrate in this concentration range. In the second region, the solution phase has a G* between 15 to 20 mPa. These solutions form weak hydrogels on addition of calcium nitrate. Finally, there is a third concentration region where the solutions have a G* between 20 to 400 mPa and which form strong hydrogels, with a G* of between 13–40 kPa (Fig. 4c). Taken together, these results show a range of four orders of magnitude difference in the values of G* between the formation of weak and strong hydrogels. Furthermore, the results show that above the cmc₁ it is possible to form hydrogels. However, only above the cmc₂ and well into the worm-like micellar region do the strongest hydrogels form. Therefore, the solution phase is structurally connected with the hydrogel phase.

Ideally, we would probe the differences between the solution phase between cmc₁ and cmc₂ to understand if any structural reorganisation is occurring on addition of the calcium salt. Unfortunately, the low concentrations here preclude many techniques that are usually used to probe the molecular assembly of such dipeptides. For example, FTIR was collected in D₂O (Fig. 5, see also Fig. S19 and S20 (ESI†) for the complete data set of the solution and hydrogel phase, respectively). The data for the solution below 0.1 wt% (Fig. 5a) did not show the presence of ordered molecular packing. Between 0.1 and 1.0 wt%, peaks at 1629 cm⁻¹ and 1664 cm⁻¹ were observed (Fig. 5a and Fig. S19, ESI†). In the case of the corresponding hydrogels, peaks at 1629 cm⁻¹ and 1664 cm⁻¹ are also present across the concentration range from 0.01 to 1.0 wt% (Fig. 5b and Fig. S20, ESI†). Overall, therefore, the hydrogel phase appears to have the molecular structure preserved with the transition from solution phase to hydrogel phase for concentrations above 0.3 wt% (Fig. S19 and S20, ESI†). However for concentrations below 0.3 wt%, a distinct peak is visible at 1643 cm⁻¹ in the hydrogel, which is not present in the solution. These IR data imply that there is possibly a molecular packing and structural transformation, at least between 0.1 wt% and 0.3 wt% when the solution phase is triggered to form a hydrogel. From data for polypeptides, these peaks would be assigned to β-sheets (1629 cm⁻¹) and random coil structures (1643 cm⁻¹),⁴² although we highlight that it is not clear if such direct assignment is possible for dipeptides.^43–45 In addition, peaks at 1548 cm⁻¹ and 1585 cm⁻¹ in the solution state, and at 1585 cm⁻¹ and 1602 cm⁻¹ in the hydrogel state can be associated with different naphthalene and phenylalanine packing.^42,46,47 To further compare the solution and gel phases, we investigated the hydrogels by microscopy. Optical microscopy did not result in any visible structures, either under bright field or cross-polarised light (data not shown). Confocal microscopy (again staining with Nile blue) showed that the hydrogels are formed of hierarchical nanofibre structures (Fig. S21, ESI†). These results suggest that the worm-like micellar structures previously observed in the solution phase now become hierarchically packed into large bundles of highly entangled nanofibres with high persistence length (over millimetre range). Again, there was a lower limit of resolution here, with no meaningful data collected below 0.05 wt% (Fig. S21, ESI†).

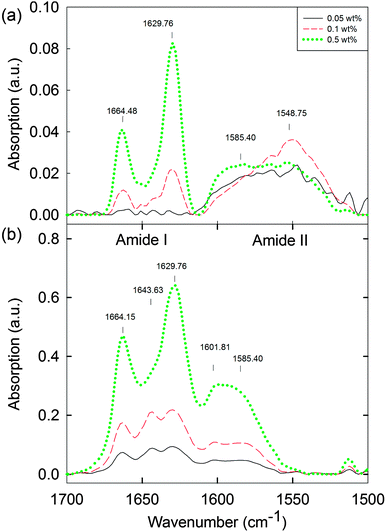Fig. 5 FTIR spectra of (a) 2NapFF solutions at high pD 11.5 ± 0.5 (0.05 to 0.5 wt%) and (b) the corresponding hydrogels (0.05 to 0.5 wt%) at the lower limits of detection. For the complete data set for the solution and gel phase, see Fig. S19 and S20 (ESI†).

Further attempts at imaging the structures formed in solution and on addition of calcium were generally fraught with difficulties due to drying artifacts and issues with concentration on drying, meaning that it was difficult to be certain whether the samples were probed at the required concentration. Attempts were made with AFM, TEM, and SEM. As an example, we imaged the samples using SEM after addition of calcium nitrate. We obtained results that initially appear to agree with our suggested sphere-to-worm transition for the samples of 2NapFF Ca-hydrogels when no coating was used and at low keV. At 0.06 wt% and above, only fibrous, worm-like structures were imaged (see Fig. S22 and S23, ESI†). Between 0.01 wt% and 0.05 wt%, spherical structures apparently co-exist with fibrous structures (example data for 0.03 wt% is shown in Fig. S24b, ESI†). However, a blank of a salt solution prepared under the same conditions (Fig. S24f, ESI†) shows similar spherical structures and hence we assume that the spheres imaged in the 0.03 wt% gel, and most likely at other low concentrations (Fig. S24, ESI†), are also from drying artifacts from the salt. As a result, we highlight the difficulties in imaging samples at such low concentration.

The primary self-assembled structures within both the worm-like micellar solution and the gel phase were probed further in situ using small angle neutron scattering (SANS). SANS can probe structures formed over a wide range of sizes from just a few to hundreds of nanometres.^48–51 The wide Q range accessed here provides information on the primary fibril dimensions and aspects of the network structure. As discussed above, as with many analytical techniques, the results from the lowest concentrations of this study are limited by the sensitivity of the technique and the measurement time required to collect data of sufficient quality, which is particularly important as access to SANS beam time is a limited resource. Therefore, only data from solutions of 0.2 to 0.5 wt% are discussed alongside data from the hydrogel at a single concentration of 0.5 wt% (Fig. 6). The data for increasing concentrations of 2NapFF solutions, from 0.3 to 0.5% are shown in Fig. S25 (ESI†). All these solutions exhibit features characteristic of scattering from worm-like micelles. The same features are not observed in the plot representing a 0.2% solution, where only weak scattering is observed, indicating a different assembly.

Fig. 6 SANS profiles for a 0.5 wt% 2NapFF solution at pD 10.5 ± 0.5 and the corresponding Ca²⁺ triggered hydrogel with the D₂O background subtracted. The model fits to the data use the hollow cylinder approach for the solution phase and a solid flexible cylinder in the gel phase. The main feature arising from the cylindrical cross-section at ∼0.13 Å⁻¹ occurs at the same position in both data sets, although it is less well defined in the gel phase.

The data have been fitted using two models, a hollow cylinder for the solution phase and a solid flexible cylinder for the gel phase.^52,53 Here, each of those cylindrical models has been combined with a power law component in order to fit the low Q region, which is influenced by the fractal scattering from the network structure. Further description of the model and details of the parameters are provided in the ESI† (Fig. S26–S28 and Table S1). The contribution from the cylindrical term in the model fits increases between 0.4 and 0.5 wt% as expected. The hollow cylinder for the 0.5 wt% data in the solution phase has dimensions of an overall radius of 3.7 ± 0.3 nm and a hollow core radius of 1.6 ± 0.3 nm. In the gel phase, the overall radius of the cylinder is the same, at 3.7 ± 0.3 nm, but the most appropriate model to fit the data is that of the flexible cylinder, demonstrated in Fig. S27 (ESI†). Thus, with the fits relatively insensitive to the scattering length density parameter, it appears there would be such a small water core in the hollow cylinder model (≤1 Å) that the structures are seen by the SANS as having a solid cross-section. Upon gelation, the power law exponent has reduced. This can be interpreted as fewer or more evenly distributed entanglement points, which define the size of the mass fractal regions. These results indicate that, while the diameter of the primary fibrils remains the same upon gelation, that there is a change in the hydration and location of the water within those structures. We interpret this as the fibres becoming more bundled, less entangled and hence larger pores are formed, in agreement with our previous NMR data.³⁰

Conclusions

At high pH, 2NapFF self-assembles into micelles, with spherical micelles being formed at low concentrations, followed by worm-like micelles. As the concentration is further increased, these worm-like micelles aggregate. The 2NapFF described here can be used as an effective surfactant, and hence knowing the concentration dependence of the self-assembled structures is key in itself. On addition of a calcium salt, gels are formed. In general, worm-like micelles need to be present for this calcium-induced gelation. However, above the first cmc, there are structural transformations that occur on addition of the calcium salt, which allows gels to form in this intermediate regime. Unfortunately, the concentration at which this occurs is very low, meaning that it is very difficult to probe this transformation. IR data implies that there are changes in the packing of the 2NapFF, at least between 0.1 wt% and 0.3 wt% when the solution phase is triggered to form a hydrogel. SANS data shows that there are structural changes at the higher concentrations, with the worm-like micelles having an aqueous core, whilst after addition of calcium there are changes in the hydration meaning that the data fits better to a solid cylinder. The addition of the calcium salt also results in a decrease in the entanglement of the structures.

These data show that the salt-triggered gelation of these dipeptides relies on the initial solution having specific structures present. Presumably this is the case of related peptide-amphiphiles. The subtle changes in structure at some concentrations may be the result of differences in hydration leading to changes in the equivalent of the packing parameter. The 2NapFF also forms gels when the pH is lowered;²⁴ whether the structure at high pH is key again or whether there are further structural changes is still an open question.

Experimental

Materials and Methods

Pre-gelator solution preparation. 2NapFF was synthesised as described previously.^18,24 All other chemicals were purchased from Sigma-Aldrich and used as received. Solutions of a specified concentration of 2NapFF were prepared by dilution in doubly distilled H₂O and adding 2.2 μL of 1 M NaOH per mg of 2NapFF. The 1 M NaOH was freshly prepared and filtered through a 0.2 μm syringe (Minisart RL 15, Sartorius Stedim) before use. The stock solution pH was adjusted with this NaOH solution and measured with a FC200 pH probe (HANNA Instruments) with a (6 mm × 6 mm) conical tip. The stated accuracy of the pH measurements is ±0.1. The basic solution was then stirred for 24 hours to yield a clear, slightly viscous solution with a pH 10.5.

Dilution of the stock solution was used to prepare solutions at lower concentrations. All diluted samples were adjusted to pH 10.5 using 1 M or 0.1 M of NaOH solution. For low concentrations of this gelator (below 0.1 wt%), we observed that there are some micellar structural differences depending on the preparation method: either diluting from a more concentrated sample or preparing the sample at that concentration. Thus, for surface tension measurements, rheological, FTIR and conductivity measurements each sample was freshly prepared at that concentration.

Salt-triggered calcium nitrate hydrogels. These gels were prepared with the previously described pre-gelation solution preparation method incubated at 22 °C for 24 hours. Subsequently, aliquots of a Ca(NO₃)₂ solution (either 20 mg mL⁻¹ or 200 mg mL⁻¹) were added to these solutions such that the final ratio of calcium ions to peptide was 2 : 1 to trigger the gelation by depositing the drop on top of the solution. The samples were left to stand for a 24 hours incubation period at 22 °C.

Surface tension. The surface tension measurements were performed on a high throughput Kibron Delta-8 Surface Tensiometer which uses a Du Nouy-Padday method (maximum pull on a rod). The results were analysed by the Delta-8 Manager software. The pre-gelation samples were prepared as described above, however the dilutions were performed using an Eppendorf epMotion 5072 for a preliminary scan and subsequently the data shown here were obtained with solutions prepared directly at the required concentrations as highlighted above. For the robotic system, 200 μL of the concentrated 2NapFF solution was transferred onto the first column of a standard Nunclon 96-well plate. A series of concentrations were prepared by sequential dilution of 2NapFF using pH 10.5 water across the plate, with the concentration being decreased by a dilution factor for each column using a transfer-and-mix protocol. Finally, 50 μL samples of each concentration were transferred to the detection plate for measurement. All measurements were conducted at 18 °C. The averaged result and standard deviation were calculated from 4 separate samples.

¹H NMR spectroscopy. ¹H NMR spectroscopy was used to characterize the solution micellar transitions. A 500 MHz Bruker Avance-III HD equipped with an 11.74 T magnet and a liquid nitrogen cooling system was used for all experiments. A common ¹H NMR experiment with 30 degrees flip angle was used to obtain the spectra. The total number of scans was 16 and the acquisition time per scan was 3 minutes for each measurement at 25 °C, except when mentioned. Aliquots of 0.5 mL of each solution were transferred to a NMR tube (NE-ML5-8, NEW ERA Enterprises).

The ¹H NMR spectroscopy integrals were calibrated against a known amount of ethanol sealed in a capillary in D₂O (approximately 6 μL ethanol in 1 mL D₂O solution) and sealed with PTFE tape. The capillary was calibrated with 8 mg mL⁻¹L-alanine solution in H₂O. Before each measurement, the reference capillary was inserted with a PTFE holder into the NMR tube with the 2NapFF solution. Additionally, a common solvent suppression experiment using pre-saturation and spoil gradient under the same conditions was conducted and used for the quantification analysis.

If the conditions are quantitative with a good signal-to-noise ratio (over 1000), it is possible to use the chemical shift and the integration of a proton resonance frequency to estimate both the molecular environment (i.e. hydrophobicity near the protons investigated) and the degree of mobility (all at relaxation delay of 1 s). The molecular environment of 2NapFF was estimated by the chemical shift of the proton on the 7-position of the naphthalene ring. The degree of mobility was evaluated by the relative intensity of the CH₂ protons of the phenylalanine groups to estimate the average amount of detectable gelator indirectly by the corresponding number of mobile protons in the sample with the same frequency. Triba et al. have showed that micellar transitions in lipids can be detected by analysis of the chemical shifts and relative integrations between two components.⁵⁴ Thus, if the 2NapFF is in dynamic equilibrium, there is a probability of each molecule either being free-flowing in solution and a complementary probability of it being self-assembled as part of a possible micellar structure. The on–off ratio can be defined as the number of free molecules divided by the number of self-assembled molecules. If this ratio is low, we expect that the molecules are forming micellar structures. However the quantification is independent from the relaxation delay used for the measurement for these low concentrations studied here (relaxation delay of 1 s). The molecules will be visible if they exchange with the solvent in the timescale of the experiment. Thus, in this case, we expect to see less of the detectable amount of surfactant only if the molecules are forming structures and they exchange with the solvent at a slower rate than the relaxation delay. Therefore quantification should be treated with caution when being used to confirm the presence of structural features in solution. The LMWG being a surfactant in the solution phase could be just partially visible, however the dominant phase could still be the one of spherical or worm-like micellar structures if the exchange with the solvent is quicker than the measurement timescale.

Rheology. Dynamic rheological experiments were performed using an Anton Paar Physica MCR301 rheometer. The rheometer was calibrated for inertia and motor every 5 days or immediately before each measurement for the solution phase measurements in order to obtain accurate measurements in the low viscosity and low torque region. These calibrations resulted in improved instrument resolution at low torque. All measurements were conducted at 25 °C. For the hydrogels, strain and frequency-sweep measurements were conducted in a vane-cup measurement system (Anton Paar ST10-4V-8.8/97.5) and samples were prepared in a plastic Sterlin cup (7 mL volume) and incubated at ≈22 °C for 24 hours before each measurement. For the solution phase, a cone–plate system (Anton Paar CP50-1) was used to improve sensitivity of the viscoelastic solutions and samples were poured onto the stage to minimize mechanical artifacts, samples were stabilized in the cone–plate system for 30 minutes before each measurement. The frequency-sweep measurements were measured at a constant strain of 0.1% for the solution phase (to capture the network features) and 0.5% for the hydrogels. These choices of parameters were based on the attempt to be on the viscoelastic region for both systems, whilst still being able to conduct the measurement in a sensible time and investigate the material properties of the bulk and not just the surface.⁵⁵ No time restrictions were made on the time needed to reach each measurement point (instrumental average over 40 recordings). To ensure the frequency measurements were carried out in the linear viscoelastic regime, strain-sweep measurements were performed for the hydrogels and the solution phase at a static frequency of 10 rad s⁻¹. The results showed no significant variation in the storage modulus (G′) and the loss modulus (G′′) measured by frequency-sweeps between a strain of 0.1 and 0.5%. For each sample, G′, G′′, the complex modulus (G*) or viscosity (η) were measured as appropriate.

Recovery measurements were conducted using a triple oscillation program of 0.5% strain for 100 seconds, 100% strain for 100 seconds and then recovery at 0.5% strain recorded until a plateau was reached (which took from 2 hours up to 2.5 days). All measurements were conducted at a frequency of 0.5 rad s⁻¹.

Conductance. Samples were prepared as described above. The instrument was calibrated with double distilled water at 25.0 ± 0.1 °C and conductance of KCl solutions were used to confirm the accuracy of the instrument (±2%) with literature values. The measurements were performed using a PCE – PHD 1 conductance probe with temperature compensation (PCE Instruments). The probe was rinsed 5 times with ddH₂O before each measurement.

UV-Vis spectroscopy. Samples were prepared as described above and poured in to a quartz cuvette. Each measurement was performed using a NanoDrop 2000c UV-Vis Spectrophotometer (Thermo Scientific).

Optical microscopy. Optical microscopy was carried out using a Nikon Eclipse Microscope and image analysis was done with ImageJ.³ Samples were prepared as described. They were poured onto a microscope slide and examined in the bright field and under cross-polarizers.

Laser scanning confocal microscopy. Confocal microscopy images were obtained on a Zeiss LSM510 and a Plan-Apo 100× (1.4 NA oil) objective. Nile blue fluorescence was excited with a 633 nm Helium Neon laser and emission detected between 638 and 758 nm using a pinhole diameter of 1 Airy unit (approx. 0.8 μm resolution). The hydrogel membrane was prepared as described previously, including a 0.001 M Nile blue in the initial solution (pipetting a selected amount from a 0.01 M stock solution). Typical pictures selected from over the 50 captured were chosen and measured for this study. The images were analysed using the Zeiss AIM software (Zeiss, Jena, Germany) and ImageJ software.³

Fourier transform infrared spectroscopy (FTIR). A Bruker Tensor 27 spectrometer at a resolution of 2 cm⁻¹, averaging over 64 scans from 4000 cm⁻¹ to 800 cm⁻¹ was used to make these experiments. The hydrogels were prepared with D₂O, NaOD and DCl for these experiments.

Scanning electron microscopy (SEM). SEM images were obtained using a Hitachi S-4800 FE-SEM at 0.5 to 1 keV. 5 × 5 mm diced silicon wafers were used to probe the gels. The gels were prepared as described above in volumes of 2 mL. A Si-wafer was dipped for 30 minutes in the solution/gel sample and subsequently allowed to dry for a further 30 minutes under a nitrogen flow (approximately 0.5 atm above atmospheric pressure). No coatings were applied to the gels. To avoid charging, a low voltage SEM was used (0.5 to 1 keV) at a 1.5 to 3 mm distance from the sample with the deceleration mode (i.e. deceleration V = 2 keV, from 3 to 1 keV).

Small angle neutron scattering. Solutions were prepared as described for other techniques, with the H₂O and NaOH replaced with D₂O and NaOD. Gels were prepared as above using Ca(NO₃)₂. UV spectrophotometer grade, quartz cuvettes (Hellma) with a 2 mm path length were filled with the solution and housed in a temperature controlled sample rack during the measurements. Small angle neutron scattering (SANS) measurements were performed using the D11 instrument (Institut Laue Langevin, Grenoble, France). A neutron beam, with a fixed wavelength of 10 Å and divergence of Δλ/λ = 9%, allowed measurements over a large range in Q[Q = 4π sin(θ/2)/λ] range of 0.001 to 0.3 Å⁻¹, by using three sample-detector distances. The high flux available from the reactor source enabled measuring times of 30 minutes or less for each instrument setting.

The data were reduced to 1D scattering curves of intensity vs. Q using the facility provided software. This involves the following key steps: the electronic background is subtracted; the full detector images for all data are normalised; scattering from the empty cell is subtracted and finally the data are radially averaged to produce the 1D curves for each detector position. The absolute scaling of the middle detector position data, taken under optimum conditions, is then used as the reference point for the other two data sets as they are scaled to form a single curve. The scattering from D₂O (the solvent) was also measured and subtracted from the data as discussed alongside the results.

The instrument-independent data were then fitted to customised models in the SasView software package,⁵⁶ these combined an absolute power law with either a hollow cylinder⁵⁷ or a (Kratky-Porod) flexible cylinder.^58,59 The Q-dependent power law (Q^−N) accounts for the mass fractal contribution to the scattering intensity, which is superimposed on that from the cylindrical structures i.e. the micelles or fibrils. While the worm-like micelles are represented by hollow cylindrical rods, the fibrils of the gel are represented as a solid flexible worm-like chain of cylindrical Kuhn segments within the flexible cylinder version of the model.

Acknowledgements

AZC thanks the University of Liverpool for funding. DA thanks the EPSRC for a Fellowship (EP/L021978/1). The experiment at the Institut Laue Langevin was allocated beam time under experiment number 9-10-1304. This work benefitted from the SasView software, originally developed by the DANSE project under NSF award DMR-0520547.

Notes and references

1. R. V. Ulijn and A. M. Smith, Chem. Soc. Rev., 2008, 37, 664–675.
2. C.-Y. Yu, W. Huang, Z.-P. Li, X.-Y. Lei, D.-X. He and L. Sun, Curr. Top. Med. Chem., 2016, 16, 281–290.
3. D. M. Leite, E. Barbu, G. J. Pilkington and A. Lalatsa, Curr. Top. Med. Chem., 2015, 15, 2277–2289.
4. X. Du, J. Zhou, J. Shi and B. Xu, Chem. Rev., 2015, 115, 13165–13307.
5. V. Jayawarna, M. Ali, T. A. Jowitt, A. F. Miller, A. Saiani, J. E. Gough and R. V. Ulijn, Adv. Mater., 2006, 18, 611–614.
6. J. B. Matson and S. I. Stupp, Chem. Commun., 2012, 48, 26–33.
7. G. Laverty, A. P. McCloskey, B. F. Gilmore, D. S. Jones, J. Zhou and B. Xu, Biomacromolecules, 2014, 15, 3429–3439.
8. D. Buenger, F. Topuz and J. Groll, Prog. Polym. Sci., 2012, 37, 1678–1719.
9. F. Rodriguez-Llansola, J. F. Miravet and B. Escuder, Chem. Commun., 2009, 7303–7305.
10. J. Ryu, S.-W. Kim, K. Kang and C. B. Park, Adv. Mater., 2010, 22, 5537–5541.
11. J. Raeburn, A. Zamith Cardoso and D. J. Adams, Chem. Soc. Rev., 2013, 42, 5143–5156.
12. S. Fleming and R. V. Ulijn, Chem. Soc. Rev., 2014, 43, 8150–8177.
13. D. J. Adams, Macromol. Biosci., 2011, 11, 160–173.
14. A. Dasgupta, J. H. Mondal and D. Das, RSC Adv., 2013, 3, 9117–9149.
15. R. Vegners, I. Shestakova, I. Kalvinsh, R. M. Ezzell and P. A. Janmey, J. Pept. Sci., 1995, 1, 371–378.
16. A. Mahler, M. Reches, M. Rechter, S. Cohen and E. Gazit, Adv. Mater., 2006, 18, 1365–1370.
17. D. J. Adams, M. F. Butler, W. J. Frith, M. Kirkland, L. Mullen and P. Sanderson, Soft Matter, 2009, 5, 1856–1862.
18. L. Chen, G. Pont, K. Morris, G. Lotze, A. Squires, L. C. Serpell and D. J. Adams, Chem. Commun., 2011, 47, 12071–12073.
19. Z. Yang, G. Liang and B. Xu, Acc. Chem. Res., 2008, 41, 315–326.
20. S. Roy, N. Javid, P. W. J. M. Frederix, D. A. Lamprou, A. J. Urquhart, N. T. Hunt, P. J. Halling and R. V. Ulijn, Chem. – Eur. J., 2012, 18, 11723–11731.
21. T. Li, M. Kalloudis, A. Z. Cardoso, D. J. Adams and P. S. Clegg, Langmuir, 2014, 30, 13854–13860.
22. S. Fleming, S. Debnath, P. W. J. M. Frederix, N. T. Hunt and R. V. Ulijn, Biomacromolecules, 2014, 15, 1171–1184.
23. T. Li, F. Nudelman, J. W. Tavacoli, H. Vass, D. J. Adams, A. Lips and P. S. Clegg, Adv. Mater. Interfaces DOI:10.1002/admi.1500601.
24. L. Chen, S. Revel, K. Morris, L. C. Serpell and D. J. Adams, Langmuir, 2010, 26, 13466–13471.
25. L. Chen, T. O. McDonald and D. J. Adams, RSC Adv., 2013, 3, 8714–8720.
26. M. Wallace, A. Z. Cardoso, W. J. Frith, J. A. Iggo and D. J. Adams, Chem. – Eur. J., 2014, 20, 16484–16487.
27. H. Cui, M. J. Webber and S. I. Stupp, Pept. Sci., 2010, 94, 1–18.
28. T. Shimada, N. Sakamoto, R. Motokawa, S. Koizumi and M. Tirrell, J. Phys. Chem. B, 2012, 116, 240–243.
29. I. W. Hamley, Soft Matter, 2011, 7, 4122–4138.
30. M. Wallace, D. J. Adams and J. A. Iggo, Soft Matter, 2013, 9, 5483–5491.
31. D. K. Chattoraj and K. S. Birdi, Adsorption and the Gibbs Surface Excess, Plenum Press, New York, 1984.
32. J.-S. Kim, C.-K. Kim, P.-S. Song and K.-M. Lee, J. Colloid Interface Sci., 1981, 80, 294–296.
33. J. N. Israelachvili, Intermolecular and surface forces, Academic Press, Burlington, 2011.
34. M. C. Moran, A. Pinazo, L. Perez, P. Clapes, M. Angelet, M. T. Garcia, M. P. Vinardell and M. R. Infante, Green Chem., 2004, 6, 233–240.
35. S. Zhang, M. A. Greenfield, A. Mata, L. C. Palmer, R. Bitton, J. R. Mantei, C. Aparicio, M. O. de la Cruz and S. I. Stupp, Nat. Mater., 2010, 9, 594–601.
36. M. Guvendiren, H. D. Lu and J. A. Burdick, Soft Matter, 2012, 8, 260–272.
37. S. Tsonchev, K. L. Niece, G. C. Schatz, M. A. Ratner and S. I. Stupp, J. Phys. Chem. B, 2008, 112, 441–447.
38. S. Banta, I. R. Wheeldon and M. Blenner, Annu. Rev. Biomed. Eng., 2010, 12, 167–186.
39. J. Raeburn, C. Mendoza-Cuenca, B. N. Cattoz, M. A. Little, A. E. Terry, A. Zamith Cardoso, P. C. Griffiths and D. J. Adams, Soft Matter, 2015, 11, 927–935.
40. http://www.nist.gov/data/nsrds/NSRDS-NBS361.pdf .
41. Z. Lin, J. J. Cai, L. E. Scriven and H. T. Davis, J. Phys. Chem., 1994, 98, 5984–5993.
42. J. T. Pelton and L. R. McLean, Anal. Biochem., 2000, 277, 167–176.
43. X. Mu, K. M. Eckes, M. M. Nguyen, L. J. Suggs and P. Ren, Biomacromolecules, 2012, 13, 3562–3571.
44. K. M. Eckes, X. Mu, M. A. Ruehle, P. Ren and L. J. Suggs, Langmuir, 2014, 30, 5287–5296.
45. K. L. Morris, L. Chen, A. Rodger, D. J. Adams and L. C. Serpell, Soft Matter, 2015, 11, 1174–1181.
46. K. Harald, L. Judith, O. Jos and D. Otto, Astrophys. J., Lett., 2009, 706, L66.
47. D. M. Hudgins, S. A. Sandford and L. J. Allamandola, J. Phys. Chem., 1994, 98, 4243–4253.
48. J.-B. Guilbaud and A. Saiani, Chem. Soc. Rev., 2011, 40, 1200–1210.
49. D. J. Pochan, L. Pakstis, B. Ozbas, A. P. Nowak and T. J. Deming, Macromolecules, 2002, 35, 5358–5360.
50. R. A. Hule, R. P. Nagarkar, A. Altunbas, H. R. Ramay, M. C. Branco, J. P. Schneider and D. J. Pochan, Faraday Discuss., 2008, 139, 251.
51. R. A. Hule, R. P. Nagarkar, B. Hammouda, J. P. Schneider and D. J. Pochan, Macromolecules, 2009, 42, 7137–7145.
52. K. L. Morris, L. Chen, J. Raeburn, O. R. Sellick, P. Cotanda, A. Paul, P. C. Griffiths, S. M. King, R. K. O'Reilly, L. C. Serpell and D. J. Adams, Nat. Commun., 2013, 4, 1480.
53. C. Colquhoun, E. R. Draper, E. G. B. Eden, B. N. Cattoz, K. L. Morris, L. Chen, T. O. McDonald, A. E. Terry, P. C. Griffiths, L. C. Serpell and D. J. Adams, Nanoscale, 2014, 6, 13719–13725.
54. M. N. Triba, D. E. Warschawski and P. F. Devaux, Biophys. J., 2006, 88, 1887–1901.
55. S. Sathaye, A. Mbi, C. Sonmez, Y. Chen, D. L. Blair, J. P. Schneider and D. J. Pochan, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2015, 7, 34–68.
56. http://www.sasview.org .
57. L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Plenum Press, New York, 1987.
58. J. S. Pedersen and P. Schurtenberger, Macromolecules, 1996, 29, 7602–7612.
59. W.-R. Chen, P. D. Butler and L. J. Magid, Langmuir, 2006, 22, 6539–6548.

---

Footnote

† Electronic supplementary information (ESI) available: Further characterisation of the micellar phase diagram, full rheological characterisation of both the solutions and hydrogels, and further SANS data and discussion. See DOI: 10.1039/c5sm03072b

---