Counter-ion distribution around flexible polyelectrolytes having different molecular architecture

Abstract

We explore the monovalent counter-ion distribution around flexible highly-charged polyelectrolytes with different molecular architectures (linear chains, stars, and unknotted and trefoil rings) using molecular dynamics simulations that include an explicit solvent that interacts with the polyelectrolyte. In particular, we find that the molecular topology influences the fraction of counter-ions transiently associating with the polyelectrolyte on a scale of the order of the chain segments, forming a “condensed” counter-ion interfacial layer. As with the hydrogen bonding of water to proteins and other polymers, the persistence time of these interfacial “bound” counter-ions is relatively short, O(1 ps), and we characterize the fluctuations in the number of the counter-ions populating the interfacial layer. We also find that the counter-ions are distributed in a non-uniform fashion on the polyelectrolyte backbone, forming dynamical clusters whose form and average size is sensitive to molecular architecture. In addition, we find that the residual bound counter-ions, not located in either the interfacial layer or the bulk solution, form a diffuse ionic cloud around the polyelectrolyte due to the uncompensated polyelectrolyte charge along the backbone. Generally charge valence strongly influences the extent of the diffuse counter-ion cloud, but in the case of monovalent counter-ions, we find that the size of the diffuse counter-ion cloud nearly coincides with the polyelectrolyte radius of gyration, independent of molecular topology.

---

1 Introduction

Polyelectrolytes form a diverse class of polymers that includes biological molecules such as DNA, RNA, proteins, and synthetic polymers such as sulfonated polystyrene and polyacrylic acid. These polymers are widely used as rheology modifiers, adsorbent materials, coatings, biomedical implant materials, encapsulating materials for pharmaceutical drug delivery systems^1–3 and, of course, they are an essential component of living systems. A microscopic understanding is needed of how the counter-ion distribution influences the polyelectrolyte configurational properties,⁴ which are of fundamental importance in the inherent tendency of polyelectrolytes to undergo supermolecular assembly,^5,6 their non-trivial phase behavior,^7,8 as well as for understanding the unique rheological and dielectric properties of these materials.^8–10

As with many ionizable materials, polyelectrolytes release their counter-ions into polar solvents in which they are dissolved,^11,12 but the extent of this counter-ion delocalization is modulated by molecular structural parameters such as charge density, charge valence, chain length, and molecular topology to name a few relevant molecular variables. It is generally appreciated that this ionization process leads to a charged chain backbone in aqueous solution and results in long-range repulsive Coulomb interactions between the polymer segments that cause the polymer to swell. The strength of this interaction must be greatly influenced by counter-ions that remain in the general proximity of the polyelectrolyte, but which are not ionically bound as in a crystal. It is these weakly bound counter-ions and their effect on chain conformation that make the modeling of polyelectrolytes challenging.^13–16 Given the evident complexity of the coupling between polymer conformation and the counter-ion distribution, analytic theories of polyelectrolytes have emphasized highly idealized models aimed at describing some essential aspects of the localization of counter-ions near the polyelectrolyte and the consequences of this association on the thermodynamics of polyelectrolyte solutions.

The classical theoretical approach to counter-ion localization in highly charged polyelectrolytes was introduced by Manning.^17,18 According to this model, when the electrostatic interactions dominate over thermal fluctuations then the fully-ionized state of the polyelectrolyte becomes unstable and counter-ions “condense” along the chain backbone, giving rise to a characteristic counter-ion “localization length” on the order of the Bjerrum length, l_B = e²/(ε_rk_BT) (e is the elementary charge, ε_r is the solvent dielectric constant, T is the temperature, and k_B is Boltzmann's constant). Manning theory^17,18 is a rather idealized model that assumes that highly charged polyelectrolytes are infinite straight threads having vanishing diameter and a uniform charge density. Counter-ion localization does not theoretically arise in the model when the polyelectrolytes have a finite chain length and this model does not consider how changes in conformation induced by the counter-ions and thermal fluctuations of the chain backbone alter the physical nature of the counter-ion localization to the polyelectrolyte. Simulation studies^7,19–27 of flexible polyelectrolytes having finite length indicate significant deviations from Manning theory, and provide evidence for the importance of the coupling of the counter-ions with polymer conformation.

The development of more realistic analytic models of polyelectrolytes have followed two approaches, namely an extension of the Manning model based on the mean-field Poisson–Boltzmann theory^28–32 and through the introduction of continuous flexible chain model^33,34 that address the influence of counter-ions on chain conformation. A valiant first attempt to better describe this coupling was made by Muthukumar³³ where counter-ion condensation on the surface of a flexible polyelectrolyte chain was modeled by an association mechanism affecting the polyelectrolyte self-interaction and, thus chain conformation. In models of the first type, the polyelectrolyte is still assumed to have a rod-like conformation so that the coupling between the counter-ion distribution and the chain conformation is simply ignored. In the second type of model, the condensed ions renormalize the charge density and the dissociated counter-ions are modeled based on a simple Debye–Hückel approximation. Shklovskii³⁵ has also made an interesting contribution to this field by showing that highly charged spherical particles can exhibit long range attractions and conductive properties that are associated with a diffuse counter-ion cloud around the particle. The influence of the diffuse counter-ion cloud on polyelectrolyte association is also emphasized in the controversial model of colloidal interactions by Sogami and Ise.³⁶ Similar arguments have been made by Kirkwood and coworkers³⁷ regarding the physical implications of a “polarizable” cloud of counter-ions around polyelectrolytes (modeled as charged spheres). We can then expect a diffuse counter-ion cloud to have significant implications for polyelectrolyte association and we take a first step in addressing this fundamental problem by quantifying the nature of the diffuse counter-ion cloud.

The present work directly address the coupling between the molecular conformation and the counter-ion distribution in highly charged polyelectrolytes in an explicit solvent by molecular dynamics (MD) simulations. We choose not to follow the historical pattern of previous polyelectrolyte conformation studies, in which polymer and salt charge concentrations are altered. Instead, we consider different molecular topologies (linear chains, stars, and unknotted and trefoil rings; see Fig. 1), since topology (i.e., the connectivity between the polyelectrolyte segments) influences the average molecular shape and segmental density even in the absence of charges; chain topology should then affect the coupling between chain conformation and the counter-ion distribution. Indeed, it is well known for neutral polymers that molecular topology plays an important role in the viscoelesticity of these material.^38–41 Variation of the molecular topology of charged polymer is also used in improving the efficiency of water-soluble polymer drug carriers for the treatment of cancer and in the development of numerous nanomedicine therapies.^42,43 Investigations on the impact of the molecular topology of polyelectrolytes are limited in comparison to linear polyelectrolytes, but there are some notable studies on star polyelectrolytes^44–48 with an implicit solvent and rings with knots.⁴⁹ By using an explicit solvent, we can account for the short-ranged solvent interactions needed to address the dynamical consequences of counter-ion and solvent association with the polyelectrolyte.

Fig. 1 (a) A schematic of a polyelectrolyte chain surrounded by ions and the shaded areas highlight the interfacial ions (dark blue), domain ions (light blue). Any ions outside these areas correspond to undisturbed ionic solvent. (b–e) Screenshots of typical molecular configurations of (b) linear chain; (c) unknotted ring; (d) ring with a trefoil knot; (e) star polymer with fM = 160. The solvent and most of the ions are not shown for clarity. For (b–d) and from left to right the molecular mass increases and for (e) the chain functionality decreases with fixed molecular mass.

We find that polyelectrolytes tend to form semi-flexible polymers whose conformation is highly sensitive to molecular topology. In this more realistic model of polyelectrolytes, counter-ions localize for all molecular models both on the scale of l_B as in the idealized Manning theory, but also on the scale of the chain as a whole, i.e., radius of gyration, R_g. This two scale localization has a fundamental significance for understanding intermolecular interactions in polyelectrolyte solutions.

This paper is organized as follows. Section 2 contains details of the model and simulation methods. Results of the characterization of the counter-ion distribution in the proximity to polyelectrolytes of different molecular architecture are presented in Section 3. Section 4 concludes the paper.

2 Model and methodology

We employ molecular dynamics (MD) simulations based on a bead-spring model of Lennard-Jones (LJ) segments bound by stiff harmonic bonds suspended in explicit LJ solvent particles, some of which are charged to represent counter-ions and ions from added salt. The particular model of polyelectrolytes that we employ was originally introduced by Yethiraj and coworkers,^50,51 and subsequently was investigated by Koplik et al.²⁵ This model incorporates minimal aspects of real polyelectrolyte solution and allows for equilibrated molecular dynamics with an explicit solvent. The added complexity and the cost in computational time required by inclusion of an explicit solvent is motivated by an important series of papers by Yethiraj and coworkers^50,51 indicating that the solvent has a significant impact on the polyelectrolyte structure and dynamics, and, of course, one cannot reasonably model the competitive binding of the solvent and counter-ions to the polyelectrolyte backbone, an essential feature of these molecules, without including the solvent explicitly. Competitive binding of the molecular spaces to macromolecules is known to greatly alter the phase behavior of polymer solutions,^52,53 leading to often counter-intuitive phase behavior. Even greater complexity can be expected when associated species have long range interactions.

All macro-ion segments, dissolved ions, and solvent particles are assigned the same mass m, size σ, strength of interaction ε, and all dissolved ions are monovalent. We set ε and σ as the units of energy and length and the cutoff distance for LJ interaction potential is r_c = 2.5σ. Polyelectrolyte molecular mass ranges from M_w = fM + 1 = 11 to 161 segments, where M corresponds to number of segments per arm and f represent the number of arms; f = 2 for all molecular architectures except for stars. All polyelectrolytes carry a total charge −Z_pe and Z_p/M_w = 1, which is distributed uniformly along the molecular structure. The bonds between polymer segments are connected via a stiff harmonic spring, V_H(r) = k(r − l₀)², where l₀ = σ is the equilibrium length of the spring, and k = 1000ε/σ² is the spring constant. To model finite size rod-like polymers, we use the same model as with flexible chains, but a bending potential is used, U_bend(θ) = k_bend(θ − θ₀)²; where θ₀ = 180° and k_bend = 1000 ε/rad². All charged particles interact via the Coulomb potential, and the particle–particle particle-mesh method is used. The operating conditions are typical of the LJ liquid state: density ρσ³ = 0.8 and reduced temperature k_BT/ε = 1, the latter maintained by a Nosé–Hoover thermostat.

The system is composed of a total of 64 000 solvent particles in a periodic cube of side L. The system includes N₋ co-ions of charge −e and N₊ = N₋ + Z_p counter-ions of charge +e so that the system of interest has neutral total charge. Aside from the Bjerrum length that specifies the strength of the Coulomb interaction, the other key length parameter for an ionic solution is the Debye screening length: λ_D = [4πl_B(ρ₊ + ρ₋)]^−1/2, where ρ_± = N_±/L³ are the ion densities. Simulations are conducted for l_B/σ = 1.85 and N₊ = 300, which results in λ_D/σ ≈ 2.5. MD time unit is τ = σ(m/ε)^1/2. Typical simulations equilibrate for 2000τ, and data is accumulated over a 7500τ interval.

3 Results and discussion

We start our discussion of the counter-ion distribution in our model polyelectrolyte with the observation that the fraction of the counter-ions located in close proximity to the polyelectrolyte forms an interfacial region having an enriched average concentration of counter-ions. This can be qualitatively understood in terms of Manning model of charge condensation,¹⁷ where the counter-ions are inferred to “condense” along the chain backbone to screen the bare charge for a high charge polyelectrolyte. Nevertheless, counter-ions found in this interfacial region only partially screen the bare charge of the polyelectrolyte due to the Coulombic repulsion between the counter-ions, leaving the remaining counter-ions at larger distances from the polyelectrolyte. In other words, there are two zones of counter-ion enrichment around the polyelectrolyte. While it is commonly assumed that the interfacial layer has a scale on the order of l_B, it has previously been observed that there is significant variation in the amount charge at shorter and larger distances than l_B.²⁵ This two-zone model just described is a bit ambiguous since there is no sharp boundary between the zones that would allow the quantification of the respective scales of counter-ion localization. For the purposes of our investigation, we set the interfacial layer based on an arbitrary distance criterion in which any counter-ion that is located at shorter distances than 1.1σ are taken to be part of the interfacial region. This particular value, i.e., 1.1σ, is chosen in order to discriminate between the counter-ions that are in contact with the polyelectrolyte from the remaining counter-ions.

Now that we have defined the interfacial region for our model based on a precise geometric picture, we calculate the average number of interfacial counter-ions, n_int, for the different molecular topologies (linear chains, rings, trefoil knots, and stars). We note that our discussion is an expansion of a preliminary study of this same topic,⁵⁴ where we found that the interfacial counter-ions exhibit a rich spectrum of behaviors for the different molecular topologies. As seen in Fig. 2a, n_int is influenced both by M_w and molecular topology. This is not surprising given that polyelectrolytes under investigation have a flexible backbone, while in the Manning model of charge condensation polyelectrolytes are assumed to be slender needles. Overall, the deviation from the linear chains is observed as the molecular complexity increases as in the case of stars and trefoil knots. In our previous investigation,⁵⁴ we found that if instead n_int is defined as the counter-ions located at shorter distances than l_B (rather than 1.1σ) then a qualitative agreement is found between Manning predictions about the fraction of condensed counter-ions and our results for n_int.

Fig. 2 (a) Average number of interfacial counter-ions, n_int (b) the average number of contacts with the polyelectrolyte the interfacial counter-ions have, n_cont, normalized by the molecular mass, M_w. Standard deviation, Σ, of (c) n_int and (d) n_cont as function of M. The symbols represent linear chains (), rings (), trefoil knots (), and stars ().

We digress to explain some dynamical aspects of the counter-ion enrichment. The value of n_int fluctuates over time, reflecting a dynamic binding and unbinding process where the residence time of the counter-ion is rather short, O(1 ps), so that the interfacial counter-ions are exchanging with the counter-ions in the solution at a reasonably high rate.^13,14,55 The solvent also interacts with the polymer with a short range interaction and likewise the interfacial solvent continuously exchanges with the solvent molecules in solution on a comparable timescale to interfacial counter-ion exchange process. Despite the rapid exchange process of both the competing counter-ion and the solvent exchange processes, there is nonetheless a time-averaged enrichment of counter-ions near the polyelectrolyte defining a “bound” layer of counter-ions; this is an equilibrium self-assembly phenomenon.²⁵ Below, we discuss the spatial organization of the counter-ions in the interfacial layer, which is normally far from uniform even in our coarse-grained model.

The magnitude of the fluctuations for n_int can be quantified by the standard deviation, Σ(n_int). Linear chains and rings exhibit similar values for n_int and for Σ(n_int) signifying that the molecular complexity of the rings is not sufficient to distinguish them from linear chains, as seen in Fig. 2a and c. On the other hand, we see that trefoil knots exhibit fluctuations of a similar magnitude, but have quite different values of n_int. Stars exhibit both n_int and fluctuations in this property that are conspicuously distinct from linear chains and ring polyelectrolytes. Based on these observations, we conclude that chain topology strongly influences the population of counter-ions at the interfacial layers, as well as fluctuations in their numbers.

In our previous work⁵⁶ exploring the effect of multivalent counter-ions on linear chains, we argued that the observed conformational changes are a result of the chain coiling around the polyelectrolytes, Fig. 2b. A coiling of the chains is suggested by the increase in the number of contacts the interfacial counter-ions have with the polyelectrolyte, n_cont. While we find similar features as for n_int, the contact number n_cont approaches a similar level, n_cont/M_w ≈ 0.37 for all molecular topologies simulated. For rings, n_cont/M_w exhibits little M_w variation, while for linear chains n_cont/M_w decreases with M_w for small M_w. On the other hand, for trefoil knots and stars there is a substantial increase in n_cont/M_w for small M_w, signifying that these molecular topologies adopt molecular conformations that wrap the interfacial counter-ions. This counter-ion enrichment in flexible polyelectrolytes can be understood by excess counter-ions found in kinks and near the branched points of charged lines.⁵⁷ This trend is also reflected in the size of the fluctuations in n_cont, as indicated in Fig. 2d. Based on the saturation behavior of n_cont, we anticipate that n_cont will be an important factor in determining the energetics and equilibrium properties, but to our knowledge this quantity has not been considered in polyelectrolyte modeling before.

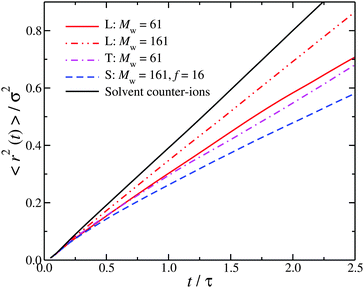
The role of molecular topology in wrapping around interfacial counter-ions suggests that this effect should also be reflected in the interfacial counter-ion dynamics. The fast dynamics probed by neutron scattering in the picosecond time scale (t/τ < 2.5, where τ ≈ 1 ps) can be utilized to define a Debye–Waller factor for the interfacial counter-ions. While a time scale on the order of a 1 ps sounds relatively short to have an impact on the macroscopic dynamics, we note that there are studies that argue that while the water dynamics in the hydration layer around proteins and other polymers is of a few picoseconds, it is sufficiently long to affect the polyelectrolyte hydrodynamics.^58–61 Accordingly, we calculate the mean-square displacement, 〈r²〉, for the interfacial counter-ions. To ensure that the 〈r²〉 is not correlated with the particular polyelectrolyte conformation and that the counter-ions in the interfacial layer have not diffused away from the polyelectrolyte, we have averaged our results from ten different uncorrelated time origins. From Fig. 3, it is clear that the association between counter-ions and chain backbone influences the interfacial dynamics, with higher branched polyelectrolytes leading to a significant reduction in mobility (as measured by 〈r²〉). In hindsight, this is not surprising. Fig. 1e shows a star polyelectrolyte with f = 16, and it clear that a significant fraction of counter-ions are located near the star core.

Fig. 3 Mean-square displacement of the interfacial counter-ions, 〈r²〉, on a relatively short time scale relevant for neutron scattering measurements. The notation L, S, and T correspond to linear chain, star, and the trefoil knot, respectively. The mean-square displacement of counter-ions that are not in the interfacial layer (i.e., solvent) are also presented.

Based on the above discussion, we now have a more detailed picture on how the interfacial counter-ions associate with polyelectrolytes having different molecular topologies, and we now shift our focus towards to the counter-ions that are in the proximity of the polyelectrolyte, but are not part of the “bound” interfacial layer, as described above. To better quantify the distribution of counter-ions around the polyelectrolyte, we calculate the average net charge, q(r), as function of distance from the polyelectrolyte segments, which is simply the sum of the counter-ion distribution q₊(r) and the co-ion distribution q₋(r). For comparison, we also calculate the distribution of counter-ions belonging to the interfacial bound layer alone, q_b. Evidently from Fig. 4, q(r) represents both the counter-ions at the interfacial layer and the counter-ion cloud that is loosely associated with the polyelectrolyte. From Fig. 4, it is also clear, that q_b follows the distribution of the polyelectrolyte segments but always corresponds to a smaller amount of charge; this is expected as the counter-ions at the interfacial layer only partially screen the polyelectrolyte bare charge. On the other hand, there are significant deviations between q(r) and q_b starting at distances on the order of l_B, signifying that q_b is insufficient metric for accounting the whole impact of counter-ions near the polyelectrolyte. To understand why q(r) is a better metric for capturing the distribution of the counter-ions, we compare the relevant distributions of each type of ion. The location of the boundary, R_b, between the counter-ion cloud around the polyelectrolyte and the bulk solvent can be identified at q(R_b) → 0, which means that q₊ = q₋. Thus, we have q(r) ≈ 0 for distances r > R_b, while on the other hand, there is an excess counter-ion charge and a depletion of co-ion charges for r < R_b, corresponding to the diffuse counter-ions around the polyelectrolyte. The latter regime apparently embodies what has been described in the literature as the “diffuse counter-ion cloud”, as discussed in the introduction. We refer to q(r) as the counter-ion distribution of the diffuse ionic cloud (including the counter-ions in the interfacial layer) and focus on characterizing the spatial extent of this distribution.

Fig. 4 Distribution of the ionic net charge, q(r), as well as the relevant distributions of the counter-ions q₊ and co-ions q₋, around a trefoil knot with molecular mass, M_w = 61. The distribution of the polymeric segments, q_p(r), as well as, the distribution of counter-ions located in the interfacial layer, q_b(r), are also presented.

At this point, one might naturally expect q(r) to track the segmental distribution since molecular conformations are coupled to the counter-ion distribution. Fig. 4 displays both the segmental and counter-ion distributions, which include the interfacial and diffusely associated counter-ions. It is clear that at short distances, near the polyelectrolyte backbone segments, there is more charge from neighboring segments than from counter-ions, q(r) < q_p(r). This means that at short distances there is a higher population of polyelectrolyte segments than counter-ions, and this imbalance results in an effective repulsion between the segments, leading to a swelling of the polyelectrolyte. Nevertheless, at larger distances there is a crossover for q(r) > q_p(r). For example, a trefoil knot having M_w = 61, as seen in Fig. 4, the crossover occurs at r > 6.5σ. This means that at distances r > 6.5σ, there is a higher probability of finding a monovalent counter-ion than a polyelectrolyte segment. This is also reflected on the slower decay of the tail of the counter-ion distribution than the segmental distribution. This is significant because it means that q(r) includes a large fraction of counter-ions that are not in the interfacial layer. Thus, the counter-ion distribution has a structure that is distinct from the segmental distribution, an effect warranting quantification.

To determine the spatial extent of the diffuse counter-ion cloud, we compute the average ionic charge at a distance r from any macro-ion segment, q(r), as can be seen in Fig. 5. In close proximity to the macro-ion, there is an oscillatory behavior in q(r), reflecting liquid-like correlations in the counter-ions around the macro-ion, and these correlations diminish beyond a scale of 2l_B. This effect is more pronounced in finite length rod polyelectrolytes due to high spatial regularity of the macro-ion charges (note that we do not observe waves of oscillatory charge for the conditions of our investigation). For relative small M_w < 41, q(r) decays to zero at larger distances. For molecular architectures other than rods and for M_w > 41, q(r) exhibits a substantial peak occurring at a scale much larger than λ_D. This strongly suggests the existence of another length scale describing the distribution of the counter-ion cloud around these polyelectrolytes.

Fig. 5 The ionic charge, q(r), around macro-ions of various molecular architecture. The notation F, L, S, R, and T correspond to finite length rod, linear chain, star, unknotted ring and ring the trefoil knot, respectively. The upward arrows (↑) mark the Bjerrum length, l_B, and Debye length, λ_D, while the downward arrows (↓) mark the size of radius of gyration, R_g.

Numerous recent experimental and computational studies of polyelectrolytes have definitively established the importance of the diffusely bound counter-ions in the understanding the properties of polyelectrolyte solutions,^13–16,24 but we are not aware of any previous computational work quantifying the scale of this “cloud”. For example, we seek to understand how the spatial extent of this diffuse counter-ion cloud varies with the polyelectrolyte mass or molecular architecture. The lack of quantification of this basic polyelectrolyte property is surprising to us given the importance of this phenomenon for understanding polyelectrolyte properties and intermolecular interactions.^{13–16,62–65}

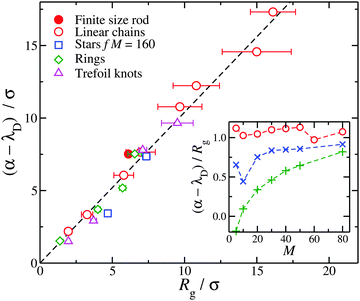
We take a cue from previous work⁶⁶ based on PB calculations for rod polyelectrolytes suggesting that a localization scale can be defined from the inflection point in the net ionic charge at a distance r from macro-ion segments. This scale is certainly larger than l_B and λ_D, so we consider this quantity for our flexible polymers to see if we can define a rational metric for counter-ion localization based on Q(r); see inset of Fig. 6. It is evident that Q(r) increases and then saturates at long distances at Q(r)/Z_p ≈ 1 for all molecular architectures examined. We observe that macro-ions with different M_w (since Z_p = λM_w) have different levels of charge saturation. We also find that the molecular complexity regulates the rate of saturation in Q(r). For all the cases examined (rings, trefoil knots, and stars) Q(r), which saturates at shorter distances in comparison to linear chains having the same M (see inset of Fig. 6).

Fig. 6 Normalized spatial distribution of the net ionic charge around a macro-ion of various molecular architectures. The notation is the same as in Fig. 2. Inset: Net ionic distribution without being normalized.

Our findings up to this point regarding the nature of the counter-ion distribution can be rationalized within existing polyelectrolyte theories, however, we find that all our Q(r) curves collapse onto a single master curve with the following functional form:

Q(r) = βZ_p tanh²[(r − μ)/α], (1)

where α, β, and μ are fitting parameters and their values are presented in Table 1. This collapse of Q(r) curves suggests that the rate of charge saturation and the size of ionic cloud surrounding a macro-ion. This means that both can be described independently of molecular architecture, a welcome simplification. For systems with β > 1, the distribution of counter-ions are affected by their periodic images, our system corresponds to a dilute polyelectrolyte solution with non-negligible concentration effects. Since we focus on the dilute regime in the current work, we restrict our attention to systems with β < 1.1. The α parameter defines a characteristic length at which Q(r) saturates; in essence it is a domain localization length describing the size of the diffuse ionic cloud around the polyelectrolyte. This scale is directly coupled to the conformational properties of the macro-ion. By plotting the parameter α versus R_g, we find all the data with β < 1.1 exhibiting a strikingly linear relationship, see Fig. 5. For example, knowing the size of the macro-ion, one can draw the size of disturbed ionic cloud by the macro-ion at R ≈ 5α/2 ≈ 5R_g/2 since Q(r) at r = R has reached charge saturation, as apparent in Fig. 4. As demonstrated in a previous study,⁵⁶ the extent of the counter-ion cloud does not scale with R_g for higher valence counter-ions; for comparison we present results for linear chains at inset of Fig. 7. This means that the relation of the extent of the counter-ion cloud with polyelectrolyte conformation is non-trivial.

Table 1 Parameters obtained from fitting eqn (1) to Q(r) (see Fig. 4 in the main manuscript). The notation L, S, R, T, and F correspond to linear chain, star, ring, trefoil knot, and finite size rod molecular architectures, respectively. The quantities f and M are related to molecular mass, M_w = fM + 1. In all cases, the charge per macro-ion segment is λ = Z_p/M_w = 1

Topology	f	M	Z p	α	β	μ
L	2	5	11	4.61	0.92	0.00
L	2	10	21	5.79	1.00	0.00
L	2	20	41	8.54	1.00	0.00
L	2	30	61	10.18	1.00	0.00
L	2	40	81	13.36	1.00	0.00
L	2	50	101	14.86	1.00	0.00
L	2	60	121	17.25	1.00	0.00
L/S	2	80	161	20.12	1.00	0.00
S	4	40	161	22.56	1.54	−0.57
S	8	20	161	10.16	1.04	1.33
S	16	10	161	6.23	1.00	0.94
R	2	5	11	3.95	0.79	−0.27
R	2	20	41	6.19	1.00	0.56
R	2	30	61	7.71	1.04	0.89
R	2	40	81	10.1	1.07	0.66
R	2	60	121	17.6	1.26	−0.18
R	2	80	161	43.11	4.01	−0.69
T	2	15	31	3.97	0.97	−0.01
T	2	30	61	5.46	0.99	0.43
T	2	51	103	10.43	1.06	0.08
T	2	80	161	12.46	1.09	0.74
F	2	10	21	10.09	1.02	−0.56
F	2	20	41	21.02	1.32	−2.22

---

Fig. 7 Extent of the counter-ion distribution α versus the mean radius of gyration, R_g, for polyelectrolytes with λ = 1 and β < 1.1. The α parameter is shifted by a factor equal to the Debye length, λ_D. The dashed line corresponds to a linear fit: α − λ_D = 1.04R_g. The uncertainty estimates indicate two standard deviations. Inset: Demonstration of the non-trivial relation between the α parameter and R_g at different multivalent counter-ion environments; symbols correspond to monovalent (), divalent (), and trivalent () counter-ions.

Why should we be concerned about the diffuse counter-ion cloud? Apart from the large effect this layer has on the dielectric properties of polyelectrolyte solutions,⁶⁷ we may expect this loosely associated cloud of counter-ions to make polyelectrolytes highly polarizable. Kirkwood and coworkers³⁷ have predicted that the presence of the “polarizable” cloud of counter-ions around polyelectrolyte chains (proteins modeled as spheres) can lead to long range attractions interactions arising from the associated fluctuations of the potential field derived from fluctuations in the positions of the counter-ions around the polyelectrolyte. Recent computational studies have shown that polarizable dielectric particles have an inherent tendency to cluster,⁶⁸ so we believe that the presence of a diffuse counter-ion cloud provides a natural physical mechanism for understanding the self-assembly of polyelectrolytes into dynamic clusters.^36,69–72 In the future, we plan to quantify the nature of the interchain interactions in our system to check this hypothesis.

The presence of the polyelectrolyte in the solution has a large impact not only on the average distribution of the counter-ions, but induces the self-assembly of the counter-ions within the interfacial region of the polyelectrolyte, an effect relevant to the understanding the charge fluctuation phenomenon just described. The local distribution of these associated counter-ions in the interfacial layer reflects a balance between the Coulomb attractive or repulsive interactions, and between the ions and the polyelectrolyte segments. While the formation of dynamical counter-ion clusters on the backbone of the polyelectrolyte chains have been noted before in this model,²⁵ here we expand upon these findings by investigating the formation of counter-ion clusters for polyelectrolytes of different molecular topology. To calculate the size of a counter-ion cluster, n_c, we use a distance criterion, where a counter-ion belongs to a cluster if it is located 1.2σ from a counter-ion belonging to the cluster. Moreover, we label the probability of finding a counter-ion cluster of size n_c as P_c(n_c), and the resulting counter-ion cluster probabilities for different molecular topologies are presented in Fig. 8. We again emphasize that these counter-ion clusters are transient, meaning that they continuously form, break apart, and then reform; no clustering is observed away from the polyelectrolyte backbone or in the absence of the polyelectrolyte under the thermodynamic conditions, i.e., salt concentration and temperature that we investigate. We find little variation in P_c(n_c) for polyelectrolyte chains having different molecular mass. Additionally, for polyelectrolyte chains and rings, the size of counter-ion clusters are relative small, e.g., for P_c(n_c) = 10⁻², we find n_c ≈ 5. The functional form of P_c appears to be nearly exponential, which is consistent with a linear chain equilibrium polymerization of the counter-ions on the polyelectrolyte backbone.⁷³ In other words, the counter-ion clusters dynamically form chains on the polyelectrolyte backbone so that the spatial organization of these clusters loosely reflects the geometry of the polyelectrolyte that they “dress”, see Fig. 1b–e. We anticipate that the timescale of these counter-ion clusters will be longer than the exchange time, discussed above, and that these clusters will influence the charge fluctuations of the polyelectrolyte as a whole. This is an additional topic for future investigation, and for the present we focus on the geometrical nature of these curious self-assembled structures.

Fig. 8 Probability of finding a counter-ion cluster of size n_c for (top) polyelectrolytes having a molecular mass, M_w = 61 and (bottom) star polyelectrolytes having M_w = fM + 1 = 161. The notation L, S, R, and T correspond to linear chain, star, unknotted ring and ring the trefoil knot, respectively. Linear chains are equivalent to stars having f = 2.

For trefoil knot and highly branched star polyelectrolytes, however, we see a new feature emerging in the interfacial counter-ion clustering. Large clusters form with respect to linear polyelectrolyte chains, having a mass cluster size several times larger. In particular, for stars having M_w = 161 and f = 16, we find n_c ≈ 45 for P_c(n_c) = 10⁻²; this cluster size is nine times larger than in the case of the linear polyelectrolytes discussed above. This is a highly counter-intuitive result given that counter-ions strongly repel each other. This suggests that the high charge density created by the star molecular topology, in conjunction with the more complex chain topological structure, triggers the formation of much larger counter-ion clusters that are themselves branched in nature. Consistent with this picture, the probability distribution, provided that n_c is sufficiently large, n_c > 5, follows a power law with cluster size, P_c(n_c) ∝ n_c^−1.9, for large polyelectrolyte stars and trefoil knots. This behavior is reminiscent of the equilibrium polymerization of branched polymers.⁷⁴

Finally, we explore the radius of gyration of the counter-ion clusters, R_g,c, in the interfacial layer. We observe that once the cluster size, n_c, is sufficiently large, i.e., n_c > 5, then two distinct behaviors emerge, Fig. 9. For 4 < n_c < 20, the size of the counter-ion clusters scales as R_g,c ∝ n_c^1/2 for all molecular architectures. This is consistent that the counter-ions forming linear chain-like clusters on the linear on the backbone of the polyelectrolyte with the statistics of linear random coils, as indicated above. We thus have further evidence that dynamic counter-ion clusters are formed along the polyelectrolyte backbone, affected by the geometrical structure of the polyelectrolyte. Unfortunately, the mass scaling of the cluster radius does not allow us to distinguish between random walk counter-ion cluster conformation and randomly branched clusters (“lattice animals”), which exhibit the same scaling behavior with cluster mass as ideal linear chain coils in three dimensions,⁷⁵i.e., R_g ∼ n_c^1/2. Stars having f = 16 and M = 10 have a high enough charge density and branched complexity for the formation of even larger counter-ion clusters n_c > 20, and in these branched polyelectrolytes we see another regime emerge. In particular, highly branched counter-ion clusters are then formed, and R_g,c scales as n_c to an apparent power that is near ν ≈ 0.2, suggesting that the counter-ion clusters have fully saturated the capacity of the polyelectrolyte to accommodate them on their surface, an effect similar to what happens in the mass scaling in gels (formed by particles) above the percolation threshold when the box size is small. In the present instance, the polyelectrolyte chain is the “box”. We note that a similar mass scaling crossover is physically observed in the radius of gyration of dendrimer molecules having a high generation number where excluded volume interactions inhibit further cluster growth.⁷⁶ The organization of the counter-ions into self-assembled structures on the polyelectrolyte backbone is evidently a physically rich phenomenon with many implications for the conformation of polyelectrolytes and the interparticle responsible for the supramolecular assembly of the polyelectrolytes. An understanding of these interactions and assembly processes is clearly important in the design of novel functional materials using polyelectrolytes.

Fig. 9 Mean-square radius of gyration of the counter-ion clusters, R_g,c², formed in the interfacial region of the polyelectrolytes having molecular mass, M_w = 161. The highlighted regions correspond to the different mass scaling of the counter-ion clusters and dashed lines are guides for eye. Note that the counter-ions are generally similar to worm-like chains for n_c < 10.

4 Conclusions

In summary, we quantify the distribution of monovalent counter-ions for molecular architectures (linear chains, stars, and unknotted and trefoil rings) using molecular dynamics simulations. The fraction of interfacially “bound” counter-ions, defined by an enrichment on a scale on the order of the size of the polyelectrolyte segments, is influenced by the molecular architecture. An effect not anticipated by Manning theory. We find that for molecular architectures having a higher molecular complexity than linear chains, the polyelectrolyte tends to wrap around these counter-ions, resulting in a modified counter-ion fast dynamics, as well as a different degree of screening of the bare charge of the polyelectrolyte. On the scale of the polymer radius of gyration, there is an additional diffuse counter-ion cloud that forms around the polyelectrolyte chain due to the residual unscreened polyelectrolyte charge. We demonstrate that this diffuse counter-ion distribution is independent of molecular topology for monovalent counter-ions, i.e., the extent of the counter-ion distribution scales comparable to the radius of gyration of polyelectrolyte. However, this effect is unique to monovalent counter-ions since for higher valent counter-ions the diffuse counter-ion cloud becomes more contracted and even partially collapses for trivalent counter-ions.⁵⁶ Finally, we characterize the self-assembly of counter-ions into dynamic clusters in the interfacial region around polyelectrolytes having different molecular topologies. We find that the counter-ions organize into dynamic polymer-like structures near the polyelectrolyte backbone and that the topology of these clusters largely follow the topology of the polyelectrolyte backbone. These counter-ion clusters are the direct physical expression of interfacial charge fluctuations and must have relevance for understanding polyelectrolyte intermolecular interactions. Experimental synthesis and characterization of polyelectrolyte systems can be used to validate the predictions of the present work. In the future, we plan to investigate how the counter-ion structure in this family of polyelectrolyte models influence the interaction between these molecules.

Acknowledgements

Financial support was provided by the NIST Fellow Postdoctoral Program. Official contribution of the U.S. National Institute of Standards and Technology – not subject to copyright in the United States.

References

1. P. G. de Gennes, P. Pincus, F. Brochard and R. M. Velasco, J. Phys., 1976, 37, 1461–1476.
2. A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118.
3. A. Yethiraj, J. Phys. Chem. B, 2009, 113, 1539–1551.
4. V. M. Prabhu, Curr. Opin. Colloid Interface Sci., 2005, 10, 2.
5. C. F. J. Faul and M. Anttonietti, Adv. Mater., 2003, 15, 673–683.
6. S. Srebnik and J. F. Douglas, Soft Matter, 2011, 7, 6897–6905.
7. R. G. Winkler, M. Gold and P. Reineker, Phys. Rev. Lett., 1997, 80, 3731–3734.
8. Polyelectrolytes Thermodynamics and Rheology, ed. P. M. Visakh, O. Bayraktar and G. Pico, Springer, 2014.
9. A. Y. Kasumov, D. V. Klinov, P.-E. Roche, S. Gueron and H. Bouchiat, Appl. Phys. Lett., 2004, 84, 1007–1009.
10. S. Duhr and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19678–19682.
11. F. Oosawa, Polyeletrolytes, Marcel Dekker, New York, 1971.
12. J.-L. Barat and J.-F. Joanny, Adv. Chem. Phys., 1996, 94, 1.
13. D. Hinderberger, G. Jeschke and H. W. Spiess, Macromolecules, 2002, 355, 9698.
14. D. Hinderberger, H. W. Spiess and G. Jeschke, J. Phys. Chem. B, 2004, 108, 3698.
15. T. E. Angelini, L. K. Sanders and R. H. Colby, J. Phys.: Condens. Matter, 2005, 17, S1123.
16. Y. Katsumoto, S. Omori, D. Yamamoto, A. Yasuda and K. Asami, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 011911.
17. G. S. Manning, J. Chem. Phys., 1969, 51, 924–933.
18. G. S. Manning, J. Chem. Phys., 1969, 51, 3249.
19. M. J. Stevens and K. Kremer, J. Chem. Phys., 1995, 103, 1669–1690.
20. J. C. Chu and C. H. Mak, J. Chem. Phys., 1999, 110, 2669–2679.
21. H. J. Limbach and C. Holm, J. Chem. Phys., 2001, 114, 9674–9682.
22. S. Liu and M. Muthukumar, J. Chem. Phys., 2002, 116, 9975.
23. M. Ullner and C. E. Woodward, Macromolecules, 2002, 35, 1437–1445.
24. M. Muthukumar, J. Chem. Phys., 2002, 116, 9975.
25. T. S. Lo, B. Khusid and J. Koplik, Phys. Rev. Lett., 2008, 100, 128301.
26. J.-M. Y. Carrillo and A. V. Dobrynin, Macromolecules, 2011, 44, 5798–5816.
27. F. Carnal and S. Stoll, J. Phys. Chem. A, 2012, 116, 6600–6608.
28. M. Le Bret and B. H. Zimm, Biopolymers, 1984, 23, 287–312.
29. T. G. Dewey, Biopolymers, 1990, 29, 1793–1799.
30. G. S. Manning and U. Mohanty, Physica A, 1998, 16, 196–204.
31. I. Borukhov, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 3598–3615.
32. A. Naji and R. R. Netz, Phys. Rev. Lett., 2005, 95, 185703.
33. M. Muthukumar, J. Chem. Phys., 2004, 120, 9343–9350.
34. E. Raphael and J.-F. Joanny, Europhys. Lett., 1990, 13, 623–628.
35. R. Zhang and B. I. Shklovskii, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 021405.
36. I. Sogami and N. Ise, J. Chem. Phys., 1984, 81, 6320–6332.
37. J. G. Kirkwood and J. B. Shumaker, Proc. Natl. Acad. Sci. U. S. A., 1952, 38, 855–862.
38. D. Vlassopoulos, G. Fytas, T. Pakula and J. Roovers, J. Phys.: Condens. Matter, 2001, 13, R855–R876.
39. M. Kapnistos, M. Lang, D. Vlassopoulos, W. Pyckhout-Hintzen, D. Richter, D. Cho, T. Chang and M. Rubinstein, Nat. Mater., 2008, 7, 997–1002.
40. S. J. Dalsin, M. A. Hillmyer and F. S. Bates, ACS Macro Lett., 2014, 3, 423–427.
41. A. Chremos and J. F. Douglas, J. Chem. Phys., 2015, 143, 111104.
42. M. E. Fox, Acc. Chem. Res., 2009, 42, 1141–1151.
43. A. Agrawal and S. Kulkarni, Int. J. Res. Dev. Pharm. Life Sci., 2015, 4, 1700–1712.
44. O. V. Borisov and E. Zhulina, Eur. Phys. J. B, 1998, 4, 205–217.
45. A. Jusufi, C. N. Likos and H. Löwen, Phys. Rev. Lett., 2001, 88, 018301.
46. N. Hoffmann, C. N. Likos and H. Löwen, J. Chem. Phys., 2004, 121, 7009–7021.
47. M. Ballauff, Prog. Polym. Sci., 2007, 32, 1135–1151.
48. A. Jusufi and C. N. Likos, Rev. Mod. Phys., 2009, 81, 1753–1772.
49. P. G. Dommersnes, Y. Kantor and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 031802.
50. R. Chang and A. Yethiraj, J. Chem. Phys., 2003, 118, 6634.
51. R. Chang and A. Yethiraj, Macromolecules, 2006, 39, 821–828.
52. J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 2015, 143, 131101.
53. J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 2015, 143, 194901.
54. A. Chremos and J. F. Douglas, MRS Advances, 2015 , submitted.
55. K. Karatasos and M. Krystallis, J. Chem. Phys., 2009, 130, 114903.
56. A. Chremos and J. F. Douglas, J. Chem. Phys., 2015 , in preparation.
57. G. S. Manning, Soft Matter, 2014, 10, 3738–3747.
58. B. Halle and M. Davidovic, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12135–12140.
59. L. Nilsson and B. Halle, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13867–13872.
60. L. Zhang, L. Wang, Y.-T. Kao, W. Qui, Y. Yang, O. Okobiah and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18461–18466.
61. Although 1 ps would appear to be a “short” time, this period of time is longer than the time required for a sound wave to propagate an interatomic distances in a condensed fluid.⁷⁷ This means that we may view the polymer and the associated interfacial ions and solvent as a single ‘rigid’ object from a hydrodynamic standpoint. Hydrodynamic measurement of proteins and other macromolecules made on picosecond and nanosecond timescales should reflect this collective unit in the decay in the self-intermediate scattering function, from which the diffusion coefficient can be estimated.⁷⁸ This time scale is also long enough for inertia effects associated with fluid complessibility to become unimportant.⁷⁹ Therefore, while a picosecond is a ‘short’ time by some standards, it is long enough to have important hydrodynamic consequences.
62. I. Morfin, F. Horkay, P. J. Basser, F. Bley, A.-M. Hecht, C. Rochas and E. Geissler, Biophys. J., 2008, 87, 2897.
63. V. M. Prabhu, E. J. Amis, D. P. Bossev and N. Rosov, J. Chem. Phys., 2004, 121, 4424.
64. V. M. Prabhu, B. D. Vogt, W. Wu, J. F. Douglas, E. K. Lin, S. K. Satija, D. L. Goldfarb and H. Ito, Langmuir, 2005, 21, 6647–6651.
65. T. E. Angelini, R. Golestanian, R. H. Coridan, J. C. Butler, A. Beraud, M. Krisch, H. Sinn, K. S. Schweizer and G. C. L. Wong, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7962–7967.
66. M. Deserno, C. Holm and S. May, Macromolecules, 2000, 33, 199–206.
67. F. Bordi, C. Cametti and R. H. Colby, J. Phys.: Condens. Matter, 2004, 16, R1423–R1463.
68. K. Barros and E. Luijten, Phys. Rev. Lett., 2014, 113, 017801.
69. K. S. Schmitz, Langmuir, 1997, 12, 5849–5863.
70. N. Grønbench-Jensen, R. J. Mashl, R. F. Bruinsma and W. M. Gelbart, Phys. Rev. Lett., 1997, 78, 2477–2480.
71. R. Messina, C. Holm and K. Kremer, Phys. Rev. Lett., 2000, 85, 872–875.
72. B. Hong, A. Chremos and A. Z. Panagiotopoulos, Faraday Discuss., 2012, 154, 29–40.
73. J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 1999, 111, 7116–7130.
74. D. Stauffer and A. Aharony, Introduction to Percolation Theory, Taylor Francis, 1994.
75. G. Parisi and N. Sourlas, Phys. Rev. Lett., 1981, 46, 871–874.
76. F. Mallamace, E. Canetta, D. Lombaro, A. Mazzaglia, A. Romeo, L. M. Scolaro and G. Maino, J. Chem. Phys., 1969, 51, 924–933.
77. R. Zwanzig and M. Bixon, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 2, 2005–2012.
78. F. Roosen-Runge, M. Henning, F. Zhang, R. M. J. Jacobs, M. Sztucki, H. Schober, T. Seydel and F. Schreiber, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11815–11820.
79. R. Zwanzig and M. Bixon, J. Fluid Mech., 1975, 69, 21–25.

---