Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular ordering in the high-temperature nematic phase of an all-aromatic liquid crystal†
Francesco
Vita
a,
Maruti
Hegde
b,
Giuseppe
Portale‡
c,
Wim
Bras
c,
Claudio
Ferrero
d,
Edward T.
Samulski
e,
Oriano
Francescangeli
*a and
Theo
Dingemans
*b
aDipartimento di Scienze e Ingegneria della Materia, dell'Ambiente ed Urbanistica and CNISM, Università Politecnica della Marche, Via Brecce Bianche, 60131 Ancona, Italy. E-mail: o.francescangeli@univpm.it
bFaculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HS Delft, The Netherlands. E-mail: t.j.dingemans@tudelft.nl
cNetherlands Organization for Scientific Research (NWO), DUBBLE CRG at the ESRF, 6 rue Jules Horowitz, 38043 Grenoble Cedex, France
dEuropean Synchrotron Radiation Facility, Boîte Postale 220, 38043 Grenoble Cedex, France
eDepartment of Chemistry, University of North Carolina, Chapel Hill, NC 27599-3290, USA
First published on 19th January 2016
Abstract
We report the structural characterization of the nematic phase of 2,6-biphenyl naphthalene (PPNPP). This lath-like all-aromatic mesogen provides a valuable benchmark for classical theories of nematic order. PPNPP exhibits a very high temperature nematic phase (417–489 °C) above an enantiotropic smectic A phase. X-ray diffraction reveals a surprisingly strong tendency towards molecular layering in the nematic phase, indicative of “normal cybotaxis” (i.e. SmA-like stratification within clusters of mesogens). Although stronger at low temperatures, the layering is evident well above the smectic A-nematic transition. The nematic order parameter is evaluated as a function of temperature from the broadening of the wide-angle diffuse diffraction feature. Measured values of the orientational order parameter are slightly larger than those predicted by the Maier–Saupe theory over the entire nematic range except for a narrow region just below the clearing point where they significantly drop below the theoretical prediction.
Introduction
Theories describing the orientational order of nematic (N) liquid crystals have been developed by Onsager,1 Flory2 and Maier and Saupe.3 These theories are based on rigid, rod- or lath-like molecules. The popular Maier–Saupe (M–S) theory describes the orientational distribution in the N phase in terms of an anisotropic potential between rod-like molecules that stabilizes parallel alignment. The theory is based on a mean field treatment of long-range contributions and ignores short-range forces. In spite of this drastic simplification, the prediction of the temperature dependence of orientational order 〈P2〉 by the M–S theory fits surprisingly well the N phases of many low molecular weight liquid crystals. It was suggested by Luckhurst and Zannoni4 that this qualitative agreement with experiment could be explained by generic aspects of a N phase comprised of locally ordered clusters of molecules persisting above the clearing point into the isotropic (I) phase. At that time this idea was merely an intriguing theoretical speculation, one that was not supported by any experimental evidence. More recently, interest in short-ranged molecular aggregation in N phases (cybotactic clusters)5 has been revived since such clusters of molecules appear to play a crucial role in determining the unusual properties of bent-core nematogens.6,7 In this context, an extension of M–S theory that explicitly takes into account the role of cybotactic clusters has been proposed by Droulias et al.8 In bent-core nematics the presence of cybotaxis seems to be a natural consequence of the highly non-linear molecular shape. By contrast, M–S and other classical theories of nematics are predicated on an idealized shape of the mesogens—rigid rods with cylindrical symmetry or rigid flat lath-like shapes.In an attempt to clarify the relationship between molecular shape, mesophase properties and theoretical predictions, an all-aromatic compound such as p-quinquephenyl (PPPPP, Fig. 1) serves as an ideal model for molecular nematics. Indeed, the PPPPP shape conforms to that of a rigid lath with conformationally-averaged cylindrical symmetry. Moreover, PPPPP does not contain polar groups or the flexible terminal chains typical of most low molar mass liquid crystals.9 Therefore, apart from the challenging experimental conditions posed by its very high temperature N phase and predisposition to sublime, PPPPP has been the subject of experimental studies aimed at measuring the temperature dependence of its orientational order.10–12 Despite some difficulties related to the orientation of a monodomain sample over macroscopic volumes, birefringence measurements eventually resulted in an observed temperature dependence of 〈P2〉 basically in agreement with the M–S prediction.12 Complimenting those findings a full characterization of PPPPP mesomorphism and molecular shape was performed via atomistic molecular dynamics simulations.13 It was reported that the N phase is favored over the smectic (Sm) phase in part because of a certain degree of internal molecular flexibility (both torsional isomerization and bending of the molecular para axis), indicating that PPPPP is not as rigid as expected especially at the elevated temperatures of the N phase.
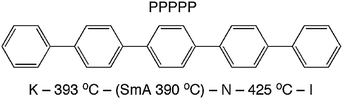 | ||
| Fig. 1 Molecular structure and phase map of PPPPP (measured by differential scanning calorimetry), revealing a monotropic SmA phase.12 | ||
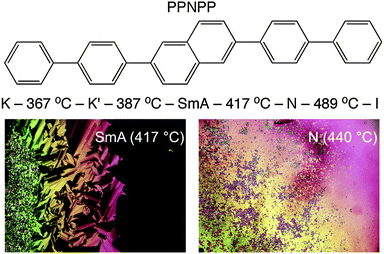
Herein we report the full structural characterization of a related all-aromatic nematogen, the 2,6-biphenyl naphthalene (PPNPP, Fig. 2). It differs from PPPPP in that the central phenyl ring is replaced by a 2,6-substituted naphthalene resulting in a slight offset in its shape relative to PPPPP, a slightly larger aspect ratio and perhaps, restricted flexibility due to the rigid naphthalene in its core. These features impart a wider N range (albeit at very high temperatures) and the presence of an enantiotropic SmA phase below the N phase; the differential scanning calorimetry (DSC) thermograms (Fig. S3, ESI†) are suggestive of a second order (or very weakly first order) SmA–N phase transition. On heating and cooling a stable SmA phase with a relatively large stability range (ΔT ≈ 30 °C) below a stable N phase (ΔT ≈ 72 °C) is observed. By contrast, PPPPP just showed a very narrow (ΔT ≈ 1 °C) monotropic SmA phase upon cooling.12 The melting transition of PPNPP is similar to that of PPPPP but the N–I transition is 64 °C higher. DSC performed on PPNPP at a rate of 20 °C min−1 revealed supercooling of all phase transitions by ∼12–15 °C on cooling.
Experimental
The synthesis and chemical characterization of PPNPP, including DSC scans, can be found in the ESI.†X-ray diffraction (XRD) measurements were carried out at the BM26B DUBBLE beamline14 of the European Synchrotron Radiation Facility (ESRF), Grenoble, France. A special set-up was used to make temperatures as high as ∼500 °C experimentally accessible. It consisted in a home-made temperature-controlled hot stage, containing a Pt100 thermal probe and connected to a PID digital temperature controller enabling a stability better than ±1.5 °C. The Pt100 probe guarantees very high sensitivity with a low magnetic field dependence. The sample holder was designed to allow insertion into a liquid nitrogen-cooled superconductive magnet. The latter was used to apply a static magnetic field of 2.2 T (measured in air) in a direction perpendicular to the incident X-ray beam, so as to align the long axis molecular director n.
The energy of the incident beam was 12.0 keV, corresponding to a wavelength of 1.03 Å, and the sample to detector distance 188.5 mm. This configuration allowed recording X-ray diffraction both in the low-angle and in the wide-angle region (q = 1–22 nm−1). Overall, the set-up resolution was estimated to be Δqres = 6 × 10−2 nm−1. Samples were placed in sealed quartz capillaries (1 mm diameter); the evolution of their diffraction pattern was studied by changing the temperature stepwise (both on heating and cooling) and allowing the sample to equilibrate at each set point. Because PPNPP sublimates easily, the temperature steps were relatively coarse (5 °C) in order to keep the measurement time as short as possible. On this scale, we found good agreement between the transition temperature values measured by XRD and DSC (see below). All diffraction patterns were background corrected by subtraction of the diffraction pattern generated by an empty capillary.
Results and discussion
Fig. 3 shows a representative sequence of PPNPP diffraction patterns in the aligned N phase, taken on cooling from the I phase under a vertical magnetic field. The onset of the N phase was observed at 470 °C when the pair of broad isotropic rings typical of the I phase (Fig. 3a) changed into the anisotropic diffraction pattern of the aligned nematic phase (Fig. 3b–f). The latter consists of: (i) a pair of diffuse wide-angle features centered on the equatorial axis (normal to n); (ii) a pair of narrower diffraction arcs centered on the meridional axis (parallel to n) at low angle; (iii) a series of weaker meridional reflections spanning the low-angle to wide-angle region. The transition from the N to the SmA phase was located between 400 °C and 395 °C, revealed by a narrowing of the low-angle peaks below the resolution limit. A similar sequence was observed on heating.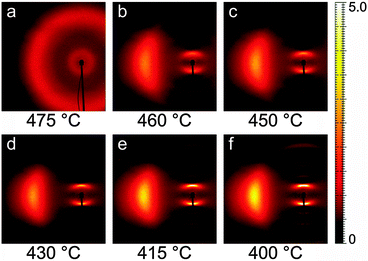 | ||
| Fig. 3 XRD patterns of PPNPP recorded on cooling under an aligning magnetic field (2.2 T, vertical). Only the left wide-angle feature is shown because of the pattern symmetry. | ||
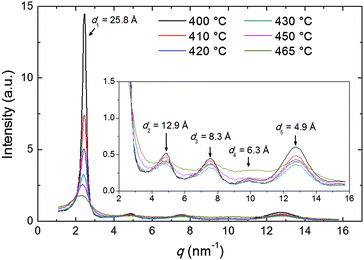
The diffraction patterns taken on cooling have been analyzed in detail. The intensity profile of the XRD pattern along the meridional direction is shown in Fig. 4. The dominant feature is the above-mentioned low-angle diffraction peak observed at q1 = 2.44 nm−1, corresponding to a d-spacing d1 = 2π/q1 = 25.8 Å (at 400 °C). This represents the average intermolecular distance in the longitudinal direction and hence provides an estimation of the molecular length L which is in good agreement with the value expected from molecular modeling (25.34 Å, calculated as 24.34 Å, the distance between the terminal H atoms, plus 2 × 0.5 Å, the VDW radius of the two H atoms). We also observe a small increase of d1 with the temperature, up to 27.8 Å at 470 °C, perhaps as a consequence of the greater longitudinal disorder. This contrasts with the behavior described by Leadbetter et al. in their classical work on conventional calamitics,15 whose flexible aliphatic tails (contrary to the rigid structure of our mesogen) result in contracted conformations at higher temperatures and shorter molecular lengths.
The experimental full width at half maximum (FWHM), Δq, of the low-angle peak (well fitted by a Voigt lineshape) can be used to estimate the longitudinal positional correlation length ξ through the relation ξ = 9.92/Δq*, based on the Hosemann's paracrystalline model.15 Here Δq* is the intrinsic FWHM of the (Lorentzian) first order diffraction peak, obtained by correction of the measured Δq for the (Gaussian) experimental set-up broadening Δqres. For a Voigt lineshape it can be obtained by inverting the approximated equation:16
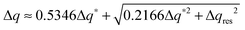 | (1) |
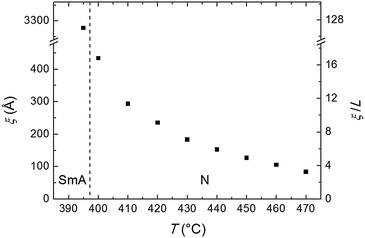 | ||
| Fig. 5 Temperature dependence of the longitudinal correlation length ξ and of its ratio with the molecular length L. The vertical dashed line separates the SmA and the N phases. | ||
Beside the main peak, another four peaks are identifiable at higher q-values (see inset of Fig. 4), corresponding to the weak meridional reflections visible in Fig. 3b–f. The q-space positions of their maxima approximate well those expected for higher order reflections (qn = nq1, n = 1, 2,…) apart from some distortion caused by the molecular form factor. For the n = 5 order, an additional distortion is caused by superposition with the tails of the wide-angle equatorial features, as discussed in the following.
The transverse positional order has been studied by analyzing the intensity profiles taken along the equatorial direction: Fig. 6 shows representative curves in the aligned N and in the I phase. Here the broad peak centered at ∼12.5 nm−1 corresponds to an average transverse intermolecular distance dt varying in the range 4.9–5.3 Å (decreasing with decreasing temperature), a typical value for nematics related to the diameter of an aromatic ring. In the I phase a second peak appears in the low-angle region (see also Fig. 3a), related to a residual intermolecular longitudinal correlation. By using the same expression used to calculate the longitudinal correlation length, the peak FWHM provides a transverse correlation length decreasing with increasing temperature: 24.6 Å (i.e., ∼5dt) at 400 °C, 21.7 Å (∼4dt) at 465 °C, and 15.0 Å (∼3dt) in the I phase at 480 °C.
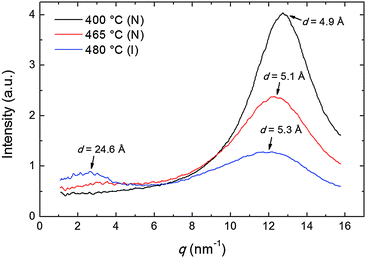 | ||
| Fig. 6 Intensity profiles of the XRD pattern along the equatorial direction at different temperatures in the N and in the I phase; arrows indicate the d-spacing corresponding to each peak. | ||
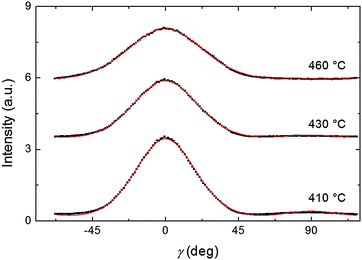
Finally, we evaluated the orientational order parameter 〈P2〉 by fitting the azimuthal profile of the wide-angle feature, following the method described by Davidson et al.17 According to this approach, the wide-angle equatorial scattering is caused by interference in the radiation transversely scattered within small clusters composed of tens of nearly parallel molecules and its azimuthal broadening originates from the orientational disorder among different clusters. The azimuthal intensity profile I(γ) can thus be numerically related to the cluster orientational distribution function (ODF) fd(θ), which generally results in a good approximation of the molecular ODF f(θ).18 Here θ is the angle formed by (a cluster of) molecules with the molecular director n, while γ is the azimuthal angle on the detector measured with respect to the equatorial axis.
Retrieval of fd(θ) is simplified if one assumes a Maier–Saupe ODF:
fd(θ) ≈ f(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) = Z−1em θ) = Z−1em![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (2) |
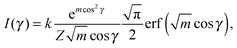 | (3) |
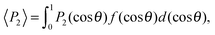 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ.
θ.
Representative azimuthal profiles (integrated in the q-range 11–14 nm−1) and the corresponding fitting curves are shown in Fig. 7 for three temperatures in the N range. The low intensity maximum at 90 deg is due to the fifth order meridional peak which has noticeable intensity in the same q-range as the equatorial reflection. Although this reflection is much weaker than the equatorial crescent, it significantly affects the fitting procedure, especially at the lower temperatures. To get rid of the problem, we fitted the data by using a superposition of two azimuthal scattering functions I(γ), one centered at 0 deg (the main peak) and the other one at 90 deg (the secondary peak). In order to limit the number of free parameters, we used two different values of k for the two peaks, but a common value of m. In fact, it seems reasonable that the two peaks are affected in a similar way by orientational disorder. No background was added to the fitting function, as the original images were already background corrected. The agreement with the experimental data is very good throughout most of the N phase, although it worsens at low temperature, where the effect of the secondary peak is more noticeable. From the m values provided by the fits, we could calculate the temperature dependence of the order parameter. The results are shown in Fig. 8 as a function of the reduced temperature T/TNI. As with our measurements we could only determine TNI within a 5 °C interval, its value was established by fitting the experimental data by a Haller-type equation:19
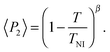 | (5) |
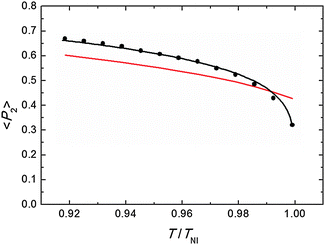 | ||
| Fig. 8 Orientational order parameter as a function of the reduced temperature: measured values (black dots), fitting by Haller equation (eqn (5), black line), and theoretical prediction from M–S theory (red line). For the last we have used the approximated expression 〈P2〉 = (1–0.98T/TNI)0.22, assuming a temperature independent molar volume.20 | ||
This provides TNI = 470.7 ± 0.3 °C and a critical exponent β = 0.165 ± 0.002. As a comparison, Olivier et al. obtain β = 0.18 from their molecular simulations on PPPPP and compare it with typical β experimental values for 5CB in the range 0.17–0.25.13a
Actually, the validity of Haller's empirical model close to the clearing point is questionable, as it does not account for the weakly first order nature of N–I phase transition. However, we verified that excluding the highest temperature point from the data set did not significantly affect the value of β. In Fig. 8 the experimental results are also compared with the order parameter behavior predicted by the M–S theory. Apart from the region very close to the clearing point, our results are slightly larger than M–S curve, although the discrepancy is of the order of our experimental accuracy (estimated to be around 10%;17 the latter is mainly due to the difficulty of an exact subtraction of background and other unrelated diffraction features). On the other hand, our values exhibit a marked decrease in a very narrow region (T/TNI > 0.99) below the isotropization temperature and depart from the M–S universal prediction of 〈P2〉 = 0.43 at the N–I transition. A similar divergence from the expected trend on approaching the I phase is not unusual in the experimental determination of the N order parameter. This has already been reported for PPPPP, when the order parameter has been measured by diamagnetic susceptibility,10 nuclear magnetic resonance (NMR),11 and XRD measurements.12 In the last case, it was attributed to the macroscopic fluctuations of the molecular director, stronger at high temperature and not completely suppressed by the aligning magnetic field. Although we cannot totally exclude this effect, especially when the sample is on the verge of isotropization, in our case fluctuations are expected to be reduced as we used a magnetic field more than twice that in the previous experiment. Nevertheless, the unequivocal confirmation of the observed reduction trend of 〈P2〉 very close to TNI would require additional measurements with a thermal stability higher than that allowed by our setup at the challenging experimental conditions.
Conclusions
We have performed a full structural characterization of the N phase of PPNPP. Like the previously studied PPPPP, this all-aromatic compound represents a prototypical embodiment of the ideal “rigid rod” mesogen, the basic ingredient of most of the theories of the N phase. PPNPP is found to show a very high temperature N phase above an enantiotropic SmA phase. While XRD measurements reveal a lateral ordering very similar to conventional nematics, longitudinal order is characterized by an unusually large correlation length (>5L) over most of the N range. This behavior is indicative of cybotactic clusters, nanoscopic-size SmA-like assemblies of stratified molecules persisting in the N phase well above the SmA–N transition.5 While conjectured long ago,4 the relevance of cybotactic order in determining mesogen thermodynamic properties has just begun to be elucidated both theoretically8 and experimentally.6,7 Our measurements of the orientational order parameter 〈P2〉 result in values which are slightly larger than M–S predictions over most of the N range, but significantly lower just below the N–I transition temperature. Higher accuracy data are required to test the significance of the observed deviation from the theoretical models close to the N–I phase transition.Acknowledgements
The authors acknowledge I. F. Placentino (Università Politecnica delle Marche) and D. Hermida Merino (ESRF) for their support during XRD measurements, and BM28-XMaS staff (ESRF) for providing the superconducting magnet. ETS acknowledges support from the Cary C. Boshamer Professorship. The Netherlands Organisation for Scientific Research (NWO) is gratefully acknowledged for making beam time available on the DUBBLE beamlines.References
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627 CrossRef CAS.
- P. J. Flory, Proc. R. Soc. London, Ser. A, 1956, 234, 73 CrossRef CAS.
- (a) W. Maier and A. Saupe, Z. Naturforsch., 1958, 15A, 287 Search PubMed; (b) W. Maier and A. Saupe, Z. Naturforsch., 1959, 14A, 882 CAS.
- G. R. Luckhurst and C. Zannoni, Nature, 1977, 267, 412 CrossRef CAS.
- E. T. Samulski, Liq. Cryst., 2010, 37, 669 CrossRef CAS.
- (a) O. Francescangeli, V. Stanic, S. I. Torgova, A. Strigazzi, N. Scaramuzza, C. Ferrero, I. P. Dolbnya, T. M. Weiss, R. Berardi, L. Muccioli, S. Orlandi and C. Zannoni, Adv. Funct. Mater., 2009, 19, 2592 CrossRef CAS; (b) O. Francescangeli and E. T. Samulski, Soft Matter, 2010, 6, 2413 RSC; (c) O. Francescangeli, F. Vita, C. Ferrero, T. Dingemans and E. T. Samulski, Soft Matter, 2011, 7, 895 RSC; (d) O. Francescangeli, F. Vita and E. T. Samulski, Soft Matter, 2014, 10, 7685 RSC.
- (a) A. Jákli, Liq. Cryst. Rev., 2013, 1, 65 CrossRef; (b) O. Francescangeli, F. Vita, F. Fauth and E. T. Samulski, Phys. Rev. Lett., 2011, 107, 207801 CrossRef PubMed; (c) F. Vita, I. F. Placentino, C. Ferrero, G. Singh, E. T. Samulski and O. Francescangeli, Soft Matter, 2013, 9, 6475 RSC; (d) T. J. Dingemans, L. A. Madsen, O. Francescangeli, F. Vita, D. J. Photinos, C.-D. Poon and E. T. Samulski, Liq. Cryst., 2013, 40, 1655 CrossRef CAS.
- S. Droulias, A. G. Vanakaras and D. J. Photinos, Liq. Cryst., 2010, 37, 969 CrossRef CAS.
- T. J. Dingemans, N. S. Murthy and E. T. Samulski, J. Phys. Chem. B, 2001, 105, 8845 CrossRef CAS.
- P. L. Sherrell and D. A. Crellin, J. Phys., 1979, 40, C3–C211 Search PubMed.
- T. J. Dingemans, L. A. Madsen, N. A. Zafiropoulos, W. B. Lin and E. T. Samulski, Philos. Trans. R. Soc. London, Ser. A, 2006, 364, 2681 CrossRef CAS PubMed.
- S. Kuiper, B. Norder, W. Jager, T. J. Dingemans, J. van Turnhout and S. J. Picken, J. Phys. Chem. B, 2011, 115, 1416 CrossRef CAS PubMed.
- (a) Y. Olivier, L. Muccioli and C. Zannoni, ChemPhysChem, 2014, 15, 1345 CrossRef CAS PubMed; (b) C.-D. Poon, et al., unpublished results.
- W. Bras, I. P. Dolbnya, D. Detollenaere, R. van Tol, M. Malfois, G. N. Greaves, A. J. Ryan and E. Heeley, J. Appl. Crystallogr., 2003, 36, 791 CrossRef CAS.
- A. J. Leadbetter, R. M. Richardson and C. N. Colling, J. Phys., 1975, 36, C1–C37 Search PubMed.
- J. J. Olivero and R. L. Longbothum, J. Quant. Spectrosc. Radiat. Transfer, 1977, 17, 233 CrossRef.
- P. Davidson, D. Petermann and A. M. Levelut, J. Phys. II, 1995, 5, 113 CrossRef CAS.
- M. Deutsch, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 8264 CrossRef.
- I. Haller, Prog. Solid State Chem., 1975, 10, 103 CrossRef.
- W. H. de Jeu, Physical properties of liquid crystalline materials, Gordon and Breach Science Publishers, New York, 1980 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis, Fourier transform infrared spectroscopy (FTIR) and mass spectroscopy (MS) data, DSC scans on heating and cooling. See DOI: 10.1039/c5sm02738a |
| ‡ Present address: Macromolecular Chemistry & New Polymeric Materials, Zernike Institute for Advanced Materials, Nijenborgh 4, 9747 AG Groningen, The Netherlands. |
| This journal is © The Royal Society of Chemistry 2016 |