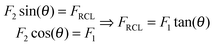Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Weak reversible cross links may decrease the strength of aligned fiber bundles
S. Soran
Nabavi
a and
Markus A.
Hartmann
*ab
aInstitute of Physics, Montanuniversitaet Leoben, Franz-Josef Strasse 18, 8700 Leoben, Austria. E-mail: markus.hartmann@univie.ac.at
bFaculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria
First published on 4th January 2016
Abstract
Reversible cross-linking is an effective strategy to specifically tailor the mechanical properties of polymeric materials that can be found in a variety of biological as well as man-made materials. Using a simple model in this paper the influence of weak, reversible cross-links on the mechanical properties of aligned fiber bundles is investigated. Special emphasis in this analysis is put on the strength of the investigated structures. Using Monte Carlo methods two topologies of cross-links exceeding the strength of the covalent backbone are studied. Most surprisingly only two cross-links are sufficient to break the backbone of a multi chain system, resulting in a reduced strength of the material. The found effect crucially depends on the ratio of inter- to intra-chain cross-links and, thus, on the grafting density that determines this ratio.
1 Introduction
Often the mechanical behavior of polymeric structures is not determined by the properties of the backbone polymers, but is carefully tailored to meet specific demands by introducing cross-links in the system.1 These cross-links may be weaker than the covalent bonds which hold the structure together and break before the backbone ruptures.2 Sometimes these cross-links are able to break and re-form reversibly. If these reversible cross-links (RCLs) connect parts of the same chain upon their rupture the previously shielded part of the chain reveals its hidden length providing an efficient energy dissipation mechanism.3 In these special cases, these cross-links are called sacrificial bonds. Sacrificial bonds can be found in a large variety of biological materials such as bone,4,5 wood,6 and some softer fibers like silk7–9 and mussel byssus threads.10–13 The strength of these bonds differs from a few hundred milli-electron volts for hydrogen bonds to a value close to the strength of covalent bonds for metal-coordination bonds.14–16Experimental as well as theoretical work showed that permanent as well as reversible cross-links have a large influence on the mechanical properties of semiflexible networks such as the cytoskeleton.17–19 Analytical evaluations for parallel-stretched polymeric chains with permanent random cross-links showed that increasing the number of cross-links reduces thermal fluctuations20,21 by reducing the number of allowed configurations.22 In ref. 23 a kinetic model is introduced to describe the dependence of the maximum force a molecule can sustain on the pulling speed as well as to study the impact of the recovery time on the mechanical response of the system.
One of the key factors determining the stability and mechanical properties of a single polymer chain is the topology of the cross-links.24–26 If the cross-link topology resembles a loop such that the applied force is distributed over all the cross-links, then the strength of the chain is directly related to the number of cross-links.27,28 The force required to break the cross-links increases by increasing the number of cross-links in the loop.27,29 In nature a configuration of cross-links maximizing strength can be found e.g., in the muscle protein titin that is forming parallel β sheets providing a material with a high mechanical performance.30
In the present paper a simple, generic model is presented to investigate the mechanical performance of a chain bundle system containing reversible cross-links. Despite the simplicity of the model, the results presented may give an insight in the mechanical behavior of these highly complex systems, including the mussel byssal plaque adhesive proteins,12,13,31–33 the influence of footprint materials in adhesion,34 membrane adhesion of E-selectin receptors immobilized on a substrate35–37 or the atomic force microscope studies on adhesion of microbial cells.38 Additionally, our model can help to understand the mechanical performance of a flexible chain bundle system such as mussel byssus threads and their cuticle which are cross-linked by metal-coordination bonds.10,11,39–44 One of the most surprising effects found in this study is that the presence of cross-links may effectively weaken the material compared to the non cross-linked chains. It is shown that this weakening is due to the premature rupture of the covalent backbone of some of the chains before reaching the contour length.
2 The model
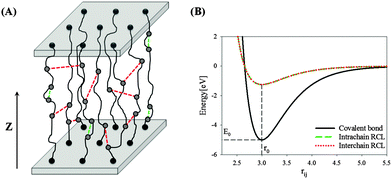
The model is motivated by experimental results obtained in ref. 10 and describes the influence of reversible cross-linking on the mechanical properties of a polymeric system. The model presented here is a generalization of the single chain model described previously.28,45 Each polymer in the system is described as a covalently linked chain of N hard spheres with diameter R oriented along the Z-axis (in the following R is set to the unit of length). Depending on the situation investigated the entire system is made of one, two or nine single chains. The first and last bead of each chain are permanently grafted to a substrate, which in the simulations is described as two hard, in-penetrable walls located at z = 0 and z = L, respectively (see Fig. 1). In the other two directions open boundary conditions were used. In the case of nine chains the grafting points are arranged to occupy a triangular lattice with lattice constant d defining the grafting density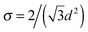 .
.
The covalent binding energy between neighboring beads is described by a Morse potential. This potential is known to provide an accurate description of covalent bonds. All inner beads i are covalently linked to their two neighbors (i − 1 and i + 1), and are allowed to move freely during the simulation, while the end beads of each chain (i = 1 and i = N) have only one neighbor and are permanently grafted to the substrate, i.e. they are held fixed during the simulation. Thus, the excluded volume and covalent interactions between two beads i and j separated a distance r can be described via:
 | (1) |
To take the cross-links into account some of the monomers are defined as sticky. ρ = Ns/N defines the sticky site density with Ns the number of sticky sites in the system. Always two of these sticky sites may form a cross-link that is allowed to open and close reversibly. These RCLs can either link two segments of the same chain providing an intrachain cross-link or connect two segments of different chains forming an interchain cross-link. Experimental results available indicate that the strength of metal coordination bonds like the dopa–Fe complex found in the His-rich domains of the mussel byssus, are 20 to 30% of the strength of a covalent bond,14,46 but the precise shape of the intermolecular potential is not known. To keep the model as simple as possible in the simulations the energetics of inter- and intra-chain cross-links are chosen to follow an identical Morse potential as the covalent bonds with a binding energy reduced by a factor of 4 (i.e. ERCL0 = 0.25E0).
The Monte Carlo moves executed during the simulation are moving the inner beads and updating the cross-links. During the simulations we keep track of the open and closed cross-links. Updating the cross-links consists in choosing one of the sticky sites randomly. If the chosen sticky site is part of a closed cross-link, then the probability for bond rupture is determined using the energy difference of the closed and open bond. If the chosen sticky site is not part of a closed cross-link then the probability of bond formation with another randomly chosen open sticky site is calculated. A new state of the system is accepted following a standard Metropolis algorithm.47,48 The temperature is set to kBT = 25 meV. In the simulations up to 3 million Monte Carlo (MC) steps were performed. One MC step defines the time scale of the simulations being one jump trial per monomer and sticky site. Load-displacement curves are obtained by averaging the force on the end beads of the chain for a given end-to-end distance (i.e. the distance between the grafting plates). A complete curve is obtained by gradually changing this distance. The correspondence of the microscopic evolution of bonds and the features observed in the load-displacement curve is found by monitoring the state (open or closed) and the extension of all bonds for each step in the load-displacement curve.
Monte Carlo simulations obtain the equilibrium properties of the investigated system. During loading and unloading the system is in equilibrium in each step. Thus, all load-displacement curves presented in this paper correspond to quasi-static deformation. Describing viscoelastic, i.e. time-dependent phenomena is beyond the scope of the present paper. Nevertheless, these phenomena are known to be of importance in polymeric materials and mechanical properties are known to be strongly rate-dependent.49,50 Investigation of these effects demands to use molecular dynamics methods that is planned for future research.
3 Results and discussion
Previous results showed that the topology and arrangement of RCLs have a strong influence on the mechanical response of single polymer chains.28,45 In the present paper the focus is put on the influence of the RCLs on the strength of the polymeric system. In this context we define the strength of the system as the maximum force it can sustain before failing catastrophically. The theoretical strength (i.e. the strength at zero temperature) of the bare backbone (i.e. without RCLs) is given by the maximum of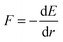 which is found as Fmax = βE0/2 at rmax = r0 + ln(2/β) ≈ r0 + 0.35 using eqn (1). In the chain bundle system the strength of the combined system is found by multiplying the strength of one chain with the number of chains. The theoretical maximum extension of the system is given by
which is found as Fmax = βE0/2 at rmax = r0 + ln(2/β) ≈ r0 + 0.35 using eqn (1). In the chain bundle system the strength of the combined system is found by multiplying the strength of one chain with the number of chains. The theoretical maximum extension of the system is given by 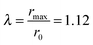 .
.
In the following sections it will be demonstrated that these theoretical values are found only for very low temperatures, while at ambient temperature the strength of the system is reduced due to entropic effects. Furthermore, it will be shown that although the RCLs are weaker than the covalent backbone of the chain, there exist topologies of RCLs exceeding the strength of the backbone. This effect is easy to understand, if several RCLs are loaded in parallel and, thus, stretched simultaneously. Then their combined strength is just the sum of the strength of the single bonds and five RCLs suffice to break the backbone which is a factor of 4 stronger than one RCL. It is more surprising that even two interchain RCLs each having just a quarter of the strength of the backbone may be sufficient to exceed the strength of the backbone. This effect crucially depends on the lateral distance of the chains, i.e. their grafting density σ. The next sections are organized as follows: first, to identify the most important processes a simplified system containing only one or two chains is investigated. Second, the results obtained for the simple setting are used to understand the behavior of a more realistic chain bundle system containing nine chains.
3.1 Single chain
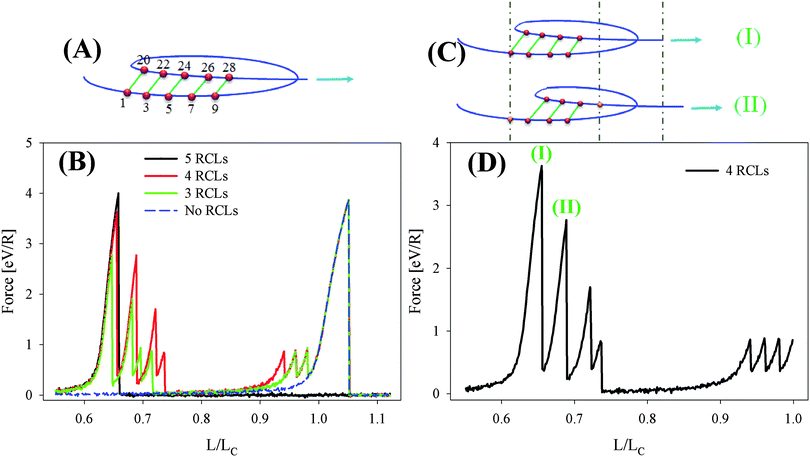
To obtain a reference load-displacement curve first a single chain of length N = 50 without any cross-links is stretched. The result is the dashed line shown in Fig. 2(B). The curve is flat until the load starts rising shortly before the contour length is reached and the backbone gets stretched. The load rises up to approximately 4 eV/R at a relative extension of L/LC ≈ 1.05. Both values, the maximum force as well as the corresponding extension, are considerably lower than the theoretical values of Fmax = 5 eV/R and λ = 1.12. This observation is consistent with the results obtained by Nabavi et al.28 where it was shown that entropic effects are responsible for reducing the efficacy of bonds, even if the bond strength drastically exceeds thermal energy. A reduction in efficacy means that at non-zero temperature the bond sustains a lower level of force than in the case of zero temperature. More exact, in this work it was demonstrated that the entropy of the fluctuating backbone of the polymer is responsible for the reduced strength. Because the entropy of the polymer backbone scales with the number of monomers, i.e., the length of the polymer, this effect strongly depends on the chain length. It was found that for a single chain with only one cross-link N = 33 is the critical number of monomers where the behavior of cross-links changes from enthalpic to entropic.In a second step a single chain with predefined RCLs as shown in Fig. 2(A) is investigated. In this structure the RCLs are formed between monomers (1,20), (3,22), (5,24), (7,26) and (9,28). Thus, the folding pattern of the molecule can be regarded as something like a minimal parallel β-sheet. The five RCLs present in the structure are loaded in parallel leading to a shear force on the backbone. The corresponding load displacement curve is the black line in Fig. 2(B). At L/LC = 0.65 the load rises to the strength of the backbone as shown by the dotted reference curve and then suddenly drops to zero and does not rise again. This behavior is characteristic for the rupture of the backbone. Thus, it may be concluded that this special configuration of RCLs retains the strength of the system, but it significantly decreases the extensibility of the chain.
The red and green curves in Fig. 2(B) show the load-displacement curves for a similar configuration as shown in Fig. 2(A) but with only 4 and 3 RCLs, respectively. These two configurations are weaker than the covalent backbone. Thus, it is the RCLs that rupture resulting in a sequence of peaks decaying in height. Most interestingly the curves show more peaks than there are cross-links in the system. This is due to the reversibility of the bonds that allow for reforming of opened sticky sites during stretching (see Fig. 2(B)). In order to understand this mechanism of RCL rupture and re-formation, the system with four RCLs as shown in Fig. 2(C) is investigated in more detail. Fig. 2(D) shows the loading response of the corresponding chain. Upon loading, first, all four RCLs break simultaneously (peak (I) in Fig. 2D) and try reforming new stable RCLs. Interestingly, upon reforming the cross-links keep their topology forming another shear resistant structure consisting of three RCLs (Fig. 2C-II). In a slightly different context such a topology is called a pseudo-knotted loop.24,28 This new structure is responsible for the second sharp peak (II) in Fig. 2(D). The reason for forming a pseudoknotted loop instead of a random formation of cross-links is that when the length of the chain increases by a tensile load, the absolute displacement for the upper sticky sites shown in Fig. 2(C) is much larger than for the sticky sites in the lower part of the chain. The six inner sticky sites are still in close vicinity favoring the formation of a pseudoknotted loop by three RCLs (see Fig. 2(C-II)). A similar mechanism occurs for the chain with three RCLs as is demonstrated by the green curve in Fig. 2(B).
In summary, all investigated configurations show the same strength. Nevertheless, the extensibility of the system containing 5 RCLs loaded in parallel is strongly reduced compared to the other configurations containing less RCLs. On the other hand the work to fracture, i.e., the area under the curve, is larger for the systems containing 4 and 3 RCLs and even no RCL compared to the 5 cross-link case. The energy to failure of the chain containing three, four and five RCLs are 41, 51.8 and 14.5 eV, respectively, while it is about 25 eV for the non cross-linked case. These results show that it is possible to tune the mechanical properties of a single polymeric chain by changing the topology and number of the involved RCLs. In particular, it is possible to tune the extensibility and work to fracture which is related to the toughness of the involved molecules.
3.2 Two chain system
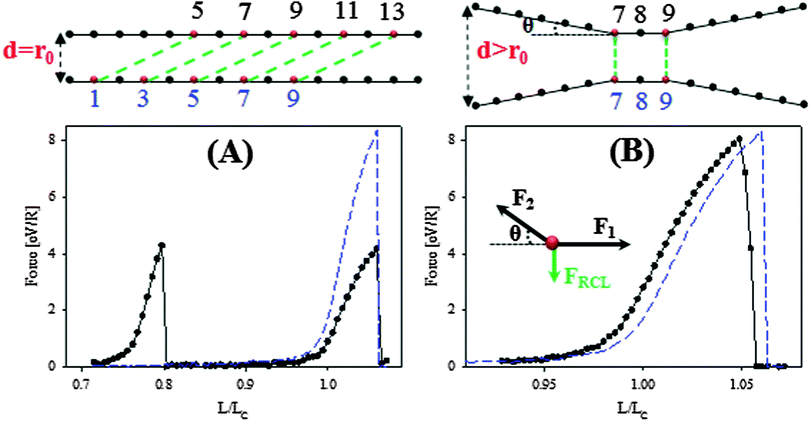
In a next step the influence of interchain cross-links on the mechanical behavior of a two-chain system is investigated. The system consists of two chains of N = 15 beads each. At the beginning of the simulations a predefined topology of RCLs is prepared as shown in Fig. 3. The configurations investigated differ in the lateral distance between the chains that is defining the grafting density σ. For the first configuration this distance is small. Here the fixed end beads of the chains have a distance equal to the equilibrium distance of the RCLs (d = r0) as is indicated in Fig. 3(A). The second configuration is characterized by a lateral distance larger than the equilibrium distance of RCLs (d = 2.6r0 > r0) as is shown in Fig. 3(B). The main physical difference of the two configurations is that in the case of the low distance an interchain cross-link does not experience any force if the involved sticky sites have the same position on their chain. This is because in this case the cross-links have their equilibrium distance.For the case of d = r0 and five interchain cross-links that are loaded in parallel the combined strength of the cross-links exceeds the strength of the backbone (see Fig. 3(A)). The peak around L/LC ≈ 0.8 in the load-displacement curve corresponds to the covalent rupture of one of the chains. The second peak around the contour length corresponds to the rupture of the second chain. While the extensibility of the system is the same as the extensibility of the reference system without cross-links, the strength of the cross-linked system is reduced by a factor of two compared to the non cross-linked case. This is because when the system is stretched to its contour length one chain is already broken and can not take up any force. Two conditions have to be fulfilled that the system behaves in the described way. First, the cross-links should not be formed between sticky sites having the same positions in their chains (see Fig. 3(A)), otherwise the cross-links would not feel any force (because the distance between the chains corresponds to the equilibrium distance of the cross-links). Second, the sticky sites forming the cross-links should show a regular spatial spacing, otherwise the force does not distribute equally on the five cross-links and the cross-links rupture separately. This behavior confirms the observations made in ref. 45 and 51 that the distribution of binding sites has a large impact on the mechanical performance.
Most interestingly, if the distance between the chains is larger than the equilibrium distance of the cross-links, i.e., d > r0, only two interchain cross-links may be sufficient to exceed the strength of the covalent backbone. This is unexpected because the strength of one cross-link is only a quarter of a covalent bond. Fig. 3(B) shows a sketch of the investigated configuration and the inset indicates the forces acting on bead number 7 in the upper chain. F1 shows the covalent force acting on bead 7 that is due to the covalent bond in the inner part of the loop formed by the two cross-links, i.e., the bond between beads 7 and 8. Because the two cross-links align the intermediate part of the chains more or less in the longitudinal direction F1 also points in the longitudinal direction, i.e. the direction of the tensile load. F2 shows the covalent force on bead 7 coming from the non-cross linked part of the backbone. In a first approximation it can be assumed that this force points in the direction of the grafting point of this chain, forming an angle θ to the longitudinal direction. θ is determined by the grafting density as well as the length of the chains. Finally, FRCL shows the force on bead 7 stemming from the closed cross-link. This force is perpendicular to the longitudinal direction. Thus, a force balance in longitudinal and transversal direction gives
This analysis demonstrates that if F1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(θ) exceeds the strength of the cross-link, the cross-link will fail, while the backbone fails if
tan(θ) exceeds the strength of the cross-link, the cross-link will fail, while the backbone fails if 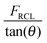 exceeds the strength of the backbone. If we insert the values of the strength of cross-link and covalent bonds FRCL = 1.25 eV/R and F1 = 5 eV/R, then the backbone ruptures when
exceeds the strength of the backbone. If we insert the values of the strength of cross-link and covalent bonds FRCL = 1.25 eV/R and F1 = 5 eV/R, then the backbone ruptures when 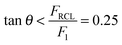 and the cross-link breaks otherwise. Therefore, the backbone of the chain fails by a rupture of one covalent bond if θ < θcritical ≈ 15°, while for θ > θcritical ≈ 15° the cross-links break. In this configuration the two cross-links hold the intermediate part of the chains parallel together. Thus, the chains are aligned in the longitudinal direction and the force on the backbone is a bit smaller than the net force on the outer part. Consequently, the failure of the backbone in the outer part of the structure results in a sharp peak in the load-displacement curve (see Fig. 3(B)) slightly before the rupture of the system without cross-links.
and the cross-link breaks otherwise. Therefore, the backbone of the chain fails by a rupture of one covalent bond if θ < θcritical ≈ 15°, while for θ > θcritical ≈ 15° the cross-links break. In this configuration the two cross-links hold the intermediate part of the chains parallel together. Thus, the chains are aligned in the longitudinal direction and the force on the backbone is a bit smaller than the net force on the outer part. Consequently, the failure of the backbone in the outer part of the structure results in a sharp peak in the load-displacement curve (see Fig. 3(B)) slightly before the rupture of the system without cross-links.
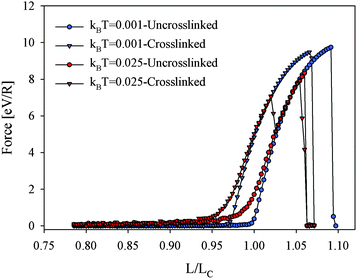
As was shown before entropy and temperature have a large impact on the mechanical response of polymeric systems. In order to investigate the impact of entropy on the loading response, a simple configuration of two chains with and without cross-links was investigated at different temperatures. The black and red curves in Fig. 4 denote the load-displacement curves of system without cross-linking at different temperatures. At low temperature kBT = 0.001 eV, the chains rupture at L/LC ≈ 1.1 showing a strength of about 10 eV/R, while at higher temperature kBT = 0.025 eV the system fails at a shorter length L/LC ≈ 1.06 with a reduced strength of ≈8.3 eV/R. These results confirm that at ambient temperature due to entropic effects the covalent bonds show a reduced strength compared to the theoretical value of 10 eV/R for the two chain system at zero temperature. Correspondingly the maximum extension of the system is reduced L/LC ≈ 1.06 < λ. As expected, entropy decreases the strength and extensibility of the system.
The distance between the chains d = 4r0 is chosen such that in a first approximation the angle θ is found as 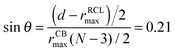 (please note that rRCLmax = rCBmax ≈ r0 + 0.35). This angle is slightly lower than the critical angle θ < θcritical. Thus, as discussed in Fig. 3(B) it is expected that the backbone of the chains fails at a slightly shorter end-to-end distance compared to the system without cross-links. In the low temperature setting the system behaves as expected (compare the two blue curves in Fig. 4). Upon increasing the temperature this behavior changes. Because θ = 12.4° is close to the critical value θcritical ≈ 15° fluctuations become important and the simple zero temperature arguments do not hold any more. The influence of temperature is shown by the red curves in Fig. 4 showing the load-displacement curve of the system with two parallel RCLs. For the high temperature (red triangles) fluctuations lead to the rupture of the cross-links instead of the expected failure of the backbone observed for the low temperature case (blue triangles) considerably changing the load-displacement curve. This cross-link rupture leads to an additional peak at L/LC ≈ 1.02 before the backbone fails at L/LC ≈ 1.06.
(please note that rRCLmax = rCBmax ≈ r0 + 0.35). This angle is slightly lower than the critical angle θ < θcritical. Thus, as discussed in Fig. 3(B) it is expected that the backbone of the chains fails at a slightly shorter end-to-end distance compared to the system without cross-links. In the low temperature setting the system behaves as expected (compare the two blue curves in Fig. 4). Upon increasing the temperature this behavior changes. Because θ = 12.4° is close to the critical value θcritical ≈ 15° fluctuations become important and the simple zero temperature arguments do not hold any more. The influence of temperature is shown by the red curves in Fig. 4 showing the load-displacement curve of the system with two parallel RCLs. For the high temperature (red triangles) fluctuations lead to the rupture of the cross-links instead of the expected failure of the backbone observed for the low temperature case (blue triangles) considerably changing the load-displacement curve. This cross-link rupture leads to an additional peak at L/LC ≈ 1.02 before the backbone fails at L/LC ≈ 1.06.
So far, simple model systems with predefined cross-link topologies were investigated to clarify the impact of RCLs on the mechanical behavior of polymeric systems. Different to the case of a single chain, in a chain bundle system already two cross-links may be sufficient to rupture the chain, although the strength of one cross-link is only a quarter of a covalent bond. In the following, results of a more realistic system containing nine chains each having a length of 50 beads will be presented. Computational stretching tests are performed to investigate the influence of the grafting density on the mechanical properties of the system.
3.3 Chain-bundles
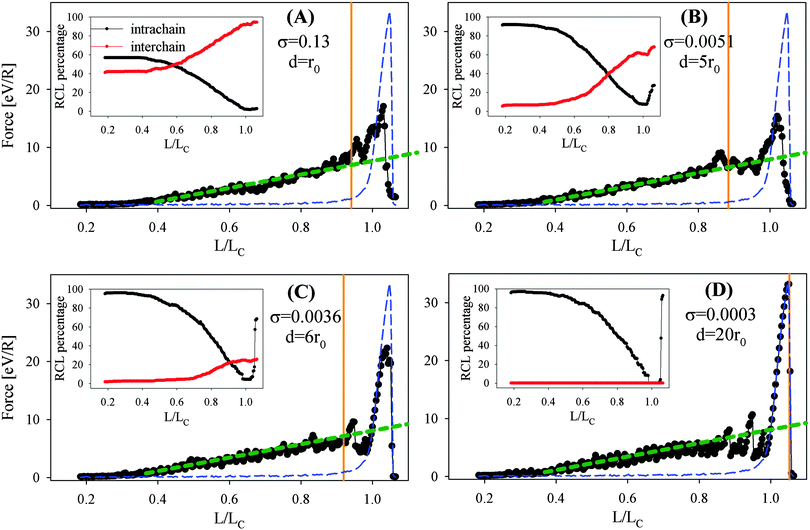
The following sections discuss the mechanical properties of chain bundles containing RCLs. Special emphasis is put on the influence of the grafting density on the mechanical properties of the bundles with a regular distribution of sticky sites. Each bundle contains nine single chains. For these simulations the starting configuration was prepared by slowly unloading the straightened bundle without sticky sites from the contour length to the starting end-to-end distance L/LC ≈ 0.18. Note that this preparation of the starting configuration precludes entanglement of the polymers. Then the sticky sites were introduced. In each of the nine chains 24 sticky sites were defined as sticky i.e., ρ = 0.48. Then the bundles are stretched from the starting end-to-end distance L/LC ≈ 0.18 until failure above the contour length at L/LC ≈ 1.06. Note, that for this system the topology of cross-links was not prescribed as in the simple one- and two chain system investigated before, but the cross-links were forming randomly in the course of the simulation. For each setting the load-displacement curve, the number of intact cross-links and the mechanical parameters such as strength, work to elongate and work to fracture are calculated. In this paper these parameters are obtained, first, as the maximum force during the loading test, second, the amount of energy that is needed to elongate the molecule from L/LC ≈ 0.18 till the contour length (L/LC = 1) and, third, the amount of energy required to stretch the bundle till failure.Simulations were performed for several grafting densities σ, i.e., distances d between the chains. Fig. 5 shows results for d = r0, 5r0, 6r0 and 20r0. The corresponding grafting densities are σ = 0.13, 0.0051, 0.0036 and 0.0003 chains per unit area, respectively. Fig. 5 shows that for small end-to-end distances, the number of intrachain cross-links is consistently larger than the interchain cross-links for all investigated grafting densities. Focusing only on the number of interchain cross-links at L/LC ≈ 0.18 it can be observed that this number decreases with decreasing grafting density. For the lowest grafting density investigated (σ = 0.0003 i.e., d = 20r0), the chains are that much separated that no interchain cross-links can form. Thus, this system behaves like nine independent chains loaded in parallel and the corresponding load-displacement curve is given by multiplying the load-displacement curve of the single chain by nine. As can be seen in the figure during stretching the number of intrachain cross-links decreases, while the number of inter-chain cross-links increases for all except the independent case of lowest grafting density. The number of interchain cross-links rises for all systems between L/LC ≈ 0.5 and L/LC ≈ 0.8, while for the system with d = 20r0 no interchain cross-link forms. Increasing the number of interchain cross-links is because during loading the crumpled starting structure straightens and the probability of forming cross-links between the chains largely increases. In particular for the systems with d = 5r0 and 6r0, at first, there are only few interchain cross-links, but upon stretching their number suddenly increases as is shown in the insets of Fig. 5.
The orange lines in Fig. 5 indicate the first covalent backbone rupture of one of the chains during stretching. As can be observed for all grafting densities—except the lowest—this rupture occurs well before the contour length is reached. Mostly the premature failure of the covalent backbone observed for this system is a combination of the two types of backbone rupture discussed in Fig. 3. The topology of the cross-links consists of cross-links that are mainly loaded in shear (corresponding to case (A) in Fig. 3), but often less than 5 cross-links suffice to prematurely rupture the backbone (corresponding to case (B) in Fig. 3). In rare cases the failure of the backbone in the 9 chain setting can also be attributed to much more complicated topologies involving the cross-linking of more than two chains.
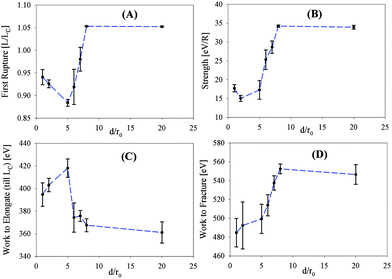
It is this premature failing of some of the chains in the system that is responsible for the observed reduction in strength compared to the non-crosslinked reference curve (see also Fig. 6B). For all investigated systems the maximum load (corresponding to the strength) occurs after the system was stretched to its contour length. Because at extensions larger than the contour length all covalent bonds rupture, the strength determined in our model is a measure of the number of unbroken chains when reaching the contour length. Because no chain ruptures prematurely in the non cross-linked reference system, all nine chains contribute to the strength of this system. It is the grafting density that significantly influences the number and topology of inter-chain cross-links and the probability of premature failure of the chains (see also Fig. 6A).
Fig. 6C and D shows that the work to fracture is significantly different from the work to elongate the system. The first is the work done to stretch the system to its contour length, while the latter one is the energy needed to elongate the system to the point, where the load-displacement curve finally drops to zero. When the chains are not inter cross-linked this additional contribution to the energy after the contour length is reached, is the same for all topologies and sticky site densities. Consequently, the work to elongate the system and the work to fracture are essentially the same. It is the chain failure before reaching the contour length that changes the situation. The work to fracture is now related to the strength of the system. The systems having a higher strength need more energy to fracture the system (see Fig. 6B and D). This is because the higher strength corresponds to a larger number of unbroken chains. On the other hand, the work to elongate the chain to its contour length is increased by a premature rupture of the chains. Thus, a large work to elongate the molecule corresponds to a low strength and work to fracture (see Fig. 6).
Fig. 6 shows the large impact that the grafting density has on the mechanical behavior of system. While changing the grafting densities from large to small the system essentially evolves from a system consisting of interacting chains to a system consisting of non-interacting, independent chains. This is shown by the steep increase in the position of the first backbone rupture from a value well below to a value well above the contour length. Simultaneously the strength as well as the work to fracture rise considerably, while the work to elongate the molecule shows a significant drop. All parameters take constant values when the grafting density is so small that the chains behave independently. Finally, it should be noted that a comparison of cross-linked and non cross-linked bundles shows that adding cross-links dramatically increases the stiffness of the system by a factor of almost 50 from Y = 1.7 meV/R2 to Y = 77 meV/R2. The stiffness Y is a measure of the slope of the load-displacement curve and is indicated by the dashed line in Fig. 5. Possibly the stiffness could be further enhanced if entanglement of the chains is allowed. When such entangled chains are stretched the points of entanglement provide an additional resistance to deformation yielding a higher slope in the load-displacement curves.
4 Conclusion
In this paper the influence of reversible cross-links on the mechanical behavior of polymeric chain-bundles was investigated. Simple systems containing only one or two short chains as well as more complicated systems made of nine, longer chains were studied. The results show that cross-links have a profound influence on the mechanical properties of the system. In particular it is the interplay of inter- and intrachain cross-links that is of utmost importance. Most interestingly the presence of cross-links may decrease the strength of the system. Depending on the grafting density only two cross-links may be sufficient to break the covalent backbone of one of the chains prematurely. On first sight, this is completely unexpected because one cross-link has only a quarter of the strength of a covalent bond. The simple systems investigated in the beginning of this paper discussed the possible topologies of cross-links responsible for such behavior. This premature rupture of the covalent bond reduces the maximum load the system can sustain before it breaks, thus it effectively decreases the strength of the system. On the other hand, the stiffness of the system is considerably enhanced.The results presented in this paper bear important implications to understand how natural materials are built to achieve their outstanding mechanical properties as well as to transfer these principles into new man-made materials. The presented results show that the grafting density is an essential parameter to tune the mechanical performance of inter cross-linked aligned fiber bundles.
Acknowledgements
We thank Oskar Paris and Peter Fratzl for fruitful discussions. Financial support from the Austrian Science Fund (FWF) in the framework of project P 22983-N20 is gratefully acknowledged.References
- F. Tanaka, Polymer Physics: Applications to Molecular Association and Thermoreversible Gelation, Cambridge University Press, 2011 Search PubMed.
- G. E. Fantner, E. Oroudjev, G. Schitter, L. S. Golde, P. Thurner, M. M. Finch, P. Turner, T. Gutsmann, D. E. Morse, H. Hansma and P. K. Hansma, Biophys. J., 2006, 90, 1411–1418 CrossRef CAS PubMed.
- B. L. Smith, T. E. Schäffer, M. Viani, J. B. Thompson, N. A. Frederick, J. Kindt, A. Belcher, G. D. Stucky, D. E. Morse and P. K. Hansma, Nature, 1999, 399, 761–763 CrossRef CAS.
- G. E. Fantner, T. Hassenkam, J. H. Kindt, J. C. Weaver, H. Birkedal, L. Pechenik, J. A. Cutroni, G. A. G. Cidade, G. D. Stucky, D. E. Morse and P. K. Hansma, Nat. Mater., 2005, 4, 612–616 CrossRef CAS PubMed.
- H. S. Gupta, P. Fratzl, M. Kerschnitzki, G. Benecke, W. Wagermaier and H. O. K. Kirchner, J. R. Soc., Interface, 2007, 4, 277 CrossRef PubMed.
- J. Keckes, I. Burgert, K. Frühmann, M. Müller, K. Kölln, M. Hamilton, M. Burghammer, S. V. Roth, S. Stanzl-Tschegg and P. Fratzl, Nat. Mater., 2003, 2, 810–814 CrossRef CAS PubMed.
- E. Oroudjev, J. Soares, S. Arcidiacono, J. B. Thompson, S. A. Fossey and H. G. Hansma, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6460 CrossRef CAS PubMed.
- N. Becker, E. Oroudjev, S. Mutz, J. P. Cleveland, P. K. Hansma, C. Y. Hayashi, D. E. Makarov and H. G. Hansma, Nat. Mater., 2003, 2, 278–283 CrossRef CAS PubMed.
- S. Keten, Z. Xu, B. Ihle and M. J. Buehler, Nat. Mater., 2010, 9, 359–367 CrossRef CAS PubMed.
- M. J. Harrington, H. S. Gupta, P. Fratzl and J. H. Waite, J. Struct. Biol., 2009, 167, 47–54 CrossRef CAS PubMed.
- M. J. Harrington, A. Masic, N. Holten-Andersen, J. H. Waite and P. Fratzl, Science, 2010, 328, 216–220 CrossRef CAS PubMed.
- D. S. Hwang, H. Zeng, A. Masic, M. J. Harrington, J. N. Israelachvili and J. H. Waite, J. Biol. Chem., 2010, 285, 25850–25858 CrossRef CAS PubMed.
- B. P. Lee, P. Messersmith, J. Israelachvili and J. H. Waite, Annu. Rev. Mater. Res., 2011, 41, 99–132 CrossRef CAS PubMed.
- D. S. Barnes and L. D. Pettit, J. Inorg. Nucl. Chem., 1971, 33, 2177–2184 CrossRef CAS.
- S. Keten and M. J. Buehler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061913 CrossRef PubMed.
- Z. Xu, Sci. Rep., 2013, 3, 2914 Search PubMed.
- O. Lieleg, J. Kayser, G. Brambilla, L. Cipelletti and A. R. Bausch, Nat. Mater., 2011, 10, 236–242 CrossRef CAS PubMed.
- K. M. Schmoller, P. Fernandez, R. C. Arevalo, D. L. Blair and A. R. Bausch, Nat. Commun., 2010, 1, 134 CrossRef CAS PubMed.
- K. W. Müller, R. F. Bruinsma, O. Lieleg, A. R. Bausch, W. A. Wall and A. J. Levine, Phys. Rev. Lett., 2014, 112, 238102 CrossRef PubMed.
- P. Benetatos, S. Ulrich and A. Zippelius, New J. Phys., 2012, 14, 115011 CrossRef.
- A. von der Heydt, D. Wilkin, P. Benetatos and A. Zippelius, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032701 CrossRef PubMed.
- P. Benetatos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 042602 CrossRef PubMed.
- C. K. C. Lieou, A. E. Elbanna and J. M. Carlson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012703 CrossRef PubMed.
- D. E. Makarov and G. J. Rodin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011908 CrossRef PubMed.
- A. E. Elbanna and J. M. Carlson, PLoS One, 2013, 8, e56118 Search PubMed.
- S. S. Nabavi, P. Fratzl and M. A. Hartmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032603 CrossRef PubMed.
- K. Eom, P.-C. Li, D. E. Makarov and G. J. Rodin, J. Phys. Chem. B, 2003, 107, 8730 CrossRef CAS.
- S. S. Nabavi, M. J. Harrington, O. Paris, P. Fratzl and M. A. Hartmann, New J. Phys., 2014, 16, 013003 CrossRef.
- K. Eom, D. E. Makarov and G. J. Rodin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 021904 CrossRef PubMed.
- H. P. Erickson, Science, 1997, 276, 1090–1092 CrossRef CAS PubMed.
- Q. Lin, D. Gourdon, C. Sun, N. Holten-Andersen, T. H. Anderson, J. H. Waite and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3782 CrossRef PubMed.
- J. H. Waite and C. C. Broomell, J. Exp. Biol., 2012, 215, 873 CrossRef CAS PubMed.
- Q. Lu, E. Danner, J. H. Waite, J. N. Israelachvili, H. Zeng and D. S. Hwang, J. R. Soc., Interface, 2013, 10, 20120759 CrossRef PubMed.
- I. Y. Phang, N. Aldered, X. Y. Ling, J. Huskens, A. S. Clare and G. J. Vancso, J. R. Soc., Interface, 2010, 7, 285 CrossRef CAS PubMed.
- E. Sackmann and A.-S. Smith, Soft Matter, 2014, 10, 1644–1659 RSC.
- E. Reister-Gottfried, K. Sengupta, B. Lorz, E. Sackmann, U. Seifert and A.-S. c. v. Smith, Phys. Rev. Lett., 2008, 101, 208103 CrossRef PubMed.
- S. F. Fenz, T. Bihr, R. Merkel, U. Seifert, K. Sengupta and A.-S. Smith, Adv. Mater., 2011, 23, 2622–2626 CrossRef CAS.
- Y. F. Dufrêne, Trends Microbiol., 2015, 23, 376–382 CrossRef PubMed.
- E. Degtyar, M. J. Harrington, Y. Politi and P. Fratzl, Angew. Chem., Int. Ed., 2014, 53, 12026–12044 CrossRef CAS PubMed.
- G. M. Moeser and E. Carrington, J. Exp. Biol., 2006, 209, 1996 CrossRef PubMed.
- T. Pearce and M. LaBarbera, J. Exp. Biol., 2009, 212, 1442 CrossRef PubMed.
- Z. Qin and M. J. Buehler, Nat. Commun., 2013, 4, 2187 Search PubMed.
- M. J. Harrington and J. H. Waite, in Fibrous Proteins, ed. T. Scheibel, Landes Bioscience, 2008, ch. Short-Order Tendons: Liquid Crystal Mesophases, Metal-Complexation and Protein Gradients in the Externalized Collagens of Mussel Byssal Threads, p. 30 Search PubMed.
- N. Holten-Andersen, H. Zhao and J. H. Waite, Biochemistry, 2009, 48, 2752–2759 CrossRef CAS PubMed.
- S. S. Nabavi, M. J. Harrington, P. Fratzl and M. A. Hartmann, Bioinspired, Biomimetic Nanobiomater., 2014, 3, 139–145 CrossRef.
- H. Lee, N. F. Scherer and P. B. Messersmith, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12999–13003 CrossRef CAS PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From algorithms to applications, Academic Press, 2002 Search PubMed.
- D. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, Cambridge University Press, 2009 Search PubMed.
- G. I. Bell, Science, 1978, 200, 618–627 CAS.
- J. Adams, G. E. Fantner, L. W. Fisher and P. K. Hansma, Nanotechnology, 2008, 19, 384008 CrossRef CAS PubMed.
- M. A. Hartmann and P. Fratzl, Nano Lett., 2009, 9, 3603–3607 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |