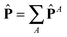Open Access Article
Open Access ArticleOpen boundary molecular dynamics of sheared star-polymer melts
Jurij
Sablić
a,
Matej
Praprotnik
*ab and
Rafael
Delgado-Buscalioni
*cd
aLaboratory for Molecular Modeling, National Institute of Chemistry, Hajdrihova 19, SI-1001 Ljubljana, Slovenia. E-mail: praprot@cmm.ki.si
bDepartment of Physics, Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia
cDepartamento Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, Campus de Cantoblanco, E-28049 Madrid, Spain. E-mail: rafael.delgado@uam.es
dCondensed Matter Physics Center, IFIMAC. Campus de Cantoblanco, E-28049 Madrid, Spain
First published on 15th January 2016
Abstract
Open boundary molecular dynamics (OBMD) simulations of a sheared star polymer melt under isothermal conditions are performed to study the rheology and molecular structure of the melt under a fixed normal load. Comparison is made with the standard molecular dynamics (MD) in periodic (closed) boxes at a fixed shear rate (using the SLLOD dynamics). The OBMD system exchanges mass and momentum with adjacent reservoirs (buffers) where the external pressure tensor is imposed. Insertion of molecules in the buffers is made feasible by implementing there a low resolution model (blob-molecules with soft effective interactions) and then using the adaptive resolution scheme (AdResS) to connect with the bulk MD. Straining with increasing shear stress induces melt expansion and a significantly different redistribution of pressure compared with the closed case. In the open sample, the shear viscosity is also a bit lowered but more stable against the viscous heating. At a given Weissenberg number, molecular deformations and material properties (recoverable shear strain and normal stress ratio) are found to be similar in both setups. We also study the modelling effect of normal and tangential friction between monomers implemented in a dissipative particle dynamics (DPD) thermostat. Interestingly, the tangential friction substantially enhances the elastic response of the melt due to a reduction of the kinetic stress viscous contribution.
1. Introduction
Die swelling1 is a well known phenomenon in polymer melts and most viscoelastic liquids which consist of the sudden expansion of the liquids after exiting a slit or orifice. The most frequent explanation has a microscopic origin: molecules elongate in the stream direction and compress perpendicularly exerting extra elastic pressure in the normal planes. This leads to the so-called normal stress differences which are the landmark of viscoelasticity. Despite this accepted view, the devil is in the details and although considerable effort has been carried out since the middle of the last century (see e.g.ref. 1 for historic details), accurate modelling of polymer melts is a very difficult task. Any of the many constitutive relationships1 for continuum models cannot generally predict the rheology of a new molecular polymer design. In turn, the huge span in time scales in any standard polymer melt limits the scope of molecular dynamics (MD) to simple rheological tests with extremely small samples under simple (usually steady) flows. However, a detailed account of bonded and non-bonded interactions in atomistic (AT) simulations (see e.g.ref. 2–4) is able to grasp relevant information, maybe then to feed continuum (fluid dynamics) models. In between, coarse grained (CG) molecular modelling is useful due to many reasons. We give at least a couple of reasons: first, polymer science has some degree of universality which benefits the use of simplified models, quite often able to provide insight and valuable predictions.4,5 Second, the theory of coarse graining to extract precise coarse potential interactions pertaining to the atomistic model at hand is now advancing at a relatively fast rate.4,6,7 More recently, the community has started to recognize the relevance of the dynamic aspects of coarse graining either based on GENERIC8 or the Mori–Zwanzig formalism.9 The idea is to perform short atomistic simulations8 to extract the quantities determining the reversible and irreversible dynamics of the slow variables, such as the friction kernels.9 These friction kernels (between polymer “blobs”) are naturally implemented in the dissipative particle dynamics (DPD) method as, notably, Español et al.9 showed (under the Markovian and pairwise approximations) that DPD can be formally derived from the Mori–Zwanzig coarse graining route. Another relatively newer route is the use of hybrid models concurrently combining continuum and molecular simulations. Yasuda et al.10 and other (mostly Japanese) groups have exploited a version of these hybrids to model polymer melts. We have also worked in this field using essentially the same technique used in this work for simple fluids.11,12 Contrary to Yasuda et al.10 and other hybrid schemes, the present method is designed to open up the simulation box so as to consider melt expansions. Here, we apply the idea to study the rheology of much larger, polymeric molecules. At present, we restrict to the open boundary molecular dynamics (OBMD) simulation,13 without connection to the continuum side. However, the present method naturally connects with continuum fluid dynamics via hybrid schemes.14–20Another aspect of this work is the use of DPD as a tool to check the effect of monomer friction on the rheological behaviour of these CG models. In particular, the tangential friction between blobs naturally arises while performing dynamic coarse graining9 but is seldom included in these sort of analyses (see for example the DPD study for melts by Fedosov et al.21). To conclude our comments on methodological aspects, we also note that the present simulations in open domains use a useful trick which consists of using an even lower detailed molecular model to feed the molecular reservoir close to the open system boundaries. The idea is taken from the so-called “adaptive resolution scheme” (AdResS)22–34 and permits to generalize the use of AdResS in standard periodic (closed) boxes (see e.g.ref. 11, 12 and 35–37).
The main physical question we pose here is what are the rheological consequences of imposing a fixed pressure load to a sheared sample of polymer melt, compared to the case of shearing at a fixed volume. This question was also raised by a bunch of groups spread over the last two decades38–43 with contradictory results. It is indeed a particularly relevant question for molecular simulations because the vast majority of numerical studies on melts have considered closed (usually periodic) systems, while many rheological experiments are carried out under a normal load: melts across slabs in ref. 44 (cited experiments therein) or a cone and plate rheometry under a fixed load.1
From the fundamental side, this question connects with the already mentioned die swelling phenomenon whose details are still not completely understood. It also connects with another interesting question which is, what consequences do boundary constraints have on flowing (far-from-equilibrium) polymer melts (see ref. 45 for a recent study). The OBMD is a flexible tool for these questions on boundary constraints because it can be tuned to permit different ensembles46 such as the grand canonical, isoenthalpic, isothermal, constant stress (Neumann-like) or constant shear (Dirichlet-like).14 In particular, it could be useful to validate theories for non-equilibrium thermodynamics (such as extended thermodynamics47,48), or the far from trivial fate of fluctuations of mass (related to sound modes) and momentum in sheared complex fluids, which often lead to undesirable instabilities in sheared or extruded melts, like the shark skin.1,49
Even in unentangled melts, the influence of boundary or global constraints on the density expansion of sheared melts is still poorly understood with the studies presenting contradicting results. At least there is a consensus on the fact that for a given shear, the shear viscosity η is larger in the isochoric (NVT) constraint than under either a constant pressure39,40 or a constant load.43,44 A clear manifestation of this effect was presented in a numerical study of Thompson et al.,44 in which a slab of lubricating liquid (20-mers) flowing between two solid walls presented a shear thinning exponent βη ≃ 2/3 under a constant normal load, while just 0.5 under a constant volume (here η ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −βη with
−βη with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) the shear rate). This effect has been ascribed to the shear dilatancy manifesting in a larger hydrostatic pressure under a constant volume.39,40 Indeed, the viscosity of polymer melts often increases with the pressure49 as also observed in ref. 44. In Section 6, we offer a more precise analysis showing that the spring stress is reduced in the open system due to the smaller intermolecular friction in the expanded melt.
the shear rate). This effect has been ascribed to the shear dilatancy manifesting in a larger hydrostatic pressure under a constant volume.39,40 Indeed, the viscosity of polymer melts often increases with the pressure49 as also observed in ref. 44. In Section 6, we offer a more precise analysis showing that the spring stress is reduced in the open system due to the smaller intermolecular friction in the expanded melt.
There are several kinds of “isobaric” conditions: a constant hydrostatic pressure (Piso) is usually termed isobaric, while a constant normal load (here P22) is closer to industrial processes like slit extrusion1 or lubricants.44 Both can show substantially different rheological behaviours when compared with constant volume studies (see e.g.ref. 44). Experimental studies of the Couette flow under a constant load are also scarce and indicate shear expansion and a measurable increase of the melt viscosity with increasing external pressure.50,51
The most striking differences in the computational literature are found in the density variation with shear. Dlugogorski38 (for a FENE dumbbell) and Daivis and Evans (modelling decane)39 seem to be the first to perform a molecular simulation showing the density decrease under shear (using isobaric conditions). Daivis and Evans use the term “shear dilatancy”, following the term used by Reynolds on the same phenomenon (see the quotation in ref. 39). Note that “shear dilatancy” has been later often used instead of “shear thinning”, but here it is not. By contrast, Xu et al.40 (attractive linear chains up to 50-mers) reported just the opposite result (compression under shear). For (purely repulsive) branched chains (under NVT), they also reported a reduction in the hydrostatic pressure with shear. A subsequent study by Matin43 for linear chains at a constant load (and chain lengths up to 50 monomers) found shear dilatancy and also a non-monotonous trend for the hydrostatic pressure (as Xu et al.40 and others2,3 did). Shear dilatancy was later also found by Bosko et al.41 while analysing dendrimer melts under isobaric conditions. Consistently, they found a pressure increase under a constant volume. Shear dilatancy is the trend we also observe but, under our imposed constant normal load (which is closer to the experimental setup1,39,44) we find that the density (and viscosity) is controlled by the load and not by the hydrostatic pressure. However, there is a lack of studies and the question remains about universality of shear dilatancy of polymer melts under a Couette flow (consistent with the die swelling phenomenon under a Poisson flow1).
To conclude the introduction some words should be said about the technological relevance of star molecules (see discussion in ref. 52–54) which certainly arises from their unique dynamic features. Star molecules present a broad range of relaxation times associated with different molecules pulsations (rotation, elastic deformation, and arm entanglements) analysed in ref. 53. Each relaxation time triggers a change in the rheological regime once the external perturbation (shear) exceeds the corresponding threshold rate. The present results also illustrate this phenomenon. Moreover, star molecules bridge the gap between linear polymers and colloids54,55 and can present interesting (colloidal-like) ordering effects, sometime enhanced due to their softer character.53,56–59 In this context, a suggesting observation in these simulations is the onset of some ordering in the neutral direction at large shear rates whose origin (hydrodynamic or entropic) remains to be established.
In Section 2, we briefly present the OBMD method which was otherwise more thoroughly explained in ref. 13. The star molecule melt model presented in Sections 3 and 4 shows that the OBMD correctly reproduces thermodynamic equilibrium according to the grand canonical ensemble. In Section 5, we present the results for sheared melts in the absence of tangential friction between monomers and analyze the results in Section 6 according to the pressure balance. This serves to enlighten the discussion on the effect of tangential friction in Section 8. Finally, Section 9 discusses some interesting results obtained for melts presenting severe viscous heating that depends on the characteristics of the DPD thermostats and their friction kernels. Comparison with the previous results is made in Section 10, while conclusions and future outlook are given in Section 11.
2 Open boundary molecular dynamics
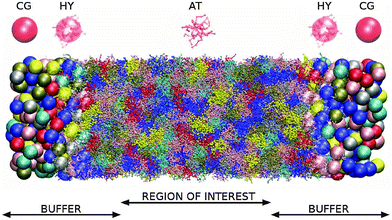
We begin by briefly explaining the OBMD method which combines features of the open MD46 and adaptive resolution.11 The reader is referred to a review on open MD14 and ref. 13 for a more detailed presentation of the present OBMD implementation to star polymers. The OBMD simulation is carried out in an open rectangular box which, in the present setup, permits the MD domain to exchange mass and momentum through two of its boundaries (along the x2 direction) with a reservoir (called buffer) which is maintained at some desired thermo-mechanic state. The two domains of finite extent of the buffer embed the central part of the box (the MD domain). They allow for molecular insertion or deletion so as to keep their average molecular density fixed (typically to a fraction between 0.5 and 0.7 of the bulk density). The OBMD is therefore not periodic in the coupling direction. Molecules are free to enter or leave the buffer from or to the MD domain, but in doing so they cross another layer where they gradually change their atomistic resolution (73 monomers for the star molecule considered hereby) to a reduced CG model, comprising one only spherical “blob” per molecule. Obviously the CG layer is placed inside the buffer domain (which here also contains a smaller atomistic part). This strategy permits to perform an otherwise impossible task: the insertion of new polymeric molecules into the melt. New molecules are inserted into the low resolution layer of the buffer, where soft CG interactions govern the dynamics of the blob-model polymers. Soft effective interactions can be obtained from the Boltzmann iteration procedure,60,61 although we shall see that in principle, the consistency of OBMD (in terms of pressure balance across the layers) does not depend on the CG potential chosen. The insertion of these blob molecules is carried out by the USHER scheme62 and the change from CG to monomer molecular resolution (usually termed atomistic resolution, AT) is carried out by the AdResS.22–34The dynamics of the monomers can be described by the following equations of motion:
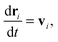 | (1) |
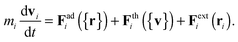 | (2) |
The adaptive resolution force Fadi is constructed to allow for a momentum conserving “alchemic” transformation of the molecules, which takes place gradually along the transition layer (where 0 < w < 1, see below). The transition is achieved by the following linear combination of the AT and CG forces (FATαβ and FCGαβ, respectively),22
| Fadαβ = w(xα)w(xβ)FATαβ + (1 − w(xα)w(xβ))FCGαβ. | (3) |
An essential function of the buffer region is the imposition of boundary conditions to the open MD box. This is done by adding an extra “external” force at the buffer regions, Fext, calculated from eqn (4) (see e.g.ref. 66).
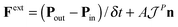 | (4) |
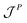 is the momentum flux tensor, while n is the outward normal vector of an open-end plane of the box.11 In general, the pressure tensor contains normal and tangential contributions, i.e.
is the momentum flux tensor, while n is the outward normal vector of an open-end plane of the box.11 In general, the pressure tensor contains normal and tangential contributions, i.e.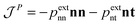 . The external force is designed to exactly conserve the linear momentum over the whole particle system (buffer + MD) and it is distributed among the buffer particles according to Fexti = G(xi)Fext. To allow a different distribution of the normal and tangential forces, the distribution function G is chosen to be a tensor defined by eqn (5),13
. The external force is designed to exactly conserve the linear momentum over the whole particle system (buffer + MD) and it is distributed among the buffer particles according to Fexti = G(xi)Fext. To allow a different distribution of the normal and tangential forces, the distribution function G is chosen to be a tensor defined by eqn (5),13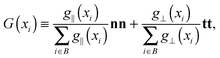 | (5) |
Many OBMD applications (as those illustrated hereby) involve transfer of momentum (the pressure tensor) from outside the MD domain. This requires a momentum conserving thermostat. In production runs, we used the DPD thermostats (while a strong damping Langevin for equilibration purposes). Our choice for the DPD thermostat is not only to conserve momentum (in principle one could use the Lowe-Andersen67) but also because of modelling purposes. The Mori–Zwanzig formalism, under Markovian conditions leads to coarse-graining dynamics with DPD-like equations of motion.9 The solid theoretical results show that the friction kernels introduce an important modelling aspect. The friction kernels in a CG model of some real melt, should ideally be measured from force–force correlations of the detailed all-atom model.9 Here, we adopt a simpler but yet useful route, which is to study how friction affects the rheology of the model melt. The generic form of the DPD thermostat used is
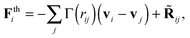 | (6) |
![[R with combining tilde]](https://www.rsc.org/images/entities/b_char_0052_0303.gif) ij is the fluctuating force constructed to satisfy the fluctuation-dissipation under equilibrium conditions. We refer the reader to ref. 68–70 for details on the DPD implementation. As in ref. 9, 69 and 70 the friction kernel has normal and tangential components,
ij is the fluctuating force constructed to satisfy the fluctuation-dissipation under equilibrium conditions. We refer the reader to ref. 68–70 for details on the DPD implementation. As in ref. 9, 69 and 70 the friction kernel has normal and tangential components,| Γ = γ∥nijnij + γ⊥tijtij, |
| Label | Kernel cutoff (RDPDcut) | γ ∥ | γ ⊥ |
|---|---|---|---|
| Sdpdshort | 21/6σ | [1.0–20.0] | 0 |
| Sdpdlong | 1.5 × 21/6σ | 1.0, 5.0 | 0 |
| Adpd | 21/6σ | 1.0, 5.0 | 0 |
| Tdpd | 1.5 × 21/6σ | 1.0 | 1.0 |
In the following sections, we present and analyse the results obtained for the DPD thermostat with no tangential friction between monomers (blobs). This analysis is then used to understand the effect of the tangential friction, considered in Section 8. In the case of the normal friction alone, the substantial heat dissipated by the sheared melt requires from us to implement a slight modification of the DPD thermostat to maintain a constant (kinetic) temperature at the largest shear rates. Details of this modified DPD thermostat (we call it “adaptive”) and friction kernels are given in Section 3.
Importantly, simulations in closed isothermal (periodic) boxes (NTV) are used as a reference to investigate the effect of open boundaries. Shear flow in the closed system has been simulated using Lees–Edwards boundary conditions71 and the SLLOD algorithm.72,73
3 Setup and melt models
The simulation setup is illustrated in Fig. 1 and 2. The polymer melt is exposed to a Couette flow in the x1 direction being sheared along the x2 direction (gradient direction). The vorticity or neutral direction is x3. In the closed box, we use the SLLOD72,73 dynamics to impose the desired shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) in a closed periodic box (with a constant particle number and volume). In the open setup, the surfaces located at x2 = ±L2/2 are subjected to equal normal pressures pext22 and (opposite sign) tangential stresses ±pext12, in such a way that the rotational part of the shear flow turns counter-clockwise in the flow–gradient (x1 − x2) plane. No constraint is imposed to the remaining component of the pressure tensor, resulting in 〈p13〉 = 0 and a self determined 〈p33〉. The box is periodic in the other two directions x1 and x3 so this setup corresponds to an slice of polymer melt with a fixed load at two of its boundaries (at x2 = ±L2/2).
in a closed periodic box (with a constant particle number and volume). In the open setup, the surfaces located at x2 = ±L2/2 are subjected to equal normal pressures pext22 and (opposite sign) tangential stresses ±pext12, in such a way that the rotational part of the shear flow turns counter-clockwise in the flow–gradient (x1 − x2) plane. No constraint is imposed to the remaining component of the pressure tensor, resulting in 〈p13〉 = 0 and a self determined 〈p33〉. The box is periodic in the other two directions x1 and x3 so this setup corresponds to an slice of polymer melt with a fixed load at two of its boundaries (at x2 = ±L2/2).
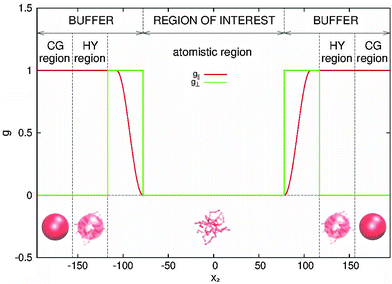 | ||
| Fig. 2 Buffer distribution function. The force Fext, that acts on buffer regions in order to impose the boundary conditions at open ends of the box to the region of interest, is distributed among molecules inside buffers via the depicted functions, forming the distribution function tensor G, given by eqn (5). The force acting on each molecule equals Fexti = G(xi)Fext. | ||
The melt is made of the star polymer model already presented in ref. 9 and 74. Each polymer consists of 73 monomers, i.e. 12 arms of 6 monomers attached to the central monomer. In what follows, we use m0, σ0 and ε0 for mass, length and energy units and we will arbitrarily set these units to m0 = 1, σ0 = 1, and ε0 = 1, respectively. The resulting time unit is τ0 = σ0(m0/ε0)1/2 = 1. Excluded volume interactions of monomers are modelled by the repulsive Weeks–Chandler–Anderson interaction with diameter parameter σ = 2.415σ0 and energy parameter ε = 1. The interactions between two adjacent bonded monomers are harmonic with a linear spring of stiffness constant K = 20.0ε/σ02. The equilibrium distance between non-central monomers is reqij = 2.77σ0, while the equilibrium distance between the central monomer and the first monomer of an arm is reqij = 3.9σ0. The size of the simulation box is 390 × 117 × 117 (in units of σ0).
Simulations were performed at a fixed constant (monomer's kinetic) temperature (T = 4.00 ± 0.01). The results presented in the following sections correspond to simulations obtained using a modified DPD thermostat which we label as “adpd”. This adpd thermostat has no tangential friction γ⊥ = 0 while γ∥ = 1 (some results also with γ∥ = 5). The cutoff of the Heaviside friction kernel is Rdpd = 21/6σ. We refer to Table 1 for thermostat and kernel details. We recall that the effect of the tangential friction is analysed in Section 8. In Section 9, we illustrate the heat dissipation and temperature increase observed upon using standard thermostats DPD with normal friction.
Thermostating sheared polymer melts is a delicate issue due to the large amount of heat they dissipate. At a large enough shear rate or large shear stress, the temperature of the melts increases. The same phenomenon is also observed in experiments and industrial processes (extrusion) at high shear rates (typically above 500 Hz).47,75,76 Phenomenological temperature “corrections” for the melt viscosity are often used in industry and experiments.77 Although this problem goes beyond the present manuscript, the temperature of a system under a non-equilibrium steady state is also a fundamental problem because equipartition is lost and the different temperature definitions present slight variations (kinetic versus configurational temperature78). In the literature, few studies report on the problem of viscous heating in molecular simulations (see the exceptions in ref. 79–81) and many published materials elude reporting on possible temperature variation in their sheared thermostated systems. After the present experience, we believe that some of the data presented in previous papers might be somehow biased by temperature. We will show an indication later in Section 9.
We considered four different thermostats: the “standard” (sdpd)69 and “transverse” (tdpd)70 DPD thermostats and also a modified DPD thermostat. The latter is able to extract larger amounts of heat by self-adapting its temperature parameter TDPD which controls its random force term. This “adaptive DPD thermostat” (adpd) as we call it, dynamically adjusts TDPD according to a sort of coupled heat equation,
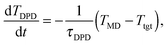 | (7) |
The thermostat time τDPD (acting like a coefficient of heat transfer to the “reservoir”) was set to τDPD = 100δt. The thermostat nominal temperature TDPD was updated using a simple explicit Euler scheme for eqn (7) with a time step of 100δt. All the thermostats used are applied to the relative velocities of monomers. The friction kernels of the DPD thermostats (damping and noise terms are constructed using the same kernel70) are chosen to be Heaviside functions with a cutoff distance RDPDcut, i.e. γ(R) = 1 for R ≤ RDPDcut and zero otherwise.
All the results presented here correspond to a normal friction kernel γ∥ = 1 (some results for the adpd thermostat were also carried out for γ∥ = 5 to test sensitivity). To test the effect of tangential friction we also run simulations with γ∥ = γ⊥ = 1 in the tdpd thermostat. The thermostat details and labels used are given in Table 1.
The integration step ranges from δt = 0.01τ0 to δt = 0.005τ0 for the highest shear rates. Note that τ0 = 1 is smaller than the standard Lennard-Jones time (monomer–monomer interaction), τ = σ(m/ε)1/2 = 2.415τ0 where m = 1 is the monomer mass.
The equilibration of the lump of melt in the OBMD simulation is conducted by a modified version of the AdResS, whereby the weighting function w in eqn (3) is gradually increased in time starting from w = 0 (CG model).83 The weighting function is therefore switched from a position-dependent to a time-dependent one. The resolution is thus gradually sharpened from CG to AT. The procedure is described in detail in ref. 13. After equilibration, each simulation is run for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ0.
000τ0.
4 Melt at equilibrium
4.1 Characteristic times
In view of the close relationship between the structure and dynamics that takes place in sheared melts (and complex fluids in general), it is interesting to present the range of physical times of the melts before analysing their structural transformation with shear. In star polymers, one can observe three types of relaxation phenomena.84 First is elastic deformation of the overall shape of polymers, second relaxation occurs via the rotational diffusion, and the third one regards disentanglement of arms of every star polymer. Each of the relaxation processes can be estimated from the integral of the corresponding normalized autocorrelation function (ACF), via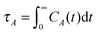 , and these are given by eqn (8)–(10), respectively.
, and these are given by eqn (8)–(10), respectively.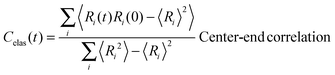 | (8) |
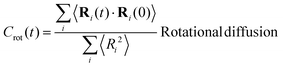 | (9) |
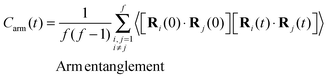 | (10) |
| Simulation | τ arm | τ elas | τ dif | τ rot |
|---|---|---|---|---|
| Open sdpdshort | 33 ± 2 | 6 ± 1 | 800 ± 100 | 55 ± 5 |
| Closed sdpdshort | 33 ± 2 | 6 ± 1 | 800 ± 100 | 55 ± 5 |
| Open sdpdlong | 55 ± 2 | 10 ± 1 | 1200 ± 100 | 100 ± 5 |
| Closed sdpdlong | 55 ± 2 | 10 ± 1 | 1100 ± 100 | 100 ± 5 |
| Open adpd | 33 ± 2 | 3 ± 1 | 700 ± 100 | 59 ± 5 |
| Closed adpd | 33 ± 2 | 3 ± 1 | 800 ± 100 | 59 ± 5 |
| Open tdpd | 195 ± 5 | 35 ± 5 | 4800 ± 400 | 332 ± 5 |
Using the adpd thermostat (normal friction alone) we get τelas = 3 ± 1, τarm = 33 ± 2, τrot = 59 ± 5 and τdif = 700 ± 100, which illustrates the wide range in time scales involved in these sort of simulations. These times are similar in the open and closed systems (in equilibrium) and are compared with those obtained with other thermostats and kernels in Table 2. However, as shown below the rheology of the melt is not determined by the molecular diffusion, but rather by the molecular relaxation times. For the star molecule under study with f = 12 arms of length la = 6σ (i.e. 6 monomers per arm), molecular rotation is slower than the elastic relaxation of arms, the ratio being τrot/τarm > 10 in all the cases considered (see Table 2). This ratio determines the type of rheological behaviour of the melt according to a theoretical approach based on solving the Fokker–Planck equation for the bond distribution.88,89 We will come back to this issue in Section 5.3.
4.2 Equation of state
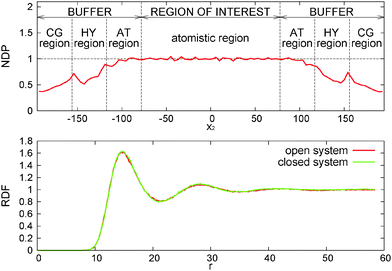
As explained in ref. 13, the OBMD simulations of the melt at equilibrium provide the correct average thermodynamic variables. The pressure equation of state obtained in OBMD agrees with that obtained from a standard NVT simulation for all the volume fractions studied.13 More precisely, the average equilibrium density 〈ρ〉 (pext22) obtained with OBMD at a fixed normal pressure pext22 is consistent with the equilibrium pressure p calculated in a closed MD simulation at a fixed density ρ = 〈ρ〉 (pext22). In passing, it should be highlighted that the same CG potential was used for all the melt densities considered, indicating that the pressure consistency at the MD domain is independent of the coarse-grained potential used in the buffer.In the following, we work with the polymer volume fraction, defined as Φ = ρNπσ3/6, where ρN = N/V is the number density (N and V respectively represent the number of monomers and the volume of the region of interest and the mass density is ρ = mρN with monomer mass m = 1, thus ρ = 0.136Φ). For the NVT ensemble, the study conducted here corresponds to p = (0.093 ± 0.001) and Φ = 0.20, fixed for any shear rate. In the open box, we fix pext22 = 0.093 and for zero shear rate (equilibrium) we get 〈Φ〉 = (0.20 ± 0.01). Fig. 3 shows the normalised density profile of polymers (ρslabM/ρavgM). Here ρslabM denotes mass density of polymers in each slab, where it is measured, and ρavgM its average value. The latter is constant in closed simulations, i.e. ρavgM = 0.0271, while its calculated value in open cases equals ρavgM = 0.0271 ± 0.0001. We observe that the obtained density profile is flat in the region of interest with some minor artefacts, which are due to the lack of statistics. Along the buffer zones the density gradually decreases as a consequence of the application of the external pressure pext22. As it has been explained in previous related studies on hybrid atomistic-continuum schemes,14,66 this inhomogeneity does not affect the transfer of pressure and stress from the exterior, provided that the density profile is flat around the hybrid interface. This is indeed the case, as it can be seen in Fig. 3 (see the interface between the “region of interest” and “buffer”). The radial distribution function (RDF) of CoMs of molecules is in perfect agreement with NVT simulations.
4.3 Mass fluctuations
In the grand canonical ensemble, mass fluctuations are related to the integral of the RDF,90 so the excellent agreement between the RDFs obtained from NVT and open boxes suggest that the fluctuations in the number of molecules inside the domain of interest should be thermodynamically consistent with the grand canonical prescription: namely, the relative fluctuation in polymer mass M = ρMV should be Std[M]/M = [kBT/(McT2)]1/2, where cT is the isothermal sound velocity cT2 = (∂p/∂ρ)T. cT, which is evaluated using the pressure equation of state from ref. 13, is shown in Fig. 4. The agreement between OBMD and the NVT ensemble is excellent. In the same figure, we plot the results for the relative mass fluctuations at different pressures (average densities) and compare with the grand canonical prediction. We find that the agreement is very good, notably because of the tiny relative mass fluctuations in the (not small V = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504
504![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384σ03 = 248
384σ03 = 248![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 805σ3) volume considered for our open box: which range between 3.6% and 0.26% at the largest density considered (Φ = 0.2). In terms of mass density variance σρ2 = ρkBT/(VcT2), for the state we considered hereafter under shear (p = 0.093ε0/σ03, Φ = 0.2 and ρ = 0.0271m0/σ03) the OBMD result is σρ2 = (5.0 ± 0.3) × 10−9m0/σ03 in excellent agreement with the variance predicted for the μVT ensemble 4.79 × 10−9. The conclusion of this study strongly supports our claim that the OBMD equilibrium simulation samples the grand canonical ensemble without any (or negligible) bias. It has to be said that the value of the external chemical potential μext = μ(pext22,T) however cannot be imposed in OBMD, although it could be reconstructed following the standard Gibbs–Duhem route with varying external pressure. New implementations of the AdResS29,65 might also be used to evaluate μ.
805σ3) volume considered for our open box: which range between 3.6% and 0.26% at the largest density considered (Φ = 0.2). In terms of mass density variance σρ2 = ρkBT/(VcT2), for the state we considered hereafter under shear (p = 0.093ε0/σ03, Φ = 0.2 and ρ = 0.0271m0/σ03) the OBMD result is σρ2 = (5.0 ± 0.3) × 10−9m0/σ03 in excellent agreement with the variance predicted for the μVT ensemble 4.79 × 10−9. The conclusion of this study strongly supports our claim that the OBMD equilibrium simulation samples the grand canonical ensemble without any (or negligible) bias. It has to be said that the value of the external chemical potential μext = μ(pext22,T) however cannot be imposed in OBMD, although it could be reconstructed following the standard Gibbs–Duhem route with varying external pressure. New implementations of the AdResS29,65 might also be used to evaluate μ.
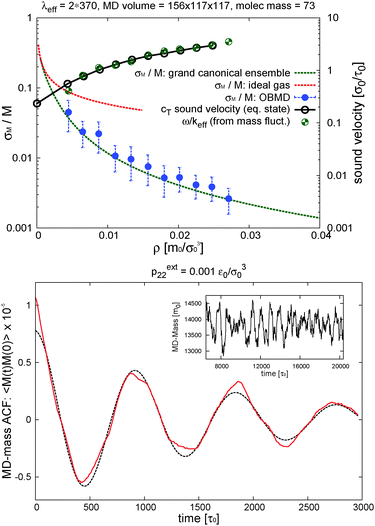 | ||
| Fig. 4 Top panel: The relative fluctuation of the polymer mass (standard deviation over average polymer mass M) in the interest MD-domain of the open setup (see Fig. 2). Comparison is made with the grand canonical theoretical result (green dashed line) Std[M]/M = [kBT/(McT2)]1/2 and, also included, the ideal gas limit (red dashed) obtained with the isothermal sound velocity cidT = (kBT/Mm)1/2 with Mm = 73m0 the molecular mass. The volume of the interest domain is V = 156 × 117 × 117σ03. Recall that the monomer LJ diameter is σ = 2.415σ0 and its mass is m0 = 1. The right ordinate axis shows the values of the isothermal sound velocity cT = (∂p/∂ρ)T (from the pressure equation of state) that is compared with ω/keff obtained from the oscillation frequency ω of the total mass autocorrelation function in the MD domain (see bottom panel). The effective wavenumber is keff = (π/370)σ0−1 and the total open box is L2 = 390σ0. Bottom panel: the time autocorrelation function of the mass in the MD domain at equilibrium with imposed external pressure pext22 = 0.001ε0/σ03 (dashed line is the fit to extract ω, see text); the inset illustrates the evolution of the total mass in the MD domain for this case. | ||
A typical outcome for the time evolution of the total mass of polymers in the MD domain is shown in Fig. 4. It presents oscillations, suggesting that it might contain some information about the sound velocity of the system.
Sound propagation can indeed be studied in our simulations because we work with momentum preserving (DPD) dynamics (by contrast, sound is damped in the standard Langevin dynamics). It is noted that an “ideal” open system should be transparent to all waves, meaning that all waves, either created by inner mass fluctuations of any wavelength or by external waves travelling across, should leave the system and do not reflect back. This implies, in particular, that in the absence of external longitudinal forces, fluctuations of the total mass should have no memory, being a white noise (or at least a broad-band signal).91 The presence of correlations in the total mass of our “region of interest” is in fact due to partial reflections of waves at the rarefied buffers, where density fluctuations are reduced (recall we fix the average total mass of these reservoirs, see e.g.ref. 66). In the autocorrelation (ACF) of the total mass fluctuation, the dominant wavelength should obviously be the largest possible one compatible with this condition and the total simulation box length. A density mode with wavenumber k = 2π/λ decays like 〈ρ(k,t)ρ(k,0)〉 = 〈δρ2〉exp[−νLk2t]cos[ωt] with νL being the sound attenuation coefficient92 and ω = cTk the oscillation frequency. Inspection of Fig. 3 indicates that the density profile of the whole system (MD + buffer) roughly conforms to Dirichlet boundary conditions with a fixed density at the end of the buffer domains ρ(x2 = ±L2/2)<ρ0. In such a case, the longest wavelength available to mass fluctuations of the system would be λeff ≃ 2L2. We fitted the time autocorrelation function of the MD mass to extract ω and compare it with the ansatz ω = cTkeff using ω = cTkeff with keff = 2π/λeff. The best fit to the simulation results corresponds to λeff = 760σ0, while 2L2 = 780σ0 and it is shown in Fig. 4 in terms of ω/keff and compared with the sound velocity of melt cT. The excellent match confirms that the mass in the MD domain has memory induced by reflections of sound waves against the low density domains (buffers). Such reflections could be reduced by coupling the MD with a continuum hydrodynamic field outside,66 or by imposing a non-reflecting boundary condition91 (still to be generalized to MD, see also ref. 92). However, in the present scenario we find that these results are quite interesting because they suggest the possibility of measuring the sound velocity cT from the fluctuations of the total MD mass. In particular, it might allow to measure how the sound velocity is modified in a sheared melt, cT(Wi). Although a detailed study would be certainly required, just as an indication, we find that cT(Wi) (estimated in this way, i.e. from mass fluctuations) decreases.
5 Sheared melt with normal friction
This section presents results for the star molecule model with zero tangential friction between monomers. Kernel and thermostat details (adpd) are given in Sections 3 and 4. We decided to first focus on this model to avoid embarrassing the discussions with details of different cases (open versus closed, normal versus tangential friction) and also because this model presents a richer dynamical behaviour, whose analysis will be useful to understand the effect of tangential friction in Section 8.5.1 Weissenberg number
The Weissenberg number Wi is a useful number to compare and dissect different regimes in polymer rheology. It is defined asWi = τrel![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , , | (11) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1 is the “shear flow time” needed to affinely deform a square box of sheared fluids into a parallelepiped with an angle of 45° between adjacent planes. As stated, in eqn (9) and Table 2, the longest relaxation of our star polymer is related to the molecular rotation so τrel = τrot in eqn (11). In fact, the diffusion of the CoM of the molecules is much slower (see Table 2). The CoM diffusion does not directly sample the structure of molecules, whose modification under flow is related to the non-Newtonian character of polymers. The Peclet number determines the ratio between CoM diffusion and flow advection Pe = τdif
−1 is the “shear flow time” needed to affinely deform a square box of sheared fluids into a parallelepiped with an angle of 45° between adjacent planes. As stated, in eqn (9) and Table 2, the longest relaxation of our star polymer is related to the molecular rotation so τrel = τrot in eqn (11). In fact, the diffusion of the CoM of the molecules is much slower (see Table 2). The CoM diffusion does not directly sample the structure of molecules, whose modification under flow is related to the non-Newtonian character of polymers. The Peclet number determines the ratio between CoM diffusion and flow advection Pe = τdif![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and for our setup it is about 10 times larger than Wi. In colloidal suspensions, the shear thinning typically starts for Pe > 1 due to shear banding. Interestingly, star polymers constitute a sort of bridge between the open structures of linear polymers and the compactness of colloids. Thus, one might elucubrate that the onset of shear thinning in compact stars could well be due to shear banding (collective molecular ordering in lanes), rather than by (individual) polymer elongations. We shall see later on that both (collective and individual) effects take place in our sheared system, although we advance that the transition to the non-Newtonian regime takes place at Wi = τrot
and for our setup it is about 10 times larger than Wi. In colloidal suspensions, the shear thinning typically starts for Pe > 1 due to shear banding. Interestingly, star polymers constitute a sort of bridge between the open structures of linear polymers and the compactness of colloids. Thus, one might elucubrate that the onset of shear thinning in compact stars could well be due to shear banding (collective molecular ordering in lanes), rather than by (individual) polymer elongations. We shall see later on that both (collective and individual) effects take place in our sheared system, although we advance that the transition to the non-Newtonian regime takes place at Wi = τrot![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > 1. Hence at least for the (not so compact) star polymer studied here, shear thinning is not determined by collective ordering at straining rates faster than the CoM diffusion. The hybrid character of star molecules (between colloids and polymers) is the subject of current research.56–58
> 1. Hence at least for the (not so compact) star polymer studied here, shear thinning is not determined by collective ordering at straining rates faster than the CoM diffusion. The hybrid character of star molecules (between colloids and polymers) is the subject of current research.56–58
5.2 Density and hydrostatic pressure
Denoting the symmetric pressure tensor (exerted by the melt) as Pα,β, the hydrostatic pressure is defined as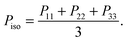 | (12) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) along with the molecular structure. The density (in the open domain) and pressures (P22 in NVT and also Piso in both cases) are quite sensible to temperature changes, as shown in Section 9.
along with the molecular structure. The density (in the open domain) and pressures (P22 in NVT and also Piso in both cases) are quite sensible to temperature changes, as shown in Section 9.
5.3 Rheology
We start by determining the zero shear viscosity, η0 = η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0). A standard way is the Green–Kubo equilibrium route (via the integral of the time autocorrelation of shear stress).93 To maintain consistency with the non-equilibrium route we follow the experimental approach which fits the trend for η(
= 0). A standard way is the Green–Kubo equilibrium route (via the integral of the time autocorrelation of shear stress).93 To maintain consistency with the non-equilibrium route we follow the experimental approach which fits the trend for η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) for a range of values of the shear rate with some suitable expression such as the popular Carreau fit.50,94 We also checked that Green–Kubo viscosities95 are similar to the Carreau-fitted ones within statistical uncertainty (about 10%). The Carreau fit has the following expression,
) for a range of values of the shear rate with some suitable expression such as the popular Carreau fit.50,94 We also checked that Green–Kubo viscosities95 are similar to the Carreau-fitted ones within statistical uncertainty (about 10%). The Carreau fit has the following expression,η = η0[1 + (τη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )2]−βη/2, )2]−βη/2, | (13) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) was calculated from the off-diagonal pressure tensor component P12 = −η
) was calculated from the off-diagonal pressure tensor component P12 = −η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , which was measured in simulations. From eqn (13), the viscosity shear thinning exponent βη, is such that,
, which was measured in simulations. From eqn (13), the viscosity shear thinning exponent βη, is such that,η → ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −βη for large −βη for large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrot > 1, coincides with the molecular deformation altering the equilibrium rotational diffusion.
τrot > 1, coincides with the molecular deformation altering the equilibrium rotational diffusion.
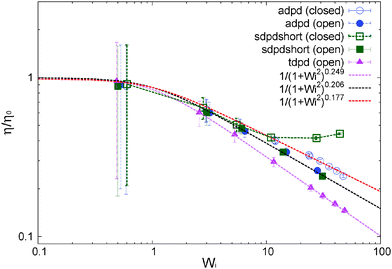 | ||
| Fig. 5 Normalized shear viscosity obtained for several models under open and closed conditions. Details of the model (varying in thermostats and kernels) are given in Table 1 and 2. Lines are best Carreau fits. | ||
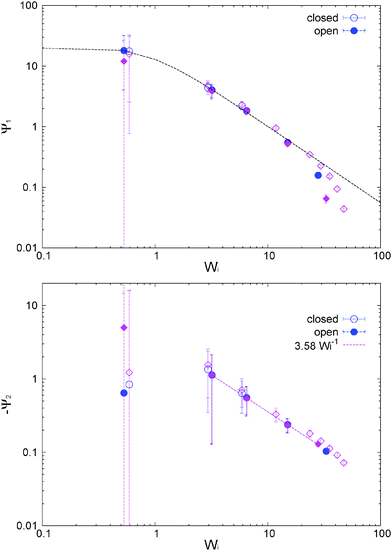
We now focus on the adpd model and defer the discussion on the tangential friction to Section 8. The system temperature is fixed to T = 4.0 ± 0.01. In this case, we get a zero shear viscosity η0 = 0.50 ± 0.05. At larger Wi, the shear thinning exponents β obtained from Carreau fits (eqn (13)) are found to be slightly steeper in the open domain βη = 0.41(2) than in the NVT box βη = 0.35(4). Thus at a fixed shear rate, the open system is slightly less viscous than the closed sample. This is in agreement with previous studies for linear and branched melts carried out at a constant and unconstrained density (see Section 10).
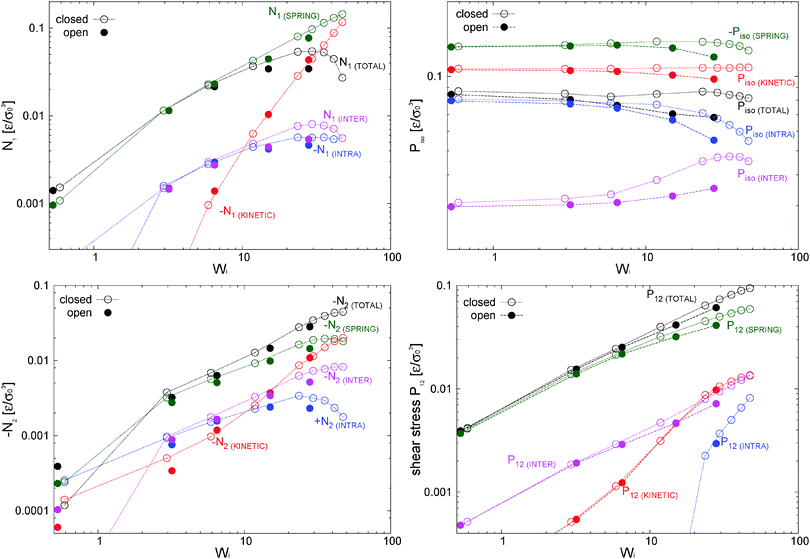
The first and second normal stress coefficients Ψ1 = N1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2 and Ψ2 = N2/
2 and Ψ2 = N2/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2 (for the adpd model, discussed in this section) are shown in Fig. 6. For Wi < 20 we find a decrease in Ψ1 consistent with the Carreau standard behaviour (eqn (13)), providing Ψ1(
2 (for the adpd model, discussed in this section) are shown in Fig. 6. For Wi < 20 we find a decrease in Ψ1 consistent with the Carreau standard behaviour (eqn (13)), providing Ψ1(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0) = 21 ± 1 and an exponent βΨ1 ≃ 1.30 ± 0.04 (i.e. N1 ∼
= 0) = 21 ± 1 and an exponent βΨ1 ≃ 1.30 ± 0.04 (i.e. N1 ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.7) quite similar for both ensembles. The relaxation time for Ψ1 obtained from the fit is also consistent with τη = τrot within error bars. At Wi > 20, we find a measurable decrease of Ψ1 with respect the Carreau trend (see Fig. 6), which takes place at slightly smaller Wi in the open case. This corresponds to a loss of the elastic component of the melt at large shear rates. The second normal stress coefficient Ψ2 = N2/
0.7) quite similar for both ensembles. The relaxation time for Ψ1 obtained from the fit is also consistent with τη = τrot within error bars. At Wi > 20, we find a measurable decrease of Ψ1 with respect the Carreau trend (see Fig. 6), which takes place at slightly smaller Wi in the open case. This corresponds to a loss of the elastic component of the melt at large shear rates. The second normal stress coefficient Ψ2 = N2/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2, shown in Fig. 6 is also quite similar in both environments and at large
2, shown in Fig. 6 is also quite similar in both environments and at large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) scales like Ψ2 ∼ −
scales like Ψ2 ∼ −![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1. The similar behaviour for N2 under open and closed boxes might be due to the fact that we just fix the normal load (in the x2 direction) and not the hydrostatic pressure as in some other studies,39,40,42 presenting different trends for N2 in NVT and NPisoT constraints.
−1. The similar behaviour for N2 under open and closed boxes might be due to the fact that we just fix the normal load (in the x2 direction) and not the hydrostatic pressure as in some other studies,39,40,42 presenting different trends for N2 in NVT and NPisoT constraints.
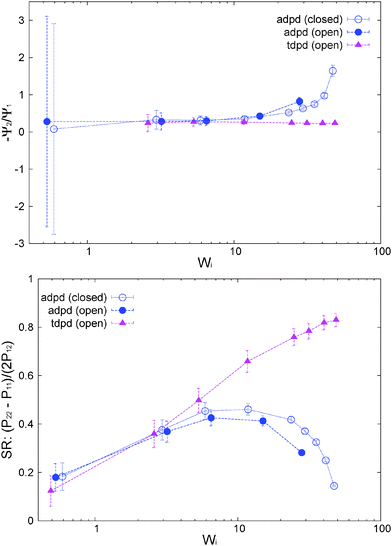
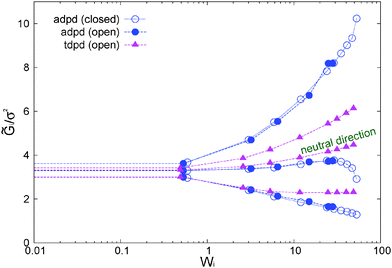
The normal stress ratio VR ≡ −Ψ2/Ψ1 and the recoverable shear strain87
SR ≡ Ψ1/(2η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = (P22 − P11)/(2P12) ) = (P22 − P11)/(2P12) | (14) |
5.4 Gyration tensor
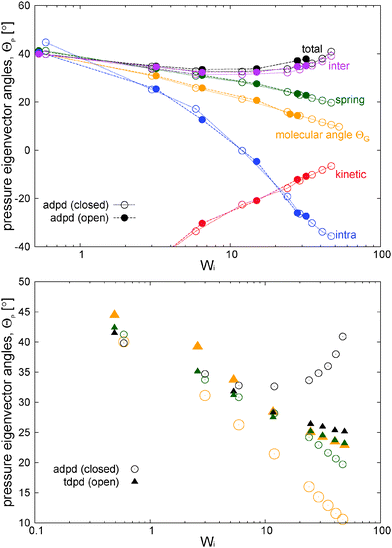
The thermodynamic and rheological properties of any polymeric system are intimately related to the deformation of the molecules induced by flow. It is therefore convenient to start by presenting the results for the average gyration tensor of our star polymer model under shear, whose components are shown in Fig. 8. At Wi > 1 the flow induces the alignment of the star molecules in the flow direction and at the same time a compression in the gradient direction. The width of the stars in the neutral direction slightly increases up to Wi ∼ 20 and AT larger shear rates, they also start to contract in this direction. It is also instructive to observe the shape of molecules in their principal deformation axes, obtained from the diagonalization of the gyration tensor. The molecular axes are s1 = cos(θG)x1 − sin(θG)x2, s2 = −sin(θG)x1 + cos(θG)x2, and s3 = x3 (since G13 = G23 = 0). The ith eigenvalue is noted as![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) i. The angle θG is the average molecular tilt over the flow direction that satisfies:
i. The angle θG is the average molecular tilt over the flow direction that satisfies: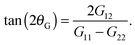 | (15) |
The results for the eigenvalues of gyration tensor are shown in Fig. 8 and reveal the strong contraction of the molecules in the s2 direction. In particular, at Wi ∼ 50 we observe that ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 21/2 ∼ 1.12σ so the chain width in the contracted axis reaches the monomer (or blob) diameter. In a real polymer at this shear rate, the flow starts altering the structure of the chain “blobs” smaller than σ. But this is precisely our modelling unit length so we will take this as the maximum Wi to be explored here (roughly Wi < 100). Above this (size dependent) shear rate, one should also expect a shear rate dependence of the blob–blob friction kernel (see ref. 97 for a related study on this issue). It is also interesting to note that the total volume of the molecules (evaluated from the product of the eigenvalues of the gyration tensor) first increases (molecules expand) up to Wi ∼ 10 and due to contraction in the neutral direction and then tends to contract (in the form of a highly extended ellipsoid) at larger Wi. In this sense, the behaviour of the arms in the neutral direction of the star have some similarities with what is found in tethered polymers,98,99 which also present a maximum volume at intermediate Wi.
21/2 ∼ 1.12σ so the chain width in the contracted axis reaches the monomer (or blob) diameter. In a real polymer at this shear rate, the flow starts altering the structure of the chain “blobs” smaller than σ. But this is precisely our modelling unit length so we will take this as the maximum Wi to be explored here (roughly Wi < 100). Above this (size dependent) shear rate, one should also expect a shear rate dependence of the blob–blob friction kernel (see ref. 97 for a related study on this issue). It is also interesting to note that the total volume of the molecules (evaluated from the product of the eigenvalues of the gyration tensor) first increases (molecules expand) up to Wi ∼ 10 and due to contraction in the neutral direction and then tends to contract (in the form of a highly extended ellipsoid) at larger Wi. In this sense, the behaviour of the arms in the neutral direction of the star have some similarities with what is found in tethered polymers,98,99 which also present a maximum volume at intermediate Wi.
6 Analysis of the stress–structure and dynamics relationship
The present analysis provides the relationship between stress components and the molecular structure and dynamics. It focuses on the results presented in the previous section, which corresponds to the adpd star model, with zero tangential friction. The conclusions will be useful for the comparison done in Section 8.6.1 Pressure balance in closed system
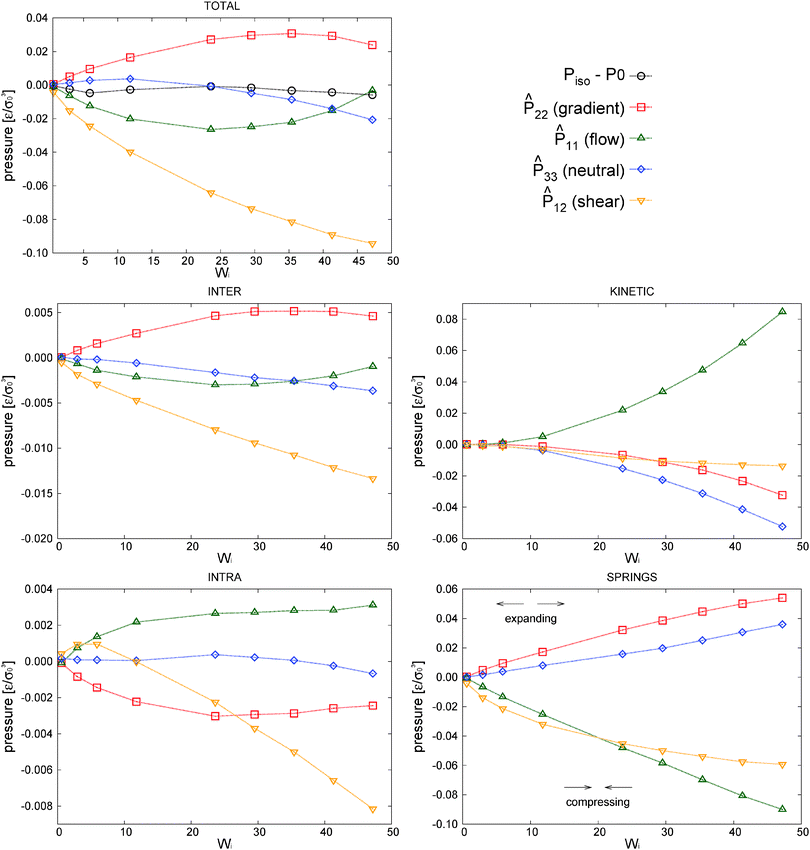
Pressure is the leading mechanical variable in rheology as it directly connects the microscopic world with material properties. We now elaborate on the pressure balance in an attempt to connect the molecular structure with the observed rheology.The pressure exerted by the melt‡ is calculated using the Irving-Kirkwood method and the method of planes,100 which is particularly suitable for the open setup as it was designed for non periodic boundaries. The pressure can be first decomposed in virial and kinetic parts. The virial pressure includes contributions from spring forces and intramolecular forces (both acting amongst pairs of monomers of the same molecule) and intermolecular forces (between monomers of different molecules). The pressure balance allows to analyze the different molecular contributions,
| Pα,β = Pkinα,β + Pspringα,β + Pintraα,β + Pinterα,β. | (16) |
| N1 = P22 − P11, | (17) |
| N2 = P33 − P22. | (18) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/b_char_0050_0302.gif) ≡ P − PisoI, ≡ P − PisoI, |
with I = δα,β the unit second rank tensor. Indeed, the hydrostatic pressure can be decomposed in different molecular contributions 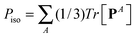 with A = kinetic, springs, etc. Also, due to the linearity of the trace operator we can decompose the traceless stress tensor P in a sum of contributions of traceless tensors, i.e.,
with A = kinetic, springs, etc. Also, due to the linearity of the trace operator we can decompose the traceless stress tensor P in a sum of contributions of traceless tensors, i.e., 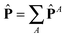 with
with ![[P with combining circumflex]](https://www.rsc.org/images/entities/b_char_0050_0302.gif) A =
A = ![[P with combining circumflex]](https://www.rsc.org/images/entities/b_char_0050_0302.gif) A − (1/3)Tr[PA]I. This is useful to simplify the analysis. In fact, before discussing the differences between open and closed ensembles, we inspect some generalities of the pressure balance focusing on the results obtained for the closed (NVT) ensemble. To that end, we present in Fig. 9 the contributions to the pressure components of the melt under shear to the hydrostatic pressure and the different traceless stress tensors (component-wise: gradient
A − (1/3)Tr[PA]I. This is useful to simplify the analysis. In fact, before discussing the differences between open and closed ensembles, we inspect some generalities of the pressure balance focusing on the results obtained for the closed (NVT) ensemble. To that end, we present in Fig. 9 the contributions to the pressure components of the melt under shear to the hydrostatic pressure and the different traceless stress tensors (component-wise: gradient ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) 22, flow
22, flow ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) 11, neutral
11, neutral ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) 33 and shear P12 obviously P13 = P23 = 0).
33 and shear P12 obviously P13 = P23 = 0).
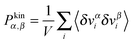 was obtained from the peculiar velocities δvi = vi − u(ri), where u(r) = u1(x2)e1 is the average velocity field obtained by binning the velocity gradient direction x2. Indeed, the ideal part of the hydrostatic pressure is one third of the trace of the kinetic pressure tensor, (1/3)Tr[Pkin] = ρT. However, its traceless part,
was obtained from the peculiar velocities δvi = vi − u(ri), where u(r) = u1(x2)e1 is the average velocity field obtained by binning the velocity gradient direction x2. Indeed, the ideal part of the hydrostatic pressure is one third of the trace of the kinetic pressure tensor, (1/3)Tr[Pkin] = ρT. However, its traceless part, ![[P with combining circumflex]](https://www.rsc.org/images/entities/b_char_0050_0302.gif) kin ≡ Pkin − ρTI, contains relevant information about the correlations in velocity fluctuations over different axes. In particular, velocity fluctuations of monomers in the x1 and x2 directions become correlated at
kin ≡ Pkin − ρTI, contains relevant information about the correlations in velocity fluctuations over different axes. In particular, velocity fluctuations of monomers in the x1 and x2 directions become correlated at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > 0 and contribute to the shear stress and viscosity. In our setup, this correlation becomes negative (owing to the imposed counter-clockwise shear) and leads to a negative contribution to Pkin12 with a non-negligible viscous contribution to the shear viscosity η = −P12/
> 0 and contribute to the shear stress and viscosity. In our setup, this correlation becomes negative (owing to the imposed counter-clockwise shear) and leads to a negative contribution to Pkin12 with a non-negligible viscous contribution to the shear viscosity η = −P12/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) which tends to reduce the shear thinning exponent (see the comparison with the case with tangential friction in Section 8). Although seldom pointed out in the literature (see ref. 4), at high enough shear rates the kinetic pressure of monomers becomes significant in polymer melts. This is in fact what we clearly observe in Fig. 9 for the star model with normal friction (adpd). The anisotropy in the kinetic pressure observed in the covariance of peculiar velocities of monomers is certainly much larger than what would be observed in a simple fluid.47,78 It is also of a different nature because in the melt, the monomer motions are constrained and they fluctuate and rotate being tethered to the center of their star molecule. This leads to different monomer peculiar velocities in the flow, gradient, and neutral directions which are reflected in the kinetic pressure. In Fig. 9, we show
which tends to reduce the shear thinning exponent (see the comparison with the case with tangential friction in Section 8). Although seldom pointed out in the literature (see ref. 4), at high enough shear rates the kinetic pressure of monomers becomes significant in polymer melts. This is in fact what we clearly observe in Fig. 9 for the star model with normal friction (adpd). The anisotropy in the kinetic pressure observed in the covariance of peculiar velocities of monomers is certainly much larger than what would be observed in a simple fluid.47,78 It is also of a different nature because in the melt, the monomer motions are constrained and they fluctuate and rotate being tethered to the center of their star molecule. This leads to different monomer peculiar velocities in the flow, gradient, and neutral directions which are reflected in the kinetic pressure. In Fig. 9, we show ![[P with combining circumflex]](https://www.rsc.org/images/entities/b_char_0050_0302.gif) kinversus Wi (recall that Pkin =
kinversus Wi (recall that Pkin = ![[P with combining circumflex]](https://www.rsc.org/images/entities/b_char_0050_0302.gif) kin + ρTI and diagonal components of Pkin are positive). At Wi > 1, the kinetic pressure contributes to the first and second normal stress Nkin1 and Nkin2. As soon as the molecules become stretched in the flow direction (for Wi > 1), velocity fluctuations in the flow direction are enhanced with respect to those along the gradient and neutral directions:
kin + ρTI and diagonal components of Pkin are positive). At Wi > 1, the kinetic pressure contributes to the first and second normal stress Nkin1 and Nkin2. As soon as the molecules become stretched in the flow direction (for Wi > 1), velocity fluctuations in the flow direction are enhanced with respect to those along the gradient and neutral directions: ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) kin11 > 0 and
kin11 > 0 and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) kin22 < 0,
kin22 < 0, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) kin33 < 0. We find that Nkin2 < 0 (see Fig. 10 below), so the kinetic stress acts in the same way as the elastic (springs) components. However, the kinetic contribution to the first normal stress differences is negative Nkin1<0 so it is just opposite of the elastic contribution of the chain. Our conclusion is that the kinetic pressure of monomers tends to reduce the elasticity of the melt in the flow–gradient direction at large shear rates.
kin33 < 0. We find that Nkin2 < 0 (see Fig. 10 below), so the kinetic stress acts in the same way as the elastic (springs) components. However, the kinetic contribution to the first normal stress differences is negative Nkin1<0 so it is just opposite of the elastic contribution of the chain. Our conclusion is that the kinetic pressure of monomers tends to reduce the elasticity of the melt in the flow–gradient direction at large shear rates.
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 3 = G33 for Wi > 20 (also observed in “sdpdshort” and “sdpdlong” thermostats). A somewhat similar rebound in the intramolecular pressure at a large shear rate has been observed in simulations of entangled and disentangled linear polymer melts (see ref. 3 and reference therein). However, in these studies the monomer–monomer interaction is attractive, and this fact modifies (reverses) the intramolecular contributions (polymer compression then reduces the intramolecular pressure, unlike for our purely repulsive potential).
3 = G33 for Wi > 20 (also observed in “sdpdshort” and “sdpdlong” thermostats). A somewhat similar rebound in the intramolecular pressure at a large shear rate has been observed in simulations of entangled and disentangled linear polymer melts (see ref. 3 and reference therein). However, in these studies the monomer–monomer interaction is attractive, and this fact modifies (reverses) the intramolecular contributions (polymer compression then reduces the intramolecular pressure, unlike for our purely repulsive potential).
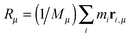 and virial pressure proportional to
and virial pressure proportional to 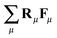 ). This “molecular pressure” formulation is however less informative because the effects of all internal forces, like the springs, are hidden in the spatial CoM distribution g({R}). Nevertheless, it serves to illustrate the central role of intermolecular forces and shed some light on the apparently striking similarity between the intermolecular pressure and the total pressure dependence with Wi, which can be seen by comparison between the corresponding (inter and total) panels of Fig. 9 (note the difference in values). This similarity between intermolecular (IM) and global magnitudes (such as IM energy and hydrostatic pressure, see Fig. 9) has also been reported as “striking” in previous sheared melt simulations.2,3 It is interesting to note that the dominant velocity gradient component of the IM force Pinter22 reaches a plateau around Wi ∼ 20 and slightly decreases at larger Wi (as the total P22 does – see Fig. 9). This is indicative of a change in the dynamics of polymers, which according to the concomitant increase observed in Pinter11, most probably start to rotate and collide more often in the flow direction.
). This “molecular pressure” formulation is however less informative because the effects of all internal forces, like the springs, are hidden in the spatial CoM distribution g({R}). Nevertheless, it serves to illustrate the central role of intermolecular forces and shed some light on the apparently striking similarity between the intermolecular pressure and the total pressure dependence with Wi, which can be seen by comparison between the corresponding (inter and total) panels of Fig. 9 (note the difference in values). This similarity between intermolecular (IM) and global magnitudes (such as IM energy and hydrostatic pressure, see Fig. 9) has also been reported as “striking” in previous sheared melt simulations.2,3 It is interesting to note that the dominant velocity gradient component of the IM force Pinter22 reaches a plateau around Wi ∼ 20 and slightly decreases at larger Wi (as the total P22 does – see Fig. 9). This is indicative of a change in the dynamics of polymers, which according to the concomitant increase observed in Pinter11, most probably start to rotate and collide more often in the flow direction.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) have also been observed for different polymers in ref. 2, 3, 40 and 43. The present analysis (see Fig. 9) reveals in fact that Piso depends on a competition of several mechanisms. Below Wi ≃ 10 the hydrostatic pressure varies little but presents a slight descend, probably due to the chain expansion (revealed by the analysis of the gyration tensor) which decreases the intramolecular pressure. At larger shear rates Wi > 10, two opposite mechanisms enter into the play: First, an increase in P11 due to the strong increase of kinetic pressure (and to a lesser extent to intermolecular collisions). This is probably due to molecular rotations similar to the tank-thread motion reported for a star molecule solution102 and also pointed out in ref. 2 and 3. And second, a decrease in P33 due to the contraction of the stars in the neutral direction (see Fig. 8) and consequent reduction of the kinetic pressure Pkin33. Both effects nearly counterbalance each other (see Fig. 9) leaving small variations in Piso. The relevance of these effects depends on the boundary conditions (the open case is analysed in next section) and type of friction (Section 8). More generally variations of Piso depend on the presence of attractive monomer interactions and the molecular structure.
) have also been observed for different polymers in ref. 2, 3, 40 and 43. The present analysis (see Fig. 9) reveals in fact that Piso depends on a competition of several mechanisms. Below Wi ≃ 10 the hydrostatic pressure varies little but presents a slight descend, probably due to the chain expansion (revealed by the analysis of the gyration tensor) which decreases the intramolecular pressure. At larger shear rates Wi > 10, two opposite mechanisms enter into the play: First, an increase in P11 due to the strong increase of kinetic pressure (and to a lesser extent to intermolecular collisions). This is probably due to molecular rotations similar to the tank-thread motion reported for a star molecule solution102 and also pointed out in ref. 2 and 3. And second, a decrease in P33 due to the contraction of the stars in the neutral direction (see Fig. 8) and consequent reduction of the kinetic pressure Pkin33. Both effects nearly counterbalance each other (see Fig. 9) leaving small variations in Piso. The relevance of these effects depends on the boundary conditions (the open case is analysed in next section) and type of friction (Section 8). More generally variations of Piso depend on the presence of attractive monomer interactions and the molecular structure.
It is interesting to note that the decrease of neutral kinetic pressure in our adpd star model starts to take place around Wi ≃ 20, which is precisely the ratio τrot/τelas ≃ 20. Above this shear rate the flow strains faster than the elastic relaxation of the molecules thus reducing the fluctuations of the arms in the neutral direction. This effect finally induces a net decrease in Piso above Wi > 30. We shall see (Section 10) that this effect is absent (or at least delayed) while introducing the tangential friction, again indicating that friction should be an essential part of any CG model.9
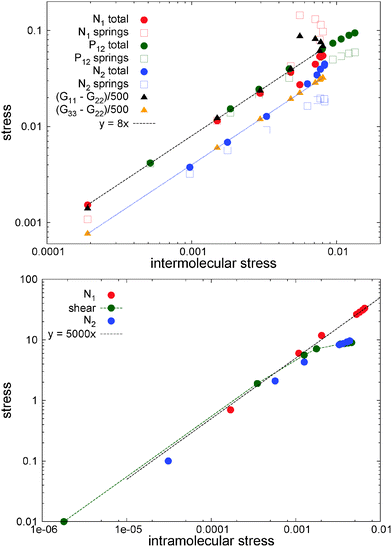
To highlight the relevancy of the intermolecular stress in the linear SOR regime, we plot in Fig. 11 (top panel) the total and elastic contributions (springs) to the normal and shear stress against the intermolecular counterparts. At low shear rates, about Wi < 10, the same linear relation is found for the first normal stress difference and shear stress, N1 ≃ 8Ninter1 and P12 ≃ 8Pinter12, while we found N2 ≃ 4Ninter1. Approximately the same linear relation holds for the elastic stress and also for the normal molecular strains evaluated with the gyration tensor (G11 − G22 and G22 − G33, scaled in Fig. 11(top panel)). This provides the Hookean limit of the melt N1 ≃ C(G11 − G22) and N2 ≃ (C/2)(G33 − G22) with C = 62.5 (we find that P12 ∼ CG12 holds only for smaller Wi < 5). In the open (adpd) setup, the linear regime for N1 and P12 perfectly agrees with closed simulations; however we found deviation from linearity in the case of N2, an issue which deserves further investigation. The bottom panel of Fig. 11 presents the results for stars with the tangential friction, analysed in Section 10.
7 Effect of open environment
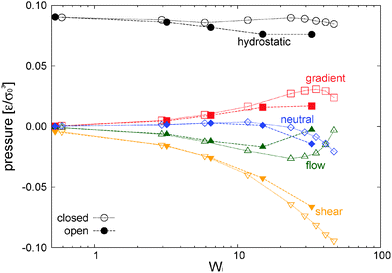
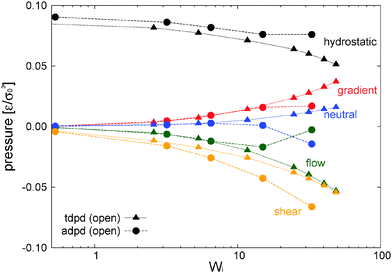
7.1 Density and hydrostatic pressure
In our open domain, we fix the load of the melt in the gradient direction (Pext22 = P22) and this produces a redistribution of the pressure tensor, reducing its component in the flow and neutral directions and also, indirectly, its shear stress. This is deduced from Fig. 12 where we compare the traceless stress tensor and the hydrostatic pressure in the open and closed setups at the fixed T = 4 temperature. Note that Pext22 = P22 =![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) 22 + (1/3)Piso is constant in the open setup (within statistical uncertainties). In the open domain, the sheared melt expands in the gradient direction; a phenomenon similar to the die swelling observed in polymer extrusion at the pipe orifice and related to other viscoelastic phenomena.103 In the open domain, this corresponds to a decreasing melt density (at faster shear rates) and brings about a smaller hydrostatic pressure than in the closed environment at similar Wi (see Fig. 12). However, the relative decrease of Piso is larger than the density jump. This fact is due to several related effects we now analyze from the inspection of Fig. 10. Indeed, at the fixed temperature, a lower density leads to a lower kinetic pressure Pkiniso = ρT found in the open domain (this trend also applies here to the intramolecular pressure Pintraiso because our model considers purely repulsive nonbonded interactions, the opposite effect could arise for attracting chains2,3). However, an even larger reduction in Piso with respect to the closed box is observed due to the smaller intermolecular pressure in the open box (see Fig. 10 for Wi > 10). Indeed, at a high shear, a less dense melt presents less molecular collisions, less intermolecular friction and thus less elastic load. As stated, at the fixed temperature, the elastic strain is essentially activated by intermolecular friction in the melt. Notably, at Wi ∼ 20, these intertwined effects induce a reduction of about 25% of hydrostatic pressure of the open domain mainly arising from the decrease of elastic stress. At this Wi, density has only decreased about 10% (see Fig. 17). In agreement with this comment, we note that this depressurizing effect is doubled when the tangential friction is added as commented in Section 10.
22 + (1/3)Piso is constant in the open setup (within statistical uncertainties). In the open domain, the sheared melt expands in the gradient direction; a phenomenon similar to the die swelling observed in polymer extrusion at the pipe orifice and related to other viscoelastic phenomena.103 In the open domain, this corresponds to a decreasing melt density (at faster shear rates) and brings about a smaller hydrostatic pressure than in the closed environment at similar Wi (see Fig. 12). However, the relative decrease of Piso is larger than the density jump. This fact is due to several related effects we now analyze from the inspection of Fig. 10. Indeed, at the fixed temperature, a lower density leads to a lower kinetic pressure Pkiniso = ρT found in the open domain (this trend also applies here to the intramolecular pressure Pintraiso because our model considers purely repulsive nonbonded interactions, the opposite effect could arise for attracting chains2,3). However, an even larger reduction in Piso with respect to the closed box is observed due to the smaller intermolecular pressure in the open box (see Fig. 10 for Wi > 10). Indeed, at a high shear, a less dense melt presents less molecular collisions, less intermolecular friction and thus less elastic load. As stated, at the fixed temperature, the elastic strain is essentially activated by intermolecular friction in the melt. Notably, at Wi ∼ 20, these intertwined effects induce a reduction of about 25% of hydrostatic pressure of the open domain mainly arising from the decrease of elastic stress. At this Wi, density has only decreased about 10% (see Fig. 17). In agreement with this comment, we note that this depressurizing effect is doubled when the tangential friction is added as commented in Section 10.
7.2 Normal stress differences and shear stress
Fig. 10 compares the different contributions to the normal stress differences and the shear rate in the open and closed systems. Much of what has been already said in the previous section applies here. The results for the shear stress nicely corroborate what we pointed out before about the close relationship between intermolecular and elastic stresses. Fig. 10 (right bottom) clearly shows that the kinetic and intra molecular shear stresses are essentially equal in the open and closed domains. The decrease in elastic shear stress found in the open case is due to the reduction in the intermolecular friction at a lower density (although seemingly paradoxical, the “nominal” contribution to Pintra12 in the monomer pressure balance is minor). In all instances, at low enough shear (Wi < 10) the elastic stress is close to the total stress (and proportional to the intramolecular stress). This is the regime of validity of the stress optic rule which is broken at larger shear due to viscous (and compressible) effects related to the “simple fluid” of monomers. Remarkably, for the present model of the star polymer melt, the kinetic normal stress becomes the dominant “viscous” contribution and at large Wi > 20 it even induces a decrease in the first normal stress difference N1.7.3 Molecular ordering under shear
Fig. 13 presents the angle of the largest eigenvector of different contributions to the pressure tensor with the flow direction (measured according to eqn (15)). We also include the molecular orientation, measured from the angle associated with the gyration tensor (eqn (15)). This plot condenses what has been already mentioned in previous sections. Recall that a spherical molecular structure provides θG = 45° and similarly from eqn (15) a Newtonian fluid without elastic component, necessarily presents θ = 45°. This is what is observed for the total pressure tensor angle θP and the molecular orientation θG at Wi → 0 in Fig. 13. As the straining rate is made faster both angles decrease in a similar fashion, however, at Wi > 10, the pressure tensor angle θP presents a minimum and starts increasing towards 45°. By contrast, the molecular orientation θG keeps aligning with the flow direction. This in an indication of the loss of the Hookean behaviour of the melt which here is mainly due to the kinetic pressure (see its principal direction in Fig. 13). The stress direction of springs also aligns with the flow, although their angle is larger than the molecular orientation (a similar outcome was observed in ref. 3). Finally, note the close match between the direction of intermolecular forces and the total pressure tensor. As stated, intermolecular forces are the driving mechanism of transformation between the viscous flow and elastic energy. Lastly, as observed by other authors,39,42,43 the open boundary does not modify the molecular structure or orientation with Wi, when compared with the closed case. Here, Fig. 13 shows another remarkable result: the significant redistribution of pressure in the open case (see Fig. 12) does not alter the orientation of the different contributions of the pressure tensor at the increasing shear rate. The orientation of pressure eigenvectors is a function of their eigenvalues which in turn determine the material properties of the polymer (its viscoelasticity87). A relevant example is the recoverable shear strain (SR) given by eqn (14). Material properties should not depend on the constraints used to perturb the polymer and this is precisely what our analyses provide.To observe the collective order of the star molecular, we calculated the CoM pair distribution function g(Rij). Fig. 14 illustrates the marginal distributions 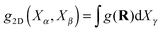 for different planes and at increasing shear rates. It is illustrative to draw the directions of the principal components of the pressure and the gyration tensor to observe the departure from the Hookean (linear SOR) regime. Above Wi > 20 molecules start to orient in lanes in the flow–gradient plane, as indicated by the elongated shape of the CoM distribution in Fig. 14. In linear polymers at large shear rates, this effect creates order and even crystallization (ref. 87). This collective order is also clearly visible in one snapshot of the system, in Fig. 15. Molecules with different relative velocities (closeby in the gradient direction) slide over creating a stress which is larger along a direction differing from the orientation of individual molecules. This direction of maximal stress is correlated with the CoM distribution (see Fig. 14) which shows bright spots where molecules slide over and depleted regions in the “wake” of each molecule. At the largest shear rates considered, we also observe some collective ordering in the neutral (vorticity) direction. In sheared colloids, lanes of particles in the neutral direction appear due to hydrodynamic interactions.104 This could be a plausible hypothesis, in view of the hybrid colloid–polymer nature of the star molecule direction.
for different planes and at increasing shear rates. It is illustrative to draw the directions of the principal components of the pressure and the gyration tensor to observe the departure from the Hookean (linear SOR) regime. Above Wi > 20 molecules start to orient in lanes in the flow–gradient plane, as indicated by the elongated shape of the CoM distribution in Fig. 14. In linear polymers at large shear rates, this effect creates order and even crystallization (ref. 87). This collective order is also clearly visible in one snapshot of the system, in Fig. 15. Molecules with different relative velocities (closeby in the gradient direction) slide over creating a stress which is larger along a direction differing from the orientation of individual molecules. This direction of maximal stress is correlated with the CoM distribution (see Fig. 14) which shows bright spots where molecules slide over and depleted regions in the “wake” of each molecule. At the largest shear rates considered, we also observe some collective ordering in the neutral (vorticity) direction. In sheared colloids, lanes of particles in the neutral direction appear due to hydrodynamic interactions.104 This could be a plausible hypothesis, in view of the hybrid colloid–polymer nature of the star molecule direction.
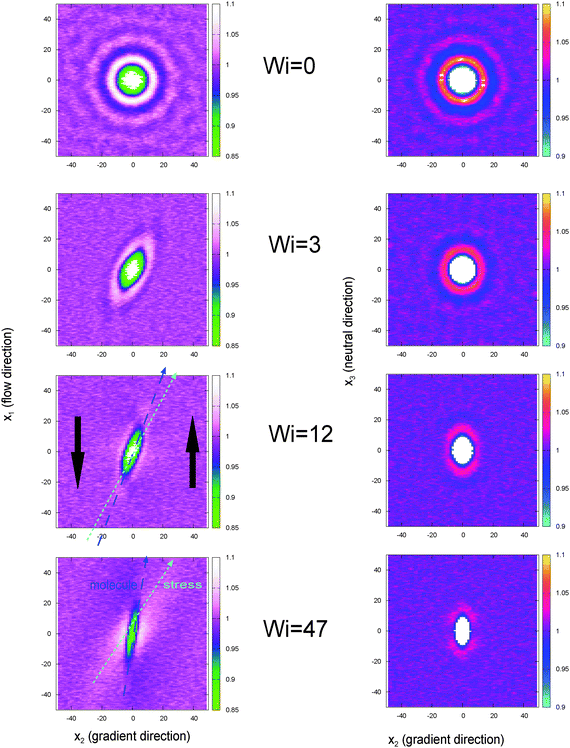 | ||
Fig. 14 The pair distribution of molecules, g(R) providing the probability of finding the CoM of a molecule at a distance (vector) R from the target molecule CoM. Left: Marginal probability 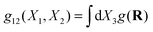 in the flow–gradient and (right) gradient–neutral planes. The results for increasing Wi in a closed domain (open simulations at similar Wi are visually indistinguishable). Green line denotes the direction of the deviatoric stress and the blue line the molecular orientation obtained from the gyration tensor eqn (15). in the flow–gradient and (right) gradient–neutral planes. The results for increasing Wi in a closed domain (open simulations at similar Wi are visually indistinguishable). Green line denotes the direction of the deviatoric stress and the blue line the molecular orientation obtained from the gyration tensor eqn (15). | ||
 | ||
| Fig. 15 Snapshot of a closed box simulation under shear rate (Wi = 42). For the sake clarity only 10% of randomly chosen molecules are shown. Colors indicate the position in the neutral direction. The snapshot clearly shows the formation of lanes tilted in the flow–gradient plane created due to sliding over rows of oriented molecules. Compared to Fig. 14, the snapshot is rotated for 180° with respect to the gradient axis. | ||
8 Effect of tangential friction
To investigate how the tangential friction between monomer blobs alters the rheology of the melt model, we use a standard (i.e. not adaptive) DPD thermostat70 with γ∥ = 1 and γ⊥ = 1 (see Section 3, 4, and 5.3 for details). As stated the friction kernels are Heaviside functions, in this case with a cutoff distance Rdpd = 1.5 × 21/6σ. In the following, we label this tangential friction thermostat as “tdpd”. This tdpd thermostat was found to be strong enough to keep the relative increase of the system temperature smaller than 5% at the largest shear rates considered.In a real system friction acts by reducing the relative velocities of interacting monomers, generally in the normal and also in the tangential directions. Under Markovian and pairwise interaction assumptions, this form of friction leads to the DPD equations as shown by the Mori–Zwanzing dynamic coarse graining applied to the microscopic Liovillian dynamics.9 The same effect is properly captured by the tdpd thermostat, although here at a qualitatively level. Reducing the monomer relative velocities immediately leads to a reduction in kinetic pressure which has large consequences on the system rheology. In particular, the behaviour of the melt is essentially ruled by its elastic component, activated by the more effective intermolecular friction. Just to illustrate this point, we plot in Fig. 16 the contributions of the first normal stress difference (a direct measure of viscoelasticity) for the tdpd case. Compared with Fig. 10 (for the γ⊥ = 0 adpd case) the tdpd model has a much smaller kinetic pressure and N1 is essentially determined by the elastic stress (particularly as Wi increases). The same conclusion applies to P12 in Fig. 16.
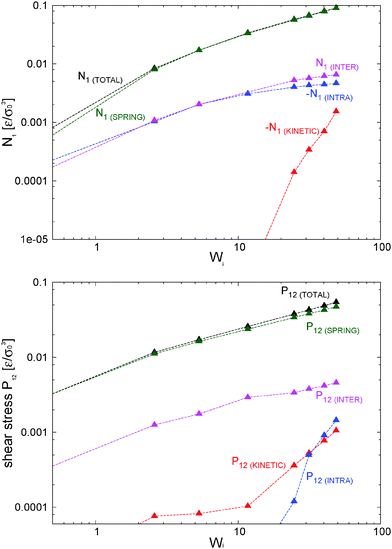 | ||
| Fig. 16 Balances for the first normal stress difference and the shear stress for the tdpd model including tangential friction. Comparison with Fig. 10 for the zero tangential friction case. Error bars of the measured quantities are approximately 0.002–0.005ε/σ03. | ||
An interesting difference related to the presence of tangential friction concerns shear dilatancy. Fig. 17(a) presents the relative density expansion δρ/ρ0 = 1 − ρ/ρ0 for different models. Let us now focus on the adpd and tdpd models which are kept isothermal (non-isothermal cases are discussed in Section 9). The density expansion of the adpd model (without tangential friction) scales like δρ/ρ0 ∼ Wi, while tangential friction (tdpd) leads to a much softer trend δρ/ρ0 ∼ Wi0.5 (although it expands relatively more at moderate shear rates). Under a constant normal load, shear dilatancy is a consequence of the growth of pressure in the velocity–gradient direction. In the case of small kinetic effects (tdpd) this growth is controlled by the expansion force arising from the compressed springs. This elastic pressure appears as soon as molecules start to align with the flow and compress in the gradient direction. Under enough tangential friction, the elastic stress is dominant and also controls the hydrostatic pressure, which in the absence of kinetic pressure effects, presents a faster decrease at large Wi compared to the adpd case (see Fig. 18). Of course, this decrease is also related to the fact that the tpdp simulations were done in the open system; notably for tdpd we get about 50% reduction in hydrostatic pressure for less than 10% reduction in density (see Fig. 17).
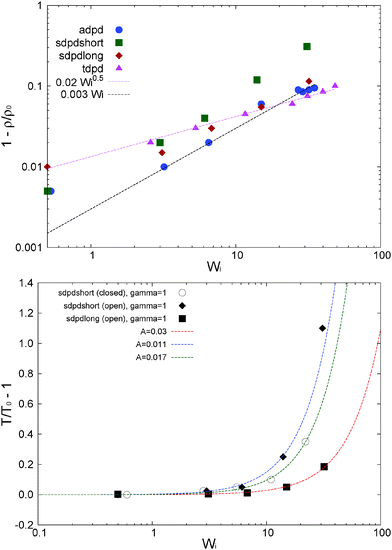 | ||
| Fig. 17 Top panel: Relative density variation for the different cases studied (open and closed, and different models and thermostats, see Table 1). Bottom panel: relative temperature increase observed in simulations with standard DPD thermostats with vanishing tangential friction. The relative variation of T for the adpd thermostat is smaller than 0.01 and less than 0.045 for the tdpd case (both of them not shown in the graph). Details of the thermostats are given in Table 1. The lines correspond to eqn (21), with the characteristic constant A defined there. Error bar estimations of the data are approximately 0.005 and 0.01 for the upper and lower graph, respectively. | ||
The eigenvalues of the gyration tensor shown in Fig. 8 also indicate that adding tangential friction makes star molecules “stiffer”, in the sense that one needs larger values of the Weissemberg number to deform them. This observation is however somewhat misleading because for a fixed Wi, the real (physical) shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = Wi/τrot is now smaller due to the increase in τrot with the friction. In any case, the tangential friction is expected to alter the stress–strain relations in the Hookean regime (related to the linear stress-optic rule coefficient). This is (indirectly) seen in Fig. 11 where we plot the normal strain differences G11 − G22 and G22 − G33 (also G12) against the corresponding intermolecular stress differences (against Pintra12). We choose this plot to illustrate two facts: first, if the kinetic pressure is minor, the intermolecular friction is the leading mechanism driving the molecular deformation (and its elastic response). Second, molecular strains (and elastic stresses, not shown in the figure) in the flow–gradient and gradient–neutral planes (corresponding to the first and second normal stress differences) present a quite similar linear scaling (the shear deformation as well) with the intermolecular stress. This is to be contrasted with the top pannel of Fig. 11 (model in the absence of tangential friction), where the second normal stress (and G22 − G33) is half of the first N1 counterpart (also G22 − G11). A perfect alignment between intermolecular forces, elastic stress and molecular strain was also found by Kroger et al.89 in linear FENE chains. It thus seems that tangential friction (tdpd) helps to reduce the second normal stress in such a way that N1 and N2 present similar scaling laws N1 ∼
= Wi/τrot is now smaller due to the increase in τrot with the friction. In any case, the tangential friction is expected to alter the stress–strain relations in the Hookean regime (related to the linear stress-optic rule coefficient). This is (indirectly) seen in Fig. 11 where we plot the normal strain differences G11 − G22 and G22 − G33 (also G12) against the corresponding intermolecular stress differences (against Pintra12). We choose this plot to illustrate two facts: first, if the kinetic pressure is minor, the intermolecular friction is the leading mechanism driving the molecular deformation (and its elastic response). Second, molecular strains (and elastic stresses, not shown in the figure) in the flow–gradient and gradient–neutral planes (corresponding to the first and second normal stress differences) present a quite similar linear scaling (the shear deformation as well) with the intermolecular stress. This is to be contrasted with the top pannel of Fig. 11 (model in the absence of tangential friction), where the second normal stress (and G22 − G33) is half of the first N1 counterpart (also G22 − G11). A perfect alignment between intermolecular forces, elastic stress and molecular strain was also found by Kroger et al.89 in linear FENE chains. It thus seems that tangential friction (tdpd) helps to reduce the second normal stress in such a way that N1 and N2 present similar scaling laws N1 ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.68±0.02 with N2 ∼ −0.3N1. This is to be compared with the adpd case in Fig. 6 (N1 ∼
0.68±0.02 with N2 ∼ −0.3N1. This is to be compared with the adpd case in Fig. 6 (N1 ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.70 and N2 ∼
0.70 and N2 ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 1.0). As shown in Fig. 7 the tdpd model yields −N2/N1 ≃ 0.3 at any Wi < 100. This value is characteristic of disentangled melts (being −N2/N1 = 2/7 the theoretical prediction for small shear rates1,88).
1.0). As shown in Fig. 7 the tdpd model yields −N2/N1 ≃ 0.3 at any Wi < 100. This value is characteristic of disentangled melts (being −N2/N1 = 2/7 the theoretical prediction for small shear rates1,88).
The monotonous increase of elastic storage with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) found in the tdpd model is reflected in the recoverable shear strain (SR) shown in Fig. 7. Somewhat paradoxically, adding tangential friction increases the melt elasticity. Albeit, this reinforces the conclusions in Section 6: the intermolecular friction is the principal mechanism loading elastic stress into an disentangled melt. In passing, we note that in the tpdp model the orientational resistance parameter mG = Wi
found in the tdpd model is reflected in the recoverable shear strain (SR) shown in Fig. 7. Somewhat paradoxically, adding tangential friction increases the melt elasticity. Albeit, this reinforces the conclusions in Section 6: the intermolecular friction is the principal mechanism loading elastic stress into an disentangled melt. In passing, we note that in the tpdp model the orientational resistance parameter mG = Wi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(2θG) grows like mG = 3.7Wi0.65 (at least for Wi < 100), a scaling which agrees with that reported for stars in solution105 (the prefactor being however about twice larger in our melt).
tan(2θG) grows like mG = 3.7Wi0.65 (at least for Wi < 100), a scaling which agrees with that reported for stars in solution105 (the prefactor being however about twice larger in our melt).
Not unexpectedly, the zero shear viscosity for the tdpd star model is larger η0 = 2.6 than the adpd case η0 = 0.5. The relaxation time is also larger τη = 287 (compared with 60). However, the tdpd shear viscosity thinning is faster; we find βη ≃ 0.5 compared with 0.4 for the adpd case (recall η ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −βη). Again, this is also a consequence of a much smaller contribution of the viscous stress coming from kinetic effects. If the tangential friction is absent, the kinetic (and intramolecular) contribution increases the shear stress and the viscosity at any Wi leading to a softer shear thinning exponent.
−βη). Again, this is also a consequence of a much smaller contribution of the viscous stress coming from kinetic effects. If the tangential friction is absent, the kinetic (and intramolecular) contribution increases the shear stress and the viscosity at any Wi leading to a softer shear thinning exponent.
9 Thermostats and heat dissipation
9.1 Density and temperature
We now briefly analyze the effect of the temperature increase due to heat dissipation in the sample. In all cases, the temperature reaches a steady state, but as shown in Fig. 17 (bottom panel) plotting δT/T0 = T/T0 − 1, we face severe viscous heating while performing the first row of simulations with the sdpdshort and (stronger) sdpdlong thermostats (see Table 1). Heating is observed at Wi > 10 and irrespective of the damping parameter (we tried up to γDPD = 50m0τ0−1). Tangential friction drastically reduces heating (δT/T0 < 0.045 for Wi < 70) however the adpd thermostat enabled us to simulate zero tangential friction at a fixed temperature, providing δT/T0 < 0.01.Let us focus on the “heated” runs at the increasing shear rate to illustrate the effect of uncontrolled temperature. Fig. 17 shows that heating introduces further melt expansion under shear and this kinetic energy induces larger hydrostatic pressure (which it is seen to increase with shear in the sdpdshort case). Pressurization due to viscous heating can also alter the rheology response. This is seen in Fig. 5 where the sdpdshort case presents shear thickening at Wi > 10, but only under closed conditions. The shear thickening reported in some of the published studies on polymer melts (closed box simulations) might be due to viscous heating (see e.g.ref. 39). More interesting than this elucubration is the results of Fig. 5 for the sdpdshort-open. The viscosity obtained for the same thermostat in an open environment is not affected by the temperature increase with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . In fact it presents the very same trend as the adpd case. This observation indicates that shear viscosity is dominated by the normal load. In fact, the same outcome was also observed for the sdpdlong model (with shear exponent βη = 0.39) and for all γ∥ ≤ 10 considered. Thus, this insensitivity of viscosity to temperature found only under normal load is not probably due to a cancellation of effects sometimes observed in experiments50 (viscosity decreasing with T and increasing with P22). Rather it should be due to the viscosity dominated by pressure as happens in highly pressurized melts.50 Here, monomers interact via purely repulsive forces (WCA) which might map a sample under large pressure, in fact, adding attractive interactions would probably trigger temperature effects on viscosity.
. In fact it presents the very same trend as the adpd case. This observation indicates that shear viscosity is dominated by the normal load. In fact, the same outcome was also observed for the sdpdlong model (with shear exponent βη = 0.39) and for all γ∥ ≤ 10 considered. Thus, this insensitivity of viscosity to temperature found only under normal load is not probably due to a cancellation of effects sometimes observed in experiments50 (viscosity decreasing with T and increasing with P22). Rather it should be due to the viscosity dominated by pressure as happens in highly pressurized melts.50 Here, monomers interact via purely repulsive forces (WCA) which might map a sample under large pressure, in fact, adding attractive interactions would probably trigger temperature effects on viscosity.
9.2 Viscous heating
The rate of heat production per unit volume due to viscous dissipation is![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) η = η
η = η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2 leading to a larger steady temperature whose value depends on the heat extraction rate. The onset of temperature increase is usually determined by a non-dimensional parameter which depends on Wi and on the rate of cooling
2 leading to a larger steady temperature whose value depends on the heat extraction rate. The onset of temperature increase is usually determined by a non-dimensional parameter which depends on Wi and on the rate of cooling ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) c (see the recent computational study in ref. 10). Although in this work we shall not focus on heat and entropy production, we believe it is interesting to share our observations on this phenomenon, partly because of the relatively small simulation literature accurately reporting heating effects in sheared, thermostatted melts. A simple equation for the heat produced in the sheared melt includes frictional gain and cooling,
c (see the recent computational study in ref. 10). Although in this work we shall not focus on heat and entropy production, we believe it is interesting to share our observations on this phenomenon, partly because of the relatively small simulation literature accurately reporting heating effects in sheared, thermostatted melts. A simple equation for the heat produced in the sheared melt includes frictional gain and cooling,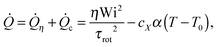 | (19) |
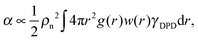 | (20) |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) = 0 we thus have,
= 0 we thus have,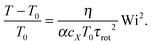 | (21) |
10 Comparison with previous studies
It is interesting to compare our results with previous rheological studies, some of them were carried out at isobaric (constant Piso) or constant load (P22) constraints. As stated in the Introduction, the number of studies of flowing melts under a constant pressure (either hydrostatic pressure or normal load) is not large. However, they present significant discrepancies in the density and pressure variations with shear. For instance, ref. 42 presents the results for dendrimer melts under the isobaric conditions (constant hydrostatic pressure) revealing a decrease in the melt density under shear. For linear chains, ref. 40 presents just the opposite effect (contraction under shear), while ref. 43 (constant load) reports shear expansion (density increase).The shear thinning exponents found here for a star polymer melt are consistent with those found in other simulations for somewhat similar systems such as hyperbranched and dendrimer polymers.41,42 Recall that the shear thinning exponent of any quantity Φ is βΦ with Φ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −βΦ at large
−βΦ at large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . For viscosity we find βη ≃ 0.4 (adpd) and βη ≃ 0.5 (tdpd), for the first normal stress coefficient βΨ1 ∼ 1.30 (adpd) and 1.31 (tdpd), while for the second one the values are βΨ2 ∼ 1.0 (adpd) and 1.31 (tdpd). For dendrimers, Bosko et al.41 reported shear thinning exponents increasing with M under NVT (βη ∈ [0.28–0.36]) while, for NPisoT the were roughly independent of M (βη ∈ [0.37–0.39]). The same work reported βΨ1 ≃ 1.27 and βΨ2 ≃ 1.23 under NPisoT, while βΨ1 ≃ 1.1 βΨ2 ≃ 1.0 under NVT. Closed simulations for hyperbranched polymer melts42 predicted βη ≃ 0.3 (slightly increasing with molecular mass M), while βΨ2 ≃ 0.95 and βΨ1 ≃ 1 (both roughly independent on M). The scaling of (first and second) normal coefficients are probably sensitive to the type of external constraint (either isobaric Piso or constant load P22). As an indication, a numerical study at constant load for linear chains43 reported the same exponents found in this work (βΨ1 = 1.35 and βΨ2 ≃ 1 respectively). Concerning shear viscosity, if the density is allowed to relax (under isobaric or constant load conditions) the shear thinning exponents reported in the literature show much less variation with the molecular weight than under a fixed density. This has been shown for linear chains under a constant load43 and also for dendrimers.42 In both cases, the shear thinning exponent in the variable density case was found to be close to 0.4, while it ranged from 0.25 to 0.4 in the closed system (increasing with the molecular weight in both cases). This larger insensitivity of shear thinning exponents under fixed load conditions agrees with our observations in simulations presenting viscous heating mentioned in Section 9.
. For viscosity we find βη ≃ 0.4 (adpd) and βη ≃ 0.5 (tdpd), for the first normal stress coefficient βΨ1 ∼ 1.30 (adpd) and 1.31 (tdpd), while for the second one the values are βΨ2 ∼ 1.0 (adpd) and 1.31 (tdpd). For dendrimers, Bosko et al.41 reported shear thinning exponents increasing with M under NVT (βη ∈ [0.28–0.36]) while, for NPisoT the were roughly independent of M (βη ∈ [0.37–0.39]). The same work reported βΨ1 ≃ 1.27 and βΨ2 ≃ 1.23 under NPisoT, while βΨ1 ≃ 1.1 βΨ2 ≃ 1.0 under NVT. Closed simulations for hyperbranched polymer melts42 predicted βη ≃ 0.3 (slightly increasing with molecular mass M), while βΨ2 ≃ 0.95 and βΨ1 ≃ 1 (both roughly independent on M). The scaling of (first and second) normal coefficients are probably sensitive to the type of external constraint (either isobaric Piso or constant load P22). As an indication, a numerical study at constant load for linear chains43 reported the same exponents found in this work (βΨ1 = 1.35 and βΨ2 ≃ 1 respectively). Concerning shear viscosity, if the density is allowed to relax (under isobaric or constant load conditions) the shear thinning exponents reported in the literature show much less variation with the molecular weight than under a fixed density. This has been shown for linear chains under a constant load43 and also for dendrimers.42 In both cases, the shear thinning exponent in the variable density case was found to be close to 0.4, while it ranged from 0.25 to 0.4 in the closed system (increasing with the molecular weight in both cases). This larger insensitivity of shear thinning exponents under fixed load conditions agrees with our observations in simulations presenting viscous heating mentioned in Section 9.
More recently, very similar papers106,107 studied the rheology and dynamics108 of star polymers with different functionalities in solution. They reported that the contribution of the stars to the sheared solution viscosity scales like Wi−0.4 which is quite close to the shear thinning exponents we find here for the melt. According to these simulations,106,107 the first normal stress coefficient scales like Ψ1 ∼ Wi−1 in solution, although the authors claim an exponent of −4/3 at very high shear rates Wi > 100. In the melt, we observe the −4/3 power law at smaller shear rates. The second normal coefficient seems also to scale slightly differently in solution Ψ2 ∼ Wi−4/3 than in the melt Ψ2 ∼ Wi−1. The strong similarities in solution and melt indicate that rheological properties are mainly ruled by conformational changes of the chains and maybe also that the hydrodynamic effects in the melt are somewhat similar to those in a liquid solvent. Finally, it is interesting to note that the range of values for βη and βΨ1 for stars, dendrimers and hyperbranched molecules are consistent with the theoretical calculation of Kroger et al.88 based on the Fokker–Planck equation for the bond vector distribution of multibead linear chains having slow rotational diffusion (compared with the entanglement relaxation) and a finite deformation energy.88 These two features are indeed consistent with the nature of short-armed stars, dendrimers and hyperbranched molecules with internal excluded volume interactions.
The number of experimental studies on rheology of sheared star polymers is not abundant either, but it is growing fast due to the foreseen technological applications.52,53 Most of these studies consider long armed stars which present entanglements. However, the shear thinning exponent we found for the tangential friction case βη = 0.5 is quite close to the star case of the experiments by Tezel et al.109 (4 arms stars with Ma = 140 kg mol−1; the lowest molecular weight considered in these experiments). Although entanglements in star polymers are not yet fully understood in the non-Newtonian regime,52 they should be responsible for the substantially increase in shear thinning (exponents close to 0.8) observed in the recent experiments with star molecule melts of Snijkers et al.52 Shear thinning exponents found in melts of linear chains are around βη = 1 (predicted by reptation theory). An open question is why star molecules significantly reduce the shear thinning.52
The analyses presented in Section 6 based on the (exact) balance of the pressure coming from the different contributions (kinetic, intramolecular, intermolecular and bonds) provide some clues which can be useful in a broader study. These types of analysis were performed by Baig et al.,2,3 Matin43 and Tschopp.45 However these balances were based on the energy budget which has less direct rheological consequences than the stress. Also, surprisingly, the kinetic contribution was not considered (leading to unbalanced analyses). The sole exception we found is the work of Kroger et al.89 for linear FENE chains which, like ours, is based on the exact stress budget. In elongational flow of linear chain melts, Kroger et al.89 found that viscous effects came mainly from intramolecular collisions (they called it “simple fluid” stress offset). Here, we find that in star molecules the kinetic pressure can be the dominant viscous contribution to the melt rheology at large shear rates (a possibility in fact recognized by Kroger et al. in their book4). The kinetic pressure is however reduced with the tangential friction and this warns about the need of dynamic coarse-graining9 to represent a realistic model. While linear chains tumble in shear flow,110 star molecules perform a quite different motion called tank-threading102,105 (whereby arms rotate around the molecule center). One can speculate that the reduction of shear thinning observed in star melts is due to an enhanced kinetic pressure related to the tank-threading. Above Wi > 10 we observe the tank-threading motion in our melt with monomer angular momentum growing much faster (ω ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.6 from the preliminary results) than it does in stars in solution (where ω is constant102,111). Concerning intermolecular interactions, quite often neglected in the literature (see e.g.ref. 87), we find that these are the key to transfer the externally imposed stress into molecular strain and elastic stress. This observation agrees with that of Kroger et al.89 Intermolecular friction is the sole possible mechanism if entanglements are not relevant (like in our short arm star molecules).
0.6 from the preliminary results) than it does in stars in solution (where ω is constant102,111). Concerning intermolecular interactions, quite often neglected in the literature (see e.g.ref. 87), we find that these are the key to transfer the externally imposed stress into molecular strain and elastic stress. This observation agrees with that of Kroger et al.89 Intermolecular friction is the sole possible mechanism if entanglements are not relevant (like in our short arm star molecules).
11 Conclusions
We have conducted OBMD simulations of the melt of star polymers (73 monomers, 12 arms of 6 monomers per arm) using a relatively new modelling technique which combines the adaptive resolution and open-MD (respectively, introduced in ref. 22 and 46 and used in many other studies). From a technical point of view, this work substantially enlarges the size of molecules exchanged between the open system and the reservoir.13 In this work, we however focus on what happens if a melt is sheared under a constant normal load instead of a constant volume. The constant load is in fact the condition in many experiments (see ref. 40 and 44) although the simulation literature on the subject is not abundant. We have also presented some conclusions on how the tangential and normal monomer–monomer frictions affect these CG molecular models.The OBMD permits to perform several new features in a molecular simulation. At equilibrium, the OBMD correctly represents the mass fluctuations of the grand canonical ensemble and interestingly, it could permit to study how fluctuations and sound velocity are altered under non-equilibrium (e.g. sheared) states. OBMD also allows to impose the external shear stress Pext12 as required for (flux based) hybrid continuum-MD simulations.15,66 It could also enable the validation of theories like extended thermodynamics47 predicting different outcomes for the “conjugate” constant stress and constant shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) non-equilibrium ensembles.
non-equilibrium ensembles.
Concerning the present study, we observe that under a constant normal pressure, the melt expands when sheared (shear dilatancy) leading to substantial depressurization and slightly decreasing the shear viscosity. This behaviour was observed in most previous simulations on sheared melts, but surprisingly it is still unclear if it is the general (universal) trend (e.g. see ref. 40). This study provides new information on the rheology of sheared melts: notably, we see that the type of monomer friction is a key aspect for the system rheology. From a theoretical standpoint,9 friction between monomers (or rather “polymer blobs”) arises as soon as one consider a CG view of the complex molecule (which is the standard case in polymer science). The pressure balance analysis reveals that in the absence of tangential friction, the monomer kinetic stress becomes significant at large shear rates, increasing the system viscosity (reducing the shear thinning exponent) and diminishing its elastic response (e.g. normal stress difference and stress recovery). We also observed viscous heating in some simulations (e.g. using the sdpdshort and sdpdlong thermostats) revealing a viscosity jump (shear thickening) in closed systems. By contrast, the viscosity of the heated (and less dense) open samples did not change in trend (shear thinning) under a constant load. This indicates that the melt viscosity is controlled by the normal pressure, at least for the present type of molecules with purely repulsive interactions and no significant entanglements. We expect the OBMD to become useful in other studies, such as adding the energy transfer63 or extending the incompressible coupling in ref. 10 to perform hybrid simulations of compressible melts including the transfer of dissipated heat through/across system boundaries. Thus, the properties related to heat conduction could be investigated.112
Acknowledgements
We thank J. J. Freire for initial configurations and K. Kremer for useful discussions. J. S. and M. P. acknowledge financial support through grants P1-0002 and J1-4134 from the Slovenian Research Agency. J. S. acknowledges financial support from Slovene Human Resources Development and Scholarship Fund (186. JR). R. D-B acknowledges support from the Spanish government under national MINECO project FIS2013-47350-C5-1-R. Partial support from the COST Action MP1305 is kindly acknowledged.References
- R. Larson and H. Brenner, Constitutive Equations for Polymer Melts and Solutions: Butterworths Series in Chemical Engineering, Elsevier Science, 2013 Search PubMed.
- C. Baig and V. G. Mavrantzas, J. Chem. Phys., 2010, 132, 014904 CrossRef PubMed.
- C. Baig, V. G. Mavrantzas and M. Kröger, Macromolecules, 2010, 43, 6886–6902 CrossRef CAS.
- M. Kröger, Models for Polymeric and Anisotropic Liquids, Springer, Berlin Heidelberg, 2005 Search PubMed.
- J. Padding, E. van Ruymbeke, D. Vlassopoulos and W. Briels, Rheol. Acta, 2010, 49, 473–484 CrossRef CAS.
- V. A. Harmandaris, N. P. Adhikari, N. F. A. van der Vegt and K. Kremer, Macromolecules, 2006, 39, 6708–6719 CrossRef CAS.
- C. F. Abrams, J. Chem. Phys., 2005, 123, 234101 CrossRef PubMed.
- P. Ilg, H. C. Öttinger and M. Kröger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011802 CrossRef PubMed.
- C. Hijon, P. Espanol, E. Vanden-Eijnden and R. Delgado-Buscalioni, Faraday Discuss., 2010, 144, 301–322 RSC.
- S. Yasuda and R. Yamamoto, Phys. Rev. X, 2014, 4, 041011 Search PubMed.
- R. Delgado-Buscalioni, K. Kremer and M. Praprotnik, J. Chem. Phys., 2008, 128, 114110 CrossRef PubMed.
- R. Delgado-Buscalioni, K. Kremer and M. Praprotnik, J. Chem. Phys., 2009, 131, 244107 CrossRef PubMed.
- R. Delgado-Buscalioni, J. Sablić and M. Praprotnik, Eur. Phys. J.: Spec. Top., 2015, 224, 2331–2349 CrossRef CAS.
- R. Delgado-Buscalioni, Numerical Analysis of Multiscale Computations, 2012, 145–166 Search PubMed.
- G. De Fabritiis, R. Delgado-Buscalioni and P. V. Coveney, Phys. Rev. Lett., 2006, 97, 134501 CrossRef CAS PubMed.
- K. Mohamed and A. Mohamad, Microfluid. Nanofluid., 2010, 8, 283–302 CrossRef.
- J. H. Walther, M. Praprotnik, E. M. Kotsalis and P. Koumoutsakos, J. Comput. Phys., 2012, 231, 2677–2681 CrossRef CAS.
- S. Yasuda and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 036308 CrossRef PubMed.
- W. E, B. Engquist, X. Li, W. Ren and E. Vanden-Eijnden, Commun. Comput. Phys., 2007, 2, 367–450 Search PubMed.
- N. D. Petsev, L. G. Leal and M. S. Shell, J. Chem. Phys., 2015, 142, 044101 CrossRef PubMed.
- D. A. Fedosov and G. E. K. B. Caswell, J. Chem. Phys., 2010, 132, 144103 Search PubMed.
- M. Praprotnik, L. Delle Site and K. Kremer, J. Chem. Phys., 2005, 123, 224106 CrossRef PubMed.
- M. Praprotnik, L. Delle Site and K. Kremer, Annu. Rev. Phys. Chem., 2008, 59, 545–571 CrossRef CAS PubMed.
- M. Praprotnik, S. Poblete and K. Kremer, J. Stat. Phys., 2011, 145, 946–966 CrossRef.
- S. Bevc, C. Junghans, K. Kremer and M. Praprotnik, New J. Phys., 2013, 15, 105007 CrossRef.
- H. Wang, C. Hartmann, C. Schütte and L. Delle Site, Phys. Rev. X, 2013, 3, 011018 Search PubMed.
- J. Zavadlav, M. N. Melo, A. V. Cunha, A. H. de Vries, S. J. Marrink and M. Praprotnik, J. Chem. Theory Comput., 2014, 10, 2591–2598 CrossRef CAS PubMed.
- J. Zavadlav, M. N. Melo, S. J. Marrink and M. Praprotnik, J. Chem. Phys., 2014, 140, 054114 CrossRef PubMed.
- A. Agarwal, H. Wang, C. Schütte and L. Delle Site, J. Chem. Phys., 2014, 141, 034102 CrossRef PubMed.
- J. Zavadlav, M. N. Melo, S. J. Marrink and M. Praprotnik, J. Chem. Phys., 2015, 142, 244118 CrossRef PubMed.
- J. Zavadlav, R. Podgornik and M. Praprotnik, J. Chem. Theory Comput., 2015, 11, 5035–5044 CrossRef CAS PubMed.
- H. Wang and A. Agarwal, Eur. Phys. J.: Spec. Top., 2015, 224, 2269–2287 CrossRef CAS.
- A. Agarwal, J. Zhu, C. Hartmann, H. Wang and L. D. Site, New J. Phys., 2015, 17, 083042 CrossRef.
- K. Kreis, A. C. Fogarty, K. Kremer and R. Potestio, Eur. Phys. J.: Spec. Top., 2015, 224, 2289–2304 CrossRef CAS.
- D. Mukherji and K. Kremer, Macromolecules, 2013, 46, 9158–9163 CrossRef CAS.
- P. Szymczak and M. Cieplak, J. Chem. Phys., 2007, 127, 155106 CrossRef CAS PubMed.
- P. Szymczak and M. Cieplak, J. Phys.: Condens. Matter, 2011, 23, 033102 CrossRef PubMed.
- B. Z. Dlugogorski, M. Grmela and P. J. Carreau, J. Non-Newtonian Fluid Mech., 1993, 48, 303–335 CrossRef CAS.
- P. J. Daivis and D. J. Evans, J. Chem. Phys., 1994, 100, 541–547 CrossRef CAS.
- Z. Xu, J. J. de Pablo and S. Kim, J. Chem. Phys., 1995, 102, 5836–5844 CrossRef CAS.
- J. T. Bosko, B. D. Todd and R. J. Sadus, J. Chem. Phys., 2005, 123, 034905 CrossRef PubMed.
- T. C. Le, B. D. Todd, P. J. Daivis and A. Uhlherr, J. Chem. Phys., 2009, 131, 044902 CrossRef CAS PubMed.
- M. L. Matin, PhD thesis, Royal Melbourne Institute of Technology, Melbourne, 2001.
- P. A. Thompson, G. S. Grest and M. O. Robbins, Phys. Rev. Lett., 1992, 68, 3448–3451 CrossRef PubMed.
- M. Tschopp, J. L. Bouvard, D. Ward, D. Bammann and M. F. Horstemeyer, 2013, arXiv:1310.0728, 1–28.
- E. G. Flekkoy, R. Delgado-Buscalioni and P. V. Coveney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 026703 CrossRef PubMed.
- D. Jou, J. Casas-Vázquez and M. Criado-Sancho, Thermodynamics of Fluids Under Flow, Springer, Netherlands, 2010 Search PubMed.
- P. Daivis, J. Non-Newtonian Fluid Mech., 2008, 152, 120–128 CrossRef CAS.
- J. Dealy and J. Wang, Melt Rheology and its Applications in the Plastics Industry, Springer, Netherlands, 2013 Search PubMed.
- J. Aho, Rheological Characterization of Polymer Melts in Shear and Extension: Measurement Reliability and Data for Practical Processing, Tampere University of Technology, 2011 Search PubMed.
- W. Friesenbichler, I. Duretek, J. Rajganesh and S. R. Kumar, Polimery, 2011, 56(1), 58–62 Search PubMed.
- F. Snijkers, K. Ratkanthwar, D. Vlassopoulos and N. Hadjichristidis, Macromolecules, 2013, 46, 5702–5713 CrossRef CAS.
- D. Vlassopoulos, G. Fytas, T. Pakula and J. Roovers, J. Phys.: Condens. Matter, 2001, 13, R855–R876 CrossRef CAS.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef CAS.
- S. M. T. Divoux, M. A. Fardin and S. Lerouge, 2015, arXiv:1503.04130, 1–16.
- S.-Q. Wang, S. Ravindranath and P. E. Boukany, Macromolecules, 2011, 44, 183–190 CrossRef CAS.
- S. T. Milner, T. C. B. McLeish and A. E. Likhtman, J. Rheol., 2001, 45, 539–563 CrossRef CAS.
- C. Koch, A. Z. Panagiotopoulos, F. Lo Verso and C. N. Likos, Soft Matter, 2013, 9, 7424–7436 RSC.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24, 1624–1636 CrossRef CAS PubMed.
- S. Bevc, C. Junghans and M. Praprotnik, J. Comput. Chem., 2015, 36, 467–477 CrossRef CAS PubMed.
- R. Delgado-Buscalioni and P. V. Coveney, J. Chem. Phys., 2003, 119, 978–987 CrossRef CAS.
- R. Potestio, S. Fritsch, P. Español, R. Delgado-Buscalioni, K. Kremer, R. Everaers and D. Donadio, Phys. Rev. Lett., 2013, 110, 108301 CrossRef PubMed.
- R. Potestio, P. Español, R. Delgado-Buscalioni, R. Everaers, K. Kremer and D. Donadio, Phys. Rev. Lett., 2013, 111, 060601 CrossRef PubMed.
- P. Español, R. Delgado-Buscalioni, R. Everaers, R. Potestio, D. Donadio and K. Kremer, J. Chem. Phys., 2015, 142, 064115 CrossRef PubMed.
- R. Delgado-Buscalioni and G. De Fabritiis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 036709 CrossRef CAS PubMed.
- E. A. Koopman and C. P. Lowe, J. Chem. Phys., 2006, 124, 204103 CrossRef CAS PubMed.
- T. Soddemann, B. Dünweg and K. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 046702 CrossRef PubMed.
- P. Espanol and P. Warren, Europhys. Lett., 1995, 30, 191 CrossRef CAS.
- C. Junghans, M. Praprotnik and K. Kremer, Soft Matter, 2008, 4, 156–161 RSC.
- A. W. Lees and S. F. Edwards, J. Phys. C: Solid State Phys., 1972, 5, 1921 CrossRef.
- D. J. Evans and G. P. Morriss, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 1528–1530 CrossRef CAS.
- A. J. Ladd, Mol. Phys., 1984, 53, 459–463 CrossRef CAS.
- J. Freire, in Branched Polymers II, ed. J. Roovers, Springer, Berlin Heidelberg, 1999, vol. 143, pp. 35–112 Search PubMed.
- M. SJ, Korea-Aust. Rheol. J., 2008, 20, 117–125 Search PubMed.
- F. Legrand and J.-M. Piau, J. Non-Newtonian Fluid Mech., 1998, 77, 123–150 CrossRef CAS.
- R. A. Mendelson, Trans. Soc. Rheol., 1965, 9, 53–63 CrossRef CAS.
- J. Casas-Vázquez and D. Jou, Rep. Prog. Phys., 2003, 66, 1937 CrossRef.
- S. Bernardi, B. D. Todd and D. J. Searles, J. Chem. Phys., 2010, 132, 244706 CrossRef PubMed.
- P. Padilla and S. Toxvaerd, J. Chem. Phys., 1996, 104, 5956–5963 CrossRef CAS.
- R. Khare, J. de Pablo and A. Yethiraj, J. Chem. Phys., 1997, 107, 2589–2596 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Christen and W. F. van Gunsteren, J. Chem. Phys., 2006, 124, 154106 CrossRef PubMed.
- G. S. Grest, K. Kremer, S. T. Milner and T. A. Witten, Macromolecules, 1989, 22, 1904–1910 CrossRef CAS.
- G. S. Grest, K. Kremer and T. A. Witten, Macromolecules, 1987, 20, 1376–1383 CrossRef CAS.
- A. Eriksson, M. N. Jacobi, J. Nyström and K. Tunstrom, J. Chem. Phys., 2008, 129, 024106 CrossRef PubMed.
- G. Strobl, The Physics of Polymers, Springer-Verlag, NY, 1997 Search PubMed.
- M. Kröger, W. Loose and S. Hess, J. Rheol., 1993, 37, 1057–1079 CrossRef.
- M. Kröger, C. Luap and R. Muller, Macromolecules, 1997, 30, 526–539 CrossRef.
- J.-P. Hansen and I. R. McDonald, in Theory of Simple Liquids, ed. J.-P. Hansen and I. R. McDonald, Academic Press, Burlington, 3rd edn, 2006, pp. 11–45 Search PubMed.
- R. Delgado-Buscalioni and A. Dejoan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 046708 CrossRef CAS PubMed.
- R. Delgado-Buscalioni and P. V. Coveney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 046704 CrossRef CAS PubMed.
- P. Allen and D. Tildesley, Computer simulation of liquids, Clarendon Press, 1987 Search PubMed.
- K. Yasuda, J. Text. Sci. Eng., 2006, 52, 171–173 CrossRef.
- J.-P. Ryckaert, A. Bellemans, G. Ciccotti and G. V. Paolini, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 259–267 CrossRef.
- P. Kindt and W. J. Briels, J. Chem. Phys., 2005, 123, 224903 CrossRef CAS PubMed.
- C. Baig and V. A. Harmandaris, Macromolecules, 2010, 43, 3156–3160 CrossRef CAS.
- S. Barsky, R. Delgado-Buscalioni and P. V. Coveney, J. Chem. Phys., 2004, 121, 2403–2411 CrossRef CAS PubMed.
- R. Delgado-Buscalioni, AIP Conf. Proceedings, 2007, 913, 114.
- B. D. Todd, D. J. Evans and P. J. Daivis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 1627–1638 CrossRef CAS.
- R. L. C. Akkermans and G. Ciccotti, J. Phys. Chem. B, 2004, 108, 6866 CrossRef CAS.
- M. Ripoll, R. G. Winkler and G. Gompper, Phys. Rev. Lett., 2006, 96, 188302 CrossRef CAS PubMed.
- J. Brandao, E. Spieth and C. Lekakou, Polym. Eng. Sci., 1996, 36, 49–55 CAS.
- X. Cheng, X. Xu, S. A. Rice, A. R. Dinner and I. Cohen, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 63–67 CrossRef CAS PubMed.
- M. Ripoll, R. Winkler and G. Gompper, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 349–354 CrossRef CAS PubMed.
- D. A. Fedosov, S. P. Singh, A. Chatterji, R. G. Winkler and G. Gompper, Soft Matter, 2012, 8, 4109–4120 RSC.
- S. P. Singh, A. Chatterji, G. Gompper and R. G. Winkler, Macromolecules, 2013, 46, 8026–8036 CrossRef CAS.
- S. P. Singh, C.-C. Huang, E. Westphal, G. Gompper and R. G. Winkler, J. Chem. Phys., 2014, 141, 084901 CrossRef PubMed.
- A. K. Tezel, J. P. Oberhauser, R. S. Graham, K. Jagannathan, T. C. B. McLeish and L. G. Leal, J. Rheol., 2009, 53, 1193–1214 CrossRef CAS.
- R. Delgado-Buscalioni, Phys. Rev. Lett., 2006, 96, 088303 CrossRef PubMed.
- S. P. Singh, D. A. Fedosov, A. Chatterji, R. G. Winkler and G. Gompper, J. Phys.: Condens. Matter, 2012, 24, 464103 CrossRef PubMed.
- J. Li and J. Lee, Acta Mech., 2014, 225, 1223–1233 CrossRef.
Footnotes |
| † An interesting remark is that the recoverable shear compliance87 obtained from Je = τrot/η0 results to be Je ≃ 110 independent of the friction kernel. |
| ‡ Traditionally, following the experiment standpoint, rheological magnitudes are expressed in terms of the pressure on the system (here given by −P). For instance, the normal stress difference is then N1 = −(P11 − P22) and this explains the opposite sign used in our (and other) simulation studies. |
| § This can be proved from the equation for the time dependence of the covariance 〈dvi/dt(t)dvi/dt(t′)〉 of the DPD Langevin's equation and can be easily checked (and the cooling rate α measured) upon observation of an exponential convergence of T towards T0 after an instantaneous change (increase or decrease) of T0. |
| This journal is © The Royal Society of Chemistry 2016 |