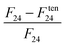Open Access Article
Open Access ArticleRelevance of saddle-splay elasticity in complex nematic geometries†
Žiga
Kos
*a and
Miha
Ravnik
ab
aFaculty of Mathematics and Physics, University of Ljubljana, Slovenia. E-mail: ziga.kos@fmf.uni-lj.si; miha.ravnik@fmf.uni-lj.si
bJosef Stefan Institute, Ljubljana, Slovenia
First published on 13th November 2015
Abstract
We demonstrate the relevance of saddle-splay elasticity in nematic liquid crystalline fluids in the context of complex surface anchoring conditions and the complex geometrical confinement. Specifically, nematic cells with patterns of surface anchoring and colloidal knots are shown as examples where saddle-splay free energy contribution can have a notable role which originates from nonhomogeneous surface anchoring and the varying surface curvature. Patterned nematic cells are shown to exhibit various (meta)stable configurations of nematic field, with relative (meta)stability depending on the saddle-splay. We show that for high enough values of saddle-splay elastic constant K24 a previously unstable conformation can be stabilised, more generally indicating that the saddle-splay can reverse or change the (meta)stability of various nematic structures affecting their phase diagrams. Furthermore, we investigate saddle-splay elasticity in the geometry of highly curved boundaries – the colloidal particle knots in nematic – where the local curvature of the particles induces complex spatial variations of the saddle-splay contributions. Finally, a nematic order parameter tensor based saddle-splay invariant is shown, which allows for the direct calculation of saddle-splay free energy from the Q-tensor, a possibility very relevant for multiple mesoscopic modelling approaches, such as Landau-de Gennes free energy modelling.
1 Introduction
The complex geometrical confinement of nematic liquid crystalline fluids by micro and nano-sized cavities, channels, topological objects and colloids is today an interesting direction for developing novel optical,1 photonic,2,3 rheological,4,5 topological6,7 and microfluidic8 materials. In such systems, the main variabilities are the geometry of the confining surfaces6–8 and the alignment of the nematic imposed by the surfaces (i.e. surface anchoring).8,9Complex surface conditions for nematic ordering can be achieved by patterning the surfaces with different surfactants, e.g. that impose partly perpendicular, partly inplane orientation of nematic molecules. In flat nematic cells, such an approach can lead to sub-millisecond switching times of the nematic with electric field and is interesting for fast switching high-resolution displays.9 Flat patterned cells may also exhibit a variety of nematic states with topological defects.10 The patterned surface can be applied also to spheres11–14 or tori,15 thus producing Janus colloids.
Geometric variability of the nematic confinement is today impressively achieved by producing complex-shaped colloidal particles that take the shape of knots,6 nematic defect conditioned fibres,16 faceted particles17–20 or handlebodies.7,21 Contact surfaces between nematic fluid and the confining geometry can also be made micro-structured, with surface corrugations22 and surface wrinkles.23,24 The geometry and surface anchoring can be designed to give a working key-lock mechanism.25 Another approach towards complex shaped objects is also by considering emulsions of nematic in host fluids, leading to complex shaped droplet fibres3 and foams.26
Nematic liquid crystalline fluids are soft materials with a long range orientational order – characterised by nematic director n with n ↔ −n symmetry – that effectively respond elastically to external stimuli imposed by external fields or surfaces. Three basic elastic modes of nematic ordering are known to emerge – splay, twist and bend – which importantly are further combined with elastic deformation modes know as saddle-splay and splay-bend. The elasticity effects are typically considered at the mesoscopic level, relying on the phenomenological expansion of the nematic free energy, as for example in Frank–Oseen or Landau–de Gennes formulation.27,28 Notably, the Landau–de Gennes free energy minimisation is today used as one of the central approaches for modelling and predicting nematic liquid crystal fields because it can well account for the formation of topological defects.29–37 It is actually well known that besides the standard splay, twist and bend elastic modes also saddle-splay elasticity is inherently incorporated into the Landau–de Gennes free energy (even with only one elastic constant), but typically little attention is paid to its actual relevance when interpreting the results.
Saddle-splay elasticity has been of interest in experimental and theoretical studies. Periodic stripe deformation patterns were observed experimentally in a nematic confined between a homeotropic and a planar surface.38,39 Numerical analysis has revealed the saddle-splay elasticity to be the driving force of the creation of a stripe pattern. In similar geometries a set of point defects and strings was also observed, allowing for an estimation of the saddle-splay elastic constant.40 In nematic droplets, various configurations are observed and predicted, depending on the droplet size, anchoring of nematic molecules, and nematic elasticity. Saddle-splay was revealed to be a key element when calculating their stability criteria.41–43 Experiments performed on biphenylic liquid crystals confined to cylindrical capillaries with homeotropic anchoring44,45 show at least four distinct configurations, whose stability is used to analytically determine the saddle-splay elastic constant. Numerical results confirm a great role of saddle-splay in capillaries, specifically in the weak anchoring regime.46 An experimental and theoretical study of lyotropic chromonic liquid crystals confined to capillaries with planar degenerate boundary conditions reveals a chiral structure, which is a result of a large saddle-splay elastic modulus.47 Similarly, saddle-splay was attributed to the chiral symmetry breaking in torus-shaped droplets.21,48 Finally, the role of saddle-splay was investigated theoretically even for cholesteric liquid crystals under capillary confinement49 and nematic shells.50
Experimental21,38,44,45 and numerical51 studies on saddle-splay free energy and its K24 elastic constant agree that K24 is indeed substantial and can be comparable in size to the standard Frank elastic constants (K1, K2, K3), at least in a typical nematic representative 5CB material. Furthermore, recently unconventional elastic regimes have been reached in experiments, as for example in chromonic liquid crystals52,53 or in twist-bend54–56 and splay-bend57 phases. Actual values of the saddle-splay elastic constant in such materials are mostly unknown, however, it might be possible that such or similar materials could also have an unconventional saddle-splay elastic constant (as predicted in ref. 47) thus exhibiting some of the effects presented in this article.
If the nematic degree of order (scalar order parameter) is homogeneous, the saddle-splay elastic free energy can be rewritten into a form of a surface term, effectively renormalising the surface anchoring. Typically, this is the main reason why its contribution to the total free energy is (and can be) ignored. However, if the nematic geometry is complex and has complex boundaries, this surface integral may be of the same size as the splay, twist or bend elastic contributions and importantly, also spanning over regions which are defects (e.g. boojums or other). Even in view of the homogeneous order parameter and defect-free configurations, there are two reasons how saddle-splay can be important: (i) if the surface anchoring is small enough to allow for deviations from the preferred order at the boundary, as is the case in ref. 38 and 39. (ii) If the anchoring is made degenerate, saddle-splay is made important by the local curvature of the boundary,21,47,48 or by patterning the surface with different anchoring regimes, as shown in this article. The idea of this paper is to show that in distinct complex confining geometries and surface anchoring configurations it is essential to consider also the saddle-splay elasticity, when exploring nematic fields. The examples of such geometries and surfaces include patterned cells9 and complex shaped colloidal particles, like knots.6
In this paper, we explore the saddle-splay free energy of nematic liquid crystalline fluids in complex geometries and in complex surface anchoring profiles, specifically demonstrating the important role of saddle-splay elasticity in patterned cells and in nematic colloidal knots. We consider saddle-splay elasticity in surface and volume free energy density formulations, taking advantage of both descriptions to demonstrate its role. Notably, we explore saddle-splay elasticity formulated by tensor order parameter free energy terms rather than the standard director based formulation. We analyse the role of the elastic anisotropy in homeotropic-planar patterned cells for local hybrid aligned nematic and for boojum structures, finding that relative (meta)stability of the structures can be strongly affected by the actual value of the saddle-splay constant. We extend our analysis to colloidal knots, showing that regions of nematic boojum defects (which form at largest curvature regions of the particle knots) contribute via the saddle-splay as much as 37% to the total elastic free energy if assuming single Landau elastic constant approximation (2K24 = Ki = K). Finally, we evaluate the mutual relation between tensor and director based formulation of the saddle-splay free energy.
2 Model and methods
The relevance of saddle-splay nematic deformation is explored within the general framework of the mesoscopic free energy, formulated in terms of nematic order parameter tensor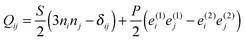 , which besides the scalar order parameter S and the director n includes also the biaxial ordering around second director e(1) with biaxiality parameter P. The free energy is most commonly written in the Landau–de Gennes form:27,58,59
, which besides the scalar order parameter S and the director n includes also the biaxial ordering around second director e(1) with biaxiality parameter P. The free energy is most commonly written in the Landau–de Gennes form:27,58,59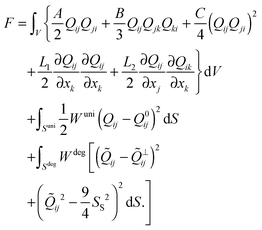 | (1) |
![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) ij = Qij + SSδij/2,
ij = Qij + SSδij/2, ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) ⊥ij = Pik
⊥ij = Pik![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) klPlj, Pij = δij − νiνj, and νi is the surface normal. SS is the surface-imposed degree of order which is set to Seq. Generally, the first two lines of eqn (1) form the Landau–de Gennes free energy FLdG and the last three lines form the surface anchoring free energy Fa. The main advantage of the Q-tensor formulation of the free energy is that – besides the deformation of the director field – it also allows for modelling of the spatial variation of the nematic degree of order, thus better describing various experimental systems, in particular those with nematic defects. The director symmetry n ↔ −n is also inherently incorporated in the tensor approach, making it a strong choice when calculating the nematic field profiles.
klPlj, Pij = δij − νiνj, and νi is the surface normal. SS is the surface-imposed degree of order which is set to Seq. Generally, the first two lines of eqn (1) form the Landau–de Gennes free energy FLdG and the last three lines form the surface anchoring free energy Fa. The main advantage of the Q-tensor formulation of the free energy is that – besides the deformation of the director field – it also allows for modelling of the spatial variation of the nematic degree of order, thus better describing various experimental systems, in particular those with nematic defects. The director symmetry n ↔ −n is also inherently incorporated in the tensor approach, making it a strong choice when calculating the nematic field profiles.
Nematic elastic free energy Fel formulated via the nematic order parameter tensor Qij can be rewritten (as well known from the literature27,28) into the form based on derivatives of the nematic director field n, if assuming uniaxial Qij and the homogeneous nematic degree of order. The result is the Frank–Oseen FF–O and saddle-splay F24 free energy:27,28
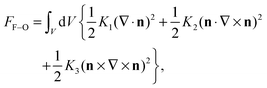 | (2) |
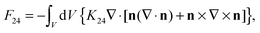 | (3) |
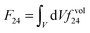 , K1, K2, K3, and K24 are splay, twist, bend, and saddle-splay elastic constants, respectively. The elastic constants depend on temperature (or concentration, if considering lyotropic liquid crystals) and as such on the nematic degree of order S. Here, primarily for simplicity, we use only two (tensorial) elastic constants L1 and L2, which correspond to K1 = K3. This identity can be broken by including the third (tensorial) elastic constant. The correspondence between the two used temperature independent (tensorial) elastic constants Li (i = 1, 2) and Frank elastic constants Ki is as follows:
, K1, K2, K3, and K24 are splay, twist, bend, and saddle-splay elastic constants, respectively. The elastic constants depend on temperature (or concentration, if considering lyotropic liquid crystals) and as such on the nematic degree of order S. Here, primarily for simplicity, we use only two (tensorial) elastic constants L1 and L2, which correspond to K1 = K3. This identity can be broken by including the third (tensorial) elastic constant. The correspondence between the two used temperature independent (tensorial) elastic constants Li (i = 1, 2) and Frank elastic constants Ki is as follows: 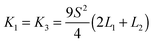 ,
, 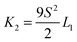 , and
, and 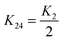 . For liquid crystal materials, the Ki set of elastic constants is typically measured. In the free energy formulation, splay-bend elastic terms can be also included,28,60–62 which includes ∇2n elastic free energy term. This is a higher order contributions; therefore we do not consider it in this article.
. For liquid crystal materials, the Ki set of elastic constants is typically measured. In the free energy formulation, splay-bend elastic terms can be also included,28,60–62 which includes ∇2n elastic free energy term. This is a higher order contributions; therefore we do not consider it in this article.
Our numerical simulations are performed by minimising the total free energy by using the finite difference relaxation algorithm on a cubic mesh.37 The notable advantage of using this computationally simple method is that it is fast and also not very computer memory demanding, allowing us to simulate rather large simulation volumes, which qualitatively and even quantitatively compare well with experiments.6,16 The minimisation is performed with the full symmetric Qij tensor, and only after the equilibrium configuration is achieved, the director, the nematic degree of order and other possible variables are calculated from the equilibrium Qij profile. In the simulations, the following values of the parameters are used: A = −0.172 × 106 J m−3, B = −2.13 × 106 J m−3, C = 1.73 × 106 J m−3, and mesh resolution Δx = 10 nm which is sufficient to avoid defect pinning by the mesh. x0, y0, and z0 are used to denote the size of the simulation box in x, y, and z directions. Mesh box equals 140 × 140 × 71 points for patterned cells and 300 × 300 × 300 points for colloidal knots. In the regime of a single elastic constant, we use L1 = 4 × 10−11 N (and L2 = 0). Chosen parameters roughly correspond to cyanobiphenilic liquid crystals.63,64 In the elastically anisotropic regime, we use different ratios between elastic constants denoting the elastic anisotropy within the Frank–Oseen formulation as K1/K2. To preserve the lower estimate for the correlation length ξ = 6.63 nm (important for numerical stability), the larger of the two elastic constants is increased when changing the elastic anisotropy at the constant nematic degree of order, while keeping the relations K3 = K1 and K24 = K2/2 preserved. The above material parameters correspond to dimensionless numerical parameters, set by L1(K1 = K2) = 1 and ξ = 1, as follows: A = −0.118, B = −2.341, C = 1.901, Δx = 1.5. Preserving the lower estimate of the correlation length, the following transformation of dimensionless L1 and L2 is performed to characterise the K1/K2 ratio: L1 = K2/K1, L2 = 2(1 − K2/K1) in the case of K1/K2 ≤ 1, and L1 = 1, L2 = 2(K1/K2 − 1) in the case of K1/K2 ≥ 1. Experimentally, similar elastic regimes could be achieved by the proper choice of the nematic material52–57 or by tuning the temperature, and thus taking advantage of large deviations of elastic constants near nematic–isotropic64,65 or nematic–smectic66,67 phase transition.
2.1 Surface form of saddle-splay elasticity
Considering the Gauss theorem, the saddle-splay free energy can be rewritten into the surface integral form in the regime of the homogeneous nematic degree of order:28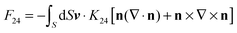 | (4) |
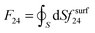 ), in contrast to bulk saddle-splay free energy density fbulk24. We provide the analysis of saddle-splay elasticity in complex nematic systems in view of volume (eqn (3)) and surface (eqn (4)) free energy density, which are calculated after the Q-tensor relaxation of the free energy (eqn (1)) has been performed.
), in contrast to bulk saddle-splay free energy density fbulk24. We provide the analysis of saddle-splay elasticity in complex nematic systems in view of volume (eqn (3)) and surface (eqn (4)) free energy density, which are calculated after the Q-tensor relaxation of the free energy (eqn (1)) has been performed.
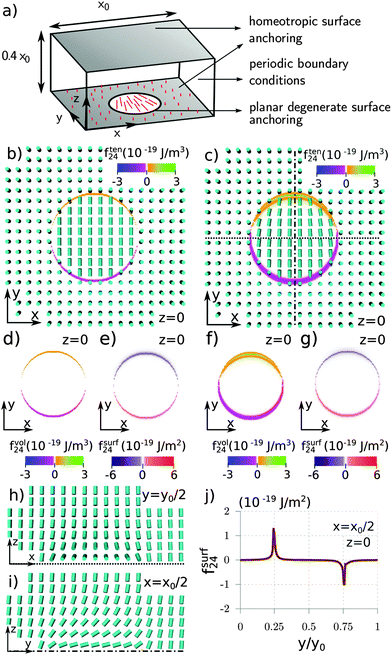
If we consider a nematic cell, bounded by two horizontal planes and periodic boundary conditions in the lateral directions (as for example in Fig. 1a), the eqn (4) can be further rewritten into
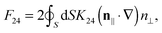 | (5) |
Alternatively, eqn (4) can be understood in terms of the curvature of the boundary.48,68 Under the assumption of strong (degenerate) planar surface anchoring, eqn (4) can be rewritten into:48
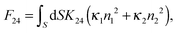 | (6) |
2.2 Tensor form of saddle-splay elasticity
Elastic anisotropy in liquid crystals is at the mesoscopic level generally described by introducing multiple invariants in the total free energy, each typically with different elastic constants, which account for different elastic responses.69–71 Saddle-splay is generally explored in the framework of the nematic director, but today the majority of (numerical) calculations are performed with the nematic order parameter tensor. Therefore, specifically writing down the Q-tensor invariants that correspond to the saddle-splay seems to be a reasonable consideration, allowing for the direct evaluation of the saddle-splay elasticity. A possible formulation of the tensor-based saddle-splay volume free energy density ften24 can be written as: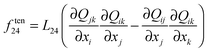 | (7) |
Eqn (7) is based on the well known and established relation between the director-based Frank–Oseen free energy and the Q-tensor-based Landau–de Gennes free energy, which can be related by assuming the uniaxial form of the Q tensor and the homogeneous profile of the nematic degree of order. Indeed, the Q tensor based saddle-splay free energy in eqn (7) can be rewritten – by assuming the uniaxial form of the Q-tensor – into:
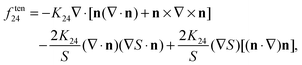 | (8) |
We use tensor based and director based formulations of saddle-splay volume and surface density to demonstrate the importance of saddle-splay elasticity in the complex geometrical confinement. Specifically, the two exemplary setups – as considered in eqn (5) and (6) – provide us with a direct insight into the relevance of saddle-splay elastic free energy and are considered in the next sections. The importance of eqn (5) can be demonstrated in nematic cells with patterned surface anchoring, where n⊥ changes along the cell's boundary, whereas eqn (6) clearly comes into account in nematics, confined by curved boundaries, as for example in the systems of knotted colloidal particles dispersed in nematic fluid.
3 Saddle-splay elasticity in nematic cells with patterned surface anchoring
In our first example we investigate saddle-splay elasticity in patterned cells, where anchoring at the one cell surface (top) is homeotropic whereas at the other surface (bottom) there is a circular patch of planar degenerate anchoring surrounded by homeotropic anchoring conditions (see Fig. 1a). In Sections 3.1 and 3.2 we simulate two elasticity regimes K1 = K2 = K3 and K1 = 2K2 = K3 (with Wuni = Wdeg = 2 × 10−3 J m−2), respectively. In Section 3.3 we investigate the nematic field for high values of K2, which is not a typical elastic anisotropy regime of nematic liquid crystals but such elastic anisotropy is shown to allow for the formation of novel field configurations.3.1 Local hybrid aligned nematic (HAN) configuration
A nematic profile with a local hybrid aligned nematic director profile emerges in patterned cells in the regime of materials with roughly equal or similar elastic constants (K1 = 2K2 = K3) (see Fig. 1). The director field in such a configuration shows a gradual transition from inplane orientation at the planar degenerate surface patch to the perpendicular at the homeotropic surfaces, as shown in Fig. 1b–e.In one elastic constant regime (K1 = K2 = K3), the in-plane director component n∥ is homogeneous throughout the bottom surface patch, with the actual direction of n∥ being arbitrary. The orientation along the y axis was chosen for an easier analysis. The saddle-splay free energy density – calculated as surface free energy density fsurf24 or as volume free energy density fvol24 – turns out to be substantial at the border line regions between the homeotropic and degenerate anchoring. The sign of saddle-splay free energy density locally depends on the structure of the nematic director, which is effectively determined by the direction of the hybrid alignment (i.e. the bend), as seen in Fig. 1e and f. Due to the symmetry of n∥, the locally negative and the positive values of fsurf24 and fvol24 add up to zero (when performing the integration over the surface or over the bulk), giving no net saddle-splay free energy F24.
In the elastically anisotropic regime (K1 = 2K2 = K3), the symmetry of the inplane director n∥ breaks and the net saddle-splay free energy F24 becomes non-zero, and actually notably contributes to the total elastic free energy (see Table 1). The regions contributing to this net value are close to the planar-homeotopic anchoring transition, where the director field gets additionally distorted compared to the elastically isotropic regime (Fig. 1b and c).
| F 24/Fel for K1 = K2 = K3 | F 24/Fel for K1 = 2K2 = K3 | |
|---|---|---|
| HAN configuration | 0 | 4.9 |
| Radial boojum | −0.34 | −0.15 |
| +1 hyperbolic boojum | 0.36 | 0.27 |
| −1 hyperbolic boojum | −0.012 | 0.038 |
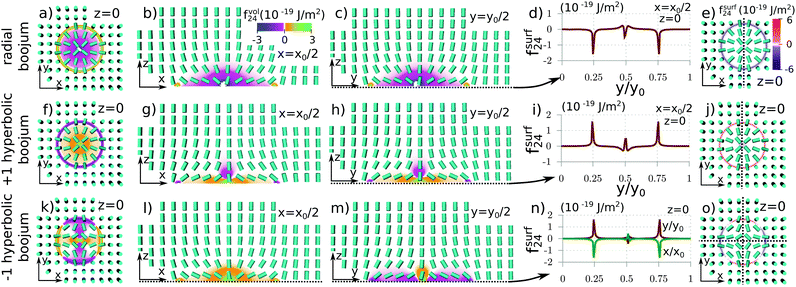
3.2 Boojum nematic configuration
The surface patterned cells allow – besides the local HAN configuration presented above – also for the formation of the nematic profile with a surface boojum defect in the center of the planar patch, as shown in Fig. 2. Actually, in the considered patterned cell, we were able to generate three different boojum configurations via the initial conditions: a radial boojum, a hyperbolic boojum with a winding number +1 (which we further call +1 hyperbolic boojum), and a hyperbolic boojum with a winding number −1 (−1 hyperbolic boojum), all of them are presented in Fig. 2. Once formed, they turned out to be long-lived but were ultimately unstable and gradually deformed into a defect-free state (i.e. the local HAN configuration). Such behaviour is also reported to be observed experimentally.72 The free energy of these induced boojum states is several 10% higher than the free energy of the HAN configuration.The boojum configurations allow us to evaluate the saddle-splay free energy in comparison to other free energy contributions (Table 1), and to analyse the spatial profiles of the saddle-splay contributions to the free energy, especially in the view of topological defects. The saddle-splay free energy density profiles are distinctly different, as compared to the HAN configuration where locally positive and negative contributions mostly cancelled each other out in the total saddle-splay free energy F24. In the boojum configurations, the saddle-splay volume free energy density fvol24 is substantial close to the degenerate surface, but moreover in the region of the central boojum defect (Fig. 2b, c, g, h, l and m). For the radial boojum in (Fig. 2a–e), fvol24 is mostly positive. For the +1 hyperbolic boojum in Fig. 2f–j, fvol24 has regions of both negative an positive values with leadingly positive regions. For the −1 hyperbolic boojum structure (Fig. 2k–o), fvol24 shows a complex spatial profile where regions of positive and negative fvol24 mostly cancel each other out and F24 thus contributes only little to the total elastic free energy (Table 1). The profile of the saddle-splay volume density in boojum configurations explains the substantial contributions of saddle-splay elasticity to the total elastic free energy for radial and +1 hyperbolic configurations and much smaller saddle-splay free energy for a −1 hyperbolic boojum. Since the main contributions arise from regions close to boojum defect cores, the knowledge of boojums could potentially suffice to deduce the amount (or the sign) of saddle-splay free energy in general systems with surface boojum defects.
Considering the saddle-splay as the surface term fsurf24, it is primarily conditioned by the contributions from the the planar-homeotropic anchoring boundary. At this boundary region, fsurf24 is negative for the radial boojum (Fig. 2d and e), it is positive for the +1 hyperbolic boojum (Fig. 2i and j), and the sign varies for the −1 hyperbolic boojum (Fig. 2n and o). The fsurf24 shows variations close to the defect cores; however, they are suppressed by the low values of the nematic degree of order. Although contributions of fsurf24 arise from the director distortions at the planar-homeotropic anchoring border, the total value of F24 is still conditioned by the possible occurrence of a boojum at the center of a planar degenerate surface. In the absence of a boojum (i.e. HAN configuration) or in the case of a −1 hyperbolic boojum, fsurf24 at the planar-homeotropic anchoring border mostly cancel each other out. In the case of a radial or a +1 hyperbolic boojum, the sign of Fsurf24 stays the same throughout the planar-homeotropic anchoring transition and thus fsurf24 contributes a substantial amount to the total elastic free energy (Table 1).
Changing the elastic constants to K1 = 2K2 = K3 has little effect on the nematic field in boojum states. The free energy of boojum states remains a few 10% higher than the free energy of HAN configuration. In radial and +1 hyperbolic configuration, the change of the elastic constants mostly increased the weight of splay and bend deformations thus reducing the saddle-splay contribution to the elastic energy, while in the −1 hyperbolic state the applied change in elastic anisotropy changed the balance towards a positive value of F24. Free energy contributions for higher elastic anisotropy are given in Table 1. We see that for HAN configuration an anisotropic elastic condition was necessary to induce a nonzero saddle-splay elasticity. For radial and +1 hyperbolic boojum configurations F24 contributed a larger amount to the total elastic free energy also in the one elastic constant regime. The change of elastic constants affected the F24/Fel ratio, however the saddle-splay free energy remains substantial. Compared to other boojum states, F24 for a −1 hyperbolic boojum is relatively small, which does not change much in the different elastic regime.
We use the calculated boojum and HAN configurations to test the relevance of eqn (4) (the surface director formulated saddle-splay free energy density). For the HAN configuration, we can calculate eqn (4) at the homogeneous nematic degree of order Seq without the numerical difficulties due to singularities in the director field. The results agree with F24, calculated from eqn (3) up to a negligible numerical relative error of 4 × 10−6. However, if spatially dependent nematic degree of order S is taken as calculated from the order parameter tensor, eqn (4) can deviate from eqn (3) for up to 24%.73 This discrepancy is rather notable not only in the boojum configurations, but actually emerges also in the elastically anisotropic hybrid aligned configuration (Section 3.1). Therefore, more generally, if the nematic degree of order S varies throughout the sample, eqn (4) can be taken (as expected) only as an estimate for calculating the the saddle-splay free energy contribution. For exact computation of the saddle-splay free energy, the bulk formulation of the saddle-splay free energy needs to be evaluated (eqn (3)).
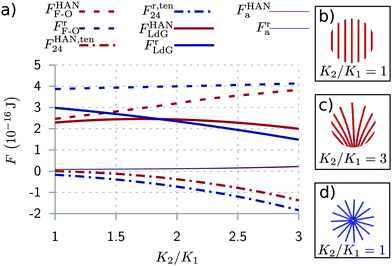
3.3 Stabilisation of radial boojum via saddle-splay
Strongly negative values of the saddle-splay free energy of the radial boojum configuration suggest that for high saddle-splay coupling such a state could potentially become not only long-lived but metastable or even stable. Indeed, we demonstrate that this can be achieved by increasing the elastic anisotropy ratio K2/K1 where K24 = K2/2 and K1 = K3, effectively increasing the saddle-splay elastic constant K24. The free energy of the radial boojum configuration falls below the free energy of the HAN configuration at K2/K1 ∼ 2 and becomes the equilibrium configuration, which is shown in Fig. 3. When increasing the K2/K1 ratio, the free energy configurations show a decrease in the difference between Frank–Oseen free energies, but a rather constant large difference between the saddle-splay free energies of the two states, which causes the stabilisation that can be attributed to the saddle-splay. More broadly, this indicates that the actual values of the saddle-splay constant in different systems can be a major factor in determining stability, metastability or non-stability of different structures.Models which include only Frank–Oseen and not the saddle-splay free energy could not properly predict the stability of a radial boojum at K2/K1 ∼ 2. Fig. 3 indicates that Frank–Oseen free energy of a radial boojum should fall below the Frank–Oseen free energy of the HAN configuration at much higher elastic anisotropy than K2/K1 ∼ 2 and therefore, such behaviour could not be fully explained in terms of solely Frank–Oseen elasticity.
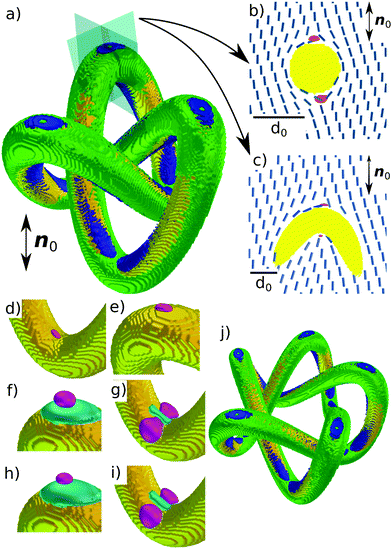
4 Saddle-splay elasticity in planar degenerate colloidal knots
The relevance of curved boundaries in the saddle-splay free energy is demonstrated for the case of colloidal knots with planar degenerate boundary conditions. Experimentally and with numerical modelling they were explored in ref. 6. We simulate the trefoil (3,2) and pentafoil (5,3) torus knots as tubes of the following parametric curves:r(3,2) = (2.1R(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ − 2.25 ϕ − 2.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ), 2.1R(sin 2ϕ), 2.1R(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + 2.25 ϕ + 2.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ), 6R 2ϕ), 6R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3ϕ), 3ϕ), | (9) |
r(5,3) = (2.75R(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3ϕ − 3 3ϕ − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ), 2.75R(sin 2ϕ), 2.75R(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3ϕ + 3 3ϕ + 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ), 6R 2ϕ), 6R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5ϕ), 5ϕ), | (10) |
The trefoil knot generates 12 boojums as shown in (Fig. 4b–e in red color), which emerge at the regions of the highest local curvature, i.e. local saddle points and local peaks. These boojums emerge as + and − pairs, satisfying the topological constraints of the knot.6 Analogously as the trefoil knot, the pentafoil knot generates 20 boojums, again at highest-local curvature locations, as seen from Fig. 4.
The saddle-splay free energy density fsurf24 shows for both the trefoil and pentafoil knots a distinctive pattern, which can be partially explained by eqn (6). Possible values of fsurf24 depend on the local curvature of the particle knot and since the major part of the knot's surface has a positive curvature fsurf24 is mostly positive. In the vicinity of the hyperbolic boojums (bottom one in Fig. 4b and c), fsurf24 > 0 if the director bends along the direction of the positive principal curvature, and fsurf24 < 0 if the director bends along the direction of the negative principal curvature. However, besides eqn (6) there are additional surface contributions to the saddle-splay free energy, which arise due to finite anchoring strength. In the vicinity of +1 hyperbolic boojums, the normal component of the director increases along the surface in a manner that is similar to the planar-homeotropic alignment border in the case of a radial boojum in a patterned cell (Fig. 2b and c). This variation of the director field along the surface explains negative areas of fsurf24 around +1 hyperbolic boojums, as seen in Fig. 4a. Elsewhere along the surface, the variations from the surface-preferred director orientation are (i) not strong enough or (ii) in agreement with saddle-splay contributions arising from the local curvature and cause no specific pattern to occur.
Fig. 4f and g show saddle-splay volume free energy density fvol24. Close to the +1 hyperbolic boojum, fvol24 is mostly positive. This shows similarity to fvol24 in patterned cells, only that in the case of knots the area with negative fvol24 is suppressed near +1 hyperbolic boojums. There is even greater similarity in the case of −1 hyperbolic boojum. Both Fig. 2l and m and 4f show a region of fvol24 > 0, surrounded by two regions where fvol24 < 0.
More generally, the calculated results agree with anticipating positive saddle-splay free energy because of the primarily positive curvature of the investigated colloidal knots. The analysis of the saddle-splay elasticity in combination with flat and curved geometry now also suggests that boojums indicate the structure of saddle-splay free energy density, where in particular +1 hyperbolic boojums give positive contributions to the saddle-splay free energy and radial boojums give negative contributions to F24. Calculating the total saddle-splay free energy of the knotted colloids F24, it is in fact positive and represents a substantial part of the total elastic free energy Fel for a trefoil and a pentafoil knot as shown in Table 2.
| Trefoil particle knot (3,2) | Pentafoil particle knot (5,3) | |
|---|---|---|
| F 24/Fel | 0.37 | 0.34 |
5 Comparison between tensor and director formulated saddle-splay free energy
Exact comparison between tensorial and director-based consideration of saddle-splay is important when exact values of free energies are needed, e.g. when predicting stability or structural transitions between different nematic (meta)stable structures or profiles. Fig. 1 and 4 reveal clearly similar profiles of the director based and tensor based saddle-splay free energy density, however, selected differences between both approaches can be observed. We show the use of Q-tensor saddle-splay free energy Ften24 for the example of a radial boojum structure in a patterned cell within one elastic constant regime (Fig. 2a–e, Section 3.2). The results are presented in Table 3, where ∇S and biaxial contributions, total discrepancy between F24 and Ften24, and the error resulting from finite mesh resolution are calculated at two mesh resolutions. Note that the tensorial saddle-splay free energy eqn (7) is not explicitly incorporated as a new free energy contribution to the total free energy, but is actually already an inseparable part of the standard one elastic constant Landau–de Gennes free energy FLdG. Single elastic invariant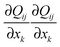 from FLdG incorporates not only splay, bend, and twist deformation modes but also saddle-splay.
from FLdG incorporates not only splay, bend, and twist deformation modes but also saddle-splay.
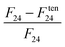
| Mesh resolution | ∇S terms (eqn (8)) | Biaxial contribution | Finite resolution error | |
|---|---|---|---|---|
| Δx | −0.11Fdir24 | −0.07Fdir24 | 0.39 | 0.21 |
| Δx/2 | −0.12Fdir24 | −0.08Fdir24 | 0.33 | 0.13 |
There are three main differences between the tensor based saddle-splay free energy Ften24 and the director based saddle-splay free energy F24: (i) possible local biaxiality of Qij (in particular in the defect cores), (ii) ∇S terms (relevant in the defect regions), and (iii) numerical error due to finite mesh resolution (we use Δx/ξ = 1.5). The biaxial contribution to Ften24 is evaluated by taking only the uniaxial part of the calculated Qij and re-evaluating eqn (7). The ∇S contributions are calculated explicitly from the diagonalisation of the Q-tensor profile. The rest of the discrepancy between Ften24 and F24 is attributed to finite resolution, which we quantify by modelling exactly the same structure with two resolutions (Δx = 10 nm and Δx/2 = 5 nm). Indeed, the finite difference algorithm with rather large mesh resolution (Δx/ξ ∼ 1) suffers from rather low precision at the determination of the exact value of the total free energy. Especially the explicit calculation of saddle-splay free energy, as done in this article at sharp surface anchoring boundaries, gives a limited precision of ∼20% due to finite resolution. Finer resolution or, especially in the case of curved interfaces, finite element methods could be used to investigate saddle-splay free energy density with higher precision. Table 3 shows that director deformations are still the most significant part of ften24, which is in agreement with the comparison between director based and tensor based free energy density profiles in Fig. 4.
To generalise, ften24 represents an easy-to-implement measure of saddle-splay elasticity in terms of the Q-tensor. Due to the nature of Q-tensor formalism, discrepancy between saddle-splay free energy, calculated in the director or tensorial approach, may occur and is actually expected to occur – in particular in systems with large variations of the nematic degree of order and possibly even biaxiality, which is often the case in complex geometrical confinements.
6 Conclusions
We have explored the relevance of saddle-splay elasticity in complex nematic geometries, with particular focus on nematic systems with inhomogeneous (patterned) surface anchoring and with complex surface curvatures. Saddle-splay elasticity was analysed in the view of volume and surface density, where specifically, we investigated the saddle-splay elasticity in patterned cells and around colloidal knots.In the first example of patterned cells, the large saddle-splay contributions F24 to the total free energy emerge from the border region between the planar and homeotropic anchoring patches, as seen from both surface and volume saddle-splay free energy formulations. To vary the magnitude of the saddle-splay free energy F24, elastic anisotropy is used, which helps in achieving a larger stability window of the simulations. Negative values of F24 of a radial structure on the surface patch make it possible to reduce its free energy below the free energy of the hybrid aligned configuration if K2 and K24 are large enough, showing that saddle-splay elasticity can condition the ground state of nematic in geometries with a complex surface.
In the second example of colloidal knots, the largest saddle-splay contributions to the total free energy are shown to emerge from the highest local curvature regions, which actually also coincide with the locations of surface boojum defects. Generally, in the colloidal knots, F24 is large due to surface variations of the normal director component and due to the high curvature of colloidal knots. The spatial profiles of the saddle-splay volume free energy are calculated, and shown to distinctly depend on the boojum-type, i.e. its topological structure. Indeed, boojum structures that appear at the trefoil (3,2) and pentafoil (5,3) colloidal knots have a similar spatial profile of the saddle-splay free energy density fvol24 to that in patterned cells.
We explored saddle-splay formulated as a Q-tensor (not director) term 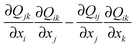 . The contributions to the tensor-based saddle-splay free energy are shown to be in the range of several 10% with the magnitudes strongly depending on the actual considered nematic geometry, in particular on the presence of topological defects. Such tensor based saddle-splay free energy is significantly influenced by ∇S and biaxial terms, but represents a directly implementable way to calculate saddle-splay contribution to the free energy in a given nematic field.
. The contributions to the tensor-based saddle-splay free energy are shown to be in the range of several 10% with the magnitudes strongly depending on the actual considered nematic geometry, in particular on the presence of topological defects. Such tensor based saddle-splay free energy is significantly influenced by ∇S and biaxial terms, but represents a directly implementable way to calculate saddle-splay contribution to the free energy in a given nematic field.
More generally, in the explored structures, the saddle-splay free energy is found to contribute substantially to the total free energy, thus affecting the stability or metastabilty of the structures. Nematic profiles in complex geometries typically form a range of (meta)stable states, with their mutual stability or metastability conditioned by the exact value of the total free energy minimum. Therefore, when considering phase-diagrams or stability in complex nematic structures the relevance of saddle-splay – i.e. the actual value of saddle-splay elastic constant K24 – has to be considered. Finally, the presented work is a contribution towards understanding the stability and formation of complex structures in general nematic complex fluids, including liquid crystal and active nematics.
Acknowledgements
The authors acknowledge stimulating discussions and joint work on topics related to this work with S. Žumer, L. Cattaneo, T. Rasing, I. Muševič, and I. I. Smalyukh. Financial support from SLO ARRS program P1-0099, project Z1-5441, USAF AFRL EOARD research project Nematic Colloidal Tilings as Tunable Soft Metamaterials, and EU MC program FREEFLUID is acknowledged.References
- F. Castles, S. M. Morris, J. M. C. Hung, M. M. Qasim, A. D. Wright, S. Nosheen, S. S. Choi, B. I. Outram, S. J. Elston, C. Burgess, L. Hill, T. D. Wilkinson and H. J. Coles, Nat. Mater., 2014, 13, 817 CrossRef CAS PubMed.
- J. Beeckman, K. Neyts and P. V. M. Vanbrabant, Opt. Eng., 2011, 50, 081202 CrossRef.
- K. Peddireddy, V. S. R. Jampani, S. Thutupalli, S. Herminghaus, C. Bahr and I. Muševič, Opt. Express, 2013, 21, 30233 CrossRef PubMed.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431 CrossRef CAS PubMed.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940 CrossRef CAS PubMed.
- A. Martinez, M. Ravnik, B. Lucero, R. Visvanathan, S. Žumer and I. I. Smalyukh, Nat. Mater., 2014, 13, 258 CrossRef CAS PubMed.
- B. Senyuk, Q. Liu, S. He, R. D. Kamien, R. B. Kusner, T. C. Lubensky and I. I. Smalyukh, Nature, 2013, 493, 200 CrossRef CAS PubMed.
- A. Sengupta, S. Herminghaus and C. Bahr, Liq. Cryst. Rev., 2014, 2, 73 CrossRef CAS.
- J. Zhang, M. I. Boamfa, A. E. Rowan and T. Rasing, Adv. Mater., 2010, 22, 961 CrossRef CAS PubMed.
- P. Guillamat, F. Sagués and J. Ignés-Mullol, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 052510 CrossRef PubMed.
- M. Conradi, M. Ravnik, M. Bele, M. Zorko, S. Žumer and I. Muševič, Soft Matter, 2009, 5, 3905 RSC.
- M. Melle, S. Schlotthauer, M. G. Mazza, S. H. L. Klapp and M. Schoen, J. Chem. Phys., 2012, 136, 194703 CrossRef PubMed.
- Y. Iwashita and Y. Kimura, Soft Matter, 2013, 9, 10694 RSC.
- S. Čopar, M. Ravnik and S. Žumer, Materials, 2014, 7, 4272 CrossRef.
- M. Cavallaro Jr, M. A. Gharbi, D. A. Beller, S. Čopar, Z. Shi, R. D. Kamien, S. Yang, T. Baumgart and K. J. Stebe, Soft Matter, 2013, 9, 9099 RSC.
- M. Nikkhou, M. Škarabot, S. Čopar, M. Ravnik, S. Žumer and I. Muševič, Nat. Phys., 2015, 11, 183 CrossRef CAS.
- F. R. Hung and S. Bale, Mol. Simul., 2009, 35, 822 CrossRef CAS.
- J. S. Evans, C. N. Beier and I. I. Smalyukh, J. Appl. Phys., 2011, 110, 033535 CrossRef.
- D. Engström, R. P. Trivedi, M. Persson, M. Goksör, K. A. Bertness and I. I. Smalyukh, Soft Matter, 2011, 7, 6304 RSC.
- D. A. Beller, M. A. Gharbi and I. B. Liu, Soft Matter, 2015, 11, 1078 RSC.
- E. Pairam, J. Vallamkondu, V. Koning, B. C. van Zuiden, P. W. Ellis, M. A. Bates, V. Vitelli and A. Fernandez-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9295 CrossRef CAS PubMed.
- N. M. Silvestre, Z. Eskandari, P. Patrício, J. M. Romero-Enrique and M. M. T. da Gama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 011703 CrossRef CAS PubMed.
- A. C. Trindade, J. P. Canejo, L. F. V. Pinto, P. Patríco, P. Brogueira, P. I. C. Teixeira and M. H. Godinho, Macromolecules, 2011, 44, 2220 CrossRef CAS.
- T. Ohzono, T. Yamamoto and J. Fukuda, Nat. Commun., 2014, 5, 3735 Search PubMed.
- N. M. Silvestre, Q. Liu, B. Senyuk, I. I. Smalyukh and M. Tasinkevych, Phys. Rev. Lett., 2014, 112, 225501 CrossRef PubMed.
- S. Shi and H. Yokoyama, Langmuir, 2015, 31, 4429 CrossRef CAS PubMed.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, New York, 1993 Search PubMed.
- M. Kleman and O. D. Lavrentovich, Soft Matter Physics: An Introduction, Springer Verlag Inc., New York, 2003 Search PubMed.
- G. Alexander and J. Yeomans, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061706 CrossRef CAS PubMed.
- M. A. Lohr, M. Cavallaro, D. A. Beller, K. J. Stebe, R. D. Kamien, P. J. Collings and A. G. Yodh, Soft Matter, 2014, 10, 3477 RSC.
- O. Henrich, K. Stratford, M. E. Cates and D. Marenduzzo, Phys. Rev. Lett., 2011, 106, 107801 CrossRef CAS PubMed.
- J. Fukuda, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061702 CrossRef PubMed.
- S. M. Hashemi and M. R. Ejtehadi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 012503 CrossRef PubMed.
- K. Tojo, A. Furukawa, T. Araki and A. Onuki, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 30, 55 CrossRef CAS PubMed.
- F. R. Hung, O. Guzmán, B. T. Gettelfinger, N. L. Abbott and J. J. de Pablo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 011711 CrossRef PubMed.
- M. Tasinkevych, N. Silvestre, P. Patrício and M. T. da Gama, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 341 CrossRef CAS PubMed.
- M. Ravnik and S. Žumer, Liq. Cryst., 2009, 36, 1201 CrossRef CAS.
- A. Sparavigna, O. Lavrentovich and A. Strigazzi, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 1344 CrossRef CAS.
- A. Sparavigna, L. Komitov, O. D. Lavrentovich and A. Strigazzi, J. Phys. II, 1992, 2, 1881 CrossRef.
- O. D. Lavrentovich, Phys. Scr., 1991, 39, 394 CrossRef.
- S. Žumer and S. Kralj, Liq. Cryst., 1992, 12, 613 CrossRef.
- D. S. Miller and N. L. Abbott, Soft Matter, 2013, 9, 374 RSC.
- J. Gupta, S. Sivakumar, F. Caruso and N. Abbott, Angew. Chem., Int. Ed., 2009, 48, 1652 CrossRef CAS PubMed.
- D. Allender, G. Crawford and J. Doane, Phys. Rev. Lett., 1991, 67, 1442 CrossRef CAS PubMed.
- R. Polak, G. Crawford, B. Kostival, J. Doane and S. Žumer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, R978 CrossRef CAS.
- S. Kralj and S. Žumer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 366 CrossRef CAS.
- Z. S. Davidson, L. Kang, J. Jeong, T. Still, P. J. Collings, T. C. Lubensky and A. G. Yodh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 050501 CrossRef PubMed.
- V. Koning, B. C. van Zuiden, R. D. Kamien and V. Vitelli, Soft Matter, 2014, 10, 4192 RSC.
- A. Kilian and A. Sonnet, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 2702 CrossRef CAS.
- S. Kralj, R. Rosso and E. G. Virga, Soft Matter, 2011, 7, 670 RSC.
- A. A. Joshi, J. K. Whitmer, O. Guzmán, N. L. Abbott and J. J. de Pablo, Soft Matter, 2014, 10, 882 RSC.
- L. Tortora and O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5163 CrossRef CAS PubMed.
- J. Jeong, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1742 CrossRef CAS PubMed.
- V. Borshch, Y.-K. Kim, J. Xiang, M. Gao, A. Jákli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635 CAS.
- S. M. Shamid, S. Dhakal and J. V. Selinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052503 CrossRef PubMed.
- D. Chen, M. Nakata, R. Shao, M. R. Tuchband, M. Shuai, U. Baumeister, W. Weissflog, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022506 CrossRef PubMed.
- P. Sathyanarayana, M. Mathew, Q. Li, V. S. S. Sastry, B. Kundu, K. V. Le, H. Takezoe and S. Dhara, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 010702 CrossRef CAS PubMed.
- M. Nobili and G. Durand, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, R6174 CrossRef CAS.
- J.-B. Fournier and P. Galatola, Europhys. Lett., 2005, 72, 403 CrossRef CAS.
- V. M. Pergamenshchik, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 1254 CrossRef CAS.
- S. Ponti, Phys. Lett. A, 1995, 200, 165 CrossRef CAS.
- G. Barbero and G. Durand, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 1942 CrossRef CAS.
- M. Cui and J. R. Kelly, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 331, 49 CrossRef.
- N. V. Madhusudana and R. Pratibha, Mol. Cryst. Liq. Cryst., 1982, 89, 249 CrossRef CAS.
- H. Schad, J. Chem. Phys., 1981, 75, 880 CrossRef CAS.
- J. Huang and J. T. Ho, Phys. Rev. Lett., 1987, 58, 2239 CrossRef CAS PubMed.
- J. Huang and J. T. Ho, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 2449 CrossRef CAS.
- R. Kamien, Rev. Mod. Phys., 2002, 74, 953 CrossRef.
- K. Schiele and S. Trimper, Phys. Status Solidi B, 1983, 118, 267 CrossRef CAS.
- L. Longa, D. Monselesan and H.-R. Trebin, Liq. Cryst., 1987, 2, 769 CrossRef.
- A. Poniewierski and T. Sluckin, Mol. Phys., 1985, 55, 1113 CrossRef.
- L. Cattaneo, Ž. Kos, M. Savoini, P. Kouwer, A. Rowan, M. Ravnik, I. Muševič and T. Rasing, Soft Matter, 2016 10.1039/C5SM01726B.
- Relative error of F24 calculated from surface or volume density is evaluated only for the structures where F24/Fel > 0.02. We were not interested in the discrepancy between surface and bulk representation of saddle-splay elasticity in the cases where F24 is in fact negligible.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm02417j |
| This journal is © The Royal Society of Chemistry 2016 |