 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formation of polyelectrolyte multilayers: ionic strengths and growth regimes
Kan
Tang
a and
Nicolaas A. M.
Besseling
*b
aDepartment of Chemical and Materials Engineering, University of Nevada, Nevada, USA
bDepartment Chemical Engineering/OMI, Delft University of Technology, Delft, Netherlands. E-mail: N.A.M.Besseling@TUDelft.NL
First published on 3rd November 2015
Abstract
This article presents a study of layer-by-layer (LbL) formation of poly-electrolyte multilayers (PEMs). Upon increasing ionic strength LbL growth patterns vary from linear for the lowest salt concentrations ([NaCl] = 0, 0.001, and 0.01 M) to exponential (for [NaCl] = 0.5 and 1 M). The slope of the linear growth at the lowest ionic strengths increases with increasing [NaCl]. During the LbL process at 0.5 M NaCl we observe a cross over from exponential to linear growth for which the slope is orders of magnitude larger than those observed at low salt concentrations. We provide a comprehensive interpretation of these growth behaviors, which are also reported for many other LbL PEM systems, based on the generic features of the phase diagram of aqueous solutions of mixtures of oppositely charged poly-electrolytes. Processes occurring in LbL formation of PEMs can be understood as moving in the direction of equilibrium, while never achieving it. The experimental model system in this study was: polydiallyldimethylammonium chloride/polystyrene sulfonate (PDADMAC/PSS). PEM formation was followed in situ by optical reflectometry in combination with well-controlled transport conditions (impinging jet stagnation point flow).
Introduction
Layer by layer (LbL) assembly of polyelectrolyte multilayers (PEMs) is a versatile way of surface modification and fabrication of novel nanostructures. It consists of alternatively exposing a substrate to a solution of poly-cations and to a solution of poly-anions, usually with rinsing steps in between. The method was invented by Hong and Decher1,2 and has been a popular research field ever since, as the method has proved to be very versatile, applicable to a large variety of macro-ions, ranging from synthetic poly-electrolytes and bio-macromolecules to nanoparticles.3 It has been demonstrated that multiple parameters such as pH,3–6 ionic strength,7–9 charge density,10–12etc., influence the LbL process and the resulting PEMs. An important distinction between formation mechanisms is that between so-called ‘linear growth’, in which the same amount gets added to the multilayer upon each subsequent LbL cycle, and ‘exponential growth’, in which the amount added to the film in each subsequent cycle is proportional to the amount already present during that cycle.3 The main purpose of the present study is to clarify the origin of these differences, and to clarify what happens during the growth steps. For that purpose we selected a relatively simple model system: a pair of strong poly-electrolytes polydiallyldimethylammonium chloride (PDADMAC) and polystyrene sulfonate (PSS). The different regimes will be probed by variation of the ionic strength. Variation of the ionic strength makes it possible to explore distinctly different regimes of behavior, while keeping all other conditions the same. Furthermore, variation of the ionic strength offers a good chance to interpret the experimental findings, as the basic effect of small ions in these systems is known, to screen the electrostatic interactions among the poly-ions and between poly-ions and the substrate. It has been argued that the formation and behavior of PEMs constituted from poly-electrolytes can be rationalized in terms of the phase diagram of aqueous solutions of mixtures of oppositely charged poly-electrolytes.13,14 In the present paper, we will take this idea further, by invoking several aspects of the aforementioned phase diagram that were not considered before in this context. This enables us to explain a range of observed features concerning the formation of poly-electrolyte multilayers, including the reasons why under certain conditions so-called linear growth of PEMs is observed, whereas under other conditions so-called exponential growth occurs and how the growth rates depend on the concentration of the added simple salt etc.Experimental section
Materials
All chemicals used in the experiments are from Sigma Aldrich. Highly quaternized (>90%) poly(diallyldimethylammonium chloride) (PDADMAC) and Poly(sodium 4-styrenesulfonate) (PSS) were chosen as the positively and negatively charged poly-electrolytes, respectively. The weight-average molecular mass (Mw) of PDADMAC and PSS are about 100 and 70 kDa, respectively. Both polymers are polydisperse. The chemical structures of these two synthetic polyelectrolytes are shown in Scheme 1. With all experiments the concentrations of PDADMAC and PSS were chosen to be 0.6 and 0.3 g L−1, respectively, corresponding to monomer concentrations of 1.6 and 1.4 mM, respectively. Sodium chloride was used to control the ionic strength.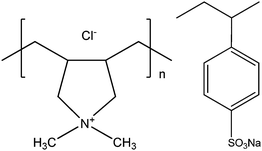 | ||
| Scheme 1 Chemical structures of poly(diallyldimethylammonium chloride) (PDADMAC) and poly(sodium 4-styrenesulfonate) (PSS). | ||
With all experiments the substrates were strips cut from an oxidized silicon wafer. N-type silicon wafers with a resistivity of 0.001–0.003 Ohm cm were purchased from Sil'tronix S. T (France). The silicon wafers were oxidized in an oven for 100 minutes at 1000 °C. The thickness of the silica layer was determined by ellipsometry to be 70 nm. The typical variation between different measuring spots on a silicon chip, and hence the uncertainty of the thickness at the reflectometry measuring spot is 2 nm. Used strips were for re-use rinsed with acetone and subsequently cleaned in a plasma cleaner (Harrick, PDC-002, Ithaca, NY).
Methods
The various solutions were supplied to the substrate in a controlled way by means of an impinging-jet stagnation-point flow cell, in which the stagnation point coincides with the measuring spot of the optical reflectometer.15,16 The reflectometry signal S, the ratio of the intensities of parallel over perpendicularly polarized reflected light, can in principle be converted into adsorbed mass per unit area as follows:Here, S0 is the signal from the bare surface, which should be tuned to be close to unity by adjusting the polarization of the incident light. The relative change of the signal (S − S0)/S0 is proportional to the adsorbed amount. The proportionality factor Qf, usually denoted the quality factor, can in principle be calculated from the refractive indices of the substrate (silicon), optical spacer (silica) and solvent (buffer solution), and the refractive-index increment dn/dc of the adsorbing material.15,16 In the case of polyelectrolytes adsorbing from aqueous solutions, such as in the present study, effective dn/dc values are unavailable because the effective dn/dc of an adsorbed polyelectrolyte is influenced by the release of unknown amounts of counter ions, both from the substrate and polyelectrolyte, which always accompanies adsorption of the polyelectrolyte at an oppositely charged substrate. Furthermore, the different polyelectrolytes constituting PEMs will in general have different dn/dc values and it is not possible to separate their contributions to the signal. Thus, as done by others in similar situations, we will report just (S − S0)/S0 values to monitor the formation of multilayers. However, a rough idea of the corresponding adsorbed amounts can be obtained by realizing that dn/dc values of aqueous polymer solutions are usually around 0.15 ml g−1, leading to a Qf of about 28 mg m−2 (as calculated using Peter Barneveld's software program Prof. Huygens, version 1.2c (Dullware Software)). This value for Qf is obtained using the following values for the relevant parameters: wavelength of the He–Ne laser = 632.8 nm, refractive index of silicon wafer nSi = 3.85,† refractive index of silica layer nSiO2 = 1.46, thickness of the silica layer dSiO2 = 70 nm, refractive index of solutions ns = 1.33, assumed value of the refractive-index increment dn/dc = 0.15 ml g−1. The value of 28 mg m−2 for Qf was calculated for an adsorbed amount Γ = 1 mg m−2 and a refractive index of the adsorbed layer na = 1.4.
Layer by layer deposition of poly-electrolyte multilayers was realized in situ using the reflectometer setup by alternatingly supplying different solutions to the substrate by the impinging jet flow. As the silica substrate is negatively charged under the given conditions the LbL procedure was always started by supplying a solution of PDADMAC, followed by a ‘rinsing step’ during which an aqueous NaCl solution was supplied with the same NaCl concentration as in the polyelectrolyte solutions. Then a solution of PSS was supplied followed by another rinsing step as described before. So, during the entire procedure of PEM formation, the substrate and the film growing on it remain inside the stagnation-point flow cell, immersed in aqueous electrolyte solution in which the NaCl concentration remains the same. The durations over which the poly-electrolyte solutions were supplied were usually above 400 s, unless the signal became stable in a shorter period. The durations of the rinsing steps were above 150 s. In order to build up PEMs this cycle was repeated many times. We will in this paper use the term ‘LbL cycle’ for two subsequent exposure steps (with rinsing after each step); first to the PDADMAC solution and subsequently to the PSS solution.
Results of PEM formation at different ionic strengths
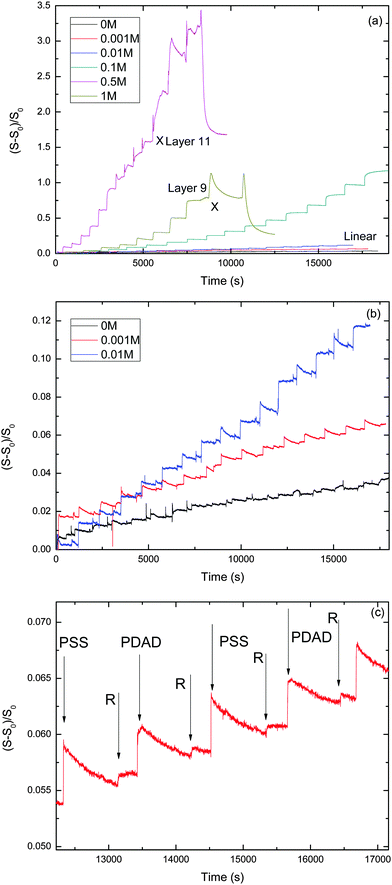
We performed a series of LbL experiments using the stagnation-point, optical reflectometer setup at various NaCl concentrations varying from 0 to 1 M. The evolution of the reduced signal vs. time for the different NaCl concentrations is shown in Fig. 1. Table 1 summarizes some characteristics for the PEM growth with the different salt concentrations.| [NaCl] (M) | Phase of PEM | Growth pattern | Slope of reflectometry signal at linear growth | Estimated mass per layer at linear growth (mg m−2) |
|---|---|---|---|---|
| 0 | Glassy | Linear | 0.0019 | 0.053 |
| 0.001 | Glassy | Linear | 0.0034 | 0.095 |
| 0.01 | Glassy | Linear | 0.0073 | 0.20 |
| 0.1 | Fluid | ‘Parabolic’ | — | — |
| 0.5 | Fluid | Exponential & linear++ | 0.2 | 5.6 |
| 1 | Fluid | Exponential | — | — |
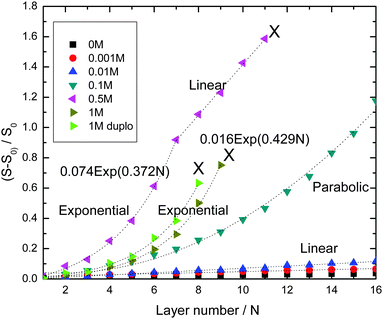
Fig. 1 shows the development of the reflectometry signal over time, while the substrate is exposed to LbL cycles. Fig. 1a gives an overview of the signal traces for all salt concentrations that were investigated. Because of the large variation of the signal magnitudes with salt concentration, we replotted the traces for the ‘low-salt’ experiments also in a separate figure (Fig. 1b). To illustrate the signal variations occurring during an LBL cycle, we added Fig. 2c, which zooms in on just a few cycles from the trace for CNaCl = 0.001. In order to emphasize the growth patterns, the end points of each adsorption step were collected and are plotted in Fig. 2.
For the lowest salt concentrations, ([NaCl] = 0, 0.01 and 0.001 M), the PEMs build up linearly. That is, upon each LbL cycle the same signal increase is observed (within experimental accuracy), which tells us that the mass increase in the PEM upon subsequent LbL cycle is the same as well. The mean signal increment per layer increases with increasing salt concentration: they are 0.0019, 0.0034 and 0.0073 for [NaCl] = 0, 0.001 and 0.01 M, respectively. This corresponds to mean increments per layer of the adsorbed mass of about 0.053 mg m−2, 0.095 mg m−2, and 0.20 mg m−2, respectively. The latter values were obtained using the value for the quality factor Qf = 28, as discussed in the Experimental section.
For the highest salt concentrations [NaCl] = 0.1 M and larger, the growth patterns turned to be non-linear. For [NaCl] = 0.5 M, the build-up becomes exponential, at least for the first 7 layers. After layer 7, the signal is about 0.9, corresponding to about 25 mg m−2 (again based on Qf = 28 mg m−2). Thereafter, build-up with the 0.5 M NaCl case continues in a linear fashion. However, with this linear growth the signal increase per cycle is orders of magnitude larger than with the above-mentioned low-salt cases. The signal increment per layer equals 0.20, corresponding to an increase of the adsorbed amount of about 5.6 mg m−2. Similar transitions from exponential to such linear growth were observed by others (e.g. for PDADMAC/PSS multilayers17 and other systems18–24). The linear growth in the later stages of the [NaCl] = 0.5 case extends up to the 11th layer. After that, the signal becomes unstable and the PEM gets partly washed away. The reflectometry trace obtained with 1 M NaCl is also shown in Fig. 1a. Growth is again exponential and there is no linear-growth regime observed. However, after the 9th layer, at which the signal is about the same as when the 0.5 M NaCl case becomes unstable, the PEM at 1 M NaCl also becomes unstable while supplying the 10th layer, as reflected by the pronounced signal decrease. Upon the injection of the polyanion solution belonging to the 11th layer nearly the entire PEM gets removed. The observation of the transition from exponential growth to linear growth has already been reported. However, the reasons behind it have not been fully understood yet. When we compare the two exponentially growing cases, at 0.5 and 1 M NaCl, we see that increments per layer at the same layer numbers are large for the lower salt concentration (0.5 M NaCl) than for 1 M NaCl. This is opposite from what was observed for the [NaCl] dependency of the linearly growing cases at the lowest salt concentrations.
For 0.1 M NaCl, growth is neither linear nor exponential, but something in between. It is fitted reasonably well by a parabolic curve.
Comprehensive interpretation for the observed growth regimes
Phase diagram for mixtures of oppositely charged poly-ions in aqueous electrolyte solutions
Above we described several distinct features observed with the growth of PEMs by LbL procedures at different concentrations of the ‘simple salt’ NaCl. These different modes of growth of PEMs by LbL fabrication procedures were observed in many other studies as well. In the present section, we will propose a comprehensive interpretation for the different regimes observed, and explain the differences. It has been proposed before13,14 that an understanding of PEMs, and mechanisms by which they are formed, can be based on known generic features of the phase diagram of aqueous solutions of mixtures of oppositely charged polyelectrolytes.25–27 We will elaborate upon this suggestion. The present discussion however will incorporate several aspects of the phase diagram that were not invoked before in the context of poly-electrolyte multilayers. This enables us to interpret a larger range of experimental observations, in much more detail than was done before. Therefore, we will first discuss briefly the generic features of a typical phase diagram of mixtures of oppositely charged poly-electrolytes in aqueous electrolyte solutions.Under certain conditions (not-too-low poly-ion concentrations, not-too-high ionic strengths), such solutions tend to phase separate into a relatively concentrated poly-electrolyte-complex phase, often called ‘complex coacervate’, and a coexisting more dilute phase. The main driving force is the screened electrostatic attraction between the oppositely charged poly-ions. This behavior can be summarized graphically as in Fig. 3. Panel (a) shows the phase diagram at some fixed value of the chemical potential (or equivalently: some fixed value of the activity) of some ‘simple electrolyte’ e.g. NaCl. There is a two-phase region in which compositions phase-separate into dilute poly-electrolyte and more concentrated poly-electrolyte solutions. The latter phases are usually highly hydrated. This two-phase region shrinks upon increasing activity of the simple salt. Especially the poly-electrolyte concentrations in the complex-coacervate phase decrease strongly. As depicted in panel (b) of Fig. 3, upon increasing the ionic strength at a constant total poly-ion concentration [+] + [−], the two-phase regime becomes narrower, and beyond a certain threshold value acs of the simple-salt activity as, phase separation does no longer occur. This is obviously due to the increasing screening of the electrostatic attraction between the oppositely charged poly-ions upon increasing activity of the ‘simple salt’. Equivalently, one can say that increasing this activity leads to a decrease of the entropy gain associated with the liberation of counter ions upon complexation of the oppositely charged poly-ions. It should be understood that these are not two alternative mechanisms. They refer to the same mechanism in different words. Screened electrostatic interactions in electrolyte solutions generally involve entropic contributions associated with the distribution of ions. Growth of PEMs at a surface will occur under conditions in which mixtures of oppositely charged poly-electrolytes tend to phase separate, and will not occur under conditions in which such mixtures are completely soluble.
Obviously, in the one-phase region the spatial distributions of the poly-electrolytes exhibit correlations. The soluble complexes of oppositely charged poly-ions occurring at low concentrations are an example. At higher concentrations, the coils will overlap and interpenetrate, as in solutions of ‘simple polymers’ above the overlap concentration.28,29
Upon decreasing the ionic strength, the effective screened electrostatic interactions within the complex-coacervate become stronger and stronger, and the poly-ion concentrations in the complex coacervate become larger and larger. Below a certain threshold as = ags, these interactions get so strong and the poly-ion concentrations become so high that the internal dynamics of the complex coacervate gets severely suppressed. The concentrated phase looses its fluidity, and becomes a kinetically trapped glassy solid. This is indicated by the thick grey pieces of line, which are drawn as continuations of the complex-coacervate line. As these glassy polyelectrolyte complexes are kinetically trapped non-equilibrium systems, their precise composition and internal structure depend to a large extend on the system history, and not just on actual conditions such as composition and temperature. As discussed in some more detail in the next subsection; stratified polyelectrolyte multilayers formed by the layer-by-layer (LbL) process at low ionic strengths constitute a specific example of such a glassy solid, whose structure is determined by the process by which it is formed.
Low ionic strength: linear growth of multilayers
As discussed in the Results section, and observed by many others the LbL procedure applied at low ionic strengths leads to linear growth of the PEMs, meaning that upon each cycle of exposure to poly-cation and poly-anion solutions the same amount of poly-electrolyte material is added to the PEM.1,9 Furthermore, in this low-ionic-strength regime, the amounts added per exposure step are in the range that is typical for adsorbed poly-electrolyte monolayers at solid substrates. This linear growth of PEMs can be understood from the above discussion on glassy states formed by oppositely charged poly-ions at low ionic strengths. With each cycle of exposure to either a poly-cation solution or a poly-anion solution, the PEM that is already present behaves in fact as a glassy solid, and adsorption of a new monolayer is essentially just adsorption at a solid substrate. It has indeed been observed that the motion of the polyelectrolyte in linearly growing PEMs is severely limited.30–32Such PEMs can only be formed when every new adsorbed poly-ion layer overcompensates the charge of the substrate at which it gets adsorbed. Such charge overcompensation by adsorbing polyelectrolytes occurs when there is some non-electrostatic contribution to the affinity between polymer and substrate (e.g. hydrophobic and Van der Waals interactions), in addition to the screened electrostatic attraction between the poly-ions and the oppositely charged substrate. After the first layer, the substrate at which adsorption takes place is in fact the polyelectrolyte film that is formed during the previous stages of the formation of the PEM. As is well understood for polyelectrolyte adsorption at oppositely charged solid surfaces, under these conditions the adsorbed amount per monolayer is limited largely by the screened electrostatic repulsion among the adsorbed poly-ions in a monolayer. It has been predicted theoretically that therefore the adsorbed amount of a monolayer increases with increasing ionic strength. This has been coined the ‘screening-enhanced regime’ of poly-electrolyte adsorption.33–35 Indeed, increasing adsorbed amounts upon increasing ionic strength have been observed in many experimental poly-electrolyte-adsorption studies.7–9 By the same mechanism, linear growth of a PEM is expected to be faster, i.e. the increase per LbL cycle is expected to be larger, for higher ionic strengths. That is indeed what we observe: the slope of accumulated amount vs. layer number increases with increasing NaCl concentration (the curves for 0, 0.001 and 0.01 M NaCl in Fig. 1).
High ionic strength; exponential growth of complex-coacervate films
However, for even higher NaCl concentrations we see that growth of the poly-electrolyte film upon subsequent LbL cycles ceases to be linear. In fact for 0.5 and 1 M NaCl, the amount accumulated in the film increases exponentially with the numder of LbL cycles. Such exponential growth has been observed in many other studies on PEM formation by LbL procedures. With these exponentially growing PEMs, the amount added upon exposure to either the poly-cation solution or the poly-anion solution exceeds by far any reasonable value for an adsorbed monolayer, especially in the later stages. The most logical explanation is that instead of adsorption of a monolayer on top of the existing PEM, in this regime the poly-electrolyte is absorbed inside the film. In fact, the proportionality of the film growth per exposure step to the amount accumulated already, which is implied by the observed exponential growth, indicates that the whole poly-electrolyte film participates in the uptake of a new poly-electrolyte. Such a behavior is to be expected when the PEM is no longer a glassy solid, as is the case at the lowest ionic strengths, but becomes fluid, allowing for diffusive transport throughout the film. If this happens, the result of an LbL process will not be a ‘frozen-in’ stratified multilayer consisting of stacked monolayers of poly-cations and poly-anions, but a homogeneous, disordered fluid complex-coacervate film. ‘PEMs’ formed by LbL procedures under certain conditions may indeed be a mixed-up films without any stratified structure, as was recognized already by others. The terminology “diffuse in and out” has been coined for this situation.21,22 Zan et al.36 also concluded (for a different PEM system than ours) that at low salt concentrations, added poly-electrolyte binds to the outside of an existing multilayer, whereas at high salt concentration the added poly-electrolyte penetrates the whole film. In fact these poly-electrolyte films at higher salt concentrations are essentially complex-coacervate wetting films. In this regime the terms ‘poly-electrolyte multilayer’ and ‘layer-by-layer’ are not really appropriate, as there are no distinguishable layers, but rather, a disordered film of interpenetrating, highly hydrated polymer coils.What happens during exponential-growth cycles can be understood in more detail on the basis of the generic features of the phase diagram sketched in panel (a) of Fig. 3. Obviously, at no stage of the LBL process the film reaches equilibrium with an outside solution. The outside solutions contain just one of the poly-ions at a time, whereas the concentration of the opposite poly-ion is 0. However, as we will elaborate shortly, what happens during the LBL process can be understood by recognizing that at each stage of the process the system is on its way towards equilibrium, which is never achieved as the outside solution is switched before equilibration processes have completed. Say that in the LbL procedure the substrate is exposed alternatively to solutions of poly-cations and of poly-anions with concentrations of say about [+] = 2[+]D+ and [−] = 2[−]D− respectively, where [+]D+ is the poly-cation concentration corresponding to point D+ of Fig. 3, and [−]D− the poly-anion concentration corresponding to point D−. At some stage of the LbL procedure, after exposure to a poly-anion solution, the substrate is covered by a complex-coacervate film with the composition indicated by point C− of Fig. 3a. In this film, the poly-anion concentration [−]C− is larger than the poly-cation concentration [+]C−, (f+ < ½). The dilute phase that would be in equilibrium with that C− film would have the composition indicated by point D−. During the subsequent exposure of the film to a poly-cation solution with concentration 2[+]D+ there is a driving force for transport of poly-cations towards the film, which is proportional to 2[+]D+ − [+]D− ≈ 2[+]D+, where [+]D− is the equilibrium concentration of poly-cations in the dilute phase D− that would coexist with the C− film.‡ At the same time, there is a driving force for transport of poly-anions away from the film, which is roughly proportional to [−]D−, as the actual value for [−] = 0.§ As initially, after the switch the driving force for uptake of poly-cations by the film is larger than that for loss of poly-anions, there is a net growth of the film. While the film grows, its composition gradually shifts from C− to C+, as the fraction f+ of poly-cations among all poly-ions in the film increases. At about the stage where film composition C+ is reached, the driving force for uptake of poly-cations has decreased to 2[+]D+ − [+]D+ = [+]D+, whereas the driving force for poly-anion loss is still proportional to [−]D−, which is about the same for more or less ‘symmetric cases’ for which poly-anions and poly-cations are similar apart from the sign of their electric charge. Hence, the film growth has leveled off.¶ Upon continued exposure of the file to the poly-cation solution, the film will gradually loose more poly-anions than it gains poly-cations, resulting in a net shrinkage of the film. Such gradual decreases are indeed observed in the experimental traces of Fig. 1. In a typical LBL procedure, the outside solution is changed before all the processes are completed. In fact, waiting for full equilibrium would ultimately lead to the disappearance of the film, leaving behind just a single adsorbed layer corresponding to the solution to which the surface is exposed. If at about the point where the net growth of the film has leveled off, exposure is switched from the poly-cation solution to the poly-anion solution with a concentration of about 2[−]D− the film will grow again because of uptake of poly-anions, which exceeds the simultaneous loss of poly-cations. This is completely analogous to what was explained in detail above for exposure of a ‘C− film’ to the poly-cation solution. The composition of the film will shift back in the direction from C+ to C−. Upon each subsequent exposure of the film to poly-cation and poly-anion solutions, the film grows by an amount which is proportional to the thickness of the film that is present, while its composition ‘oscillates’ from C− to C+, and back from C+ to C−, respectively.
In other words, using certain concentrations [+] and [−] for the poly-cation solution, respectively, the poly-anion solution from which the PEM is formed, the composition of the complex-coacervate film tends to ‘oscillate’ between compositions C+ and C− such that the coexisting dilute solutions D+ and D− have concentrations [+]D+ = ½[+] and [−]D− = ½[−].
We observe that for [NaCl] = 1 M, exponential growth is ‘slower’ than for [NaCl] = 0.5 M. That is, the net change of the accumulated amount at a certain stage of the LbL procedure is smaller at [NaCl] = 1 M than at [NaCl] = 0.5 M. Note that this change of the LbL growth rate upon increase of the salt concentration is opposite from what happened in the low-salt, linear-growth regime discussed in the previous subsection. Indeed the mechanism behind this salt-concentration dependency of the LbL growth rate is totally different from what was discussed for the linearly growing multilayers at the lowest salt concentration. The effect of the salt concentration upon the exponential growth rate at these highest salt concentrations can be explained from generic features of the phase diagram. The two-phase region in the representation in panel (a) of Fig. 3 shrinks upon increasing activity of the ‘simple salt’, that is, upon increasing NaCl concentration in the applied solutions. When the poly-ion concentrations [+] and [−] of the solutions to which the substrate is exposed are the same, concentrations of the coexisting dilute phases [−]D− and [+]D+ are expected to stay the same according to the above arguments. As the two-phase region shrinks upon increased salt concentration, this implies that [+]D− and [−]D+ increase. In other words, composition D− shifts upwards in the graph and composition D+ to the right. Then the variation of the composition of the complex-coacervate phase e.g. from C− to C+ upon exposure to a poly-cation solution is at a higher [NaCl] to a lesser extend caused by uptake of poly-cations and to a larger extend by loss of poly-anions. The latter is roughly the same. However, in 2[+]D+ − [+]D−, which measures the driving force for poly-cation uptake, the term [+]D− is larger for higher ionic strength. Hence the driving force for poly-cation uptake is smaller. As a consequence, the net growth of a film with a certain amount of poly-ions is smaller at higher [NaCl]. A completely analogous argument applies for (subsequent) exposure of a C+ film to a poly-anion solution.
From exponential to linear growth at high ionic strength
As said, the exponential nature of the growth is a consequence of the whole film participating in the uptake of poly-ions. However, at some stage the film becomes so thick that the duration t of a single exposure to a poly-ion solution is not enough for the entering poly-ions to penetrate the whole film. This stage is reached when the film thickness l reaches the order of the typical diffusion distance associated with the exposure time t: that is as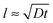 , where D is the diffusion coefficient of the poly-ions inside the complex-coacervate film, which will in general be different for the two poly-electrolytes involved. From thereon, only an outer region of the film, with a thickness
, where D is the diffusion coefficient of the poly-ions inside the complex-coacervate film, which will in general be different for the two poly-electrolytes involved. From thereon, only an outer region of the film, with a thickness 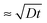 participates in the growth of the film, whereas the inner parts lag behind in equilibrating the local composition. Therefore, growth could be linear, albeit with much larger amounts added per exposure than for the low-ionic-strength case discussed above. This could be the explanation for the ‘fast linear growth’ that we observed with the 0.5 M NaCl case after layer 7 in Fig. 1a. Indeed, although the curves are somewhat noisy in that region, the traces of the signal increase during separate exposure steps have not yet leveled off when the switch to a subsequent solution is made. This suggests that exponential growth could have been maintained longer when the duration of the separate exposures had been longer. Others have argued that such a transition from exponential to linear growth is caused by a film restructuring in which the inner part of the film is inaccessible because of structural features, whereas only an outer layer, which is supposed to maintain a fixed thickness, allows for sufficient internal mobility to be accessible.22,23,37 Although we cannot exclude that such special structuring occurs in certain cases, in our argument this assumption is not needed in order to explain the transition towards linear growth. According to our explanation the transition towards ‘fast linear growth’ should be a quite general phenomenon and the cycle-number at which the transition towards ‘fast linear growth’ occurs should depend upon the duration of the separate exposures, something that is interesting to test in further research.
participates in the growth of the film, whereas the inner parts lag behind in equilibrating the local composition. Therefore, growth could be linear, albeit with much larger amounts added per exposure than for the low-ionic-strength case discussed above. This could be the explanation for the ‘fast linear growth’ that we observed with the 0.5 M NaCl case after layer 7 in Fig. 1a. Indeed, although the curves are somewhat noisy in that region, the traces of the signal increase during separate exposure steps have not yet leveled off when the switch to a subsequent solution is made. This suggests that exponential growth could have been maintained longer when the duration of the separate exposures had been longer. Others have argued that such a transition from exponential to linear growth is caused by a film restructuring in which the inner part of the film is inaccessible because of structural features, whereas only an outer layer, which is supposed to maintain a fixed thickness, allows for sufficient internal mobility to be accessible.22,23,37 Although we cannot exclude that such special structuring occurs in certain cases, in our argument this assumption is not needed in order to explain the transition towards linear growth. According to our explanation the transition towards ‘fast linear growth’ should be a quite general phenomenon and the cycle-number at which the transition towards ‘fast linear growth’ occurs should depend upon the duration of the separate exposures, something that is interesting to test in further research.
We observed that the poly-electrolyte films become unstable when they grow beyond a certain mass. We do not yet know at this stage what actually happens there. A possible explanation may be that dewetting occurs, upon which a smooth wetting film converts into sitting droplets with some non-zero contact angle.
Conclusions
Optical reflectometry in combination with well-controlled transport conditions (impinging jet, stagnation point flow) is a convenient method to follow the formation of poly-electrolyte multilayers (PEMs) by LbL procedures in situ, and in real time. The formation of the poly-electrolyte multilayers depends strongly on the concentration of added NaCl. At the lowest salt concentrations ([NaCl] = 0, 0.001, 0.01) the PEMs grow linearly with LbL cycles. The slopes of this linear growth are consistent with adsorbed poly-electrolyte monolayers, and increase with increasing [NaCl]. This can be understood by assuming that at these low salt concentrations the PEMs are glassy solids, and that adsorption of every new layer is analogous to adsorption of a poly-electrolyte at an oppositely charged solid surface. The surface charge of the existing PEM is overcompensated by each newly adsorbed layer. The salt-concentration dependency reflects the ‘screening-enhanced’ adsorption behavior as observed for many cases of poly-electrolyte adsorption. In addition to the electrostatic interactions, there is also a non-electrostatic affinity between the polymer and the substrate.For the highest salt concentrations ([NaCl] = 0.5 and 1 M) the poly-electrolyte films grow exponentially with LbL cycles, at least initially. The increments to the films occurring upon each LbL cycle are orders of magnitude larger than for the low-salt linear growth regime, and not-at-all consistent with the notion of adsorbing monolayers. These observations can be understood by assuming that in this regime the poly-electrolyte films consist of the fluid complex-coacervate, which allows for diffusive internal dynamics, and hence for absorption of the polyelectrolyte throughout the film, rather than just for adsorption at the outer surface. For this regime, accumulation of mass in the film upon LbL cycles is slower with higher salt concentration. These behaviors are all explained by careful consideration of the generic features of the phase diagram of solutions of oppositely charged poly-electrolytes, where it should be recognized that equilibrium is never reached in an LbL process.
References
- G. Decher, J. D. Hong and J. Schmitt, Buildup of ultrathin multilayer films by a self-assembly process: III. Consecutively alternating adsorption of anionic and cationic polyelectrolytes on charged surfaces, Thin Solid Films, 1992, 210/211, 831–835 CrossRef.
- G. Decher, Fuzzy Nanoassemblies: Toward Layered Polymeric Multicomposites, Science, 1997, 277, 1232–1237 CrossRef CAS.
- J. Borges and J. F. Mano, Molecular Interactions Driving the Layer-by-Layer Assembly of Multilayers, Chem. Rev., 2014, 114, 8883–8942 CrossRef CAS PubMed.
- P. Bieker and M. Schönhoff, Linear and Exponential Growth Regimes of Multilayers of Weak Polyelectrolytes in Dependence on pH, Macromolecules, 2010, 43, 5052–5059 CrossRef CAS.
- J. Hiller and M. F. Rubner, Reversible Molecular Memory and pH-Switchable Swelling Transitions in Polyelectrolyte Multilayers, Macromolecules, 2003, 36, 4078–4083 CrossRef CAS.
- K. Itano, J. Choi and M. F. Rubner, Mechanism of the pH-Induced Discontinuous Swelling/Deswelling Transitions of Poly(allylamine hydrochloride)-Containing Polyelectrolyte Multilayer Films, Macromolecules, 2005, 38, 3450–3460 CrossRef CAS.
- S. T. Dubas and J. B. Schlenoff, Swelling and Smoothing of Polyelectrolyte Multilayersby Salt, Langmuir, 2001, 17, 7725–7727 CrossRef CAS.
- S. T. Dubas and J. B. Schlenoff, Factors Controlling the Growth of Polyelectrolyte Multilayers, Macromolecules, 1999, 32, 8153–8160 CrossRef CAS.
- R. A. McAloney, M. Sinyor, V. Dudnik and M. C. Goh, Langmuir, 2001, 17, 6655–6663 CrossRef CAS.
- K. Glinel, A. Moussa, A. M. Jonas and A. Laschewsky, Influence of Polyelectrolyte Charge Density on the Formation of Multilayers of Strong Polyelectrolytes at Low Ionic Strength, Langmuir, 2002, 18, 1408–1412 CrossRef CAS.
- R. Steitz, W. Jaeger and R. v. Klitzing, Influence of Charge Density and Ionic Strength on the Multilayer Formation of Strong Polyelectrolytes, Langmuir, 2001, 17, 4471–4474 CrossRef CAS.
- U. Voigt, W. Jaeger, G. H. Findenegg and R. v. Klitzing, Charge Effects on the Formation of Multilayers Containing Strong Polyelectrolytes, J. Phys. Chem. B, 2003, 107, 5273–5280 CrossRef CAS.
- D. Kovacevic, S. van der Burgh, A. de Keizer and M. A. Cohen Stuart, Kinetics of Formation and Dissolution of Weak Polyelectrolyte Multilayers: Role of Salt and Free Polyions, Langmuir, 2002, 18, 5607–5612 CrossRef CAS.
- D. Kovacevic, S. van der Burgh, A. de Keizer and M. A. Cohen Stuart, Specific Ionic Effects on Weak Polyelectrolyte Multilayer Formation, J. Phys. Chem. B, 2003, 107, 7998–8002 CrossRef CAS.
- J. C. Dijt, M. A. Cohen Stuart, J. E. Hofman and G. J. Fleer, Kinetics of Polymer Adsorption in Stagnation Point Flow, Colloids Surf., 1990, 51, 141–158 CrossRef CAS.
- J. C. Dijt, M. A. Cohen Stuart and G. Fleer, Reflectometry as a Tool for Adsorption Study, Adv. Colloid Interface Sci., 1994, 50, 79–101 CrossRef CAS.
- T. Radeva, V. Milkova and I. Petkanchin, Electro-optics of Colloids Coated with Multilayers from Strong Polyelectrolytes:Surface Charge Relaxation, J. Colloid Interface Sci., 2003, 266, 141–147 CrossRef CAS PubMed.
- P. Lavalle, V. Vivet, N. Jessel, G. Decher, J.-C. Voegel, J. M. Philippe and P. Schaaf, Direct Evidence for Vertical Diffusion and Exchange Processes of Polyanions and Polycations in Polyelectrolyte Multilayer Films, Macromolecules, 2004, 37, 1159–1162 CrossRef CAS.
- J. M. Garza, P. Schaaf, S. Muller, B. Vincent, J.-F. Stoltz, J.-C. Voegel and P. Lavalle, Multicompartment Films Made of Alternate Polyelectrolyte Multilayers of Exponential and Linear Growth, Langmuir, 2004, 20, 7298–7302 CrossRef CAS PubMed.
- P. Nestler, M. Paßvogel and C. A. Helm, Influence of Polymer Molecular Weight on the Parabolic and Linear Growth Regime of PDADMAC/PSS Multilayers, Macromolecules, 2013, 46, 5622–5629 CrossRef CAS.
- P. Lavalle, C. Picart, J. Mutterer, C. Gergely, H. Reiss, J.-C. Voegel, B. Senger and P. Schaaf, Modeling the Buildup of Polyelectrolyte Multilayer Films Having Exponential Growth, J. Phys. Chem. B, 2004, 108, 635–648 CrossRef CAS.
- C. Porcel, P. Lavalle, V. Ball, G. Decher, B. Senger, J.-C. Voegel and P. Schaaf, From Exponential to Linear Growth in Polyelectrolyte Multilayers, Langmuir, 2006, 22, 4376–4383 CrossRef CAS PubMed.
- E. Hubsch, V. Ball, B. Senger, G. Decher, J.-C. Voegel and P. Schaaf, Controlling the Growth Regime of Polyelectrolyte Multilayer Films: Changing from Exponential to Linear Growth by Adjusting the Composition of Polyelectrolyte Mixtures, Langmuir, 2004, 20, 1980–1985 CrossRef.
- C. Porcel, P. Lavalle, G. Decher, B. Senger, J.-C. Voegel and P. Schaaf, Influence of the Polyelectrolyte Molecular Weight on Exponentially Growing Multilayer Films in the Linear Regime, Langmuir, 2007, 23, 1898–1904 CrossRef CAS PubMed.
- E. Spruijt, A. H. Westphal, J. W. Borst, M. A. Cohen Stuart and J. van der Gucht, Binodal Compositions of Polyelectrolyte Complexes, Macromolecules, 2010, 43, 6476–6484 CrossRef CAS.
- R. Chollakup, W. Smitthipong, C. D. Eisenbach and M. Tirrell, Phase Behavior and Coacervation of Aqueous Poly(acrylic acid) – Poly(allylamine) Solutions, Macromolecules, 2010, 43, 2518–2528 CrossRef CAS.
- J. Y. Wang, M. A. Cohen Stuart and J. van der Gucht, Phase diagram of Coacervate Complexes Containing Reversible Coordination Structures, Macromolecules, 2012, 45, 8903–8909 CrossRef CAS.
- G. J. Fleer, M. A. Cohen Stuart, T. Cosgrove and B. Vincent, Polymers at Interfaces, Springer, 1993 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford, 2007 Search PubMed.
- D. Finkenstadt and D. D. Johnson, Model of Ionization Response of Weak Polyacids in a Layered Polyelectrolyte Self-Assembly, Langmuir, 2002, 18, 1433–1436 CrossRef CAS.
- M. Castelnovo and J. F. Joanny, Formation of Polyelectrolyte Multilayers, Langmuir, 2000, 16, 7524–7532 CrossRef CAS.
- L. Y. Wang, M. Schönhoff and H. Möhwald, Lipids Coupled to Polyelectrolyte Multilayers: Ultraslow Diffusion and the Dynamics of Electrostatic Interactions, J. Phys. Chem. B, 2002, 106, 9135–9142 CrossRef CAS.
- H. G. M. Van de Steeg, M. A. Cohen Stuart, A. de Kerizer and B. H. Bijsterbosch, Polyelectrolyte Adsorption: A Subtle Balance of Forces, Langmuir, 1992, 8, 2538–2546 CrossRef CAS.
- F. Xie, T. Nylander, L. Piculell, S. Utsel, L. Wagberg, T. Akesson and J. Forsman, Polyelectrolyte Adsorption on Solid Surfaces: Theoretical Predictions and Experimental Measurements, Langmuir, 2013, 29, 12421–12431 CrossRef CAS PubMed.
- C. H. Tong, The interplay of the polyelectrolyte-surface electrostatic and non-electrostatic interactions in the polyelectrolytes adsorption onto two charged objects – A self-consistent field study, J. Chem. Phys., 2012, 137, 104904 CrossRef PubMed.
- X. J. Zan, B. Peng, D. A. Hoagland and Z. H. Su, Polyelectrolyte uptake by PEMs: Impact of salt concentration, Polym. Chem., 2011, 2, 2581–2589 RSC.
- M. Salomaki, I. A. Vinokurov and J. Kankare, Effect of Temperature on the Buildup of Polyelectrolyte Multilayers, Langmuir, 2005, 21, 11232–11240 CrossRef PubMed.
Footnotes |
| † As the imaginary part of the refractive index of silicon is negligible in the present context it is taken to be 0, as usual in the calculation of the Q factor for reflectometry studies. |
| ‡ As we do not claim to quantitatively predict diffusion rates, and as the concentrations considered are quite low, we do not consider activity effects while mentioning concentration differences as driving forces for diffusion. |
| § The following argument assumes that diffusion coefficients of poly-anions and poly-cations are about the same, which is reasonable for the ‘symmetric case’ in which the poly-anions and poly-cations are similar apart from the sign of their electric charge. Disparate diffusion coefficients further complicates the argument slightly, in a quite obvious way. |
| ¶ In fact, the above reasoning started out from concentration 2[+]D+ so that the resulting composition of the film would tend towards C+. According to the present reasoning, upon alternating exposure to poly-cation and poly-anion solutions, the composition of the film ‘oscillates’ between two more or less fixed points (C− and C+ in the figure). The composition of the film after exposure to a poly-cation solution tends toward the point C+ that coexists with a dilute phase D+ in which the poly-cation concentration is roughly half of the poly-cation concentration to which the film was exposed. Analogously, subsequent exposure to a poly-anion solution causes the composition of the film to ‘move back’ to the composition C− which coexists with a dilute composition D− in which the poly-anion concentration is half of that of the solution to which the film was exposed. |
| This journal is © The Royal Society of Chemistry 2016 |

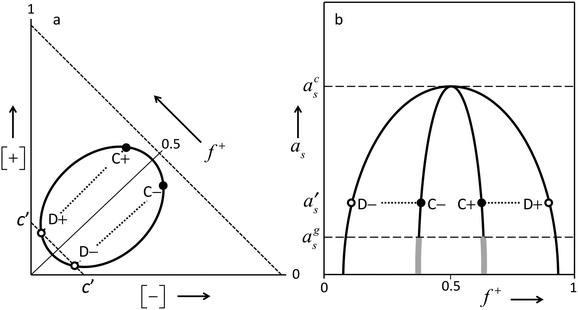
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) [+]/([+] + [−]) is the fraction of poly-cations among all poly-ions. Along the dashed diagonals, and lines parallel to these, the total concentration of poly-ions [+] + [−] is constant, whereas
[+]/([+] + [−]) is the fraction of poly-cations among all poly-ions. Along the dashed diagonals, and lines parallel to these, the total concentration of poly-ions [+] + [−] is constant, whereas