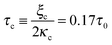Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Contribution of myosin II activity to cell spreading dynamics†
Noam
Nisenholz
a,
Aishwarya
Paknikar
b,
Sarah
Köster
b and
Assaf
Zemel
*a
aInstitute of Dental Sciences and Fritz Haber Center for Molecular Dynamics, Hebrew University of Jerusalem, 91120, Israel. E-mail: Assaf.Zemel@ekmd.huji.ac.il
bUniversity of Göttingen, Institute for X-Ray Physics, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
First published on 20th October 2015
Abstract
Myosin II activity and actin polymerization at the leading edge of the cell are known to be essential sources of cellular stress. However, a quantitative account of their separate contributions is still lacking; so is the influence of the coupling between the two phenomena on cell spreading dynamics. We present a simple analytic elastic theory of cell spreading dynamics that quantitatively demonstrates how actin polymerization and myosin activity cooperate in the generation of cellular stress during spreading. Consistent with experiments, myosin activity is assumed to polarize in response to the stresses generated during spreading. The characteristic response time and the overall spreading time are predicted to determine different evolution profiles of cell spreading dynamics. These include, a (regular) monotonic increase of cell projected area with time, a non-monotonic (overshooting) profile with a maximum, and damped oscillatory modes. In addition, two populations of myosin II motors are distinguished based on their location in the lamella; those located above the major adhesion zone at the cell periphery are shown to facilitate spreading whereas those in deeper regions of the lamella are shown to oppose spreading. We demonstrate that the attenuation of myosin activity in the two regions may result in reciprocal effects on spreading. These findings provide important new insight into the function of myosin II motors in the course of spreading.
I. Introduction
Actin polymerization at the leading edge of a cell provides the driving force for cell spreading and locomotion.1 Facilitated by cell–substrate friction, actin polymerization drives the extension of thin lamellipodia protrusions that act as motor units at the leading edge of the cell and elastically pull on the cell body forward. A few lines of evidence support this elastic picture. Experiments consistently show that both the cell area and force are monotonically increasing functions of substrate rigidity,2–6 and the total (steady-state) force exerted into the matrix has been reported to linearly increase with cell projected area.2,3,5,7 Furthermore, we have recently demonstrated with endothelial cells that the development of cellular stress occurs concurrently with the increase in cell area during spreading.8 The origin of this apparent long-term elasticity of the cytoskeleton on the time scale of spreading (see also ref. 9) is however not fully understood; an attempt to explain it has recently been proposed.10Myosin II activity is known to be a major factor in cellular force generation,11–14 however, the impact of this activity on the ability of a cell to spread is not fully understood. Experiments monitoring the consequences of myosin inhibition using various drug treatments (e.g., Rho kinase inhibitor, ML-7, blebbistatin and others) yielded controversial results; in some experiments myosin II forces were found to facilitate spreading (inhibition caused impaired spreading),15–18 in others to inhibit it14,19–21 and some showed no effect.21 Recent investigations have indicated that the two myosin isoforms, non-muscle myosin IIA and IIB, may have distinct functions during spreading. Experiments on fibroblasts,11,14 and similarly on T-cells,22 have shown that the contractile activity of myosin IIA inhibits spreading since the depletion of this protein resulted in faster spreading and larger cell spread areas. In addition, the non-muscle myosin IIA has been shown to be essential for maintaining the integrity of the cytoskeleton and for transmitting forces from one cell end to the other.11,14 In contrast, inhibition of the myosin IIB isoform had little effect on fibroblast spreading.11,14 Similar conclusions have been reached by Betapudi et al.23,24 with breast cancer cells and other cell types who found myosin IIA to inhibit spreading and myosin IIB to facilitate spreading. The measured differences in the spatial distribution of the two myosin isoforms have shown to be consistent with the observed behavior but accurate interpretation of these data is difficult in these cells due to the significant degree of overlap in the spatial distributions of these proteins.11,14,23,24 Interestingly, the contrasting effects of the two myosin isoforms are consistent with the reported roles of the myosin IIB isoform in neurite outgrowth,25,26 and of the myosin IIA isoform in neurite retraction.27,28 In this cell type myosin IIB concentrates mainly in the peripheral domain of the growth cone while the myosin IIA is found more posteriorly in the growth cone and along the axon.29
These studies exemplify the complexity of myosin functions during spreading and the need for a quantitative theoretical investigation of this phenomenon. A number of computational and analytical models have been focused on the role of myosin in force generation10,30,31 and cytoskeleton organization.32–35 However, to the best of our knowledge, no previous study has theoretically investigated the contribution of myosin forces to the dynamics and the extent of spreading, nor is there a quantitative analysis of the consequences of the spatial distribution of myosin motors on the regulation of cell area and force. In addition, it is unknown how the intrinsic dynamics of myosin II activity (that generally, are governed both by signaling mechanisms as well as by the physical characteristics of acto–myosin interactions) influence the dynamics of spreading. In a recent study,8 we presented a minimal elastic theory of cell spreading dynamics that quantitatively demonstrated how the dynamics of spreading on elastic substrates is limited by the rate of actin polymerization at the cell front and cell–substrate adhesion kinetics. Treating the cytoskeleton as an elastic network has shown to be essential for explaining the universal dependence of the cell area and force on substrate rigidity. We nevertheless deliberately did not make explicit account of myosin forces and their dynamics since our goal has been to derive a minimal model of spreading dynamics; myosin activity has only been implicitly accounted for via its contribution to the effective elastic moduli of the cell.
In this paper, we extend our theory to explicitly investigate the consequences of myosin activity on cell spreading dynamics and mechanics. Because cell–substrate adhesions and the tractions exerted onto the substrate often tend to localize at the cell periphery8,12,36 we adopt a coarse-grained model and theoretically distinguish two populations of myosin II molecular motors: those that locate above the adhesion zone at the cell periphery and facilitate the pulling forward of the cell, and those located more centrally in the cytoskeleton and generally inhibit spreading. Biochemically, these two populations may be identical (e.g., be the same isoform) and could therefore be indistinguishable by various drug treatments, however, we show theoretically that myosin activity in the two spatial locations possesses distinct functions during spreading. We demonstrate that the steady-state radius of the cell is dictated by a balance between myosin exerted forces in the two spatial locations; those at the lamella front facilitate spreading, and those in the lamella bulk oppose spreading. The steady-state force is shown to be dictated by myosin activity in the lamellar front that augments the frictional interaction between the cell and the substrate. These conclusions shed light on the ambiguity revolving the effects of myosin inhibition on cell spreading area, and are consistent with the generic tendency of cellular forces to decrease with myosin inhibition.
In addition, we demonstrate that the dynamics of myosin activity in the lamellar bulk may dictate different spreading profiles. These include a “regular” monotonic increase of cell area with time, an over-damped mode in which the cell area first rises to a maximum and then decreases with time to a steady state, and damped oscillations. Such slow modulations of cell area with time have been discussed in the literature in terms of late myosin contraction22 (and the reciprocal effects of Rac and Rho activity) but have not been quantitatively and systematically studied. Our analysis thus provides important new insight into the function of myosin activity during spreading.
II. Model
Our starting point is a linear theory of cell spreading dynamics described in detail in ref. 8. Accordingly, we model the cell lamella as a homogeneous and isotropic elastic disc of thickness h and radius R that is actively stretched by the propulsion of the cell front forward (see Fig. 1). The cell adheres to the substrate via multiple (transient) adhesion contacts that are assumed to concentrate in a narrow rim between R and R + L (thus neglecting the limited distribution of adhesions underneath the cell body).37 This coarse-grained approximation separates the lamella into two distinct zones: the adhesion zone at R < r < R + L, and an adhesion-free zone at r < R. The width L is taken to be fixed during spreading and smaller than the cell size, L ≪ R.8,37 The radial extension speed of the cell front is dictated by two oppositely oriented velocities:| Ṙ(t) = vpol − vF(t) | (1) |
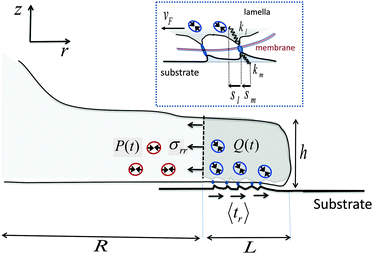 | ||
| Fig. 1 Schematic illustration of major mechanical elements at the cell front. The temporal force balance expressed in eqn (3) is demonstrated with the solid arrows that indicate the mean tractions on the adhesion zone interfaces; P and Q represent the respective (active) contributions of actomyosin contractility to the radial and shear stresses on those interfaces as expressed in eqn (4) and (5). Small circles with double-arrowheads represent the localized distribution of actomyosin force dipoles from which Q and P originate. Note in particular, the opposite effects that Q and P have on the force balance during spreading. While strengthening of Q assists in pulling the cell forward, strengthening of P resists this motion. The top inset provides a zooming into the force balance at the cell–substrate interface. The local displacements of individual adhesion contacts in both the lamella and the substrate are shown along with the associated effective spring constants that characterize the local stiffness. The displacements are produced due to the retrograde flow, vF, that is driven by the forces generated in the cytoskeleton according to vF = f/ξs (cf.eqn (11)). | ||
The retrograde flow arises from the forces generated in the cytoskeleton, which in turn are sustained by the frictional interaction between the lamellar network and the substrate, see Fig. 1. This frictional interaction arises from the distribution of transmembrane adhesion receptors (e.g., integrins) that physically and transiently link the actin network to ligands on the substrate. The retrograde flow of the actin network induces local elastic displacements in the vicinity of each adhesion contact. We denote as sl the local tangential displacement of the lamella, and as sm the corresponding local displacement of the substrate; s = sl + sm is the total local displacement, see the box in Fig. 1. The lipid membrane is assumed to be stationary with respect to the substrate (although lipids can still flow in the plane of the membrane). Using a simple stochastic model for the binding kinetics of these adhesion contacts one may relate the mean displacement and the mean number of contacts to the drag velocity, vF, as follows (see ref. 8 and 44 and Section III in the ESI† for a detailed derivation):
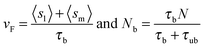 | (2) |
The mean displacements and the retrograde flow are dictated by the forces generated in the cytoskeleton. Denoting as σrr the mean radial stress exerted by the cytoskeleton at r = R, averaged over the lamella height, h, and as 〈tr〉 the mean radial traction acting parallel to the cell basis and averaged over the width of the adhesion layer, L, one has (for L ≪ R§) the following force balance condition at the cell front,2 see Fig. 1:
| hσrr = L〈tr〉 = f | (3) |
| 〈tr〉 = Nbkm〈sm〉 = Nbkl〈sl〉 − Q, | (4) |
σrr = 2κcurr + ξc![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) rr − P rr − P | (5) |
In eqn (5), urr(t) = [R(t) − R0]/R0 and ![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) rr(t) = durr/dt denote, respectively, the mean radial strain and strain-rate of the cytoskeleton where κc is an effective area-expansion modulus and ξc is an effective viscosity coefficient.¶ The quantity P = P(t) represents the mean contribution of acto-myosin contraction in the adhesion-free zone (r < R) to the radial stress in the cytoskeleton. The reference length, R0, is used here as a constant for simplicity, although it may have its own dynamics and is generally expected to be increasing in the early stages of cell adhesion as the lamella network assembles at the cell basis.50
rr(t) = durr/dt denote, respectively, the mean radial strain and strain-rate of the cytoskeleton where κc is an effective area-expansion modulus and ξc is an effective viscosity coefficient.¶ The quantity P = P(t) represents the mean contribution of acto-myosin contraction in the adhesion-free zone (r < R) to the radial stress in the cytoskeleton. The reference length, R0, is used here as a constant for simplicity, although it may have its own dynamics and is generally expected to be increasing in the early stages of cell adhesion as the lamella network assembles at the cell basis.50
Since acto-myosin forces are generally contractile, Q and P are taken as negative quantities and the minus sign in eqn (4) and (5) indicates that the stresses they generate are positive (tensile and pointing inward). We take both Q and P to be zero at t = 0, hence only the increase in myosin dipolar stress from its baseline level in the suspended cell in solution is included; thus the cross-linking function of myosin motors is included in the value of the elastic moduli kl and κc. As will be shown below, the variations in Q and P induce opposite effects on cell spreading dynamics. While the enhancement of Q(t) facilitates spreading and results in more extended cell sizes and stronger forces, an increase in P(t) opposes spreading and renders the cytoskeleton stiffer.
A variety of experimental and theoretical studies have indicated that the magnitude and the orientation of acto-myosin forces are regulated by the local stress in the cytoskeleton.33,35,51–54 Motivated by these studies, we include a simplified account of the dynamics of the acto-myosin polarization response,35,50,52,55 and study the effect on cell spreading dynamics. Accordingly, Q(t) and P(t) are assumed to polarize in accordance with the elastic part of the corresponding stress in the particular regime, namely Q ∼ Nbkl〈sl〉 and P ∼ κcurr. For simplicity, we associate only one (major) time scale with each response, and we denote them as τq and τp, respectively. We thus write the following phenomenological relaxation response as:50,55
τq![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) + Q = −βNbkl〈sl〉 + Q = −βNbkl〈sl〉 | (6) |
| τpṖ + P = −2ακcurr | (7) |
Eqn (1)–(7) constitute a closed set of equations to solve for the evolution of the cell size, R(t), force, f(t), and myosin exerted stress P(t) and Q(t). The steady-state solution can be examined by setting ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) = Ṗ = Ṙ = 0 and noting that in this case vF = vpol (see eqn (1)). Substituting the steady-state values of Q and P in eqn (4) and (5), respectively, and using eqn (2) and (3) one finds the following expressions for the steady-state values of cell radius and force:
= Ṗ = Ṙ = 0 and noting that in this case vF = vpol (see eqn (1)). Substituting the steady-state values of Q and P in eqn (4) and (5), respectively, and using eqn (2) and (3) one finds the following expressions for the steady-state values of cell radius and force:
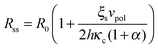 | (8) |
| fss = ξsvpol | (9) |
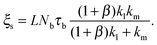 | (10) |
The set of eqn (1)–(7) can be reduced to a third-order linear differential equation in P(t) and consequently solved for all other variables (see ESI†). To demonstrate the essential properties of the solution, however, it is instructive to specialize in the simpler situation where the dynamics expressed in eqn (6) of Q(t) towards a steady-state are neglected; physically this may arise in cases where the reorganization of actomyosin forces more deeply in the cytoskeleton is slower than that in more peripheral locations. The neglect of Q(t) dynamics is examined in the ESI† and shown to provide a fairly good approximation to the full solution.
Assuming τq to be sufficiently small, eqn (6) can be restated as follows: Q = −βNbkl〈sl〉. Substituting this in eqn (4) and combining it with eqn (1) and (2) result in the following expression for the dependence of cellular force on spreading velocity:
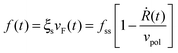 | (11) |
Combining eqn (5) and (11), using eqn (7) and noting that urr(t) = (R(t) − R0)/R0 we find the following differential equation for R(t):
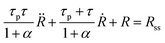 | (12) |
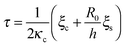 is a characteristic spreading time.8 This equation can be now solved to find explicit expressions for the evolution of the cell size and force; assuming P(0) = 0 and R(0) = R0 one finds:
is a characteristic spreading time.8 This equation can be now solved to find explicit expressions for the evolution of the cell size and force; assuming P(0) = 0 and R(0) = R0 one finds: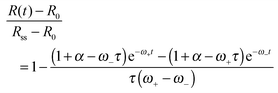 | (13) |
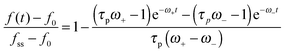 | (14) |
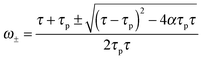 | (15) |
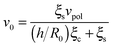 , is obtained from eqn (5) by setting urr = P = 0. An explicit expression for the evolution of the myosin stress, P(t), can readily be derived by the usage of eqn (5) and (11). Analysis of these equations is presented next.
, is obtained from eqn (5) by setting urr = P = 0. An explicit expression for the evolution of the myosin stress, P(t), can readily be derived by the usage of eqn (5) and (11). Analysis of these equations is presented next.
III. Results and discussion
A. Effects of myosin activity on the steady-state cell radius and force
The formulation described above allows us to investigate the effects of myosin II activity on the extent and dynamics of cell spreading and force generation. As has already been mentioned above, myosin activity plays a dual role in the overall force balance during spreading. While strengthening of myosin forces above the adhesion zone at the cell front facilitates spreading, the enhancement of myosin stress in deeper regions of the lamella opposes spreading. This may also be explained in terms of the effects of myosin activity on the effective rigidity of these two regimes. We note the appearance of the two effective moduli,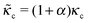 and
and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) l = (1 + β)kl in eqn (8) and (10). These provide a model for the effective stiffening of the two lamellar regions by myosin polarization behavior.54 Thus, on the one hand, via the effect of β, the inhibition of myosin activity reduces the effective rigidity of the lamella front (
l = (1 + β)kl in eqn (8) and (10). These provide a model for the effective stiffening of the two lamellar regions by myosin polarization behavior.54 Thus, on the one hand, via the effect of β, the inhibition of myosin activity reduces the effective rigidity of the lamella front (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) l = (1 + β)kl), this reduces the frictional interaction with the substrate and impairs the ability of the cell to spread. The active stiffening of the lamella front by myosin activity is thus seen to provide it with more strength to stretch the interior of the cytoskeleton forward, while inhibition has the opposite effect of loosening the lamella, as indeed often observed by its “floppy” appearance in the microscope.1,14 On the other hand, via the effect of α, the inhibition of myosin II motors loosens deeper regions of the lamella (
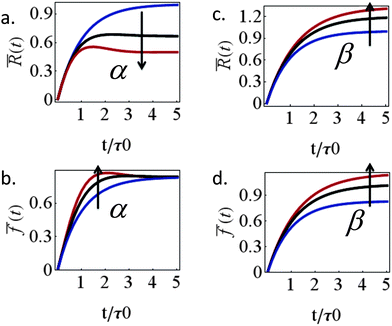
l = (1 + β)kl), this reduces the frictional interaction with the substrate and impairs the ability of the cell to spread. The active stiffening of the lamella front by myosin activity is thus seen to provide it with more strength to stretch the interior of the cytoskeleton forward, while inhibition has the opposite effect of loosening the lamella, as indeed often observed by its “floppy” appearance in the microscope.1,14 On the other hand, via the effect of α, the inhibition of myosin II motors loosens deeper regions of the lamella (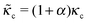 ) and this facilitates the elastic stretching of the cell. These two contrasting effects of myosin activity in the lamella are illustrated in panels a and c of Fig. 2.
) and this facilitates the elastic stretching of the cell. These two contrasting effects of myosin activity in the lamella are illustrated in panels a and c of Fig. 2.
Interesting is the different way in which the two myosin populations affect the cellular force. Panel 2b shows that with higher values of α larger stresses develop during spreading but all curves converge to the same value at the steady-state. Myosin contractility in the lamellar bulk, P(t), is thus seen to only affect the temporal value of the cellular stress during spreading but to have no effect on the steady-state stress. The steady-state stress in our model is dictated by the frictional interaction ξsvF = ξs(β)vpol between the cell and the substrate which monotonically increases with myosin activity in the adhesion zone, as shown in panel 2d. As mentioned above, this conclusion is likely to hold so long as the cytoskeleton is free to flow past the substrate and contract; once long-lived stable contacts are established between the actin cytoskeleton and the ECM myosin contractility in the lamellar bulk would naturally also contribute to the generated force. The general increase of steady-state cellular stress with myosin activity is well known.11,14 Assuming 1 + β to inversely scale with blebbistatin concentration or volume fraction, χbleb, as 1/χbleb one finds fss ∼ 1/[km/kl + χbleb] which is consistent with the results of Mitrossilis et al.10,13
Similar structural arguments have been invoked to explain the effects of myosin IIA and IIB on cell spreading dynamics. While the inhibition of both resulted in a reduction of cellular force,11,14 it has been reported in ref. 23 and 24 that the depletion of the myosin IIB isoform resulted in impaired spreading while the depletion of myosin IIA facilitated spreading. Measurements of the spatial distribution of the two isoforms showed that the IIB protein is concentrated slightly more peripherally; while this picture is consistent with our analysis it must be emphasized that the spatial distribution of the two myosin isoforms shows significant overlapping which makes a quantitative interpretation nontrivial. The distribution of the two myosin isoforms is perhaps more apparent in neuronal cells. The myosin IIB isoform mainly concentrates at the peripheral zone of the growth cone whereas the myosin IIA isoform is found in more central locations of the growth cone and along the axon.29 Consistent with this spatial segregation, the inhibition of myosin IIB impedes neurite outgrowth25,26 while the myosin IIA drives neurite retraction.27,28 Our analysis does not distinguish between two myosin isoforms but illustrates that differences in their location may oppositely affect spreading.
Our theory also predicts the effects of matrix rigidity on the extent and dynamics of cell spreading. Consistent with experiments, eqn (8)–(10) predict that both the cell radius and force monotonically increase with matrix rigidity and combining eqn (5) and (11) reveals that the initial spreading speed is given by v0 = ξsvpol/[(h/R0)ξc + ξs], which in agreement with experiment is also an increasing function of matrix rigidity. A detailed examination of these predictions in comparison to experimental data is presented in ref. 8. Our extension here to account for myosin polarization response allows us to predict how the matrix rigidity might affect the responsiveness of cell spreading to myosin inhibition. On very stiff substrates eqn (10) predicts that ξs ∼ (1 + β)kl; on very soft substrates ξs is independent of β. One consequently finds Rss ∼ (1 + β)/(1 + α) for very stiff substrates, and Rss ∼ 1/(1 + α), for very soft substrates. Thus in the case of stiff substrates, myosin inhibition is expected to have a reduced effect on cell spreading in comparison to soft substrates where spreading is predicted to be facilitated. This is consistent with the recent observations of Dillard et al.21 with T cells spreading on mobile and fixed ligands on a supported lipid bilayer.
B. Effects of myosin activity on cell spreading dynamics
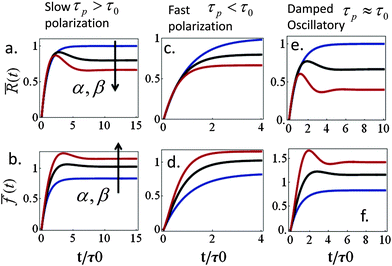
Spreading dynamics and force generation have been described by two major characteristic times, the spreading characteristic time, τ, and the polarization response time, τp, of myosin motors in the lamellar bulk; the less prominent consequences of myosin dynamics in the lamellar front are examined in the ESI.† The frequencies ω+ and ω− are combinations of the two time scales that also depend on the polarizability factors α and β; the spreading time, τ(β), is generally an increasing function of β (via the dependence of ξs on β). While spreading experiments reveal that τ is on the order of minutes (e.g., as in blood platelets) to tens of minutes (other cell types), we are still uncertain about the characteristic time of acto-myosin polarization; measurements of force generation in clamped cells held between cantilevers reveal an active polarization of force that occurs on a time scale of minutes to tens of minutes.13,56 This suggests a time scale for P(t), however, even in those experiments it is unclear to what extent do spreading forces contribute to the actual measurement. Our formalism here allows us to investigate how the ratio between τp and τ may be reflected in cell spreading dynamics.We first examine the predicted behavior in the two extreme cases where: (i) cell spreading is faster than the polarization response, τ < τp and (ii) polarization response is faster than spreading, τp < τ. In the former case (i) actomyosin polarization occurs with a delay relative to spreading. For sufficiently strong polarization response we find that R(t) and f(t) may evolve non-monotonically with time, showing a characteristic “overshoot” in early spreading, as exhibited by the black and red curves in Fig. 3a and b. Similar behavior has been observed, for instance, in ref. 22 (see Fig. 1c in that paper) as well as in our experiments on platelets (data not shown). Mathematically one finds that for long τp and small enough α early spreading behaves as: R(t) ≈ R0 + (R0ss − R0)(1 − e−t/τ) and f(t) ≈ f0 + (fss − f0)(1 − e−t/τ). Thus, in early spreading the cell extends with minor (opposing) polarization forces, as if it tries to reach the steady-state cell size, R0ss, that would be obtained with α = β = 0. However, at longer times, when t > τ, a gradual decrease in cell size may be observed once myosin motors start pulling on the cytoskeleton. Interestingly, this behavior may also be interpreted as an effective stiffening of the cytoskeleton from the initial value κc to the final value κc(1 + α). The gradual decrease in cell size may result in the overall decrease in cell force (e.g., red curve in panel 3b).
In the opposite case (ii) where acto-myosin forces polarize more quickly than cell spreading one finds: R(t) ≈ R0 + (Rss − R0)(1 − e−t/![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) ). This is similar to the previous case, but here both the steady-state size Rss and the time scale
). This is similar to the previous case, but here both the steady-state size Rss and the time scale ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) = τ/(1 + α) are reduced by the cytoskeletal stiffening factors, 1 + α and 1 + β (cf. panel 3c). For the force we find the following behavior:
= τ/(1 + α) are reduced by the cytoskeletal stiffening factors, 1 + α and 1 + β (cf. panel 3c). For the force we find the following behavior: 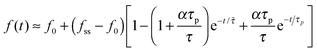 . At early times where f(t) and its elastic contribution are still small, the acceleration of P(t) may dominate the behavior of f(t) (with large enough α) and give rise to an apparent sigmoidal appearance of f(t) (see for instance Fig. S2b and c, ESI†).
. At early times where f(t) and its elastic contribution are still small, the acceleration of P(t) may dominate the behavior of f(t) (with large enough α) and give rise to an apparent sigmoidal appearance of f(t) (see for instance Fig. S2b and c, ESI†).
Finally, eqn (15) predicts the occurrence of damped oscillations when the discriminant is negative (red curve in Fig. 3e and f). As the equation shows, the closer the time scales τ and τp are, the more likely are these oscillations to be observed. We find that for τp ≈ τ the frequency of these oscillations scales as 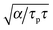 , i.e., increases with α and decreases with τp and τ as one expects. This predicted global oscillatory behavior of cell area should be distinguished from the more rapid protrusion–retraction cycles that occur locally at the cell periphery as reported for instance in ref. 15 and 57.
, i.e., increases with α and decreases with τp and τ as one expects. This predicted global oscillatory behavior of cell area should be distinguished from the more rapid protrusion–retraction cycles that occur locally at the cell periphery as reported for instance in ref. 15 and 57.
A phase diagram summarizing when damped oscillations of this sort are to be expected is shown in Fig. 4a for the case kl = km; the ordinate measures the ratio τp/τ0 between the polarization time and the spreading time, where τ0 = τ (β = 0), and the abscissa is the myosin susceptibility α = β. Interestingly, the phase diagram predicts that substrate rigidity may oppositely affect the profile of spreading dynamics (R(t)) for cells located in the upper or lower halves of the phase diagram. Substrate rigidity is predicted to modulate the spreading time, 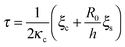 , via the augmenting effect it has on ξs (see, eqn (10)). Hence, if a cell is located on the lower branch of the diagram (e.g., point a in panel 4a), a lowering of substrate rigidity will increase the ratio τp/τ0 and cause the cells to enter the oscillatory regime; as seen in panel 4b (dark-red shows regular spreading versus light-red that shows damped oscillatory behavior). The opposite effect is predicted for cells located on the upper branch of the phase diagram, see 4c; in this case an oscillatory mode (dark red curve) is observed on the more rigid substrate. Note that all curves in panels 4a and b were deliberately scaled by the steady-state change in cell radius Rss − R0 in order to emphasize the effects of matrix rigidity on the dynamics of spreading. However, as noted above eqn (8)–(10) predict that Rss is a monotonically increasing function of matrix rigidity, as commonly observed experimentally.2–6,8
, via the augmenting effect it has on ξs (see, eqn (10)). Hence, if a cell is located on the lower branch of the diagram (e.g., point a in panel 4a), a lowering of substrate rigidity will increase the ratio τp/τ0 and cause the cells to enter the oscillatory regime; as seen in panel 4b (dark-red shows regular spreading versus light-red that shows damped oscillatory behavior). The opposite effect is predicted for cells located on the upper branch of the phase diagram, see 4c; in this case an oscillatory mode (dark red curve) is observed on the more rigid substrate. Note that all curves in panels 4a and b were deliberately scaled by the steady-state change in cell radius Rss − R0 in order to emphasize the effects of matrix rigidity on the dynamics of spreading. However, as noted above eqn (8)–(10) predict that Rss is a monotonically increasing function of matrix rigidity, as commonly observed experimentally.2–6,8
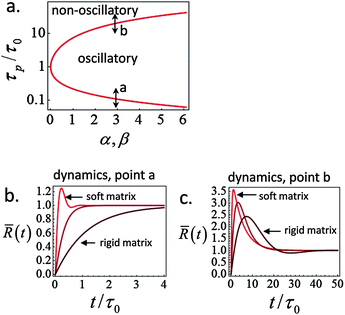 | ||
Fig. 4 Phase diagram (panel a) showing regimes of oscillatory and non-oscillatory spreading dynamics in the relevant parameter space: τp/τ0 and α, β. The boundary curve is calculated for km = kl and τc = 0.17τ0. Panels b and c demonstrate (respectively) the predicted dynamics of the scaled cell radius, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) (t) = (R(t) − R0)/(Rss − R0), for three choices of matrix rigidity, around points a and b in the phase diagram; soft, intermediate and rigid matrices correspond to km/kl = 0.1, 1, and 10, respectively. The effect of matrix rigidity enters via its modulation of the cell–substrate friction coefficient, ξs, as predicted by eqn (10). Note that all plots are normalized by the steady-state change in cell radius, Rss − R0, which by eqn (8) is an increasing function of matrix rigidity; hence all curves converge to 1 at t → ∞. Complementary calculations of (t) = (R(t) − R0)/(Rss − R0), for three choices of matrix rigidity, around points a and b in the phase diagram; soft, intermediate and rigid matrices correspond to km/kl = 0.1, 1, and 10, respectively. The effect of matrix rigidity enters via its modulation of the cell–substrate friction coefficient, ξs, as predicted by eqn (10). Note that all plots are normalized by the steady-state change in cell radius, Rss − R0, which by eqn (8) is an increasing function of matrix rigidity; hence all curves converge to 1 at t → ∞. Complementary calculations of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) (t), (t), ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (t) and (t) and ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) (t) for the dynamics observed in panels b and c are presented in Fig. S2 (ESI†). (t) for the dynamics observed in panels b and c are presented in Fig. S2 (ESI†). | ||
Fig. 2–4 show an interesting means of investigating the contribution of myosin activity to cell spreading dynamics. It is predicted that the stimulation of myosin activity would increase the likelihood of observing non-monotonic spreading patterns that are otherwise more rarely observed; this is illustrated by the effect of increasing α or β on the evolution of cell area and force. Furthermore, our prediction of a phase diagram that distinguishes different effects of substrate rigidity on the cell spreading profile (panels b and c in Fig. 4) suggests another interesting way to investigate the coupling of myosin polarization dynamics to spreading induced stresses. To this end, however, it is essential for first experimentally quantifying the time scale of actomyosin polarization in the course of spreading (τp). One way to achieve this is by measuring the course of force generation in cells whose spreading area has been restricted using the micro-patterning technique.58 An experiment in this spirit has been reported by Aratyn-Schaus et al.59 who used blebbistatin washout to set the initiation of myosin force generation in an already full spread cell; these authors reported a time scale of a few minutes for myosin force generation in U2OS osteosarcoma cells.
IV. Concluding remarks
We presented a theoretical analysis of the contribution of myosin II generated stress to the extent and dynamics of cell spreading, and of the force generation in this process. The theory distinguishes two myosin populations according to their location in the lamella. Since cell–substrate adhesions tend to concentrate near the cell periphery we used a coarse grained picture and distinguished between myosin motors above the adhesion zone and those that locate more deeply in the lamella. The two myosin populations are shown to affect cell spreading in opposite ways. Those located above the adhesion zone facilitate spreading since they effectively strengthen the frictional interaction between the cell and the substrate and more efficiently allow the cell to extend forward. Myosin II motors in the lamella bulk have the opposite effect of pulling the cell inwards, thereby resisting cell spreading. We have demonstrated that the time scale of actomyosin polarization plays a crucial role in shaping the time course of cell spreading and predicted a phase diagram which shows the conditions for the occurrence of global oscillatory changes in cell area. The closed form expressions we derived for the evolution of cell area and force provide a simple quantitative framework for analyzing the contribution of myosin dynamics during spreading.Acknowledgements
Funding to SK was provided by the Deutsche Forschungs-Gemeinschaft (DFG) in the framework of the SFB 937/A12 and the Excellence Initiative. AZ thanks the Israel Science Foundation (grant no. 1396/09) and the Niedersachsen, German-Israeli Lower Saxony Cooperation for their support.References
- U. S. Schwarz and M. L. Gardel, J. Cell Sci., 2012, 125, 3051 CrossRef CAS PubMed.
- N. Wang, I. M. Tolic-Norrelykke, J. X. Chen, S. M. Mijailovich, J. P. Butler, J. J. Fredberg and D. Stamenovic, Am. J. Physiol.: Cell Physiol., 2002, 282, C606 CrossRef CAS PubMed.
- J. P. Califano and C. A. Reinhart-King, Cell. Mol. Bioeng., 2010, 3, 68–75 CrossRef PubMed.
- T. Yeung, P. C. Georges, L. A. Flanagan, B. Marg, M. Ortiz, M. Funaki, N. Zahir, W. Ming, V. Weaver and P. A. Janmey, Cell Motil. Cytoskeleton, 2005, 60, 24 CrossRef PubMed.
- C. Reinhart-King, M. Dembo and D. Hammer, Biophys. J., 2005, 89, 676 CrossRef CAS PubMed.
- L. Trichet, J. Le Digabel, R. J. Hawkins, S. R. K. Vedula, M. Gupta, C. Ribrault, P. Hersen, R. Voituriez and B. Ladoux, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6933 CrossRef CAS PubMed.
- S. Schwarz G.Henriques, R. Sandmann, A. Strate and S. Köster, J. Cell Sci., 2012, 125, 3914 CrossRef PubMed.
- N. Nisenholz, K. Rajendran, Q. Dang, H. Chen, R. Kemkemer, R. Krishnan and A. Zemel, Soft Matter, 2014, 10, 7234–7246 RSC.
- S. Yang and T. Saif, Exp. Cell Res., 2005, 305, 42–50 CrossRef CAS.
- J. Étienne, J. Fouchard, D. Mitrossilis, N. Bufi, P. Durand-Smet and A. Asnacios, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2740 CrossRef PubMed.
- Y. Cai, N. Biais, G. Giannone, M. Tanase, G. Jiang, J. M. Hofman, C. H. Wiggins, P. Silberzan, A. Buguin and B. Ladoux, Biophys. J., 2006, 91, 3907 CrossRef CAS PubMed.
- M. L. Gardel, B. Sabass, L. Ji, G. Danuser, U. S. Schwarz and C. M. Waterman, J. Cell Biol., 2008, 183, 999 CrossRef CAS PubMed.
- D. Mitrossilis, J. Fouchard, A. Guiroy, N. Desprat, N. Rodriguez, B. Fabry and A. Asnacios, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18243 CrossRef CAS PubMed.
- Y. Cai, O. Rossier, N. C. Gauthier, N. Biais, M. A. Fardin, X. Zhang, L. W. Miller, B. Ladoux, V. W. Cornish and M. P. Sheetz, J. Cell Sci., 2010, 123, 413 CrossRef CAS PubMed.
- G. Giannone, B. J. Dubin-Thaler, H.-G. Döbereiner, N. Kieffer, A. R. Bresnick and M. P. Sheetz, Cell, 2004, 116, 431 CrossRef CAS PubMed.
- G. Johnson, L. Leis, M. Krumwiede and J. White, J. Thromb. Haemostasis, 2007, 5, 1516 CrossRef CAS PubMed.
- F. Rehfeldt, A. E. Brown, M. Raab, S. Cai, A. L. Zajac, A. Zemel and D. E. Discher, Integr. Biol., 2012, 4, 422 RSC.
- Y. Qiu, A. C. Brown, D. R. Myers, Y. Sakurai, R. G. Mannino, R. Tran, B. Ahn, E. T. Hardy, M. F. Kee and S. Kumar, et al. , Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14430 CrossRef CAS PubMed.
- T. Wakatsuki, R. B. Wysolmerski and E. L. Elson, J. Cell Sci., 2003, 116, 1617 CrossRef CAS PubMed.
- J. D. Mih, A. Marinkovic, F. Liu, A. S. Sharif and D. J. Tschumperlin, J. Cell Sci., 2012, 125, 5974 CrossRef CAS PubMed.
- P. Dillard, R. Varma, K. Sengupta and L. Limozin, Biophys. J., 2014, 107, 2629 CrossRef CAS PubMed.
- S. Kumari, S. Vardhana, M. Cammer, S. Curado, L. Santos, M. P. Sheetz and M. L. Dustin, Front. Immunol., 2012, 3, 230 CAS.
- V. Betapudi, L. S. Licate and T. T. Egelhoff, Cancer Res., 2006, 66, 4725 CrossRef CAS PubMed.
- V. Betapudi, PLoS One, 2010, 5, e8560 Search PubMed.
- S. R. Wylie, P.-J. Wu, H. Patel and P. D. Chantler, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 12967 CrossRef CAS.
- P. C. Bridgman, S. Dave, C. F. Asnes, A. N. Tullio and R. S. Adelstein, J. Neurosci., 2001, 21, 6159 CAS.
- M. Amano, K. Chihara, N. Nakamura, Y. Fukata, T. Yano, M. Shibata, M. Ikebe and K. Kaibuchi, Genes Cells, 1998, 3, 177 CrossRef CAS PubMed.
- S. R. Wylie and P. D. Chantler, Mol. Biol. Cell, 2003, 14, 4654 CrossRef CAS PubMed.
- D. M. Suter and K. E. Miller, Prog. Neurobiol., 2011, 94, 91 CrossRef CAS PubMed.
- U. S. Schwarz, T. Erdmann and I. B. Bischofs, BioSystems, 2006, 83, 225 CrossRef CAS PubMed.
- P. Marcq, N. Yoshinaga and J. Prost, Biophys. J., 2011, 101, L33 CrossRef CAS PubMed.
- C. Borau, T. Kim, T. Bidone, J. M. Garca-Aznar and R. D. Kamm, PLoS One, 2012, 7, e49174 CAS.
- V. S. Deshpande, R. M. McMeeking and A. G. Evans, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14015 CrossRef CAS PubMed.
- T. Luo, K. Mohan, V. Srivastava, Y. Ren, P. A. Iglesias and D. N. Robinson, Biophys. J., 2012, 102, 238 CrossRef CAS PubMed.
- A. Zemel, F. Rehfeldt, A. E. X. Brown, D. E. Discher and S. A. Safran, Nat. Phys., 2010, 6, 468 CrossRef CAS PubMed.
- C. M. Edwards and U. S. Schwarz, Phys. Rev. Lett., 2011, 107, 128101 CrossRef PubMed.
- A. Alexandrova, K. Arnold, S. Schaub, J. Vasiliev, J. Meister, A. Bershadsky and A. Verkhovsky, PLoS One, 2008, 3, e3234 Search PubMed.
- J. Zimmermann, C. Brunner, M. Enculescu, M. Goegler, A. Ehrlicher, J. Käs and M. Falcke, Biophys. J., 2012, 102, 287 CrossRef CAS PubMed , ISSN 1542-0086.
- A. Babich, S. Li, R. S. O'Connor, M. C. Milone, B. D. Freedman and J. K. Burkhardt, J. Cell Biol., 2012, 197, 775 CAS , ISSN 1540-8140.
- W. C. Salmon, M. C. Adams and C. M. Waterman-Storer, J. Cell Biol., 2002, 158, 31 CrossRef CAS PubMed , ISSN 0021-9525.
- A. Ponti, M. Machacek, S. Gupton, C. Waterman-Storer and G. Danuser, Science, 2004, 305, 1782 CrossRef CAS PubMed.
- C.-H. Lin and P. Forscher, Neuron, 1995, 14, 763 CrossRef CAS PubMed.
- C. Jurado, J. R. Haserick and J. Lee, Mol. Biol. Cell, 2005, 16, 507 CrossRef CAS PubMed.
- S. Walcott and S. Sun, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7757 CrossRef CAS PubMed.
- B. T. Marshall, M. Long, J. W. Piper, T. Yago, R. P. McEver and C. Zhu, Nature, 2003, 423, 190 CrossRef CAS PubMed.
- F. Kong, A. J. Garca, A. P. Mould, M. J. Humphries and C. Zhu, J. Cell Biol., 2009, 185, 1275 CrossRef CAS PubMed.
- E. V. Sokurenko, V. Vogel and W. E. Thomas, Cell Host Microbe, 2008, 4, 314 CAS.
- E. A. Novikova and C. Storm, Biophys. J., 2013, 105, 1336 CrossRef CAS PubMed.
- J. M. Maloney, E. B. Walton, C. M. Bruce and K. J. Van Vliet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041923 CrossRef PubMed.
- Y. Brill-Karniely, N. Nisenholz, K. Rajendran, Q. Dang, R. Krishnan and A. Zemel, Biophys. J., 2014, 107, L37 CrossRef CAS PubMed.
- H. J. Hsu, C. F. Lee and R. Kaunas, PLoS One, 2009, 4, e4853 Search PubMed.
- A. Zemel, F. Rehfeldt, A. E. X. B. D. E. Discher and S. A. Safran, J. Phys.: Condens. Matter, 2010, 22, 194110 CrossRef CAS PubMed.
- P. G. Torres, I. Bischofs and U. Schwarz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 011913 CrossRef PubMed.
- A. Zemel, R. De and S. Safran, Curr. Opin. Solid State Mater. Sci., 2011, 15, 169–176 CrossRef.
- N. Nisenholz, M. Botton and A. Zemel, Soft Matter, 2014, 10, 2453 RSC.
- P. Fernadez, P. A. Pullarkat and A. Ott, Biophys. J., 2006, 90, 3796 CrossRef PubMed.
- G. L. Ryan, H. M. Petroccia, N. Watanabe and D. Vavylonis, Biophys. J., 2012, 102, 1493 CrossRef CAS PubMed.
- P. W. Oakes, S. Banerjee, M. C. Marchetti and M. L. Gardel, Biophys. J., 2014, 107, 825 CrossRef CAS PubMed.
- Y. Aratyn-Schaus, P. W. Oakes and M. L. Gardel, Mol. Biol. Cell, 2011, 22, 1330 CrossRef CAS PubMed.
- Y.-L. Wang, Sci. Signaling, 2007, 2007, pe10 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01733e |
| ‡ Each adhesion connection may break on either side of the integrin molecule, i.e., either on the actin–intergin or the integrin–ligand (substrate) side. Thus, τb generally reflects the life time of the weaker of the two bonds. Because experiments show that integrins are less mobile than the actin filaments they associate with,60τb is better associated with the actin–integrin life time. |
| § Eqn (3) generally includes a tangential (hoop) stress term, (hL/R) 〈σθθ〉L,h on the left hand side that can be neglected for L ≪ R. |
| ¶ In the adhesion-free region, r < R, the cytoskeleton is treated as a thin, isotropic and homogeneous disc and generalized plane stress conditions are assumed on the two interfaces z = 0 and z = h, namely σiz(0) = σiz(h) = 0. |
| This journal is © The Royal Society of Chemistry 2016 |