Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nanorings with copper(II) and zinc(II) centers: forcing copper porphyrins to bind axial ligands in heterometallated oligomers†
Jonathan
Cremers
a,
Sabine
Richert
b,
Dmitry V.
Kondratuk
a,
Tim D. W.
Claridge
a,
Christiane R.
Timmel
b and
Harry L.
Anderson
 *a
*a
aDepartment of Chemistry, University of Oxford, Chemistry Research Laboratory, Oxford OX1 3TA, UK. E-mail: harry.anderson@chem.ox.ac.uk
bDepartment of Chemistry, University of Oxford, Centre for Advanced Electron Spin Resonance, Oxford OX1 3QR, UK
First published on 3rd August 2016
Abstract
The affinity of copper(II) porphyrins for pyridine ligands is extremely weak, but oligo-pyridine templates can be used to direct the synthesis of Cu-containing cyclic porphyrin oligomers when they also have Zn centers. We report the synthesis of two heterometallated nanorings: a six-porphyrin ring prepared from a Zn/Cu/Zn linear trimer and a ten-porphyrin ring prepared from a Zn/Zn/Cu/Zn/Zn pentamer. Both these macrocycles have copper porphyrins at two specific positions across the diameter of the ring and zinc at other sites. The presence of a paramagnetic metal results in broadening of the 1H NMR spectra and reduces the relaxation time constants (T1 and T2). The changes in T1 provide quantitative information on the distance of each proton from the copper atom. The Zn/Zn/Cu/Zn/Zn linear porphyrin pentamer binds strongly to a penta-pyridyl template, despite the weakness of the Cu–N interaction, because of the chelate cooperativity of the neighboring Zn–N coordination. The stabilities of a family of four linear porphyrin pentamer complexes were determined by UV-vis-NIR titration and analyzed using a chemical double-mutant cycle. The results show that the free energy of interaction of a copper center to axial pyridine ligands is −6.2 kJ mol−1 when the entropy cost of bringing together the two molecules has already been paid by pyridine–zinc interactions. The development of template-directed approaches to the synthesis of nanorings with combinations of different metals at specific positions around the ring opens up many possibilities for controlling the photophysical behavior of these supramolecular systems and for probing their conformations by EPR.
Introduction
The use of templates to control the formation of covalent bonds, via non-covalent interactions, has provided access to many fascinating molecular structures.1–4 Various types of reversible interactions can be used in template-directed synthesis. The most versatile of these approaches is arguably the coordination of zinc porphyrins to oligo-amine templates.5–15 Zinc porphyrin nanorings exhibit intriguing photophysical and ligand-binding behavior,12–17 yet their scope would be dramatically expanded if we could include other transition metal centers. Here we present a strategy for the synthesis of nanorings with copper(II) porphyrins at two specific positions across the diameter of the macrocycle and zinc at the other sites, c-P6Cu2 and c-P10Cu2, using templates T6 and T5, respectively (Fig. 1). This methodology should be applicable for the synthesis of many other heterometallated porphyrin nanorings. | ||
| Fig. 1 Chemical structures of the porphyrin nanorings c-P6Cu2 (n = 2) and c-P10Cu2 (n = 4), P1M (where M = Zn, Cu, or 2H), and the templates T4, T5 and T6. Ar = 3,5-bis(tert-butyl)phenyl. | ||
Heterometallated porphyrin oligomers have been widely investigated as model systems for exploring electron transfer,18–20 energy transfer,21–24 nonlinear optical activity25 and molecular recognition.26–28 The presence of an open-shell copper(II) ion in a porphyrin oligomer provides a local fluorescence-quenching site, due to relaxation via d–d transitions, although phosphorescence from trip-doublet states is sometimes observed.29–31 Thus the quenching of fluorescence from a free-base or zinc porphyrin by a remote copper center provides a test for long-range energy migration.23 EPR measurements have been used to probe the structure of DNA strands covalently attached to copper(II) porphyrin units.32 The through-space dipolar coupling between two paramagnetic copper(II) centers can be measured by EPR using double electron-electron resonance (DEER).33 This technique provides accurate information on Cu⋯Cu distances in the range 2–5 nm.34 The ability to place two copper(II) centers at precisely defined positions in a nanoring enables the conformation and flexibility of the whole assembly to be probed by EPR.35
While the binding of zinc(II) porphyrins to amines has been studied extensively,36,37 little is known about the coordination of axial ligands to copper(II) porphyrins (Fig. 2). The interaction appears to be extremely weak, as expected from a consideration of the relevant orbitals. In Cu(II) (d9) complexes, there is strong ligand binding in the equatorial plane, due to a single vacancy in the 3dx2−y2 orbitals. Bonding in the equatorial plane is also enhanced by hybridization of the 4s and 3dz2 orbitals which leads to a build-up of electron density along the z-axis, causing a reduction in axial binding strength. When the d-shell is full, as in Zn(II), the driving force for bonding in the equatorial plane is reduced, as is the 4s/3dz2 hybridization, and axial ligands bind more strongly.38 During the 1950s, Miller and Dorough reported that copper(II) tetraphenyl porphyrins bind pyridine with an association constant of 0.05 ± 0.02 M−1 (in benzene at 303 K).36 This value was supported by subsequent studies,39,40 but it is not clear whether such a weak interaction can be measured reliably by a simple UV-vis titration, since an association constant of 0.05 M−1 requires a pyridine concentration of 20 M for 50% saturation, which is greater than the concentration of pyridine in neat pyridine (12 M). Here we demonstrate that heterometallated linear porphyrin oligomers can be used to measure the weak interaction of a copper center with axial nitrogen ligands, without requiring high concentrations of the pyridine ligand, by utilizing the cooperative effect of neighboring zinc centers in a chemical double-mutant cycle.41
 | ||
| Fig. 2 (a) Axial coordination of pyridine to a metalloporphyrin (M = Zn or Cu). (b) Total SCF energy differences as a function of the metal–pyridine separation distance for M = Zn (red) and M = Cu (green). DFT calculations were carried out with Turbomole V6.1 (ref. 42) under C2 symmetry, DFT/B3LYP with the TZVP basis set,43 RI-approximation,44 empirical dispersion corrected energies.45 (c) Scheme of a metal center (M) bound in a porphyrin coordinating an axial pyridine ligand; d1 is the distance between the central metal and the axial pyridine, while d2 is the displacement of the metal atom from the plane of the porphyrin ligand. | ||
Some insights into the interaction of copper and zinc porphyrins with pyridine are provided by DFT calculations.42–45 A plot of the self-consistent field (SCF) energy vs. distance (d1) from constrained DFT geometry optimizations at fixed metal–pyridine distances (Fig. 2b) reveals that the binding energy is significantly smaller for copper porphyrins than for zinc. As a result, a shorter equilibrium M–N bond length (d1) of 2.18 Å is found for M = Zn compared to 2.35 Å for M = Cu. The calculations also show that the zinc atom is pulled out of the porphyrin plane by d2 = 0.28 Å in the equilibrium geometry, whereas the copper atom is only slightly displaced when it coordinates pyridine, d2 = 0.12 Å, reflecting stronger equatorial binding. The calculated distances d1 and d2 agree well with data from X-ray crystallography. The only known structure of a neutral copper(II) porphyrin with a 5-coordinate metal bound to a nitrogen-ligand is a pyridine complex reported by Lipstman and Goldberg,46,47 whereas the Cambridge Structural Database48 contains 362 crystal structures of zinc porphyrin amine complexes. The mean zinc–pyridine distance is d1 = 2.16(3) Å and the out of plane distance is d2 = 0.24(6) Å.9c The parameters for the Cu(II) complex are d1 = 2.47 Å and d2 = 0.12 Å.46 The scarcity of crystallographic data and the length of this Cu–N bond illustrate the weakness of the interaction.
Results and discussion
Synthesis of linear porphyrin oligomers
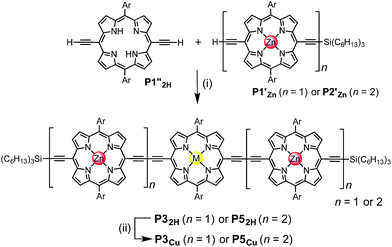
Two linear porphyrin oligomers with a copper porphyrin in the middle of the chain, P3Cu and P5Cu, were prepared by coupling the free-base deprotected porphyrin monomer P1′′2H with a large excess of mono-protected monomer P1′Zn or dimer P2′Zn, as shown in Scheme 1 (n = 1 and n = 2, respectively). Copper was then inserted into the central free-base porphyrin unit at the final stage of the synthesis. This route was adopted because the free-base intermediates have better solubility than the corresponding copper porphyrins, and because it can easily be modified to insert other metals at the centers of the oligomers. Copper-free palladium catalyzed coupling conditions were used to avoid premature insertion of copper into the free-base porphyrin units.49 All of the compounds were fully characterized by MALDI-ToF mass spectroscopy, UV-vis-NIR and NMR spectroscopy (see ESI, Section S6†).Synthesis of heterometallated porphyrin nanorings
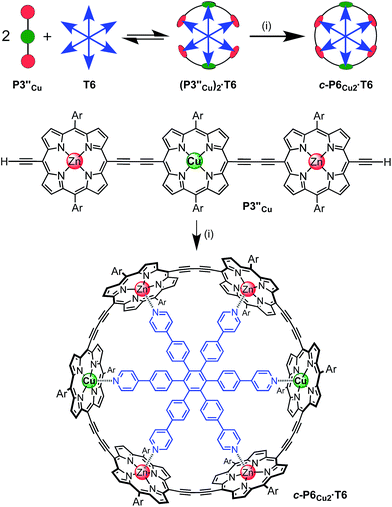
The six-porphyrin nanoring with two copper centers, c-P6Cu2, was prepared by the oxidative homocoupling of two deprotected trimers, P3′′Cu, in the presence of the hexadentate template T6 (Scheme 2). Polymerization predominated in this reaction, and the desired product, c-P6Cu2·T6, was isolated in only 2% yield, reflecting the weak binding of the Zn/Cu/Zn trimer to the T6 template.15The ten-porphyrin nanoring with two copper centers, c-P10Cu2, was prepared using a ‘caterpillar-track’ templating strategy,12 by oxidative homocoupling of the deprotected pentamer, P5′′Cu, in the presence of a pentadentate template T5 (Scheme 3). In this case, the larger number of zinc binding sites leads to stronger binding of the template and a more efficient synthesis. The desired heterometallated nanoring was isolated as its template-complex c-P10Cu2·(T5)2 in a 17% yield. The T5 template was removed from this complex in quantitative yield by addition of excess pyridine.
NMR spectroscopy of copper-containing oligomers
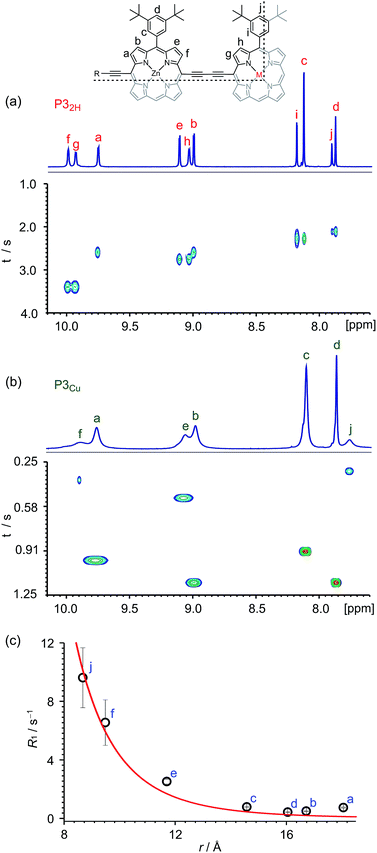
Many copper porphyrins have been synthesized, but their NMR spectra are rarely reported, because they tend to give broad unresolved resonances.50,51 NMR measurements on paramagnetic compounds are often uninformative since the unpaired electron causes rapid relaxation, resulting in broad signals,52 however the heterometallated porphyrin oligomers used in this study are large enough to give informative 1H NMR spectra, and the effect of the paramagnetic center provides extra information. Protons close to the copper ion give extremely broad peaks, whereas those further from the paramagnetic center are well resolved.The aromatic regions of the 1H NMR spectra of the linear trimers containing either a free-base, P32H, or a copper porphyrin, P3Cu, are compared in Fig. 3. The NMR spectrum of the diamagnetic compound P32H shows sharp signals for both the β-protons (at 8.9–10.0 ppm) and the aryl-protons (at 7.8–8.2 ppm). In the spectrum of the copper-containing trimer, P3Cu, the signals for the β-protons nearest to the copper (g and h) are completely unobservable, whereas the signals further removed from the copper (a–d) are well resolved.
The deterioration observed in the 1H NMR spectrum of P3Cu is a direct result of the presence of the paramagnetic copper center and can be attributed to shortening of the T1 and T2 relaxation time constants. Values of T1 and T2 were determined for P3Cu and P32H using the inversion-recovery and Carr–Purcell–Meiboom–Gill (CPMG) sequences, respectively.53 As expected, analysis of the data for the signals a–j in P32H shows little variation; the T1 times are in the range 2–3 s (Fig. 3a) and the T2 times are 0.05–0.78 s (see ESI, Fig. S36†). These values fall in the range expected for molecules of this size and reflect the local environment of the protons within the molecule. As a result of the paramagnetic copper center, P3Cu has considerably shorter relaxation times; T1 = 0.10–1.12 s (Fig. 3b) and T2 = 0.005–0.083 s for signals a–j (see ESI, Fig. S36†). Many factors contribute to relaxation rates, but a clear trend is observed when comparing oligomers with and without copper. The relaxation rates are considerably faster for P3Cu than for P32H indicating that all protons are affected by the copper center. Additionally, the relaxation rates are noticeably greater for the signals in closer spatial proximity to the copper center in P3Cu, allowing us to estimate the relative distances between the protons and the copper center based on their relaxation times. The difference in relaxation rate R1 between protons in P3Cu and P32H can be defined as ΔR1 according to eqn (1).
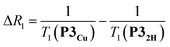 | (1) |
Dipolar relaxation rates are expected to depend on the inverse 6th power of the distance between two magnetic dipoles, eqn (2).54
 | (2) |
Fig. 3c shows a plot of the experimental values of ΔR1 against the distance (r) between the copper center and the corresponding proton, estimated from crystal structures of similar oligomers.55 The good fit to eqn (2) confirms the expected distance dependence and shows that changes in T1 relaxation rate can be used to gain structural information.
The NMR spectra of the porphyrin pentamer P5Cu are more complicated than those of P3Cu, because there are twice as many zinc porphyrin environments (see ESI, Section S3†). Protons further from the copper center give rise to sharp signals, but many of the signals overlap so T1 and T2 were not measured for these oligomers.
Quantification of the Cu–porphyrin pyridine interaction
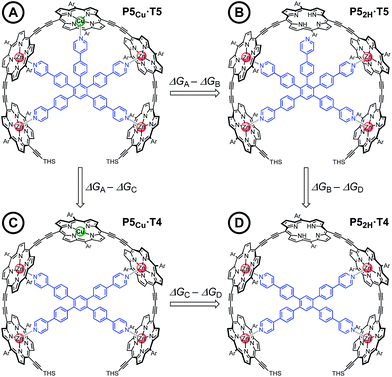
Chemical double-mutant cycles (DMCs) are a way to probe weak, non-covalent interactions by utilizing the cooperative binding effect of stronger neighboring interactions.41,56 This approach allows one to disentangle the free energy contribution due to chelate cooperativity associated with the formation of intramolecular non-covalent interactions. We envisioned that we could utilize the cooperative binding effect of the four zinc porphyrins in P5Cu to force the copper center to interact with the template and determine its contribution to the binding strength. The DMC illustrated in Fig. 4 quantifies and eliminates all secondary and allosteric effects associated with single mutations and provides a measure of the free energy benefit associated with the Cu⋯N interaction by comparing the affinities of T4 and T5 for P52H and P5Cu.Simply comparing the stabilities of P5Cu·T5 and P52H·T5 (complexes A and B respectively) would give an estimate of the energy of the Cu⋯N interaction, but this approach could lead to false conclusions because a mutation in one part of the molecule (P5Cu → P52H) may influence other interactions; for example, a free-base porphyrin might be more flexible than a copper porphyrin, which would add to the stability of P52H·T5, or there might be a contact between the pyridine ligand and the free-base porphyrin which could destabilize P52H·T5. Similar issues apply to a simple comparison of complexes A and C, where a single mutation is made in the ligand (T5 → T4). The DMC approach overcomes these problems by cancelling the secondary free energy effects of the mutations in a pairwise fashion in the thermodynamic cycle.41 The cycle is completed by probing the stability of complex D (P52H·T4), in which both the copper center and the central binding leg are removed.
The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes shown in Fig. 4 were generated by titrating solutions of the corresponding porphyrin pentamers dissolved in chloroform with the ligands T5 or T4. These UV-vis-NIR titrations gave sharp end points, and the complexes are too stable for their formation constants to be determined directly from their formation curves. Therefore, denaturation titrations were performed to determine the formation constant Kfvia the denaturation constant Kdn.14,15,57 A large excess of pyridine was titrated into solutions of the 1
1 complexes shown in Fig. 4 were generated by titrating solutions of the corresponding porphyrin pentamers dissolved in chloroform with the ligands T5 or T4. These UV-vis-NIR titrations gave sharp end points, and the complexes are too stable for their formation constants to be determined directly from their formation curves. Therefore, denaturation titrations were performed to determine the formation constant Kfvia the denaturation constant Kdn.14,15,57 A large excess of pyridine was titrated into solutions of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes (ca. 10−6 M in CHCl3 at 298 K) to displace the multidentate ligands. Our analysis assumes that the denaturation processes are essentially all-or-nothing two state equilibria (i.e. that intermediate partially denatured species do not build up to significant concentration). This assumption is supported by the isosbestic nature of the UV-vis-NIR titrations and by the good fits of the curves to the calculated binding isotherm for a two-state equilibrium (Fig. 5). Denaturation constants were used to calculate the formation constants Kf using eqn (3):
1 complexes (ca. 10−6 M in CHCl3 at 298 K) to displace the multidentate ligands. Our analysis assumes that the denaturation processes are essentially all-or-nothing two state equilibria (i.e. that intermediate partially denatured species do not build up to significant concentration). This assumption is supported by the isosbestic nature of the UV-vis-NIR titrations and by the good fits of the curves to the calculated binding isotherm for a two-state equilibrium (Fig. 5). Denaturation constants were used to calculate the formation constants Kf using eqn (3):
 | (3) |
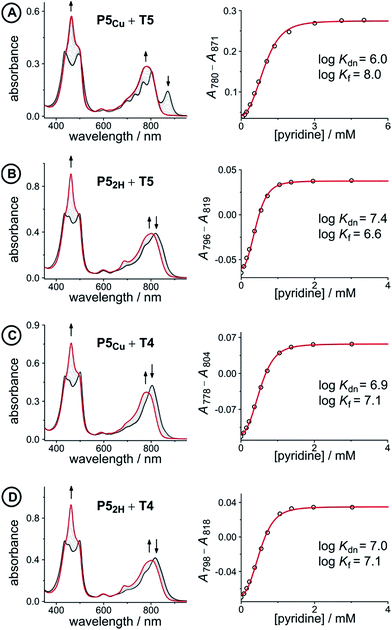 | ||
Fig. 5 UV-vis-NIR denaturation titrations of linear porphyrin oligomer complexes with templates T4 and T5 (all in CHCl3 at 298 K). The spectra shown on the left are those of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes (black) and the end spectra of the pyridine-saturated oligomers (red). On the right the experimental (black circles) and calculated binding isotherms (red lines) are shown. All titrations were performed at least twice (see ESI, Section S1.2†). 1 complexes (black) and the end spectra of the pyridine-saturated oligomers (red). On the right the experimental (black circles) and calculated binding isotherms (red lines) are shown. All titrations were performed at least twice (see ESI, Section S1.2†). | ||
The denaturation titrations of the complexes with pyridine are illustrated in Fig. 5 and the results are summarized in Table 1. The absorption spectra of the complexes with multidentate ligands are more red-shifted (black lines) than the final spectra (red lines) in which the complex is completely denaturated. The observed red-shift is caused by the more rigid structures and reduced porphyrin–porphyrin dihedral angles in the template complexes, compared to the free oligomers. The absorption spectrum of the template complex P5Cu·T5 (A) clearly reveals more structure in the Q-bands compared to P52H·T5 (B), P5Cu·T4 (C), and P52H·T4 (D), which is further evidence for the interaction of the copper center with the template. Binding to T5 locks every porphyrin unit in P5Cu into position and the rotational freedom of the central copper porphyrin is lost, giving rise to the observed characteristic fine structure in the absorption spectrum. In the complexes P52H·T5 (B), P5Cu·T4 (C), and P52H·T4 (D), motion of the central porphyrin is less restricted resulting in a broader absorption band. The spectral changes observed in the denaturation of complexes B–D are similar because in all cases there is no interaction between the central porphyrin and the template.
| Complex (X) | K dn (M−3) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kf(X) Kf(X) |
ΔGX (kJ mol−1) |
|---|---|---|---|
| P5Cu·T5 (A) | 9.1 ± 2.0 × 105 | 8.0 ± 0.1 | −35.6 ± 0.3 |
| P52H·T5 (B) | 2.4 ± 0.3 × 107 | 6.6 ± 0.1 | −29.2 ± 0.2 |
| P5Cu·T4 (C) | 8.1 ± 0.3 × 106 | 7.1 ± 0.1 | −30.2 ± 0.2 |
| P52H·T4 (D) | 9.0 ± 0.3 × 106 | 7.0 ± 0.1 | −29.9 ± 0.2 |
The stability constants of complex P5Cu·T4 (C) and P52H·T4 (D) are nearly identical, indicating that there is no inductive effect on the binding interaction due to the presence of copper and that the flexibility of copper and free-base porphyrins are comparable. A slightly lower stability constant is found for complex P52H·T5 (B), which might reflect steric repulsion of the central template leg with the central free-base unit of the oligomer. The formation constant of the complex P5Cu·T5 (A) is roughly an order of magnitude higher than the others, due to interaction of the copper center with the template.
The energy of the copper–pyridine interaction (ΔΔGCu) was calculated from eqn (4):
| ΔΔGCu = ΔGA − ΔGB − ΔGC + ΔGD | (4) |
 | (5) |
Analysis of these data reveals that the energy of interaction between the copper center and the template is ΔΔGCu = −6.2 ± 0.4 kJ mol−1. This interaction energy is substantially less than the energy of the copper porphyrin pyridine interaction from DFT calculation (56.6 kJ mol−1, Fig. 2), which is not surprising as the DFT calculations do not take account of solvation. The free energy changes associated with single mutations ΔGA − ΔGB = −6.4 ± 0.3 kJ mol−1 and ΔGA − ΔGC = −5.4 ± 0.3 kJ mol−1 differ significantly from the value from the double-mutant cycle, showing the benefit of the DMC approach. Its use in this system provided clearer insights into the weak binding interaction than would have been achieved from single mutations.
The free energy term ΔΔGCu = −6.2 ± 0.4 kJ mol−1 is an estimate of the enthalpy of the copper–pyridine interaction, because it is measured in a situation where the loss of translational entropy of bringing together two molecules has already been paid, and the interaction probed by the DMC is effectively intramolecular. In general, the entropy cost of bringing two molecules together to form a non-covalent complex in solution at 298 K contributes approximately −TΔS ≈ +6 kJ mol−1 to ΔG,60,61 which would correspond to a free energy for a bimolecular copper porphyrin pyridine interaction of ΔGCu ≈ 0 (i.e. K ≈ 1 M−1). However there are reports that the coordination of pyridine to a metalloporphyrin is more entropically unfavorable which would explain the very weak association constant.40,62
When two molecules bind together through more than one point of interaction, the increased stability resulting from chelate cooperativity can be quantified by the effective molarity (EM).57,63 Comparison of the stability constants of P5Zn·T5 (Kchem = 1.1 ± 0.2 × 1012 M−1) with those of P52H·T5 (Kchem = 1.3 ± 0.2 × 105 M−1) and P1Zn with 4-phenylpyridine (Kchem = 2.1 ± 0.1 × 103 M−1) indicates that the effective molarity of the central Zn–N interaction in P5Zn·T5 is EM = 4 ± 1 × 103 M (see ESI, Section S1.3†). If we assume that the effective molarity is the same for the central Cu–N interaction in P5Cu·T5, then the single-site microscopic binding constant for copper porphyrins to pyridyl ligands, KCu, can be estimated by dividing the observed equilibrium constant (ΔΔGCu = −6.2 kJ mol−1 ⇒ KCuEM = 12) by the effective molarity, giving KCu = 3.1 × 10−3 M−1. This value illustrates how a high effective molarity enables very weak interactions to be measured.
Conclusions
We have demonstrated that linear porphyrin oligomers can be prepared containing a central free-base porphyrin unit and zinc at the other sites. The free-base porphyrin can be metallated with copper(II), without transmetallation at the zinc centers, to prepare heterometallated linear oligomers, which are precursors to mixed-metal nanorings.1H NMR spectroscopy can be used to gain structural information on porphyrin oligomers containing paramagnetic copper(II) centers. While the signals corresponding to protons in close proximity to the copper are broadened to the extent that they can no longer be observed, protons further from the copper are well resolved. The changes in proton relaxation rate constants (R1 = 1/T1) due to the presence of the copper center depend on the inverse 6th power to the distance, providing information on the molecular geometry.
The axial binding interaction between a copper porphyrin and pyridine can be quantified with the help of a chemical double-mutant cycle, revealing that the energy of the Cu⋯N interaction is ΔΔGCu = −6.2 ± 0.4 kJ mol−1. It is tempting to compare this energy with that for coordination of pyridine to a zinc porphyrin monomer (ΔGZn = −20.0 ± 0.2 kJ mol−1 for P1Zn in CHCl3 at 298 K). However such a comparison is misleading because ΔGZn includes the loss of translational entropy associated with bringing two molecules together, whereas ΔΔGCu is measured in a situation where the interaction is effectively intramolecular with a high effective molarity.
The heterometallated porphyrin nanoring complexes c-P6Cu2·T6 and c-P10Cu2·(T5)2 have been prepared by template-directed synthesis. The molecular geometry and metal ligand interactions in the nanoring c-P10Cu2 have been investigated using EPR, the results of this study are presented in an accompanying paper.35
Acknowledgements
We thank the EPSRC and the European Research Council (grant 320969) for support, and the EPSRC UK Mass Spectrometry Facility at Swansea University for mass spectra. We are grateful to Prof. John E. McGrady for valuable discussion.Notes and references
- K. S. Chichak, S. J. Cantrill, A. R. Pease, S.-H. Chiu, G. W. V. Cave, J. L. Atwood and J. F. Stoddart, Science, 2004, 304, 1308 CrossRef CAS PubMed.
- K. Suzuki, S. Sato and M. Fujita, Nat. Chem., 2010, 2, 25 CrossRef CAS PubMed.
- J. Guo, P. C. Mayers, G. A. Breault and C. A. Hunter, Nat. Chem., 2010, 2, 218 CrossRef CAS PubMed.
- J. B. Beves, B. A. Blight, C. J. Campbell, D. A. Leigh and R. T. McBurney, Angew. Chem., Int. Ed., 2011, 50, 9260 CrossRef CAS PubMed.
- (a) S. Anderson, H. L. Anderson and J. K. M. Sanders, Acc. Chem. Res., 1993, 26, 469 CrossRef CAS; (b) D. W. J. McCallien and J. K. M. Sanders, J. Am. Chem. Soc., 1995, 117, 6611 CrossRef CAS.
- J. Li, A. Ambroise, S. I. Yang, J. R. Diers, J. Seth, C. R. Wack, D. F. Bocian, D. Holten and J. S. Lindsey, J. Am. Chem. Soc., 1999, 121, 8927 CrossRef CAS.
- S. Rucareanu, A. Schuwey and A. Gossauer, J. Am. Chem. Soc., 2006, 128, 3396 CrossRef CAS PubMed.
- (a) P. C. M. van Gerven, J. A. A. W. Elemans, J. W. Gerritsen, S. Speller, R. J. M. Nolte and A. E. Rowan, Chem. Commun., 2005, 3535 RSC; (b) R. Wakabayashi, Y. Kubo, O. Hirata, M. Takeuchi and S. Shinkai, Chem. Commun., 2005, 5742 RSC; (c) K.-T. Youm, S. T. Nguyen and J. T. Hupp, Chem. Commun., 2008, 3375 RSC; (d) J. Taesch, V. Heitz, F. Topic and K. Rissanen, Chem. Commun., 2012, 48, 5118 RSC.
- (a) M. Hoffmann, C. J. Wilson, B. Odell and H. L. Anderson, Angew. Chem., Int. Ed., 2007, 46, 3122 CrossRef CAS PubMed; (b) M. Hoffmann, J. Kärnbratt, M.-H. Chang, L. M. Herz, B. Albinsson and H. L. Anderson, Angew. Chem., Int. Ed., 2008, 47, 4993 CrossRef CAS PubMed; (c) J. K. Sprafke, D. V. Kondratuk, M. Wykes, A. L. Thompson, M. Hoffmann, R. Drevinskas, W.-H. Chen, C. K. Yong, J. Kärnbratt, J. E. Bullock, M. Malfois, M. R. Wasielewski, B. Albinsson, L. M. Herz, D. Zigmantas, D. Beljonne and H. L. Anderson, J. Am. Chem. Soc., 2011, 133, 17262 CrossRef CAS PubMed.
- M. C. O'Sullivan, J. K. Sprafke, D. V. Kondratuk, C. Rinfray, T. D. Claridge, A. Saywell, M. O. Blunt, J. N. O'Shea, P. H. Beton, M. Malfois and H. L. Anderson, Nature, 2011, 469, 72 CrossRef PubMed.
- B. Zhu, H. Chen, W. Lin, Y. Ye, J. Wu and S. Li, J. Am. Chem. Soc., 2014, 136, 15126 CrossRef CAS PubMed.
- S. Liu, D. V. Kondratuk, S. A. L. Rousseaux, G. Gil-Ramírez, M. C. O'Sullivan, J. Cremers, T. D. W. Claridge and H. L. Anderson, Angew. Chem., Int. Ed., 2015, 54, 5355 CrossRef CAS PubMed.
- P. Neuhaus, A. Cnossen, J. Q. Gong, L. M. Herz and H. L. Anderson, Angew. Chem., Int. Ed., 2015, 54, 7344 CrossRef CAS PubMed.
- S. A. L. Rousseaux, J. Q. Gong, R. Haver, B. Odell, T. C. W. Claridge, L. M. Herz and H. L. Anderson, J. Am. Chem. Soc., 2015, 137, 12713 CrossRef CAS PubMed.
- L. Favereau, A. Cnossen, J. B. Kelber, J. Q. Gong, R. M. Oetterli, J. Cremers, L. M. Herz and H. L. Anderson, J. Am. Chem. Soc., 2015, 137, 14256 CrossRef CAS PubMed.
- C.-K. Yong, P. Parkinson, D. V. Kondratuk, W.-H. Chen, A. Stannard, A. Summerfield, J. K. Sprafke, M. C. O'Sullivan, P. H. Beton, H. L. Anderson and L. M. Herz, Chem. Sci., 2015, 6, 181 RSC.
- C. E. Tait, P. Neuhaus, M. D. Peeks, H. L. Anderson and C. R. Timmel, J. Am. Chem. Soc., 2015, 137, 8284 CrossRef CAS PubMed.
- J. A. Cowan and J. K. M. Sanders, J. Chem. Soc., Chem. Commun., 1985, 1213 RSC.
- (a) A. M. Brun, A. Harriman, V. Heitz and J.-P. Sauvage, J. Am. Chem. Soc., 1991, 113, 8657 CrossRef CAS; (b) A. Harriman, V. Heitz and J.-P. Sauvage, J. Phys. Chem., 1993, 97, 5940 CrossRef CAS.
- J. Fortage, J. Boixel, E. Blart, L. Hammarström, H. C. Becker and F. Odobel, Chem.–Eur. J., 2008, 14, 3467 CrossRef CAS PubMed.
- R. L. Brookfield, H. Ellul and A. Harriman, J. Chem. Soc., Faraday Trans. 2, 1985, 81, 1837 RSC.
- V. V. Borovkov, J. M. Lintuluoto and Y. Inoue, Helv. Chim. Acta, 1999, 82, 919 CrossRef CAS.
- (a) M. Asano-Someda, A. van der Est, U. Krüger, D. Stehlik, Y. Kaizu and H. Levanon, J. Phys. Chem. A, 1999, 103, 6704 CrossRef CAS; (b) N. Toyama, M. Asano-Someda, T. Ichino and Y. Kaizu, J. Phys. Chem. A, 2000, 104, 4857 CrossRef.
- M. Speckbacher, L. Yu and J. S. Lindsey, Inorg. Chem., 2003, 42, 4322 CrossRef CAS PubMed.
- J. Fortage, A. Scarpaci, L. Viau, Y. Pellegrin, E. Blart, M. Falkenström, L. Hammarström, I. Asselberghs, R. Kellens, W. Libaers, K. Clays, M. P. Eng and F. Odobel, Chem.–Eur. J., 2009, 15, 9058 CrossRef CAS PubMed.
- (a) A. Vidal-Ferran, N. Bampos and J. K. M. Sanders, Inorg. Chem., 1997, 36, 6117 CrossRef CAS PubMed; (b) S. J. Webb and J. K. M. Sanders, Inorg. Chem., 2000, 39, 5912 CrossRef CAS PubMed.
- (a) T. Fujihara, K. Tsuge, Y. Sasaki, Y. Kaminaga and T. Imamura, Inorg. Chem., 2002, 41, 1170 CrossRef CAS PubMed; (b) P. D. Harvey, N. Proulx, G. Martin, M. Drouin, D. J. Nurco, K. M. Smith, F. Bolze, C. P. Gros and R. Guilard, Inorg. Chem., 2001, 40, 4134 CrossRef CAS PubMed.
- S. Rucareanu, O. Mongin, A. Schuwey, N. Hoyler and A. Gossauer, J. Org. Chem., 2001, 66, 4973 CrossRef CAS PubMed.
- (a) D. Kim, D. Holten and D. Gouterman, J. Am. Chem. Soc., 1984, 106, 2793 CrossRef CAS; (b) M. Asano, Y. Kaizu and H. Kobayashi, J. Chem. Phys., 1988, 89, 6567 CrossRef CAS.
- F. Liu, K. L. Cunningham, W. Uphues, G. W. Fink, J. Schmolt and D. R. McMillin, Inorg. Chem., 1995, 34, 2015 CrossRef CAS.
- G. Szintay and A. Horváth, Inorg. Chim. Acta, 2001, 324, 278 CrossRef CAS.
- T. Nguyen, P. Hakansson, R. Edge, D. Collison, B. A. Goodman, J. R. Burns and E. Stultz, New J. Chem., 2014, 38, 5254 RSC.
- (a) G. Jeschke, ChemPhysChem, 2002, 3, 927 CrossRef CAS PubMed; (b) G. Jeschke and Y. Polyhach, Phys. Chem. Chem. Phys., 2007, 9, 1895 RSC.
- (a) J. S. Becker and S. Saxena, Chem. Phys. Lett., 2005, 414, 248 CrossRef CAS; (b) Z. Yang, D. Kise and S. Saxena, J. Phys. Chem. B, 2010, 114, 6165 CrossRef CAS PubMed; (c) A. M. Bowen, M. W. Jones, J. E. Lovett, T. G. Gaule, M. J. McPherson, J. R. Dilworth, C. R. Timmel and J. R. Harmer, Phys. Chem. Chem. Phys., 2016, 18, 5981 RSC.
- S. Richert, J. Cremers, H. L. Anderson and C. R. Timmel, Chem. Sci., 2016 10.1039/C6SC01810F.
- J. R. Miller and G. D. Dorough, J. Am. Chem. Soc., 1952, 74, 3977 CrossRef CAS.
- (a) R. J. Abraham, P. Leighton and J. K. M. Sanders, J. Am. Chem. Soc., 1985, 107, 3472 CrossRef CAS; (b) I. Tabushi, S. Kugimiya, M. G. Kinnaird and T. Sasaki, J. Am. Chem. Soc., 1985, 107, 4192 CrossRef CAS; (c) I. Beletskaya, V. S. Tyurin, A. Y. Tsivadze, R. Guilard and C. Stern, Chem. Rev., 2009, 109, 1659 CrossRef CAS PubMed; (d) S. Durot, J. Taesch and V. Heitz, Chem. Rev., 2014, 114, 8542 CrossRef CAS PubMed.
- (a) F. A. Cotton and G. W. Wilkinson, Advanced Inorganic Chemistry, 5th edn, Wiley, New York, 1988 Search PubMed; (b) N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, 2nd edn, Elsevier, London, 1997 Search PubMed.
- P. Hambright, Chem. Commun., 1967, 470 RSC.
- (a) G. Szintay, A. Horváth and G. Grampp, J. Photochem. Photobiol., A, 1999, 126, 83 CrossRef CAS; (b) G. Szintay and A. Horváth, Inorg. Chim. Acta, 2001, 324, 278 CrossRef CAS.
- (a) S. L. Cockroft and C. A. Hunter, Chem. Soc. Rev., 2007, 36, 172 RSC; (b) A. Camara-Campos, D. Musumeci, C. A. Hunter and S. Turega, J. Am. Chem. Soc., 2009, 131, 18518 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119 CrossRef CAS.
- (a) S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS PubMed; (b) S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- S. Lipstman and I. Goldberg, Cryst. Growth Des., 2010, 10, 4596 CAS.
- Crystal structures have been reported of a copper porphyrin radical cation M. W. Renner, K. M. Barkigia and J. Fajer, Inorg. Chim. Acta, 1997, 263, 181 CrossRef CAS and of two copper porphyrins with 6-coordinate Cu(II) atoms B. Zimmer, M. Hutin, V. Bulach, M. W. Hosseini, A. De Cian and N. Kyritsakas, New J. Chem., 2002, 26, 1532 RSC.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380 CrossRef.
- R. W. Wagner, T. E. Johnson, F. Li and J. S. Lindsey, J. Org. Chem., 1995, 60, 5266 CrossRef CAS.
- G. M. Godziela and H. M. Goff, J. Am. Chem. Soc., 1986, 108, 2237 CrossRef CAS PubMed.
- M. W. Renner, K. M. Barkigia, Y. Zhang, C. J. Medforth, K. M. Smith and J. Fajer, J. Am. Chem. Soc., 1994, 116, 8582 CrossRef CAS.
- K. E. Schwarzhans, Angew. Chem., Int. Ed., 1970, 9, 946 CrossRef CAS.
- T. D. W. Claridge, High-Resolution NMR Techniques in Organic Chemistry, 2nd edn, Elsevier Science, Oxford, 2009 Search PubMed.
- (a) J. Koehler and J. Meiler, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 59, 360 CrossRef CAS PubMed; (b) I. Bertini, C. Luchinat and G. Parigi, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 40, 249 CrossRef CAS; (c) I. Bertini, C. Luchinat, G. Parigi and R. Pierattelli, ChemBioChem, 2005, 6, 1536 CrossRef CAS PubMed.
- P. N. Taylor, J. Huuskonen, G. Rumbles, R. T. Aplin, E. Williams and H. L. Anderson, Chem. Commun., 1998, 909 RSC.
- (a) H. Sun, C. A. Hunter and E. M. Llamas, Chem. Sci., 2015, 6, 1444 RSC; (b) H. Sun, C. A. Hunter, C. Navarro and S. Turega, J. Am. Chem. Soc., 2013, 135, 13129 CrossRef CAS PubMed.
- H. J. Hogben, J. K. Sprafke, M. Hoffmann, M. Pawlicki and H. L. Anderson, J. Am. Chem. Soc., 2011, 133, 20962 CrossRef CAS PubMed.
- The analysis of the titration of P5Cu·T5 with pyridine in terms of eqn (3) assumes that coordination of pyridine to the copper porphyrin center in P5Cu·T5 does not significantly contribute to its denaturation, which is valid since copper porphyrins show negligible binding to pyridine at a concentration of 6 mM in CHCl3 at 298 K.
-
K
σ = 64 for P5Cu·T4 and P52H·T4; T5 has a lower symmetry than T4 resulting in Kσ = 32 for P52H·T5; the rotational freedom of the central porphyrin in P5Cu·T5 is lost due to template binding, giving Kσ = 64. Analysis of the DMC in Fig. 4 without considering statistical factors would change ΔΔGCu by RT
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to −7.9 kJ mol−1.
2 to −7.9 kJ mol−1. - C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310 CrossRef CAS PubMed.
- D. H. Williams, E. Stephens, D. P. O'Brien and M. Zhou, Angew. Chem., Int. Ed., 2004, 43, 6596 CrossRef CAS PubMed.
- (a) S. J. Cole, G. C. Curthoys, E. A. Magnusson and J. N. Phillips, Inorg. Chem., 1972, 11, 1024 CrossRef CAS; (b) G. C. Vogel and J. R. Stahlbush, Inorg. Chem., 1977, 16, 950 CrossRef CAS; (c) F. A. Walker and M. Benson, J. Am. Chem. Soc., 1980, 102, 5530 CrossRef CAS; (d) G. Szintay and A. Horváth, Inorg. Chim. Acta, 2000, 310, 175 CrossRef CAS.
- (a) C. A. Hunter and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 7488 CrossRef CAS PubMed; (b) G. Ercolani and L. Schiaffino, Angew. Chem., Int. Ed., 2011, 50, 1762 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and characterization of new compounds, UV-vis-NIR titrations and binding data for reference compounds and for the formation of linear oligomer complexes, error analysis and calculation of statistical factors. See DOI: 10.1039/c6sc01809b |
| This journal is © The Royal Society of Chemistry 2016 |