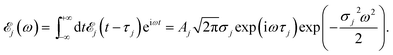Open Access Article
Open Access ArticleStudy of double core hole excitations in molecules by X-ray double-quantum-coherence signals: a multi-configuration simulation†
Weijie
Hua
 ab,
Kochise
Bennett
a,
Yu
Zhang
a,
Yi
Luo
bc and
Shaul
Mukamel
*a
ab,
Kochise
Bennett
a,
Yu
Zhang
a,
Yi
Luo
bc and
Shaul
Mukamel
*a
aDepartment of Chemistry, University of California, Irvine, CA 92697-2025, USA. E-mail: smukamel@uci.edu
bDepartment of Theoretical Chemistry and Biology, School of Biotechnology, KTH Royal Institute of Technology, S-10691 Stockholm, Sweden
cHefei National Laboratory for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei, Anhui 230026, China
First published on 12th May 2016
Abstract
The multi-configurational self-consistent field method is employed to simulate the two-dimensional all-X-ray double-quantum-coherence (XDQC) spectroscopy, a four-wave mixing signal that provides direct signatures of double core hole (DCH) states. The valence electronic structure is probed by capturing the correlation between the single (SCH) and double core hole states. The state-averaged restricted-active-space self-consistent field (SA-RASSCF) approach is used which can treat the valence, SCH, and DCH states at the same theoretical level, and applies to all types of DCHs (located on one or two atoms, K-edge or L-edge), with both accuracy and efficiency. Orbital relaxation introduced by the core hole(s) and the static electron correlation is properly accounted for. The XDQC process can take place via different intermediate DCH state channels by tuning the pulse frequencies. We simulate the XDQC signals for the three isomers of aminophenol at 8 pulse frequency configurations, covering all DCH pathways involving the N1s and O1s core hole (N1sN1s, O1sO1s and N1sO1s), which reveal different patterns of valence excitations.
Introduction
X-ray spectroscopies of core level electronic excitations serve as efficient tools in characterizing chemical and electronic structures, thanks to their element selectivity and high sensitivity.1 With recent development of X-ray laser technology, bright and ultrashort pulses can be generated by the X-ray free electron laser (XFEL)2 and high harmonic generation (HHG) tabletop3 sources. This opens up all-X-ray nonlinear spectroscopy which provides higher level of information compared to linear absorption and emission. Various nonlinear X-ray spectroscopies have been proposed and realized experimentally.4–11 All-X-ray four-wave-mixing (FWM) signals require high intensity light sources. Very recently, FEL-based FWM experimental setup at the extreme ultraviolet (EUV) and soft X-ray regions has been reported,12 and signals stimulated by EUV transient gratings had been measured.13Two-dimensional (2D) X-ray double-quantum-coherence (XDQC) is a promising FWM technique.5,14,15 Sequences of pulses are used to probe the valence structure by capturing the correlation between single (SCH) and double core hole (DCH) excited states [note that here SCH/DCH denote excited states of neutral molecules rather than SCH/DCH ionized states (i.e., cations)]. The signal is generated in the kIII = k1 + k2 − k3 direction, with k1, k2, and k3 the wave vectors of the three incident pulses in chronological order. This technique was originally developed in NMR and has been successfully applied to elucidate the coupling of two nuclei. It was then extended to the infrared and visible regimes.16 Theoretical studies on the X-ray analogue are thus required to explore its potential and performance, help interpret the signals and understand the underlying chemistry.
Double vacancies in core orbitals were studied theoretically by Cederbaum et al.18,19 in the 1980s and the extreme sensitivity of chemical shifts of the DCH ionized states was found. In recent years, inner-shell double photo-ionization attracted much attention by researchers. Experiments were performed for inert gases20–22 and small molecules [CO, CO2, N2, N2O, H2O, NH3, CH4, C6H6, C2H2n (n = 1–3), H2S, SO2, CS2, aminophenols, etc.] in the gas phase based on third-generation synchrotron and newly developed XFEL light sources,23–36 see ref. 37 and 38 for recent reviews. A double core-hole in a molecule can reside on the same atom (single-site or 1-site DCH) or on two different atoms (two-site or 2-site DCH). The double core vacancy can be generated by sequential absorption of two X-ray photons or simultaneously by one photon. With EUV or hard X-ray FEL lasers, multiple X-ray ionization atoms can be prepared and highly charged Xe and fully-stripped Ne cations were observed.20,21 Instead of ionization to continuum, one or two of the K-shell core electrons can also be excited to the unoccupied molecular orbitals.23,30,31,33,39 DCH excitations of 1s2s or 1s2p core electrons to unoccupied levels had been observed in SiX4 (X = H, F, Cl, Br, CH3) molecules.40 Extensive simulations on molecular DCH states were carried out mainly using the restricted-active-space self-consistent field (RASSCF) method23,27,28,35,41,42 and the many-body Green's function based algebraic diagrammatic construction (ADC) method truncated at different orders.18,26,43 Other approaches include the density functional theory (DFT),5,26,32,34 time-dependent DFT (TDDFT),15 second-order Møller–Plesset (MP2),25 MP4SDQ,44 Configuration Interaction with singles and doubles (CISD),33 and multi-reference CI (MRCI)26 methods. Methods for core hole states and X-ray spectra such as DCH states are reviewed in ref. 8.
The experimental setup for XDQC signal is schematically shown in Fig. 1. We use g, e/e′, and f to denote the ground, SCH, and DCH states, respectively. The ground state energy is set as 0. The two contributing terms to this signal are given by loop diagrams shown in Fig. 1c. During the interaction with the first two pulses k1 and k2, the molecular density matrix is promoted from the ground state population to the ground–SCH coherence, and then to the ground–DCH coherence, i.e.,  . This holds the same for both diagrams. The third pulse k3 then sets the system to be in ρe′g or ρfe′ coherence (diagrams A and B respectively) during the final propagation time. Making the rotating wave approximation (RWA)45 for all interactions between the electromagnetic field and molecule, the field frequency and molecule excitation frequency have opposite signs (expressions for signals are given in the Appendix). Thus, by tuning the central carrier frequencies of the four pulses ω1–ω4 to match the ground–SCH or SCH–DCH transitions energies, various excitations are probed as resonances in XDQC signals.
. This holds the same for both diagrams. The third pulse k3 then sets the system to be in ρe′g or ρfe′ coherence (diagrams A and B respectively) during the final propagation time. Making the rotating wave approximation (RWA)45 for all interactions between the electromagnetic field and molecule, the field frequency and molecule excitation frequency have opposite signs (expressions for signals are given in the Appendix). Thus, by tuning the central carrier frequencies of the four pulses ω1–ω4 to match the ground–SCH or SCH–DCH transitions energies, various excitations are probed as resonances in XDQC signals.
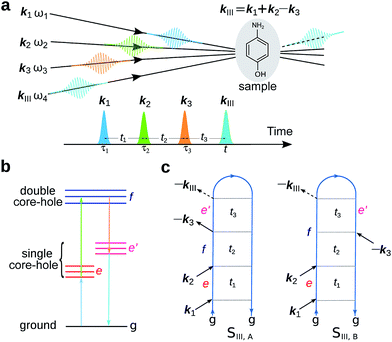 | ||
| Fig. 1 Setup for the X-ray double-quantum-coherence signal measurement. (a) Pulse sequence. (b) Molecular energy level scheme. g, e/e′, and f denote the ground, single, and double core-hole states, respectively. For instance, when f is a N1sO1s DCH state, e/e′ can be either a N1s or O1s SCH state; when f is a N1sN1s DCH state, e/e′ refers to a N1s SCH state. (c) Two contributing loop diagrams. Both diagrams show a wavefunction evolution pathway of g → e → f → e′ → g (see ref. 17 for diagram rules). | ||
The challenge of XDQC signal simulations lies in computing valence, SCH and DCH excited states with both accuracy and efficiency, and the corresponding transition dipole moments (TDMs) for valence–SCH and SCH–DCH state pairs.8 Previous signal calculations5,15 only considered the 2-site DCH states at the DFT level. The earlier work5 treated the two core holes by using the equivalent core hole (ECH) approximation (also known as the Z + 1 approximation).46 Within this approximation, the core excited atom is replaced by the next element in the periodic table while the number of electrons remains unchanged. This approximation can adequately describe deep 1s core excited states, in good agreement with experimental K-edge X-ray absorption spectra [XAS, i.e., X-ray absorption near edge structure (XANES) or near-edge X-ray fine-structure (NEXAFS)] of various large molecules and materials (see ref. 47 and references therein). When both core holes are treated by the ECH approximation, calculation of DCH states is turned into a ground-state-like, single-determinant problem of the di-cation.5 This holds the simplest level of theory to describe DCH-related signals and is limited only for 2-site DCHs on the 1s orbitals. The ECH approximation had been combined with the linear-response TDDFT to model molecules with both a core and a valence holes, and to calculate the shake-up satellites in K-edge X-ray photoelectron spectra.48 We recently15 developed a new scheme to model the DCH states, where one of the two excited atoms is treated by the excited core hole (XCH) approximation,49 and based on this XCH reference state (Kohn–Sham single determinant) the other core hole is considered by linear response (TDDFT with restricted excitation window).50 Since unrestricted reference is used, spin contaminated states over a threshold are omitted after the calculations.51 This method treats orbital relaxation and electronic correlations better than the ECH approximation and is still practical for relatively large systems. However, treating two core holes at different levels introduces nonphysical bias as there are two possibilities in assigning the two levels. Intuitively, both core holes can be explicitly considered within this TDDFT framework. But a double core hole within a single-determinant may easily lead to SCF convergence problems and the collapse of the wavefunction to a low-energy state. More practical method is necessary to better describe double core holes.
In this work we employ the state-averaged RASSCF (SA-RASSCF) method52 for XDQC signal simulations. Within this multi-configurational approach, the two core holes (whether single or two site) are explicitly treated at the same theoretical level. Multiple configurations better describe the static electron correlation. The core hole can reside in any inner shells including the 1s levels. Using RASSCF to calculate core-excited states dated back to the 1980s study of Ågren and coworkers,41,53 where state-specific RASSCF was used for the lowest SCH and DCH states, and correlation and relaxation effects on energies were systematically analyzed. In recent years, Tashiro et al.23,42 had employed the method to calculate double ionized states and spectra of various small molecules. Calculating a manifold of core excited states requires state-averaging. The SA-RASSCF method52 has been used to calculate a series of valence and SCH states for spectroscopy use. Odelius and coworkers54 had employed RASSCF and second-order perturbation theory restricted active space (RASPT2) for L-edge XANES and resonant inelastic X-ray scattering (RIXS) spectra of transitional-metal based complexes, computations were performed for other various similar systems.11,55 Cost and sensitivity of this method have been carefully investigated.56 Hua et al.57 employed SA-RASSCF to calculate core-excited states of conical intersection structures and time-resolved stimulated X-ray Raman signals during the photo-induced furan ring-opening reaction pathway. The RASSCF method is commonly viewed as the basis for more accurate multi-configurational electron correlation methods. More accurate signals can be expected by extension, for example, using the RASPT2 method.58
We study the double core excitations of three isomers of aminophenols by XDQC signals simulated at the RASSCF level. These molecules have two strong electron-donating groups –NH2 and –OH bonded to benzene, at the para-, meta-, and ortho- (abbreviated as p-, m-, o- respectively) positions (also known as 4-, 3-, and 2-aminophenol, respectively). Aminophenols are important electrochemical materials used in dye industry,59 and the para isomer is used as a π-donor in charge transfer complexes.60 These molecules serve as simple models to demonstrate the multidimensional nonlinear X-ray signals involving double core holes4 and were employed in DCH ionization studies.26,34 We examine and compare the spectra of these isomers via different DCH pathways selected by varying the pulse frequencies. All possible DCHs created on the 1s orbitals of nitrogen and/or oxygen are considered, including 1-site DCHs on nitrogen (N1sN1s) or oxygen (O1sO1s) and 2-site DCHs on both atoms (N1sO1s).
Results and discussion
XANES
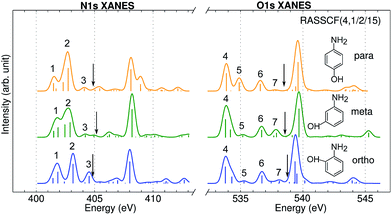
XANES spectra serve as a guide to set up the pulse parameters in XDQC, and provide a window to estimate the accuracy of the simulated XDQC signals. To calibrate our method, we also calculate the XANES spectra at the N1s and O1s edges by RASSCF with different active spaces, and compare it with various DFT methods. Two RASSCF active spaces were (6, 1/4/14) and (4, 1/2/15), where the numbers in parentheses refer to the number of electrons, and numbers of active orbitals in the RAS1, RAS2, and RAS3 space, respectively. The DFT methods include static DFT with the full core hole (FCH) and ECH approximations, and TDDFT with the Tamm–Dancoff approximation (TDA),63 all using the B3LYP functional.64Fig. 2 compares N1s and O1s XANES spectra of p-aminophenol simulated by different methods. Results show good agreement between RASSCF and DFT, which are not sensitive to the variation of the active space. Three main features appear below the ionic potentials (IP) in both edges. In Fig. 2a, the pre-shoulder peak 1 (401.6 eV) comes from the N1s → σ*N–H transitions (see orbitals in Fig. 2c). The strong peak 2 is dominated by transitions of the same type, with also contributions from the N1s → π* resonance. The separation to peak 1 differs from these approaches (in ascending order): 0.8 eV by TDDFT/TDA, 1.1 eV by the two RASSCF methods, 1.2 eV by DFT-FCH and 1.9 eV by DFT-ECH. A weak peak 3 appears at 404–405 eV, originating from the N1s → σ*N–C transition. In Fig. 2b, peaks 4, 5, 6 are assigned as O1s → σ*O–H, O1s → π*, and O1s → σ*O–C transitions, respectively. All methods give the three peaks with similar relative positions and intensities, except that peak 6 almost vanishes in TDDFT/TDA. Comparison of different levels verifies the accuracy of our RASSCF approach. To our knowledge no experimental XANES spectra of this molecule are available. The theoretical spectra [calibrated according to the ΔKohn–Sham (ΔKS) scheme61] are estimated to have ∼1–2 eV accuracy in absolute excitation energies according to our experience (for comparison of light-element K-edge XANES spectra predicted by this procedure to experiment, see, e.g., ref. 65). Our computed IPs (404.9 and 538.5 eV) compare well with previous theoretical (404.9 and 538.3 eV)26 and experimental (405.4 and 539.2 eV)34 results. Note that this work focuses on bound states (region below IP), and we used constant small hwhm in spectral broadening for better comparison of different methods. To better resolve the continuum region, a different convolution scheme66 with larger hwhm above the IP was employed and given in Fig. S1.†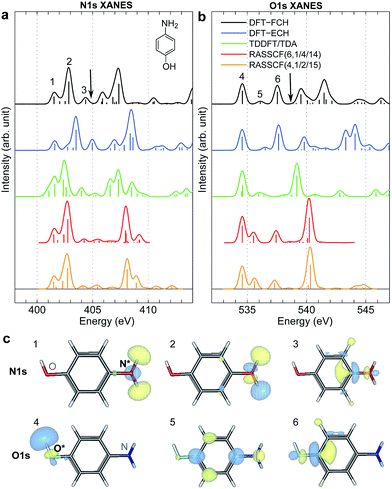 | ||
| Fig. 2 (a) N1s and (b) O1s XANES spectra of p-aminophenol simulated by different methods. Arrows mark the calculated IPs (404.9 and 538.5 eV) by the DFT-FCH method. Major peaks below IP are labeled. The DFT-FCH energies have been shifted using the ΔKohn-Sham scheme61 and scalar relativistic corrections;62 other methods were then calibrated to it by aligning the first resolved peak. Shifts applied: DFT-FCH (−5.7 and −6.7 eV for N1s and O1s spectra), DFT-ECH (−123.1, −141.2 eV), TDDFT/TDA (11.7, 13.7 eV), RASSCF (6, 1/4/14) (−3.9, −3.9 eV), RASSCF (4, 1/2/15) (−4.9, −5.1 eV). (c) DFT-ECH final-state molecular orbitals for each peak (contour isovalue = 0.08). Core excited nitrogen and oxygen are labeled by N* and O*. | ||
Fig. 3 shows the calculated N1s and O1s XANES spectra of the three aminophenol isomers at the RASSCF (4, 1/2/15) level. The spectra are very similar and show 3 main features below the IPs in both the N and O K-edges. Peak positions differ by less than 0.4 eV. Peak 3 and 5 intensities also show notable differences: peak 3 is the strongest for o-aminophenol, and peak 5 is the strongest for p-aminophenol. These fine details could be observed by high-resolution measurements.
Selection of states and pulse parameters
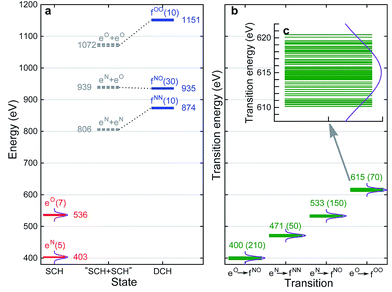
With XANES at hand, only bound SCH states (sticks up till the IPs) were considered in XDQC signal simulations, which only include several states of 3–5 eVs. We selected DCH states such that the SCH–DCH transition energies are within a 10 eV window. Each pulse frequency was set at the middle of the corresponding transition energy range. Fig. 4a and b depict these energy levels and transition energies for p-aminophenol with the indicated pulse frequencies. This include 5 N1s and 7 O1s excited states, respectively, as well as 10 N1sN1s and O1sO1s DCH states and 30 N1sO1s DCH states (all state energies given in Table S1†).To set up XDQC simulations, four pulse frequencies ω1, ω2, ω3, ω4, should be specified. These were chosen to select the desired state-to-state transition energies: two from the ground–SCH state transitions (i.e., XANES, or SCH state energies with ground state energy set as 0), and two from the SCH–DCH transitions, as can be seen from the pulse envelope factors in eqn (5) and (6). For instance, to generate N1sN1s intermediate DCH states, ω1 is tuned to the N1s resonance ω(eN), followed by the second pulse frequency ω2 to match the energy difference between N1sN1s and N1s states, ω(fNN) − ω(eN). ω3 and ω4 are then set to be ω(fNN) − ω(eN) and ω(eN) respectively to select the diagram-A pathway, or vice versa for the diagram-B pathway. Our RASSCF calculations show clear (∼68 eV) separation of the two transition energies. Therefore, only one diagram (A or B) contributes given our pulse bandwidth (∼10 eV), which simplifies the signal interpretation. The physical reason is as follows: two electrons in the same shell (N1s orbitals) have strong repulsion, so that ω(fNN) is blue shifted from twice of ω(eN). The same applies for O1sO1s intermediate DCH states, with energies ω(fOO) − ω(eO) and ω(eO) differing by ∼79 eV. The 2-site N1sO1s DCH states have much higher density of states (DOS) than others. A single diagram is also selected but for a different reason. Their energies (around 935 eV) can be estimated by adding the two corresponding SCH states (around 403 eV and 536 eV which sum to 939 eV; see Fig. 4a). A few eVs relaxation energy shows that the two core holes are weakly coupled, so that ωe′g and ωfe′ difference is approximately the N1s and O1s core orbital energy difference (∼130 eV).
We had examined 8 pulse configurations listed in Table 1. Based on the excitation sequences of the first two pulses (ω1, ω2), we classified them as ON, NO, NN, and OO to denote the SCH and DCH resonances. For example, for the ON pulse configuration, the system is excited to O1s SCH states by ω1 = 536 eV (g → eO resonance), and then to O1sN1s DCH states by ω2 = 400 eV (eO → fON resonance). ω3 and ω4 determine whether the active pathway corresponds to diagram A or B [see eqn (5) and (6)], and the full notation for pulse configuration is thus labeled as for example, ON-A. Diagram B is selected by swapping ω3 and ω4.
| Pulse configurationa,b | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω1 ω1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω2 ω2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω3 ω3 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω4 ω4 |
|---|---|---|---|---|
| a E.g., ON means that the molecule is excited to O1s SCH states by ω1 first, and then to O1sN1s DCH states by ω2. b A (or B) denotes whether the dominant pathway in Fig. 1 is diagram A or B. | ||||
| ON-A | 536 | 400 | 533 | 403 |
| NO-A | 403 | 533 | 400 | 536 |
| NN-A | 403 | 471 | 471 | 403 |
| OO-A | 536 | 615 | 615 | 536 |
XDQC signals for p-aminophenol
Fig. 5 shows the simulated XDQC signals for p-aminophenol at 8 pulse configurations, recorded versus Ω1–Ω2. As can be seen from the denominators in eqn (5) and (6), the detection windows Ω1, Ω2 and Ω3 are chosen according to the transition energy range. The Ω1–Ω2 plot directly correlates the SCH (ωeg) and DCH (ωfg) energies. Both SIII,A and SIII,B have the same detection windows. For instance, at ON-A and ON-B, the detection window Ω1 is set to [532, 539] eV according to the O1s state energies, and Ω2 set to [932, 940] eV according to the O1sN1s state energies (see respectively the denominators Ω1 − ξeg and Ω2 − ξfg in eqn (5) and (6)). ON and OO pulse configurations have the same Ω1 but different Ω2 windows ([932, 940] eV versus [1147, 1152] eV) as the O1sN1s and O1sO1s DCH states are respectively involved. While in the ON and NO set up, the same N1sO1s DCH states are reached via different paths, so they have different Ω1 windows in accordance with the O1s and N1s state energies. We find that ON, NO, NN, OO give distinct patterns of the signals at different energy regions. While diagram A or B has a weaker influence. The signals look similar, and only differ in absolute intensities. Due to this similarity, the following discussions are limited to diagram-B, while diagram-A signals (ON-A, NO-A, NN-A, OO-A) of all isomers are given in Fig. S2–S5.† Note that diagrams A and B have different Ω3 range (ωe′gversus ωfe′), so the Ω2–Ω3 plot can provide complementary information. The XDQC technique can select the most sensitive channel to map and distinguish between similar structures.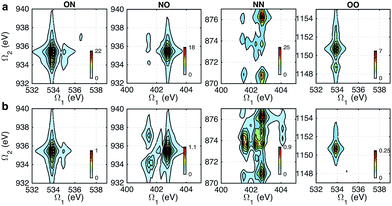 | ||
| Fig. 5 XDQC signals SIII(t3 = 6.1 fs, Ω2, Ω1) (absolute values) of p-aminophenol for 8 pulse configurations calculated at the RASSCF level. ON, NO, NN, and OO are selected by tuning pulse frequencies ω1 and ω2. ON and NO pulse configurations create two-site N1sO1s DCH states (generated via O1s and N1s SCH excited states, respectively); NN and OO generate one-site N1sN1s and O1sO1s DCH states, respectively. Different ω3 and ω4 frequency settings select either (a) diagram A or (b) diagram B (see diagrams in Fig. 1c). Both diagrams do not contribute to the same signal for our parameter regime. All pulses have duration of σ = 100 as. | ||
XDQC signals with two-site DCH intermediates for different isomers
Fig. 6 displays the simulated XDQC signals at the ON-B pulse setting, which demonstrates the sensitivity of XDQC for resolving isomers of similar structures. Panel a recaptures the calculated O1s XANES spectra for easy comparison of the peak positions. On the Ω1–Ω2 plot (Fig. 6b), the strongest peak appears at Ω1 = 534 eV in all molecules. This resonates with the g → eO1 transition (eO1 is the first O1s core excited state), and corresponds to the strong peak 4 in the XANES spectra. para-Aminophenol shows a well-separated shoulder in the region 1 eV higher, in resonance with the g → eO2 transition (peak 5 in XANES, O1s → π*). This shoulder is hardly seen in the other two isomers, consistent with their much weaker XANES peak 5 intensities. It is clear that the para isomer has more stable resonance structures or more delocalized π electrons. This feature reflects the coupling of the two groups through the π* orbitals. The meta and ortho isomers instead exhibit more diffuse patterns in this region than the para one, related to the broader, unsymmetric XANES main peak 4 (O1s → σ*OH). In addition, at Ω1 = 536.7 eV another evident feature distinguishes the 3 molecules, which strengths increased in the order of p-, m-, and o- isomers. The related XANES peak 6 shows almost the same intensity. These results illustrate that XDQC can amplify the difference seen in XANES, as the more complex signal expression enforces XDQC has a stricter selectivity than XANES. A strong peak in XDQC signal requires both relatively large values of the four transition dipole moments terms and a good match in energy. Above we have identified the dominant O1s states for each peak feature. While multiple N1sO1s core excited states contribute due to their much denser DOS, and the peaks span an energy region of Ω2 = 934–936 eV.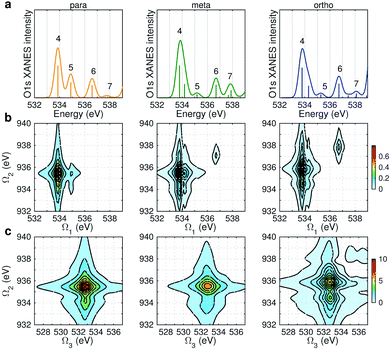 | ||
| Fig. 6 (a) Simulated O1s XANES spectra of p-, m-, and o-aminophenols (left to right) from Fig. 3. (b–c) ON-B XDQC signals (absolute values) (see Table 1 for notation): (b) SIII(t3 = 6.1 fs, Ω2, Ω1), (c) SIII(Ω3, Ω2, t1 = 0 fs). | ||
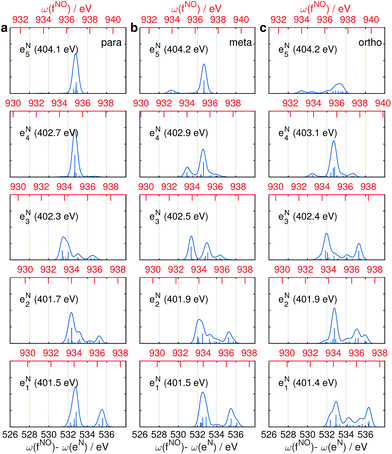
The same Ω2 region is found in the Ω2–Ω3 plot (Fig. 6c), which shows more diffuse patterns. Ω3 is related to eN → fON transition energies, and peaks fall in a narrow region around 533 eV. To further interpret the XDQC signals, we show the oscillator strengths between N1s SCH and O1sN1s DCH states in Fig. 7, which more vividly explains the peaks in XDQC signals. For each isomer, the strongest absorption happens at 533 eV (see bottom axes). For example, this applies to the four states eN1,2,4,5 in the para isomer. The corresponding DCH state energies are ca. 934 eV (eN1,2) and 936 eV (eN4,5), see top axes. The above analysis reveals the N1s states involved. The multiple contributing N1sO1s DCH states are shown by the many vertical sticks for each peak.
Fig. 8 displays signals simulated at the NO–B pulse configuration. The Ω1–Ω2 plot (panel a) reveals the correlation between N1s and N1sO1s states, which are sensitive to isomers. In the para isomer, the peaks involve double core hole states at ca. 934.2, 935.5, and 937.0 eV. Compared with signals at ON-B pulse setting (Fig. 6a), the active DCH states are not the same. The resonance with N1s states happens at 401.5 and 402.7 eV, which corresponds to peaks 1 and 2 respectively in N1s XANES (Fig. 3). The dominant N1s states are interpreted as eN1 and eN4, respectively, as clearly shown in Fig. 7a. The corresponding XANES peaks for the meta and ortho isomers are also peaks 1 and 2. The difference in XANES has been evidently enhanced. The meta isomer has broader peaks 1 and 2 (contributed from the lowest 4 states with comparable oscillator strengths), which lead to richer XDQC features than other isomers. The ortho isomer has a weak peak at Ω1 = 404.5 eV, which is absent in others. This is related to peak 3 in N1s XANES, where the ortho isomer has much larger intensity than others. The Ω2–Ω3 plot in Fig. 8b shows much simpler patterns. Only some of the DCH states (ca. 935.5 eV) contribute, as selected by the energy match and oscillator strengths between the O1s and N1sO1s states.
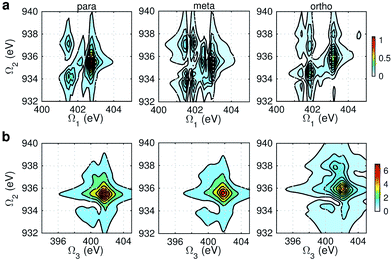 | ||
| Fig. 8 NO–B XDQC signals (absolute values) of p-, m-, and o-aminophenols (left to right). (a) SIII(t3 = 6.1 fs, Ω2, Ω1), (b) SIII(Ω3, Ω2, t1 = 0 fs). | ||
XDQC signals with single-site DCH intermediates for different isomers
Fig. 9 and 10 respectively show the NN-B and OO-B signals, where the 1-site DCH states are activated. The Ω1–Ω2 plot directly gives the correlation between SCH and DCH states, which show more isomer sensitivity than the 2-site DCH case. The N1s or O1s SCH resonances in XDQC are still limited by the corresponding XANES peak intensities. The dominant DCH sates for each feature can be more easily distinguished, as the 1-site DCHs have lower DOS. Fig. 11 gives the oscillator strengths between O1s and O1sO1s states. With this map and the O1s XANES spectra, the dominant states which contribute to the main peaks can be identified. For instance, the only major peak of p-aminophenol at Ω1 = 534 eV and Ω2 = 1151 eV are assigned as eO1 and fOO3 (Fig. 9a). They are also responsible for the main peak in the Ω2–Ω3 plot (Fig. 9b) at Ω2 = 617 eV. Fig. 11a shows that only state eO1 (bottom box) contributes at this transition energy.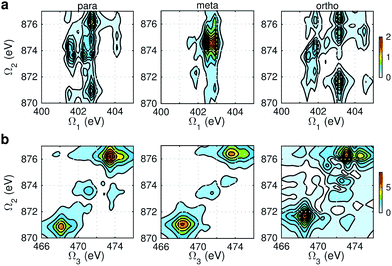 | ||
| Fig. 9 NN-B XDQC signals (absolute values) of p-, m-, and o-aminophenols (left to right). (a) SIII(t3 = 6.1 fs, Ω2, Ω1), (b) SIII(Ω3, Ω2, t1 = 0 fs). | ||
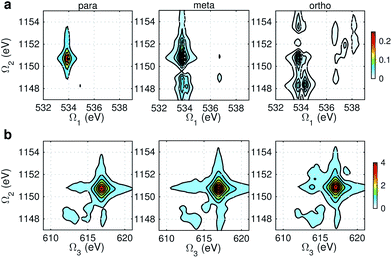 | ||
| Fig. 10 OO-B XDQC signals (absolute values) of p-, m-, and o-aminophenols (left to right). (a) SIII(t3 = 6.1 fs, Ω2, Ω1), (b) SIII(Ω3, Ω2, t1 = 0 fs). | ||
Conclusions
We have implemented the state-averaged RASSCF method for simulating double core hole states in molecules and their signatures in the XDQC signals. For the three isomers of aminophenols, we have considered different intermediate DCH states on a single (N1sN1s, O1sO1s) and two sites (N1sO1s) by tuning the pulse frequencies, and interpreted the signals by comparing with the XANES spectra and the oscillator strengths between SCH and DCH states. The XDQC technique is sensitive to the correlation between SCH and DCH states and can distinguish molecules with similar structures. The Ω1–Ω2 plot directly records the correlation between SCH and DCH states, which shows more sensitivity to structural variations than the Ω2–Ω3 window. Signals recorded via 1-site DCH pathway are more sensitive to different isomers than the 2-site DCH one.XDQC directly reveals the correlation of different core excited states, and thus reveals spatial correlation information inside a molecule (since core excited states are localized). In other types of nonlinear X-ray techniques, for instance, Stimulated X-ray Raman Spectroscopy (SXRS),6 this coupling can only be inferred through valence excited states. Combining with the high temporal resolution, this spatial correlation can be used to detect ultrafast electron dynamics. This will be an interesting future direction.
RASSCF can treat various DCH and SCH states at the same theoretical level, and better incorporates the static correlation and orbital relaxation introduced by the core hole(s), which gives higher accuracy for XDQC signals than DFT-based methods used previously.5,15 It can treat all types of 1- and 2-site DCH states accurately and can be used for simulations of other nonlinear X-ray signals involving DCHs. More accurate energies can be expected from a multi-state RASPT2 method. RASSCF also gives a reasonable estimate of the absolute core excitation energies. Creating a DCH on the same shell requires higher energy than twice of the energy to create a SCH. Creating a DCH on two weakly coupled orbitals (e.g., N1s and O1s in aminophenols) requires approximately the sum of energies used to create an individual SCH. Both cases show good energy separation and the signals are dominated by a single diagram, which simplifies the interpretation of the signals. The 2-site DCH of the same element and shell (e.g., a 2-site DCH on the Cα 1s and Cβ 1s orbitals in furan which separate by 1 eV (ref. 67)) is an interesting issue for future study.
XDQC signals with two-site double core hole intermediates can reveal the coupling of the two core holes. In our aminophenol models, both side groups are electron donors. When one group is changed to an acceptor, it can represent a large class of push–pull chromophores (also known as donor–acceptor molecules; e.g., p-nitrophenolate, p-aminobenzoic acid) which show intramolecular charge transfer transitions and serve as building blocks of optical materials.68 By properly tuning two-site DCH excitations on the two side groups, the XDQC signals could provide a novel probe for intramolecular charge transfer.
Computational methods
Electronic structure
Geometries were optimized at the B3LYP/aug-cc-pVTZ69 level with the Gaussian 09 program.70 All valence, SCH, and DCH states were calculated with the cc-pVDZ basis set71 by using the Molpro2012 program.72 SA-CASSCF method with 6 orbitals and 6 electrons were used to generate the 10 low-lying valence states, though only the lowest root (ground state) was used in signal calculations. SCH and DCH states were computed starting from the converged valence wavefunction. The excited core orbital was chosen in the RAS1 space with freezed occupation, which the size being 1 for the SCH and 1-site DCH states, and 2 for the 2-site DCH states. 2 orbitals were set in the RAS2 space, and 15 orbitals in the RAS3 space. 30 states were calculated spanning an energy range of several eVs. With resulting wavefunctions, TDMs between the ground and SCH states (Vge) and between the SCH and DCH states (Vef) as well as the XDQC signals were then calculated by our in-house code. For instance, Vef is given by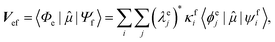 | (1) |
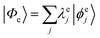 and
and 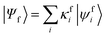 are the SA-RASSCF wavefunctions for the SCH and DCH states, with |ϕej〉 and |ψfi〉 the Slater's determinants, and λej and κei the CI coefficients. 〈ϕej|
are the SA-RASSCF wavefunctions for the SCH and DCH states, with |ϕej〉 and |ψfi〉 the Slater's determinants, and λej and κei the CI coefficients. 〈ϕej|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ψfi〉 were calculated using the Löwdin rules.73
|ψfi〉 were calculated using the Löwdin rules.73
XANES spectra
The N1s and O1s XANES spectra were first calculated for all molecules. The orientationally averaged oscillator strengths are given by | (2) |
To calibrate our simulations, we had calculated the spectra of p-aminophenol at different levels of theory, including RASSCF with two different active spaces (6, 1/4/14) and (4, 1/2/15), and the static and the time-dependent DFT methods with the B3LYP functional. DFT-FCH calculations were performed by the GAMESS-US package74 (maximum overlap method75 used for SCF convergence) and DFT-ECH calculations by the Gaussian 09 package. The IGLO-III basis set76 was set for the excited atom while the cc-pVDZ basis for the rest. With wavefunctions and integrals in hand, spectra were generated with our in-house code. The restricted excitation window TDDFT/TDA calculations were performed using the NWChem package50,77 with the cc-pVDZ basis for all atoms.
Calibration was first carried out for the DFT-FCH method using the ΔKS scheme.61 The IP was calculated as the energy difference between FCH and ground state. N1s (O1s) core excited state energies were then uniformly shifted by 0.21 (0.38) eV to include the scalar relativistic effect for the core hole.62 Such a protocol can yield transition energies in good agreement with experiment. Stick spectra were convoluted with a Gaussian line shape with hwhm of 0.3 eV. Then, resolved spectra from other methods were calibrated by aligning the first resolved main peak (shifts given in caption of Fig. 2). Meta and and ortho-aminophenols were only calculated at the DFT-FCH and RASSCF (4, 1/2/15) levels, and the same set of shift values as p-aminophenol was obtained. The DCH state energies were taken as sums of the shifts of the corresponding SCH states.15
XDQC signals
The XDQC signals were calculated using Gaussian pulse shapes with duration of σj = 100 as (j = 1, 2, 3, 4), which spans an energy bandwidth of 10.96 eV (fwhm in power spectrum). 8 pulse carrier frequencies were set to select different double core excitations (N1sN1s, O1sO1s, N1sO1s) and different pathways (diagrams A and B). We performed Fourier transformation of the 3D frequency-domain signal, with respect to either Ω3 or Ω1 to obtain SIII(Ω3, Ω2, t1 = 0 fs) and SIII(t3 = 6.1 fs, Ω2, Ω1), see eqn (7) and (8). The core hole lifetime broadening have been chosen as follows: 0.01 eV for ground state, 0.09 eV and 0.13 eV for N1s and O1s SCH states,78 and 0.4 eV for all DCH states. The lifetime broadening for DCH excited states was set larger than the SCH states. We had tested different DCH lifetime parameters, these only lead to elongation/compression of the 2D signals along the Ω2 axis and does not affect our analysis.Appendix
Sum-over-states expressions for XDQC signals
The X-ray electric field at time t and position r is given by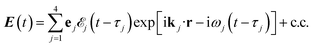 | (3) |
Here ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) j(t − τj) denotes the complex envelope of the jth pulse, and ej is the electric polarization vector. We assumed a Gaussian envelope
j(t − τj) denotes the complex envelope of the jth pulse, and ej is the electric polarization vector. We assumed a Gaussian envelope 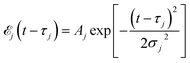 for all pulses with σj the pulse duration, and Aj the complex amplitude. The pulse spectral envelope is given by
for all pulses with σj the pulse duration, and Aj the complex amplitude. The pulse spectral envelope is given by
The sum-over-states kIII signal is given by14,15
| SIII(Ω3,Ω2,Ω1) = SIII,A(Ω3,Ω2,Ω1) + SIII,B(Ω3,Ω2,Ω1), | (4) |
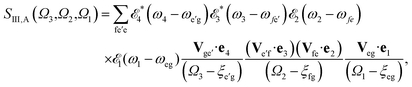 | (5) |
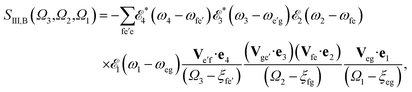 | (6) |
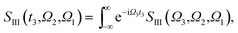 | (7) |
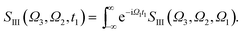 | (8) |
We took all parallel pulse configurations and considered the orientationally averaged given by15
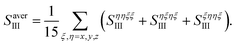 | (9) |
Acknowledgements
The support of the Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy (DOE) through award no. DE-FG02-4ER15571 and the National Science Foundation award CHE-1361516 is gratefully acknowledged. WH was supported by the DOE grant at UCI. S. M. wishes to thank the Freiburg Institite of Advanced Science (FRIAS) for their support. The work at KTH was supported by Knut and Alice Wallenberg Foundation (Grant No. KAW-2013.0020) for the project “Strong Field Physics and New States of Matter”, Göran Gustafsson Foundation for Research in Natural Sciences and Medicine, and the Hefei Science Center CAS (2015HSC-UE008). This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 and from the Swedish National Infrastructure for Computing (SNIC).References
- J. Stöhr, NEXAFS Spectroscopy, Springer, Berlin, 1992 Search PubMed.
- (a) P. Emma, R. Akre, J. Arthur, R. Bionta, C. Bostedt, J. Bozek, A. Brachmann, P. Bucksbaum, R. Coffee, F.-J. Decker, Y. Ding, D. Dowell, S. Edstrom, A. Fisher, J. Frisch, S. Gilevich, J. Hastings, G. Hays, P. Hering, Z. Huang, R. Iverson, H. Loos, M. Messerschmidt, A. Miahnahri, S. Moeller, H.-D. Nuhn, G. Pile, D. Ratner, J. Rzepiela, D. Schultz, T. Smith, P. Stefan, H. Tompkins, J. Turner, J. Welch, W. White, J. Wu, G. Yocky and J. Galayda, Nat. Photonics, 2010, 4, 641–647 CrossRef CAS; (b) J. Ullrich, A. Rudenko and R. Moshammer, Annu. Rev. Phys. Chem., 2012, 63, 635–660 CrossRef CAS PubMed.
- (a) J. Krause, K. Schafer and K. Kulander, Phys. Rev. Lett., 1992, 68, 3535–3538 CrossRef CAS PubMed; (b) P. Corkum, Phys. Rev. Lett., 1993, 71, 1994–1997 CrossRef CAS PubMed; (c) H. Kapteyn, O. Cohen, I. Christov and M. Murnane, Science, 2007, 317, 775–778 CrossRef CAS PubMed; (d) K. T. Kim, D. M. Villeneuve and P. B. Corkum, Nat. Photonics, 2014, 8, 187–194 CrossRef CAS.
- I. V. Schweigert and S. Mukamel, Phys. Rev. Lett., 2007, 99, 163001 CrossRef PubMed.
- V. Schweigert and S. Mukamel, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 052509 CrossRef.
- J. D. Biggs, Y. Zhang, D. Healion and S. Mukamel, J. Chem. Phys., 2012, 136, 174117 CrossRef PubMed.
- S. Mukamel, D. Healion, Y. Zhang and J. D. Biggs, Annu. Rev. Phys. Chem., 2013, 64, 101–127 CrossRef CAS PubMed.
- Y. Zhang, W. Hua, K. Bennett and S. Mukamel, Top. Curr. Chem., 2016, 368, 273–345 CrossRef PubMed.
- T. E. Glover, D. M. Fritz, M. Cammarata, T. K. Allison, S. Coh, J. M. Feldkamp, H. Lemke, D. Zhu, Y. Feng, R. N. Coffee, M. Fuchs, S. Ghimire, J. Chen, S. Shwartz, D. A. Reis, S. E. Harris and J. B. Hastings, Nature, 2012, 488, 603–608 CrossRef CAS PubMed.
- M. Beye, S. Schreck, F. Sorgenfrei, C. Trabant, N. Pontius, C. Schüßler-Langeheine, W. Wurth and A. Föhlisch, Nature, 2013, 501, 191–194 CrossRef CAS PubMed.
- P. Wernet, K. Kunnus, I. Josefsson, I. Rajkovic, W. Quevedo, M. Beye, S. Schreck, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M. F. de Groot, K. J. Gaffney, S. Techert, M. Odelius and A. Föhlisch, Nature, 2015, 520, 78–81 CrossRef CAS PubMed.
- F. Bencivenga, M. Zangrando, C. Svetina, A. Abrami, A. Battistoni, R. Borghes, F. Capotondi, R. Cucini, F. Dallari, M. Danailov, A. Demidovich, C. Fava, G. Gaio, S. Gerusina, A. Gessini, F. Giacuzzo, R. Gobessi, R. Godnig, R. Grisonich, M. Kiskinova, G. Kurdi, G. Loda, M. Lonza, N. Mahne, M. Manfredda, R. Mincigrucci, G. Pangon, P. Parisse, R. Passuello, E. Pedersoli, L. Pivetta, M. Prica, E. Principi, I. Rago, L. Raimondi, R. Sauro, M. Scarcia, P. Sigalotti, M. Zaccaria and C. Masciovecchio, J. Synchrotron Radiat., 2016, 23, 132–140 CrossRef PubMed.
- F. Bencivenga, R. Cucini, F. Capotondi, A. Battistoni, R. Mincigrucci, E. Giangrisostomi, A. Gessini, M. Manfredda, I. P. Nikolov, E. Pedersoli, E. Principi, C. Svetina, P. Parisse, F. Casolari, M. B. Danailov, M. Kiskinova and C. Masciovecchio, Nature, 2015, 520, 205–208 CrossRef CAS PubMed.
- D. Abramavicius, B. Palmieri, D. V. Voronine, F. Šanda and S. Mukamel, Chem. Rev., 2009, 109, 2350–2408 CrossRef CAS PubMed.
- Y. Zhang, D. Healion, J. D. Biggs and S. Mukamel, J. Chem. Phys., 2013, 138, 144301 CrossRef PubMed.
- S. Mukamel, D. Abramavicius, L. Yang, W. Zhuang, I. V. Schweigert and D. V. Voronine, Acc. Chem. Res., 2009, 42, 553–562 CrossRef CAS PubMed.
- J. D. Biggs, J. A. Voll and S. Mukamel, Philos. Trans. R. Soc. London, Ser. A, 2012, 370, 3709–3727 CrossRef PubMed.
- L. S. Cederbaum, F. Tarantelli, A. Sgamellotti and J. Schirmer, J. Chem. Phys., 1986, 85, 6513–6523 CrossRef CAS.
- L. S. Cederbaum, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 622–631 CrossRef CAS.
- A. A. Sorokin, S. V. Bobashev, T. Feigl, K. Tiedtke, H. Wabnitz and M. Richter, Phys. Rev. Lett., 2007, 99, 213002 CrossRef CAS PubMed.
- L. Young, E. P. Kanter, B. Krässig, Y. Li, A. M. March, S. T. Pratt, R. Santra, S. H. Southworth, N. Rohringer, L. F. DiMauro, G. Doumy, C. A. Roedig, N. Berrah, L. Fang, M. Hoener, P. H. Bucksbaum, J. P. Cryan, S. Ghimire, J. M. Glownia, D. A. Reis, J. D. Bozek, C. Bostedt and M. Messerschmidt, Nature, 2010, 466, 56–61 CrossRef CAS PubMed.
- L. J. Frasinski, V. Zhaunerchyk, M. Mucke, R. J. Squibb, M. Siano, J. H. D. Eland, P. Linusson, P. v. d. Meulen, P. Salén, R. D. Thomas, M. Larsson, L. Foucar, J. Ullrich, K. Motomura, S. Mondal, K. Ueda, T. Osipov, L. Fang, B. F. Murphy, N. Berrah, C. Bostedt, J. D. Bozek, S. Schorb, M. Messerschmidt, J. M. Glownia, J. P. Cryan, R. N. Coffee, O. Takahashi, S. Wada, M. N. Piancastelli, R. Richter, K. C. Prince and R. Feifel, Phys. Rev. Lett., 2013, 111, 073002 CrossRef CAS PubMed.
- J. H. D. Eland, M. Tashiro, P. Linusson, M. Ehara, K. Ueda and R. Feifel, Phys. Rev. Lett., 2010, 105, 213005 CrossRef CAS PubMed.
- P. Lablanquie, T. P. Grozdanov, M.
![[Z with combining breve]](https://www.rsc.org/images/entities/char_005a_0306.gif) itnik, S. Carniato, P. Selles, L. Andric, J. Palaudoux, F. Penent, H. Iwayama, E. Shigemasa, Y. Hikosaka, K. Soejima, M. Nakano, I. H. Suzuki and K. Ito, Phys. Rev. Lett., 2011, 107, 193004 CrossRef CAS PubMed.
itnik, S. Carniato, P. Selles, L. Andric, J. Palaudoux, F. Penent, H. Iwayama, E. Shigemasa, Y. Hikosaka, K. Soejima, M. Nakano, I. H. Suzuki and K. Ito, Phys. Rev. Lett., 2011, 107, 193004 CrossRef CAS PubMed. - P. Lablanquie, F. Penent, J. Palaudoux, L. Andric, P. Selles, S. Carniato, K. Bu
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ar, M.
ar, M. ![[Z with combining breve]](https://www.rsc.org/images/entities/char_005a_0306.gif) itnik, M. Huttula, J. H. D. Eland, E. Shigemasa, K. Soejima, Y. Hikosaka, I. H. Suzuki, M. Nakano and K. Ito, Phys. Rev. Lett., 2011, 106, 063003 CrossRef CAS PubMed.
itnik, M. Huttula, J. H. D. Eland, E. Shigemasa, K. Soejima, Y. Hikosaka, I. H. Suzuki, M. Nakano and K. Ito, Phys. Rev. Lett., 2011, 106, 063003 CrossRef CAS PubMed. - N. V. Kryzhevoi, R. Santra and L. S. Cederbaum, J. Chem. Phys., 2011, 135, 084302 CrossRef PubMed.
- N. Berrah, L. Fang, B. Murphy, T. Osipov, K. Ueda, E. Kukk, R. Feifel, P. v. d. Meulen, P. Salen, H. T. Schmidt, R. D. Thomas, M. Larsson, R. Richter, K. C. Prince, J. D. Bozek, C. Bostedt, S.-i. Wada, M. N. Piancastelli, M. Tashiro and M. Ehara, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16912–16915 CrossRef CAS PubMed.
- P. Linusson, O. Takahashi, K. Ueda, J. H. D. Eland and R. Feifel, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 022506 CrossRef.
- P. Salén, P. van der Meulen, H. T. Schmidt, R. D. Thomas, M. Larsson, R. Feifel, M. N. Piancastelli, L. Fang, B. Murphy, T. Osipov, N. Berrah, E. Kukk, K. Ueda, J. D. Bozek, C. Bostedt, S. Wada, R. Richter, V. Feyer and K. C. Prince, Phys. Rev. Lett., 2012, 108, 153003 CrossRef PubMed.
- M. Mucke, J. H. D. Eland, O. Takahashi, P. Linusson, D. Lebrun, K. Ueda and R. Feifel, Chem. Phys. Lett., 2013, 558, 82–87 CrossRef CAS.
- M. Nakano, P. Selles, P. Lablanquie, Y. Hikosaka, F. Penent, E. Shigemasa, K. Ito and S. Carniato, Phys. Rev. Lett., 2013, 111, 123001 CrossRef CAS PubMed.
- M. Nakano, F. Penent, M. Tashiro, T. P. Grozdanov, M.
![[Z with combining breve]](https://www.rsc.org/images/entities/char_005a_0306.gif) itnik, S. Carniato, P. Selles, L. Andric, P. Lablanquie, J. Palaudoux, E. Shigemasa, H. Iwayama, Y. Hikosaka, K. Soejima, I. H. Suzuki, N. Kouchi and K. Ito, Phys. Rev. Lett., 2013, 110, 163001 CrossRef CAS PubMed.
itnik, S. Carniato, P. Selles, L. Andric, P. Lablanquie, J. Palaudoux, E. Shigemasa, H. Iwayama, Y. Hikosaka, K. Soejima, I. H. Suzuki, N. Kouchi and K. Ito, Phys. Rev. Lett., 2013, 110, 163001 CrossRef CAS PubMed. -
(a) S. Carniato, P. Selles, L. Andric, J. Palaudoux, F. Penent, M.
![[Z with combining breve]](https://www.rsc.org/images/entities/char_005a_0306.gif) itnik, K. Bu
itnik, K. Bu![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ar, M. Nakano, Y. Hikosaka, K. Ito and P. Lablanquie, J. Chem. Phys., 2015, 142, 014307 CrossRef CAS PubMed;
(b) S. Carniato, P. Selles, L. Andric, J. Palaudoux, F. Penent, M.
ar, M. Nakano, Y. Hikosaka, K. Ito and P. Lablanquie, J. Chem. Phys., 2015, 142, 014307 CrossRef CAS PubMed;
(b) S. Carniato, P. Selles, L. Andric, J. Palaudoux, F. Penent, M. ![[Z with combining breve]](https://www.rsc.org/images/entities/char_005a_0306.gif) itnik, K. Bu
itnik, K. Bu![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ar, M. Nakano, Y. Hikosaka, K. Ito and P. Lablanquie, J. Chem. Phys., 2015, 142, 014308 CrossRef CAS PubMed.
ar, M. Nakano, Y. Hikosaka, K. Ito and P. Lablanquie, J. Chem. Phys., 2015, 142, 014308 CrossRef CAS PubMed. - V. Zhaunerchyk, M. Kamińska, M. Mucke, R. J. Squibb, J. H. D. Eland, M. N. Piancastelli, L. J. Frasinski, J. Grilj, M. Koch, B. K. McFarland, E. Sistrunk, M. Gühr, R. N. Coffee, C. Bostedt, J. D. Bozek, P. Salén, P. v. d. Meulen, P. Linusson, R. D. Thomas, M. Larsson, L. Foucar, J. Ullrich, K. Motomura, S. Mondal, K. Ueda, R. Richter, K. C. Prince, O. Takahashi, T. Osipov, L. Fang, B. F. Murphy, N. Berrah and R. Feifel, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 244003 CrossRef.
- M. Mucke, V. Zhaunerchyk, L. J. Frasinski, R. J. Squibb, M. Siano, J. H. D. Eland, P. Linusson, P. Salén, P. v. d. Meulen, R. D. Thomas, M. Larsson, L. Foucar, J. Ullrich, K. Motomura, S. Mondal, K. Ueda, T. Osipov, L. Fang, B. F. Murphy, N. Berrah, C. Bostedt, J. D. Bozek, S. Schorb, M. Messerschmidt, J. M. Glownia, J. P. Cryan, R. N. Coffee, O. Takahashi, S. Wada, M. N. Piancastelli, R. Richter, K. C. Prince and R. Feifel, New J. Phys., 2015, 17, 073002 CrossRef.
- J. H. D. Eland, S. Plogmaker, P. Lablanquie, F. Penent, J. Palaudoux, C. Nicolas, E. Robert, C. Miron and R. Feifel, Chem. Phys. Lett., 2016, 646, 31–35 CrossRef CAS.
- F. Penent, M. Nakano, M. Tashiro, T. P. Grozdanov, M.
![[Z with combining breve]](https://www.rsc.org/images/entities/char_005a_0306.gif) itnik, K. Bu
itnik, K. Bu![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ar, S. Carniato, P. Selles, L. Andric, P. Lablanquie, J. Palaudoux, E. Shigemasa, H. Iwayama, Y. Hikosaka, K. Soejima, I. H. Suzuki, N. Berrah, A. H. Wuosmaa, T. Kaneyasu and K. Ito, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 303–312 CrossRef CAS.
ar, S. Carniato, P. Selles, L. Andric, P. Lablanquie, J. Palaudoux, E. Shigemasa, H. Iwayama, Y. Hikosaka, K. Soejima, I. H. Suzuki, N. Berrah, A. H. Wuosmaa, T. Kaneyasu and K. Ito, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 303–312 CrossRef CAS. - O. Takahashi, N. V. Kryzhevoi and K. Ueda, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 290–302 CrossRef CAS.
- J. P. Cryan, J. M. Glownia, J. Andreasson, A. Belkacem, N. Berrah, C. I. Blaga, C. Bostedt, J. Bozek, C. Buth, L. F. DiMauro, L. Fang, O. Gessner, M. Guehr, J. Hajdu, M. P. Hertlein, M. Hoener, O. Kornilov, J. P. Marangos, A. M. March, B. K. McFarland, H. Merdji, V. S. Petrović, C. Raman, D. Ray, D. Reis, F. Tarantelli, M. Trigo, J. L. White, W. White, L. Young, P. H. Bucksbaum and R. N. Coffee, Phys. Rev. Lett., 2010, 105, 083004 CrossRef PubMed.
- S. Bodeur, P. Millié, E. Lizon, I. Nenner, A. Filipponi, F. Boscherini and S. Mobilio, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 5075–5081 CrossRef CAS.
- H. Ågren and H. J. Å. Jensen, Chem. Phys., 1993, 172, 45–57 CrossRef.
- (a) M. Tashiro, M. Ehara, H. Fukuzawa, K. Ueda, C. Buth, N. V. Kryzhevoi and L. S. Cederbaum, J. Chem. Phys., 2010, 132, 184302 CrossRef; (b) M. Tashiro, M. Ehara and K. Ueda, Chem. Phys. Lett., 2010, 496, 217–222 CrossRef CAS; (c) O. Takahashi, M. Tashiro, M. Ehara, K. Yamasaki and K. Ueda, Chem. Phys., 2011, 384, 28–35 CrossRef CAS; (d) M. Tashiro, K. Ueda and M. Ehara, Chem. Phys. Lett., 2012, 521, 45–51 CrossRef CAS.
- (a) P. Kolorenč, V. Averbukh, K. Gokhberg and L. S. Cederbaum, J. Chem. Phys., 2008, 129, 244102 CrossRef PubMed; (b) R. Santra, N. V. Kryzhevoi and L. S. Cederbaum, Phys. Rev. Lett., 2009, 103, 013002 CrossRef PubMed; (c) V. Stumpf, K. Gokhberg and L. S. Cederbaum, Nat. Chem., 2016, 8, 237–241 CrossRef CAS PubMed.
- T. D. Thomas, J. Phys. Chem. A, 2012, 116, 3856–3865 CrossRef CAS PubMed.
- S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, New York, Oxford, 1999 Search PubMed.
- (a) W. L. Jolly and D. N. Hendrickson, J. Am. Chem. Soc., 1970, 92, 1863 CrossRef CAS; (b) D. W. Davis and D. A. Shirley, Chem. Phys. Lett., 1972, 15, 185 CrossRef CAS; (c) O. Plashkevych, T. Privalov, H. Ågren, V. Carravetta and K. Ruud, Chem. Phys., 2000, 260, 11 CrossRef CAS.
- W. Hua, B. Gao and Y. Luo, Prog. Chem., 2012, 24, 964–980 CAS.
- (a) B. Brena, Y. Luo, M. Nyberg, S. Carniato, K. Nilson, Y. Alfredsson, J. Åhlund, N. Mårtensson, H. Siegbahn and C. Puglia, Phys. Rev. B, 2004, 70, 195214 CrossRef; (b) B. Brena, S. Carniato and Y. Luo, J. Chem. Phys., 2005, 122, 184316 CrossRef PubMed.
- D. Prendergast and G. Galli, Phys. Rev. Lett., 2006, 96, 215502 CrossRef PubMed.
- K. Lopata, B. E. V. Kuilen, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284 CrossRef CAS PubMed.
- (a) M. Casida, A. Ipatov and F. Cordova, Time-Dependent Density Functional Theory, Spinger-Verlag, Berlin, 2006, vol. 706, p. 243 Search PubMed; (b) A. Ipatov, F. Cordova, L. J. Doriol and M. E. Casida, J. Mol. Struct.: THEOCHEM, 2009, 914, 60–73 CrossRef CAS.
- P. A. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- (a) H. J. A. Jensen, P. Jørgensen and H. Ågren, J. Chem. Phys., 1987, 87, 451–466 CrossRef CAS; (b) H. Ågren and H. J. Å. Jensen, Chem. Phys. Lett., 1987, 137, 431–436 CrossRef; (c) H. Ågren, A. Flores-Riveros and H. J. Å. Jensen, Phys. Scr., 1989, 40, 745 CrossRef.
- I. Josefsson, K. Kunnus, S. Schreck, A. Föhlisch, F. de Groot, P. Wernet and M. Odelius, J. Phys. Chem. Lett., 2012, 3, 3565–3570 CrossRef CAS PubMed.
- (a) P. Wernet, K. Kunnus, S. Schreck, W. Quevedo, R. Kurian, S. Techert, F. M. F. de Groot, M. Odelius and A. Föhlisch, J. Phys. Chem. Lett., 2012, 3, 3448–3453 CrossRef CAS PubMed; (b) K. Atak, S. I. Bokarev, M. Gotz, R. Golnak, K. M. Lange, N. Engel, M. Dantz, E. Suljoti, O. Kühn and E. F. Aziz, J. Phys. Chem. B, 2013, 117, 12613–12618 CrossRef CAS PubMed; (c) S. I. Bokarev, M. Dantz, E. Suljoti, O. kühn and E. F. Aziz, Phys. Rev. Lett., 2013, 111, 083002 CrossRef PubMed; (d) E. Suljoti, R. Garcia-Diez, S. I. Bokarev, K. M. Lange, R. Schoch, B. Dierker, M. Dantz, K. Yamamoto, N. Engel, K. Atak, O. Kühn, M. Bauer, J.-E. Rubensson and E. F. Aziz, Angew. Chem., Int. Ed., 2013, 52, 9841–9844 CrossRef CAS PubMed; (e) R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Chem. Phys., 2014, 141, 124116 CrossRef PubMed; (f) K. Kunnus, I. Josefsson, I. Rajkovic, S. Schreck, W. Quevedo, M. Beye, C. Weniger, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, K. J. Gaffney, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M. F. de Groot, S. Techert, M. Odelius, P. Wernet and A. Föhlisch, Struct. Dyn., 2016, 3, 043204 CrossRef CAS PubMed; (g) M. Guo, L. K. Sørensen, M. G. Delcey, R. V. Pinjari and M. Lundberg, Phys. Chem. Chem. Phys., 2016, 18, 3250–3259 RSC.
- R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Comput. Chem., 2016, 37, 477–486 CrossRef CAS PubMed.
- W. Hua, S. Oesterling, J. D. Biggs, Y. Zhang, H. Ando, R. de Vivie-Riedle, B. P. Fingerhut and S. Mukamel, Struct. Dyn., 2016, 3, 023601 CrossRef PubMed.
- J. Finley, P. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- S. C. Mitchell, P. Carmichael and R. Waring, Kirk-Othmer Encyclopedia of Chemical Technology, John Wiley & Sons, Inc., 2000 Search PubMed.
- N. Chouhan, M. L. Kalra, S. Kumar, Y. N. Singh and S. C. Ameta, Mol. Cryst. Liq. Cryst., 2007, 469, 99–110 CrossRef CAS.
- (a) P. S. Bagus, Phys. Rev., 1965, 139, A619–A634 CrossRef; (b) L. Triguero, O. Plashkevych, L. G. M. Pettersson and H. Ågren, J. Electron Spectrosc. Relat. Phenom., 1999, 104, 195–207 CrossRef CAS.
- L. Triguero, L. G. M. Pettersson and H. Ågren, Phys. Rev. B: Condens. Matter, 1998, 58, 8097–8110 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS.
- (a) G. Fronzoni, O. Baseggio, M. Stener, W. Hua, G. Tian, Y. Luo, B. Apicella, M. Alfé, M. d. Simone, A. Kivimäki and M. Coreno, J. Chem. Phys., 2014, 141, 044313 CrossRef PubMed; (b) W. Hua, H. Yamane, B. Gao, J. Jiang, S. Li, H. S. Kato, M. Kawai, T. Hatsui, Y. Luo, N. Kosugi and H. Ågren, J. Phys. Chem. B, 2010, 114, 7016–7021 CrossRef CAS PubMed.
- H. Li, W. Hua, Z. Lin and Y. Luo, J. Phys. Chem. B, 2012, 116, 12641–12650 CrossRef CAS PubMed.
- W. Hua, J. D. Biggs, Y. Zhang, D. Healion, H. Ren and S. Mukamel, J. Chem. Theory Comput., 2013, 9, 5479–5489 CrossRef CAS PubMed.
- (a) M. J. Cho, D. H. Choi, P. A. Sullivan, A. J. P. Akelaitis and L. R. Dalton, Prog. Polym. Sci., 2008, 33, 1013–1058 CrossRef CAS; (b) M.-B. Suhr Kirketerp, M. Åxman Petersen, M. Wanko, L. Andres Espinosa Leal, H. Zettergren, F. M. Raymo, A. Rubio, M. Brøndsted Nielsen and S. Brøndsted Nielsen, ChemPhysChem, 2009, 10, 1207–1209 CrossRef CAS PubMed; (c) M. Wanko, J. Houmøller, K. Støchkel, M.-B. S. Kirketerp, M. Å. Petersen, M. B. Nielsen, S. B. Nielsen and A. Rubio, Phys. Chem. Chem. Phys., 2012, 14, 12905–12911 RSC; (d) A. G. Thomas, M. J. Jackman, M. Wagstaffe, H. Radtke, K. Syres, J. Adell, A. Lévy and N. Martsinovich, Langmuir, 2014, 30, 12306–12314 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria and M. A. Robbet al., Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schützet al., MOLPRO, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net Search PubMed.
- (a) P.-O. Löwdin, Phys. Rev., 1955, 97, 1474–1489 CrossRef; (b) D. B. Cook, Handbook of computational quantum chemistry, Dover Publications, Mineola, N.Y., 2005, pp. 66–69 Search PubMed.
- (a) M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS; (b) M. S. Gordon and M. W. Schmidt, in Advances in electronic structure theory: GAMESS a decade later, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, ch. 41, pp. 1167–1189 Search PubMed; (c) http://www.msg.chem.iastate.edu/GAMESS/GAMESS.html .
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- W. Kutzelnigg and U. Fleischer and M. Schindler, in NMR Basic Principles and Progress, Springer Verlag, Heidelberg, 1990, vol. 23, p. 165 Search PubMed.
- M. Valiev, E. Bylaska, N. Govind, K. Kowalski, T. Straatsma, H. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. Windus and W. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- G. H. Zschornack, Handbook of X-Ray Data, Springer, New York, 2007 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Simulated XANES spectra with better resolved continuum region; RASSCF energy levels of p-aminopheol; XDQC signals via diagram-A pathway. See DOI: 10.1039/c6sc01571a |
| This journal is © The Royal Society of Chemistry 2016 |