Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics versus thermodynamics in the proline catalyzed aldol reaction†
M.
Orlandi
,
M.
Ceotto
* and
M.
Benaglia
*
Dipartimento di Chimica, Università degli Studi di Milano,
via C. Golgi, 19, 20133 Milano, Italy. E-mail: michele.ceotto@unimi.it; maurizio.benaglia@unimi.it
First published on 6th May 2016
Abstract
In this paper the equilibrium properties of the proline catalyzed aldol reaction was studied. The use of well-established methodologies, like reaction progress kinetic analysis and linear free energy relationship analysis, led to the quantification of the reaction reversibility and to its correlation with the substrate electronic activation. Due to these experimental observations, common computational approaches based on a one way transition state analysis become unsuitable. Therefore, a computational model based on the integration of a system of kinetic differential equations associated to the multiple equilibrium reactions was proposed. Such a model was found to successfully rationalize the chemical and stereochemical outcomes of this paradigmatic reaction for the first time.
Introduction
After the pioneering works by List and Barbas,1 Jacobsen,2 and MacMillan,3 organocatalyzed reactions have been studied through experimental techniques and theoretical methods to rationalize the stereochemical behavior of a great number of catalysts.4 Among the others, Blackmond, List and Houk have extensively investigated the intra- and inter-molecular proline catalyzed aldol reactions of ketones and aldehydes.5,6 In particular, by using Reaction Progress Kinetic Analysis (RPKA), Blackmond et al. studied the proline catalyzed addition of acetone to 2- and 3-chlorobenzaldehyde, defining for the first time the kinetic rate law of this important reaction.5a–c Earlier, Houk and List provided the first evidence of the reaction mechanism, which involves the stereoselectivity model commonly known as the Houk–List model.6 Despite first reports about proline catalysis going back to more than fifteen years ago, new efforts are still ongoing from researchers in order to improve the knowledge about the nature of this kind of reaction and to better explain in detail some aspects of these transformations.7Here we report a study about the equilibrating nature of this reaction and about the influence of such reversibility on its stereochemical outcome. Eventually, this study leads to the application of a multiple transition state approach for the first quantitative computational rationalization of the observed yields, dr and ee.
Results and discussion
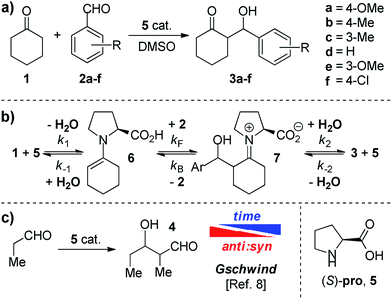
In this work, we focused our attention on the proline catalyzed addition of cyclohexanone 1 to several benzaldehydes 2a–2f (Scheme 1a). In particular, we wondered about the reversibility of these reactions accordingly with Scheme 1b. Indeed, NMR studies by Gschwind et al.8 have clearly shown the time dependence of the syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti ratio of aldol 4 in the presence of (S)-proline 5 (Scheme 1c), which is a symptom of reversible processes.
anti ratio of aldol 4 in the presence of (S)-proline 5 (Scheme 1c), which is a symptom of reversible processes.
By monitoring racemic anti ketols 3a, 3d and 3f in the presence of proline in DMSO-d6 through 1H NMR techniques, we observed the delivery of the corresponding aldehydes (see Table S1, ESI† for additional details). In order to determine the dependence of the retro aldol reaction on the proline, we mixed racemic anti-3a with 5 (30 mol%) and cyclohexanone 1 (4 eq.) in DMSO-d6 and the appearance of syn-3a was detected (Scheme 2). In particular, the CSP-HPLC analysis of the crude mixture after 72 h revealed a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 syn
3 syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti ratio and 53% ee for the (R,S) enantiomer of anti-3a, proving a kinetic resolution of the racemic starting material (Scheme 2) as a clear indication of the reversibility of the reaction.
anti ratio and 53% ee for the (R,S) enantiomer of anti-3a, proving a kinetic resolution of the racemic starting material (Scheme 2) as a clear indication of the reversibility of the reaction.
The effect of this equilibration in the proline catalyzed aldol reaction has already been detected,8 yet, it has never been studied in detail. Hence, in the present work, we will employ well-established methodologies, such as RPKA, LFERs (Linear Free Energy Relationships) and DFT computational methods to investigate this equilibrating phenomenon and rationalize its effect on the reaction outcome.
The RPKA approach, developed by Blackmond, represents one of the most powerful tools for the study of reaction mechanisms.9 It has been also used for the clarification of the role of water in the proline catalyzed aldol reaction5b and for the determination of the power rate law for the addition of acetone to 3-chlorobenzaldehyde.5a Such a reaction was found to proceed up to complete conversion and it is very well described by the following equation:5a
| Rate = k[ketone]0.59[aldehyde]0.9[H2O]−0.7 | (1) |
Eqn (1) represents the current state of the art equation and it is an excellent description for aldol reactions that provide near complete conversions. Given the reaction of acetone with 3-chlorobenzaldehyde, a rate law that considers reversibility was not required in those cases, and the possibility of reverse reactions was not included in eqn (1).5a However, in our specific cases, eqn (1) cannot be applied straightforwardly due to the presence of a substantial retro aldol reaction.
This can be observed through the “graphical rate laws” reported in Fig. 1. Fig. 1a shows the rate law for the electron poor aldehyde 2f. Fig. 1b is the same plot but for aldehyde 2c, which presents an intermediate reactivity, and Fig. 1c is for the poorly reactive aldehyde 2a. From a direct comparison of the three graphs, it is clear that the ability of eqn (1) to fit the reaction progress fails as the reaction conversion decreases (see the black dashed lines in Fig. 1a–c for the data fitting with eqn (1)). This observation motivated us to improve eqn (1) into a new rate law that includes reversible processes.
 | ||
| Fig. 1 “d[3f]/dt vs. [2]” graphical rate laws for aldehydes (a) 2f, (b) 2c and (c) 2a. Blue circles: experimental. Dashed black lines: fitting with eqn (1). Dashed red lines: fitting with eqn (2). | ||
To reach such a goal, we have chosen 1H NMR as the analytical technique because it allows monitoring of the concentration of reagents and products, as well as diastereoselectivity, versus time. The reaction between cyclohexanone 1 and 4-chlorobenzaldehyde 2f was chosen as a benchmark reaction, since it provides higher reaction rates with respect to aldehydes 2a–2e. Firstly, a “same excess”9 experiment was performed by running two reactions at different concentrations but with the same catalyst amount and the same excess of 1 with respect to 2f. This experiment highlighted the absence of catalyst deactivation in the presence of water 0.73 M (see Fig. S4, ESI†), in accordance with previous observations by Pihko5p,q and rationalization by Blackmond.5b,c Then “different excess”9 experiments were run with [exc] = 0.0, 0.24, 0.93, 1.53 and 2.6 M. Interestingly, we found that a good description of the reaction kinetics can be obtained only by considering the overall process that involves not only the forwards addition of enamine 6 to the aldehyde 2, but also the backwards aldol reaction that takes place by interaction of the catalyst 5 with the product 3 (Scheme 1b). Moreover, pre-equilibrium kinetics for the formation of enamine 6 was accounted for to rationalize the observed dependence of the reaction rate on [1] and [H2O] (Fig. S5, ESI†).
The observed first order dependence of the retro aldol reaction on 3 was confirmed through additional RPKA experiments. Indeed, by monitoring the retro aldol reaction of 3a and by plotting the disappearance rate of 3a (−d[3a]/dt) against [3a], a linear dependence was observed. This behavior has been rationalized by assuming a large dissociation constant (k2/k−2) for 7 (see page S9, ESI†).
Eventually, we derived the following rate law and a detailed derivation of these equations can be found on pages S5–S9 of the ESI.†
 | (2) |
 | (3) |
It is important to note that eqn (2) represents an extension of the Blackmond's power law (1), where the reversible process has been included. By putting kobsB equal to zero, eqn (1) is recovered. Eqn (2) allows us to reproduce the experimental reaction progress curves even for those aldehydes with lower reactivity (see Fig. 1a–c, red dashed lines).
After proving that eqn (2) provides a complete kinetic description of the catalytic system, we acquired reaction profiles of the reactions involving aldehydes 2a–2f.
The presence of different substituents at the 3- or 4-position on the phenyl ring of the aldehyde are not expected to effect this aldol reaction via steric interactions. However, the modulation of the electron-withdrawing/electron-donating properties of such substituents can strongly affect the activation and the reactivity of the carbonyl moiety. Indeed, from the experimental plots reported in Fig. 1, a strong dependence of the reaction's profile, and more surprisingly, of the final reaction conversion on the aldehyde substituent is evident. In Fig. 1 the linear dependence of the rate to equilibrium on the aldehyde concentration (d[3]/dt vs. [2]) is highlighted. Note that the non-zero intercepts, especially in Fig. 1c, are a clear indication of equilibration, since the final conversions of the reactions are not quantitative (Fig. S8 of the ESI† reports the experimental profiles for all of the aldehydes).
The kinetics study hereby presented is evidence of the dependence of the reaction on the electronic properties of the substrate 2. Thus, for a better rationalization of these observations and to provide a quantitative analysis of the observed electronic effects, we looked at the Hammett equation.10 Indeed, while the dependence of both reaction rate and reaction conversion on the aldehyde's electronic properties has been qualitatively highlighted in Fig. 1, a quantitative description can be provided by correlating the amounts ln(kX/kH) and ln(KX/KH)11 against σ+ (the Hammett electrophilic constant10d).
The plots obtained are reported in Fig. 2, and demonstrate a good correlation. Here an intercept near to zero and an angular coefficient ρ of ca. 3 were found in both cases. This same dependence of ΔΔGact (or ln(kX/kH)) and ΔΔRG (or ln(KX/KH)) on σ+ suggests that the only variation in the energetic profile of the reaction is the relative energy level of the ground state reagents. Further support for this observation can be given by a direct comparison of the measured rate constants kF and kobsB (Fig. 2): while kF strongly depends on the aldehyde's activation, kB presents a roughly constant value. This means that, intuitively, while different aryl rings affect the reactivity of the aldehyde's carbonyl group, they do not strongly affect the reactivity of the ketols' 3a–3f carbonyl group. In conclusion, increasing the reactivity of the aldehyde (i.e. by increasing its HOMO energy) affects both the rate constant kF and the equilibrium constant K.
Most information about the processes affecting a stereoselective chemical reaction can be found by monitoring the isomer distribution. The use of 1H NMR as a detection technique for the obtainment of the reaction profiles allows us to monitor the syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti ratio as a function of the reaction time. Gschwind et al. already reported the epimerization of diastereomeric products in the proline catalyzed auto-addition of propionaldehyde (Scheme 1c).8 For the present case, the syn
anti ratio as a function of the reaction time. Gschwind et al. already reported the epimerization of diastereomeric products in the proline catalyzed auto-addition of propionaldehyde (Scheme 1c).8 For the present case, the syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti ratios of compounds 3a–3f are plotted against time in Fig. 3. In the graphs the epimerization from the anti to the syn diastereoisomer for ketols 3b–3f is evident, where the syn
anti ratios of compounds 3a–3f are plotted against time in Fig. 3. In the graphs the epimerization from the anti to the syn diastereoisomer for ketols 3b–3f is evident, where the syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti ratios change from ca. 40
anti ratios change from ca. 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 to 58
60 to 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42. Thus, the anti isomer is the kinetic product, as correctly predicted by the Houk–List model,6 whereas the syn isomer is the thermodynamic one. The presence of epimerization is consistent with the retro aldol reaction, and once the reaction equilibrates, the dr will change from the kinetic towards the most stable thermodynamic product.
42. Thus, the anti isomer is the kinetic product, as correctly predicted by the Houk–List model,6 whereas the syn isomer is the thermodynamic one. The presence of epimerization is consistent with the retro aldol reaction, and once the reaction equilibrates, the dr will change from the kinetic towards the most stable thermodynamic product.
Interestingly, we found that ketol 3a exhibits a constant dr. We attribute this phenomenon to the very similar values of kF and kB for the aldol reaction of 2a (Fig. 2). Indeed, since the forward and backward processes proceed with similar rates, the epimerization and the aldol addition occur simultaneously and at a comparable rate.
As expected, enantioselectivity is also affected by equilibration. The ee of the six monitored reactions have been evaluated after 6 d of reaction and then after 3 weeks. In Table 1 the obtained results are reported. From these data the following observations are summarized: (i) all the products are affected by racemization, (ii) products characterized by electron-donating groups usually lead to higher ee erosion, and (iii) anti diastereoisomers undergo faster racemization than syn ones.
| Substrate | t (d) | Conv.a (%) | drb | eec (%) | |
|---|---|---|---|---|---|
| syn | anti | ||||
a Evaluated through 1H NMR analysis of the crude product.
b Expressed as syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti ratio.
c Evaluated through CSP-HPLC analysis. anti ratio.
c Evaluated through CSP-HPLC analysis.
|
|||||
| 2a | 6 | 58 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 45 |
59 | 76 |
| 21 | 68 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 45 |
34 | 48 | |
| 2b | 6 | 87 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 47 |
73 | 79 |
| 21 | 87 | 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 44 |
54 | 54 | |
| 2c | 6 | 90 | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
64 | 60 |
| 21 | 90 | 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 44 |
41 | 19 | |
| 2d | 6 | 95 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 47 |
77 | 77 |
| 21 | 95 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
69 | 60 | |
| 2e | 6 | 95 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 47 |
82 | 83 |
| 21 | 95 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
72 | 63 | |
| 2f | 6 | 98 | 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 52 |
87 | 84 |
| 21 | 98 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
84 | 78 | |
Thus, the stereochemical analysis of the system supports the evidence of a substantial and specific equilibration in accordance with our preliminary experiments (Scheme 2) and kinetic analysis.
Since the observed equilibration has a strong effect on the stereochemical outcome of the reaction, we wondered whether this feature might be responsible for the missing computational rationalization of these reactions. Indeed, although many papers have been published4,5e,i,j,n,o,6 that qualitatively rationalize the stereochemical outcome of intra and intermolecular proline catalyzed aldol reactions, the quantitative prediction of such a reaction outcome is still an open issue. Rzepa et al.7a have recently revisited the proline catalyzed addition of 1 to aldehyde 2d in a comprehensive paper, where the inadequacy of DFT methods in the evaluation of the weak interactions occurring at the TS level is ascribed to be the main responsible factor of such limitations. One can resort to the Curtin–Hammett Principle (CHP),12 which has been extensively employed in the determination of the stereoselectivity of organic reactions to better understand these reactions. However, it is well known that this approximation is applicable only if (i) rapidly interconverting reagents, such as conformers, are involved and (ii) the considered processes lead irreversibly to the products.13 Hence, its application should be limited only to irreversible processes affording non-interconverting products. The experiments here reported have highlighted the equilibrating nature of the proline catalyzed aldol reaction. Given such dynamic nature, which depends on the electronic nature of the aldehyde, as shown in this study, traditional transition state approaches can no longer be applied.
Thus, in order to include both kinetics and thermodynamics in the description of the catalytic system, an alternative theoretical approach for the description of the reactivity is required. In particular, we propose that the reaction evolution can be obtained by integrating the rate law of the simplified reaction scheme reported in Scheme 3. More specifically, by calculating the rate constants of Scheme 3a and by numerically integrating the system of differential equations reported in Scheme 3b, a time-dependent picture of product concentration is obtained. Scheme 3a is a simplification of the reaction based on the considerations that: (i) the inclusion of additional species that are in fast equilibrium with the considered compounds (such as water, oxazolidinones and iminium ions) is considered a higher order precision level of calculation, and that (ii) the considered species are the prevalent compounds that characterize the kinetics of the reaction in the presence of water, which is known to suppress side reactions ascribed to the catalyst's deactivation.5b,c In addition, we indeed consider that water has a fundamental role, but its concentration is constant during the reaction. Hence, when considering the qualitative and relative behavior of different reactions involving different aldehydes under the same reaction conditions, it can be neglected. Finally, in Scheme 3b we consider enamine 6 both as a single conformer (s-trans) and as a mixture of two conformers (s-trans and s-cis), each one leading to a couple of product diastereoisomers and we found that this does not affect the final outcome of the simulation.14
 | ||
| Scheme 3 (a) Simplified reaction scheme. (b) System of differential equations associated to the reaction scheme. | ||
The numerical resolution of complicated systems of differential equations is commonly known in the field of chemical kinetics.15 However, to the best of our knowledge, this is the first time that it has been applied to the field of organic computational chemistry as a tool for the simulation of stereoselective reaction outcomes, going beyond a static single transition state picture. It is important to recall that one can recover the CHP result as the time zero approximation of the present approach, while the infinite time approximation represents the thermal distribution of reagents and products. Since, as just highlighted, both kinetics and thermodynamics play an important role in this reaction, it is important to find a DFT functional capable of evaluating at best the ΔRG, the ΔG‡ and the ΔΔG‡ values. We focused on the M06/2X functional, since Houk et al.16 and Hubin and coworkers17 showed that it gives the best thermodynamic description for this class of reactions. After a wide screening of several computational set ups, we identified M06-2X/6-311G(2d,2p) as the best compromise for fast and accurate computations of a huge number of structures. More than thirty computational set ups have been tested (Table S6, ESI†) including B3LYP, CAM-B3LYP, mPW1PW91, wB97XD, M06, M06L, M06HF, M052X, BMK and LC-wPBE. Several polarizable continuum models for the inclusion of the solvent effect have also been tested, but these usually provided endorgonic profiles (ΔRG > 0). Thus, the structures of the species depicted in Scheme 3a and the TSs connecting the involved processes have been computed for aldehydes 2a–2f, in compliance with the extended conformational analysis reported by Rzepa et al.7a In Table 2 the calculated ΔRG values for both syn- and anti-3a–3f and the ΔG‡ values for the pathway involving the favourite TS (leading to 3-SR) are reported for all the substrates.
| Substrate | ΔG‡ | ΔRG | |
|---|---|---|---|
| syn | anti | ||
| a All the energy values reported are in kcal mol−1. | |||
| 2a | 20.1 | 0.24 | 0.57 |
| 2b | 18.8 | −1.95 | −0.51 |
| 2c | 18.6 | −0.84 | −0.68 |
| 2d | 18.7 | −1.42 | −0.62 |
| 2e | 18.9 | −1.62 | −0.44 |
| 2f | 18.7 | −2.45 | −1.47 |
From the values reported in Table 2, it can be observed that computations are only partially able to predict the experimentally observed trend. Indeed, while 2a is correctly predicted to be the least reactive aldehyde (Table 2), the other substrates were calculated to have roughly the same reactivity (Table 2). However, a quite good description of ΔRG was found, since on increasing the electron-withdrawing character of the aldehyde substituent, the product stability becomes higher (with a few exceptions).
The rate constants required to obtain the system of differential equations in Scheme 3b, were calculated by means of transition state theory.18 According to the Eyring equation, rate constants with an order of magnitude of 102 s−1 are obtained with calculated energy barriers of ca. 19 kcal mol−1. However, the experimentally obtained values for kF have a magnitude of 10−4 s−1. Thus, we may expect a substantial error in the time scale when simulating these reactions which might be considerably shorter. Nevertheless, the simulations should in principle still maintain a good relative description of the reactions including the reversibility of the system, especially when compared with the simple TS analysis.
The numerical integration of the equations in Scheme 3b, under adequate boundary conditions (in compliance with the experimentally used reagent concentrations), was performed by means of the ODE15s algorithm provided by MatLab suite of codes.19 In Table 3 the results obtained with this Multiple Transition State Approach (MTSA) and with the CHP are reported for the reactions relative to aldehydes 2a–2f.
| Substrate | Multiple transition state approach | Curtin–Hammett principle | ||||||
|---|---|---|---|---|---|---|---|---|
| t (h) | Conv. (%) | drb | ee (%) | drb | ee (%) | |||
| syn | anti | syn | anti | |||||
a Energy values obtained with the M06-2X/6-311G(2d,2p) level of theory were used for the obtainment of all the results reported in the table.
b Expressed as syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti ratio. anti ratio.
|
||||||||
| 2a | 34 | 68 | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 34 |
62 | 79 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 85 |
99 | >99 |
| 95 | 73 | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 34 |
30 | 53 | ||||
| 2b | 40 | 93 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
71 | 85 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 94 94 |
99 | >99 |
| 105 | 94 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
43 | 66 | ||||
| 2c | 32 | 93 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 47 |
76 | 48 | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92 92 |
99 | >99 |
| 103 | 93 | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
43 | 10 | ||||
| 2d | 30 | 96 | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 21 |
78 | 75 | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95 95 |
97 | >99 |
| 108 | 96 | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 21 |
54 | 49 | ||||
| 2e | 30 | 96 | 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12 |
92 | 90 | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95 95 |
99 | >99 |
| 105 | 96 | 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12 |
83 | 77 | ||||
| 2f | 32 | 99 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 18 |
97 | 89 | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92 92 |
99 | >99 |
| 92 | 99 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 17 |
94 | 77 | ||||
It is evident that the CHP provides only a poor qualitative agreement with the experimental data of Table 1. Indeed, the dr is predicted in favor of the anti diastereoisomer and the enantioselectivity is always predicted to be higher than 97%, in accordance with the recent report by Rzepa et al.7a (a discussion about the difficulty of the prediction of low levels of enantioselectivity can be found at page S14 of the ESI†). Moreover, no information about the reversibility of the process can be obtained.
When applying the MTSA, as expected (vide infra), the reaction times relative to the simulation are shorter than the corresponding experimental values. The evolution times of the kinetics equations were chosen in such a way that the selectivity of the first reaction (Table 3) matched with the corresponding experimental data (Table 1), that is ca. 30 h. Given the reaction time ratio of 6 d versus 21 d (experimental times of Table 1), the second measurement of the simulated reaction has been done at ca. 90/105 h (Table 3, entry 2).20 The same reaction times have been selected for the other reactions in order to obtain a comparison between reactions characterized by different substrates. The conversions are well reproduced, and respect the activity/stability trend reported above (compare Tables 1 and 3). Most importantly, a correct qualitative description of the dr is obtained, since the syn diastereoisomer is predicted to be favored, especially when compared with the CHP results in the left columns of Table 3. Analogously, the MTSA ee results are in good agreement with the experimental ones. These results are explained by the ability of the MTSA to take into account the equilibrating nature of the system, correctly predicting the erosion of the stereoselectivity. Moreover, the relative trends observed for the experimental results can be, in most cases, recognized also in the reported simulation outcomes: (i) all the products are affected by racemization, (ii) products characterized by electron-donating groups present higher ee erosion, and (iii) the anti diastereoisomers present faster racemization.
Conclusions
In conclusion, new mechanistic insight into the proline catalyzed aldol reaction is presented. RPKA has been used to prove the reversibility of the reaction and to obtain a rate law that integrates the previously reported power law by Blackmond et al.5a by taking into account the reaction reversibility. This makes the obtained kinetics law applicable to a wider range of substrates, even when the reaction does not provide quantitative conversions. LFERs have been used to rationalize the dependence of the reaction rates and of the final reaction conversion on the aldehyde activation. The analysis of the stereochemistry of the reaction has supported the evidence of the equilibrating process, which affects both diastereo- and enantioselectivity. This strong evidence makes the CHP unsuitable as a model for the computational rationalization of the experimentally observed stereochemical outcome and enabled us to introduce a MTSA for the elaboration of the computed energies that is based on the inclusion of both kinetics and thermodynamics in the description of the process. The use of this MTSA allowed us to computationally predict key features of the proline catalyzed aldol reaction and to compute realistic stereoselectivities for the first time.Acknowledgements
M. O. thanks Università degli Studi di Milano for a Ph.D. fellowship. We acknowledge the CINECA and the Regione Lombardia award under the LISA initiative, for the availability of high performance computing resources and support. Authors thank Prof. L. Raimondi, Dr M. F. Gerini and C. Aieta for useful discussions.Notes and references
- B. List, R. A. Lerner and C. F. Barbas III, J. Am. Chem. Soc., 2000, 122, 2395 CrossRef CAS.
- (a) M. S. Sigman and E. N. Jacobsen, J. Am. Chem. Soc., 1998, 120, 4901 CrossRef CAS; (b) M. S. Sigman, P. Vachal and E. N. Jacobsen, Angew. Chem., Int. Ed., 2000, 39, 1279 CrossRef CAS.
- K. A. Ahrendt, C. J. Borths and D. W. C. MacMillan, J. Am. Chem. Soc., 2000, 122, 4243 CrossRef CAS.
- (a) C. Allemann, R. Gordillo, F. R. Clemente, P. H.-Y. Cheong and K. N. Houk, Acc. Chem. Res., 2004, 37, 558 CrossRef CAS PubMed; (b) P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Chem. Rev., 2011, 111, 5042 CrossRef CAS PubMed; (c) R. B. Sunoj, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 920 CrossRef CAS; (d) A. Fu, C. Zhao, H. Li, F. Tian, F. Yuan, Y. Duan and Z. Wang, J. Phys. Chem. A, 2013, 117, 2862 CrossRef CAS PubMed; (e) K. N. Rankin, J. W. Gauld and R. J. Boyd, J. Phys. Chem. A, 2002, 106, 5155 CrossRef CAS.
- Selected examples: (a) N. Zotova, L. J. Broadbelt, A. Armstrong and D. G. Blackmond, Bioorg. Med. Chem. Lett., 2009, 19, 3934 CrossRef CAS PubMed; (b) N. Zotova, A. Franzke, A. Armstrong and D. G. Blackmond, J. Am. Chem. Soc., 2007, 129, 15100 CrossRef CAS PubMed; (c) J. S. Mathew, M. Klussmann, H. Iwamura, F. Valera, A. Futran, E. A. C. Emanuelsson and D. G. Blackmond, J. Org. Chem., 2006, 71, 4711 CrossRef CAS PubMed; (d) Y. Hayashi, M. Matsuzawa, J. Yama-guchi, S. Yonehara, Y. Matsumoto, M. Shoji, D. Hashizume and H. Koshino, Angew. Chem., Int. Ed., 2006, 45, 4593 CrossRef CAS PubMed; (e) J. E. Hein, J. Burés, Y.-Y. Lam, M. Hughes, K. N. Houk, A. Armstrong and D. G. Blackmond, Org. Lett., 2011, 13, 5644 CrossRef CAS PubMed; (f) D. Sánchez, D. Bastida, J. Burés, C. Isart, O. Pineda and O. Vilarrasa, Org. Lett., 2012, 14, 536 CrossRef PubMed; (g) M. Klussmann, H. Iwamura, S. P. Mathew, D. H. Wells Jr, U. Pandya, A. Armstrong and D. G. Blackmond, Nature, 2006, 441, 621 CrossRef CAS PubMed; (h) M. Klussmann, S. P. Mathew, H. Iwamura, D. H. Wells Jr, A. Armstrong and D. G. Blackmond, Angew. Chem., Int. Ed., 2006, 45, 7989 CrossRef CAS PubMed; (i) L. Hoang, S. Bahmanyar, K. N. Houk and B. List, J. Am. Chem. Soc., 2003, 125, 16 CrossRef CAS PubMed; (j) A. K. Sharma and R. B. Sunoj, Angew. Chem., Int. Ed., 2010, 49, 6373 CrossRef CAS PubMed; (k) D. Seebach, A. K. Beck, D. M. Badine, M. Limbach, A. Eschenmoser, A. M. Treasurywala and R. Hobi, Helv. Chim. Acta, 2007, 90, 425 CrossRef CAS; (l) B. List, L. Hoang and H. Martin, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5839 CrossRef CAS PubMed; (m) K. Sakthivel, W. Notz, T. Bui and C. F. Barbas III, J. Am. Chem. Soc., 2001, 123, 5260 CrossRef CAS PubMed; (n) F. R. Clemente and K. N. Houk, Angew. Chem., Int. Ed., 2004, 43, 5766 CrossRef CAS PubMed; (o) H. Zhu, F. R. Clemente, K. N. Houk and M. P. Meyer, J. Am. Chem. Soc., 2009, 131, 1632 CrossRef CAS PubMed; (p) A. I. Nyberg, A. Usano and P. M. Pihko, Synlett, 2004, 1891 CAS; (q) P. M. Pihko, K. M. Laurikainen, A. Usano, A. Nyberg and J. A. Kaavi, Tetrahedron, 2006, 62, 317 CrossRef CAS.
- (a) S. Bahmanyar and K. N. Houk, J. Am. Chem. Soc., 2001, 123, 12911 CrossRef CAS PubMed; (b) S. Bahmanyar, K. N. Houk, H. J. Martin and B. List, J. Am. Chem. Soc., 2003, 125, 2475 CrossRef CAS PubMed.
- Recent examples: (a) A. Armstrong, R. A. Boto, P. Dingwall, J. Contreras-Garcia, M. J. Harvey, N. J. Mason and H. S. Rzepa, Chem. Sci., 2014, 5, 2057 RSC; (b) M. H. Haindl, J. Hioe and R. M. Gschwind, J. Am. Chem. Soc., 2015, 137, 12835 CrossRef CAS PubMed.
- M. B. Schmid, K. Zeitler and R. M. Gschwind, J. Org. Chem., 2011, 76, 3005 CrossRef CAS PubMed.
- In the two following references the methodology and an excellent collection of many examples is reported. (a) D. G. Blackmond, Angew. Chem., Int. Ed., 2005, 44, 4302 CrossRef CAS PubMed; (b) D. G. Blackmond, J. Am. Chem. Soc., 2015, 137, 10852 CrossRef CAS PubMed. This powerful tool has also been used for the rationalization of very challenging reactions, for example see: (c) J. J. Devery, J. C. Conrad, D. W. C. MacMillan and R. A. Flowers, Angew. Chem., Int. Ed., 2010, 49, 6106 CrossRef PubMed. For an application of the method to the supported proline catalyzed aldol reaction in flow see: (d) O. Bortolini, A. Cavazzini, P. P. Giovannini, R. Greco, N. Marchetti, A. Massi and L. Pasti, Chem.–Eur. J., 2013, 19, 7802 CrossRef CAS PubMed.
- (a) E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Mill Valley, CA, 2006 Search PubMed; (b) K. C. Harper and M. S. Sigman, J. Org. Chem., 2013, 78, 2813 CrossRef CAS PubMed; (c) C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165 CrossRef CAS; (d) H. C. Brown and Y. Okamoto, J. Am. Chem. Soc., 1958, 80, 4979 CrossRef CAS.
- Where k is the rate constant describing the forward kinetic process defined in eqn (2) as kF and K is the thermal equilibrium constant calculated from the final conversions.
- (a) D. Y. Curtin, Rec. Chem. Prog., 1954, 15, 111 CAS; (b) P. I. Pollak and D. Y. Curtin, J. Am. Chem. Soc., 1950, 72, 961 CrossRef CAS; (c) J. I. Seeman, J. Chem. Educ., 1986, 63, 42 CrossRef CAS.
- J. I. Seeman, Chem. Rev., 1983, 83, 83 CrossRef CAS.
- The free rotation of the C–N bond of enamine 4, becomes important only at the TS level. In other words, since the two enamine conformers are converting at a higher speed with respect to the stereodetermining step of the reaction, only the most stable conformer (s-trans enamine) can be taken in consideration.
- J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall, Upper Saddle River, NJ, 2nd edn, 1998 Search PubMed.
- S. E. Wheeler, A. Moran, S. N. Pieniazek and K. N. Houk, J. Phys. Chem. A, 2009, 113, 10376 CrossRef CAS PubMed.
- P. O. Hubin, D. Jacquemin, L. Leherte and D. P. Vercauteren, Chem. Phys., 2014, 434, 30 CrossRef CAS.
- The used rate constants
were calculated with the formula
 where kB and h are respectively the Boltzmann's and Planck's constants, R the gas constant, QR(T) is the partition function of the reactants and Q‡(T) of the transition state. ΔE‡ is the reaction activation energy. For monomolecular reactions the dimensions are s−1, while for bimolecular reactions the units are M−1 s−1.
(a) E. Wigner, Trans. Faraday Soc., 1938, 34, 29 RSC;
(b) H. Eyring, Chem. Rev., 1935, 17, 65 CrossRef CAS;
(c) H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS;
(d) W. H. Miller, Acc. Chem. Res., 1993, 26, 174 CrossRef CAS;
(e) W. H. Miller, J. Chem. Phys., 1974, 61, 1823 CrossRef CAS;
(f) E. Pollak, J. Chem. Phys., 1986, 85, 865 CrossRef CAS;
(g) M. Ceotto, S. Yang and W. H. Miller, J. Chem. Phys., 2005, 122, 044109 CrossRef PubMed;
(h) M. Ceotto and W. H. Miller, J. Chem. Phys., 2004, 120, 6356 CrossRef CAS PubMed;
(i) W. H. Miller, Y. Zhao, M. Ceotto and S. Yang, J. Chem. Phys., 2003, 119, 1329 CrossRef CAS;
(j) M. Ceotto, Mol. Phys., 2011, 110(9–19), 547–559 Search PubMed.
where kB and h are respectively the Boltzmann's and Planck's constants, R the gas constant, QR(T) is the partition function of the reactants and Q‡(T) of the transition state. ΔE‡ is the reaction activation energy. For monomolecular reactions the dimensions are s−1, while for bimolecular reactions the units are M−1 s−1.
(a) E. Wigner, Trans. Faraday Soc., 1938, 34, 29 RSC;
(b) H. Eyring, Chem. Rev., 1935, 17, 65 CrossRef CAS;
(c) H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS;
(d) W. H. Miller, Acc. Chem. Res., 1993, 26, 174 CrossRef CAS;
(e) W. H. Miller, J. Chem. Phys., 1974, 61, 1823 CrossRef CAS;
(f) E. Pollak, J. Chem. Phys., 1986, 85, 865 CrossRef CAS;
(g) M. Ceotto, S. Yang and W. H. Miller, J. Chem. Phys., 2005, 122, 044109 CrossRef PubMed;
(h) M. Ceotto and W. H. Miller, J. Chem. Phys., 2004, 120, 6356 CrossRef CAS PubMed;
(i) W. H. Miller, Y. Zhao, M. Ceotto and S. Yang, J. Chem. Phys., 2003, 119, 1329 CrossRef CAS;
(j) M. Ceotto, Mol. Phys., 2011, 110(9–19), 547–559 Search PubMed. - MATLAB 8.0 and Statistics Toolbox 8.1, The MathWorks, Inc., Natick, Massachusetts, United States Search PubMed.
- Since the differential equations are solved by a numerical method, only discrete reaction times are available. Thus, the simulation times may differ from different reactions accordingly with the availability of similar time values in the numerical solution.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, calculated energies, geometries and simulations. See DOI: 10.1039/c6sc01328g |
| This journal is © The Royal Society of Chemistry 2016 |