Open Access Article
Open Access ArticleThermostability and photoluminescence of Dy(III) single-molecule magnets under a magnetic field†
Ye
Bi
a,
Cheng
Chen
b,
Yi-Fang
Zhao
a,
Yi-Quan
Zhang
c,
Shang-Da
Jiang
a,
Bing-Wu
Wang
*a,
Jun-Bo
Han
b,
Jun-Liang
Sun
a,
Zu-Qiang
Bian
a,
Zhe-Ming
Wang
a and
Song
Gao
*a
aBeijing National Laboratory for Molecular Sciences, State Key Laboratory of Rare Earth Materials Chemistry and Applications, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China. E-mail: wangbw@pku.edu.cn; gaosong@pku.edu.cn
bWuhan National High Magnetic Center, Huazhong University of Science and Technology, Wuhan 430074, China
cJiangsu Key Laboratory for NSLSCS, School of Physical Science and Technology, Nanjing Normal University, Nanjing 210023, China
First published on 12th May 2016
Abstract
A series of compounds [ADyL4]·[solvent] composed of a dysprosium(III) ion coordinated by four chelated naphthyridine-like ligands (L = 4-hydroxy-8-methyl-1,5-naphthyridine-3-carbonitrile) and an alkali metal ion (A = Na, K, Rb, Cs) were synthesized and characterized. They behave as single-molecule magnets under a zero dc field with an effective energy barrier of around 95 cm−1. Meanwhile, the main part, [ADyL4], of these SMMs is thermostable and sublimable. The geometric structures of three sublimed compounds are identical to the original ones without solvents, which is confirmed by X-ray diffraction using single crystal and powder samples. The static and dynamic magnetic properties remain unchanged before and after sublimation. Luminescence measurements at 5–77 K were performed to verify the energy gap between low-lying states and to understand the pathway of the thermal relaxation process of magnetization, as well as to inspect the tiny variation in magnetic sublevels for the ground term of Dy(III). The photoluminescence spectra under a magnetic field (0–36 T) for the Dy-SMMs are investigated for the first time. The energy splitting of the two lowest sublevels of the ground term 6H15/2 of Dy(III) are analyzed using the Zeeman formula.
Introduction
In recent years many novel and modern electronic products bear witness to how fast hi-tech has changed the lives of human beings. As candidate materials for applications in high-density information storage,1,2 molecular spintronics3,4 and quantum computing,5,6 single-molecule magnets (SMMs) have been explored deeply and widely.7,8 Development of syntheses for these compounds offers the opportunity for generalizing SMM design rules empirically9,10 and understanding the magnetic relaxation mechanism in depth,11,12 as well as organizing various molecules on a surface for device fabrication.13,14 So far some interesting SMMs are transferred to the substrates via the vapor (e.g. sublimation) or liquid (e.g. drop casting, spin-coating, immersing)15–18 phase. Moreover, they could be arranged on a surface in the solid state by mechanical exfoliation which is explored to isolate an ultrathin layer of a 2-D complex on the surface.19 There are a lot of choices of suitable methods to transfer materials onto substrates, and plenty of amazing SMMs containing f-electrons have been investigated.20–26 However, lanthanide-based SMMs which could be successfully transferred or arranged on surfaces are few.27–29 One of the important factors affecting Ln-SMM behavior on surfaces is that the splitting of the magnetic sublevels of 4f-electrons by the ligand field is sensitive to the coordination environment,30–35 which would change dramatically before and after transfer onto the substrates.To investigate the behavior of individual molecules on surfaces,36–39 more methods to comprehensively characterize bulk properties, especially the energies of the magnetic sublevels for the ground term, are required. For the definition of a qubit, the SMMs' states for encoding quantum information ought to be scalable, that is well-defined.40 A common way of scaling magnetic low-lying states is fitting the dynamic magnetic susceptibilities through one or several magnetic relaxation processes (Direct, Raman and Orbach processes) in a certain temperature range, while multi-parameter nonlinear fitting may lead to a large range of energy barriers for spin reversal. The fitted energy barriers under zero and weak magnetic fields are different for Ln-SMMs with large ligand field splitting, and there is no evidence to corroborate which value signifies the energy gap between the magnetic low-lying states. Usually, ab initio calculations are employed to confirm the energy gap between the sublevels.41 Other approaches have been reported, such as FIR42 and luminescence.43 Among these methods the energy barriers obtained from luminescence spectra coincide well with the results derived from AC susceptibilities, either at room temperature or around 10 K for different systems.44–46 As far as we know, the effect of an external magnetic field on the luminescence of Ln-SMMs has not been reported yet. It is notable that luminescence spectra under varying external magnetic fields present the positions of the sublevels of the ground term, while this energy splitting may be difficult to obtain via the electron paramagnetic resonance technology, since the large ligand field splitting of Ln ions challenges the faculties of EPR in high frequency and high magnetic field.47
Following the discussion above, the sublimable SMMs featuring luminescence are good candidates for the manufacture of a molecular spintronics device, determination of the low-lying states at low temperature and even potential application in single molecule detection or quantum read-out. The molecule 8-hydroxyquinoline aluminum salt is famously thermostable, photoluminescent, has mobility for electron transfer, and is a wonderful material for organic electroluminescent diodes.48 The interesting magnetic properties of multi-nuclear Dy compounds based on 8-hydroxyquinoline have been reported.49,50 The compound NaEuL4 (HL = 4-hydroxy-8-methyl-1,5-naphthyridine-3-carbonitrile, abbreviated as 8-mCND) with a ligand similar to 8-hydroxyquinoline is found to be an outstanding red light emitting material.51 The way to make NaEuL4 is not as common as designing Ln-SMMs with bidentate ligands such as derivatives of β-diketonates.52–55 Inspired by this europium compound, a series of dysprosium complexes ADyL4 were synthesized. Each mononuclear dysprosium compound contains four chelate anions and a Dy(III) ion with an alkali metal counter cation (A = Na (1), K (2), Rb (3), Cs (4)). The structure, thermostability, static/dynamic magnetism, and photoluminescence properties were examined in detail for these four compounds; also the sublimed samples were characterized to check if they maintain their original properties after sublimation. Notably, luminescence spectra under a pulsed magnetic field which reveal the optical properties of the inorganic materials containing europium56 and erbium57–60 are recorded for the first time for Dy-SMMs to view the Zeeman splitting of the two lowest sublevels of 6H15/2.
Experimental section
General methods
All starting materials and solvents were commercially available and used without further purification. Ligand HL (8-mCND) was synthesized according to a published procedure.51Elemental analysis was performed using an Elementary Vario EL analyzer at Peking University. ESI-MS spectra were recorded on a Bruker APEX IV Fourier transform ion cyclotron resonance mass spectrometer detecting cations and anions.
{DyA} (A = Na (1), K (2), Rb (3), Cs (4))
A 20 ml ethanol solution of base (4 mmol NaOH (1), 4 mmol tBuOK (2), 2 mmol Rb2CO3 (3), 2 mmol Cs2CO3 (4)) was added to a slurry of HL (4 mmol 0.74 g) in 50 ml of alcohol in a 250 ml round flask. Then, DyCl3·6H2O (1 mmol 0.38 g) was dissolved in 20 ml of ethanol and decanted into the flask. The liquid was almost transparent. The solution was refluxed with stirring for one day. The yellow raw product precipitated and was filtered and washed with ethanol. To obtain the pure target product as crystals, it was necessary to refine the raw product before recrystallization. The dried solid was dissolved in 200 ml of anhydrous acetone, then filtered under atmosphere. The filtrate was rotary evaporated under vacuum and concentrated until a small amount of precipitate was generated. The mixture was poured into a beaker and dried in a fume cupboard. An amorphous product was obtained (in yields of more than 65% for 1–4).The amorphous solids (0.2803 g (1), 0.2923 g (2), 0.2974 g (3), 0.3092 g (4)) were dissolved in 10 ml of acetone, and 2 ml of methanol was added. Then the mixture was filtered into the beaker containing 1 ml of acetone. The transparent filtrate was slowly evaporated at room temperature. After several days, yellow crystals were obtained (more than 20% for 1–4).
[Na2Dy2(8-mCND)8(CH3OH)(Me2CO)]·[Me2CO]0.5 (1). IR: ν = 3582 (br), 3516 (br), 3044 (w), 2985 (w), 2923 (w), 2655 (w), 2575 (w), 2490 (w), 2218 (m), 1709 (w), 1634 (w), 1595 (w), 1558 (m), 1505 (s), 1472 (m), 1412 (m), 1376 (m), 1366 (sh), 1300 (w), 1281 (w), 1260 (w), 1231 (w), 1201 (m), 1096 (w), 1033 (w), 987 (w), 931 (w), 866 (w), 848 (w), 822 (w), 731 (m), 714 (w), 666 (w), 633 (w), 611 (w) cm−1. IR spectra for compounds 2–4 are nearly the same with the one for compound 1 (see ESI†). Calculated for C85.50H61O10.50N24Dy2Na2 (%) C: 52.30, N: 17.12, H: 3.13; found (%) C: 52.16, N: 17.09, H: 3.21.
[KDy(8-mCND)4(CH3OH)(Me2CO)]2·[Me2CO]2 (2). Calculated for C94H80O14N24Dy2K2 (%) C: 51.96, N: 15.47, H: 3.71; found (%) C: 51.79, N: 15.50, H: 3.55.
[RbDy(8-mCND)4(CH3OH)(Me2CO)]2·[Me2CO]2 (3). Calculated for C94H80O14N24Dy2Rb2 (%) C: 49.83, N: 14.84, H: 3.56; found (%) C: 49.82, N: 14.80, H: 3.47.
[CsDy(8-mCND)4(CH3OH)(Me2CO)]2·[Me2CO]2 (4). Calculated for C94H80O14N24Dy2Cs2 (%) C: 47.83, N: 14.24, H: 3.42; found (%) C: 49.81, N: 14.19, H: 3.33.
Sublimation
The amorphous products of 1–4 ({DyNa} (1), {DyK} (2), {DyRb} (3), {DyCs} (4)) were warmed up to 200 °C at 100 Pa, then the samples were gradually heated to 350 °C for 1, 350 °C for 2, 335 °C for 3, and 330 °C for 4, at around 10−4 Pa. The sublimed products was collected at ca. 270 °C. Two or three days later, the surface material was slightly carbonized, and it was cooled slowly. Faint yellow crystalline powders of 5–8 sublimed from 1–4 respectively ({DyNa}sub (5) in a yield of 15%, {DyK}sub (6) in a yield of 15%, {DyRb}sub (7) in a yield of 15%, and {DyCs}sub (8) in a yield of 25%) were obtained. A crystal of 8 suitable for SXRD was obtained through cooling by resting ([Cs2Dy2(8-mCND)8(H2O)0.5]2 (8)). Though 5–8 were produced in low yield, the heated raw material could be recycled using acetone. It was attempted to heat the crystal sample of 3 to sublimation, and sublimed compound 7 was attained in the same way but in a lower yield.Elementary analysis of C, N, and H and mass spectrometry data for compounds 5–8 are listed in Table S1.† IR spectra of compounds 5–8 are comparable with the ones of compounds 1–4 respectively except for one peak at 1709–1713 cm−1 which is assigned to the asymmetric stretching vibration of the carbonyl group from acetone lost after sublimation (see the ESI†).
Crystallography
Crystallographic data at 180 K for single crystals were collected on an Aglient Technologies Super Nova Atlas Dual System, with two sorts of microfocus sources (Mo Kα = 0.71073 Å for compounds of 1–4, Cu Kα = 1.5406 Å for 8) and focusing multilayer mirror optics. Determination of the crystal system and unit cell parameters was executed by the CrysAlisPro9 program. The integration, reduction and absorption correction of raw frame data was performed using the same program. All the structures were solved by a direct method and refined by full-matrix least-squares on F2 SHELX program. The H atoms of coordinated solvents with hydrogens bond were able to be located from difference Fourier synthesis, and other H atoms could be added according to the ideal geometry. Crystallographic data have been deposited with the Cambridge Crystallographic Data Centre as supplementary publication numbers CCDC 1446709 (1), CCDC 1446710 (2), CCDC 1446711 (3), CCDC 1446712 (4), and CCDC 1446713 (8).†Powder X-ray diffraction (PXRD) data for compound 5 were collected using synchrotron radiation (λ = 0.826651 Å) at the Beamline I11, Diamond Light Source, Didcot, UK. High resolution PXRD for 6–8 was performed on a PANalytical Empyrean diffractometer equipped with a Pixel detector and using Cu Kα radiation (λ = 1.5418 Å), and the data were collected in transmission mode. Le Bail fitting of the unit cell parameters for 5–8 was performed using JANA software.61
TGA
Characterization of thermostability for 1–8 was performed using a Q600 SDT under an air atmosphere at a heating rate of 5 °C min−1 from room temperature to 800 °C.Magnetic measurement
Magnetic measurements were carried out on a Quantum Design MPMS XL-5 SQUID magnetometer in RSO mode for DC susceptibility except {DyNa}sub by VSM option of PPMS-9, and ACMS option of PPMS-9 for AC susceptibilities. Samples of 1–4 were encapsulated by N-grease in a capsule, while the crystalline powders of 5–8 were wrapped by parafilm in the capsule. Magnetic data were corrected with N-grease or parafilm, capsule and Pascal’s constants.Photoluminescence measurements
The determination of excitation wavelength for compounds 1–4 was carried out on a FLS 920 at 77 K by fixing the detection wavelength of 485 nm or 575 nm and continuously changing the wavelength of incident light. For compound 8, the emission signal was collected on a FLS980 at 77 K using a picosecond pulse light emitting diode in the wavelength of 340 ± 10 nm (40 μW) with a 5 nm scan slit, 1 nm step, 0.5 s dwell time and 2 cycles. Under the same conditions, it was not successful when using the 450 W Xe arc lamp.More detailed luminescence spectra were attained in a photoluminescence measurement setup under a pulsed high magnetic field.56,60,62 A laser beam doubled from a Ti:sapphire laser (Mira 700, Coherent; 76 MHz, 130 fs; 1 mW) was launched and focused into a fiber by a quartz lens. The sample was compacted and contacted with the fiber which transmitted the input laser and collected the photoluminescence emission. Then the signal was recorded using an EM-CCD (Andor DU970P) through a monochromator (Andor SR500). The exposure time of each luminescence spectrum was about 1 ms unless indicated otherwise. The sample was cooled in a cryostat, wherein the temperature was varied from 77 K to 5 K. The magnitude of magnetic field is detected at the falling side of a magnetic pulse. Emission spectra in a temperature range from 10 to 77 K for 4 and from 10 to 55 K for 8 were excited using a diode pumped solid laser of 355 nm (4000 Hz, less than 10 mW), since the Ti:sapphire laser stopped working accidentally.
Ab initio calculations
Complete active space self-consistent field (CASSCF) calculations on the Dy fragments extracted from compounds 1–4 and 8 on the basis of X-ray determined geometries were carried out with the MOLCAS 7.8 program package63 (see Fig. 8(a) and (b), S41–S43†). The solvent molecules are omitted in the figures but partly included in calculations with an O atom from methanol or water and with an O atom and a C atom containing a carbonyl group from acetone. Since the Dy⋯Dy distances in the five compounds are very long, we did not consider Dy⋯Dy interactions in the calculations. For CASSCF calculations, the basis sets for all atoms are atomic natural orbitals from the MOLCAS ANO-RCC library: ANO-RCC-VTZP for the DyIII ion, VTZ for close O and N, and VDZ for distant atoms. The calculations employed the second order Douglas–Kroll–Hess Hamiltonian, where scalar relativistic contractions were taken into account in the basis set and spin–orbit coupling was handled separately in the restricted active space state interaction (RASSI-SO) procedure. The active electrons in the 7 active spaces include all f electrons CAS (9 in 7) for compounds 1–4 and 8 in the CASSCF calculations. To exclude all the doublets, all the roots in the active space are calculated. We have mixed the maximum number of spin-free states which was possible with our hardware (all from 21 sextets, 128 from 224 quadruplets and 130 from 490 doublets for DyIII fragments).Results and discussion
Crystallography
Crystals of compounds 1–4, which are simplified as {DyNa} (1), {DyK} (2), {DyRb} (3), {DyCs} (4), respectively, were prepared suitably for single crystal X-ray diffraction. 1 crystallized in the P21/n space group, and the other three isostructural compounds 2–4 are in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group (Tables 1 and S2–S5†). There are 4 (for 1) or 1 molecules (for 2–4) per unit cell. Two identical Dy(III) ions are located in a centrosymmetric molecule in compounds 2–4. Each Dy ion is chelated by N and O atoms from four identical ligands, [L]−. To compensate for the electric neutrality, an alkali metal ion lies near a Dy ion at a distance of 3.4362(13) Å or 3.4200(14) Å for 1 and 3.8616(6) Å, 4.0553(5) Å and 4.2668(3) Å for 2–4, respectively, by sharing three O atoms from the ligands with the trivalent lanthanide ion (Fig. 1 and S1–S4†). Each counter ion in 2–4 is surrounded by O atoms from two solvent molecules (methanol and acetone) and N atoms from the three cyan groups. One of the N atoms coordinating to the counter ion links the adjacent asymmetric unit to a whole molecule with an inversion center (Fig. S2–S4†). The Na ion of small radius carries only one methanol molecule for Na1 and one acetone for Na2, thus the two units are without an inversion center (Fig. S1†). The interaction between Na and N atoms from the nearby molecules extends the compound to a 2-D structure within the ab plane which stacks along the c axis by H bonding and π–π interactions (Fig. S5 and S6†). However, the structural differences between compounds 1–4 are small when considering Dy(III) and their surroundings. In compounds 1–4, each Dy(III) ion is located in a distorted dodecahedron with CShM64 values of 0.993 and 1.089 for (1) and 1.232, 1.195 and 1.247 for 2–4, respectively. Different from the compounds containing short bridged Dy(III) ions,65,66 there is no short bridge between Dy(III) ions in compounds 1–4. For compounds 1–4, the ranges of bond lengths for Dy–O and Dy–N are close to each other (Table S7†). The distance of intramolecular dysprosium in 1–4 is in the range from 10.4861(2) to 11.0659(6) Å, and the shortest distance of intermolecular dysprosium is from 9.9659(4) to 10.4445(3) Å. The H-bonds of N⋯O between molecules (2.851(4) Å for 1, 2.830(3) Å for 2, 2.816(5) Å for 3, and 2.810(4) Å for 4) and π–π stacking are depicted in Fig. S6–S8.†
space group (Tables 1 and S2–S5†). There are 4 (for 1) or 1 molecules (for 2–4) per unit cell. Two identical Dy(III) ions are located in a centrosymmetric molecule in compounds 2–4. Each Dy ion is chelated by N and O atoms from four identical ligands, [L]−. To compensate for the electric neutrality, an alkali metal ion lies near a Dy ion at a distance of 3.4362(13) Å or 3.4200(14) Å for 1 and 3.8616(6) Å, 4.0553(5) Å and 4.2668(3) Å for 2–4, respectively, by sharing three O atoms from the ligands with the trivalent lanthanide ion (Fig. 1 and S1–S4†). Each counter ion in 2–4 is surrounded by O atoms from two solvent molecules (methanol and acetone) and N atoms from the three cyan groups. One of the N atoms coordinating to the counter ion links the adjacent asymmetric unit to a whole molecule with an inversion center (Fig. S2–S4†). The Na ion of small radius carries only one methanol molecule for Na1 and one acetone for Na2, thus the two units are without an inversion center (Fig. S1†). The interaction between Na and N atoms from the nearby molecules extends the compound to a 2-D structure within the ab plane which stacks along the c axis by H bonding and π–π interactions (Fig. S5 and S6†). However, the structural differences between compounds 1–4 are small when considering Dy(III) and their surroundings. In compounds 1–4, each Dy(III) ion is located in a distorted dodecahedron with CShM64 values of 0.993 and 1.089 for (1) and 1.232, 1.195 and 1.247 for 2–4, respectively. Different from the compounds containing short bridged Dy(III) ions,65,66 there is no short bridge between Dy(III) ions in compounds 1–4. For compounds 1–4, the ranges of bond lengths for Dy–O and Dy–N are close to each other (Table S7†). The distance of intramolecular dysprosium in 1–4 is in the range from 10.4861(2) to 11.0659(6) Å, and the shortest distance of intermolecular dysprosium is from 9.9659(4) to 10.4445(3) Å. The H-bonds of N⋯O between molecules (2.851(4) Å for 1, 2.830(3) Å for 2, 2.816(5) Å for 3, and 2.810(4) Å for 4) and π–π stacking are depicted in Fig. S6–S8.†
| SXRD | PXRD | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| {DyNa} (1) | {DyK} (2) | {DyRb} (3) | {DyCs} (4) | {DyCs}sub (8) | {DyNa}sub (5) | {DyK}sub (6) | {DyRb}sub (7) | {DyCs}sub (8) | |
| Space group | P21/n |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/n | P21/n | P21/n | P21/n | P21/n |
| a (Å) | 19.0396 | 12.3164 | 12.1604 | 12.1005 | 19.5421 | 27.3614 | 19.5033 | 19.5585 | 19.6076 |
| b (Å) | 20.9444 | 14.0599 | 14.3443 | 14.5976 | 19.8322 | 10.3860 | 19.7216 | 19.7786 | 19.8579 |
| c (Å) | 20.8471 | 14.9899 | 14.9780 | 14.9807 | 20.8863 | 19.8914 | 20.8554 | 20.9091 | 21.1585 |
| α (°) | 90 | 85.328 | 83.549 | 82.535 | 90 | 90 | 90 | 90 | 90 |
| β (°) | 93.561 | 68.185 | 68.800 | 69.080 | 97.266 | 135.672 | 97.3815 | 97.3815 | 97.6077 |
| γ (°) | 90 | 84.879 | 83.086 | 81.967 | 90 | 90 | 90 | 90 | 90 |
| V (Å3) | 8297.2 | 2396.98 | 2411.43 | 2438.30 | 8029.7 | 3949.9 | 7955.6 | 8021.4 | 8165.9 |
| Z | 4 | 1 | 1 | 1 | 2 | 4 | 2 | 2 | 2 |
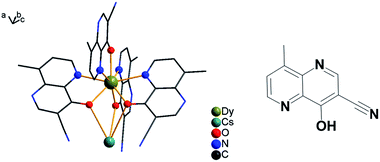 | ||
| Fig. 1 Asymmetric structural unit for compound {DyCs} (4) is shown; solvents are omitted and other coordination bonds are avoided for clarity (left). The ligand of HL is depicted (right). | ||
The structure of sublimed sample 8, named {DyCs}sub, has been determined by X-ray diffraction. The compound 8 crystallizes in the P21/n space group, with 2 molecules in a unit cell (Table S6†). In each centrosymmetric molecule, the coordination polyhedron of two different Dy ions are akin to the one in 4 (Fig. S9†). Similar bond lengths of Dy–O and Dy–N and similar bond angles of Dy ions are found for 8 (Tables S7 and S8,† CShM values: 0.724 for Dy1 and 1.496 for Dy2). The shortest intra- and inter-molecular distances of dysprosium is 9.6614(4) and 10.4406(4) Å, respectively. Also the intramolecular H bonds are 2.873(18) and 3.103(16) Å in length between the N and O atoms. The intermolecular interaction is the electrostatic interactions between N atoms from the cyan groups and Cs ions in Fig. S10†.
The intensity data vs. diffraction angle of the powder sample 8 is plotted and indexed to give the parameters of the unit cell after the background has been subtracted (Table 1, Fig. 2). The powder diffraction plot is in good agreement with the one calculated from the single crystal structure, and the unit cell parameters are comparable with the ones at 180 K from SXRD, with the small disparity probably due to the influence of temperature. The diffraction data of powder samples for {DyNa}sub (5), {DyK}sub (6) and {DyRb}sub (7) were obtained and are plotted in Fig. S11.† The peaks of diffraction patterns for samples 6 and 7 both coincide with those of 8 but those for 6 are slightly shifted to a higher 2θ angle which may be attributed to the decrease of its unit cell (Fig. S11(a)†, Table 1). However, the PXRD pattern of 5 is different both to the other sublimed samples 6–8 and to the original compound 1 (Fig. S11(b)†, Table 1). The unit cell parameters are attained through indexing the intensity curves and confirmed by Le Bail fitting,61 and it is obvious that compounds 6–8 are isostructural, while 5 is distinct from 1 and from 8. (Fig. S12†).
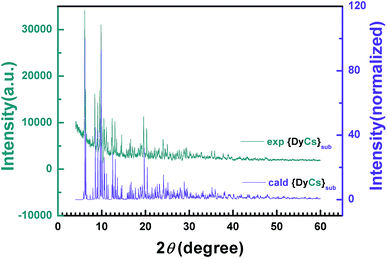 | ||
| Fig. 2 2-D diffraction patterns from PXRD experiments and the calculated data from SXRD are compared with each other. | ||
Thermostability and composition
The weights of samples 1–8 are recorded when gradually heated to 800 °C under an air atmosphere (Fig. 3 and S13†). From room temperature to 200 °C, the weight loss for 1–4 coincides with the mass proportion of methanol and acetone for the whole molecule, indicating that the solvents, both coordinated and in the lattice, are totally lost. The small weight loss in the range from room temperature to 200 or to 300 °C for compounds 5–8 (0.3158% or 0.5429% for 8) is possibly ascribed to the loss of trace water coordinated (calcd 0.434% for 8) and/or adsorbed in the molecules (Fig. S13†). Afterwards, the thermogravimetric plots for 1–8 remain independent of temperature, implying that the entity ADyL4 is stable up to 400 °C. Then, the compounds start to decompose, and finally burn into metallic oxides. Noting that all compounds decomposed before sublimation at barometric pressure, the sublimation was executed in high vacuum.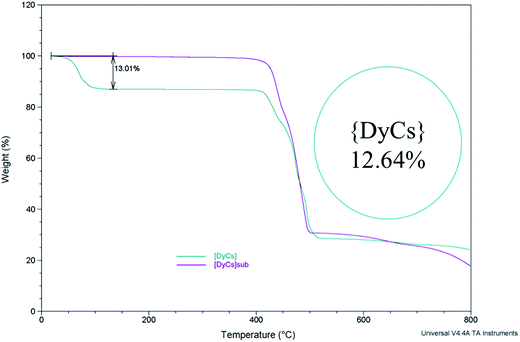 | ||
| Fig. 3 The thermogravimetry curves show the stability of compounds {DyCs} (4) and {DyCs}sub (8) while heating; the inset shows the calculated mass percentage of all the solvent in a molecule. | ||
The similar temperature range of decomposition for 5–7 to compounds 1–3 respectively might demonstrate the existence of the entity ADyL4. Indeed, the compositions of 5–7 could be deduced from mass spectra with [DyL4]− and [H + ADyL4]+, and are confirmed by elementary analysis (see the Experimental section and Table S1†). Therefore, the compositions of 5–7 are determined to be NaDyL4, KDyL4 and RbDyL4, respectively, thus the molecular formulae are simply defined as [NaDyL4], [KDyL4]4 and [RbDyL4]4, considering that 6 and 7 are isostructural with 8 the Z values for compounds 5–7 in Table 1 are derived.
From the discussions above, we can come to three conclusions on the structures and compositions of 1–8: (I) the structure of the entity [DyL4]− of 1–4 remains unchanged mostly, though alkali metal ions with increased radii are induced. The larger counter ion results in a longer Dy⋯A distance but no significant distinction of the polyhedron of Dy ions. (II) After sublimation, the entity [DyL4]− is almost unaltered with only slightly shorter Dy–N and Dy–O bond lengths observed when comparing 4 with 8. Compounds 6 and 7 are isomorphic with 8. (III) The structure of 5 is different to that of 1. To summarise, the essential stability of the entity [DyL4]− with its counter ion is almost unchanged constituently and structurally, whatever alkali metal ion is linked (1–4) and however the compounds have been synthesized, in solvent or in vapor (4 or 8).
Static magnetic properties
The direct current (dc) susceptibilities under 1000 Oe were obtained from 2–300 K for the eight compounds 1–8 (Fig. 4 and S14†). The χMT values at 300 K were 27.71, 27.69, 27.01 and 27.75, and 13.60, 57.52, 58.55 and 58.25 emu K mol−1 for compounds 1–4 and 5–8, respectively, agreeing well with those anticipated for single (14.17 emu K mol−1), double (28.34 emu K mol−1) or quadruple (56.68 emu K mol−1) free Dy ions (6H15/2). On cooling, the χMT value gradually decreases until ca. 50 K and then tends to drop sharply from 5 K. This gentle decline could be ascribed to the depopulation of Stark levels and/or inter-/intra-molecular interactions.67,68 At 2 K, the molar magnetization increases along with the dc field and reaches 9.91, 9.95, 9.63, 9.92, 5.28, 21.57, 22.23 and 20.95 Nβ up to 50 kOe, but is smaller than the saturation value (10 Nβ per Dy) (Fig. S15†). This large deviation from the saturated values may be attributed to the magnetic anisotropy of the Dy(III) ion that eliminates the 16-fold degeneracy of the 6H15/2 ground state.69,70 The non-superposition of the plots of M vs. HT−1 at 2, 3, 5, 8 and 10 K indicates the existence of zero-field splitting which is caused by the ligand field of the Dy ion71 (Fig. S16–S17†). At an average sweeping rate of 10 Oe s−1 for scanning the external field, no magnetic hysteresis loop is observed at 1.8 K for compounds 1–4 and 6–8 (Fig. S18 and S19†).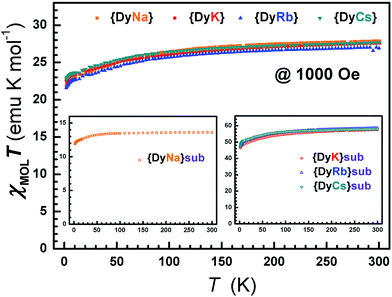 | ||
| Fig. 4 The dc susceptibilities demonstrate the static magnetic behavior with temperature for compounds 1–8. | ||
Dynamic magnetic properties
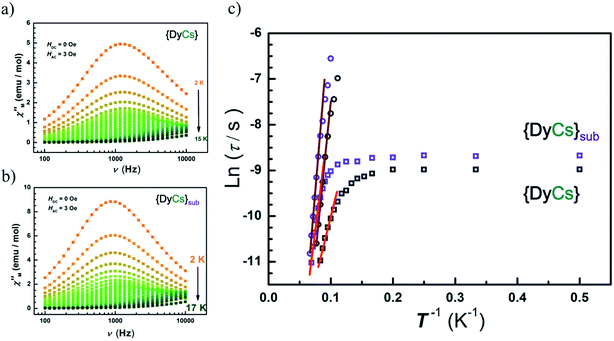
Alternative current (AC) magnetic susceptibility data were collected under a 3 Oe oscillating field at a frequency between 100 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz below 25 K. The peaks of χ′′(T) plots are clearly observed in the temperature range from 10 to 14 K for all compounds except 5 of which χ′′(T) shows a platform instead (Fig. S20–S21†). The maxima of χ′′(υ) emerge in temperature range from 2 K to 14 K for compounds 1–4, and 6–8, while no maximum is found for any χ′′(υ) curves of compound 5 (Fig. S22–S23†). Apparently, the presence of a frequency dependence of AC susceptibilities at variable temperature in zero external field for compounds 1–4 and 6–8 demonstrates a typical property of SMMs featuring thermal activated transition accompanied by temperature independent quantum tunnelling of magnetization, ascribed to the single paramagnetic center. Also, the peak centers in the χ′′(υ) plots at the same temperature are close for compounds 4 and 8 (Fig. 5(a) and (b)).
000 Hz below 25 K. The peaks of χ′′(T) plots are clearly observed in the temperature range from 10 to 14 K for all compounds except 5 of which χ′′(T) shows a platform instead (Fig. S20–S21†). The maxima of χ′′(υ) emerge in temperature range from 2 K to 14 K for compounds 1–4, and 6–8, while no maximum is found for any χ′′(υ) curves of compound 5 (Fig. S22–S23†). Apparently, the presence of a frequency dependence of AC susceptibilities at variable temperature in zero external field for compounds 1–4 and 6–8 demonstrates a typical property of SMMs featuring thermal activated transition accompanied by temperature independent quantum tunnelling of magnetization, ascribed to the single paramagnetic center. Also, the peak centers in the χ′′(υ) plots at the same temperature are close for compounds 4 and 8 (Fig. 5(a) and (b)).
In order to analyze the thermal process, a certain dc field is optimized by depicting the plots of τ vs. H, and is applied to suppress the quantum tunnelling of magnetization (QTM) (Fig. S24–S25†). Then, AC susceptibilities under 1000 Oe were measured below 25 K for compounds 1–8. Peaks of χ′′(T) between 5 K and 15 K are clearly presented in sequence of increasing frequency (Fig. S26–S27†), while the positions of the peak centers of χ′′(υ) increase along with temperature from 6 K to 15 K (Fig. S28–S29†).
The Arrhenius formula (τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ueff/kBT)) is employed to fit the temperature dependent region in the plots of ln
exp(Ueff/kBT)) is employed to fit the temperature dependent region in the plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. 1/T, then the energy barriers for spin reversal under 0 Oe (Ueff = 18 cm−1 (1), 34 cm−1 (2), 42 cm−1 (3), 38 cm−1 (4), 54 cm−1 (6), 59 cm−1 (7), 74 cm−1 (8)) and τ0 (1.24 × 10−6 s (1), 3.74 × 10−7 s (2), 1.73 × 10−7 s (3), 1.86 × 10−7 s (4), 5.59 × 10−8 s (6), 3.82 × 10−8 s (7), 1.06 × 10−8 s (8)) are derived, while the QTM rate (time) could be read out in the temperature independent region (τQTM = 0.038 ms (1), 0.09 ms (2), 0.09 ms (3), 0.13 ms (4), 0.27 ms (6), 0.19 ms (7), 0.17 ms (8)). Eliminating interference from the process of QTM under 1000 Oe, the effective energy barriers for spin reversal are also obtained (Ueff = 96 cm−1 (1), 99 cm−1 (2), 99 cm−1 (3), 93 cm−1 (4), 56 cm−1 (5), 80 cm−1 (6), 103 cm−1 (7), 112 cm−1 (8)) in same way as with τ0 (1.69 × 10−10 s (1), 4.16 × 10−10 s (2), 7.23 × 10−10 s (3), 7.58 × 10−10 s (4), 2.74 × 10−9 s (5), 4.73 × 10−9 s (6), 7.89 × 10−10 s (7), 4.04 × 10−10 s (8)) (Fig. 5(c), S23(h) and S25(g)–(h)†). For compounds 1–4, the values of Ueff under 1000 Oe are very close to each other, while the Ueff values under zero dc field vary slightly, which may attribute to the different contributions from the temperature independent process. The more rapid the QTM is, the lower the value of Ueff that is observed for compounds 1–4. Additionally, the values of energy barrier under 1000 Oe for sublimed samples (6–8) agree well with those for the crystals grown from solvents (2–4). For compounds 1 and 5, the Ueff value is halved after sublimation.
τ vs. 1/T, then the energy barriers for spin reversal under 0 Oe (Ueff = 18 cm−1 (1), 34 cm−1 (2), 42 cm−1 (3), 38 cm−1 (4), 54 cm−1 (6), 59 cm−1 (7), 74 cm−1 (8)) and τ0 (1.24 × 10−6 s (1), 3.74 × 10−7 s (2), 1.73 × 10−7 s (3), 1.86 × 10−7 s (4), 5.59 × 10−8 s (6), 3.82 × 10−8 s (7), 1.06 × 10−8 s (8)) are derived, while the QTM rate (time) could be read out in the temperature independent region (τQTM = 0.038 ms (1), 0.09 ms (2), 0.09 ms (3), 0.13 ms (4), 0.27 ms (6), 0.19 ms (7), 0.17 ms (8)). Eliminating interference from the process of QTM under 1000 Oe, the effective energy barriers for spin reversal are also obtained (Ueff = 96 cm−1 (1), 99 cm−1 (2), 99 cm−1 (3), 93 cm−1 (4), 56 cm−1 (5), 80 cm−1 (6), 103 cm−1 (7), 112 cm−1 (8)) in same way as with τ0 (1.69 × 10−10 s (1), 4.16 × 10−10 s (2), 7.23 × 10−10 s (3), 7.58 × 10−10 s (4), 2.74 × 10−9 s (5), 4.73 × 10−9 s (6), 7.89 × 10−10 s (7), 4.04 × 10−10 s (8)) (Fig. 5(c), S23(h) and S25(g)–(h)†). For compounds 1–4, the values of Ueff under 1000 Oe are very close to each other, while the Ueff values under zero dc field vary slightly, which may attribute to the different contributions from the temperature independent process. The more rapid the QTM is, the lower the value of Ueff that is observed for compounds 1–4. Additionally, the values of energy barrier under 1000 Oe for sublimed samples (6–8) agree well with those for the crystals grown from solvents (2–4). For compounds 1 and 5, the Ueff value is halved after sublimation.
The thermal activated process is classified as an Orbach process only, since it fits well in the temperature-dependent region under 0 Oe and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ is almost proportional to 1/T under 1000 Oe (Fig. 5(c)). Also, Cole–Cole72 plots reveal the concentrated distribution of magnetic relaxation time by factor α (0.15–0.36 for 4 and 0.04–0.15 for 8 under 1000 Oe for example), indicating a single process for the spin relaxation dynamics (Fig. S30–S31, Table S9†).
τ is almost proportional to 1/T under 1000 Oe (Fig. 5(c)). Also, Cole–Cole72 plots reveal the concentrated distribution of magnetic relaxation time by factor α (0.15–0.36 for 4 and 0.04–0.15 for 8 under 1000 Oe for example), indicating a single process for the spin relaxation dynamics (Fig. S30–S31, Table S9†).
Photoluminescence properties
The lanthanides, especially in their trivalent state, are interesting for their fluorescence properties.73,74 High resolution fluorescence spectra are also an effective means to determine the energy levels of coordination compounds. In recent years they have been used to confirm the energy gaps between magnetic low-lying states for Ln-SMMs.43 Considering the {EuNa} analogy with the same ligands as “antenna” featuring outstanding red light emission,51 luminescence properties were explored to gain the magnetic energy levels under zero and pulsed magnetic fields. We analyze the experimental energy difference between the two lowest states of the ground term 6H15/2 of Dy(III).The emission spectra of compounds 1–4 were obtained in solid state at 77 K after excitation by light at 350 nm from a Xe lamp, with well-resolved peaks centered at 485 and 575 nm (Fig. S32(a)–(g)†). However, high resolution data for compound 8 was not possible to obtain with the Xe lamp and ps LED excitation sources, due to their very weak intensity (Fig. S32(h)†).
PL spectra under zero magnetic field
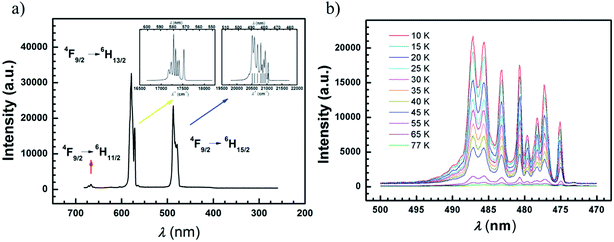
In order to gain accurate and fine luminescence spectra, measurements for compounds 1–4 were performed at 77 K using an equipment setup with a 350 nm laser (or diode pumped solid 355 nm laser) as a bright and monochromatic light source and an EMCCD as a spectrum recorder. The compound 4 was chosen for further characterization at lower temperature. The transitions of 4F9/2 → 6H11/2, 4F9/2 → 6H13/2, 4F9/2 → 6H15/2 at 5 K are classified for the Dy ion (Fig. 6(a)). Among them, the fine spectrum of the 4F9/2 → 6H15/2 transition is fitted by Gaussian function convolution of 8-components which are responsible for the 6H15/2 magnetic sublevels (Fig. S33†). The eight energy levels of the 6H15/2 term are listed in Table S10,† and the energy gap between the two lowest sublevels is 90 cm−1 ± 1 cm−1. This result is comparable with the value of the effective energy barrier (93 cm−1) deduced from the AC susceptibilities under a DC field of 1000 Oe, indicating that the first excited state is involved in the Orbach type relaxation of this compound. Similarly, the energy differences between the two lowest states for compounds 1–3 are derived from photoluminescence spectra at 77 K, and are comparable with the Ueff values under 1000 Oe (Fig. S34–S36, Tables S11–13†). However, due to the low intensity of the sublimed samples 5–7 the spectra are not well-resolved for Gaussian analyses (Fig. S37†). On cooling sample 8 down to 10 K, the well-resolved spectrum can be obtained, compared with the one for 4, and fitted by Gaussian functions (Fig. S38, Table S14†). The energy difference between the two lowest sublevels is 104 ± 3 cm−1, which is in a good agreement with the value of Ueff (112 cm−1).The transition of 4F9/2 → 6H15/2 for compound 4 and 8 at various temperatures (10–77 K for 4, 10–50 K for 8) does not shift but behaves more weakly upon warming, indicating that the transition from 4F9/2 to 6H15/2 arises from the ground state of 4F9/2 (Fig. 6(b) and S38(c)).† More than 8 peaks are observed at 10 K in compound 8, which may be due to the asymmetric environment of the two Dy ions. It is necessary to remark that fine luminescence spectra of rare earth ions can work as a reliable tool to evaluate the tiny energetic differences caused by structural variation.
PL spectra under pulsed magnetic fields
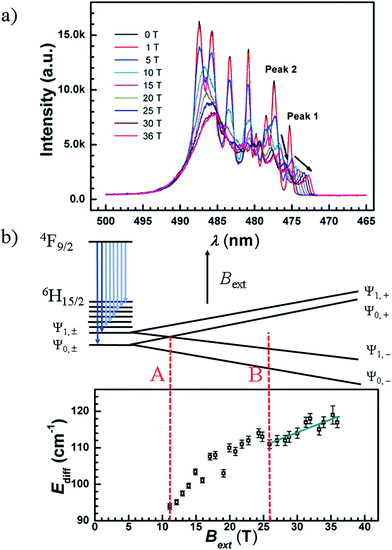
The luminescence spectra for compound 4 were recorded at 5 K under weak and strong pulsed magnetic fields at damping part. Under a weak external magnetic field (≤0.6 T), the spectrum lines are superimposed to the zero magnetic field one, the estimated Zeeman splitting energy is less than 2.8 cm−1 (far less than Ueff, Fig. S39†). This illustrates that when a weak external magnetic field is applied to the Ln-SMMs of high Ueff, the QTM is suppressed and the influence of the magnetic field on the energy gap is negligible. In a way, the Ueff under a weak magnetic field signifies the energy gap between the ground and excited states, and the one under zero dc field is employed to demonstrate the property of the SMM for potential applications in the absence of a magnetic field.Under a strong magnetic field up to 36 T, a shift of the emission peaks is observed, demonstrating the Zeeman effect (Fig. 7(a) and S40(a)†). Along with the field increasing to 36 T, the luminescence peaks blue shift. In Fig. 7(a), the emission peaks of longer wavelengths are strongly mixed and changed into an unstructured band, whereas the two emission peaks of the shortest wavelengths (peak 1 and peak 2) remain distinguishable from the others (Fig. S40(b)†). We took compound 4 to analyze the Zeeman effect. Since the compound behaves as an SMM with a large Ueff under an applied dc field of 1000 Oe, the ground (|Ψ0,±〉) and first excited states (|Ψ1,±〉) of 6H15/2 are assumed to be Ising type of MJ = ±15/2 and MJ = ±13/2, respectively (MJ represents the quantum number of the total angular momentum along the quantized axis). Therefore, for each paramagnetic ion, the Zeeman effect is simplified by only considering the splitting energy on the z axis which is proportional to the magnetic field. Given that the paramagnetic ions of the powder sample are randomly oriented, an average g-value is postulated, gave, and the Zeeman splitting energy is depicted in Fig. 7(b) and given by
| EZee = βgaveMJBext | (1) |
| Ediff = βgaveΔMJBext + E0, | (2) |
It is interesting to see that, the two emissions with the shortest wavelengths in the fine structure of the 4F9/2 → 6H15/2 transition are split into two pairs, when Bext = 4, 5, 6 or 7 T (Fig. S41†). Under a 7 T magnetic field, the relative splitting energy caused by the magnetic field corresponds to 63 cm−1 (|Ψ0,±〉) and 52 cm−1 (|Ψ1,±〉), comparable with the estimations of 64 cm−1 and 56 cm−1 from eqn (1) with gave = gJ (gJ = 4/3, the Landé g-factor for the Dy ion).
Noting that splitting of doublets under the magnetic field could be observed, an appropriate Bext range was cautiously selected for the analyses. The spectra at various fields cover the level crossing of the two lowest doublets which is depicted as case A (the summation of the absolute value of the EZee for |Ψ0,+〉 and |Ψ1,−〉 is equal to 90 cm−1, Bext ≈ 11 T, Fig. 7(b)), while the relative emissions are highly mixed, it is difficult to resolve the shift of these lines as a function of the magnetic field at and below the crossing field. When the applied magnetic field is above 26 T, the emission peaks of the transitions to |Ψ0,−〉 and |Ψ1,−〉 are well separated from the other lines, depicted as case B in Fig. 7(b), offering the ease of analyzing energy difference vs. field formulated in eqn (2). The gave is fitted to be 1.5 ± 0.2 with an intercept, E0, of 100 ± 2 cm−1 which is comparable with the 90 ± 1 cm−1 derived from the luminescence spectrum under zero magnetic field. It is notable that the fitted value of gave is consistent with the theoretical expectation (gJ = 4/3 ≈ 1.33), indicating that the ground and first excited states are dominated by the MJ = ±15/2 and MJ = ±13/2 states, respectively. The relatively large uncertainty may result from the experimental values of Ediff fitted simply by Gaussian functions. At a high magnetic field, the luminescence intensity decreases and the profile of peaks becomes worse fitted (Fig. S42†). Another reason is the assumption that the ground and first excited states are pure Ising type (Table S17†).
Theoretical analysis
In order to understand the direction of the magnetic easy axis and fine electronic structure of the molecules, we performed post-Hartree–Fock ab initio calculations based on the relativistic quantum chemistry method CASSCF/RASSI/SINGLE_ANISO.75 This approach, implemented in the MOLCAS package,63 has already been widely used as a powerful tool to extract information about the electronic structure of ground and low-lying excited states.The calculated energies of the sublevels for 6H15/2 and the diagonal elements of effective g tensors for the ground Kramers doublets are tabulated in Tables S15 and S16.† The calculated values of χMT in the temperature range of 2–300 K and magnetization at 2 K are consistent with the experimental data ((a)–(e) in Fig. S14–S15†).
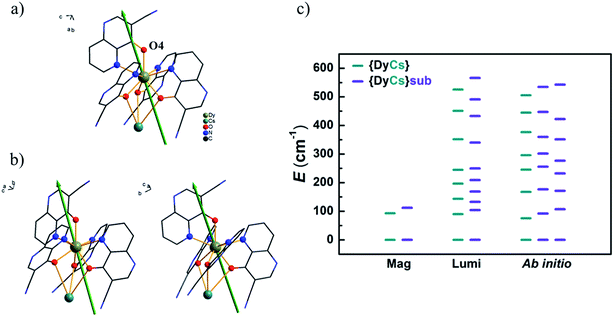
Usually the gz values of the reported prominent Dy-SMMs always approach 20, as expected for pure states of |±15/2〉 in a pseudospin model for Ising limit ground doublets. For compounds 1–4 and 8, the calculated gz values are from 19.61 to 19.78 and the components in the xy-plane of gx and gy are less than 0.03, which indicates that these molecules are in good uniaxial anisotropy. The unnegligible transverse term of g values induces fast quantum tunnelling of magnetization ((c) in Fig. S43–S45† and (a)–(c) in Fig. S46, Tables S15 and S16†). Taking compound 4 as an example, the easy axis of magnetization is orientated closely to the Dy–O4 bond. The angle between the easy axis and Dy–O4 bond is 19° (Fig. 8(a)). It is the same situation for compounds 1–3 and 8; the intersection angles are 22° and 21° for Dy1 and Dy2 of 1, 21° for 2, 19° for 3, and 17° and 19° for Dy1 and Dy2 of 8, respectively (Fig. 8(b) and (b) in Fig. S43–S45†). Additionally, for compounds 1–4 and 8, the calculated energy differences between the two lowest sublevels confirm the results of the AC susceptibilities under 1000 Oe and the luminescence spectrum at low temperature, demonstrating that the thermal process of magnetization relaxation is the first excited states involved (Fig. 8(c) and (a) in Fig. S43–S45†). The consistency of the above indicates that the robust entity [DyL4]− steadily sustains magnetic properties, whatever counter metal ion is linked. CASSCF calculations confirm that magnetic properties, characterized by Ueff and gz for the ground magnetic sublevels, are maintained after sublimation for compounds without a sodium ion.
The energies of the sublevels of the ground term are important for understanding the magnetic properties of SMMs. Based on the results of magnetic and luminescence characterization and ab initio calculations above, these three methods used to obtain the sublevel energies are compared in Fig. 8(c). (I) The ab initio calculations are based on the atom coordinates from SXRD measurements which are able to view the different Dy ions. For compound 8, two sets of sublevel energies are obtained. (II) Magnetic characterization is an experimental method to obtain the energy gap between the ground and the first or higher excited states by deducing the effective energy barrier for spin reversal from AC susceptibilities. Sometimes, magnetic characterization cannot distinguish the magnetic sublevels of Ln ions with slight variations in structure. For compound 8, only one thermal relaxation process of magnetization is viewed from the AC data. (III) Luminescence characterization is another experimental method to obtain the energies of sublevels. Especially, a low temperature is beneficial for decreasing noise and increasing resolution. Well resolved spectra provide more reliable energy differences between the magnetic sublevels and even distinguish emitting centers with tiny variations in structure, such as the luminescence spectra for compound 8. Two sets of energies for sublevels are mixed, and it is difficult to classify these energies to the two different Dy ions separately. The luminescence results provide intercomparison with the ab initio calculations on the ground and low-lying excited magnetic states, which are very difficult to determine precisely, for example, the eight Kramers doublets of Dy SMMs. Actually, the luminescence method has been developed as a useful tool for determining the quantum states of single Ln ions.76–78 It is perspected to inspect the energies for sublevels of single or few molecules of Ln-SMMs on substrates, so does other absorption spectrum.13,79 Additionally, it is feasible to obtain the information about the low-lying states split by a magnetic field through the measurement of luminescence.
Conclusions
A series of Dy compounds coordinated by four naphthyridine-like ligands, containing the [DyL4]− entity, and linked with an alkali metal ion were crystallized in solvents or in vapor by sublimation. The four compounds from solvents behave as single-molecule magnets, featuring photoluminescence based on the Dy ion. The [DyL4]− entity is hardly perturbed by the linked counter ion in the structure and magnetism with the similar ground Kramers doublets which are quantized in the same direction. The SMM magnetic properties of the sublimed samples 6–8 remain unchanged in comparison with those of the samples from solvents. These sublimable SMMs are promising materials for device manufacturing.The photoluminescence spectra offer verification of the energy gap between the two lowest sublevels of the ground term, and show that the pathway of the thermal magnetic relaxation process is the first excited states involved for compounds 1–4 and 8. The luminescence spectra at low temperature discriminate the small difference in energies for the magnetic sublevels of Dy ions in compound 8. Additionally, lanthanide luminescence under a pulsed magnetic field for SMMs is observed for the first time. The average g value is deduced from the luminescence spectra, analyzed using a reduced Zeeman model, while the information about the Zeeman splitting on Kramers doublets of the ground term 6H15/2 of Dy(III) may be difficult to obtain by normal EPR measurements. We think that luminescence spectroscopy under a strong magnetic field will be a new and complementary method to study the lowest magnetic sublevels and give insightful information on SMMs. These SMMs will be also attractive multifunctional materials in the application of molecular spintronics and quantum computing.
Acknowledgements
We appreciate Dr Hui-Bo Wei for his help in the synthesis of the ligand, Dr Zhao-Sha Meng and PhD student Xiao-Nan Yao for their efforts in detection by single crystal X-ray diffraction, and PhD student Xiao-Huan Lin for detection by powder X-ray diffraction. We also appreciate Professor Jian Pei and PhD student Ke Shi for their help in the operation of the FLS980, and Dr Ming-Xing Chen for his technical assistance with the FLS 920. We thank Dr Yan Guan for her technical support in early luminescence determination on Nanolog and Prof. Da-Hui Zhao for offering the cryostat. We appreciate all members in Professor Jun-Bo Han's group for their help with luminescence measurements and discussions. We appreciate Professor Bin Hu and PhD student Lin Luan for providing the 355 nm laser source and for the help with operation. This work was supported by the NSFC (21290171, 21321001, 91422302 and 21571008) and the National Basic Research Program of China (2013CB933401).References
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klyatskaya, J. P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502–506 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360 CrossRef CAS PubMed.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- G. A. Timco, T. B. Faust, F. Tuna and R. E. P. Winpenny, Chem. Soc. Rev., 2011, 40, 3067–3075 RSC.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341 CrossRef CAS.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C. Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC.
- M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156 RSC.
- A. Cornia, M. Mannini, P. Sainctavit and R. Sessoli, Chem. Soc. Rev., 2011, 40, 3076–3091 RSC.
- T. Komeda, H. Isshiki, J. Liu, K. Katoh and M. Yamashita, ACS Nano, 2014, 8, 4866–4875 CrossRef CAS PubMed.
- V. Corradini, A. Ghirri, U. del Pennino, R. Biagi, V. A. Milway, G. Timco, F. Tuna, R. E. P. Winpenny and M. Affronte, Dalton Trans., 2010, 39, 4928–4936 RSC.
- A. Ghirri, V. Corradini, V. Bellini, R. Biagi, U. del Pennino, V. De Renzi, J. C. Cezar, C. A. Muryn, G. A. Timco, R. E. P. Winpenny and M. Affronte, ACS Nano, 2011, 5, 7090–7099 CrossRef CAS PubMed.
- L. Margheriti, M. Mannini, L. Sorace, L. Gorini, D. Gatteschi, A. Caneschi, D. Chiappe, R. Moroni, F. B. de Mongeot, A. Cornia, F. M. Piras, A. Magnani and R. Sessoli, Small, 2009, 5, 1460–1466 CrossRef CAS PubMed.
- X. Yi, K. Bernot, F. Pointillart, G. Poneti, G. Calvez, C. Daiguebonne, O. Guillou and R. Sessoli, Chem.–Eur. J., 2012, 18, 11379–11387 CrossRef CAS PubMed.
- A. Abherve, S. Manas-Valero, M. Clemente-Leon and E. Coronado, Chem. Sci., 2015, 6, 4665–4673 RSC.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875 CrossRef CAS PubMed.
- S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS PubMed.
- M. Jeletic, P.-H. Lin, J. J. Le Roy, I. Korobkov, S. I. Gorelsky and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 19286–19289 CrossRef CAS PubMed.
- K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957 CrossRef CAS PubMed.
- L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413–4417 CrossRef CAS PubMed.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. Liddle, Chem. Sci., 2016, 7, 155–165 RSC.
- L. Margheriti, D. Chiappe, M. Mannini, P. E. Car, P. Sainctavit, M.-A. Arrio, F. B. de Mongeot, J. C. Cezar, F. M. Piras, A. Magnani, E. Otero, A. Caneschi and R. Sessoli, Adv. Mater., 2010, 22, 5488–5493 CrossRef CAS PubMed.
- K. Katoh, T. Komeda and M. Yamashita, Dalton Trans., 2010, 39, 4708–4723 RSC.
- M. Gonidec, R. Biagi, V. Corradini, F. Moro, V. De Renzi, U. del Pennino, D. Summa, L. Muccioli, C. Zannoni, D. B. Amabilino and J. Veciana, J. Am. Chem. Soc., 2011, 133, 6603–6612 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310–3316 RSC.
- K. R. Meihaus, S. G. Minasian, W. W. Lukens, S. A. Kozimor, D. K. Shuh, T. Tyliszczak and J. R. Long, J. Am. Chem. Soc., 2014, 136, 6056–6068 CrossRef CAS PubMed.
- V. E. Campbell, H. Bolvin, E. Rivière, R. Guillot, W. Wernsdorfer and T. Mallah, Inorg. Chem., 2014, 53, 2598–2605 CrossRef CAS PubMed.
- F. Habib, G. Brunet, V. Vieru, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 13242–13245 CrossRef CAS PubMed.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- S.-S. Liu, L. Xu, S.-D. Jiang, Y.-Q. Zhang, Y.-S. Meng, Z. Wang, B.-W. Wang, W.-X. Zhang, Z. Xi and S. Gao, Inorg. Chem., 2015, 54, 5162–5168 CrossRef CAS PubMed.
- L. Vitali, S. Fabris, A. M. Conte, S. Brink, M. Ruben, S. Baroni and K. Kern, Nano Lett., 2008, 8, 3364–3368 CrossRef CAS PubMed.
- S. Stepanow, J. Honolka, P. Gambardella, L. Vitali, N. Abdurakhmanova, T.-C. Tseng, S. Rauschenbach, S. L. Tait, V. Sessi, S. Klyatskaya, M. Ruben and K. Kern, J. Am. Chem. Soc., 2010, 132, 11900–11901 CrossRef CAS PubMed.
- A. Lodi Rizzini, C. Krull, T. Balashov, A. Mugarza, C. Nistor, F. Yakhou, V. Sessi, S. Klyatskaya, M. Ruben, S. Stepanow and P. Gambardella, Nano Lett., 2012, 12, 5703–5707 CrossRef CAS PubMed.
- D. Klar, A. Candini, L. Joly, S. Klyatskaya, B. Krumme, P. Ohresser, J.-P. Kappler, M. Ruben and H. Wende, Dalton Trans., 2014, 43, 10686–10689 RSC.
- D. P. DiVincenzo, Fortschr. Phys., 2000, 48, 771–783 CrossRef.
- L. Chibotaru, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer, Berlin Heidelberg, 2015, vol. 164, ch. 171, pp. 185–229 Search PubMed.
- R. Marx, F. Moro, M. Dorfel, L. Ungur, M. Waters, S. D. Jiang, M. Orlita, J. Taylor, W. Frey, L. F. Chibotaru and J. van Slageren, Chem. Sci., 2014, 5, 3287–3293 RSC.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- J. Long, R. Vallat, R. A. S. Ferreira, L. D. Carlos, F. A. Almeida Paz, Y. Guari and J. Larionova, Chem. Commun., 2012, 48, 9974–9976 RSC.
- F. Pointillart, B. L. Guennic, S. Golhen, O. Cador, O. Maury and L. Ouahab, Chem. Commun., 2013, 49, 615–617 RSC.
- J. Long, J. Rouquette, J.-M. Thibaud, R. A. S. Ferreira, L. D. Carlos, B. Donnadieu, V. Vieru, L. F. Chibotaru, L. Konczewicz, J. Haines, Y. Guari and J. Larionova, Angew. Chem., Int. Ed., 2015, 54, 2236–2240 CrossRef CAS PubMed.
- M. Baker, S. Blundell, N. Domingo and S. Hill, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer, Berlin Heidelberg, 2015, vol. 164, ch. 155, pp. 231–291 Search PubMed.
- C. W. Tang and S. A. VanSlyke, Appl. Phys. Lett., 1987, 51, 913–915 CrossRef CAS.
- N. F. Chilton, G. B. Deacon, O. Gazukin, P. C. Junk, B. Kersting, S. K. Langley, B. Moubaraki, K. S. Murray, F. Schleife, M. Shome, D. R. Turner and J. A. Walker, Inorg. Chem., 2014, 53, 2528–2534 CrossRef CAS PubMed.
- E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef CAS PubMed.
- H. Wei, Z. Zhao, C. Wei, G. Yu, Z. Liu, B. Zhang, J. Bian, Z. Bian and C. Huang, Adv. Funct. Mater., 2016, 26, 2085–2096 CrossRef CAS.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 Search PubMed.
- S. D. Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448–7451 CrossRef CAS PubMed.
- D.-P. Li, T.-W. Wang, C.-H. Li, D.-S. Liu, Y.-Z. Li and X.-Z. You, Chem. Commun., 2010, 46, 2929–2931 RSC.
- Y. Bi, Y.-N. Guo, L. Zhao, Y. Guo, S.-Y. Lin, S.-D. Jiang, J. Tang, B.-W. Wang and S. Gao, Chem.–Eur. J., 2011, 17, 12476–12481 CrossRef CAS PubMed.
- J.-B. Han, Y.-B. Han and L. Li, Physics, 2016, 45, 26–35 Search PubMed.
- V. K. Tikhomirov, L. F. Chibotaru, D. Saurel, P. Gredin, M. Mortier and V. V. Moshchalkov, Nano Lett., 2009, 9, 721–724 CrossRef CAS PubMed.
- L. F. Chibotaru, V. K. Tikhomirov, D. Saurel and V. V. Moshchalkov, J. Appl. Phys., 2009, 106, 053502 CrossRef.
- Y. Liu, D. Wang, J. Shi, Q. Peng and Y. Li, Angew. Chem., Int. Ed., 2013, 52, 4366–4369 CrossRef CAS PubMed.
- Z.-W. Ma, J.-P. Zhang, X. Wang, Y. Yu, J.-B. Han, G.-H. Du and L. Li, Opt. Lett., 2013, 38, 3754–3757 CrossRef CAS PubMed.
- V. Petříček, M. Dušek and L. Palatinus, Journal, 2014, 229, 345–352 Search PubMed.
- J. Zhang, Z. Ma, J. Han, G. Du, Y. Zhou, L. Li and Z. Cheng, J. Lumin., 2013, 144, 53–56 CrossRef CAS.
- G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239 CrossRef.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- S.-J. Liu, J.-P. Zhao, W.-C. Song, S.-D. Han, Z.-Y. Liu and X.-H. Bu, Inorg. Chem., 2013, 52, 2103–2109 CrossRef CAS PubMed.
- S.-D. Han, Q.-L. Wang, J. Xu and X.-H. Bu, Eur. J. Inorg. Chem., 2015, 5379–5386 CrossRef CAS.
- M. L. Kahn, J.-P. Sutter, S. Golhen, P. Guionneau, L. Ouahab, O. Kahn and D. Chasseau, J. Am. Chem. Soc., 2000, 122, 3413–3421 CrossRef CAS.
- M. L. Kahn, R. Ballou, P. Porcher, O. Kahn and J.-P. Sutter, Chem.–Eur. J., 2002, 8, 525–531 CrossRef CAS.
- Y. Gao, G. F. Xu, L. Zhao, J. Tang and Z. Liu, Inorg. Chem., 2009, 48, 11495 CrossRef CAS PubMed.
- S. Osa, T. Kido, N. Matsumoto, N. Re, A. Pochaba and J. Mrozinski, J. Am. Chem. Soc., 2004, 126, 420–421 CrossRef CAS PubMed.
- G. Abbas, Y. Lan, G. E. Kostakis, W. Wernsdorfer, C. E. Anson and A. K. Powell, Inorg. Chem., 2010, 49, 8067–8072 CrossRef CAS PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- J.-C. G. Bunzli and C. Piguet, Chem. Soc. Rev., 2005, 34, 1048–1077 RSC.
- J.-C. G. Bunzli and S. V. Eliseeva, Chem. Sci., 2013, 4, 1939–1949 RSC.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- R. Kolesov, K. Xia, R. Reuter, R. Stöhr, A. Zappe, J. Meijer, P. R. Hemmer and J. Wrachtrup, Nat. Commun., 2012, 3, 1029 CrossRef CAS PubMed.
- R. Kolesov, K. Xia, R. Reuter, M. Jamali, R. Stöhr, T. Inal, P. Siyushev and J. Wrachtrup, Phys. Rev. Lett., 2013, 111, 120502 CrossRef PubMed.
- P. Siyushev, K. Xia, R. Reuter, M. Jamali, N. Zhao, N. Yang, C. Duan, N. Kukharchyk, A. D. Wieck, R. Kolesov and J. Wrachtrup, Nat. Commun., 2014, 5, 3895 CAS.
- M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M. A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional magnetic data, additional figures and computational details. CCDC 1446709–1446713. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6sc01157h |
| This journal is © The Royal Society of Chemistry 2016 |