Length-independent transport rates in biomolecules by quantum mechanical unfurling

Abstract

Experiments on hole transfer in DNA between donor and acceptor moieties revealed transfer rates which are independent of the molecular bridge length (within experimental error). However, the physical origin of this intriguing observation is still unclear. The hopping model implies that the hole propagates in multiple steps along the bridge from one localized state to another, and therefore the longer the bridge, the slower the transfer. This can explain weak length-dependence but not a length-independent transfer rate. We show that the rigid molecular structure of a poly-A bridge supports single step transitions from a localized hole state to delocalized states, spread over the entire bridge. Since propagation to the bridge end is a single step process (termed quantum unfurling) the transfer rate becomes independent of the bridge length. This explanation is consistent with experimental results, and emphasizes the importance of structural order in charge transfer through bio-molecular systems.

---

Natural processes, at their molecular level, require highly efficient charge and energy transport (CT) through biomolecules.^1–5 Indeed, CT is cardinal in numerous natural processes including respiration, vision, photosynthesis and mutation formation (or repair). In DNA, the study of CT has been attracting attention for several decades.⁶ Numerous experimental and theoretical studies suggest that CT in DNA is promoted by the overlapping π orbitals of adjacent nucleobases, stacked in the closely packed double helical structures.^7–13 In particular, hole transport through positively charged DNA,^14–17 as well as charge separation/recombination through DNA bridges,^18,19 have been studied intensively. Among the nucleobases composing natural DNA (guanine (G), adenine (A), thymine (T) and cytosine (C)), Gs have the lowest ionization potential and are therefore the energetically favorable sites for hole occupation.

The seminal work by Giese et al.²⁰ on hole transport through poly-A bridges of various lengths at ambient conditions has provided a unique insight into hole transport through DNA. The population ratio following hole transfer between a donor (G⁺) and an acceptor (GGG⁺) was measured for B-DNA sequences of type [5′-G(T)_NGGG-3′]⁺ in water. For short distances (i.e., N ≲ 4), the reported population ratio (P_GGG⁺/P_G⁺) dropped sharply with the length of the poly-A bridge, and for longer distances (4 < N < 8) the drop was significantly milder, where between N = 8 and N = 16, the donor/acceptor population ratio was essentially indistinguishable. In view of the water trapping mechanism²⁰ the relative acceptor population is indicative of the rate of hole transfer through the bridge separating the donor from the acceptor.^14,21 The sharp drop was therefore attributed to exponentially decreasing CT rates via an off-resonant (super-exchange) or resonant (flickering²¹) quantum tunneling mechanism, whereas the observed mild dependence on the bridge length for longer bridges was attributed to thermally activated charge propagation through the poly-A stack by sequential hopping.^{18,20,22–28} The hopping mechanism implies that the hole propagates in multiple steps along the bridge and therefore the longer the bridge, the slower the transfer, with a typical 1/N fall of the transfer rate with the number of bridge sites. Therefore, the observation that doubling the donor–acceptor separation had strictly no effect on the CT efficiency (and presumably on the CT rate) through long bridges is not accounted for by any of these mechanisms, and calls for revisiting some basic assumptions underlying models of CT through DNA and biomolecules in general.

In this work we explain the observed independence of the CT rate on the donor–acceptor distance, by considering the electronic structure of the poly-A bridge in [5′-G(T)_NGGG-3′]⁺ in its rigid equilibrium configuration, and accounting for the effect of structural and dynamical fluctuations about this configuration. Assuming strong deviations from the rigid double helix geometry, the transport rate for long bridges is shown to drop with increasing donor–acceptor distance. However, when the rigid structure dominates and the fluctuations are weak, the transport rate for long bridges becomes strictly independent of the donor–acceptor separation, particularly for N ≳ 8, in accordance with the experimental observation.

Previous work on DNA bridges (poly-A, in particular) has shown that the hole orbitals tend to delocalize over several nucleobases in such structures.^{10,12,17,19,29–32} Indeed, the inclusion of long range correlations within a stepwise kinetic model (the variable range hopping model²²) significantly improved the success of the hopping model to describe weak length dependence of the rate for transport through long (≳10 base pairs) bridges.^22,30 Moreover, the possibilities of coherent hole scattering^33–37 or ballistic transport of hole wave packets^38,39 through DNA bridges were attributed to the presence of delocalized states in a band-like electronic structure. These ideas are based primarily on physically motivated model Hamiltonians^31,37,40,41 for rigid ordered DNA sequences, which support nearly length-independent electric conductance, when an applied potential bias injects high energy holes into the frozen, rigid bridge.³⁷ In this work we show that thermal fluctuations about the equilibrium structure of poly-A DNA promote hole transfer by inducing charge transfer from a localized donor state into poly-A bridge states, delocalized over the entire bridge. When this “quantum unfurling” becomes the dominant mechanism for long-range CT, the observed transport rates become length-independent.

A straight-forward approach for theoretical analysis of CT through complex biomolecules is to refer to well defined building blocks. In the case of DNA the nucleobases are the natural choice. Accurate ab initio quantum mechanical computational methods are currently limited in application to short DNA segments of 2–4 nucleobases^42,43 and can't be applied to longer sequences where long-range interactions should come into play. Nevertheless, an approximate glimpse into the electronic structure of long DNA molecules can be based on their local building blocks and the interactions between them.^29,42–47 Neighboring nucleobases in DNA are coupled via local π-stacking interactions imposed by the double helix structure, where the local ionization potential (hole energy) and the inter-base coupling depend on the relative orientation between the nucleobases.^29,42–47 The positively charged DNA is represented below as a tight-binding ladder molecular Hamiltonian.^31,33,34 The model takes explicit account of the building blocks of the double stranded DNA, [5′-G(T)_NGGG-3′]⁺. Each nucleobase is associated with a local (on-site) ionization (hole) energy, and with hole-transfer integrals to nearest-neighbor nucleobases.^34–36

For the rigid equilibrium Watson–Crick geometry we use the parameterization of Voityuk et al.^44–46 who calculated local ionization potentials of DNA fragments⁴⁴ and nonadiabatic coupling matrix elements^45,46 between them. In the calculations of local ionization energies⁴⁴ for internal nucleobases, account was made of the two nearest neighbors, π-stacked in the strand at the equilibrium geometry of the three dimensional helix. For the terminal nucleobases, the local ionization energy depends on the internal neighboring nucleobase as well as on the external molecular environment. Our detailed analysis of the transport rates in the equilibrium geometry (see the ESI, Fig. S1†) shows that: (i) changes in the local ionization potentials at the terminal nucleobases have no effect on the CT rate for N > 4, except for at the 5′-guanine (the donor). (ii) As long as the energy gap from the 5′-guanine to the bridge energy levels exceeds K_BT, the dependence of the CT rate on N exhibits a clear transition from an exponential drop to a plateau. (iii). For a specific realistic choice of the local 5′-guanine ionization potential the transition between two transport mechanisms occurs at N ∼ 4. A comprehensive description of the Hamiltonian is given in the ESI.† Diagonalizing this Hamiltonian, one obtains the respective quasiparticle eigenstates, which dominate the hole transport dynamics.

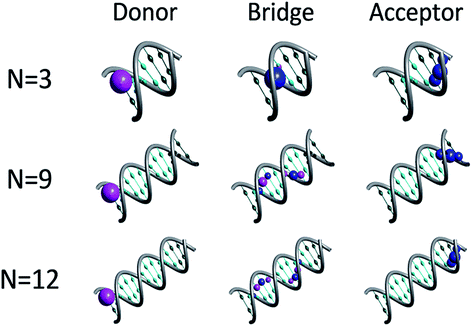
Fig. 1 depicts representative quasiparticle eigenstates (hole orbitals) for sequences of type [5′-G(T)_NGGG-3′]⁺ at the equilibrium geometry. A remarkable characteristic of these hole orbitals is that (regardless of N) each one can be related specifically to the donor ([G]⁺), to the poly-A bridge ([(T)_N]⁺), or to the acceptor ([GGG]⁺). Similarly to the results of other experimental observations and model computations^48–50 for poly-A DNA in various conformations, orbitals that are related to the bridge are not restricted to specific nucleobases. Moreover, our model for rigid [5′-G(T)_NGGG-3′]⁺ shows that most of the bridge orbitals are delocalized over the entire poly-A sequence. This delocalization is a direct consequence of the potential landscape imposed by the rigid Watson–Crick structure for the positively charged poly-A DNA, and it points to the importance of long-range interactions in this system. Another important characteristic of the hole orbitals according to the present parameterization is that regardless of N, there is only one orbital that has a significant projection on the donor (G⁺) nucleobase site (see Fig. 1). This implies that preparation of the hole at the donor G site amounts to populating primarily a single quasiparticle eigenstate. The vanishingly small projection of the donor site wave function on other eigenstates would lead to coherent oscillations between the donor and the acceptor,^26,28 even if the system retains its equilibrium geometry, but the majority of the hole population would remain at the donor site at all times in this case. Fluctuations in the DNA molecule and/or in its environment are therefore necessary in order to facilitate the hole transfer kinetics from the donor ([G]⁺) to the acceptor ([GGG]⁺).^40,51–61

Fig. 1 Quasiparticle orbitals for DNA sequences of type [5′-G(T)_NGGG-3′]⁺. The representative plots illustrate the association of specific orbitals with the donor, bridge and acceptor moieties. The probability density at each nucleobase site is marked by a corresponding sphere, where the blue and magenta correspond to positive and negative amplitudes respectively. For clarity, nucleobases associated with the bridge and the donor/acceptor moieties are marked by cyan and emerald, respectively.

Geometrical fluctuations and the nature of the coupling between the electronic and nuclear degrees of freedom are indeed of major concern for understanding CT phenomena in DNA. Many studies emphasize the effect of short-range interactions of the DNA building blocks with their local environment. Classical molecular dynamics simulations of the molecule in its surroundings, employing different force fields,^40,51–61 yield energy fluctuations in the range of a few tenths of an eV.^51,58 In order to account for the effect of such fluctuations on the hole transfer kinetics, the on-site energies (local nucleobase ionization potentials) were displaced below by a random energy shift, R_nΔE, where −1 < R_n < 1 for the n^th nucleobase site. Such a static noise changes the extension of the hole eigenstates over the bridge sites, and in particular, when ΔE reaches ∼0.1 eV, the quasiparticle eigenstates tend to localize over only a few nucleobases (in accordance with the conclusions of numerous studies of DNA in different conformations^48–50,62) rather than span the entire bridge. Nevertheless, as long as the donor G site overlaps primarily with a single quasiparticle eigenstate (i.e. the energy gap from the donor to the bridge is sufficiently large), static noise doesn't lead to charge transfer kinetics from the donor state. To account for hole kinetics, the nuclear degrees of freedom must be coupled explicitly to the charge transfer coordinate in the Hamiltonian. Below, the nuclear degrees of freedom are regarded as a weakly coupled harmonic bath with an ohmic⁶³ spectral density, and a spectral width covering the entire relevant nuclear frequencies for DNA in water. The bath modes are linearly coupled to the electronic degrees of freedom via a uniform projector onto the bridge nucleobase sites (see ESI† for details). This model implies that only transitions into or out of the poly-A bridge are coupled to the nuclear modes. Bath fluctuations⁵⁸ at the individual bridge sites are therefore fully correlated (uncorrelated fluctuations between A nucleobases within the bridge do not change the length-independence in the perturbative coupling regime, and will be discussed in details elsewhere). Note that even in this uniform coupling model the projection operator onto the bridge sites does not commute with the quasiparticle Hamiltonian, and therefore any two eigenstates of the quasiparticle Hamiltonian are coupled by the bath. In particular, eigenstates related to the donor or acceptor, are coupled to eigenstates related to the bridge, which drives the charge transport dynamics.

A reduced density matrix approach based on a second order perturbation theory is adequate for following the CT dynamics in this case. The Redfield theory⁶⁴ can be used for formulating the quasiparticle dynamics in the reduced basis of hole-orbitals (see Fig. 1). Earlier applications of this approach to models of donor–bridge–acceptor molecules demonstrated its ability to account for both short-time coherences and long-time population transfer between the reduced system eigenstates.^65,66 Considering the eigenstates of the [5′-G(T)_NGGG-3′]⁺ DNA sequences (see Fig. 1), and setting the initial state to a single (donor-based) eigenstate, coherences between the orbitals throughout the time evolution are expected to be negligible. It is then possible to decouple the coherences from the populations dynamics, and to solve the quantum master equations⁶⁴ for fluctuations-induced population transfer between the quasiparticle eigenstates (see ESI† for details).

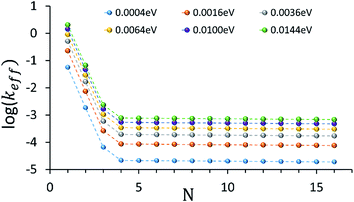
In Fig. 2 effective hole transfer rates are plotted for [5′-G(T)_NGGG-3′]⁺ molecules of different length (N), at different static noise levels, ΔE (populations dynamics underlying the rate process is demonstrated in the inset). As one can see, when the static noise is significant, ΔE = 0.1 eV, the average rate continues to drop down with the bridge length (not necessarily monotonously^49,62,68) even for the longer poly-A bridges. Such length dependencies agree with experimental observations of charge transfer through long DNA bridges of different sequences,^49,50,62 which are usually attributed to sequential or variable range hopping, or a mixture of coherent and incoherent hops.⁶² However, as ΔE → 0, corresponding to a perfectly rigid DNA at the equilibrium geometry, the transfer rate becomes length independent for the longer bridges, in accordance with the experimental observation of ref. 20.

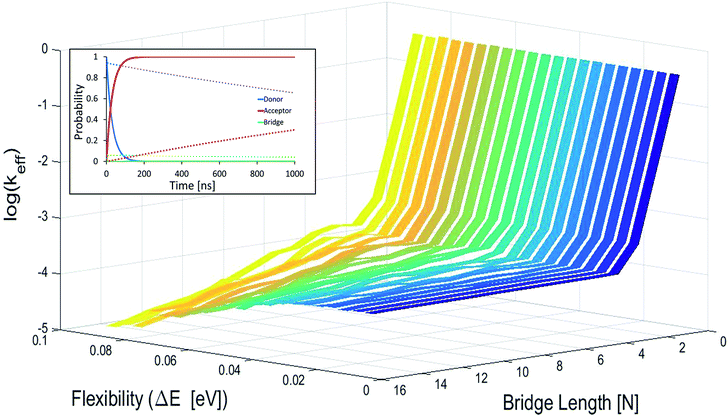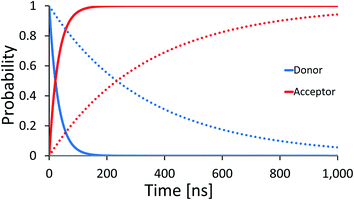
Fig. 2 Average effective transfer rates for [5′-G(T)_NGGG-3′]⁺, plotted as a function of the poly-A bridge length (N) and flexibility (static noise level, ΔE). Rates are in units of ns⁻¹ and obtained by averaging the effective rate over 60 randomly set realizations of the local ionization potentials. The nuclear bath parameters are: T = 298 K, η = 0.007 eV, ℏω_c = 0.1 eV (see the ESI† for details). Inset: simulated donor (blue), bridge (green) and acceptor (red) populations in representative [5′-G(T)_NGGG-3′]⁺ sequences of DNA. The plots demonstrate fast and slow population transfer kinetics for short (N = 2, solid) and long (N = 8, dotted) poly-A bridges, respectively. The donor, bridge and acceptor populations are defined as sums over the populations of the eigenstates related to each moiety. The buildup of the acceptor population, P_GGG⁺(t) (defined as the sum over the acceptor related eigenstates) is nearly exponential, which enables to define an effective hole transfer rate constant as follows, k_eff = −dln(1 − P_GGG⁺(t))/dt.

The degree of poly-A flexibility (expressed as ΔE within the present model) is therefore crucial for determination of the length-dependence of the transport rate through long poly-A bridges. While poly-A was identified long ago as the most rigid DNA sequence due to its optimal π-stacking interactions and its tendency to re-optimize these interactions under strain,⁶⁷ there is no experimental test for the degree of rigidity of [5′-G(T)_NGGG-3′]⁺ in a water solution during hole transport. Nevertheless, it is not unlikely that for long ordered sequences (as the poly-A studied in this work) long-range electronic interactions stabilize the equilibrium double helix structure, to the extent that CT dynamics would be dominated by transitions between the delocalized quasiparticle eigenstates of this structure, rather than by the localized states associated with fluctuating individual building blocks. Notice that calculations based on currently available classical force fields (which don't account for long-range electronic correlations) predict on-site fluctuations of order ΔE ∼ 0.1 eV, which can't explain strictly length-independent transport rates.

Fig. 3 depicts the effective rate constant as a function of the bridge length for the [5′-G(T)_NGGG-3′]⁺ sequences assuming perfect rigidity (ΔE = 0). The decay of the rate with the number of bridging AT base pairs (N) exhibits a transition from a sharp drop for short bridges to a length-independent rate for long bridges. A change of the transport mechanism at N_trans = 4 is reproduced by the minimal model considered here, based upon the electronic model Hamiltonian as discussed above (and detailed in the ESI†).

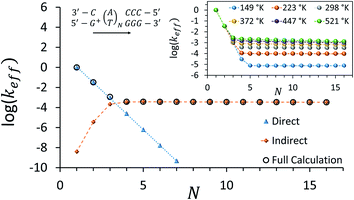Fig. 3 Calculated effective donor–acceptor transfer rate in DNA sequences of type [5′-G(T)_NGGG-3′]⁺, plotted as a function of the poly-A bridge length (N). The black circles demonstrate the transition from a sharp drop of the rate for short bridges to a length-independent rate for long bridges, as the unfurling mechanism comes into play. Blue triangles: rates calculated on the basis of direct transitions between donor and acceptor related eigenstates. Orange diamonds: rates calculated on the basis of indirect transitions through the bridge related orbitals. Rates are in units of ns⁻¹ and correspond to the DNA parameterization of ref. 44–46, corrected for the terminal sites' energies. The bath parameters are: T = 298 K, η = 0.007 eV, ℏω_c = 0.1 eV (see the ESI† for details). Inset: the same plot, repeated for different bath temperatures as indicated in the legend.

The nature of the transition between two distinctive mechanisms is highlighted by two approximate calculations, also presented in Fig. 3. The blue triangles were obtained by retaining population transfer rates only between the donor-related and acceptor-related eigenstates (setting all other rates to zero). The orange diamonds were obtained by retaining transfer rates only between bridge-related eigenstates and either donor-related or acceptor-related eigenstates (transfer rates between different bridge eigenstates and direct transitions between the donor and the acceptor eigenstates were excluded). The two fits suggest that for short bridges the transport is dominated by direct inelastic transitions between eigenstates related to the donor and acceptor sites, whereas for long bridges the transport is indirect and mediated by hole transfer into and out of the bridge orbitals.

The inset of Fig. 3 demonstrates the temperature-dependence of the effective rates. For short bridges the rate is temperature-independent as it involves primarily “downhill” inelastic transitions from the donor to the acceptor where the bath serves merely as an energy sink. Notice that this predicted temperature-independence for N < 3 in [5′-G(T)_NGGG-3′]⁺ is different than what was observed for CT through adenine bridges with different donor and acceptor, at a different molecular environment.⁶⁸ Indeed, for short adenine bridges there is strong sensitivity of the rate to the energy gaps from the donor to the bridge and from the bridge to the acceptor (see Fig. S1c and d in the ESI†), suggesting that the temperature-dependence of the rate can change significantly with changes in the donor and acceptor moieties.

For long bridges, an apparent temperature dependence is predicted in [5′-G(T)_NGGG-3′]⁺, as the “uphill” transitions to the delocalized bridge orbitals are thermally activated, and require energy absorption from the bath. The thermally activated transport through the long poly-A bridge involves unfurling of the hole from the localized state at the donor into individual high energy states, delocalized over the entire bridge (see Fig. 1), which is consistent with length-independent transfer rates, as observed in Fig. 3 for long bridges at low temperatures.

Notice that for each delocalized quasiparticle state, phase relations between the different nucleobase building blocks are fully preserved (the coherences between different quasiparticle eigenstates are the ones that vanish during the unfurling). This picture should prevail in long ordered DNA sequences (and other ordered bio-molecular bridges in general), when long-range electronic interactions and long range forces stabilize the molecular structure.⁶⁹ It complements the local picture of sequential hopping, in which phase relations between electronic states at neighboring building blocks are lost due to the structure flexibility. Interestingly, while only quantum unfurling explains a strictly length-independent transport rate (this is derived for an analytic model in the ESI†), the two theories of thermally activated transport (unfurling and hopping) seem to be in harmony with a mild length-dependence of the hole transfer rate through the poly-A sequence (see Fig. 2). This suggests that both strong local fluctuations away from the equilibrium molecular structure in its environment, and weak global fluctuations near the equilibrium structure, can contribute to long-range CT through different ordered biomolecules.

An intriguing question relates to the predicted onset of the thermally activated unfurling mechanism. Our model predicts (see inset of Fig. 3) that N_trans is controlled by the temperature, and changes (from 5 to 3) as the temperature increases. In contrast, changing the strength of the electronic nuclear coupling (the nuclear reorganization energy parameter) at a given temperature does not affect the value of N_trans, as apparent in the parallel curves in Fig. 4. In particular, the length-independence of the transfer rate is not affected by the electronic nuclear coupling strength. This result is unique to the unfurling mechanism, and reflects the linear effect of the coupling strength on inelastic transition rates between the quasiparticle eigenstates. Experimental observation of such trends and particularly the mild effect of the global reorganization energy (e.g., the solvent polarity) on N_trans, would be indicative for the unfurling mechanism.

Fig. 4 The dependence of the effective donor–acceptor transfer rate in DNA sequences of type [5′-G(T)_NGGG-3′]⁺, on the electronic nuclear coupling strength, η (See ESI† for the coupling strength definition). The different plots correspond to different values of η (as indicated on the plot). The dependence of the effective rates on the coupling strength for any N characterizes the effect of weak fluctuations around the equilibrium DNA structure. Rates are in units of ns⁻¹ and correspond to the DNA parameterization of ref. 44–46, corrected for the terminal sites energies. The bath parameters are: T = 298 K, ℏω_c = 0.1 eV (see the ESI† for details).

The dominance of the rigid double helix structure of the molecule should have another important consequence. Comparing hole transport from [G]⁺ to [GGG]⁺ in [5′-G(T)_NGGG-3′]⁺ and [3′-G(T)_NGGG-5′]⁺, we find a dramatic directionality effect. Considering for example the case with N = 2, the results in Fig. 5 show that transport in the 5′ to 3′ direction is preferred. The difference between the two directions can be attributed in this case to the relative ordering of the quasiparticle orbital energies in the two different DNA structures, as calculated by diagonalizing the respective model Hamiltonians (see Table S1, and Fig. S1 in the ESI† for the internal and terminal site energies). The numerical analysis reveals that the donor-related orbital of the [5′-G(T)₂GGG-3′]⁺ structure is higher in energy than the three acceptor-related orbitals (associated with high amplitude at the GGG⁺ moiety), but this is not the case for [3′-G(T)₂GGG-5′]⁺, which hinders the direct ‘downhill’ kinetics in this case. Experimental verification of such directionality effects would suggest that the transport is indeed dominated by energetics attributed primarily to the rigid DNA structures, and that the thermal fluctuations which promote the hole transfer kinetics are sufficiently small, such that the imprint of the rigid structure eigenstates is preserved. Sensitivity to the directionality is not expected in the presence of large on-site energy fluctuations (thermal hopping) which obscure the underlying energetics of the rigid structures, and would tend to minimize the difference between different DNA structures.

Fig. 5 Donor (blue) and acceptor (red) populations as functions of time for two DNA sequences [5′-G(T)_NGGG-3′]⁺ (solid) and [3′-G(T)_NGGG-5′]⁺ (dashed). The plots demonstrate a strong effect of the helix direction on the population transfer kinetics.

In conclusion, a new mechanism, termed “quantum unfurling”, is proposed for ultra-long-range CT in biomolecules. Quantum unfurling is the process in which a localized hole state at the donor moiety transfers in one step to a delocalized state, spread over the entire molecular bridge. The presence of delocalized states is attributed to the potential landscape set by ordered rigid molecular structures, as in the case of poly-A DNA. The unfurling is triggered by thermal fluctuations of the molecule and its environment, but since propagation to the bridge end is a single step process, the transfer rate becomes independent on the bridge length. This differs from a classical hopping picture, where the hole propagates in multiple steps along the bridge from one localized state to another, which implies that the longer the bridge, the slower the transfer.

The correspondence between previous measurements and the present theoretical results indicates the important contribution of quantum delocalized states to ultra-long-range CT through DNA. New experiments proposed here could further establish this contribution. In particular, we predicted the effects of temperature, sequence directionality (3′ to 5′ vs. 5′ to 3′ in poly-A DNA) and solvent polarity on the transport rates. Notice that while molecular rigidity and long range order which support delocalized bridge states seem to be essential for the observation of length-independent transport rates via quantum unfurling, these are by no means sufficient conditions. As in any thermally activated process, the unfurling from the localized donor state to the delocalized bridge states is sensitive to the energy gap from the donor to the bridge. Our analysis (see ESI†) suggests that length-independence of the rate will be observed only in the off-resonant regime, where the donor energy lies well below the bridge (as seems to be the case in [5′-G(T)_NGGG-3′]⁺). It is therefore important to notice that chemical changes to the bridge or the donor, which affect the energy gap, can result in different length-dependencies of the transport rate, as observed in different experiments on different DNA systems, and explained by different transport mechanisms.

The orderly packed aromatic moieties claimed to promote ultra-long range CT in poly-A via the unfurling mechanism, are abundant in other biomolecules as well. For example, electron transfer proteins such as cytochrome P450 are known to have unusually high occurrence of aromatic amino acids,⁴ which may facilitate their ultra-long-range CT functionality. Further studies are needed, however, in order to establish the effect of their organization within the bio-molecular environment on CT efficiency.

Finally, this research emphasizes the significant role of quantum mechanical phase preserving transport through biomolecules in their ambient conditions. Strictly length-independent charge transport rates via quantum unfurling manifest the non-locality of quantum mechanics. This should be considered in the context of nature's most efficient charge and energy transfer processes, and could provide a key for future molecular device applications for energy conversion and storage, or information processing.

Acknowledgements

This research was supported by the German Israeli Science Foundation and Adelis Foundation. A. D. L. acknowledges scholarship by the Technion graduate school. Barbara A. Levine is acknowledged for reviewing the manuscript.

References

1. J. R. Winkler and H. B. Gray, Electron Flow Through Metalloproteins, Chem. Rev., 2014, 114, 3369.
2. G. S. Engel, et al., Evidence for Wavelike Energy Transfer Through Quantum Coherence in Photosynthetic Systems, Nature, 2007, 446, 782.
3. H. Lee, Y. C. Cheng and G. R. Fleming, Coherence Dynamics in Photosynthesis: Protein Protection of Excitonic Coherence, Science, 2007, 316, 1462.
4. J. R. Winkler and H. B. Gray, Long-Range Electron Tunneling, J. Am. Chem. Soc., 2014, 136, 2930.
5. P. Rebentrost, M. Mohseni, I. Kassal, S. Lloyd and A. Aspuru-Guzik, Environment-assisted Quantum Transport, New J. Phys., 2009, 11, 033003.
6. D. I. Spivey and D. D. Eley, Semiconductivity of Organic Substances, Trans. Faraday Soc., 1962, 58, 411.
7. S. O. Kelley and J. K. Barton, Electron Transfer Between Bases in Double Helical DNA, Science, 1999, 283, 375.
8. E. M. Boon, D. M. Cere, T. G. Drummond, M. G. Hill and J. K. Barton, Mutation detection by electrocatalysis at DNA-modified electrodes, Nat. Biotechnol., 2000, 18, 1096.
9. C. R. Treadway, M. G. Hill and J. K. Barton, Charge Transport Through a Molecular Pi-stack: Double Helical DNA, Chem. Phys., 2002, 281, 409.
10. A. A. Voityuk, Conformations of PolyG–PolyC Pi-stacks with High Hole Mobility, J. Chem. Phys., 2008, 128, 045104.
11. Y. A. Berlin, A. A. Voityuk and M. A. Ratner, DNA Base Pair Stacks with High Electric Conductance: A Systematic Structural Search, ACS Nano, 2012, 6, 8216.
12. N. Renaud, Y. A. Berlin and M. A. Ratner, Impact of a Single Base Pair Substitution on the Charge Transfer Rate Along Short DNA Hairpins, Proc. Natl. Acad. Sci. U. S. A., Early Ed., 2013, 110(37), 14867.
13. E. L. Albuquerque, et al., DNA-based Nanobiostructured Devices: The Role of Quasiperiodicity and Correlation Effects, Phys. Rep., 2014, 535, 139.
14. M. Bixon, et al., Long-range Charge Hopping in DNA, Proc. Natl. Acad. Sci. U. S. A., Early Ed., 1999, 96, 11713.
15. J. C. Genereux and J. K. Barton, Mechanisms for DNA Charge Transport, Chem. Rev., 2010, 110, 1642.
16. R. Venkatramani, S. Keinan, A. Balaeff and D. N. Beratan, Nucleic Acid Charge Transfer: Black, White and Gray, Coord. Chem. Rev., 2011, 255, 635.
17. K. Kawai and T. Majima, Hole Transfer Kinetics of DNA, Acc. Chem. Res., 2013, 46, 2616.
18. F. D. Lewis, et al., Direct Measurement of Hole Transport Dynamics in DNA, Nature, 2000, 406, 51.
19. N. Renaud, Y. A. Berlin, F. D. Lewis and M. A. Ratner, Between Superexchange and Hopping: An Intermediate Charge Transfer Mechanism in Poly(A)–Poly(T) DNA Hairpins, J. Am. Chem. Soc., 2013, 135, 3953.
20. B. Giese, J. Amaudrut, A. K. Kohler, M. Spormann and S. Wessely, Direct Observation of Hole Transfer Through DNA by Hopping Between Adenine Bases and by Tunneling, Nature, 2001, 412, 318.
21. Y. Zhang, C. Liu, A. Balaeff, S. S. Skourtis and D. N. Beratan, Biological Charge Transfer via Flickering Resonance, Proc. Natl. Acad. Sci. U. S. A., Early Ed., 2014, 111(28), 10049.
22. T. Renger and R. A. Marcus, Variable-Range Hopping Electron Transfer through Disordered Bridge States: Application to DNA, J. Phys. Chem. A, 2003, 107, 8404.
23. Y. A. Berlin, A. L. Burin and M. A. Ratner, Charge Hopping in DNA, J. Am. Chem. Soc., 2001, 123, 260.
24. M. Bixon and J. Jortner, Long-range and Very Long-range Charge Transport in DNA, Chem. Phys., 2001, 281, 393.
25. M. Bixon and J. Jortner, Shallow Traps for Thermally Induced Hole Hopping in DNA, Chem. Phys., 2006, 326, 252.
26. S. Skourtis and A. Nitzan, Effects of Initial State Preparation on the Distance Dependence of Electron Transfer through Molecular Bridges and Wires, J. Chem. Phys., 2003, 119, 6271.
27. E. G. Petrov, V. Shevchenko Ye and V. May, On the Length Dependence of Bridge-mediated Electron Transfer Reactions, Chem. Phys., 2003, 288, 269.
28. G. Kalosakas and E. Spanou, Distance Dependence of Hole Transfer Rates from G Radical Cations to GGG Traps in DNA, Phys. Chem. Chem. Phys., 2013, 15, 15339.
29. E. Rengifo, G. Murillo and J. C. Arce, Modeling the Band Structures of B-DNA Base Stacks, J. Appl. Physiol., 2013, 113, 173703.
30. M. Jakobsson and S. Stafström, A Monte Carlo Study of Charge Transfer in DNA, J. Chem. Phys., 2008, 129, 125102.
31. Q. Cui and M. Elstner, Density Functional Tight Binding: Values of Semi-empirical Methods in an ab initio Area, Phys. Chem. Chem. Phys., 2014, 16, 14368.
32. J. C. Genereux, S. M. Wuerth and J. K. Barton, Single-Step Charge Transport through DNA over Long Distances, J. Am. Chem. Soc., 2011, 133, 3863.
33. C.-T. Shin, S. Roche and R. A. Romer, Point-Mutation Effects on Charge-Transport Properties of the Tumor-Suppressor Gene p53, Phys. Rev. Lett., 2008, 100, 018105.
34. D. Brisker-Klaiman and U. Peskin, Coherent Elastic Transport Contribution to Currents through Ordered DNA Molecular Junctions, J. Phys. Chem. C, 2010, 114, 19077.
35. D. Brisker-Klaiman and U. Peskin, Ballistic Charge Transport Through Bio-molecules in a Dissipative Environment, Phys. Chem. Chem. Phys., 2012, 14(40), 13835.
36. T. Simon, D. Brisker-Klaiman and U. Peskin, Bath Correlations Effects on Inelastic Charge Transport through DNA Junctions, Progress in Theoretical Chemistry and Physics B, 2013, vol. 27, p. 361.
37. N. Grib, D. Ryndyk, R. Gutiérrez and G. Cuniberti, Distance-dependent Coherent Charge Transport in DNA: Crossover from Tunneling to Free Propagation, J. Biophys. Chem., 2010, 1, 77.
38. Y. A. Berlin, A. L. Burin and M. A. Ratner, Elementary Steps for Charge Transport in DNA: Thermal Activation vs. Tunneling, Chem. Phys., 2002, 275, 61.
39. B. Oetzel, et al., Large Bandwidths in Synthetic One-dimensional Stacks of Biological Molecules, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195407.
40. R. Gutierrez, et al., Charge Transport through Biomolecular Wires in a Solvent: Bridging Molecular Dynamics and Model Hamiltonian Approaches, Phys. Rev. Lett., 2009, 102, 208102.
41. E. M. Conwell and S. M. Bloch, Base Sequence Effects on Transport in DNA, J. Phys. Chem. B, 2006, 110, 5801.
42. J. Sponer, et al., Nature and Magnitude of Aromatic Base Stacking in DNA and RNA: Quantum Chemistry, Molecular Mechanics, and Experiment, Biopolymers, 2013, 99, 978.
43. M. Kabelc, E. C. Sherer, C. J. Cramer and P. Hobza, DNA Base Trimers: Empirical and Quantum Chemical Ab initio Calculations versus Experiment in vacuo, Chem.–Eur. J., 2007, 13, 2067.
44. A. A. Voityuk, J. Jortner, M. Bixon and N. Rösch, Energetics of hole transfer in DNA, Chem. Phys. Lett., 2000, 324, 430.
45. A. A. Voityuk, N. Rosch, M. Bixon and J. Jortner, Electronic Coupling for Charge Transfer and Transport in DNA, J. Phys. Chem. B, 2000, 104, 9740.
46. A. A. Voityuk, M. Bixon, J. Jortner and N. Rösch, Electronic Coupling Between Watson–Crick Pairs for Hole Transfer and Transport in Deoxyribonucleic Acid, J. Chem. Phys., 2001, 114, 5614.
47. P. Hobza and J. Sponer, Toward True DNA Base-Stacking Energies: MP2, CCSD(T), and Complete Basis Set Calculations, J. Am. Chem. Soc., 2002, 124, 11802.
48. A. Capobianco, T. Caruso and A. Peluso, Hole Delocalization Over Adenine Tracts in Single Stranded DNA Oligonucleotides, Phys. Chem. Chem. Phys., 2015, 17, 4750.
49. M. A. O'Neil and J. K. Barton, DNA Charge Transport: Conformationally Gated Hopping Through Stacked Domains, J. Am. Chem. Soc., 2004, 126, 11471.
50. K. Kawai and T. Majima, Hole Transfer Kinetics of DNA, Acc. Chem. Res., 2013, 46, 2616.
51. A. A. Voityuk, K. Siriwong and N. Rosch, Environmental Fluctuations Facilitate Electron Hole Transfer from Guanine to Adenine in DNA π-Stacks, Angew. Chem., Int. Ed., 2004, 43, 624.
52. A. A. Voityuk, Electronic Couplings and On-site Energies for Hole Transfer in DNA: Systematic Quantum Mechanical/Molecular Dynamic Study, J. Chem. Phys., 2008, 128, 115101.
53. A. Troisi and G. Orlandi, Hole Migration in DNA: A Theoretical Analysis of the Role of Structural Fluctuations, J. Phys. Chem. B, 2002, 106, 2093.
54. J. Matulewski, S. D. Baranovskii and P. Thomas, Effects of Dynamic Disorder on the Charge Transport via DNA Molecules, Phys. Chem. Chem. Phys., 2005, 7, 1514–1517.
55. Y. A. Mantz, F. L. Gervasio, T. Laino and M. Parrinello, Solvent Effects on Charge Spatial Extent in DNA and Implications for Transfer, Phys. Rev. Lett., 2007, 99, 058104.
56. T. Steinbrecher, T. Koslowski and D. A. Case, Direct Simulation of Electron Transfer Reactions in DNA Radical Cations, J. Phys. Chem. B, 2008, 112, 16935.
57. F. C. Grozema, et al., Effect of Structural Dynamics on Charge Transfer in DNA Hairpins, J. Am. Chem. Soc., 2008, 130, 5157.
58. T. Kubar, U. Kleinekathofer and M. Elstner, Solvent Fluctuations Drive the Hole Transfer in DNA: A Mixed Quantum-Classical Study, J. Phys. Chem. B, 2009, 113, 13107.
59. T. Kubar, R. Gutierrez, U. Kleinekathofer, G. Cuniberti and M. Elstner, Modeling Charge Transport in DNA Using Multi-scale Methods, Phys. Status Solidi B, 2013, 250, 2277.
60. S. S. Skourtis, D. H. Waldeck and D. N. Beratan, Fluctuations in Biological and Bioinspired Electron-transfer Reactions, Annu. Rev. Phys. Chem., 2010, 461.
61. H. Yin, Y. Ma, J. Mu, C. Liu and M. Rohlfing, Charge-Transfer Excited States in Aqueous DNA: Insights from Many-Body Green's Function Theory, Phys. Rev. Lett., 2014, 112, 228301.
62. L. Xiang, J. L. Palma, C. Bruot, V. Mujica, M. A. Ratner and N. Tao, Intermediate Tunneling–Hopping Regime in DNA Charge Transport, Nat. Chem., 2015, 7, 221.
63. U. Weiss, Quantum Dissipative Systems, World Scientific, Singapore, 1999.
64. H. P. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford Univ. Press, New York, 2002.
65. K. Felts, W. T. Pollard and R. A. Friesner, Multilevel Redfield Treatment of Bridge-Mediated Long-Range Electron Transfer: A Mechanism for Anomalous Distance Dependence, J. Phys. Chem., 1995, 99, 2929.
66. R. Volkovich and U. Peskin, Contact Effects on Electronic Transport in Donor–Bridge–Acceptor Complexes Interacting with a Thermal Bath, J. Chem. Phys., 2006, 125, 244505.
67. F. Lankas, J. Sponer, P. Hobza and J. Langowski, Sequence-dependent Elastic Properties of DNA, J. Mol. Biol., 2000, 299, 695.
68. M. A. O'Neill and J. K. Barton, DNA-mediated Charge Transport Requires Conformational Motion of the DNA Bases: Elimination of Charge Transport in Rigid Glasses at 77 K, J. Am. Chem. Soc., 2004, 126, 13234.
69. J. B. Mills and P. J. Hagerman, Origin of the Intrinsic Rigidity of DNA, Nucleic Acids Res., 2004, 32, 4055.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sc03495g

---