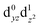A five-coordinate Mn(IV) intermediate in biological water oxidation: spectroscopic signature and a pivot mechanism for water binding

Abstract

Among the four photo-driven transitions of the water-oxidizing tetramanganese–calcium cofactor of biological photosynthesis, the second-last step of the catalytic cycle, that is the S₂ to S₃ state transition, is the crucial step that poises the catalyst for the final O–O bond formation. This transition, whose intermediates are not yet fully understood, is a multi-step process that involves the redox-active tyrosine residue and includes oxidation and deprotonation of the catalytic cluster, as well as the binding of a water molecule. Spectroscopic data has the potential to shed light on the sequence of events that comprise this catalytic step, which still lacks a structural interpretation. In this work the S₂–S₃ state transition is studied and a key intermediate species is characterized: it contains a Mn₃O₄Ca cubane subunit linked to a five-coordinate Mn(IV) ion that adopts an approximately trigonal bipyramidal ligand field. It is shown using high-level density functional and multireference wave function calculations that this species accounts for the near-infrared absorption and electron paramagnetic resonance observations on metastable S₂–S₃ intermediates. The results confirm that deprotonation and Mn oxidation of the cofactor must precede the coordination of a water molecule, and lead to identification of a novel low-energy water binding mode that has important implications for the identity of the substrates in the mechanism of biological water oxidation.

---

Introduction

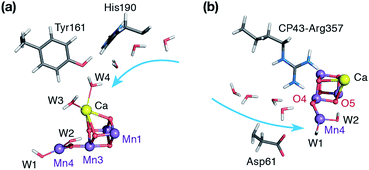
Nature's water splitting catalyst, the oxygen-bridged tetramanganese–calcium cofactor known as the oxygen-evolving complex (OEC), is found in the unique protein–pigment complex photosystem II (PSII) of oxygenic photosynthesis.^1–7 The catalytic cycle of the cofactor is comprised of five distinct redox intermediates, the S_n states, where the subscript indicates the number of stored oxidizing equivalents (n = 0–4) required to split two water molecules and release dioxygen.⁸ Light absorption and subsequent charge separation leads to the generation of the primary oxidant of PSII (P680˙⁺), an oxidized multi-chlorophyll pigment assembly. P680˙⁺ is coupled to the chemical catalysis occurring at the Mn₄O₅Ca cofactor via a redox-active tyrosine residue Y_Z which acts as a single-electron gate. After four charge separation events, the transiently formed S₃Y_Z˙ state decays to the S₀ state via an unknown mechanistic sequence, with concomitant release of triplet dioxygen and rebinding of one water molecule. The catalytic cycle is summarized in Fig. 1, which also shows the geometric conformations, protonation states and oxidation state distributions of the inorganic core of the OEC in each of the S₀–S₃ states.⁹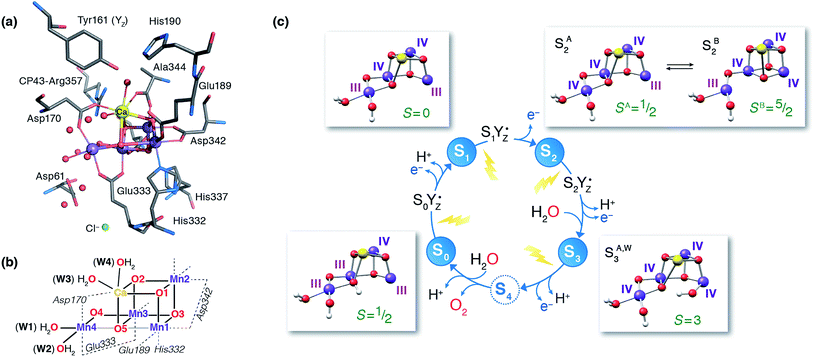

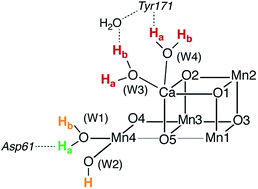
Fig. 1 (a) A view of the Mn₄Ca cluster and its environment, according to one of the S₁-state XFEL crystallographic models of Suga et al.¹⁰ (monomer A of dataset 4UB6). (b) Schematic depiction and labeling scheme for the inorganic core of the OEC. (c) The catalytic cycle with spectroscopically consistent models of the inorganic core and their spin states, adapted from ref. 9. In the present work we focus on the multi-step S₂–S₃ transition.

Recent crystallographic studies that utilized femtosecond X-ray free-electron laser (XFEL) pulses provided a reliable atomistic structure of the OEC in its dark-stable S₁ state,¹⁰ correcting, supplementing and extending the structural information that was available from previous X-ray diffraction (XRD)^11–13 and extended X-ray absorption fine structure (EXAFS) studies.^14–17 One intriguing feature of certain S-states is their heterogeneity. Specifically, in the S₂ state, with Mn oxidation states of Mn(IV)₃Mn(III), the cluster exists in two interconvertible structural forms^18,19 that correspond to two distinct EPR signals.^18,20 They differ in the distribution of Mn oxidation states and the internal connectivity of the cluster with respect to the O5 bridge (see Fig. 1) and are referred to as the “open-cubane” S^A₂ (spin S = 1/2, g ≈ 2.0 multiline signal) and the “closed-cubane” S^B₂ (spin S ≥ 5/2, g ≥ 4.1 signals).

The S₃ state of the OEC is similarly characterized by heterogeneity, but in contrast to S₂ the relevant phenomenology has not been fully rationalized in terms of well-defined structural forms.^21,22 It remains also unclear whether these forms are interconvertible. The majority S₃ state species is an EPR detectable spin S = 3 form.^21,23 The OEC cluster in this state is composed of four octahedrally coordinated Mn(IV) ions,^9,14,21 and is insensitive to near-infrared (NIR) light; Fig. 1 depicts a computational model of the inorganic core that is consistent with these observables. The minority S₃ state species, for which no EPR signal has yet been detected, has yet to be directly accessed experimentally. This population responds to NIR illumination at cryogenic temperatures by forming a split S^′₂Y_Z˙ EPR signal, where the inorganic cluster is reduced by the nearby Y_Z residue to an “S₂-like” electronic configuration.^24–32 As such, this species is expected to represent a precursor of the all-octahedral S₃ state form. The structural identity of this species is unknown and its properties are puzzling because Mn NIR photochemistry, observed also in lower S-states, is typically associated with the oxidation state 3+, whereas an all-Mn(IV) cluster is expected for the S₃ state.^9,21

The primary difficulty in combining all these observations is the complexity of the S₂–S₃ transition, which involves two structurally and electronically distinct but interconvertible starting points and encompasses oxidation of the Mn cofactor, proton removal, binding of a water molecule, and possibly further rearrangements. Beyond a better understanding of the catalyst itself, developing spectroscopically consistent atomistic models for species involved in the S₂–S₃ transition has implications for the mechanism of O–O bond formation. Two mechanisms are commonly discussed in current literature: (i) a nucleophilic attack type mechanism involving a terminal oxo ligand at the outer Mn4 and a Ca²⁺-bound water or hydroxide,^33–37 and (ii) radical-type coupling between two Mn bound oxygen ligands.^38–41 In principle both mechanisms would involve a structural change in the S₂ to S₃ transition. For the nucleophilic attack type mechanism, a coordination change at the outer Mn site has been proposed to stabilize a high-spin Mn(V) species in the S₄ state,^42,43 whereas in the radical coupling scenario this step instead involves the binding/relocation of the final substrate site, and as such it more readily rationalizes the increase in coordination number of the catalyst upon forming the S₃ state and recent substrate exchange experiments.^14,21,44,45

The identity of the two water substrates is inextricably linked with S-state progression. Experimental data shows that the two water molecules bind at different steps of the cycle. The first one binds after O₂ release and is incorporated into the oxo-bridge framework of the cofactor upon formation of the S₀ state. This water has been assigned to the O5 bridge of the cluster, which is thought to be a bridging OH in the S₀ state^9,46 and a fluxional oxo bridge in the S₂ state.^18,19 The second water binds, or at least is reorganized, during the S₂–S₃ transition^{21,41,44,45,47} that prepares the catalyst for the O–O bond formation step. The origin of this water is uncertain, and discussions regarding its incorporation cannot be easily disentangled from those regarding the identity of substrate oxygens.^37,48 Existing information on the structure of the catalyst has allowed formulation of two reasonable suggestions for water binding to a Mn ion during the S₂–S₃ transition: it may represent a loosely bound second-sphere water that coordinates a metal site progression to the S₃ state,^40,41,49 or instead it may be a Ca-bound water, specifically W3,¹⁹ that simply shifts to a Mn ion.

To better appreciate the differences between these suggestions, it is important to keep in mind that in the S₂ state the cluster exists in the two interconvertible structures depicted in Fig. 1 and it is not a priori clear if only one of them is catalytically relevant, and if so, which one. The first water binding scenario,⁵⁰ an element of Siegbahn's detailed computational water oxidation model,^40,41,51 involves binding of a (non-crystallographic) spectator water molecule to the open coordination site of the Mn1 ion of an S^A₂-type structure (Fig. 2a). According to this scenario, after Y_Z oxidation by P680˙⁺ the W1 ligand loses a proton. Subsequently Mn1, a Mn(III) in the S^A₂ state, is oxidized to Mn(IV) and thus can bind an additional water molecule. Binding and deprotonation of the incoming water molecule are coupled, with deprotonation assisted by the hydrogen bonding network on the side of the chloride ion, as shown in Fig. 2a.⁵⁰ An alternative mechanism was proposed by Guidoni and coworkers.¹⁹ In this scenario, after deprotonation of W1 the cluster assumes an S^B₂-type structure upon Mn oxidation and a water that is already bound to calcium (W3), moves to occupy the empty coordination site of Mn4, the Mn(III) ion of the S^B₂ structure.^19,52 This W3 shift would be accompanied by reorganization of water molecules along a channel associated with Ca, resulting in replenishment of the Ca-bound waters (Fig. 2b).¹⁹

Fig. 2 Schematic depiction of two major suggestions for water binding during the S₂–S₃ transition. Top: A model involving water binding to the Mn1 ion of an S^A₂-type conformer.⁵⁰ Bottom: A model involving the shift of a Ca-bound water to the Mn4 ion of an S^B₂-type conformer.¹⁹

Both suggestions involve water binding at Mn ions present as pentacoordinate Mn(III) in the S₂ state, at a site that lies along the Jahn–Teller axis of the former Mn(III) ion, located opposite the O5 bridge, i.e. they can both be described as “internal” water insertion within the Mn₄O₅Ca framework. On the other hand, they involve ions on opposite sides of the cluster and may differ fundamentally in substrate identity, a critical mechanistic determinant. Moreover, they have distinct implications for the role of the S₂ valence/structural isomerism in the mechanism, the role of calcium, and the regulation of the enzyme's substrate access and delivery mechanisms.

It is not obvious which mode of progression from the S₂ state can best accommodate the available spectroscopic information on the S₃ state and the experimentally detected S₂–S₃ intermediates. Here we attempt to address this question by identifying plausible intermediates in the S₂ to S₃ transition by matching predicted properties of computational models with available experimental data, principally from near-infrared (NIR) absorption studies and EPR spectroscopy. The outcomes of this work are: (a) an understanding of the central mechanistic role of the S₂-state structural polymorphism, (b) the characterization of an S₃-state intermediate that contains a five-coordinate Mn(IV) site, which rationalizes NIR absorption activity and is consistent with EPR spectroscopic observations, and (c) the identification of a new low-energy water binding pathway that has important implications for understanding PSII regulation and the biological water oxidizing mechanism.

Methodology

Structural models

Quantum chemical models for the structure of the OEC have been developed that combine information and constraints from X-ray crystallography, EXAFS, XAS profiles, and magnetic resonance spectroscopy.⁹ As in previous work,^{9,18,21,53–56} the models comprise 238–241 atoms (depending on protonation state and inclusion of an additional water ligand) and include the amino acid residues coordinating the Mn₄O₅Ca cofactor (from protein chain D1 unless otherwise indicated): Asp170, Glu189, His332, Glu333, Asp342, Ala344, and CP43-Glu354, as well as two H₂O molecules on Ca²⁺ ion and an H₂O plus a hydroxide on the terminal Mn4 ion. They also include the structurally and electronically critical residues Asp61, Tyr161 (Y_Z), His190, His337, and CP43-Arg357, the backbones of Leu343, Ser169, and Gly171, plus eight hydrogen-bonded crystallographic water molecules. The protonation states of all ligands were set consistently with previous studies that focused on state-specific evaluation of spectroscopic parameters,⁵⁷ and by self-consistent and experimentally corroborated modeling of the S₀, S₁, S₂, and S₃ states.⁹ Density functional theory calculations employed initial geometries originating from the S₂ state isomers reported in Pantazis et al.¹⁸ (S^A₂Y_Z and S^B₂Y_Z) and Retegan et al.⁵⁶ (S^A₂Y_Z˙ and S^B₂Y_Z˙), using permutations of protonation states (for water-derived ligands), hydrogen-bond orientations (for second-sphere waters) and side-chain rotations of non-coordinating amino acid residues.

Computational details

All calculations were performed with ORCA.⁵⁸ Geometry optimizations used the BP86 functional^59,60 with self-consistently applied atom-pairwise dispersion corrections⁶¹ and the zero-order regular approximation (ZORA) to account for scalar relativistic effects.^62–64 Backbone constraints from the 1.9 Å crystallographic model of PSII were applied to α-carbon atoms and to one α-carbon hydrogen in order to maintain the overall protein chain conformation. The ZORA-TZVP basis sets⁶⁵ were used for all elements except carbon and hydrogen, for which the basis set was reduced to ZORA-SVP. The calculations used the resolution of the identity (density fitting) approximation; to eliminate any potential errors arising from this approximation, a large decontracted def2-TZVP/J auxiliary basis set was used.⁶⁶ Optimizations were performed with the conductor-like screening model (COSMO)⁶⁷ with a dielectric constant of 8.0. Tight SCF convergence and increased integration grids (Grid6 and IntAcc 6.0 in ORCA convention) were applied.

The transition state searches for water binding were initiated from multiple starting arrangements of the incoming water molecule and used the “hybrid Hessian” feature of ORCA: this involves a frequent exact recomputation of the part of the Hessian that corresponds to the terminal Mn4 ion, its direct ligands and the incoming water molecule, in order to best identify and follow the water binding mode. To facilitate the search for water-binding transition states, Asp61, CP43-Arg357 and some crystallographic water molecules in the vicinity of Asp61 were omitted from the transition state optimizations. Exploratory calculations with the presence of Asp61 and vicinal crystallographic waters led to technical complications because of formation of various hydrogen-bonding rearrangements that led all transition state searches towards directions not relevant to the water binding event, thus the residue had to be omitted. Although this is an approximation, we can estimate that the effect is not major, in view of the flexibility of the Asp61 seen in molecular dynamics simulations,^52,68 and specifically because the side chain was shown to rotate upon W1 deprotonation,⁵² which makes its involvement in water binding ambiguous. A unique transition state was optimized through these searches and conclusively identified as a first-order saddle point by calculation of its analytic second derivatives that led to a single imaginary frequency corresponding to the water binding mode.

Magnetic and spectroscopic parameters were computed by the broken-symmetry DFT (BS-DFT) approach using the TPSSh functional⁶⁹ with the RIJCOSX approximation⁷⁰ to Coulomb and exact exchange (with GridX6), using the same scalar relativistic Hamiltonian and basis sets. Details regarding the application of BS-DFT for magnetic and EPR parameters of manganese-oxo systems can be found in recent work.^{9,18,57,71–74} All possible BS determinants (M_S eigenfunctions) were computed and from their energy differences the values of all six pairwise exchange coupling constants were determined using singular value decomposition. These values were subsequently used to construct the Heisenberg–Dirac–van Vleck (HDvV) Hamiltonian which was diagonalized using the orca_eca utility program to obtain the full spectrum of spin eigenvalues. Time-dependent (TD-DFT) calculations of excitation energies followed the same setup as for the single-point calculations described above, but employed the long-range corrected CAM-B3LYP functional.⁷⁵ Complete active space self-consistent field (CASSCF) and N-electron valence perturbation theory (NEVPT2) calculations^76,77 employed an active space of 12 electrons in 20 orbitals. Local zero-field splitting (ZFS) parameters were obtained with the recently introduced local complete active space configuration interaction (L-CASCI) approach,⁷⁸ using the same active space as for the CASSCF calculations.

Results and discussion

Initial formation of tyrosyl radical species

The presence of two structural forms in the S₂ state raises the question whether both forms are mechanistically relevant, or if instead only one form proceeds to the S₃ state. In the mechanistic progression suggested by Siegbahn, it is only the open-cubane S^A₂ form that progresses to the S₃ state. In stark contrast, computational studies by Guidoni favor the progression of the closed-cubane S^B₂ form. Given the correspondence of these two structural forms to the two EPR signals of the S₂ state, the experimental EPR literature also contains apparently contradictory suggestions regarding the progression of the multiline g ≈ 2 or of the g ≈ 4.1 S₂ state signals to the S₃ state.^22,79

By modeling the initial S₂ oxidation event we observe that upon one-electron oxidation of the S₂ state models the resultant electronic state contains the Y_Z radical, as expected, i.e. S^A₂Y_Z˙ and S^B₂Y_Z˙.⁵⁶ The phenolic proton of Y_Z in both these forms is transferred from the tyrosyl to its hydrogen-bonding partner, His190. Both structural forms remain close in energy in our calculations, with the closed-cubane form higher in energy as in the S₂-state models: S^B₂Y_Z˙ is 2.7 kcal mol⁻¹ higher than S^A₂Y_Z˙, compared to 2.4 kcal mol⁻¹ for the S^B₂/S^A₂ pair. This electronic S₂Y_Z˙ state represents the first intermediate in the S₂ to S₃ transition, formed during electron shuttling between the Mn₄O₅Ca cofactor and P680˙⁺. Importantly, neither of these structural models can progress to S₃, that is, they do not convert to a valence isomer where the electron hole shifts to the Mn cluster,⁵⁶ presumably because the intrinsic redox potential of the Mn₄CaO₅ cluster at this state is not low enough to reduce the Y_Z˙ radical. Therefore, oxidation of the cofactor must be coupled to one of the additional chemical processes described above in connection with the S₂–S₃ transition: cofactor deprotonation and/or water binding. Of these, only deprotonation rationalizes the required redox tuning of the complex. Experimental results also favor deprotonation on the donor side preceding the oxidation event.^5,80

Deprotonation of the cluster in the S₂–S₃ transition

Asp61, a second-sphere amino acid that forms a hydrogen bond with the terminal water W1 of Mn4, has been implicated in deprotonation of the OEC.^{5,13,41,49,50,52,68,81,82} This would suggest that the two titratable Mn4-bound ligands (W1, W2) situated most closely to Asp61, are probable sites for deprotonation in the S₂–S₃ transition. To address this point we compared relative energies of deprotonated structures to estimate relative acidities of the titratable groups W1, W2, W3, and W4 in both the open and the closed-cubane configurations of the S₂ and S₂Y_Z˙ states. Similar calculations have been reported by Robertazzi et al. for the S₁ state.⁸³ In these calculations, prohibiting structural relaxation and repulsive electrostatic interactions from second-sphere residues (including omission of Asp61) allows us to include in our comparison deprotonation of Ca-bound waters, for which the extensive reorganization of the hydrogen-bonding network upon relaxation would be hard to capture adequately.

The energetically most favorable proton removal site in both S₂ and S₂Y_Z˙ states for both structural forms (open and closed-cubane) is on W1, specifically the proton H-bonding to Asp61 (see Table 1 and Fig. 3). Removal of any other proton from W1 or W2 costs at least 10 kcal mol⁻¹ more in energy and deprotonation of Ca-bound waters in either the open or the closed-cubane structures is strongly disfavored. Upon deprotonation of W2 in the open-cubane form, Mulliken spin populations of 0.4 on O(W2) and 2.7 on Mn4 are found, indicating development of Mn(III)-oxyl radical character at this site prior to structural relaxation.⁸⁴ In models with a deprotonated W3 or W4 significant spin population develops on the resulting OH ligands, up to −0.5 for W3 deprotonation in the open-cubane form. Formation of the tyrosyl radical does not alter the observed trends, but it increases the relative acidities of Ca-bound waters. Table 1 reports relative energies referenced to the most acidic group within each given model. If we instead compare relative energies between different structural types (S^A₂/S^B₂), we observe that W1 and W2 deprotonation in the closed-cubane form is consistently disfavored by more than 10 kcal mol⁻¹ relative to W1 or W2 deprotonation in the open-cubane form (see Table S1†), implying that the S^A₂ forms are more susceptible to deprotonation than their S^B₂ isomers. This is a reasonable conclusion that relates to the oxidation states of the Mn4 ion in these forms: the Mn4(IV) in the open-cubane form is better stabilized by a negatively charged ligand than the Mn4(III) ion in the closed-cubane form.

Table 1 Relative single-point energies (kcal mol⁻¹) of deprotonated S₂Y_Z and S₂Y_Z˙ models

Site	S^A2YZ	S^B2YZ	S^A2YZ˙	S^B2YZ˙
W1a	0.0	0.0	0.0	0.0
W1b	16.3	13.8	16.6	13.1
W2	17.9	13.5	17.1	10.8
W3a	56.4	44.0	39.4	26.0
W3b	50.6	38.1	35.6	21.2
W4a	50.6	34.5	34.6	19.8
W4b	51.5	34.9	36.3	21.0

---

Fig. 3 Relative acidities of titratable groups for the S₂ and S₂Y_Z˙ species indicated by color: green for the most favorable site, orange for relative energies in the range 10–20 kcal mol⁻¹, and red for more than 20 kcal mol⁻¹.

Oxidation of the cluster in the S₂–S₃ transition

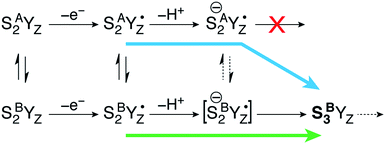
Moving on to the next event that occurs in the S₂–S₃ transition, the present calculations provide a definitive answer to the question which structural form of S₂ can be oxidized by the Y_Z˙ radical after deprotonation of W1: oxidation of the Mn(III) ion of the inorganic core occurs exclusively in the closed-cubane form. Specifically, a deprotonated S^A(−)₂Y_Z˙ species retains its electronic configuration even after complete structural relaxation; the Mn1(III) ion of the inorganic cluster is stable. It cannot be oxidized by the tyrosyl radical and does not appear to be affected by the deprotonation of the Mn4(IV) ligand W1 at the opposite side of the cluster. By contrast, the deprotonated closed-cubane S^B(−)₂Y_Z˙ form proved to be unstable and spontaneously relaxed to a form where the Mn4(III) ion of the cluster is oxidized to Mn(IV) and the tyrosyl radical is reduced to its closed-shell form with concomitant proton transfer from His190. Spin populations confirm the presence of four high-spin Mn(IV) ions (2.80–2.89 unpaired electrons on all Mn centers) and the absence of any other spin accumulation site. This type of electronic configuration corresponds to the S₃ state of the OEC and the closed-cubane species thus obtained will be referred to as S^B₃. This state nominally corresponds to an intermediate proposed in a recent ab initio molecular dynamics study of the S₂–S₃ transition by Narzi et al.⁵² Note that according to the present results, an S^A₃ species does not exist as a distinct minimum because it is electronically unstable and reverts via internal electron transfer to S^A(−)₂Y_Z˙. Since the S^B₃ structure is the first S₃-type species formed in the catalytic progression, it can be considered as the “entry point” to the S₃ state. Importantly, compared to its isomeric S^A(−)₂Y_Z˙ form, S^B₃ is found to be stabilized by 15.4 kcal mol⁻¹.

The above theoretical results are consistent with chemical intuition. Within the interconvertible S₂ state model the Mn(III) is located at the outer Mn (Mn4 for S^B₂) or within the cubane (Mn1 for S^A₂).^18,19 Of these two structures, only S^B₂ contains a Mn(III) ion with titratable ligands, and thus only the S^B₂ structure can be “redox tuned” with deprotonation, allowing advancement to S₃.

This is a clear conclusion, but it can be realized via at least two conceivable pathways. According to the first scenario (green pathway in Fig. 4), the closed cubane form becomes stabilized upon tyrosine oxidation, in contrast to the parent S^A₂Y_Z/S^B₂Y_Z species for which the open-cubane form is instead more stable.⁵² This implies that the S^B₂Y_Z˙ species may directly proceed via coupled proton and electron transfer to S^B₃. This sequence of events emerges from the computational study of Narzi et al.,⁵² which suggests that Y_Z oxidation stabilizes the closed-cubane form by 2.6 kcal mol⁻¹ compared to the open-cubane form, and facilitates proton shuttling from the W1 ligand of Mn4 to Asp61, coupled to electron transfer from Mn4 to the tyrosyl radical.

Fig. 4 The progression of the open-cubane S^A₂ and closed-cubane S^B₂ structures during the S₂–S₃ transition of the Kok cycle. The deprotonated form of S^A(−)₂Y_Z˙ is stable and cannot progress any further by Mn oxidation. A low-barrier open/closed-cubane rearrangement however induces intramolecular electron transfer (with or without direct involvement of an unstable S^B(−)₂Y_Z˙ species as transient intermediate) and formation of the stabilized S^B₃Y_Z state. Two conceivable progression pathways that converge to the same closed-cubane S^B₃ species are indicated with the green and blue arrows, the latter being the one favored by the present computational results.

With the methods used in the present paper, however, we do not observe such stabilization of the closed-cubane S^B₂Y_Z˙ form compared with S^A₂Y_Z˙ (see above).⁸⁵ Additionally, if we consider deprotonation as a distinct step, the S^A₂Y_Z˙ form must be easier to deprotonate for the reasons raised in the preceding section, i.e. a Mn4(IV)-bound water is intrinsically more acidic than a Mn4(III)-bound water. This leads us to propose an alternative scenario (blue pathway in Fig. 4), which requires separate proton transfer and electron transfer steps. The barrier for structural interconversion through transposition of the O5, which was computed at ca. 6 kcal mol⁻¹ for the preceding S^A₂/S^B₂ states¹⁸ must be even lower after deprotonation because of the trans-effect of the newly formed OH(W1) ligand. Specifically, deprotonation of W1 results in reduction of the Mn4–O5 Mayer bond order^86,87 by 26%, from 0.88 to 0.66. Therefore, the more easily formed S^A(−)₂Y_Z˙ species can readily shift towards a closed-cubane structural rearrangement that is, however, coupled to intramolecular electron transfer. Since [S^B(−)₂Y_Z˙] cannot be identified as a distinct stationary point, it is not possible to confirm whether it is a requisite transient intermediate in the transformation of S^A(−)₂Y_Z˙ to S^B₃, or whether it is avoided altogether in the case O5 transposition and electron transfer from the Mn cluster to the Y_Z radical occur simultaneously. However, even if [S^B(−)₂Y_Z˙] would form transiently, it would spontaneously evolve into S^B₃, which lies 15.4 kcal mol⁻¹ lower than S^A(−)₂Y_Z˙, an energy difference suggestive of a strong thermodynamic driving force. Regardless of the details of the progression, the identical conclusion is reached: only the closed-cubane form, a structural form that appears for the first time in the S₂ state of the catalytic cycle, progresses to the S₃ state. It is noted that EPR data suggest that Ca²⁺ is necessary to proceed past the low-spin S₂Y_Z˙ state.^88–90 Based on the above, Ca²⁺ may play a role in allowing efficient open/closed cubane interconversion, in stabilizing the closed-cubane state, or in enabling reduction of the tyrosyl radical by the Mn(III) ion of the inorganic cluster.⁵⁶

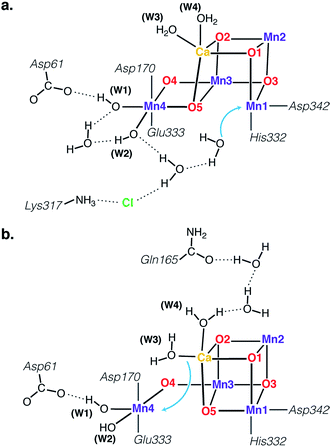
Structure of the S^B₃ intermediate

The species obtained immediately upon the spontaneous electronic reorganization described above contains a Mn4 site that is approximately square pyramidal as in the S^B₂ structure from which it is derived, with a wide O4–Mn4–O(W2) angle of 154.7°. This angle defines a free coordination site in the internal side of the cluster, opposite the O5 bridge of the closed cubane subunit and in the orientation that the Mn(III) Jahn–Teller axis had in the S₂ state. This site can serve as coordination site for an incoming water, possibly W3 (Fig. 2b).¹⁹ However, we find that structural relaxation of this structure occurs by rotation of the hydroxy ligands W1 and W2 within the plane perpendicular to the Asp170/Glu333 Mn–O bonds, affording an energy stabilization of ca. 5 kcal mol⁻¹ and leading to the S^B₃ minimum where Mn4 adopts a coordination geometry intermediate between trigonal bipyramidal and square pyramidal (Fig. 5). The widest angle is now O4–Mn4–O(W1) at 146.2° (compared to 97.3° at the initial point). The OH(W2) group is rotated towards the O5 bridge of the Mn₃O₄Ca cubane subunit, forming an intramolecular hydrogen bond.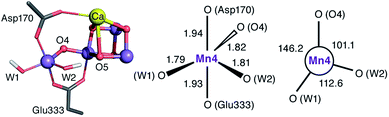

Fig. 5 Depiction of the inorganic core of the S^B₃ species and geometric parameters (Å and degrees) of its Mn4 center.

Five-coordinate Mn(IV) centers are uncommon, but not unprecedented. We are not aware of crystallographically characterized examples of synthetic complexes that display a similar coordination environment, but trigonal bipyramidal complexes supported by N₄-donor ligands have been reported by Borovik.^42,91,92 As will be shown in the following, this unusual coordination geometry at the Mn4(IV) site of S^B₃ is responsible for a range of properties that rationalize a large part of the available experimental observations.

Electronic structure and absorption profile of the S^B₃ intermediate

To study the S₃ state by EPR, dark-adapted (S₁-state) samples are illuminated by two flashes at room temperature and rapidly frozen to cryogenic temperatures.^24,25,93 As described in the introduction, this procedure captures an EPR signal consistent with a structure that contains four octahedrally coordinated Mn(IV) ions, which is considered the end point of the S₂–S₃ transition.²¹ Compared to the structural forms present in the S₂ state, this “final” S₃ species is characterized by an open-cubane topology, but with the crucial difference that the coordination number of all Mn ions is six, due to insertion of a water-derived ligand (see the S₃ state model of Fig. 1). To facilitate the following discussion we refer to this all-octahedral model as S^A,W₃, that is an S₃ state structure with metal-oxo connectivity of the open-cubane type, where “W” in the superscript indicates the ligation of an additional terminal ligand (H₂O or OH).

But as described in the introduction, a second, minority S₃-state population has been inferred from the development of additional features in the EPR spectrum following NIR illumination at cryogenic temperatures, without modification of the original EPR signal.^24,25 NIR sensitivity is not limited to the S₃ state. It is a common feature of the lower S states, where the inability of the reaction center (P680) to absorb in the 740–900 nm spectral range has pointed towards the OEC cluster acting as the chromophore.⁹⁴ The absorption which promotes the conversion of the multiline signal to the g = 4.1 signal, has been assigned to a ligand field transition localized on the unique Mn(III) ion,^94,95 in line with the presence of a near-infrared band in the MCD spectrum of a mixed valent Mn(III, IV) complex.^96,97 Similarity of the action spectrum induced in the 720–860 nm region in both S₂ and S₃ states, indicated the presence of an analogous mechanism for the NIR sensitivity of the cluster in the S₃ state, therefore extending the requirement of a Mn(III) ion to this state.³⁰ It was nevertheless argued by Havelius et al. that the assignment is circumstantial, and that other mechanisms can give rise to the observed NIR sensitivity without the constraint related to the presence of a Mn(III) ion.³² In the following we demonstrate that the S^B₃ structure described above is indeed NIR active and explains all relevant experimental observations owing to the unique five-coordinate Mn(IV) center.

The structural models that we have discussed as different S₃-state species, S^B₃ and S^A,W₃, have to account for the different photochemistry of the S₃-state populations based on the different coordination environment of the Mn4(IV) ion. To test this, we calculated the absorption spectra of the two structures using time-depended density functional theory. The reliability of TD-DFT to predict the position of d–d transitions for mononuclear Mn(IV) complexes has been previously established, with reported deviations of less than 500 cm⁻¹ compared to experiment for the low energy transitions that are of interest in the present context.^98,99 The present results confirm that the change in the local geometry of the outer Mn4 ion from five-coordinate (S^B₃) to six-coordinate (S^A,W₃) has a significant effect on the position of the d–d excitations. Using the CAM-B3LYP functional, no near-infrared absorptions were computed for the S^A,W₃ structure, with the lowest transition around 18 230 cm⁻¹ (549 nm), whereas in S^B₃ the first transition is significantly lower in energy and occurs at ca. 11 930 cm⁻¹ (838 nm). A similar picture is obtained with the PBE0 functional, which predicts the same transitions as CAM-B3LYP, only red-shifted for both models by 30–40 nm.

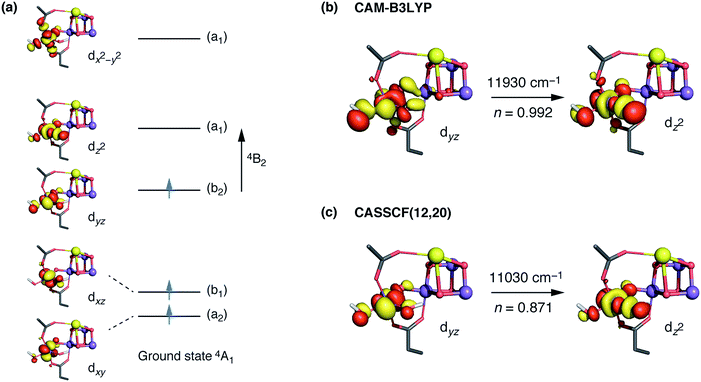
The interpretation of the absorption spectra is facilitated by the use of natural transition orbitals (Fig. 6b). These reduce the inherent complexity of dealing with several molecular orbitals that contribute to a given excited state to a simple picture of one electron being promoted from a donor to an acceptor orbital. Fig. 6 shows the orbital diagram for the Mn4 ion of species S^B₃, along with the CAM-B3LYP natural transition orbitals that describe the lowest excitation, a near-IR d–d transition from the d_yz to the d_z² orbital of Mn4(IV). The change of ligand field to the approximately octahedral geometry of S^A,W₃ increases the separation between the t_2g-derived d_yz and the e_g-derived d_z² orbitals of Mn4, shifting the excitation energy to much higher values.

Fig. 6 (a) CASSCF d orbitals on the Mn4 center of S^B₃. Symmetry labels correspond to idealized local C_2v point group symmetry (intermediate between D_3h trigonal bipyramidal and C_4v square pyramidal). (b) The dominant natural transition orbital pair for the first excited state obtained from TD-DFT calculations (n indicates the contribution of the pair to the overall transition). (c) The corresponding CASSCF orbitals, where n indicates the weight of the Mn4 configuration in the first excited state.

CASSCF calculations using an active space comprising all d electrons and orbitals of all four Mn ions, CAS(12,20), agree with the TD-DFT results. Specifically, the lowest-energy d–d transition for S^B₃ is predicted by CASSCF at ca. 11 030 cm⁻¹ (907 nm), whereas that of S^A,W₃ at 18 160 cm⁻¹ (551 nm). The CASSCF orbitals that dominate the lowest-energy transition are depicted in Fig. 6 and show very close agreement with the TD-DFT natural transition orbitals. The corresponding TD-DFT natural transition orbital pair and CASSCF orbitals for S^A,W₃ are shown in Fig. S2.† To refine the CASSCF energies we included the effects of dynamical electron correlation by performing N-electron valence state perturbation theory (NEVPT2) calculations on top of the CASSCF(12,20) reference wave functions. These calculations represent the highest level of theory employed in the present work. The NEVPT2 excitation energies are blue-shifted compared to the CASSCF energies: the lowest S^A,W₃ transition is shifted to 22 000 cm⁻¹ (454 nm), while the lowest-energy transition for the five-coordinate S^B₃ species is predicted to be at 13 610 cm⁻¹ (735 nm), in even better agreement with the experimental absorption maximum of ca. 740–760 nm.^30,31 Overall, both TD-DFT and multiconfigurational ab initio methods confirm that the unusual geometry of the five-coordinate Mn4(IV) ion in S^B₃ leads to absorption in the NIR region, consistent with the experimental observations for the population of the S₃ state that remains unobserved by EPR.

This result also implies that the response of the OEC to near-IR has a different electronic structure origin in different S-states, since NIR absorption in the S₃ state clearly does not arise from—and does not require—the presence of a Mn(III) ion.

Spin state and EPR properties of the S^B₃ intermediate

In the previous section it was shown that S^B₃ and S^A,W₃ are consistent with their assignment as NIR-active and NIR-inactive species, respectively. The close agreement of the S^A,W₃ properties (spin state of S = 3, ⁵⁵Mn hyperfine coupling constants and small fine structure splitting) with EPR data has been theoretically confirmed in our recent work.²¹ Here, we address the more complicated question whether the predicted properties of the NIR-active S^B₃ can be consistent with the fact that the NIR-active component of the S₃ state has not been identified so far in EPR studies. Two factors play a role in this respect: the ground state spin multiplicity of the cluster and the magnitude of the zero-field splitting.

Broken-symmetry DFT calculations on the S^B₃ model suggest that it is characterized by a high-spin ground state. As expected from previous work on synthetic Mn₃CaO₄ cubanes,^100,101 ferromagnetic coupling is dominant within the cubane subunit, with J₁₂ and J₂₃ exceeding 30 cm⁻¹, while J₁₃ is somewhat weaker at 10 cm⁻¹ (see Fig. S3† for depiction of all computed exchange coupling constants). Thus, the Mn₃(IV)CaO₄ cube is an intrinsically high-spin unit (S = 9/2).¹⁰¹ The coupling between Mn3 and Mn4, J₃₄, further regulates the total spin state. In the present model of S^B₃ the weakly ferromagnetic (1.3 cm⁻¹) J₃₄ leads to a ground state total spin of S = 6, the maximum spin possible for the given system. J₃₄ is quite sensitive to small structural perturbations, therefore the ground state multiplicity can be lowered if we allow for only small changes in the Mn3–Mn4 interaction, but our simulations indicate a lower bound of S = 3 for the present magnetic topology.

EPR-detected states originating from the S₃ species identified here with the S^B₃ model are known to correspond to high-spin states of the inorganic cluster. Specifically, the state formed after NIR excitation at 77 K of the NIR-active form of S₃ contains a tyrosyl radical (with an EPR signal at g ≈ 2) interacting with a high-spin form of the inorganic cluster (attributed to S = 7/2, with an EPR signal observed around g ≈ 5).^24–29,32 Since this state results from the one-electron oxidation of tyrosine Y_Z by the inorganic cofactor, it is designated as S^′₂Y_Z˙, where S^′₂ denotes an electronic configuration of the Mn cluster that is singly reduced compared to S₃, but at a geometry similar to its parent S₃ state. A comparable EPR signal measured in samples advanced to S₃ and stored for extended periods at liquid nitrogen temperature, points towards a similar configuration of the OEC formed in the absence of the Y_Z˙ radical, where the reduced state of the cluster is generated via charge recombination with the plastoquinone Q_A⁻.¹⁰² This S^′′₂Y_Z state is also associated with a similar high-spin configuration of the inorganic cluster.²⁶ Both of these states are stricto sensu “off-cycle” states with respect to physiological catalytic progression and not directly accessible with our computational methods (see the ESI† for a more detailed discussion). Nevertheless, the high-spin nature of S^B₃ is clearly consistent with the high-spin states attributed to EPR signals of the S^′₂Y_Z˙ and S^′′₂Y_Z states.

Next, we focus on the zero-field splitting of S^B₃. High field EPR measurements of a mononuclear Mn(IV) complex found that in an octahedral ligand field the D parameter is small and axial, ca. 0.25 cm⁻¹,¹⁰³ a result in line with ligand-field theory considerations. Experimental results are also available for five-coordinate Mn(IV) complexes. In a trigonal bipyramidal ligand field much larger D values, from 0.88 up to 3.0 cm⁻¹, are obtained compared to the six-coordinate metal ion, depending on the protonation of the axial oxygen atom.^42,91,104 To investigate the corresponding properties of S^B₃ we employed a recently developed ab initio method for the calculation of the on-site ZFS splitting in polynuclear complexes of arbitrary nuclearity. The method, termed L-CASCI,⁷⁸ essentially represents a multireference calculation in an active space constructed from the orbitals localized on the metal center of interest. Using this approach we calculated sequentially the ZFS parameters of all four Mn ions of S^B₃. In line with experimental results from synthetic mononuclear complexes, the largest value was calculated for the five-coordinate Mn4 ion, D = 2.14 cm⁻¹, with significant rhombicity E/D = 0.10.

It is interesting to analyze the dependence of the ZFS parameters on the principal structural modifications that define the coordination geometry at the Mn4 ion, since this also allows one to understand the connection with the EPR-detectable form of the S₃ state (S^A,W₃). In this respect the O4–Mn4–W1 angle represents a critical parameter, and to establish a connection with the local D of Mn4, the spectroscopic parameters were re-evaluated for geometries where modifications were limited to this particular angle (Fig. 7). The calculated values show that increasing the O4–Mn4–W1 angle from its optimized equilibrium value of 146°, in essence opening up a sixth coordination site at the Mn4 ion, results in diminished local zero-field splitting, whereas even larger values for D are obtained if this angle is made less obtuse.

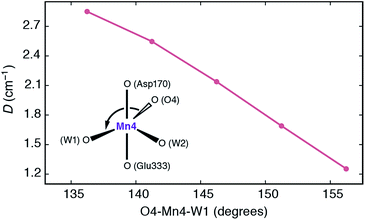Fig. 7 Dependence of the local zero-field splitting parameter D for the Mn4 ion of S^B₃ on the O4–Mn4–W1 angle.

The trend can be rationalized by decomposing the D value in terms of state contributions. This reveals that the first excited state, which is also responsible for the NIR sensitivity of the OEC cluster (see Fig. 6), has the largest contribution to the total D value among the spin conserving excited states. This state results from a transition between the d_yz and d_z² orbitals (Fig. 6a). An increase in the O4–Mn4–W1 angle would affect the two orbitals in opposite ways, with d_yz being stabilized and d_z² being destabilized. The net effect would be an increase in the energy separation between the ground state and the first excited state, which, due to the fact the energy difference enters at the denominator of the equations used to calculated the ZFS parameters, leads to a smaller D value—and vice versa. The correlation between the O4–Mn4–W1 angle and the d_yz–d_z² orbital energy difference is shown in Fig. S4.†

Given the above properties of S^B₃, it is expected that the interplay between the large zero field splitting and the high-spin state would either lead to a very broad EPR signal that would be difficult to detect at low microwave frequencies (X and Q-band), or to complex signals that underlie the signal of the final majority S₃ state species (attributed to S^A,W₃), explaining why it has yet to be characterized.

Water binding in the S₂–S₃ transition

As discussed above, the S^B₃ structure can be identified with the NIR-active component of the S₃ state, while simultaneously its spin state and unusually high local ZFS of the five-coordinate Mn4 ion support its assignment as the EPR “silent” species of the S₃ state. It is evident that the S^B₃ structure does not represent the end point of the S₂ to S₃ transition, but the entry point to the S₃ state. To complete the transition an additional water molecule needs to bind to the Mn₄O₅Ca cluster, rendering all Mn ions octahedral, as required by the S^A,W₃ structure identified and described in Cox et al.²¹ Having established a structurally defined sequence of events, we can address the question highlighted in the introduction (Fig. 2), namely how water binds to the OEC at this catalytic step.

First of all, the requirement to progress through the closed-cubane S^B₃ intermediate cannot be reconciled in any obvious way with the water binding hypothesis depicted in Fig. 2a. The only way for this binding event to be realized would be for the S^B₃ state to isomerize to an “S^A₃” state, thus creating an available coordination site at Mn1. However, as explained above such a state is not stable and would exist only in the form of S^A(−)₂Y_Z˙, with a Mn(III) ion at the Mn1 position. Its associated Jahn–Teller axis along the internally available coordination site eliminates any driving force for binding of an additional ligand.

Instead, the requisite S^B₃ intermediate imposes the five-coordinate Mn4(IV) ion as the water binding site. Two possibilities exist in this respect. The first one involves the “internal” water binding depicted in Fig. 2b, with the incoming ligand probably originating from the W3 Ca-bound water, as suggested by Bovi et al.¹⁹ The second possibility is indicated by the wide O4–Mn4–W1 angle of S^B₃ (Fig. 5) and would involve “external” water binding to the OEC, at the Mn4 site previously occupied by W1 in the S₂ state. Both possibilities would be consistent with the S^B₃ geometry and with the presence of distinct water channels that terminate at Mn4 and Ca (see Fig. 8).^{11,81,105–111}

Fig. 8 The Mn₄O₅Ca core of the optimized S^B₃ model showing the two possible pathways for water delivery to the five-coordinate Mn4 site: (a) “internal”-side delivery through the water channel associated with Ca, and (b) “external”-side delivery through the water channel terminating close to O4. Potential movement of water molecules is indicated with the light blue arrows.

We have tried to locate a transition state for a W3-binding event or for coordination of the water that bridges W2 and W3, but our attempts have been unsuccessful. Possible reasons may be that the concerted rearrangements for this type of water binding cannot be adequately incorporated in our quantum cluster models, or that the immediate coordination product is disfavored energetically owing to structural congestion in the internal side of the cluster. To test the second possibility we tried to optimized directly the “internal” and “external” water coordination products for a variety of hydrogen-bonding interactions of the new water with its environment (see Table S2†). The results indicate that in the absence of any secondary rearrangements, “external” water binding is favored over “internal” water binding at Mn4 by ca. 10 kcal mol⁻¹.¹¹² Therefore, although the “internal” water binding pathway cannot be excluded in principle, the “external” pathway seems more easily realizable. Indeed, locating a transition state for this type of water binding proved straightforward.

The water molecule that binds to Mn4 according to this pathway was already positioned at close proximity to Mn4 by hydrogen bonding interaction with O4. The transition state displays an imaginary frequency which corresponds to formation of a bond between Mn4 and this new ligand (“W_new”) with a simultaneous widening of the O4–Mn4–W1 angle and pivoting of OH(W1) towards OH(W2) (Fig. 9). The metal ion eventually adopts an octahedral geometry upon completion of the W_new binding; the adduct is labeled S^B,W₃ according to the nomenclature conventions adopted in the present work. The energy barrier for this water addition was computed to be only 4.5 kcal mol⁻¹. Interestingly, the addition product S^B,W₃ is predicted to be essentially isoenergetic with the reactants (stabilized by 0.2 kcal mol⁻¹), indicating a fine balance between ligand field stabilization of the two distinct coordination geometries (distorted trigonal bipyramidal for S^B₃, distorted octahedral for S^B,W₃), the Mn4–W_new bond energy, and the reorganization of the hydrogen-bonding network. We note that these energy values should be considered approximate because the present computational models do not fully include the response of the protein and of the surrounding hydrogen-bonding network to the structural rearrangements described above, and they also do not incorporate entropic contributions. Interestingly, despite not modeling exactly the same molecular process, the computed barrier is in good agreement with the activation energy of 5 kcal mol⁻¹ reported by Vassiliev et al. for the end-point of this channel in their multiple steered molecular dynamics simulations of water permeation in PSII,¹⁰⁹ showing that two vastly different theoretical approaches converge to a similar conclusion regarding the energetics of water access to the Mn4 site.

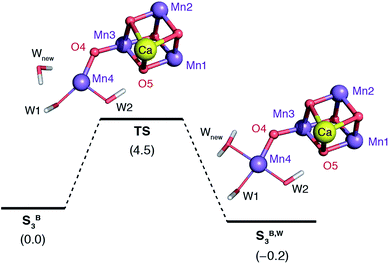Fig. 9 Schematic diagram for the binding of a water molecule (W_new) to the Mn4 of a reduced-size model of S^B₃ (coordinating amino acids are omitted for clarity). Relative energies in kcal mol⁻¹.

Importantly, this type of water binding is not only favorable based on computed energetics, but is also aligned with recent experimental and theoretical studies of ammonia interaction with the OEC.^{53,55,113,114} These studies suggest that NH₃ interacts with the inorganic cluster in the S₂ state through coordination at Mn4, from precisely the same side of the cluster and at the same coordination site, that is, by displacement of W1. This supports the notion that NH₃ accesses the cluster through the same water channel (referred to in the literature as “narrow channel”¹⁰⁶ or “channel 2”¹¹¹) suggested here to be involved in the delivery of W_new during the S₂–S₃ transition. It can also explain the partial inhibition of NH₃-treated PSII samples under steady-state conditions, in the sense that ammonia competes for a water binding site.¹¹⁵

We note that for any water binding mechanism (“internal” or “external”) that involves Mn4 as the water binding site of a closed-cubane species, a subsequent reorganization would be required to reach the end-point of the transition, the S^A,W₃ state (Fig. 1). This can be achieved, for example, with a transposition of the Mn3-oxo bonds as described in ref. 116 and 117. The associated barrier for this process is estimated at more than 10 kcal mol⁻¹.^116,117 This final step stabilizes the coordination of the new Mn-bound water by ca. 10 kcal mol⁻¹,^9,21 (or even more according to ref. 117) providing a driving force for second substrate binding/inclusion.

Identities of substrates

Even though the S^B₃ intermediate and the mode of water binding resulting from this work implicate a completely different sequence of events in the S₂–S₃ transition than that proposed by Siegbahn, the “end-point” S^A,W₃ species represents the same structural type and connectivity. Therefore, the subsequent steps for O–O bond formation may well be similar to what has been previously suggested by computational studies based on this type of S₃-state model. However, even if the catalytic evolution of the OEC past the S₃ state actually follows an oxo–oxyl coupling^38,40,41,51 at the interior of the cluster, the water binding mechanism proposed in the present study has fundamentally different consequences for enzymatic regulation and the identity of substrates. This is because within the oxo–oxyl coupling scenario the sequence described above implies that the second substrate of the reaction (besides the O5 bridge^49,53,118) is not the water molecule that binds during the S₂ to S₃ transition (W_new) but may instead be W2, as suggested by the observation that W2 pivots in close proximity to O5 upon formation of the S^B₃ intermediate (Fig. 5).

Experimental support for this assignment, as opposed to the binding of a non-crystallographic water as substrate at Mn1 (Fig. 2a), comes from membrane-inlet mass spectrometry (MIMS) measurements, which monitor the uptake of H₂¹⁸O into the product O₂ molecule.¹¹⁹ MIMS data has shown that the exchange kinetics for both substrates are very similar for the S₂ and S₃ states,^7,48,120 hence they are probably both associated with the Mn₄O₅Ca cofactor in the S₂ and S₃ states in the same way.^48,120 Within the S₂–S₃ transition mechanism proposed here, the incoming water W_new is unlikely to be a substrate. This can be in principle consistent with the experimental observations under two mechanistic scenarios for O–O bond formation: if the substrates are O5 and W2, as suggested by Cox and Messinger,⁴⁸ then they represent an oxo bridge and a hydroxyl in both the S₂ and the S₃ states and thus are consistent with the above, while the same can be true if one substrate is instead a Ca-bound water that becomes involved in O–O bond formation as a nucleophile at a subsequent step of the catalytic cycle.^34,35,37 In either case, the water that binds to form the final S₃ state is not required to be a substrate.

Conclusions

We have investigated the S₂–S₃ transition in the catalytic cycle of the oxygen evolving complex with the aim to discover structural models that can explain the available spectroscopic observations on intermediates. Our results suggest that after formation of the tyrosyl radical in the S₂ state, deprotonation of S₂Y_Z˙ is a necessary condition for catalytic progression. Regardless of whether deprotonation has to precede Mn oxidation by the tyrosyl radical or whether the two processes are coupled, the outcome is the same, that is the formation of an S₃-state intermediate with all-Mn(IV) ions, which contains a closed-cubane subunit and a terminal “dangler” five-coordinate Mn(IV) ion with a coordination geometry intermediate between square pyramidal and trigonal bipyramidal. We note that a trigonal bipyramidal dangler Mn has recently been suggested as the active form of the catalyst in the S₄ state from model chemistry studies.^42,43 However, the S₂ to S₃ intermediate proposed here is not the final S₃ state and the putative activated oxygen (substrate) site is an equatorial ligand.

The spectroscopic properties of this species explain fully the observations regarding the presence of a near-IR-active population in the S₃ state of the OEC, without the need to invoke the presence of a Mn(III) ion. The formation of this species is also consistent with the OEC rearrangements proposed by molecular dynamics studies of Guidoni and coworkers.⁵² At this point of the catalytic cycle the OEC switches completely to a high-spin topology, which may be important for allowing subsequent low-barrier single product formation to proceed.

The presence of this species as a requisite intermediate in the S₂–S₃ transition implies that water binding takes place only after deprotonation and oxidation of the inorganic cluster. Thus, the new water molecule binds not to a Mn(III) site, but to a five-coordinate Mn(IV) ion. The transition state for a low-energy water binding mode from the external side of the cluster has been identified. This mode implicates the water channel of PSII which terminates close to the O4 bridge and the Mn4 ion of the cluster. The new water ligand binds to the five-coordinate Mn4(IV) at the “external” side of the inorganic cluster in a similar way that ammonia was shown to interact with the OEC in the S₂ state,^{53,55,113,114} indicating a common delivery pathway. The most significant mechanistic implication is that the water molecule that binds in the S₂–S₃ transition does not serve as an immediate substrate, in agreement with the recent suggestion by Cox and Messinger.⁴⁸ In addition, its binding is coupled to the proton shuttle terminating at the dangler Mn4, suggesting that Asp61 gates both proton release and water coordination in a concerted fashion.^{68,111,121,122}

The S₂–S₃ progression model and water binding pathway proposed here form a good basis for structural rationalization of several complex experimental observations. These include experiments that require reinterpretation to account for the structural heterogeneity in the S₃ state, and experiments on PSII mutants or PSII samples subjected to special chemical or physical treatments such as Ca²⁺/Sr²⁺ exchange. Structure-based explanations of such data will follow soon. Most importantly, the enhanced atomistic understanding of the S₂–S₃ transition provides strong support to the idea that structural flexibility and polymorphism is not an incidental feature of the OEC, but a means by which access to active forms of the catalyst is controlled and regulated.

Acknowledgements

We thank the Max Planck Society for financial support and the COST Action CM1305 ECOSTBio (Explicit Control Over Spin States in Technology and Biochemistry). FM was supported by the Swedish Research Council, the Knut and Alice Wallenberg Foundation and the Swedish Energy Agency.

Notes and references

1. R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Blackwell, Oxford, 2001.
2. J. P. McEvoy and G. W. Brudvig, Chem. Rev., 2006, 106, 4455–4483.
3. V. Krewald, M. Retegan and D. A. Pantazis, Top. Curr. Chem., 2016, 371, 23–48.
4. N. Cox, D. A. Pantazis, F. Neese and W. Lubitz, Acc. Chem. Res., 2013, 46, 1588–1596.
5. H. Dau and M. Haumann, Coord. Chem. Rev., 2008, 252, 273–295.
6. D. J. Vinyard, G. M. Ananyev and G. C. Dismukes, Annu. Rev. Biochem., 2013, 82, 577–606.
7. W. Hillier and J. Messinger, in Photosystem II. The Light-Driven Water:Plastoquinone Oxidoreductase, ed. T. Wydrzynski and K. Satoh, Springer, Dordrecht, 2005, pp. 567–608.
8. B. Kok, B. Forbush and M. McGloin, Photochem. Photobiol., 1970, 11, 457–475.
9. V. Krewald, M. Retegan, N. Cox, J. Messinger, W. Lubitz, S. DeBeer, F. Neese and D. A. Pantazis, Chem. Sci., 2015, 6, 1676–1695.
10. M. Suga, F. Akita, K. Hirata, G. Ueno, H. Murakami, Y. Nakajima, T. Shimizu, K. Yamashita, M. Yamamoto, H. Ago and J.-R. Shen, Nature, 2014, 517, 99–103.
11. Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55–60.
12. B. Loll, J. Kern, W. Saenger, A. Zouni and J. Biesiadka, Nature, 2005, 438, 1040–1044.
13. K. N. Ferreira, T. M. Iverson, K. Maghlaoui, J. Barber and S. Iwata, Science, 2004, 303, 1831–1838.
14. M. Haumann, C. Müller, P. Liebisch, L. Iuzzolino, J. Dittmer, M. Grabolle, T. Neisius, W. Meyer-Klaucke and H. Dau, Biochemistry, 2005, 44, 1894–1908.
15. A. Grundmeier and H. Dau, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 88–105.
16. C. Glöckner, J. Kern, M. Broser, A. Zouni, V. Yachandra and J. Yano, J. Biol. Chem., 2013, 288, 22607–22620.
17. J. Yano and V. Yachandra, Chem. Rev., 2014, 114, 4175–4205.
18. D. A. Pantazis, W. Ames, N. Cox, W. Lubitz and F. Neese, Angew. Chem., Int. Ed., 2012, 51, 9935–9940.
19. D. Bovi, D. Narzi and L. Guidoni, Angew. Chem., Int. Ed., 2013, 52, 11744–11749.
20. A. Haddy, Photosynth. Res., 2007, 92, 357–368.
21. N. Cox, M. Retegan, F. Neese, D. A. Pantazis, A. Boussac and W. Lubitz, Science, 2014, 345, 804–808.
22. A. Boussac, A. W. Rutherford and M. Sugiura, Biochim. Biophys. Acta, Bioenerg., 2015, 1847, 576–586.
23. A. Boussac, M. Sugiura, A. W. Rutherford and P. Dorlet, J. Am. Chem. Soc., 2009, 131, 5050–5051.
24. N. Ioannidis and V. Petrouleas, Biochemistry, 2000, 39, 5246–5254.
25. A. Boussac, M. Sugiura, Y. Inoue and A. W. Rutherford, Biochemistry, 2000, 39, 13788–13799.
26. Y. Sanakis, N. Ioannidis, G. Sioros and V. Petrouleas, J. Am. Chem. Soc., 2001, 123, 10766–10767.
27. N. Ioannidis and V. Petrouleas, Biochemistry, 2002, 41, 9580–9588.
28. A. Boussac, M. Sugiura, T.-L. Lai and A. W. Rutherford, Philos. Trans. R. Soc., B, 2008, 363, 1203–1210.
29. N. Ioannidis, G. Zahariou and V. Petrouleas, Biochemistry, 2006, 45, 6252–6259.
30. A. Boussac, M. Sugiura, D. Kirilovsky and A. W. Rutherford, Plant Cell Physiol., 2005, 46, 837–842.
31. J.-H. Su, K. G. V. Havelius, F. M. Ho, G. Han, F. Mamedov and S. Styring, Biochemistry, 2007, 46, 10703–10712.
32. K. G. V. Havelius, J.-H. Su, G. Han, F. Mamedov, F. M. Ho and S. Styring, Biochim. Biophys. Acta, Bioenerg., 2011, 1807, 11–21.
33. V. L. Pecoraro, M. J. Baldwin, M. T. Caudle, W.-Y. Hsieh and N. A. Law, Pure Appl. Chem., 1998, 70, 925–929.
34. J. S. Vrettos, J. Limburg and G. W. Brudvig, Biochim. Biophys. Acta, Bioenerg., 2001, 1503, 229–245.
35. J. P. McEvoy and G. W. Brudvig, Phys. Chem. Chem. Phys., 2004, 6, 4754–4763.
36. E. M. Sproviero, J. A. Gascon, J. P. McEvoy, G. W. Brudvig and V. S. Batista, J. Am. Chem. Soc., 2008, 130, 3428–3442.
37. D. Vinyard, S. Khan and G. Brudvig, Faraday Discuss., 2015 10.1039/c1035fd00087d.
38. P. E. M. Siegbahn and R. H. Crabtree, J. Am. Chem. Soc., 1999, 121, 117–127.
39. P. E. M. Siegbahn, Chem.–Eur. J., 2008, 14, 8290–8302.
40. P. E. M. Siegbahn, Acc. Chem. Res., 2009, 42, 1871–1880.
41. P. E. M. Siegbahn, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1003–1019.
42. R. Gupta, T. Taguchi, B. Lassalle-Kaiser, E. L. Bominaar, J. Yano, M. P. Hendrich and A. S. Borovik, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5319–5324.
43. R. D. Britt, D. L. M. Suess and T. A. Stich, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5265–5266.
44. T. Noguchi, Philos. Trans. R. Soc., B, 2008, 363, 1189–1195.
45. H. Suzuki, M. Sugiura and T. Noguchi, Biochemistry, 2008, 47, 11024–11030.
46. R. Pal, C. F. A. Negre, L. Vogt, R. Pokhrel, M. Z. Ertem, G. W. Brudvig and V. S. Batista, Biochemistry, 2013, 52, 7703–7706.
47. H. Dau, P. Liebisch and M. Haumann, Phys. Scr., 2005, 2005, 844.
48. N. Cox and J. Messinger, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1020–1030.
49. P. E. M. Siegbahn, J. Am. Chem. Soc., 2013, 135, 9442–9449.
50. P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2012, 14, 4849–4856.
51. P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2014, 16, 11893–11900.
52. D. Narzi, D. Bovi and L. Guidoni, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8723–8728.
53. M. Pérez Navarro, W. M. Ames, H. Nilsson, T. Lohmiller, D. A. Pantazis, L. Rapatskiy, M. M. Nowaczyk, F. Neese, A. Boussac, J. Messinger, W. Lubitz and N. Cox, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15561–15566.
54. M. Retegan, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2013, 9, 3832–3842.
55. T. Lohmiller, V. Krewald, M. Pérez Navarro, M. Retegan, L. Rapatskiy, M. M. Nowaczyk, A. Boussac, F. Neese, W. Lubitz, D. A. Pantazis and N. Cox, Phys. Chem. Chem. Phys., 2014, 16, 11877–11892.
56. M. Retegan, N. Cox, W. Lubitz, F. Neese and D. A. Pantazis, Phys. Chem. Chem. Phys., 2014, 16, 11901–11910.
57. W. Ames, D. A. Pantazis, V. Krewald, N. Cox, J. Messinger, W. Lubitz and F. Neese, J. Am. Chem. Soc., 2011, 133, 19743–19757.
58. F. Neese, WIREs Computational Molecular Science, 2012, 2, 73–78.
59. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
60. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
61. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
62. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
63. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
64. C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399.
65. D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919.
66. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
67. A. Klamt and D. Schüürman, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
68. I. Rivalta, M. Amin, S. Luber, S. Vassiliev, R. Pokhrel, Y. Umena, K. Kawakami, J. R. Shen, N. Kamiya, D. Bruce, G. W. Brudvig, M. R. Gunner and V. S. Batista, Biochemistry, 2011, 50, 6312–6315.
69. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
70. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
71. D. A. Pantazis, M. Orio, T. Petrenko, S. Zein, E. Bill, W. Lubitz, J. Messinger and F. Neese, Chem.–Eur. J., 2009, 15, 5108–5123.
72. M. Orio, D. A. Pantazis, T. Petrenko and F. Neese, Inorg. Chem., 2009, 48, 7251–7260.
73. F. Neese, W. Ames, G. Christian, M. Kampa, D. G. Liakos, D. A. Pantazis, M. Roemelt, P. Surawatanawong and S. F. Ye, Adv. Inorg. Chem., 2010, 62, 301–349.
74. N. Cox, W. Ames, B. Epel, L. V. Kulik, L. Rapatskiy, F. Neese, J. Messinger, K. Wieghardt and W. Lubitz, Inorg. Chem., 2011, 50, 8238–8251.
75. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
76. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
77. C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153.
78. M. Retegan, N. Cox, D. A. Pantazis and F. Neese, Inorg. Chem., 2014, 53, 11785–11793.
79. M. Chrysina, G. Zahariou, N. Ioannidis and V. Petrouleas, Biochim. Biophys. Acta, Bioenerg., 2010, 1797, 487–493.
80. A. Klauss, M. Haumann and H. Dau, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16035–16040.
81. F. M. Ho, in Molecular Solar Fuels, ed. T. J. Wydrzynski and W. Hillier, The Royal Society of Chemistry, Cambridge, 2012, pp. 208–248.
82. H. Ishikita, W. Saenger, B. Loll, J. Biesiadka and E.-W. Knapp, Biochemistry, 2006, 45, 2063–2071.
83. A. Robertazzi, A. Galstyan and E. W. Knapp, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1316–1321.
84. B. Lassalle-Kaiser, C. Hureau, D. A. Pantazis, Y. Pushkar, R. Guillot, V. K. Yachandra, J. Yano, F. Neese and E. Anxolabehere-Mallart, Energy Environ. Sci., 2010, 3, 924–938.
85. The structural models used in the present work assume that the proton has left the system, as indicated by the minus charge used on the state designations, and is no longer residing on Asp61.
86. I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274.
87. I. Mayer, Int. J. Quantum Chem., 1984, 26, 151–154.
88. A. Boussac and A. W. Rutherford, Biochemistry, 1988, 27, 3476–3483.
89. A. Boussac, J. L. Zimmermann and A. W. Rutherford, Biochemistry, 1989, 28, 8984–8989.
90. M. Sivaraja, J. Tso and G. C. Dismukes, Biochemistry, 1989, 28, 9459–9464.
91. T. H. Parsell, R. K. Behan, M. T. Green, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2006, 128, 8728–8729.
92. S. A. Cook and A. S. Borovik, Acc. Chem. Res., 2015, 48, 2407–2414.
93. T. Matsukawa, H. Mino, D. Yoneda and A. Kawamori, Biochemistry, 1999, 38, 4072–4077.
94. A. Boussac, J.-J. Girerd and A. W. Rutherford, Biochemistry, 1996, 35, 6984–6989.
95. A. Boussac, S. Un, O. Horner and A. W. Rutherford, Biochemistry, 1998, 37, 4001–4007.
96. R. Baxter, E. Krausz, T. Wydrzynski and R. J. Pace, J. Am. Chem. Soc., 1999, 121, 9451–9452.
97. P. J. Smith, S. Peterson, V. M. Masters, T. Wydrzynski, S. Styring, E. Krausz and R. J. Pace, Biochemistry, 2002, 41, 1981–1989.
98. S. Chattopadhyay, R. A. Geiger, G. Yin, D. H. Busch and T. A. Jackson, Inorg. Chem., 2010, 49, 7530–7535.
99. K. Bane, R. A. Geiger, S. A. Chabolla and T. A. Jackson, Inorg. Chim. Acta, 2012, 380, 135–140.
100. S. Mukherjee, J. A. Stull, J. Yano, T. C. Stamatatos, K. Pringouri, T. A. Stich, K. A. Abboud, R. D. Britt, V. K. Yachandra and G. Christou, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2257–2262.
101. V. Krewald, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2013, 135, 5726–5739.
102. J. H. A. Nugent, S. Turconi and M. C. W. Evans, Biochemistry, 1997, 36, 7086–7096.
103. C. Duboc and M.-N. Collomb, Chem. Commun., 2009, 2715–2717.
104. R. Gupta, T. Taguchi, A. S. Borovik and M. P. Hendrich, Inorg. Chem., 2013, 52, 12568–12575.
105. J. W. Murray and J. Barber, J. Struct. Biol., 2007, 159, 228–237.
106. F. M. Ho and S. Styring, Biochim. Biophys. Acta, Bioenerg., 2008, 1777, 140–153.
107. F. M. Ho, Photosynth. Res., 2008, 98, 503–522.
108. A. Gabdulkhakov, A. Guskov, M. Broser, J. Kern, F. Müh, W. Saenger and A. Zouni, Structure, 2009, 17, 1223–1234.
109. S. Vassiliev, T. Zaraiskaya and D. Bruce, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 1671–1678.
110. S. Vassiliev, P. Comte, A. Mahboob and D. Bruce, Biochemistry, 2010, 49, 1873–1881.
111. S. Vassiliev, T. Zaraiskaya and D. Bruce, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1148–1155.
112. For completeness, we compared the possible product for insertion of water at the Mn1 site of an open-cubane topology. This was found to be the least favorable binding mode, more than 12 kcal mol⁻¹ higher than the water binding at Mn4 from the external side of the cluster, and requires a proton transfer to the O5 bridge in order to be stabilized.
113. J. Schraut and M. Kaupp, Chem.–Eur. J., 2014, 20, 7300–7308.
114. P. H. Oyala, T. A. Stich, R. J. Debus and R. D. Britt, J. Am. Chem. Soc., 2015, 137, 8829–8837.
115. A. Boussac, A. W. Rutherford and S. Styring, Biochemistry, 1990, 29, 24–32.
116. M. Shoji, H. Isobe and K. Yamaguchi, Chem. Phys. Lett., 2015, 636, 172–179.
117. M. Capone, D. Bovi, D. Narzi and L. Guidoni, Biochemistry, 2015, 54, 6439–6442.
118. L. Rapatskiy, N. Cox, A. Savitsky, W. M. Ames, J. Sander, M. M. Nowaczyk, M. Rögner, A. Boussac, F. Neese, J. Messinger and W. Lubitz, J. Am. Chem. Soc., 2012, 134, 16619–16634.
119. J. Messinger, M. Badger and T. Wydrzynski, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 3209–3213.
120. H. Nilsson, T. Krupnik, J. Kargul and J. Messinger, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1257–1262.
121. R. J. Debus, Biochim. Biophys. Acta, Bioenerg., 2015, 1847, 19–34.
122. L. Vogt, D. J. Vinyard, S. Khan and G. W. Brudvig, Curr. Opin. Chem. Biol., 2015, 25, 152–158.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sc03124a

---