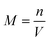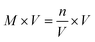An investigation into student perceptions towards mathematics and their performance in first year chemistry: introduction of online maths skills support

Abstract

An online Maths Skills Site was developed as an integrated support programme for first year Chemistry students, the content of which, was based on an analysis of their high-school mathematical backgrounds. This study examined the students’ perceptions of Maths, their patterns of usage of the Maths Skills Site and whether there was a relationship between usage of the site and performance in first year chemistry. A questionnaire and surveys were administered to obtain data on student perceptions, confidence and anxiety. Hit-count tracking was enabled for the Maths Skills Site items (notes, questions, answers, online multiple choice questions), to establish usage patterns for the cohort and individuals, over time and against topic (significant figures, algebra, etc.). Student perceptions changed over the semester. Increased confidence with chemistry and mathematics was observed, however, a significant proportion were still anxious when having to answers questions requiring calculations. Students who were already confident did not use the Maths Skills Site, whereas the students who did use the site displayed improved achievements in the credit grade category, as compared to non-users and employed a self-directed approach, tailoring their individual learning around topics important to them.

---

Introduction and background

Science is becoming increasingly interdisciplinary and dependent on mathematics and statistics, yet the deficit in basic mathematical skills of first year science students remains a problem (Tariq, 2013). In Australia there is concern over the decline in the number of high school students studying maths and science (Wilson and Mack, 2014; Wienk, 2015) and the poor mathematical skills of students entering University STEM degree programs. The “mathematics problem” has been around for decades, however, it appears that little has changed even over recent years, and it is also a world-wide phenomenon (Hunt and Lawson, 1996; Tariq, 2002; Rylands and Coady, 2009; Matthews et al., 2012; Groen et al., 2015).

The problem is exacerbated with the removal of mathematics as a pre-requisite for studies in the sciences in some institutions, which has a negative impact on progression of students through university mathematics programmes and other programmes where the application of mathematics is important (King and Cattlin, 2015). It has been reported that high school courses in physics, chemistry and biology prepare students for college courses in the same discipline, which is not surprising. Furthermore, the study of advanced mathematics was also a significant predictor of performance across all college science subjects including introductory biology (Sadler and Tai, 2007). In a more recent study, the level of high school mathematics undertaken, and the grade achieved, were found to be predictive of overall pass rates in a number of STEM degree programmes (Nakakoji et al., 2014).

The decline in the number of Australian students taking more advanced mathematics subjects at high school has previously been highlighted (McPhan et al., 2008). The Queensland Studies Authority provides a context for a flat enrolment trend in mathematics in Queensland high schools over the last 10 years (Queensland Studies Authority, 2014). In addition, there has been a slight upward trend in higher level Maths C enrolments since 2009, which can be attributed to the bonus point scheme being offered by some Universities for students who have studied the advanced subject, Maths C (including vectors, matrices, real and complex numbers) (Queensland Studies Authority, 2014). However, the number of students taking Maths A (basic: financial maths, applied geometry, elementary statistics and probability) exceeds that of the other two mathematics subjects combined and there is a consistent migration from Maths B (intermediate: including functions, calculus, exponential and log functions, applied statistics) into Maths A in year 12, the final year of school (Queensland Studies Authority, 2015).

The problem of mathematics deficiency and the impact on subjects such as chemistry, starts even before university. An investigation into why high school chemistry students have difficulty with chemistry calculations showed that this was due to a lack of understanding of basic mathematical operations such as division and multiplication, fractions and ratios (Scott, 2012). Of even greater concern is the report that science graduates (particularly in the biosciences), lack quantitative skills, so not only are they coming to university with inadequate mathematical skills, they are also leaving with a lack of mathematical skills (Matthews et al., 2013).

In a comprehensive review of factors affecting student performance in physical chemistry, it was found that the strong predictors of student success are mathematical proficiency and logical thinking skills (Bain et al., 2014; Bain and Towns, 2016). Another school of thought proposes that it is not deficiencies in mathematics per se which affects student performance in chemistry, but the inability to transfer between mathematical and chemistry contexts (Becker and Towns, 2012 and references therein). Hoban et al. (2013) examined this question in detail and concluded that student difficulties were not due to an inability to transfer mathematical knowledge but due to lack of the necessary mathematical knowledge. They also found that students who are able to explain their answers of a mathematical item in a maths context are able to transfer to an equivalent item in a chemistry context.

Maths anxiety is known to affect performance (Ashcraft and Moore, 2009), as is student confidence (Parsons et al., 2009). Many students are demotivated by any activity that requires quantitative skills (Quinnell et al., 2013). A recent study (Tariq et al., 2013) examined the roles that emotional intelligence (EI; the cognitive ability to perceive, use, understand, and regulate emotional stressors) and emotional self-efficacy (ESE; confidence to use emotional competencies) play on undergraduates’ mathematical literacy. They found that EI and ESE play a greater role in performance for female students compared to male students. Thus, enhancing students’ emotional capabilities may lead to improvements in learning strategies and increased mathematics literacy. Another study (Nicholson et al., 2013) reported that students who were confident, who held realistic views of undergraduate study and who took responsibility for their own learning had higher academic performance. While confidence is positively correlated with achievement, there is also the phenomenon of the Dunning Kruger effect, whereby poorly performing students grossly overestimate their own abilities (i.e. they don’t know what they don’t know) and hence are not able to improve (Pazicni and Bauer, 2014). Sadly, this meta-cognitive deficiency persisted over time and was more pronounced in males than females.

For STEM students, including chemistry students, who do not have the required prerequisite knowledge, many universities offer short mathematics bridging courses before the beginning of first semester. These courses offer considerable challenges to teachers in conveying complex mathematical concepts to a diverse group of students in a short period of time (from one to a few weeks) (Gordon and Nicholas, 2010). From the student's perspective these courses appear to help with their approaches to learning mathematics, reducing anxiety and increasing confidence (Gordon and Nicholas, 2013), however there is a limit to what can be achieved in such a short time (Nicholas et al., 2015).

In recent years, a range of maths support centres and online approaches have emerged (Croft, 2000; Jackson and Johnson, 2013; Mac an Bhaird et al., 2013) which are often stand alone and are not embedded within any specific discipline. Our support programme was inspired by the Maths Skills programme developed at another Australian University; La Trobe University (Jackson and Johnson, 2013), where an extra-curricular programme was introduced and tailored to support large enrolment first year courses with a diverse cohort of students. The La Trobe programme offered the choice of three learning modes – online delivery, worksheets and drop-in sessions. The emphasis was on discipline relevance and mathematical problem solving in context. Student perceptions of the support programme were positive with participating students self-reporting increased confidence, increased appreciation of the relevance of mathematics to their disciplines and improved mathematical skills. A positive correlation was found between engagement with the programme and success in completion of the respective science courses. However, participation levels were low, typically engaging only from 9–18% of the student enrolments. The authors also reported difficulty in determining whether those students who most needed support, participated. Another study in Ireland (Ní Fhloinn et al., 2014) found that students reported a positive impact of mathematics support on retention, confidence, performance and ability to cope with the mathematical demands of their courses. It is interesting to note that these studies rely on student self-reporting, and have not tracked individual student's progress with engagement in a support programme. A major challenge of support programmes is catering for diverse student needs (Jackson et al., 2014). In addition, online learning, such as can be experienced in a support programme, requires high motivation and self-regulated learning, and negative learning emotions form significant impediments to online learning (Tempelaar et al., 2012).

The present study is unique in two aspects: firstly, it focuses on mathematical skills in the context of a chemistry higher education first year cohort with diverse mathematical backgrounds and secondly, it incorporates usage tracking data from students who used a maths skills support programme. This study created a support programme for Maths Skills that was integrated in the first year chemistry curricula. In particular, we sought to understand;

• What are first year chemistry students’ perceptions towards Mathematics?

• What are students’ patterns of usage of a Maths Skills support programme integrated into first year chemistry?

• What is the relationship between students use of a Maths Skills support programme and their performance in first year chemistry?

Research methodology

Mathematics background of students in Queensland

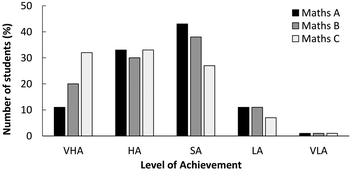
Senior secondary students in Queensland can choose to study mathematics at three levels; Maths A (basic), Maths B (intermediate) and Maths C (advanced). Analysis of the general trends was carried out for achievement in Year 12 mathematics studies (Fig. 1), based on data reported by the Queensland Studies Authority (Queensland Studies Authority, 2014), as well as the pre-requisite/prior assumed entry requirements for science programmes in Queensland (Fig. 2), as itemised on institution websites and cross checked with the summary QTAC guide (Queensland Tertiary Admission Centre, 2015). This analysis provided the relevant context for the development of the Maths Skills programme for chemistry support.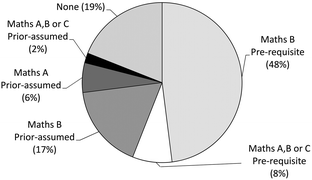

Fig. 1 Level of achievement given by the Queensland Studies Authority at the end of year 12 (2014) for students in Maths A (n = 26 524), Maths B (n = 18 076), or Maths C (n = 4780), where VLA = very low achievement, LA = low achievement, SA = sound achievement, HA = high achievement and VHA = very high achievement. SA is required for University admission.

Fig. 2 Admission requirements for Science degrees (n = 16) offered within Queensland in 2015. Double degrees, food science, environmental, medical or veterinary sciences degrees were excluded.

University chemistry course context

The first year chemistry course was offered in Semester 1 of Year 1 in about 20 degree programmes, which were predominantly in science (including the biosciences, biomedical and medical science, environmental science, and forensic science). The different degree programmes have a range of mathematics entry requirements. All except the biomedical and medical science programmes (16.2%) require concurrent studies in mathematics. The chemistry course is theory and laboratory-based, and is presented through traditional lectures, tutorials and wet laboratories to explain and discuss fundamental chemical concepts. The lectures provide the theoretical content including topics such as measurement, solutions, energy and thermodynamics, chemical reaction equilibria and kinetics including acid/base equilibria; the tutorials focus on solving problem sets; and the laboratory practical sessions provide hands-on learning experience that complements related theory material. Solving and answering chemical problems in the chemistry course during tutorials, laboratory and assessment requires students to use foundational mathematical skills, such as algebra, logarithms and quadratic equations, along with simpler concepts of exponents, significant figures and positive and negative numbers. The combination of learning activities provides active engagement and participation in the learning processes required to gain a thorough understanding of the course material and content, and the use of mathematical skills is embedded throughout the curriculum. The curriculum, assessment and lecture teaching team were the same for the course in 2014 and 2015.

Student sample

Students enrolled in the chemistry course either directly from high-school or via other pathways [mature-age entry, TAFE (Technical and Further Education) etc.] and had a range of mathematical backgrounds. The data were collected from the students in the course for two academic years (2014–2015). Students who had withdrawn or dropped their enrolment by census date (end of week 4 of a 13-week semester) were not included in the detailed analysis of the study. A total number of 942 students completed the course during 2014–2015.

In this study the dependent variables are the level of achievement and academic mathematical background of students, as well as the grade (Pass, Fail or numerical values of 1–7) and percentage marks that the students received for assessment items within the Chemistry course. Table 1 presents the correlation of the grades (and the numerical coding) with the percentage marks. The distribution of grades in the Chemistry course in 2014–2015 was typical for a first year course and previous offerings of the course.

Table 1 The grade percentages ranges and descriptors in chemistry

Grade (numerical)	1–3	4	5	6	7
Mark range (%)	0–49	50–64	65–74	75–84	85–100
Grade descriptor	Fail (F)	Pass (P)	Credit (Cr)	Distinction (D)	High distinction (HD)

---

Mathematics support programme

In this project, we define the ‘Maths Skills Site’ (MSS) as a mathematical support for chemistry resource, featuring tools that directly support students in doing chemistry problems to enable their chemistry learning, and to help them build on their prior knowledge and understanding to construct new knowledge from authentic experience (Rodgers, 1994). The MSS we implemented is based on a similar programme employed at another Australian University (Jackson and Johnson, 2013) and was linked to the Chemistry course via the student online learning management system (LMS). Accordingly, all students were automatically enrolled in the MSS. Awareness of the site and how to access the materials was communicated through announcements in lectures, on the LMS, and through emails and notices to students. Students voluntarily chose to use the MSS or not. The site was developed by experienced academics who had taught into the course and related courses for over ten years and could identify topics (numerical and mathematical calculations in chemistry) that students previously (and repeatedly) had difficulty in performing. The topics available in 2014 were positive and negative numbers, exponents, significant figures, scientific notation, algebra and logarithms; which were expanded to include quadratic equations, simultaneous equations and graphing in 2015. Development of the topic sections was through a process of academic peer-review as well as input from a first year maths tutor.

Features of the Maths Skills Site

Table 2 indicates the main features of the MSS. Each topic had four key sections and was designed to guide students to advance their knowledge and skills in the chosen topic and therefore build confidence. The topic Notes explained the topic clearly and contained many worked examples. Provision of context-based notes should enable weaker students to see the contextual basis of mathematical methods related to their specific discipline. An example from the Scientific Notation section illustrates the use of clear language and instructive illustrations (Fig. 3).

Table 2 Maths Skills Site topic sections and section descriptors

Notes	Written and illustrated to explain topic clearly including many discipline worked examples, directly applied to chemistry
Questions	Cross-referenced to notes and a range of simple to difficult questions
Answers	Worked answers were provided to assist self-directed learning and build confidence
Online problems	Were available to provide further practice in an adaptive learning environment

---

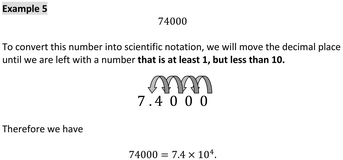Fig. 3 Example of an instructive illustration from the Scientific Notation Notes section of the Maths Skills Site.

The Questions were cross referenced to the notes and ranged in difficulty to scaffold skill development. An example from the “Logarithms and pH” section illustrates the use of simple and more challenging self-paced questions (Fig. 4). Worked answers for every question were available to help build student confidence and provided self-paced feedback on questions.

Fig. 4 Example of simple and more challenging questions from the logarithms and pH Note section of the Maths Skills Site.

Links to Multiple-choice online questions that were chemistry based and required mathematical manipulations (sourced from the publisher's online database in the Chemistry textbook) were available to help build student confidence and enable the students to practice the appropriate mathematical skills, in a low-stress environment, until they have mastered the required skill and gained confidence.

Data collection and analysis

Questionnaire. Students enrolled in the course were invited to voluntarily respond to a survey questionnaire at the commencement of their course and participate in using the MSS. The questionnaire was administered during laboratory sessions during weeks two and three of semester. The sample of students who participated in the study was 347, representing 36.8% of the student cohort. All students were asked to participate in the study and gave their informed consent before participating in the research and for the researcher's use of individuals existing data for research purposes. Students had the right to make a free choice over whether to contribute to the study or not. All student data were de-identified by an independent person prior to analysis, and stored in a secure location. In order to maintain confidentiality, participants’ names were not revealed and all data were aggregated. Preliminary analysis of an initial questionnaire completed by the 2014 student cohort has been reported elsewhere (Loughlin et al., 2015). In the present study, all aggregated student data (2014 and 2015) was de-identified for analysis (Table 3).

Table 3 Summary of Maths Skills Questionnaire responses

Question
a Refers to the level of achievement given by the Queensland Studies authority where VLA = very low achievement, LA = low achievement, SA = sound achievement, HA = high achievement and VHA = very high achievement. SA is required for University admission.
	Yr10 N (%)	Yr11 N (%)	Yr12 N (%)	Other N (%)	None N (%)
1. What level of Chemistry did you successfully complete at School or later (e.g. TAFE)?	61(18)	15(4)	206(59)	13(4)	52(15)
2. What level of Biology did you successfully complete at School or later?	57(16)	12(3)	215(62)	14(4)	48(14)
	None N (%)	Other N (%)	Maths A N (%)	Maths B N (%)	Maths C N (%)
3. What level of Maths did you successfully study at School in year 11?	5(1)	18(5)	61(18)	172(50)	88(26)
4. What level of Maths did you successfully study at School in year 12?	6(2)	20(6)	87(25)	152(44)	80(23)
	VLA N (%)	LA N (%)	SA N (%)	HA N (%)	VHA N (%)
5. If you completed year 12 Maths A, what grade did you achieve? (VLA to VHA)^a	1(1)	1(1)	26(28)	39(42)	26(28)
6. If you completed year 12 Maths B, what grade did you achieve?	1(1)	4(2)	75(32)	85(37)	66(29)
7. If you completed year 12 Maths C, what grade did you achieve?	0(0)	1(1)	16(19)	28(33)	39(46)
	Yes N (%)	No N (%)
8. Did you do the Chemistry Bridging Course?	27(9)	306(91)
9. Did you do the Maths bridging course?	17(5)	318(95)
	Not at all important N (%)	Not important N (%)	Neutral N (%)	Important N (%)	Very important N (%)
10. How important do you think Mathematics is for the study of Chemistry?	0(0)	9(3)	42(12)	169(49)	127(37)
11. How important do you think Mathematics is for the study of Biology?	24(7)	95(28)	140(41)	69(20)	72(21)
	Not at all confident N (%)	Not confident N (%)	Neutral N (%)	Confident N (%)	Very confident N (%)
12. Rate your confidence in your current chemistry knowledge?	26(8)	56(16)	145(42)	94(27)	23(7)
13. Rate your confidence in your mathematical skills?	14(4)	39(11)	135(39)	109(32)	48(14)

---

In addition, the students who responded to the questionnaire self-identified their achievement and academic background in chemistry, biology and mathematics, using the Queensland Studies Authority (QSA) levels of achievement (Fig. 1 caption). This was cross checked with the high school grades obtained from their admission records, where such data was available, and indicated that students were self-reporting their achievement and background correctly. Non-school leavers also reported their prior studies and included the categories of other studies (not years 10, 11 or 12) or no study. School leaver respondents self-reported any participation in bridging courses for chemistry and/or mathematics. All data were de-identified and aggregated for reporting.

Students’ perceptions

As part of the initial questionnaire, students answered four Likert-style questions (Q10–13, Table 3) on whether they thought mathematics is important for the study of chemistry and rated their confidence with chemistry and maths. Further questions on confidence perceptions were included in the Maths Skills usage surveys (Q6, 7 and 9, Table 4; Q7, 8 and 9, Table 5) and the follow up survey with Second year students (see below).

Table 4 Summary of follow-up survey responses for students who completed the questionnaire and did not use the Maths Skills Site in 2014–2015

Question
	Strongly disagree N (%)	Disagree N (%)	Neutral N (%)	Agree N (%)	Strongly agree N (%)
1. I did not use the Maths Skills Site as I was unaware of the site linked to Chemistry 1A	4(13.8)	5(17.2)	3(10.3)	11(37.9)	6(20.7)
2. I aware of the Maths Skills Site but did not feel I needed to use it	4(13.8)	6(20.7)	5(17.2)	8(27.6)	7(24.1)
3. I did not use the Maths Skills Site as I did not have enough time during semester	3(10.3)	9(31.0)	11(37.9)	2(6.9)	1(3.4)
4. I did not use the Maths Skills Site as it was not assessable for Chemistry	3(10.3)	13(44.8)	5(17.2)	5(17.2)	3(10.3)
5. I did not use the Maths Skills Site as I was told not use it by others	10(34.5)	10(34.5)	4(13.8)	2(6.9)	3(10.3)
6. After semester 1 my confidence in doing chemistry problems has increased	2(6.9)	0(0)	9(31.0)	11(37.9)	7(24.1)
7. After semester 1 my confidence with mathematics has increased	2(6.9)	4(13.8)	12(41.4)	7(24.1)	4(13.8)
8. Mathematics skills are important for the study of chemistry.	0(0)	0(0)	6(20.7)	9(31.0)	14(48.3)
	Never N (%)	Rarely N (%)	Sometimes N (%)	Regularly N (%)	Almost always N (%)
9. I feel anxious when I have to answer chemistry problems requiring calculations	7(24.1)	8(27.6)	8(27.6)	4(13.8)	2(6.9)

---

Table 5 Summary of follow-up survey for students who completed the questionnaire and did use the Maths Skills Site in 2015

Question
	Never N (%)	Rarely N (%)	Sometimes N (%)	Regularly N (%)	Almost always N (%)
1. I used or read the Maths Skills module notes	1(12.5)	0(0)	3(37.5)	2(25)	2(25)
2. The Maths Skills module notes were helpful for my study of Chemistry	1(12.5)	0(0)	2(25)	4(50)	1(12.5)
3. I attempted the problems in the Maths Skills modules.	1(12.5)	1(12.5)	0(0)	5(62.5)	1(12.5)
4. The answer sheets in the Maths Skills module were useful	1(12.5)	0(0)	2(25)	4(50)	1(12.5)
5. The Maths Skills module notes provided enough examples to understand problems in Chemistry	1(12.5)	0(0)	2(25)	3(37.5)	2(25)
6. The Maths Skills module notes did not help me when solving chemistry problems	4(50)	1(12.5)	3(37.5)	0(0)	0(0)
7. l feel anxious when I have to answer chemistry problems requiring calculations	1(12.5)	1(12.5)	3(37.5)	3(37.5)	0(0)
	Strongly disagree N (%)	Disagree N (%)	Neutral N (%)	Agree N (%)	Strongly agree N (%)
8. After using some/or all of the Maths Skills modules my confidence in doing chemistry problems has increased	1(12.5)	0(0)	2(25)	4(50)	1(12.5)
9. My confidence with mathematics has increased	1(12.5)	0(0)	2(25)	4(50)	1(12.5)
10. Overall I am satisfied with the maths skills modules	1(12.5)	0(0)	2(25)	4(50)	1(12.5)

---

Follow-up surveys

Follow-up surveys were carried out within two months of completion of the course of two groups of students: those who answered the questionnaire but did-not use the MSS and those who did use the MSS. Unfortunately, the response rate, of 20% and 7% respectively, was very poor for both surveys, but is typical of response rates observed in other studies (Sax, 2003). Interestingly, those students who responded to the follow-up survey were a minor cohort which used the MSS and also attempted the Questions and used the Answer Sheets (Q 3 and 4, Table 5).

Students who progressed to second year chemistry were asked to voluntarily respond to a follow-up survey (∼ one year after completing the Chemistry course). Whilst only a small cohort (n = 13) of students responded, it none-the-less provided some insight into students’ perceptions and usage of the resource and suggested reasons why students were not using the extra maths support in first year chemistry.

Usage of the Maths Skills Site

Statistics tracking was enabled in the Learning Management System of the Chemistry course which allowed us to determine the use of the individual items on the MSS (e.g.: Logarithms notes, logarithms questions, etc.) as well as the number of ‘hits per content area’. Use of the site was recorded from the point at which the site was initially made public the student cohort until the end of semester exam (Weeks 4–16 in 2014; weeks 2–16 in 2015). Access to the site was (a) mapped against the semester chronology and (b) hit count on the site by individual student, which was correlated with individual overall grade for the course. All student usage data was de-identified, and aggregated for analysis.

Limitations

This study focuses on two cohorts of students namely those enrolling in 2014 and those enrolling in 2015. Our analysis shows that these students are typical for this university and represent a full spectrum of Queensland students entering Queensland universities. Only limited numbers of students (n = 5 and 12; 2014 and 2015 respectively) in this study enrolled in any of the mathematics bridging courses offered at this institution and they were students who were able to commit both time and finances to the endeavour. Questionnaires were sent to all students in the study, without prior recruitment. The response rates to the follow-up surveys were low. Variables such as individual student motivation levels or alternate mathematics support during a student's semester of study are unknown and cannot be controlled or reported.

Results

Student mathematical backgrounds in Queensland

Understanding the mathematical background of students entering first year chemistry at university assisted the development of the MSS. We carried out an analysis of the mathematical background and performance of students completing Maths A, B or C. The achievement distribution in 2014 (Fig. 1) typifies the trends over recent years. Students who completed Maths C perform very strongly, with 32% obtaining the top grade of VHA at high school. In comparison, students who completed Maths A generally perform at a lower achievement level with only 11% obtaining a VHA and 43% obtaining an average grade of SA (Fig. 1).

We carried out a survey of the entry requirements on mathematics pre-requisites for science programmes in Queensland (from QTAC Sciences section), as listed for entry by the Queensland Tertiary Admissions Centre for 2015 (Fig. 2). Of the 48 degrees listed, 56% had a maths prerequisite, 25% had combinations of maths prior-assumed knowledge. Of concern, were nine science degrees (19%) that had no prior assumed or prerequisite maths knowledge needed for university entry. The students in this study were enrolled in a first year chemistry course that was offered in degree programmes with varying mathematical pre-requisites and prior assumed entry requirements. A snapshot of the mathematical backgrounds of the 2014 sub-cohort has been reported previously (Loughlin et al., 2015). Success in formative and summative assessment within the chemistry course was enabled by prior study of Mathematics B or B/C in combination with chemistry prior knowledge (Loughlin et al., 2015).

We developed the MSS, (vide supra), in the context of the varied mathematical backgrounds and performance levels of students entering with Maths A, B or C or no year 12 mathematics. Consideration of the mathematical background of students guided the curriculum of the resource and resulted in the inclusion of topics ranging from elemental numeracy skills, such as positive and negative numbers and significant figures to more mathematical concepts such as algebra, simultaneous and quadratic equations.

Usage of the Maths Skills Site

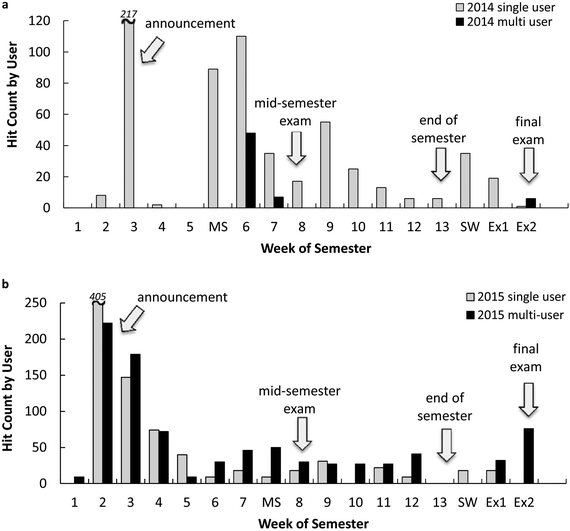
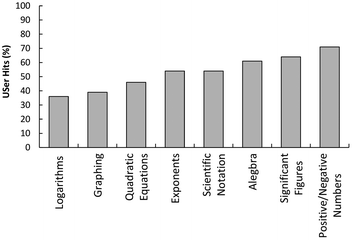
Distributed and variable usage, obtained from the user statistics tracking system, was observed for the site throughout semester for single and multiple users (Fig. 5a and b). The item hit-count indicated a total of 38 and 115 users in 2014 and 2015, representing 8% and 24% of the course total cohort, respectively. The overall patterns of usage of the site by students indicated peak usage after the in-class announcements advertising the site to students. Minor increases in usage occurred before major assessment items, such as the mid-semester exam in 2014 and the end-of semester exam in 2015, although the curriculum was identical for both years of the study.

Fig. 5 Diagram of usage vs. time fpr 2014 (a) and 2015 (b), with key semester milestones; MS (mid semester break – easter); SW (study week); Ex1 (exam week 1); Ex2 (exam week 2); Vac (vacation break).

Tracking of usage by individual students revealed that a typical usage was single on-off log-in to survey all topics (69% of users). The remaining students (31%) logged-in to the site 2–5 times during semester, accessing individual specific items (module notes, questions, etc.) anywhere between 18–120 times across the various Maths Skills topics. Aggregated access by students to the topic notes (Fig. 6) indicated the overall preferences, with the positive and negative numbers topic being the most accessed. We mapped the student usage (by single and multiple user) of topics against the chemistry curriculum; e.g. algebra and exponents were used in the energy and thermochemistry unit in weeks 7–8 of semester and areas such as positive/negative numbers were used more widely in the curriculum. It was noted that student usage of the topics in the MSS was variably distributed across the semester (c.f.Fig. 5a and b), and no correlation was observed with the timing of the chemistry curriculum.

Fig. 6 Usage of Maths Skills Site Notes by Topic.

Further analysis indicated students were individual in their choices within the site. This is illustrated by three examples of typical usage ‘types’ of the MSS resources:

• Student Usage Type A: Accessed all the notes, questions, and answers available on the topics of positive and negative numbers, significant figures, scientific notation and exponents, but did not access other topics, such as algebra.

• Students Usage Type B: Accessed all the notes for every topic, and the online multiple-choice questions, but did not access the self-instruction questions and answers for any topic

• Student Usage Type C: Accessed the significant figures, scientific notation and graphing notes, and had a mixed approach to problems by accessing the online multiple-choice questions, and selectively choosing the significant figures self-instruction questions and answers.

Use of the Maths Skills Site and student performance in first year chemistry

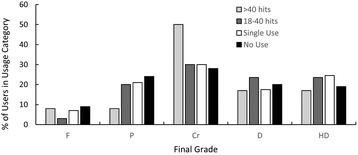
We mapped the final grade in the Chemistry course, excluding students with no assessment submission, against the hit-counts for the students who accessed the site, and aggregated the data. Four broad usage categories were used as shown in Fig. 7. These were: one off log-ins to ‘visit’ and survey all the topics; 18–40 hits for students with 2–3 days of log-in and ‘use’ of each of the items such as questions; >40 hits for students with more than three days of log-in and more active ‘use’ of items; and non-usage of the Maths Skills Site. Usage and non-usage of the site was distributed across all grades. Due to the small sample size and variable use of the site across the final grade categories, no general trends could be drawn. However, multiple hit users were more strongly represented in the credit grade category, as compared to the non-users.

Fig. 7 Diagram of usage hits on Maths Skills Site vs. final grade for chemistry.

Student perceptions towards Maths

The questions for confidence and anxiety were captured in the early-in-semester questionnaire (Table 3) and the follow-up surveys administered after completion of the course (Tables 4 and 5), when students had almost completed a full semester of study at this University. In the early semester phase, less than half the questionnaire cohort were confident/very confident with their current chemistry knowledge (34%), or mathematical skills (46%). After a full semester of study, students who responded to the survey, self-reported feeling more confident in doing chemistry (62% agree/strongly agree), more confident with mathematics (37–62% agree/strongly agree) yet still a significant proportion of students who used the Maths Skills Site (37% agree/strongly agree), as well as those who did not use the site (21% agree/strongly agree), reported feeling anxious when having to answer problems requiring calculations.

The survey of the students who completed the questionnaire but did not use the MSS (Table 4) indicated that the predominant reasons for non-use was that students felt they did not need to use it (52%) or they were unaware of the site (59%) even though it was linked in the LMS to the Chemistry course. The follow-up survey of second year students indicated that students who did not use the site were ‘already confident’ with their own mathematics ability and had found alternative resources to study for the Mathematics needed for chemistry. Those who did use the site reported problems with the website lagging, which may be due to external factors, but also provided open ended responses about the Maths Skills Site: ‘helped with problems I came across’, ‘practice (was good)’ and ‘it helped me understand’.

Discussion and conclusions

This study has attempted to understand: first year chemistry students’ perceptions towards Mathematics; students patterns of usage of a Maths Skills support programme integrated into first year chemistry; and the relationship between students use of a Maths Skills support programme and their performance in first year chemistry.

The student's perceptions were identified from the questionnaire and follow-up surveys (research question 1). From the questionnaire data it is evident that students at the beginning of the semester realised the importance of mathematical skills to their science studies (both chemistry and biology), however, their confidence levels were low irrespective of their background. At the end of semester, the students who responded to the survey, felt more confident but there was still anxiety associated with mathematical calculations. Despite feeling anxious few students availed themselves of the online Maths Skills Site self-help resources although there was some increase in usage just before assessments were due.

Student patterns of usage for the site were identified through user statistics tracking within the LMS (research question 2). The ‘peak and trough’ pattern of usage of the resource by students was suggestive of ‘in the moment’ responses and a ‘just-in-time’ study for assessment mind-set. The types of usage indicate that usage by type (notes, questions, answers, online problems) indicated a preferred usage by some students for the notes (suggestive of passive learning) and a preferred usage by other students for the multiple-choice online problems (suggestive of interactive learning). A self-directed problem solving approach, through accessing the questions and answers sections, was poorly used by students, as compared to the usage of the notes and online problems. The usage preference of students who accessed the topic notes was towards scientific and numeracy skills, positive and negative numbers, significant figures, scientific notation and exponents (Fig. 6). Apart from algebra, the more challenging topics of logarithms, quadratic equations were less used; which is likely to be a reflection of the frequency of use of such topics in the chemistry curriculum. Further analysis of the usage indicated students were selecting topics and individual items (notes, questions, answers, online multiple choice questions) through a self-directed approach where the student would tailor their own individual learning.

Correlation of the patterns of usage for the site with student final grades, albeit from a small sample, nonetheless suggest a positive relationship between the use of a Maths Skills support programme and student performance in first year chemistry (research question 3). It was interesting to note the distribution of grades was similar for users or non-users of the MSS, with a peak occurring for the credit grade of 5 (Fig. 7). Users who accessed the MSS >40 times were more highly represented in the credit grade category. Although the academic outcomes for the students that used the MSS are distributed across the grades, it may be that the more motivated students are self-selecting to use the site.

High achieving students are intrinsically motivated as well as extrinsically (for example by a desire to earn a competitive place in graduate Medical School). The majority of tertiary students however appear to be extrinsically motivated by assessment stressors (Armstrong et al., 2013). The modularisation of units focuses students’ attention on end of semester exams and other summative assessments, and this fosters surface learning and memorisation (Armstrong et al., 2013). It does not allow integration to conceptual knowledge which takes time and a deeper approach. The problem therefore is how to motivate those students who most need extra help to adopt a deeper approach and make use of the online support provided. Research has shown that the learning strategies and self-efficacy of the students determines in part their success in an online developmental mathematics course (Wadsworth et al., 2007) and there is a positive correlation between self-assessment and academic performance (McDonald and Boud, 2003; Ibabe and Jauregizar, 2010). Interestingly, there is a negative correlation between students’ grades and their own estimation about their grades indicating a deficit in metacognitive skills (Vadhan and Stander, 1994). It has been suggested that we better train students in metacognitive capacities (Pintrich, 2002) and indeed learning strategies and self-efficacy can be developed (Weinstein et al., 2000). Thus it is recommended that systematic formative self-assessment activities are incorporated into the curriculum to improve students’ metacognitive skills (Ibabe and Jauregizar, 2010). In this way the use of self-help resources by those students who need them will increase and consequently their understanding of mathematics in context should improve. In addition, raising students’ awareness of their mathematical knowledge base through diagnostic testing has been trialled elsewhere (Kemp et al., 2011; Wilkes, 2015).

In conclusion, after a semester of study, the chemistry students who were surveyed had increased confidence with chemistry and mathematics, yet a significant proportion of students (37%) were still anxious when having to answer questions requiring calculations. The usage of the resources was varied. Students who were already confident with their abilities tended not to use the site. Students who accessed the site displayed improved achievements in the credit grade category, as compared to non-users. They used a self-directed approach, choosing to tailor their individual learning within the Maths Skills Site and did not correlate their usage of the site with the timing of the chemistry curriculum. Those who used the site were positive about the usefulness of the content (notes, questions, and answers) and the help provided for problem solving in Chemistry. However, the implementation of digital approaches to Maths Skills support requires smoother technological solutions. Significantly, this study indicated the facility for students to ‘tailor’ an individual approach to self-directed learning assisted in students’ usage of mathematical skills support in chemistry, and apparently led to sound academic outcomes. Future studies will thus focus on the contextualisation of mathematical skills within scientific disciplines, such as biochemistry, and find ways to motivate the students to use the self-help resources and make the technology more efficient and engaging.

Appendix 1

Example of module introduction for significant figures

In the lab, despite our best efforts, we are never going to have perfect measurements as there are limits on our equipment. Because of this, we need to use significant figures when taking measurements and when performing calculations on these measurements. This module looks at using significant figures in chemistry.

Now open the module folder, work through the notes, do the questions, and check your answers.

Extract from page 1 of notes for significant figures – introduction

Alternatively, imagine that you are in the lab and are trying to calculate the molarity of a solution that you just made. You used 0.4 moles of solute to create 7 litres of solution. Calculating molarity gives

But does it really make sense to write down all the decimal places? Was the number of moles of solute measured accurately to the same number of decimal places? We need a rule to know how many decimal places to use when 'combining' two quantities (or two numbers). The answer is to use significant figures.

Extract from page 13 of notes for algebra

Now let's try to rearrange the formula so that it will calculate the number of moles if we are given the molarity and the volume. To begin, we start with the formula.

We want to calculate number of moles so we need to have by itself (only on one side of the equals sign and everything else on the other side). To do this, we need to use a very important rule for equations.

Whatever you do to one side of the equation, you MUST do to the other side of the equation

We are allowed to do anything we like to one side of an equation, as long as we do the exact same thing to the other side of the equation.

To leave n by itself, we need to ‘remove’ the divide by volume. But we can’t just ‘remove’ something from an equation just because we don’t want it there. Instead, we need to ‘move it to the other side’. As we are dividing by volume, we will multiply both sides of the equation by volume.

While this now looks different from our initial formula, we haven’t actually changed anything. By doing the exact same thing to both sides of the equation, we have not changed the formula, only the way the formula ‘looks’. On the right hand side, we can now cancel the volumes. (If you are unsure about cancelling, have a look back at the ‘Division in Algebra’ section in these notes.) End of extract from page 13 of algebra notes.

Extract of from pages 1, 4–5 of Notes for positive and negative numbers

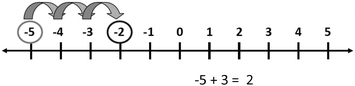
Negative numbers can also be found in many formulas found in chemistry. Understanding negative numbers and how to do operations on them (addition, subtraction, multiplication and division) is very important. Extract from page 1.

Example 4 extract from page 4–5

−5 + 3 = ?

The first number is −5, so we start at −5 on the number line. It is addition, so we will be moving to the right. The second number is 3, so we will be moving 3 spaces.

Examples of questions for logarithms

Question 4. Calculate the pH of the following solutions. You may use a calculator. (Refer to example 6 of the logarithms notes).

(a) [H+] = 0.058 M

(b) [H+] = 0.0004 M

(c) [H+ ] = 4.5 × 10⁻⁶ M

(d) [H+] = 8.2 × 10⁻⁴ M

Question 7. In test tube A, there is a solution with a pH of 6. In test tube B, there is a solution with a pH of 8. Because there is a difference of 2 in the pH (8 − 6 = 2), does this mean that the [H+] in test tube B is twice that of test tube A? Explain your answer.

Examples of questions for quadratic equations

Solve the following quadratic equations using the quadratic formula. Remember that if the quadratic is not in standard form, it first has to be rearranged so that it is in standard form before using the quadratic formula. Where necessary, round your answer to two decimal places.

(Question 1) x² − 3x + 2 = 0

(Question 2) x² − 2x − 3 = 0

………

Question 13. What are the equilibrium concentration of products and reactants for the following reaction with an equilibrium constant (KC) of 0.012.

HSO₄⁻(aq) + H₂O(l) ⇌ H₃O⁺(aq) + SO₄²⁻(aq)

Initially the concentration of HSO₄⁻ was 0.50 M, the initial concentration of H₃O⁺ was 0.02 and the initial concentration of SO₄²⁻ was 0.08 M.

Examples of questions for simultaneous equations

Solve the following simultaneous equations.

Question 1.

x + y = 5

4x + 2y = 14

Question 11. How many grams of Na₂HPO₄ (which has a molecular weight of 142) and NaH₂PO₄·2H₂O (which has a molecular weight of 156) would you need to prepare 0.5 L of 0.3 M sodium phosphate buffer with a pH of 7.1? (The pK_a of dissociation of H₂PO₄⁻ to HPO₄²⁻ and H⁺ is 6.86).

Example of a question from online multiple choice – significant figures

Round 5241.43 to three significant figures and express the result in scientific notation.

(a) 5.24 × 10³; (b) 5.241 × 10³; (c) 0.52 × 10⁴; (d) 5.241 × 10³.

Acknowledgements

This work was supported by a Griffith University Grant for Learning and Teaching. Human Ethics Approval BPS/20/13/HREC. The authors would like to thank David Harman for expert assistance.

References

1. Armstrong S., Brown S., and Thompson G. (Ed.) (2013). Motivating Students, Routledge, Oxford and New York.
2. Ashcraft M. H. and Moore A. M., (2009), Mathematics anxiety and the affective drop in performance, J. Psychoeduc. Assess., 27(3), 197–205.
3. Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics. Chem. Educ. Res. Pract., 17(2), 246–262.
4. Bain K., Moon A., Mack M. R. and Towns M. H., (2014), A review of research on the teaching and learning of thermodynamics at the university level. Chem. Educ. Res. Pract., 15(3), 320–335.
5. Becker N. and Towns M., (2012), Students’ understanding of mathematical expressions in physical chemistry contexts: an analysis using Sherin's symbolic forms, Chem. Educ. Res. Pract., 13(3), 209–220.
6. Croft A. C., (2000). A guide to the establishment of a successful mathematics learning support centre. Int. J. Math. Educ. Sci. Technol., 31(3), 431–446.
7. Gordon S. and Nicholas J., (2010), Teachers’ reflections on the challenges of teaching mathematics bridging courses, Proceedings of The Australian Conference on Science and Mathematics Education, 16, 35–40.
8. Gordon S. and Nicholas J., (2013), Students’ conceptions of mathematics bridging courses, Journal of Further and Higher Education, 37(1), 109–125.
9. Groen L., Coupland M., Langtry T., Memar J., Moore B. and Stanley J., (2015), The mathematics problem and mastery learning for first-year, undergraduate STEM students, International Journal of Learning, Teaching and Educational Research, 11(1), 141–160.
10. Hoban R. A., Finlayson O. E. and Nolan B. C., (2013), Transfer in chemistry: a study of students’ abilities in transferring mathematical knowledge to chemistry. Int. J. Math. Educ. Sci. Technol., 44(1), 14–35.
11. Hunt D. N. and Lawson D. A., (1996), Trends in mathematical competency of A-level students on entry to university, Teaching Mathematics and its Applications, 15(4), 167–173.
12. Ibabe I. and Jauregizar J., (2010), Online self-assessment with feedback and metacognitive knowledge, J. Higher Educ., 59, 243–258.
13. Jackson D. C. and Johnson E. D., (2013), A hybrid model of mathematics support for science students emphasizing basic skills and discipline relevance, Int. J. Math. Educ. Sci. Technol., 44(6), 846–864.
14. Jackson D. C., Johnson E. D. and Blanksby T. M., (2014), A practitioner's guide to implementing cross-disciplinary links in a mathematics support program, International Journal of Innovation in Science and Mathematics Education, 22(1), 67–80.
15. Kemp M., Fletcher D. and Middleton H., (2011), Encouraging preparedness for first-year subjects involving quantitative concepts and skills, In 14th Pacific Rim Conference in First Year Higher Education. http://www.fyhe.com.au/past_papers/papers11/FYHE-2011/content/pdf/6A.pdf, accessed 13 May, 2016.
16. King D. and Cattlin J., (2015), The impact of assumed knowledge entry standards on undergraduate mathematics teaching in Australia, International Journal of Innovation in Science and Mathematics Education, 1–14, (ahead-of-print).
17. Loughlin W. A., Johnston P. R., Watters D., Brown C. L. and Harman D., (2015), Snapshot of mathematics skills of first year science students from diverse backgrounds, International Journal of Innovation in Science and Mathematics Education, 23(1), 21–36.
18. Mac an Bhaird C., Fitzmaurice O., Fhloinn E.N. and O’Sullivan C., (2013). Student non-engagement with mathematics learning supports. Teaching mathematics and its applications, 32(4), 191–205.
19. Matthews K. E., Belward S., Coady C., Rylands L., Simbag V., Adams P., Peleaz N., Thompson K., Parry M. and Tariq V., (2012), The state of quantitative skills in undergraduate science education: Findings from an Australian study. Office for Learning and Teaching: Canberra, http://researchonline.jcu.edu.au/26400/1/QS_report_July2012.pdf, accessed 13 May, 2016.
20. Matthews K. E., Hodgson Y. and Varsavsky C., (2013), Factors influencing students’ perceptions of their quantitative skills, Int. J. Math. Educ. Sci. Technol., 44(6), 782–795.
21. McDonald B. and Boud D., (2003), The impact of self- assessment training on performance in external examinations, Assessment in Education, 10(2), 209–220.
22. McPhan G., Morony W., Pegg J., Cooksey R. and Lynch T., (2008), Maths? Why not? Final report prepared for the Department of Education, Employment and Workplace Relations. Canberra (Australia).
23. Nakakoji Y., Wilson R. and Poladian L., (2014), Mixed methods research on the nexus between mathematics and science, International Journal of Innovation in Science and Mathematics Education, 22(6), 61–76.
24. Nicholson L., Putwain D., Connors L. and Hornby-Atkinson P., (2013), The key to successful achievement as an undergraduate student: confidence and realistic expectations? Stud. High. Educ., 38(2), 285–298.
25. Ní Fhloinn E., Fitzmaurice O., Mac an Bhaird C., O’Sullivan C., (2014), Student perception of the impact of mathematics support in higher education, Int. J. Math. Educ. Sci. Technol., 45(7), 953–967.
26. Nicholas J., Poladian L., Mack J. and Wilson R., (2015), Mathematics preparation for university: entry, pathways and impact on performance in first year science and mathematics subjects, International Journal of Innovation in Science and Mathematics Education, 23(1), 37–51.
27. Parsons S., Croft T. and Harrison M., (2009), Does students’ confidence in their ability in mathematics matter? Teaching Mathematics and its Applications, 28(2), 53–68.
28. Pazicni S. and Bauer C. F., (2014), Characterizing illusions of competence in introductory chemistry students. Chem. Educ. Res. Pract., 15(1), 24–34.
29. Pintrich P. R., (2002), The role of metacognitive knowledge in learning, teaching, and assessing. Theory into practice, 41(4), 219–225.
30. Queensland Studies Authority, (2014), Trends and Issues in curriculum and assessment: Identifying enrolment trends in senior mathematics and science subjects in Queensland schools, http://https://www.qcaa.qld.edu.au/downloads/publications/trends_and_issues_01_enrolment_trends.pdf, accessed 13 May, 2016.
31. Queensland Studies Authority, (2015), Subject enrolments and levels of achievement—2015, http://https://www.qcaa.qld.edu.au/downloads/publications/qcaa_stats_sen_subjects_2015.pdf, accessed 13 May, 2016.
32. Queensland Tertiary Admission Centre, (2015), QTAC Guide to Tertiary Courses: Starting September 2015 through to August 2016, 201–207.
33. Quinnell R., Thompson R. and LeBard R. J., (2013), It's not maths; it's science: exploring thinking dispositions, learning thresholds and mindfulness in science learning, Int. J. Math. Educ. Sci. Technol., 44(6), 808–816.
34. Rodgers C. R. and Frieberg H. J., (1994), Freedom to learn, 3rd edn. Columbus, OH: Merrill/MacMillan.
35. Rylands L. J. and Coady C., (2009), Performance of students with weak mathematics in first-year mathematics and science, Int. J. Math. Educ. Sci. Technol., 40(6), 741–753.
36. Sadler P. M. and Tai R. H., (2007), The two high-school pillars supporting college science, Science, 317(5837), 457.
37. Sax L. J., Gilmartin S. K. and Bryant A. N., (2003). Assessing response rates and nonresponse bias in web and paper surveys. Res. High. Educ., 44(4), 409–432.
38. Scott F. J., (2012), Is mathematics to blame? An investigation into high school students' difficulty in performing calculations in chemistry, Chem. Educ. Res. Pract., 13(3), 330–336.
39. Tariq V. N., (2002), A decline in numeracy skills among bioscience under graduates, J. Biol. Educ., 36(2), 76–83.
40. Tariq V. N., Qualter P., Roberts S., Appleby Y. and Barnes L., (2013), Mathematical literacy in undergraduates: role of gender, emotional intelligence and emotional self-efficacy, Int. J. Math. Educ. Sci. Technol., 44(8), 1143–1159.
41. Tempelaar D. T., Niculescu A., Rienties B., Gijselaers W. H. and Giesbers B., (2012), How achievement emotions impact students' decisions for online learning, and what precedes those emotions, Internet and Higher Education, 15(3), 161–169.
42. Vadhan V. and Stander P., (1994), Metacognitive ability and test performance among college students, J. Psychol., 128, 307–309.
43. Wadsworth L. M., Husman J., Duggan M. A., and Pennington M. N., (2007), Online Mathematics Achievement: Effects of Learning Strategies and Self-Efficacy J. Developmental Education, 30(3), 6–14.
44. Weinstein C. E., Husman J. and Dierking D. R., (2000), Self-regulation interventions with a focus on learning strategies. in Boekaerts M., Pintrich P. R. and Zeidner M. (ed.), Handbook of Self-Regulation, San Diego, Calif.: Academic Press, pp. 727–747, http://onlinelibrary.wiley.com/doi/10.1002/tl.443/epdf, accessed 13 May, 2016.
45. Wienk M., (2015), Discipline Profile of the Mathematical Sciences 2015, Australian Mathematical Sciences Institute, http://amsi.org.au/wp-content/uploads/2015/08/discipline-profile-2015.pdf, accessed 13 May, 2016.
46. Wilkes J. and Burton L. J. (2015). Get Set for Success: Applications for engineering and applied science students, International Journal of Innovation in Science and Mathematics Education, 23(1), 94–105.
47. Wilson R. and Mack J., (2014), Declines in high school mathematics and science participation: evidence of students’ and future teachers’ disengagement with maths, International Journal of Innovation in Science and Mathematics Education, 22(7), 35–48.

---