Realist ontology and natural processes: a semantic tool to analyze the presentation of the osmosis concept in science texts

Abstract

In this work, we developed an ontological tool, based on the scientific realism of Mario Bunge, for the analysis of the presentation of natural processes in science textbooks. This tool was applied to analyze the presentation of the concept of osmosis in 16 chemistry and biology books at different educational levels. The results showed that more than 50% of the books present the process of osmosis connected just with concentration properties associated with the hydrodynamic state of the osmotic process, forgetting the properties of osmotic pressure to define the state of osmotic equilibrium. This omission creates confusion between the state of osmotic equilibrium with the isotonic state by reducing the entire osmosis process to a mere process of diffusion by differences in concentrations. Moreover, in 4 of the biology textbooks, the presentation of the osmosis concept and osmotic equilibrium in cell system illustrations generates confusion between hydrostatic pressure generated by gravity vs. hydrostatic pressure generated by membrane tension or turgor pressure. Our results show that in most of the texts, the osmotic process is not connected with the non-equilibrium state, macroscopic dynamic state or equilibrium state, whereas in other textbooks, equivalence between these states and hypo–hyper and isotonic states is incorrectly presented.

---

Introduction

Scientific knowledge uses a conceptual language supported on a materialist ontology (Bunge, 1974a, 1974b). Most of the philosophers and historians of science agree that the development of scientific knowledge can be partially understood through the conceptual change of its theories (Lakatos et al., 2002; Kindi and Arabatzis, 2013). On the other hand ideas about conceptual change from the history and philosophy of science have been widely applied in the field of psychology of learning through the work of Susan Carey or Michael Posner for science education (Vosniadou, 2013).

According to Vosniadou “conceptual change requires fundamental changes in students' ontological and epistemological commitments and in their representations” (2013, p. 14). These requirements can be detected when the ontological categorization of a scientific concept in the conceptual system of a novice differs from the ontological categorization in the conceptual systems of experts. For example, Chi and colleagues have suggested that there is a difference in the ontological categorization in the concept of “heat” while a novice considers heat as “hot molecules” or “hot stuff” (an entity), instead of the speed of molecules (a process) (Chi, 2008).

Studies that use ontological tools for a disciplinary analysis of the content of natural science textbooks are scarce (Niaz, 2001; Scharmann and Smith, 2001; Rodriguez and Niaz, 2004; Niaz and Fernández, 2008; Niaz and Maza, 2011). The philosophy of science, particularly ontology, can be transformed into a powerful tool for this purpose. According to Science Magazine, among the most influential living science philosophers we have Mario Bunge (Michel et al., 2011), who proposed a philosophical system called Scientific Realism. In his proposal, five ontological categories are defined that address all areas of material reality (Bunge, 1977). These categories are:

– Thing or object

– Property

– State

– Event

– Process

This ontology has semantic connotations for text analysis because scientific knowledge is composed of concepts, and such concepts can be connected to material reality through the above ontological categories. Historically, many scientific concepts have come to be understood due to an ontological interrogation. For example, we now know that the concept of energy refers to a property, contrary to the former belief that the concept of energy is associated with an object or thing under the caloric theory (Müller, 2007).

According to this philosophical approach, a thing or object is an entity endowed with all its substantial properties (Bunge, 1977). This means that things or objects have their own existence. Scientific concepts referring to categories of things include, for example, the concepts of atom, molecule, electron, dog, or planet, unlike properties that have no existence but are part of our conceptions of things; this means that there are no properties per se but rather only properties of things. Examples of scientific concepts that refer to properties of things include mass, volume, energy, and viscosity. The thing–property relationship is essential to elucidating a scientific concept and improving the teaching thereof. Not all things or natural objects have the same properties. It was the same Mario Bunge who proposed that energy is the only property that is shared by all objects of our reality (Bunge, 2000a, 2000b). However, it is known that general properties such as mass do not appear in all objects of material reality—the photon being one such exception.

In one of our previous studies, we analyze the ontology of Boyle's law. It is clear that both concepts of volume (V) and pressure (P), present in this law in the relationship P·V = k, are properties of a gas (thing). Boyle's law does not refer to the properties of a piston or to the act of measuring the magnitudes of these variables. The application of the philosophical system of Mario Bunge allowed us to clarify these issues and to establish with a solid philosophical basis that the volume (V) of gas is the cause and the pressure (P) of gas is the effect in the relationship being studied. When we applied this ontology to the semantic analysis of 15 chemistry university textbooks, we realized that 14 of them had serious ontological and semantic shortcomings in the presentation of Boyle's law in both the texts and the illustrations (Quiroz and Rubilar, 2015).

Scientific concepts do not only refer to laws, as in the case of Boyle's law. Concepts also exist that refer to states, events or processes. In this philosophical system, the “state” concept is defined as the framework or list of properties that characterize or identify an object in a determined instant. An example of state is the liquid states of a substance, which are defined by a number of characteristic properties such as viscosity, formless, capillary, etc. In the case of events, this concept relates to the change in natural objects. The transformation of one object into another or the passage from one state of an object to another state is considered an event. Given the above reasoning, we wonder how natural processes are presented in science textbooks. We are particularly interested in the concept of osmosis as it is approached in many chemistry and biology textbooks.

Ontological analysis of natural processes

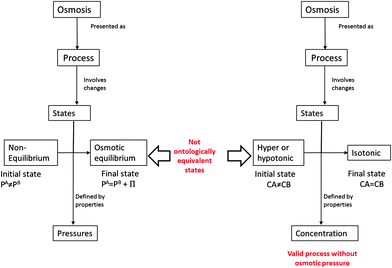
The semantic analysis of scientific concepts that refer to natural processes becomes one of the most complex analyses in the natural sciences—this as a process must necessarily be connected to an object, its properties and states, and a time sequence, as shown in the following diagram of Fig. 1.

Fig. 1 Ontological connections for the presentation of a natural process and possible errors.

Fig. 1 shows that, independent of the way in which a natural process is presented from a semantic-ontological point of view, natural processes must be connected with a change of states. Therefore, these changes of states must have a temporary connection, meaning a sequence that connects the initial and final states of a material system, an object. In this scheme, the categorization of a concept that refers to a process and categorizes it as a property, state or thing thus becomes an ontological error.

Things or objects such as the moon, a uranium atom or a human being have their own existence. Then processes, properties or states have no existence but appear on objects. For example, there is no rotation process, but there is rotation of the moon; the aging process does not exist independently, but there is aging of a human being; in reality fission does not exist, but there is a process of fission of the uranium nucleus.

The importance of a correct ontological categorization of a scientific concept is demonstrated with the concept of energy. Today energy is considered as a property; however, in the past times in the context of caloric theory it was ontologically classified as a thing, as a fluid that can be obtained from the bodies. The same happens today with the concept of heat, which is a process of energy transfer due to temperature differences; however, heat tends to be classified as a thing (i.e. a caloric fluid) or a property (i.e. heat energy), which becomes an ontological error under this framework. Table 1 shows the types of errors with an explanation provided for each error.

Table 1 Types of errors in the presentation of natural processes and their respective explanation based on realist ontology

Error	Explanation
Type 1 error (E1)	This is an error of ontological type. It occurs when a process is mistakenly assigned to a different ontological category, such as property (E1A), state (E1B) or thing (E1C).
Type 2 error (E2)	This is an error of omission. It occurs when a process is presented without associating it with its respective states.
Type 3 error (E3)	This error occurs when a state is associated with properties that are unrelated to the context or the time in which the state is manifested.
Type 4 error (E4)	This error occurs when a change of state is not associated with a thing or a particular material system—its material reference does not exist (E4A) or is ambiguous (E4B).

---

Ontological analysis of the osmotic process

Osmosis is a process that occurs in a system composed of two solutions in contact with a semipermeable membrane, wherein there must be a pressure difference between the two solutions for the process to occur. These differences in pressure or, in a more general context, differences in potential or internal energies are given by differences in solvent concentration as shown in Fig. 2.

Fig. 2 States during the osmotic process. On the left, we have a non-equilibrium state; in the center, we have a macroscopic dynamic state when the osmotic flow starts; and to the right, we have an osmotic equilibrium state. The osmotic process begins due to differences in solvent concentration.

At a macroscopic level, we can ontologically analyze the concepts involved to define the system of osmosis. On one side, we have a solution A; a solution having a solute concentration that we will call C^A_solute and a concentration of solvent denominate C^A_solvent. Similarly, the B solution is also an object that has properties C^A_solut and C^B_solvent.

According to the definition of the process as a temporary change in the state of a thing, in this case, the thing or object is the complete system of A + membrane + B. The initial non-equilibrium state is set when the pressures of both solutions are different, due to differences in concentrations as shown in Fig. 2. Given these initial conditions, we move to the macroscopic dynamic state in which the osmotic flow begins as a spontaneous solvent transfer from solution A to solution B, as shown in the same Fig. 2. The spontaneity is generated by solvent concentration differences in which C^A_solvent > C^B_solvent according to Fick's diffusion law. When the height of the B solution level rises above the height of A, the hydrostatic pressure of the B solution begins to increase—the latter being an emergent property of the system A + B when the membrane height level B is greater than A. Finally, the equilibrium state is reached, though based on one additional property. The additional pressure exerted by the column of solution B increases until it reaches the osmotic flow stop point, which is the state of osmotic equilibrium.

Osmotic flow stops due to the additional height “h” that solution B reaches, which in this case is C^A_solvent ≠ C^B_solvent. This is the osmotic pressure Π. Then, that pressure, which is hydrostatic pressure, can be calculated as Π = d·h·g, where d is the density, h is the height level, and g is the gravity constant. In general terms, any pressure that stops an osmotic flow from reaching the state of osmotic equilibrium is an osmotic pressure independent, as this is generated either by increasing levels of a solution or through a piston or a membrane tension. Next, we will discuss the 3 states of the osmotic process.

Initial state of non-equilibrium

On the left of Fig. 3, there is a system of non-equilibrium where the pressure difference is due to differences in concentration, that is C^A_solvent > C^B_solvent. In this case, the initial state of non-equilibrium occurs because solution A is a hypotonic state relative to B, which in turn is in a hypertonic condition relative to A. Both A and B have the same height levels, so there is no difference in the hydrostatic pressure. It is clear that the pressure difference between A and B is generated at the membrane due to concentration differences.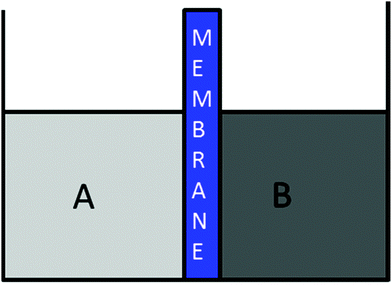

Fig. 3 A system in a state of non-equilibrium. Pressure differences occur due to differences in concentration which is considered the first state of the osmosis process.

Macroscopic dynamic state and the beginning of the osmotic flow

The second state of the osmotic process involves a mass transport of solvent from the solution with the higher pressure to the lower pressure solution. This flow condition is generated by differences in concentration. Part of the osmotic process thus can be understood as a diffusion process, although osmosis cannot be reduced to this because the osmotic process includes a final state of osmotic equilibrium which, as discussed below, cannot be defined only by the concentrations because this is not necessarily achieved when they are equal.

Ontological status of equivalence between the osmotic equilibrium state and the isotonic state

The equivalence between the osmotic equilibrium state and the isotonic state can be true under two specific conditions: the first is that both solutions in contact through the membrane have solute (i.e. neither of the solutions possesses pure solvent). The second condition is that the solutions in contact have the same hydrostatic pressures (i.e. without membrane tension or with equal height levels). An illustration of the experimental set where the solutions are in contact via a membrane, which is presented as a movable wall, is shown in Fig. 4. Under the experimental scheme, no difference in hydrostatic pressure generated by gravity exists, the flow of solvent is diffusional due to concentration differences and the equilibrium state is reached when the concentrations are equal. The final state of osmotic equilibrium in this particular case is reached when the concentrations of both solvents A and B are equal. This means that in this case, we have equivalence between the osmotic equilibrium state and the isotonic state. When a hydrostatic pressure is present, generated either by gravity (Fig. 2) or, as discussed below, by the tension of a membrane, this equivalence is not valid.

Fig. 4 Osmotic process example where the osmotic equilibrium state is equivalent to the isotonic state.

Osmosis in cell systems

Ontological equivalence between turgor pressure and osmotic pressure

In a cell system, the osmosis process also occurs but in different contexts. Cytoplasmic fluid has a different solute concentration than the plasma fluid. As in the previous examples, when there is a concentration difference between A and B, the osmotic flow of solvent will occur; however, in the absence of hydrostatic pressure, this macroscopic dynamic state is governed by a diffusional process because C^A_solvent > C^B_solvent. If the solute concentration is higher in the cytoplasm than in the external medium, the solvent will flow from the outside to the inside of the cell, thus increasing its volume. Then, in the absence of hydrostatic pressure, cell membranes, depending on their rigidity, will generate an internal pressure, which, if it equals the osmotic pressure, will stop the osmotic flow. In this case, the osmotic equilibrium state is not equivalent to the isotonic state. This pressure is known as turgor pressure, which is ontologically equivalent to osmotic pressure, as shown in Fig. 5. The process illustrated in Fig. 5 can occur only in cases where the turgor pressure that the cell membrane can generate before it breaks is greater than the osmotic pressure. If such is not the case, then membrane rupture occurs.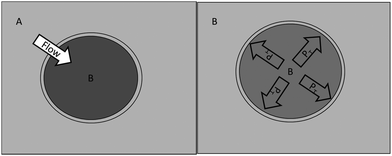

Fig. 5 Initial and final state of an osmotic process in a model of a turgid cell. To the left (A) is the initial state of non-equilibrium, where the solvent osmotic flow occurs from the outside towards the inside of the cell due to differences in concentrations of solvent (C^A_solvent > C^B_solvent), and to the right (B) is the state of osmotic equilibrium, which is achieved by turgor pressure (PT), which stops the osmotic flow because of membrane tension (Pritchard, 2001).

The ontological equivalence between the isotonic state and the osmotic equilibrium state in cell systems

It is common for the osmotic equilibrium state to be confused with the isotonic state. In many biology textbooks, the line sequence of states of the osmotic process starts from a hypertonic or hypotonic state and finishes in an isotonic state. The hypertonic state in a cellular system is a state in which the property of the solvent concentration inside the cell is lower than the concentration of solvent on the outside of the cell, due to the greater amount of solute in the cytoplasm.

This condition also satisfies the requirement that C^A_solvent > C^B_solvent. The same reasoning applies inversely and can be used to define the hypotonic state. Analogously, the isotonic state is the state where the solvent concentration in the cytoplasm is equal to the concentration of solvent in the plasma, so that C^A_solvent = C^B_solvent. With no hydrostatic pressure in cell systems, there exists an ontological equivalence between the osmotic state of non-equilibrium and the hypertonic and hypotonic states, because all these states are defined by the same properties: the solvent concentration differences on both sides of the membrane. However, many biology textbooks claim that the osmotic flow to or from the cytoplasm is stopped when the isotonic state is reached, which is not always correct. The state of osmotic equilibrium is equal to the isotonic state in a cellular context only when there is no membrane pressure (i.e. turgor pressure), because equal concentrations of A and B imply equal pressures on both sides of the membrane, as shown in Fig. 6.

Fig. 6 On the left is a hypertonic condition with an osmotic solvent flow from the plasma into the cytoplasm C^A_solvent > C^B_solvent, and on the right, the isotonic state is achieved when the solvent concentration is equalized C^A_solvent = C^B_solvent which occurs only for cells with a flaccid membrane (without turgor pressure).

It is important to mention that the isotonic state is not equivalent to the state of osmotic equilibrium when turgor pressure exists. As discussed earlier in Fig. 5, turgor pressure is equivalent to osmotic pressure because it can stop the osmotic flow even when the solvent concentrations are different on both sides of the membrane. In a system that has turgor pressure, the osmotic equilibrium state is not equivalent to the isotonic state because the properties that define the state of osmotic equilibrium (pressures) are not the same properties that define the isotonic state of equilibrium (concentrations). The poor definition of the osmotic process as a succession of states defined by concentrations (i.e., hyper-, hypo- and isotonic states) is very common. As previously discussed, however, equivalence is correct only under certain conditions, as shown in Fig. 7.

Fig. 7 Comparing ontological osmotic processes. On the left is the connection of the ontological categories in the context of a traditional osmosis membrane system and piston system, as presented in chemistry texts. On the right is a particular case of osmosis in cell systems in the absence of osmotic pressure (which is valid only for cells with a flaccid membrane as shown in Fig. 6) as presented in some biology textbooks.

Based on the present ontological analysis and in the general tool of Fig. 1, we are able to build a concrete tool for identifying errors in the presentation of osmosis. Fig. 8 shows this proposal. The tool in Fig. 8 enables us to perform an ontological-semantic analysis of the presentation of osmosis in science texts. Four errors therein are identified: the first (E₁) is when the concept of osmosis is assigned to a different ontological category than a process. The second error (E₂) is associated with bypassing the states involved in the osmosis process and defining the concept only from its properties. The third error (E₃) corresponds to defining osmosis states by concentration as a property—an error that could be remedied by explaining the conditions under which this equivalence is valid in the absence of osmotic pressure in chemical systems or biological systems. Finally, the fourth error (E₄) is associated with assigning the wrong material system; for example, assigning a cell system, an osmotic process regulated by hydrostatic pressure. Table 2 shows the 4 types of errors and their definitions.

Fig. 8 Semantic tool for the presentation of osmosis in textbooks based on the ontology of scientific realism. Potential errors are distinguished in red.

Table 2 Types of errors in the presentation of the osmosis concept and their respective explanation based on realist ontology

Error	Explanation
Type 1 error (E1)	This error is generated when osmosis is not presented as a process but as a colligative property (E1A).
	This error is presented in textbooks that confuse the osmosis concept with the osmotic pressure concept. It may also be generated by confusing the osmosis concept with a state (E1B) or an object (E1C).
Type 2 error (E2)	This error occurs when the osmosis process is explained only from the properties of chemical potential or osmotic pressure or internal energy, without specifying any of the three states, especially the osmotic equilibrium states.
Type 3 error (E3)	This error occurs when non-equilibrium states or the state of osmotic equilibrium are confused with other states, such as the hypertonic, hypotonic or isotonic states. This happens when osmosis is presented just as a diffusion process.
	We have defined a special error type 3 (E3′) that occurs when the osmotic equilibrium relates only to the hydrostatic pressure generated by gravity and not to the concept of osmotic pressure, which is an ontological reductionism.
Type 4 error (E4)	This error occurs when osmosis is not associated with a material system (E4A) or when osmosis occurs in multiple material associated systems, which are not necessarily equivalent (E4B)—such as systems with or without hydrostatic pressure, dehydrated plant cells vs. turgid cells, etc.

---

Textbook analysis

One of the basic pillars on which the action of teaching is based in all educational levels is the textbook. Today its powerful influence on classroom work for both teachers and students is unquestionable, becoming in many occasions the sole benchmark of scientific knowledge (Palacios and de Dios Jiménez, 2002). The implications in the teaching and learning process that the use of the textbook has for a science teacher refer to the fact that their own teaching may be based on a textbook (Dillon et al., 1994).

There has been research on how teachers use the textbook of science in the classroom (Digisi and Willett, 1995) and how this use can influence the teaching–learning process. For example, Martins and Assunçao Brigas (2005) highlight the ways in which textbooks (school and/or university) can be used by teachers considering:

(a) The treatment of the concepts in some books promotes the formation of alternative conceptions, so the teacher must be aware of these deficiencies in school and/or university textbooks (Dall'Alba et al., 1993).

(b) The main ideas of the text should ideally correspond to both; the main ideas in the science class and the information in the text that has been considered important for the students. This structural significance of the text itself is underestimated (Alexander and Kulikowich, 1994).

(c) Most text promotes memorizing facts and vocabulary, putting less emphasis on the understanding of knowledge and the applications of this knowledge in the daily life of students (Stinner, 1992).

Considering that scientific knowledge has an ontological material reference (Bunge, 1974a, 1974b), and further, that scientific concepts are systematized in theories (Bunge, 2000a, 2000b), we believe that teachers should keep in mind the role that the textbook can play in helping students to build appropriate concepts (Martins and Assunçao Brigas, 2005). At the university level this means that the learning of a scientific concept is more than memorizing definitions. This implies also connect both with material reality through their respective ontological category as to associate with the other concepts of the theory on which this is embedded. In this work 15 university scientific texts, 14 of them in Spanish and 1 in English where the osmosis concept is presented, were analyzed.

Guidelines for selection of textbooks

To select textbooks, we applied the criteria used by Binn and Bell (Binns and Bell, 2015), Vesterinen et al. (2013) and Niaz and Fernandez (2008), which are:

(a) Availability of textbooks in our university and nearby libraries.

(b) Inclusion of recent textbooks.

(c) Inclusion of textbooks that have published various editions, which show their acceptance by the science education community.

(d) Consultations with colleagues in different parts of the world revealed that various textbooks selected for this study are used for translations.

(e) Various studies published in science education journals have used these textbooks.

Table 3 shows the analysis of the presentation of the osmosis concept in 15 science textbooks based on the tool presented in Fig. 8. The first 5 texts (L1 to L5) correspond to biology textbooks and other texts (L6 to L15) correspond to Chemistry. These books have issues ranging from 1969 to 2013. Table 4 shows the result of this analysis based on the 4 error types described in Table 2. In all 15 books, both text (T) and illustrations (I) were analyzed.

Table 3 Analyzed science texts and their respective encodings

Textbook	Editorial	Author	Year	Pages	ID	Language
Introducción a la Botánica	Compañía editorial Continental	Cronquist A.	1969	38–41	L1	Spanish
Botánica	McGraw-Hill	Lüttge U., Kaluge M. and Bauer G.	1993	63–65, 69–70, 145, 394–395, 426, 437, 451, 466, 502	L2	Spanish
Fundamentos de la Fisiología Vegetal	McGraw-Hill	Azcón J. and Talón M.	2000	26–27	L3	Spanish
Biología	McGraw-Hill	Ville C.	1996	45	L4	Spanish
Biología	Panamericana	Curtis H., Barnes S. and Schneck Massarini A.	2008	64	L5	Spanish
Química 9 ed	McGraw-Hill	Chang, R	2007	523–525	L6	Spanish
Química 11 edn	McGraw-Hill	Chang R. and Goldsby K.	2013	541–543	L7	Spanish
Principios de química general 3 edn	Panamericana	Atkins P. and Jones L.	2006	308–310	L8	Spanish
Principios de química general 5 edn	Panamericana	Atkins P. and Jones L.	2012	360–362	L9	Spanish
Chemistry & Chemical Reactivity 2 edn	Harcourt college Pub	Kotz J. and Purcell	1991	583–586	L10	English
Química y reactividad Química 5 edn	Thomson international	Kotz J. and Treichel P.	2003	582–585	L11	Spanish
Conceptos básicos de Química	Compañía editorial Continental	Sherman A., Sherman S. and Russikokk L.	1999	348–351	L12	Spanish
Química general	McGraw-Hill	Longo F.	1975	171–173	L13	Spanish
Química general 3 edn	McGraw-Hill	Whitten K., Gailey K. and Davis R.	1998	525–528	L14	Spanish
Química general 8 edn	Cengage learning	Whitten K., Davis R., Peck M. and Stanley G	2008	527–531	L15	Spanish

---

Table 4 Evaluation of error in biology and general chemistry textbooks (n = 15) in text (T) and illustration (I)

No.	Textbook	Criteria^a
		1	2	3	4
a T′ and I′ indicate an E3′ error type.
1	Cronquist, A. (Cronquist, 1969) (1969)		I		I
2	Lüttge (Lüttge et al., 1993) (1993)				I
3	Azcón and Talón (Azcón-Bieto and Talón, 2000) (2000)		T
4	Curtis (Curtis et al., 2008) and Barnes (2008)			T
5	Ville (Villee, 1996) (1996)		T	T	I
6	Chang R. (2007)			T′	IT
7	Chang R. and Goldsby K. (2013)			T′	IT
8	Atkins P. and Jones L. (2006)	T		T	T
9	Atkins P. and Jones L. (2012)	T		T	T
10	Kotz J. and Treichel P. (2003)	T	T	TT′
11	Kotz J. and Treichel P. (2005)	T	T	TT′
12	Sherman A., Sherman S. and Russikokk L. (1999)		T	TI′
13	Longo F. (1975)		T	T
14	Whitten K., Gailey K. and Davis, R. (1998)		T	TI′	TI
15	Whitten K., Davis R., Peck M. and Stanley, G. (2008)		T	TI′	T

---

The general analysis of Table 4 shows that the least reiterated error is E₁. Only 4 out of 16 analyzed texts misclassified the osmosis concept primarily as a colligative property, thus confusing the concept of osmosis with the concept of osmotic pressure. Another interesting tendency is that the E₂ error can be found in 8 of the 16 texts analyzed, with mainly chemistry books presenting this error. Apparently, the association between the osmotic process and the states occurs mostly in biology texts, but as we shall see with the E₃ error, this association was established erroneously with the hyper, hypo- and isotonic states in different cellular contexts. Error E₃ was the most frequent error in the analysis. It appeared in 13 of the 16 texts analyzed. In these books, osmotic states are defined by ownership concentration properties instead of pressure properties. On the other hand, the osmosis equilibrium state is reduced to a fact related only to hydrostatic pressure. It is very interesting to note that the only error that is mostly presented in the illustrations in biology textbooks was the E₄ error. Of the 6 biology textbooks, 4 had errors associated with using a reference material not equivalent to a cell system. This trend occurred mostly in biology textbooks because many of their illustrations appealed to concepts of osmotic pressure in contexts of hydrostatic pressure and then applied this to cellular systems in which hydrostatic pressure does not exist; only 2 books consider the osmotic pressure as turgor pressure.

Individual textbook analysis

L1

Two errors in this book are presented: the first one (E₂) is found in Fig. 2.15 on page 39 and mentions that the property that changes over time is the concentrations of substances such as water and sugar, but no reference to the initial and final states can be found. The second error (E₄) also relates to the aforementioned image; in vegetable cells, system osmosis is not related to a hydrostatic pressure relationship, which is the error presented in the text.

L2

The text speaks about plant cells and diffusion by concentration. However, the illustration used to explain osmosis in cell systems includes an example with hydrostatic pressure, which is an E₄ error.

L3

The text presents a type 3 error, as it presents a state of osmotic equilibrium related to the concentration of solute in both solutions, which is valid only without turgor pressure.

L4

The analysis presented an E3 error, as the state of osmotic equilibrium is compared with the isotonic state. Further mentions of stopping osmotic flow through differences in concentrations without connecting with turgor pressure also occurred.

L5

In the analysis of this text, 3 errors occur: the first relates to the process of osmosis, which is explained without explicitly alluding to the osmotic states and with only with its pressure properties (E₂) or the more general property of the chemical potential. Furthermore, when osmotic pressure is defined, it is incorrect, as the third paragraph on page 45 states the following:

“The osmotic pressure is produced by the tendency of water molecules to pass through the membrane to equalize the concentration of water molecules on both sides”

The errors here include relating osmotic pressure to a diffusion process and not defining it as a property that stops the osmotic flow, which is also not necessarily diffusional. For the second error, the osmotic equilibrium state is related to the properties of the concentrations (E₃)—i.e., the isotonic state—, which does not occur in any type of turgor cell. Finally, a type 4 error is detected because they use an illustration that includes osmotic pressure related to concentration differences and not turgor pressure.

L6 and L7

These correspond to general chemistry books by the same author but of different editions, thus maintaining exactly the same information. Both books therefore contain the same mistakes. The first error (E_3′) is in the text on page 541, which mentions the osmotic equilibrium state when the hydrostatic pressure of the column stops the osmotic flow without making explicit the equivalence with osmotic pressure. The second error E₄B is shown in Fig. 12.12 on page 541: this illustration is intended to demonstrate how the process of osmosis takes place by analogy with what happens when two solutions with different vapor pressures are together inside a sealed box. However, one of the solutions is a pure solvent and the other is a solution. Over time, a net transfer of pure solvent to the vessel containing the solution occurs, and the figure indicates that a similar phenomenon occurs during osmosis. In this case, osmosis is associated with a material system that is not necessarily equivalent (E₄; without membrane).

Even if the molecular discrimination is equivalent (De Berg, 2006) and the air space can act as a membrane our main objection for using this analogy is that there is no osmotic pressure to stop the solvent transport. We recognize that the use of this analogy to explain the osmotic process can be considered as correct from the point of view of the molecular mechanism or erroneous from the ontological point of view of the final stage of the process so we recommend that our objection must be taken with caution. A third error (E₃) is detected on page 542. On this page, it is mentioned that the osmotic equilibrium state corresponds to the state where the isotonic concentration and osmotic pressure are the same on both sides of the semipermeable membrane.

L8 and L9

These correspond to general chemistry books by the same author but with different issues that retain exactly the same information. In both books are therefore the same mistakes. The first error (E₁A) is detected twice in the text, on page 360 and 361, the osmosis is classified as a property instead of being classified as a process; specifically, it is classified as a colligative property of solutions and then as a thermodynamic property. A second error (E₃) is shown in the text on page 360, mentioning that the osmotic flow occurs when the solvent flows into the more concentrated solution; that is, the equilibrium state is confused with the isotonic state. A third error (E₄) lies in the text on page 361, where examples of osmosis in everyday life occur. As in the previous books (L6 and L7), there are no hydrostatic or osmotic pressures, so only a diffusional process occurs.

L10 and L11

These correspond to general chemistry books by the same author but with different issues that retain exactly the same information. Both books therefore contain the same mistakes. Just as in the L8 and L9 textbooks, in this case, on page 582, an E₁A error is detected, as osmosis is classified as a colligative property of the solutions instead of as a process. The second and third errors (E₂ and E₃) can be found on page 582 in the text, when osmosis is defined as the movement of solvent molecules across a semi-permeable membrane from a lower solute concentration to another, higher concentration; therefore, the equilibrium state is omitted and the definition also associates the osmotic process with the concentration property.

An E_3′ error can be found on page 582, where the state of osmotic equilibrium is associated with the hydrostatic pressure but without explicit mention of its equivalence with osmotic pressure. As in other texts, it is assumed that the height of the column of the solution is a measure of the osmotic pressure and not just a particular case of it.

L12

Three errors in this book can be found. The first and second errors are on page 348, where the diffusion of solvent through the semipermeable membrane is explained as a product of the difference in concentrations without reference to the initial and final states of the osmotic process. The third error (E_3′), was detected in Fig. 15.14 on page 350, where it is mentioned that osmotic pressure is due to the height of the column (hydrostatic pressure) without indicating that this is just a particular case of osmotic pressure.

L13

The osmotic process is presented as associated only with the properties of pressure without mention of any state (E₂). Additionally, it presents a type 3 error in the text because when discussing an illustration that contains a bladder with a solution of sugar, it states that:

“…there will be displacement of water from the solution into the bladder until the concentrations become equal”

Thus, the text clearly relates the osmotic equilibrium state to the isotonic state without specifying the conditions where this equivalence is valid.

L14 and L15

These correspond to general chemistry books by the same author but with different issues that retain exactly the same information. Both books therefore contain the same mistakes. First, osmosis is properly defined as a process but is defined as the passage of solvents due to concentration differences, which means a merely diffusional process (E₃). In Fig. 14.16 of L14, the author attempts to draw an analogy with a material system where mass transport occurs due to solvent vapor pressure, which is an example that has neither equilibrium states nor any osmotic pressure (E₄).

Another error in this text is that no states are mentioned to explain the osmotic process; it always mentions only the properties of pressure and concentration, even in the same examples of its illustrations (E₂). In its latest version (L15), this text removes an illustration without osmotic pressure, and its replacement includes the example of cell systems embedded in solutions in hyper-, hypo- and isotonic states, thus defining the osmotic process according to concentration and not pressure (E₃).

Conclusion

Based on our results, we can state that our tool for the analysis of natural processes based on the ontology of the scientific realism of Mario Bunge allows for the detection of errors in university science textbooks. In the case of the presentation of the osmosis concept, the most frequent error in the scientific textbooks analyzed is the confusion between the osmotic equilibrium state and the isotonic state. Furthermore, the reduction of the osmotic process to a mere diffusional process generated by concentration differences is a systematic error in most of the analyzed texts, and the illustrations are a reinforcement of this misconception.

Figure use in biology texts has been generally counterproductive when trying to extrapolate examples with hydrostatic osmotic pressure generated by gravity to cell systems with turgor osmotic pressure generated by cell tension, thus confusing the material reference where both are equivalent.

It is a projection of this work to evaluate the alternative conceptions about osmosis held by students who use these texts. On the other hand, the connection of a natural process with their respective states and properties for the presentation in scientific texts is possible and desirable for texts aimed at younger readers. Can we use the same ontological strategy to lower the learning achievement level? We believe that it is possible to consider making ontological concessions to facilitate the learning of younger readers, something that deserves a separate investigation, and a special analysis of high school textbooks is mandatory for this purpose.

Acknowledgements

This scientific product is derived from FONDECYT research 1150659 CONICYT – CHILE and the VRIEA of the Pontificia Universidad Católica de Valparaíso (project DREAMS 0.37.307/2015). Cecilia Morales and Michelle Spinelli Barria also thanks to the graduate program “Magister en Didáctica de las Ciencias Experimentales” of the Pontificia Universidad Católica de Valparaíso and CONICYTPCHA/Magíster Nacional 2015-22151311 for the fellowship granted.

References

1. Alexander P. A. and Kulikowich J. M., (1994), “Learning from physics text: a synthesis of recent research”, J. Res. Sci. Teach., 31(9), 895–911.
2. Azcón-Bieto J. and Talón M., (2000), Fundamentos de la fisiología vegetal, España: Mac Graw Hill.
3. Binns I. C. and Bell R. L., (2015), “Representation of Scientific Methodology in Secondary Science Textbooks”, Sci. Educ., 24(7–8), 913–936.
4. Bunge M., (1974a), “The relations of logic and semantics to ontology”, Journal of Philosophical Logic, 3(3), 195–209.
5. Bunge M., (1974b), Treatise on Basic Philosophy: Semantics I: Sense and Reference, Springer Netherlands.
6. Bunge M., (1977), Treatise on Basic Philosophy: Volume 3: Ontology I: The Furniture of the World, D. Reidel.
7. Bunge M., (2000a), “Energy: Between physics and metaphysics”, Sci. Educ., 9(5), 457–461.
8. Bunge M., (2000b), La investigación científica: su estrategia y su filosofía, Siglo XXI.
9. Cronquist A., (1969), Introducción a la botánica, México: Compañia Editorial Continental.
10. Chi M. T. H, (2008), Three Types of Conceptual Change: Belief Revision, Mental Model Transformation, and Categorical Shift, in Vosniadou S. (ed.) International Handbook of research on conceptual change, Hillsdale, NJ: Erlbaum.
11. Curtis H., Schnek A., Barnes S. and Massarini A., (2008), Biología, Buenos Aires: Editorial Medica Panamericana.
12. Dall'Alba G., Walsh E., Bowden J., Martin E., Masters G., Ramsden P. and Stephanou A., (1993), “Textbook treatments and students' understanding of acceleration”, J. Res. Sci. Teach., 30(7), 621–635.
13. De Berg K. C, (2006), “The kinetic-molecular and thermodynamic approaches to osmotic pressure: a study of dispute in physical chemistry and the implications for chemistry education”, Sci. Educ., 15(5), 495–519.
14. Digisi L. L. and John B. Willett, (1995), “What high school biology teachers say about their textbook use: a descriptive study.” J. Res. Sci. Teach., 32(2), 123–142.
15. Dillon D. R., O'Brien D. G., Moje E. B. and Stewart R. A., (1994), “Literacy learning in secondary school science classrooms: a cross-case analysis of three qualitative studies”, J. Res. Sci. Teach., 31(4), 345–362.
16. Kindi V. and Arabatzis T., (2013), Kuhn's The Structure of Scientific Revolutions Revisited, Taylor & Francis.
17. Lakatos I., Worall J., Currie G. and Zapatero J. C., (2002), Escritos filosóficos: La metodología de los programas de investigación científica, vol. 1, Alianza.
18. Lüttge U., Kluge M. and Bauer G., (1993), Botánica, España: Mac Graw Hill.
19. Martins I. P. and Assunçao Brigas M., (2005), “Libros de texto de Química y aprendizaje de los alumnos: pensamiento y prácticas del profesorado”, Tarbiya: Revista de investigación e innovación educativa, 36, 149–166.
20. Michel J. B., Kui Shen Y., Presser Aiden A., Veres A., Gray M. K., Pickett J. P., Hoiberg D., Clancy D., Norvig P., Orwant J., Pinker S., Nowak M. A. and Aiden E. L., (2011), “Quantitative analysis of culture using millions of digitized books”, Science, 331(6014), 176–182.
21. Müller I., (2007), A History of Thermodynamics: The Doctrine of Energy and Entropy, Springer.
22. Niaz M., (2001), “A rational reconstruction of the origin of the covalent bond and its implications for general chemistry textbooks”, Int. J. Sci. Educ., 23(6), 623–642.
23. Niaz M. and Fernández R., (2008), “Understanding quantum numbers in general chemistry textbooks”, Int. J. Sci. Educ., 30(7), 869–901.
24. Niaz M. and Maza A., (2011), Nature of Science in General Chemistry Textbooks, Springer.
25. Palacios J. P. and de Dios Jiménez J., (2002), “Las ilustraciones en la enseñanza-aprendizaje de las ciencias”, Enseñanza de las Ciencias, 20, 369–386.
26. Pritchard J., (2001), Turgor Pressure, eLS, John Wiley & Sons, Ltd.
27. Quiroz W. and Rubilar C. M., (2015), “Natural laws and ontological reflections: the textual and didactic implications of the presentation of Boyle's law in general chemistry”, Chem. Educ. Res. Pract., 16(3), 447–459.
28. Rodriguez A. J. and Niaz M., (2004), “A reconstruction of structure of the atom and its implications for general physics textbooks: a history and philosophy of science perspective”, J. Sci. Educ. Technol., 13(3), 409–424.
29. Scharmann L. C. and Smith M. U., (2001), “Further thoughts on defining versus describing the nature of science: A response to Niaz”, Sci. Educ., 85(6), 691–693.
30. Stinner A., (1992), “Science textbooks and science teaching: from logic to evidence”, Sci. Educ., 76(1), 1–16.
31. Vesterinen V. M., Aksela M. and Lavonen J., (2013), Quantitative Analysis of Representations of Nature of Science in Nordic Upper Secondary School Textbooks Using Framework of Analysis Based on Philosophy of Chemistry, Sci. Educ., 22(7), 1839–1855.
32. Villee C. A., (1996), Biología, México: Mac Graw Hill.
33. Vosniadou S., (2013), International Handbook of Research on Conceptual Change, Taylor & Francis.

---