Unequivocal evidence of enhanced magnetodielectric coupling in Gd³⁺ substituted multiferroic Bi₂Fe₄O₉

Abstract

We report an enhanced magnetodielectric (MD) coupling in antiferromagnetic Bi₂Fe₄O₉ (BFO) lightly substituted by gadolinium (Gd³⁺). Rietveld refined X-ray diffraction and Raman spectra reveal the formation of orthorhombic phase for all the synthesized samples. Gd³⁺ substitution results in a notable increase of antiferromagnetic transition (T_N) from 250 K (x = 0, BFO) to 256 K (x = 0.02, BGFO2). At the same time, deviation from linear M–H behaviour in the substituted samples at T ≤ 30 K implies the onset of weak ferromagnetic ordering, along with a sudden rise in magnetisation around ∼30 K. This result indicates the magnetically active nature of Gd³⁺ ions possessing a large magnetic moment of ∼8 μ_B and this is explained by considering the two sub-lattice mode. The temperature dependence of the dielectric study shows unusual oppression in ε′ and tan loss plots at T ∼ T_N which hints a plausible MD coupling in the above studied samples. A contrasting behaviour in the temperature dependant MD% is seen for BFO and the substituted samples have an enhancement of ∼30% for BGFO2 at 300 K. Further, confirmation to this coupling is drawn by studying frequency and magnetic field dependant MD% at 300 K, where it is found that both obey a power law of the form ∝exp(ω)ⁿ and ∝(H)^m respectively. Interestingly, the values of ‘n’ and ‘m’ obtained from fitting are found to lie in the range 0.45–0.5, thus signifying a similar dependence of MD on frequency as well as magnetic field. Lastly, the effect of Gd³⁺ substitution on P–E loop of BFO and its substituted samples at room temperature have been discussed.

---

1. Introduction

In recent decades, magnetoelectrically coupled multiferroic materials have been under the intensive focus of contemporary academic interest owing to their diversified physical aspects along with remarkable multifunctional device applications.^1–5 These materials manifest the interaction of magnetic and electrical order parameters, often known as ‘magnetoelectric (ME) effect’.² The coupling of these two ferroic order parameters lends an additional degree of freedom in device designing where magnetic and electric polarization can be sensitively tuned with electric and magnetic field, respectively.⁶ Moreover, the simultaneity of these ferroic orders at room temperature is of both fundamental and technological interest. However, the natural occurrence of room temperature ME materials possessing novel technological applications is very uncommon due to their mutually exclusive features.² Although, several single-phase systems such as BiFeO₃, BiFeO₃-based compositions, hexagonal RMnO₃ (R = rare earth) and LuFe₂O₄ have been explored, they are found to exhibit weak coupling between the order parameters due to the occurrence of magnetic and electric ordering at different temperatures.^7–11 Usually, most of the known ME multiferroic systems till date are functional much below room temperature. So, the quest for developing single phase multiferroic materials with optimum ME effect at ambient temperature still continues and is a matter of practical challenge.

The compound of our interest is multiferroic Bi₂Fe₄O₉ (BFO), a well-known antiferromagnetically ordered system and a material prototype of Cairo spin lattice.^12–14 BFO has been widely studied over the past few decades and shows numerous functional applications.^15–17 The most peculiar feature exhibited by BFO is the unique pentagon spin frustration which arises due to the interactions among different kind of Fe³⁺ ions present in the BFO unit cell, thus leading to a non-collinear magnetic structure.¹⁸ Fig. 1(a) shows the unit cell of BFO along with the direction of spins (arrows) of different kind of Fe³⁺ ions. In fact, BFO comprises of two stacked octahedral coordinated Fe atoms (denoted as Fe(O)). Here, we observe four tetrahedral coordinated Fe³⁺ ions (Fe(T)) in the interior of the unit cell whereas on the sides of the cell there are four octahedral coordinated Fe³⁺ ions. It can also be seen that the spins of tetrahedral Fe³⁺ ions interact antiferromagnetically among themselves denoting the superexchange interaction while spins of octahedral Fe³⁺ ions interact ferromagnetically (FM) within a pair of octahedral spins. These competing exchange interactions of different kinds of Fe atoms generate pentagon spin frustration in the BFO system. Moreover, Fe(T) being antiferromagnetically interacting among themselves are considered to display the strongest coupling.¹⁵ However, despite being well-known for its multiferroicity, the urge for further improving its properties and achieve room temperature magnetodielectric effect has motivated researchers to chemically substitute Bi and Fe-site of BFO.^19–22

Fig. 1 (a) A unit cell of Bi₂Fe₄O₉ showing schematic crystal structure and magnetic spins in ab plane along c-axis where the competing exchange interactions between octahedral (Fe(O)) and tetrahedral (Fe(T)) coordinated Fe ions generates pentagon spin frustration. (b) Rietveld refinement of room temperature XRD patterns of BFO, BGFO0.5, BGFO1, BGFO1.5 and BGFO2. (c) The magnified pattern of (002) and (220) diffraction peaks.

The main aim of this manuscript is to investigate the dielectric, magnetic and magnetodielectric properties of Bi_2(1−x)Gd_2xFe₄O₉ (0 ≤ x ≤ 0.02) compounds. In the literature, it is well established that the doping of Gd (a rare-earth magnetic element) at Bi-site of BiFeO₃ is very effective in increasing the magnetization.^23,24 Also, Gd³⁺ ion is magnetically active and has larger effective magnetic moment (∼8 μ_B) as compared to Fe³⁺ ions (∼6 μ_B). Therefore, substitution of smaller ionic radii i.e. Gd³⁺ (1.05 Å) at Bi³⁺-site (1.17 Å) and the coupling between Gd³⁺ and Fe³⁺ ions would be interesting to search for emerging physical properties. In the present context, we report enhanced antiferromagnetic transition (T_N) temperature along with the unambiguous evidence of ME coupling and enhanced magnetodielectric effect at room temperature in Gd³⁺ substituted Bi₂Fe₄O₉ ceramics.

2. Experimental procedure

The polycrystalline samples of Bi_2(1−x)Gd_2xFe₄O₉ (0 ≤ x ≤ 0.02) were prepared using high purity oxides (>99.9%, Sigma Aldrich) namely Bi₂O₃, Gd₂O₃ and Fe₂O₃ by conventional solid state reaction route. The above raw materials taken in stoichiometric proportions were mixed thoroughly, grounded for 2 h and calcined at 800 °C for 12 h followed by a sintering at 850 °C for 10 h. The sintered samples were characterized by room temperature X-ray diffraction (XRD) measurement, RIGAKU JAPAN for detecting the phase formation. XRD was carried out using Cu-Kα radiation (λ = 1.54 Å) in a wide range of Bragg angles (10° ≤ 2θ ≤ 70°) with a step size of 0.002° and at a slow scan rate of 3° min⁻¹. The room temperature Raman spectra were recorded using an Nd-Yag 532 nm laser in the back scattering geometry in a spectrometer (WiTec, alpha 200) equipped with a confocal microscope and CCD camera. The magnetization measurements were done using cryogen free 7T-SQUID-VSM, Magnetic Property Measurement System (Quantum Design, USA). The dielectric measurements were performed using high precession impedance analyser (Wayne Kerr 6500B) over a frequency range of 0.1 kHz to 100 kHz. The temperature variation from 15–320 K was attained using closed cycle refrigerator (Cryo industries, USA). The magnetodielectric measurements were carried out in presence of an external magnetic field (up to 1.3 T) using an electromagnet (GMW 5403) equipped with bipolar DC power supply. Finally, room temperature ferroelectric property (polarizations–electric field loops) of the samples were measured on a standard ferroelectric tester using a Radiant precision premier II unit.

3. Results and discussion

3.1 X-ray diffraction (XRD) study

Fig. 1(b) shows the room temperature Rietveld refined X-ray diffraction (XRD) patterns of parent (BFO) as well as the gadolinium substituted samples (Bi_2(1−x)Gd_2xFe₄O₉ (0 ≤ x ≤ 0.02)). The synthesized samples are abbreviated depending on x (Gd) concentration, such as BFO (x = 0), BGFO0.5 (x = 0.005), BGFO1 (x = 0.01), BGFO1.5 (x = 0.015) and BGFO2 (x = 0.02). All the XRD pattern reveals a well crystallized orthorhombic phase with space group ‘Pbam’ (JCPDS no. 76-1098). The Rietveld refinement was done using FULLPROF software²⁵ to study the detailed crystal structure and the fitting parameters are listed in Table 1. Substitution of Gd³⁺ ions having lower ionic radius than that of Bi³⁺ ions results in reduction of lattice parameters and cell volume as seen from Table 1. A closer view of obtained XRD peaks around 29–32° in Fig. 1(c) shows slight shifting of the main peaks i.e. (002) and (220) to higher 2θ angles with increase in x concentration. This feature can also be attributed to lower ionic radii substitution thus, confirming substitution of Gd³⁺ ions at Bi³⁺ site. Also, the variation in tetrahedral and octahedral coordinated Fe–O bond lengths and O–Fe–O bond angles due to substitution are estimated and listed in Table 2. The comparative variation of Fe(T)–O as well as Fe(O)–O bond lengths in BFO and BGFO2 are schematically depicted in Fig. 2(a) and (b). Here, we observe a slight increase (∼0.2%) in average bond length of Fe–O due to Gd³⁺ substitution in BGFO2 samples with respect to BFO. This has given an insight to explore the effect of Gd³⁺ substitution on the bond lengths of strongly coupled tetrahedral coordinated Fe³⁺ ions i.e. Fe(T)–O as discussed in Fig. 1(a). Interestingly, we observed significant reduction in Fe(T)–O bond lengths of BGFO2 sample as compared to that of parent (BFO) sample. This feature is expected to play a vital role in governing the magnetic and magnetodielectric properties of substituted samples which will be discussed later.

Table 1 Rietveld refined X-ray diffraction parameters of Bi_2(1−x)Gd_2xFe₄O₉ (0 ≤ x ≤ 0.02)

Samples	Lattice parameters				χ^2
	a (Å)	b (Å)	c (Å)	Vol (Å)
BFO	7.97350	8.44142	6.00277	404.0324	3.66
BGFO0.5	7.97316	8.44124	6.00272	404.0032	3.01
BGFO1	7.97279	8.44118	6.00238	403.9587	2.71
BGFO1.5	7.96758	8.43569	5.99818	403.1498	3.13
BGFO2	7.96737	8.43496	5.99978	403.2118	3.06

---

Table 2 Different bond lengths and bond angles of BFO and BGFO2 samples obtained from the Rietveld refinements of respective XRD patterns

Samples	BFO	BGFO2
Bond lengths (Å)
Fe(O)–O2 (×2)	1.956	2.064
Fe(O)–O3 (×2)	1.949	1.989
Fe(O)–O4 (×2)	2.048	2.045
Fe(T)–O1	1.837	1.808
Fe(T)–O2 (×2)	1.930	1.876
Fe(T)–O3	1.847	1.736
〈Fe–O〉a	1.945	1.949
Bond angles (degree)
O3–Fe(O)–O2	87.51	92.85
O2–Fe(O)–O4	92.60	94.17
O3–Fe(O)–O4	97.31	96.72
O4–Fe(O)–O4	82.25	75.39
O2–Fe(O)–O2	175.07	178.21
O3–Fe(O)–O3	83.12	92.05
O1–Fe(T)–O2	113.25	114.71
O2–Fe(T)–O2	106.05	105.45
O3–Fe(T)–O2	108.18	104.26
O1–Fe(T)–O3	111.72	112.35

---

Fig. 2 Fe(T)–O and Fe(O)–O bond lengths of (a) BFO and (b) BGFO2 samples.

3.2 Raman spectroscopy study

To have better insight to the vibrational, structural and lattice properties, the room temperature Raman spectra of parent (BFO) and its substituted samples (BGFO1 and BGFO2) were performed at wave number ranging from 100–1000 cm⁻¹ and is illustrated in Fig. 3(a). Using group theoretical irreducible representation, Iliev et al. have estimated 42 Raman modes (Γ = 12A_g + 12B_1g + 9B_2g + 9B_3g) for orthorhombic Bi₂Fe₄O₉.²⁶ But, due to the insufficient intensity arising from small polarizability of several modes, we could observe less number of modes as compared to above group theoretical calculations. As shown in Fig. 3, all the samples exhibits similar Raman vibrations, confirming the ‘Pbam’ symmetry with seven dominant Raman modes. All the observed Raman modes for parent and substituted samples are listed in Table 3. However, a close look at the spectra shows a slight shifting of major Raman modes to higher wave number (shown in dashed arrows) along with decrease in peak intensity with increase in Gd content. The reason for slight shifting of Raman modes could be attributed to the substitution of Gd atom (∼157 u) which is lighter than Bi atom (∼209 u) and lattice disorder in terms of contraction of unit cell volume as detected from XRD analysis. On the other hand, stronger force constants in general causes blue shift of Raman spectra lines.²⁷ Moreover, decrease in peak intensity with increase in Gd³⁺ content may be due to substitutional disorder which has been recently argued to cause broadening of Raman modes and reduction in intensities.²⁸ Although, the reduction in peak intensities in the present case is not very significant due to small amount of substitution. Another possible reason could be attributed to the decrease in dipole moment (arising due to Bi³⁺ lone s² pair) in substituted samples leading to reduction in intensities. Here, we found that the experimentally obtained Raman modes are in good agreement with the predicted values.²⁶ In fact, the low frequency modes (up to 167 cm⁻¹) are assigned to Bi atoms, high frequency modes (above 262 cm⁻¹) involve mainly oxygen-stretching motions while the Fe atoms actively participate in the modes between 152 cm⁻¹ and 262 cm⁻¹.²⁹ Furthermore, we observed suppression of peak at ∼165 cm⁻¹ while peaks at ∼360 cm⁻¹ and ∼640 cm⁻¹ stabilizes with increase in x content. In order to clearly assign the active Raman modes, we have deconvoluted Raman spectra of BGFO2 sample as shown in Fig. 3(b). The spectra is fitted to the sum of eight Lorentzian peaks with multiple Lorentzian oscillators of the form I = I₀ + ∑A_iΓ_i/[4(ω − ω_i)² + Γ_i²] where, i is the peak number, I₀ is the background intensity, ω_i is the centre frequency, Γ_i is the full width at half maxima (FWHM), and A_i is the area of i^th peak.³⁰ The deconvoluted Raman spectra of BGFO2 with seven major Raman modes at 204 cm⁻¹ (A_g(3), B_1g(3), B_2g(3), B_3g(3)), 278 cm⁻¹ (B_1g(4)), 325 cm⁻¹ (A_g(6), B_1g(5), B_2g(6)), 364 cm⁻¹ (A_g(7), B_1g(6)), 429 cm⁻¹ (A_g(8), B_1g(7), B_2g(7), B_3g(6)), 552 cm⁻¹ (A_g(9), B_1g(8), B_3g(8)) and 641 cm⁻¹ (A_g(10), B_1g(9)) are discernible from the Fig. 3(b).

Fig. 3 (a) Room temperature Raman spectra of BFO, BGFO1 and BGFO2 samples and (b) deconvoluted Raman spectrum of BGFO2 fitted to the sum of eight Lorentzian peaks.

Table 3 Various active Raman modes observed for Bi_2(1−x)Gd_2xFe₄O₉ (x = 0, 0.01 and 0.02) samples recorded at room temperature

Active Raman modes	Raman shifts (cm^−1)
	BFO	BGFO1	BGFO2
Ag(3), B1g(3), B2g(3), B3g(3)	202	203	204
B1g(4)	276	277	278
Ag(6), B1g(5), B2g(6)	321	323	325
Ag(7), B1g(6)	359	362	364
Ag(8), B1g(7), B2g(7), B3g(6)	426	427	429
Ag(9), B1g(8), B3g(8)	549	551	552
Ag(10), B1g(9)	638	640	641
Ag(11)	724	725	727

---

3.3 DC magnetization study

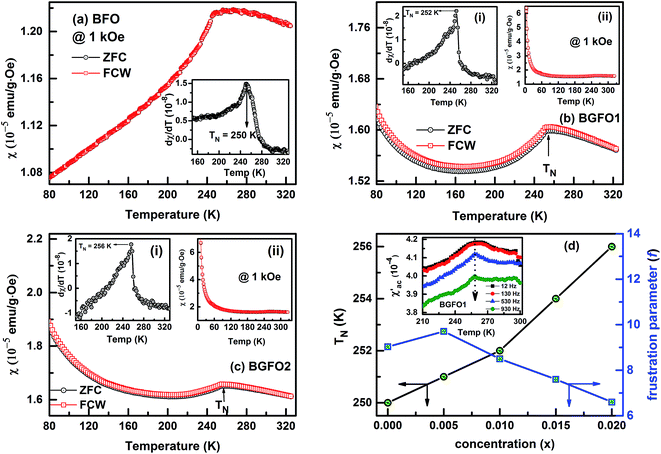
Fig. 4(a–c) illustrates temperature dependant DC magnetization plot of BFO, BGFO1 and BGFO2 under zero field cooled (ZFC) and field cooled warming (FCW) conditions performed at an external field of 1 kOe. A broad cusp around 250 K is noticed in the parent (BFO) sample, characteristically revealing the antiferromagnetic (AFM) behaviour and is consistent to previous reports,^13,15,31 while for the substituted samples, the AFM transition (T_N) is found to increase with substitution. To ascertain the exact AFM transition, the dχ/dT versus temperature is plotted which confirms the AFM transition (T_N) of BFO = 250 K, BGFO1 = 252 K and BGFO2 = 256 K as shown in the insets of Fig. 4(a), (b-i) and (c-i) respectively. The variation of AFM transition (T_N) with concentration (x) is depicted in Fig. 4(d). The origin of enhancement in the AFM transition (T_N) upon Gd³⁺ substitution may be attributed to the Fe–Gd interaction. Moreover, as observed in the XRD analysis, increase in Gd³⁺ concentration leads to decrease in lattice parameters and reduction in strongly antiferromagnetically coupled Fe(T)–O bond lengths. This might be modifying the Fe(T)–O–Fe(T) super-exchange interaction in terms of the lattice distortion in the unit cell causing enhancement in T_N. Also, BFO is known to be magnetically frustrated system showing a unique pentagon spin frustration and the degree of frustration (f) in a spin frustrated system is generally defined as f = |θ_CW|/T_N, where |θ_CW| is the Curie–Weiss temperature.³² The value of f for BFO is determined to be ∼9 revealing a highly frustrated AFM spin in the material but a decrease in f parameter with increase in substitution can be clearly seen from Fig. 4(d). A clear quantitative picture of f parameter can be obtained by performing high temperature χ–T measurement in order to have a wide range of paramagnetic region, which is beyond the scope of present study. It is to be noted that ZFC–FCW of BFO exactly superimposes thus ruling out the possibility of magnetic glassiness or spin glass behaviour in the material. Whereas, a slight mismatch of ZFC–FCW curve is observed in case of BGFO1 samples. So as to confirm the possibility of magnetic glassiness, we have performed the ac susceptibility (χ′_ac) measurement of BGFO1 sample at selected frequencies as shown in inset of Fig. 4(d). Usually, for a spin glass system, χ′_ac versus temperature gives frequency dependant behaviour, but no such feature is seen for BGFO1 sample which implies absence of spin glass or magnetic glassiness in the materials. One of the interesting features in Gd substituted samples is that the magnetization sharply increases below ∼30 K which may be due to the ordering of Gd³⁺ magnetic moments.³³ The enhanced magnetisation due to Gd substitution is also seen in isothermal M–H plots.

Fig. 4 (a–c) dc magnetic susceptibility (χ) versus temperature (80–325 K) of BFO, BGFO1 and BGFO2 samples under 1 kOe. Insets [(a-i), (b-i) & (c-i)] show the corresponding dχ/dT plots indicating the AFM transition (T_N) and [(b-ii) & (c-ii)] shows χ versus T plot for a temperature range of 2–325 K respectively. (d) Variation of AFM transition (T_N) and frustration parameter (f) with concentration (x) and its inset display χ′_ac versus T of BGFO1 sample at several static frequencies.

Fig. 5(a–c) shows M–H curves of BFO, BGFO1 and BGFO2 samples at selected temperatures up to a maximum field of 60 kOe. A linear behaviour of magnetisation can be seen for BFO sample for all the recorded temperatures typically revealing its AFM/PM characteristics, as discussed earlier. Interestingly, the substituted samples also shows a linear magnetisation which signifies AFM/PM nature being intact for 30 K ≤ T ≤ 320 K but for T < 30 K, magnetisation shows a non-linear curve implying an onset of weak FM in the samples. Eventually, the presence of weak FM ordering in the substituted samples were evaluated from the Arrott plots (M² versus H/M) based on the Weiss-molecular field theory.^34,35 Fig. 5(d) shows the Arrott plots of BFO (inset), BGFO1 and BGFO2 samples at 5 K. A consistent linear increase for BFO is observed whereas BGFO1 and BGFO2 show a non-linear increase of the curves. Also, the linear extrapolation of the high field region of M²–H/M plot of both the samples yields a negative intercept on the M² axis which specifies the crossover from AFM/PM to weak FM ordering.³⁶ Further, to strengthen the indications of the growing weak FM interactions along with AFM/PM, we have analysed the M–H loop K using the following expressions consisting of both FM and AFM/PM parts:³⁷

where, M^S_FM is FM saturation magnetisation, M^R_FM is remanant magnetisation, H_ci is intrinsic coercivity, χ is magnetic susceptibility for AFM/PM part, M is the observed magnetisation and H is the applied magnetic field. Here, first term represents FM component and the second term is related to the linear component representing AFM/PM contribution. Inset of Fig. 5(b) and (c) exhibits the fitting of M–H curve of BGFO1 and BGFO2 samples respectively at 5 K using the above eqn (1). From the fitting, the values of M^S_FM, M^R_FM and H_ci is determined to be ∼2.7 emu g⁻¹, ∼0.02 emu g⁻¹ and ∼575 Oe for BGFO1 while ∼3.6 emu g⁻¹, ∼0.7 emu g⁻¹ and ∼1035 Oe for BGFO2. Also, AFM/PM susceptibility (χ) increases monotonically from ∼3.3 × 10⁻⁵ emu g⁻¹ Oe⁻¹ to ∼5 × 10⁻⁵ emu g⁻¹ Oe⁻¹, as x increases from x = 0.01 to 0.02 respectively.

Fig. 5 The isothermal M–H curves of (a) BFO, (b) BGFO1 and (c) BGFO2 samples at several fixed temperatures up to 60 kOe. Inset (b and c) illustrates experimental M–H curve of BGFO1 and BGFO2 samples respectively at 5 K with the fitted (solid line) and theoretically simulated AFM/PM and FM part (dotted lines). (d) Arrott plots of BFO, BGFO1 and BGFO2 samples at 5 K.

It is to be noted that value of magnetisation increases with increase in x content and a sudden rise in magnetisation is more prominently seen towards the lowest temperature i.e. T < 30 K (insets of Fig. 4(b-ii and c-ii)). This can be explained by considering two sub-lattice mode model.^30,38 In the present studied compound, we have Fe as well as Gd sub-lattice which have their own temperature dependence of magnetisation. Usually, Gd being a rare earth element, orders at preferably lower temperature.³⁹ Generally, AFM material comprising of two spin sub-lattices have zero net magnetic moment due to complete compensation of spins between these two sub-lattices. However, if any resultant small magnetic moment arises in AFM materials, then it could be possibly due to uncompensated spins in the two sub-lattices. In our case, substitution of Gd³⁺ causes enhancement in magnetisation below T ∼ 30 K because Gd³⁺ having large effective magnetic moment (∼8 μ_B) than Fe³⁺ (∼5.9 μ_B) orders FM at preferably low temperature and coupling between Gd³⁺ and Fe³⁺ ions (f–d coupling) creates a possibility of enhanced magnetization.

3.4 Temperature dependant dielectric study

Fig. 6(a–c) depicts the temperature dependant (150–300 K) dielectric permittivity (ε′) in the main plot for BFO, BGFO1 and BGFO2 samples at several static frequencies. The insets of the respective plots show the variation of tan loss and dε′/dT in the same temperature window. For all the above samples, the values of ε′ decreases with the decrease in temperature i.e. ∼27 (BFO), ∼23 (BGFO2) at room temperature to ∼25.5 (BFO), ∼21.5 (BGFO2) at 150 K. The dielectric plot of parent as well as modified samples can be divided in two regions namely the low temperature almost linearly rising dispersion-less region (T < 180 K) and dispersedly rising region for T > 180 K. From the dielectric data, we observe a slight oppression (shown in circle) in the studied samples and to exactly trace the dielectric transition or peak, derivative of ε′ at 12 kHz of all the samples are shown in the respective insets. The dε′/dT plot shows a sharp peak at 250 K, 252 K and 256 K for BFO, BGFO1 and BGFO2 respectively, which also happens to be the AFM transition (T_N). Along with, a change in slope around T_N was seen in the respective tan loss plots taken at 12 kHz. This strongly indicates a plausible coupling of magnetic and electric order parameters in our samples. Moreover, Fig. 6(d) shows temperature and field dependant tan loss plot of parent and BGFO2 samples which indicate that with the application of magnetic field, tan loss factor decreases and a clear distinction of broad shoulders around T_N can be seen. This further provides the evidence of ME coupling in BFO as well as in BGFO1 and BGFO2.

Fig. 6 (a–c) Temperature dependant ε′ of BFO, BGFO1 and BGFO2 samples and respective insets show tan loss and dε′/dT of the same. (d) tan loss factor is plotted as a function of temperature at 0 T and 1.3 T for BFO (upper panel) and BGFO2 (lower panel). Dotted circles and arrows indicate the T_N while dotted lines are guide to the eye.

3.5 Magnetodielectric study

Strong evidence of ME coupling encouraged us to observe the influence of magnetic field on the dielectric property and investigate the magnetodielectricity in our samples. The magnetodielectric (MD) effect is expressed as:⁴⁰where, ε′(H) and ε′(0) are dielectric permittivity with applied field (1.3 T) and zero field respectively. Fig. 7(a) shows temperature variation of MD% at 12 kHz for BFO (inset), BGFO1 and BGFO2. All the samples exhibited negative MD effect along with a contrasting behaviour in case of parent and substituted samples. The parent BFO sample shows almost negligible MD effect at low temperatures but as temperature approaches T_N (250 K), a sudden rise in negative MD is seen which continues till 300 K and the MD% value becomes ∼−0.3%. On the contrary, BGFO1 and BGFO2 shows an abrupt change in MD values, one at lower temperature i.e. ∼50 K (marked in dotted circle) which might be due to the ordering of Gd³⁺ as discussed above, and the other around magnetic transition (T_N, marked by an arrow). In BGFO1 and BGFO2, as temperature approaches T_N, the magnitude of MD% increases with rise in temperature and reaches room temperature with values −0.31% (BGFO1) and −0.39% (BGFO2). This shows a remarkable enhancement of ∼7% and ∼30% in MD% for BGFO1 and BGFO2 samples respectively at 300 K as compared to that of BFO sample.

Fig. 7 (a) Temperature dependent MD% of BFO (inset), BGFO1 and BGFO2 samples at 12 kHz. Dotted circle indicates Gd³⁺ ordering. (b) Frequency variation of MD% under H = 1.3 T of BFO, BGFO1 and BGFO2. The dotted lines show the power law fitting of the form MD% ∝ exp(ω)ⁿ. (c) Field variation of MD% of BFO, BGFO1 and BGFO2. The solid lines are fitted using the power law of the form MD% ∝ (H)^m. (d) Variation of MD% with M² for BFO (inset), BGFO1 and BGFO2 samples.

Now, we shall discuss the variation of MD% with frequency (0.1–100 kHz) at room temperature as shown in Fig. 7(b). A negative MD effect is seen for BFO, BGFO1 and BGFO2 samples. The MD% for BFO shows a maximum value of ∼−6% at 0.1 kHz whereas the substituted samples shows a very less value (<35%), but with increase in frequency MD% approaches to zero varying non-linearly in the log scale of frequency. Further, to analyse the frequency dependant behaviour, our MD plot was fitted using power law of the form, MD% ∝ exp(ω)ⁿ, distinctly for lower frequency regions (<10 kHz) and higher frequency regions (>10 kHz). The low frequency process is vulnerable to space-charge polarizations, leakage currents, dc conductivity etc., whereas high frequency process may be regarded as the intrinsic contribution. The exponent n ∼ −0.2 shows a reasonably good fit for low frequency regions while n ∼ −0.5 fits well for higher frequency regions for all the samples. Thus, the MD result suggests that both the lower and higher frequency processes are responsible for observed MD in these samples.

To elucidate the above feature, field dependant MD% is done for BFO, BGFO1 and BGFO2 samples at room temperature. Fig. 7(c) shows variation of MD% versus field at 50 kHz in order to nullify the effect of interfacial space-charge artifacts.⁴¹ The change in MD% observed with a change in the applied magnetic field indicates strong coupling of electric and magnetic order parameters. We observe a negative MD% in all the cases with values ∼−0.03%, ∼−0.06% and ∼−0.12% for BFO, BGFO1 and BGFO2 samples at an applied field of 1.3 T. The field dependence of MD% is found to obey power law of the form MD% ∝ (H)^m and the value of ‘m’ is found to lie in the range of 0.45–0.5 for all the studied samples. The value of ‘m’ obtained is very close to that of the value of ‘n’ in the frequency dependant MD plot of the intrinsic region (>10 kHz), thus confirming a similar dependence of MD on frequency as well as the applied magnetic field. Also, from Fig. 7(c), it is clear that the relationship between MD% and H is nearly quadratic in nature and can be explained in the framework of the Ginzburg–Landau free energy theory for the second order phase transition. This free energy expression can be used to determine the magnetic ordering effect on dielectric susceptibility. It was concluded that the magnetic ordering effect on a dielectric constant will be proportional to γM² (i.e., MD% ∼ γM²).⁴² Fig. 7(d) shows the linear variation of MD% with the square of magnetization (M²) for BFO, BGFO1 and BGFO2 samples which clearly emphasises that the MD effect emerges from the magnetoelectric coupling term ‘γP²M²’ obtained from free energy expression. From linear fitting, the absolute values of γ was calculated to be ∼0.35 (emu g⁻¹)⁻², ∼0.7 (emu g⁻¹)⁻² and ∼1.55 (emu g⁻¹)⁻² for BFO, BGFO1 and BGFO2 respectively.

3.6 Ferroelectric study

Since, BFO and Gd³⁺ substituted samples show room temperature MD effect, we expect the ferroelectric hysteresis behaviour for the same. Also, BFO has been reported to exhibit room temperature ferroelectric behaviour.^16,19 Fig. 8 shows P–E hysteresis loops of BFO, BGFO1 and BGFO2 samples at room temperature. No saturation in hysteresis curve could be obtained for all the samples up to the maximum applied electric field of ±40 kV cm⁻¹ which implies partial reversal of the polarisation. A clear yet unsaturated hysteresis curve is observed for BFO while the highest substituted sample (BGFO2) shows a slim P–E loop. In case of BFO, it has been reported that a lone s² pair of electrons of the Bi³⁺ ions hybridizes with 2p- orbital of O²⁻ ions and forms a localised lobe which leads to the non-centrosymmetric distortions and causes ferroelectricity.¹⁹ But with gradual increase in x content, we obtain slim P–E loops and decrease in remanant polarisation (2P_r) and coercive field (2E_c). This shows that the substitution has a significant effect on the ferroelectric property of the system which suppresses the Bi³⁺ ions lone s² pair effect. Moreover, the slim P–E loop in case of BGFO2 suggest a comparatively less insulating behaviour of the sample and this fact is also revealed from the increased value of tan loss in BGFO2 as compared to BFO. Though the main plot of Fig. 8 shows a slim P–E loop but a smaller hysteresis in P–E loop can be seen for BGFO2 sample as illustrated in inset of Fig. 8. For BFO remanant polarisation (2P_r) and coercive electric field (2E_c) are found to be 0.119 μC cm⁻² and 16.89 kV cm⁻¹ respectively while the values are 0.05 μC cm⁻² (2P_r) and 5.83 kV cm⁻¹ (2E_c) for BGFO1 and 0.009 μC cm⁻² (2P_r) and 1.17 kV cm⁻¹ (2E_c) for BGFO2.

Fig. 8 Room temperature polarization hysteresis (P–E) loops of BFO, BGFO1 and BGFO2 samples. Inset shows magnified P–E loop of the above samples up to a range of ±4.5 kV cm⁻¹.

4. Conclusion

We have investigated structural, magnetic, magnetodielectric and ferroelectric behaviour of Bi_2(1−x)Gd_2xFe₄O₉ (0 ≤ x ≤ 0.02) ceramics. XRD confirms the formation of well crystalized samples of orthorhombic phase along with the decrease in lattice parameters while Raman spectra depicts slight shifting of Raman modes to higher wave number due to partial substitution of Gd³⁺ at Bi³⁺-site. The temperature dependence of magnetization and dχ/dT plot shows a sharp AFM (T_N) transition which is found to increase with Gd³⁺ substitution i.e. from 250 K (BFO) to 256 K (BGFO2). The values of magnetization are found to increase rapidly towards lower temperature (T < 30 K) and is explained in terms of two sub-lattice mode model. Also, the magnetic measurements disclose the onset of weak FM along with AFM phase in the system for T < 30 K. Moreover, evidence of plausible magnetodielectric coupling in all the samples are observed from the concomitant anomaly realized in the temperature dependant dielectric and tan loss data around T_N. At room temperature, enhanced magnetodielectricity (MD) of ∼7% and ∼30% are determined for x = 0.01 and 0.02 respectively with respect to parent (BFO) sample. Further, frequency and field dependant MD at 300 K is studied to establish a strong coupling of dielectric and magnetic order parameters and both are found to obey power law of the form ∝exp(ω)ⁿ and ∝(H)^m respectively. Thus, we expect that the above striking features would make it a worthy candidate for various multifunctional device applications.

Acknowledgements

AKS acknowledges the Board of Research in Nuclear Science (BRNS), Mumbai (Sanction No. 2012/37P/40/BRNS/2145), UGC-DAE-CSR Mumbai (Sanction No. CRS-M-187, 225) and Department of Science and Technology (DST), New Delhi (Sanction No. SR/FTP/PS-187/2011) for funding. AKS acknowledges Dr P. Kumar for P–E loop measurement. Lastly, SRM is thankful to the BRNS for the financial assistance.

References

1. N. A. Hill, J. Phys. Chem. B, 2000, 104(29), 6694–6709.
2. W. Erenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759–765.
3. D. Khomskii, Physics, 2009, 2, 20.
4. N. A. Spaldin, S.-W. Cheong and R. Ramesh, Phys. Today, 2010, 63, 38.
5. H. J. Zhao, W. Ren, Y. Yang, J. Íñiguez, X. M. Chen and L. Bellaiche, Nat. Commun., 2014, 5, 4021.
6. K. Dey, A. Indra, D. De, S. Majumdar and S. Giri, ACS Appl. Mater. Interfaces, 2016, 8, 12901–12907.
7. C. Ederer and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 060401.
8. S. N. Tripathy, D. K. Pradhan, K. K. Mishra, S. Sen, R. Palai, M. Paulch, J. F. Scott, R. S. Katiyar and D. K. Pradhan, J. Appl. Phys., 2015, 117, 144103.
9. R. A. M. Gotardo, L. F. Cótica, I. A. Santos, M. Olzon-Dyonisio, S. D. Souza, D. Garcia, J. A. Eiras and A. A. Coelho, Appl. Phys. A, 2013, 111, 563–567.
10. A. K. Singh, S. Patnaik, S. D. Kaushik and V. Siruguri, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 184406.
11. J. Yong Park, J. Hwan Park, Y. Kyu Jeong and H. M. Jang, Appl. Phys. Lett., 2007, 91, 152903.
12. N. Niizeki and M. Wachi, Z. Kristallogr., 1968, 127, 173–187.
13. S. R. Mohapatra, B. Sahu, T. Badapanda, M. S. Pattanaik, S. D. Kaushik and A. K. Singh, J. Mater. Sci.: Mater. Electron., 2016, 27, 3645–3652.
14. I. Rousochatzakis, A. M. Lauchli and R. Moessner, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 104415.
15. A. K. Singh, S. D. Kaushik, B. Kumar, P. K. Mishra, A. Venimadhav, V. Siruguri and S. Patnaik, Appl. Phys. Lett., 2008, 92, 132910.
16. S. R. Mohapatra, B. Sahu, M. Chandrasekhar, P. Kumar, S. D. Kaushik, S. Rath and A. K. Singh, Ceram. Int., 2016, 42, 12352.
17. S. Sun, W. Wang, L. Zhang and M. Shang, J. Phys. Chem. C, 2009, 113, 12826–12831.
18. E. Ressouche, V. Simonet, B. Canals, M. Gospodinov and V. Skumryev, Phys. Rev. Lett., 2009, 103, 267204.
19. Z. M. Tian, Y. Qiu, S. L. Yuan, M. S. Wu, S. X. Huo and H. N. Duan, J. Appl. Phys., 2010, 108, 064110.
20. C. M. Raghavan, J. W. Kim, J. Y. Choi, J.-W. Kim and S. S. Kim, Ceram. Int., 2014, 40, 14165–14170.
21. S. Huang, L. R. Shi, Z. M. Tian, S. L. Yuan, C. M. Zhu, G. S. Gong and Y. Qiu, J. Solid State Chem., 2015, 227, 79–86.
22. M. G. Rozova, V. V. Grigoriev, I. A. Bobrikov, D. S. Filimonov, K. V. Zakharov, O. S. Volkova, A. N. Vasiliev, E. V. Antipov, A. A. Tsirlin and A. M. Abakumov, Dalton Trans., 2016, 45, 1192–1200.
23. R. Guo, L. Fang, W. Dong, F. Zheng and M. Shen, J. Phys. Chem. C, 2010, 114, 21390–21396.
24. P. Uniyal and K. L. Yadav, Mater. Lett., 2008, 62, 2858–2861.
25. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–67.
26. M. N. Iliev, A. P. Litvinchuk, V. G. Hadjiev, M. M. Gospodinov, V. Skumryev and E. Ressouche, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 024302.
27. A. Ubaldini and M. M. Carnasciali, J. Alloys Compd., 2008, 454, 374–378.
28. K. K. Mishra, A. K. Arora, S. N. Tripathy and D. Pradhan, J. Appl. Phys., 2012, 112, 073521.
29. P. Hermet, M. Goffinet, J. Kreisel and P. Ghosez, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 220102.
30. S. Chauhan, M. Kumar, S. Chhoker, S. C. Katyal and M. Singh, RSC Adv., 2016, 6, 43080–43090.
31. A. A. Zatsiupa, L. A. Bashkirov, I. O. Troyanchuk, G. S. Petrov, A. I. Galyas, L. S. Lobanovskii, S. V. Trukhanov and I. M. Sirota, Inorg. Mater., 2013, 49, 616–620.
32. A. P. Ramirez, Annu. Rev. Mater. Sci., 1994, 24, 453–480.
33. V. A. Khomchenko, V. V. Shvartsman, P. Borisov, W. Kleemann, D. A. Kiselev, I. K. Bdikin, J. M. Vieira and A. L. Kholkin, Acta Mater., 2009, 57, 5137–5145.
34. S. Blundell, Magnetism in condensed matter, Oxford University press Inc., New York, 1st edn, 2001.
35. P. Kumar, N. Shankhwar, A. Srinivasan and M. Kar, J. Appl. Phys., 2015, 117, 194103.
36. P. Tong, B. Kim, D. Kwon, T. Qian, S.-I. Lee, S.-W. Cheong and B. G. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184432.
37. S. Duhalde, M. F. Vignolo and F. Golmar, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 161313.
38. T.-J. Park, G. C. Papaefthymiou, A. J. Viescas, A. R. Moodenbaugh and S. S. Wong, Nano Lett., 2007, 7, 766–772.
39. P. Suresh, P. D. Babu and S. Srinath, Ceram. Int., 2016, 42, 4176–4184.
40. P. Uniyal and K. L. Yadav, J. Phys.: Condens. Matter, 2009, 21, 405901.
41. D. M. Evans, M. Alexe, A. Schilling, A. Kumar, D. Sanchez, N. Ortega, R. S. Katiyar, J. F. Scott and J. M. Gregg, Adv. Mater., 2015, 27, 6068–6073.
42. T. Kimura, S. Kawamoto, I. Yamada, M. Azuma, M. Takano and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 180401.

---