A bubble-based EMMS model for pressurized fluidization and its validation with data from a jetting fluidized bed
Abstract
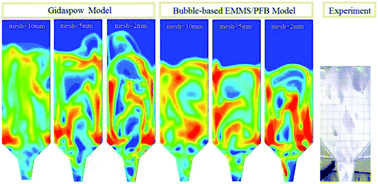
A bubble-based EMMS model for a Pressurized Fluidized Bed (PFB) was revised on the basis of an energy minimization multi-scale (EMMS) method. In the new revised model, in order to calculate the heterogeneous index accounting for the hydrodynamic disparity between heterogeneous and homogeneous fluidization, a bubble size correlation derived from experiments on a pressurized jetting fluidized bed with a conical distributor was introduced. With given operating pressure and gas superficial velocity, a heterogeneous index was calculated by integrating the bubble size correlation under elevated pressure with the EMMS model. The heterogeneous index, which decreased with the height above the distributor and also had its lowest lever when the mean voidage is in the range of (εmf, 1.0), was fitted into a surface and incorporated into Fluent as a user-defined function (UDF). The new bubble-based EMMS/PFB drag model was validated by predicting successfully the solid concentration distribution, the velocity of particles near the wall above the distributor, the radial profiles of particles' vertical motion and the average bubble size.

 Please wait while we load your content...
Please wait while we load your content...