Structure and property optimization of perfluorinated short side chain membranes for hydrogen fuel cells using orientational stretching

Abstract

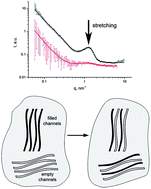
Small-angle neutron scattering has been applied to study the structure peculiarities of perfluorinated proton conducting polymer samples containing sulfonic groups of the Aquivion® type in dry and moistened conditions, which differ from Nafion® type membranes by the length of the side chains with sulfonic acid groups. The fine structure of the membranes is revealed, which is based on a system of regular proton conducting channels in the perfluorinated polymer matrix. The way this fine structure changes was determined as a function of the equivalent weight of the membrane, and the relation of these changes with proton conductivity value is established. The neutron contrast variation method enabled us to study the effect of orientational stretching on the fine structure. It was found that stretching is accompanied by an increase in proton conductivity due to changes in the fine structure of the channel system. Our investigations confirm that a reduction in the side chain length affects the fine structure of the perfluorinated proton conducting membranes, which is accompanied by an improvement in their performance in hydrogen fuel cells. Therefore, Aquivion® type systems will allow to reduce and possibly remove the existing operational restrictions of Nafion®.

---

Introduction

The investigations of the last decade have demonstrated that the categories of perfluorinated polymer membranes for hydrogen fuel cells can be ranked according to their operational properties due to side chain structural changes. Although DuPont has been responsible for the production of Nafion® with a certain length of functionalized side groups (long side chains, LSC) since 1972 and has taken the leading position, other materials with short side chains (SSC) with sulfonic groups at the end (Aquivion®) were introduced by the Solvay Solexis Company during recent years. The special interest in Aquivion® is associated with the possibility of extending the temperature range of operation in fuel cells. Specifically, SSC membranes achieve higher proton conductivity, which remains with an increase in temperature, while LSC membranes lose their conductivity when heated above 90 °C. The perfect proton conductivity value should be at the level of 0.1 S cm⁻¹, which is easily implemented in SSC membranes. The possibility of operating at higher temperatures close to 130 °C (thermodynamic critical temperature of hydrogen adsorption on a catalyst surface) allows the use of less pure hydrogen as fuel (with CO impurities), which leads to the contamination of catalysts at low temperatures.^1–4

The proton conductivity of Aquivion® type membranes is affected by their chemical structure (composition and nature of the polymer chain), water content, and morphology of the material. However, the influence of polymer structure features on their macroscopic properties, such as proton conductivity, remains unclear. Investigations of the structure and conductivity of model materials will provide insight into the proton transport mechanism and lead to optimization of next generation membranes for fuel cells.⁵

The additional factor causing interest in recent time, which affects proton conductivity, is the orientational one-direction stretching of these membranes. It is assumed that stretching can change the channel morphology making the channels straighter, thus leading to simplification of the proton paths in the membrane and an increase in proton conductivity along the stretching direction.^6–8

The main parameter of the composition of perfluorinated membranes is their equivalent weight (EW). EW is equal to the molecular weight of the polymer chain fragment per one sulfonic acid group and characterizes the concentration of sulfonic acid groups in the polymer volume. It is convenient to plot and analyze the dependences of the macroscopic and structural characteristics vs. EW, using a set of similar samples with different EW.

Experimental

The SSC samples in the present work were synthesized at the Boreskov Institute of Catalysis, St. Petersburg Department (Russia) via an original method of aqueous emulsion copolymerization.^1,3 As compared to the traditional solution method to obtain LSC Nafion® type membranes, the aqueous emulsion method has a number of advantages. Thus, this method provides a constant copolymer composition with a high degree of sulfonic monomer conversion. The emulsion method also yields perfluorinated proton conducting membranes (Nafion, Aquivion) with nanostructures different from the structures obtained by solution polymerization.^3,4 A feature of this method is the use of a special perfluorinated modifying additive (perfluorokerosene), which leads to samples with a higher EW. It was found that this additive also affects the molecular weight (MW) of the resulting polymer, by reducing it.

A series of SSC samples with different EW was prepared for the present work (Table 1), which was synthesized both without additive (higher MW) and with additive (lower MW). All samples were in the form of plain films with a 0.15–0.25 mm thickness in the dry state. Additionally, samples with orientational stretching were studied (Table 2). Stretching of the membranes was performed at a velocity of 1–2 mm min⁻¹, 180 °C and zero humidity. This mode of stretching was selected experimentally in order to prevent disruption of the membranes during stretching. The degree of stretching was specified by a certain time of stretching. After completion of the stretching procedure, the membrane sample was subjected to rapid cooling to room temperature to provide the conservation of the internal membrane structure.

Table 1 List of studied SSC samples without stretching

Sample	EW, g mol^−1 SO3H	Notes
SSC-5	769 ± 12	Synthesized without additive, higher molecular weight
SSC-1	787 ± 7
SSC-3	807 ± 7
SSC-7	780 ± 10	Synthesized with additive, lower molecular weight
SSC-2	810 ± 9
SSC-8	827 ± 7
SSC-9	830 ± 3
SSC-6	870 ± 8
SSC-4	1021 ± 21
SSC-10	1205 ± 15

---

Table 2 List of studied SSC samples with stretching

Sample	Stretching degree	EW, g mol^−1 SO3H	Notes
SSC-5	200%	769 ± 12	Synthesized without additive, higher molecular weight
SSC-1	150%	787 ± 7
	200%
SSC-3	100%	807 ± 7
	200%
SSC-7	100%	780 ± 10	Synthesized with additive, lower molecular weight
	150%
	200%
	300%
SSC-2	100%	810 ± 9
	200%
SSC-6	200%	870 ± 8
SSC-4	100%	1021 ± 21
	200%
	300%

---

The EW of the samples was determined by the titration method, according to the value of the ion-exchange capacity (IEC), which is proportional to the amount of ionic sulfonic acid groups.⁹ EW is reciprocal to IEC (EW = IEC⁻¹).

The proton conductivity and the maximum water uptake of the samples were also measured.

Proton conductivity was measured by impedance spectroscopy at 20 °C in the equilibrium state of saturation with water after boiling at 100 °C for 1 h. A Z-3000X impedance meter (Elins, Russia) using a cell with stainless steel electrodes in the four-electrode scheme in the frequency range 10–150 000 Hz was used.

The maximum water uptake was defined according to the weight of saturated samples, W_w, after boiling in water at 100 °C for 2 h compared to the weight of dried in vacuum membranes at 70 °C to a constant weight, W_d.¹ Water uptake, C_w, was calculated as follows: C_w = (W_w − W_d)/W_w × 100%.

Small-angle neutron scattering (SANS) was used for the structure determination of 6 standard (initial) SSC samples (SSC-1–SSC-6) and 3 samples with orientational stretching: SSC-3 and SSC-2 stretched at 100% (2 times stretching) and SSC-6 stretched at 200% (3 times stretching).

Small-angle neutron scattering (SANS) experiments were carried out at the “YuMO” facility^10,11 (Joint Institute for Nuclear Research, Dubna, Russia) in the range of momentum transfer q = (4π/λ)sin(θ/2) = 0.06–10 nm⁻¹, where θ is the scattering angle, and the neutron wavelength λ = 0.05–0.8 nm. The q-range allows structure peculiarities to be found at the scale of ∼2π/q ∼ 1–100 nm. Samples were packed in several layer stacks for measurements to obtain optimal scattering intensity. The measured scattering curves (scattering intensities, I vs. momentum transfer, q) were calculated by normalization to samples thicknesses and to vanadium measurements, which were used as a standard for absolute intensity calibration in the program SAS package.¹² Four samples (SSC-1–SSC-4) were also measured and analyzed earlier at other SANS facilities with a lower resolution,¹ however the present work improves their structural parameters and complements them with 2 new samples (SSC-5 and SSC-6). All samples were studied in air-dry condition (dry series) and saturated in H₂O (H series). SANS measurements of samples saturated in D₂O (D series) were also carried out. The use D₂O allows the nuclear contrast sample-environment (polymer–water) to be changed and in some cases identify additional structural features. Samples were wrapped in aluminum foil, which is transparent for neutrons and prevents saturated samples from drying during measurements, and measured at 20 °C. Test measurements of several samples at 80–110 °C showed insignificant differences in the scattering curves and structural parameters obtained at 20 °C. Thus, the structural features measured at the low temperature of 20 °C may be considered as coincident with those obtained at high temperatures close to the operating mode for membranes in fuel cells.

Results and discussion

Proton conductivity

To match the neutron scattering data for membranes in the H and D states, the proton conductivity was determined for H₂O-saturated membranes along with deuterium conductivity at saturation with D₂O. Deuteron conductivity was measured after saturation in D₂O for 1 h, without heating.

Fig. 1 shows conductivity in H₂O and D₂O as a function of the EW of the sample. The optimal range of EW, in which the conductivity remains high, is 750–900 g mol⁻¹ SO₃H. The conductivity in D₂O for all the membranes is 60–70% of the proton conductivity in H₂O (inset in Fig. 1), except the SSC-4 sample with an EW of 1021 g mol⁻¹ SO₃H (the largest EW for which both conductivities were measured). This supports the conductivity mechanism associated with charge mobility, which according to the authors^13,14 is a superposition of two components: (1) slow Stokes proton diffusion in the composition of the hydronium ion H₃O⁺ and (2) fast hopping of protons across a network of hydrogen bonds between adjacent water molecules by the Grotthus mechanism. Our results demonstrate that the conductivity is mainly associated with the rapid Grotthus mechanism, which in the case where hydrogen is replaced by deuterium significantly slows down and reduces the charge carrier velocity. The Stokes diffusion of H₃O⁺ and D₃O⁺ differs insignificantly; therefore, it can only give a small contribution to the conductivity mechanism. The more rapid decline of deuteron conductivity for the SSC-4 sample with a large EW is apparently associated with the lower water uptake for this sample, which can cause a difference in the velocities of proton and deuteron transmission. Also the deuteron conductivity value for all the samples can be influenced by the absence of the necessary conditions to obtain maximum conductivity (no boiling in D₂O was performed). Our preliminary estimates show that this can reduce the resulting conductivity by 5–10%, and the influence on the samples with different EW can be also different. However, it does not qualitatively affect the results. Generally it was found that the conductivity in D₂O is significantly lower and is 60% of the average proton conductivity in H₂O.

Fig. 1 Proton and deuteron conductivity of membranes with different EW, saturated with H₂O and D₂O. The inset shows the conductivity ratios.

The proton conductivity upon stretching changes, depending on the direction and the degree of stretching. Fig. 2a shows an example of the changes in conductivity after stretching for the four samples. Conductivity measured along the stretching direction increases, and in the cross direction decreases. Most of the samples show a small effect at 100% elongation (twice), however significant changes are observed for larger degrees of stretching. Fig. 2b shows an increase in conductivity along the stretching direction by 200% and decrease across the direction of 200% stretching, depending on the EW.

Fig. 2 (a) Proton conductivity of membranes depending on the degree and direction of stretching. ▲ – conductivity along the stretching direction and ▼ – across the stretching direction. (b) Proton conductivity of the initial and 200% stretched membranes, depending on their EW. The conductivity of the initial membranes is shown in black, and the conductivity of the stretched membranes measured along the stretching direction is red and across the stretching direction is green.

Water uptake

Saturation in light and heavy water demonstrates that no abnormalities in H₂O to D₂O replacement occur (Fig. 3). The maximum uptake of D₂O for the majority of samples is almost identical with the uptake of H₂O, which allows an adequate comparison of the structure of membranes moistened in light and heavy water.

Fig. 3 Maximum water uptake for the membranes saturated with H₂O and D₂O, depending on their EW.

It should be noted that sample saturation for SANS measurements was performed by simple immersion in light or heavy water at room temperature for at least 1 h. These conditions allowed a certain equilibrium water saturation level to be achieved, which turned out to be significantly less than the maximum water uptake (Table 3). The saturated samples were compared with samples in air-dry conditions (dried in air, without heating under vacuum), which may contain up to 5% bound water, which also reduces the estimated water uptake level. It is interesting to note the effect of stretching the membranes on their water uptake. The SSC-3 and SSC-2 samples, which were stretched at 100%, did not lose their water uptake compared to the initial membranes, whereas the SSC-6 sample, which was stretched at 200%, significantly lost its ability to absorb water. These results are in good agreement with the changes in proton conductivity, which slightly varies at 100% stretching, and changes significantly at 200% stretching.

Table 3 Water saturation level for the samples studied by SANS

Sample	Max. water uptake, not stretched	Water uptake for SANS, not stretched	Water uptake for SANS, stretched
SSC-5 H	76.8%	36.4%	—
SSC-5 D	68.8%	37.5%	—
SSC-1 H	72.3%	38.9%	—
SSC-1 D	69.0%	40.9%	—
SSC-3 H	50.8%	33.0%	35.0%
SSC-3 D	47.0%	34.9%	36.7%
SSC-2 H	50.1%	32.7%	31.8%
SSC-2 D	47.7%	34.8%	33.7%
SSC-6 H	39.1%	30.4%	20.7%
SSC-6 D	43.7%	31.3%	14.4%
SSC-4 H	35.7%	18.1%	—
SSC-4 D	32.2%	15.5%	—

---

Small-angle neutron scattering

The SANS curves for the initial non-stretched samples are shown in Fig. 4. As discussed below, neutron scattering in membranes occurs due to significant nuclear contrast between the polymer and vacant volume within the polymer matrix (cavities and channels), which can be filled with light or heavy water, and this changes the degree of contrast relative to the polymer. Thus, comparison of the data in these cases allows the number and geometric properties of the conducting channels filled with water to be discussed.

Fig. 4 SANS curves for initial non-stretched samples in dry (a), H (b) and D (c) conditions. Points are experimental data, and curves are the fitting results.

The measured SANS curves are well approximated by the model scattering function (1), which is also used to describe the membranes structure:¹

The squared form factor in this model, , generally describes curved and branched cylindrical channels (cylinder squared form factor is ), with a cross-section radius, R_g (channel diameter is ), much less than the channel length, R_g ≪ L. Such asymptotic approximation is valid in the momentum transfer range 1/L ≪ q ≤ 1/R_g for the form factor of structures, which geometry is defined by the fractal index, n.^15,16 The value of n = 1 corresponds to straight cylinders, 1 < n < 2 means bent cylinders, n = 2 characterizes statistically bent tubes, similar to Gaussian polymer chains, and 2 < n < 3 means branched structures. The parameter I₀ characterizes the intensity of forward scattering, depending on the scattering ability of the structural elements.

The structure factor in model (1), , describes the pair spatial correlations of channels at several (k) characteristic distances, R_i. The coefficient C_i is the average number of channels correlating with the selected channel at the distance R_i, and B is a constant (incoherent background scattering).

The number of correlation distances, k, published earlier¹ was 3–4. The present work reports on an expanded q-range and improved data statistics, which allow more precise structure data to be obtained. Due to this fact the number of correlating distances is extended and is k = 5–6 for dry samples (dry series), and for the samples saturated with light and heavy water (H and D series, respectively) k = 4–6 and k = 3–4, respectively. The obtained sets of correlation distances correspond to the measured scattering curves details. Fig. 5 shows an example analysis for the SSC-4 dry membrane. The correlations at i = 2, 5 and 6 are positive, R₂ corresponds to the ionomer peak observed on the curve and characterizes the ordered structure at the distance R ∼ 2π/q ∼ 3–5 nm, and R₅ corresponds to the additional peak or knee at the lower q-range and describes the scale of crystalline areas of ∼20 nm. Several samples also display other larger scale correlations between channels, in which R₆ ∼ 30–35 nm. The correlations at i = 1, 3 and 4 are negative and show the forbidden zones, which are the distances the neighbouring channel cannot occupy. The entire approximation results are shown in the tables in the ESI material.†

Fig. 5 Interpretation of the structural factor parameters of the fitting model (1) on the example of the SSC-4 dry sample.

The most important are the following structural parameters: R_g – gyration radius, which indicates the diameter of individual channels, n – fractal index as a measure of channel morphology and R₂ – the correlation distance between adjacent channels. Also the parameter R₅ should be mentioned and associated with the C₅ coefficient, which shows the degree of sample crystallinity. These parameters are analyzed below depending on the EW of the samples in the dry and H₂O-saturated states. D₂O-saturation leads to a reduction in scattering ability in SANS due to a reduction in the nuclear contrast between the polymer and water, however, the obtained parameters are generally similar to that found for the H₂O-saturated membranes. Therefore, isotopic substitution in water molecules does not affect their interaction with the polymer, which is already a known fact for fluorinated membranes. D₂O-filled channels present weaker contrast to areas of crystallinity in membranes, which results in a reduced k number for the D samples. Additionally, on the scale characterized by the ionomer peak, these parameters are similar to the values obtained for the H membranes. Therefore, it is of special interest to compare the parameters of the dry and H₂O-saturated membranes.

The gyration radius, R_g, in all the dry membranes is 0.2–0.35 nm (channel diameter is = 0.55 ÷ 1.0 nm). The change in R_g after humidification (dynamicity of channels) is approximately the same for all the studied samples, and an increase in R_g by 2.0–2.5 times is observed with a result of 0.5–0.7 nm (diameter 1.4–2.0 nm).

Along with this tendency, a reduction in the cross-size of channels with an increase in EW is observed (Fig. 6). This can be rationally explained by the fact that a higher EW corresponds to a lower amount of sulfonic groups in the polymer bulk, since they are on the inner surface of the channels. As a result, a lower amount of sulfonic groups leads to the formation of thinner channels in the dry state. Saturation with water enhances this effect since the samples with a larger EW absorb less water.

Fig. 6 Cross gyration radius of the channels in the dry and moistened membranes depending on their EW.

It should be mentioned that the opposite effect occurs for molecular weight on the cross dimension of the channels. A lower MW, which results when a modifying additive is used in the synthesis, leads to some expansion of the channels. This is probably due to the lower melt viscosity at a lower MW, and the channel system in the membrane being formed faster and more effectively than at higher MW when the polymer melt is too viscous, and thus channel formation is slow. The effect of polymer inertia with a higher MW is also known for polyethylene.^17–20

The distance between adjacent channels is similar in all the dry samples, in which R₂ ∼ 3.5 nm, and corresponds to the position of the ionomer peak on the SANS curves, q ∼ 2 nm⁻¹ (Fig. 7).

Fig. 7 Distance between adjacent channels in the dry and moistened membranes depending on their EW.

SANS on the moistened membranes caused a shift in the ionomer peak to a lower momentum transfer, q ∼ 1.2–1.5 nm⁻¹, which means that there was an increase in the distance between channels to R₂ ∼ 4.4–5.2 nm due to the larger elasticity of the wet membranes. The R₂ scale in humidified membranes tends to decrease with an increase in EW by reducing their water uptake. Thus, on the 5 nm scale, all the studied samples look similar to each other and consist of an ordered channel system in the polymer matrix. Noticeable changes are observed only for the channel diameter, depending on the EW and MW of the polymer. However, the parameter n, which describes the channel geometry on a scale up to 100 nm, varies considerably (Fig. 8). The values of n for the dry and moistened membranes demonstrate the growth trend with EW increasing for samples with different MW, which can be seen directly from the scattering curve profiles. The dry samples with the lowest EW (SSC-5 and SSC-2) result in lower intensity SANS curves with the lowest slopes (Fig. 4a). Upon moistening, the parameter n increases for all the samples. The inset on Fig. 8 shows the ratio of n of the humidified and dry samples, which is larger than unity for all the samples. Therefore, swelling of the membranes results in complicated channel structures, which become more curved and branched.

Fig. 8 Parameter n for the dry and moistened membranes depending on their EW. Inset shows the ratio of n_H/n_dry for the moistened and dry samples.

Apparently, the structure of the dry samples contains unopened channels, which are not observable in SANS. These channels, since they are filled with water, obtain volume and become visible. Thus the membrane structure becomes more complicated.

Additional attention should be paid to the behaviour of the ratio n_H/n_dry for samples with low and high MW, which are synthesized with or without additive (Fig. 8, inset). In both cases the increase in EW prevails over the decrease in n_H/n_dry, i.e. at a higher EW the effect of the change in channel geometry becomes weaker. This is a natural fact, because an increase in EW entails a reduction in water uptake. It is also interesting to note that the observed dynamic range of n_dry = 1.23–2.1 (n_max/n_min ≈ 1.7) declines after saturation with water, to become n_H = 1.82–2.6 (n_max/n_min ≈ 1.4). A weakening of the structural differences between the samples upon moistening is observed.

In addition to affecting the channel geometry an increase in EW leads to enhanced polymer chain ordering and packing density (crystallinity) in nanoscale domains. Areas of reduced density and free volume (channels) between the polymer chains exist, which are separated by a typical domain diameter distance. These areas correspond to the local maximum at q ∼ 0.3 nm⁻¹ on the SANS curves, which corresponds to the correlation distance R₅ ∼ 2π/q ∼ 20 nm. This type of structuring is consistent with the results published by other authors.²¹ The parameter C₅ is a measure of coherence in scattering on such structure of dense and sparse areas on a specified scale, which is better expressed at a higher EW (Fig. 4). The effect of enhancing the crystalline trends in the dry samples is better expressed at a lower MW of the polymer. The effects of structure ordering are less noticeable upon saturation of the membranes with water, which leads to total amorphization of the samples, as evidenced by a decrease in the C₅ parameter (Fig. 9).

Fig. 9 Parameter C₅ for the dry and moistened membranes depending on their EW.

Stretching effect in SANS

To determine the structure changes under stretching, three samples stretched in one direction were examined via SANS: SSC-3 and SSC-2, which were stretched by 100% (2 times) and SSC-6, which was stretched by 200% (3 times). The “YuMO” spectrometer used in these initial experiments allowed the distribution of scattered intensities as a function of the scattering vector module (momentum transfer) to be obtained, which is averaged data over all possible angles between the stretching direction axis and the scattering vector. Measurements on the 2D-detector are also planned with the analysis of scattering cross sections anisotropy in the plane of the scattering vectors.

A comparison of the measured SANS curves for the initial and stretched membranes, dry and moistened in light and heavy water, are shown in Fig. 10 and 11. The stretched samples scattering data are also adequately described by model (1). Comparison of the key structure parameters for the initial and stretched samples is shown in Table 4.

Fig. 10 SANS curves for the stretched samples SSC-3 and SSC-2 (red, 2 times stretching) compared to the initial non-stretched samples (black) in dry (a and d), H (b and e) and D (c and f) conditions. Points are experimental data, and curves are the fitting results.

Fig. 11 SANS curves for the stretched sample SSC-6 (red, 3 times stretching) compared to the initial non-stretched sample (black) in dry (a), H (b) and D (c) conditions. Points are experimental data, and curves are the fitting results.

Table 4 Comparison of the key structural parameters for the initial and stretched samples

Sample	n		Rg, nm		R2, nm
	Initial	Stretched	Initial	Stretched	Initial	Stretched
SSC-3 dry	2.1	1.83 ± 0.15	0.21 ± 0.04	0.34 ± 0.04	3.53 ± 0.08	3.58 ± 0.20
SSC-3 H	2.4	1.87 ± 0.29	0.536 ± 0.007	0.71 ± 0.05	4.73 ± 0.03	5.06 ± 0.06
SSC-2 dry	1.23 ± 0.08	1.31 ± 0.13	0.291 ± 0.019	0.328 ± 0.027	3.534 ± 0.025	3.51 ± 0.04
SSC-2 H	1.90 ± 0.10	1.8 ± 0.4	0.652 ± 0.019	0.74 ± 0.06	4.80 ± 0.03	5.01 ± 0.07
SSC-6 dry	1.69 ± 0.15	1.70 ± 0.16	0.33 ± 0.04	0.38 ± 0.09	3.56 ± 0.06	2.5
SSC-6 H	2.07 ± 0.14	1.66 ± 0.08	0.682 ± 0.026	0.496 ± 0.017	5.12 ± 0.03	3.82 ± 0.04

---

Comparison of the SANS curves of the initial and stretched samples in dry and H conditions shows that with 100% stretching (SSC-3 and SSC-2 samples) the structure does not change much, and the scattering curves are almost identical. The ionomer peak position remains the same or slightly shifts to a smaller q, which means a small increase in the distance between adjacent channels. The dry samples demonstrate some additional ordering after stretching (a slight increase in the scattering density is observed).

200% stretching (SSC-6 sample) in dry and H conditions leads to significant changes in the structure, and the ionomer peak is shifted to a larger q, which demonstrates the convergence of adjacent channels. At the same time, an additional local maximum at a lower q (matrix knee, which characterizes the crystallinity on the scale of the typical distance between channel bands) is also moved to a larger q.

Thus it should be concluded that 200% stretching for the averaged orientation axis in the scattering vector plane leads to a reduction in the distances between the characteristic structural elements observed in the whole scale of distances, whereas 100% stretching leaves these structural features substantially unchanged. At the same time, the gyration radius of the individual channels, R_g, significantly increases after 100% stretching, especially for the SSC-3 sample, according to fitting results in Table 4. Further stretching (200% for SSC-6 sample) causes R_g in the dry condition to become quite close to its value for the initial sample. However R_g in the H state is considerably reduced due to a reduction in the amount of absorbed water after stretching. The parameter n has a tendency to decrease upon stretching, which corresponds to channel straightening.

It can be concluded that the fist stretching step makes the channels wider and more straight, while the distance between channels remains unchanged, and more extended ordering associated with crystallinity also remains. Further stretching makes the channels more narrow, similar to their initial values and become closer, as well as the bundles of channels between crystalline areas (Fig. 12).

Fig. 12 Proposed consequential change in channel morphology under stretching: 1 – initial membrane, 2 – 100% stretching, and 3 – 200% stretching.

SANS on the membranes in the D condition shows an intriguing effect. The observed scattering intensity distributions upon stretching differ greatly for the polymers with different MW. In the case of the SSC-2 and SSC-6 samples with a lower MW due to the use of a modifier during polymerization, heavy water saturation leads to the fact that the ionomer peak in the SANS curves becomes hardly noticeable for the stretched samples, whereas it remains very pronounced for the same samples in the initial non-stretched state (Fig. 10f and 11c). At the same time, in the SSC-3 sample with a larger MW (synthesized without any modifying additive), the ionomer peak is observed in all cases, including heavy water saturation for the stretched sample.

As shown above, isotopic substitution does not affect the water content in the swollen samples. The conductivity profiles in these cases, depending on EW, are also almost the same. Thus, it can be concluded that the distribution of light and heavy water inside the membranes does not vary. Therefore, the effect of the ionomer peak disappearing may be associated only with the peculiarities of the channel contrasting being filled with light or heavy water, taking into account the specifics of the internal structure of the membranes with different MW.

Ionomer peak discussion

The ionomer peak in SANS and small-angle X-ray scattering (SAXS) curves is an interesting feature of various ionomers. It is typically associated with the distribution of ionic group multiplets (0.3–1.3 nm size) at typical distances (2–9 nm), since these polar groups are segregated in the nonpolar polymer environment.²²

Several cases that describe the disappearance of the ionomer peak for various ionomer systems, including perfluorinated membranes, are known. As an example, the ionomer peak is not observed for the free acid form of hydrocarbon copolymers, but exists in the sulfonic acid form of fluorocarbon ionomers.

Deformation studies of the ethylene cesium carboxylate ionomer showed azimuthal dependence of the X-ray peak position on sample elongation.²³ This relationship was explained by a lamellar intracluster scattering model, and a spherical intracluster model can also be used.

The ionomer peak in SANS for the Cs methacrylate/ethylene ionomer disappears when it is saturated with water.²⁴ However Cs sulfonate/ethylene displays the ionomer peak. The peak disappearance in ethylene/carboxylate samples was interpreted as the decay of cluster ordering after saturation with water,^24,25 although the ionic groups were stored in a separate phase. The evident retention of order for the ethylene/sulfonate ionomer may be due to the fact that sulfonic acid is much stronger than carboxylic acid. Shifting of the ionomer peak to a smaller q at a high water content may occur due to ionic phase rearrangement. At a water content above 30%, the peak may be a result of scattering interference from random distributed water spheres.²⁶ The authors²² demonstrated by SAXS and SANS, peaks corresponding to Bragg distances of 3–9 nm with a variation in the proportion of ionic groups and the amount of retained water in polypentenamer sulfonate. At a high content of ionic groups in the dry sample, SANS peaks were not observed due to low contrast, however they appeared after the addition of D₂O, and shifted to smaller q values with an increase in D₂O content.²² The absence of the ionomer peak in the dry state is attributed to the formation of a two-phase system, in which ionic groups exist in a separate phase, and the scattering intensity depends on the contrast of Cs-sulfonic groups and amorphous polypentenamer chains. The addition of D₂O molecules increases the contrast.

The effect of no SAXS peak in dry Nafion® membranes and the appearance peaks upon moistening has also been recorded.²⁷ According to²⁸ ionic clusters of a small size with a small number of ionic groups may also exist in the dry membrane (Nafion®-117, annealed at 100 °C under vacuum). When water is removed, the cluster size is reduced, since they are formed by close spaced sulfonic groups. Disappearance of the ionomer peak in this case occurs due to the decrease in the ion clusters volume fraction and increase in the distances between them.²⁷

A temperature effect on the SAXS data is known for ionomers based on sulfonated copolymers (ethylene-co-propylene-co-ethylidene norbornene) with zinc stearate inclusions.²⁹ The ionomer peak in SAXS disappears above 190 °C, which is explained by the dissolving of ion aggregates in the polymer matrix (transition from order to disorder). It is shown that ionomers with a Zn salt have an aging effect, where the peak increases within 20 days, which characterizes ordering, and increase in ionic aggregates with aging.³⁰

The closest effect to our situation is SANS data describing the change in membrane morphology upon swelling of the block copolymer poly(sulphonate phenylene)-b-poly(arylene ether ketone).²¹ The dry and swollen in D₂O membranes are compared, and it is found that the dry sample demonstrates a lower scattering intensity because of the low contrast between the polymer components. The scattering intensity in small q-range increases according to the law ∼q⁻² (lamellar structure), and then ∼q⁻⁴ (Porod's law). A small ionomer peak characterizes the average distance between ionic sulfonic clusters randomly distributed along the polymer chain. The crystalline peak in the intermediate q-range is not observed for the dry membrane. After saturation with D₂O, the scattering intensity increased (except for a larger q) due to the increased contrast in the scattering between the hydrophobic regions and areas filled with water. The ionomer peak in the saturated membrane becomes more pronounced. Additionally a strong maximum appears at an intermediate q due to the formation of hydrogenated areas and microphase separation. At a lower q the curve profiles still correspond to a lamellar structure.²¹

The polymers described in ref. 21 are amorphous–crystalline. Typically such polymers with a low degree of sulfonation show two scattering peaks in SANS (as in the case of Nafion®), which corresponds to ionomer and crystalline domains. Part of the crystalline areas decreases with an increase in the degree of sulfonation, and as a result, the membranes become more amorphous (second peak in SANS disappears), which is confirmed in the present work. A decrease in the crystalline peak is observed with a decrease in EW.

Obviously, the membrane structure should be independent of the isotopic content of water (H₂O or D₂O). Therefore, an appropriate model should give similar results at any contrast. Membranes swollen in H₂O/D₂O mixtures at different ratios were also studied.²¹ At 50% D₂O, the ionomer peak almost disappears, which means that the scattering length density of the hydrophobic blocks becomes equal to that of the hydrophilic parts. Calculations of the scattering length densities confirm their match for the used H₂O/D₂O mixture and hydrophilic part of the copolymer, without taking in account ionic solvation groups.^21,31 A similar effect was observed for the intermediate q-range with a crystalline peak, which was described by the hard sphere (HS) model.²¹ Partially saturated membranes compared to the fully swollen samples have the same peak position. This fact not only confirms the validity of the HS-model for the studied systems, but also suggests that other possible periodic models (lamellar and cylindric) are not valid to describe the crystalline peak, since the peak position in these models should be shifted with a change in water content.²¹ However this is contrary with our results for SSC perfluorinated membranes (peak position shifts), which confirms the correctness of using the cylindrical model for our case.

Thus the disappearance of the ionomer peak has been observed in numerous ionomer systems under various conditions and is usually interpreted as a decrease in the degree of ordering in the sample.

In our case, in the interpretation of the data it should be considered that the samples were saturated by simple immersion in water for SANS measurements, which does not provide maximum saturation, i.e. moistened membranes contain both water-filled channels and dry channels, in which water does not penetrate upon simple immersion. This situation is not unique. Measurements of proton conductivity by the cantilever of an atomic force microscope have shown that Nafion® has vast non-conductive areas, which means that some of the channels are unavailable for water.³²

It is important in neutron scattering experiments that wet and dry channels have different signs of nuclear contrast, ΔK (difference in the coherent neutron scattering lengths densities). Dry membranes contain only one type of object (dry pores with surfaces covered with sulfonic acid groups). Calculations according to the known coherent scattering lengths of the elements show that the contrast factor for dry channels is ΔK_dry = −4.57 × 10¹⁰ cm⁻².

Channels filled with light water have a slightly higher contrast factor, ΔK_H = −5.129 × 10¹⁰ cm⁻². Therefore in the case of light water, saturated dry and wet channels do not compensate each other upon interference from scattered waves from neighbouring channels. Thus the ionomer peak remains.

If heavy water is used to fill the channels, the contrast factor between the wet channels and the polymer is positive: ΔK_D = 1.80 × 10¹⁰ cm⁻². The interference of the scattering on the adjacent channels (dry and containing D₂O) with different signs of contrast may lead to possible weakening of the scattering in the area of the ionomer peak. Stretching of the membranes is able to enhance the effect of interference and suppression of scattering due to unaxial channels orientation, i.e. a more ordered mutual channel arrangement.

Besides, stretching leads to rearrangement of the water domains in the membrane, as shown in Fig. 13. The initial samples have pores that can be filled with water and areas inaccessible to water. Stretching may break the connections between channels and form new connections, which will result in closure of some previously available water channels and opening of some inaccessible channels, which greatly modify the membrane structure. It can be assumed that large closed areas will split into a system of smaller tight areas, surrounded by opened channels. Thus the resulting structure will consist of a neighbourhood of empty and filled channels, which is not observed in the initial non-stretched sample. Such mixing will lead to the disappearance of the ionomer peak due to the interference of scattering on the channels with different signs of contrast, which makes a negative contribution to the total scattering intensity of the entire channel system.

Fig. 13 Schematic of channel adjustment under stretching. In D₂O: ΔK_D = 1.80 × 10¹⁰ cm⁻² and ΔK_dry = −4.57 × 10¹⁰ cm⁻². These values have different signs, and may be compensated at the interference. In H₂O: ΔK_H = −5.129 × 10¹⁰ cm⁻² and ΔK_dry = −4.57 × 10¹⁰ cm⁻², which are close values of the same sign, thus compensation in scattering is impossible.

It is obvious, that this effect of plastic cleavage of closed areas works best for low MW polymers (SSC-2 and SSC-6), in which the chains in the sample volume are less mixed and plastic deformation occurs easily. The SSC-3 sample with a larger MW is expected to preserve its original system of opened and closed pores.

The fact that the peak in the stretched sample SSC-3, which is saturated with H₂O, is well observed, confirms the partial preservation of the contrast ratios when dry channels do not compensate scattering on wet channels, which is the same as in the initial sample without deformation.

Polymers with a high MW are obviously more inert to stretching, which does not allow the channels to easily open and close, whereas a low MW may contribute to more structural changes under stretching.^17–20 According to the authors,³³ high MW SSC membranes lead to greater aggregation of the fluorocarbon chain to reduce the bending of the chains during the formation of phase-separated structures, which result in larger, more elongated water domains. Thus the copolymers with a higher MW have hydrophilic areas (channels) that are more extensive and more resistant to external influences such as stretching.

It is necessary to consider another possible cause of the decrease in neutron scattering length density, which results in the loss of the ionomer peak. The authors²¹ examined ionomers, where the peak disappears in H₂O/D₂O mixtures of certain ratios to compensate the scattering on the polymer matrix, while saturation of pure H₂O or D₂O makes no compensation with a clearly observed ionomer peak.

In our case, the stretched SSC membrane peak disappears in pure D₂O, however, taking in account the deformation processes discussed above, which lead to the closure of some old channels and possibility of new channels opening, we also cannot exclude the possibility of incomplete saturation of channels with heavy water. Thus at a filled volume fraction, X, the zero contrast condition between this volume and the polymer matrix is given by the equation, XK_D = K_P, where K_D = 6.37 × 10¹⁰ cm⁻² and K_P = 4.57 × 10¹⁰ cm⁻² are coherent scattering length densities for heavy water and the polymer, respectively. Hence the degree of filling the channels with heavy water is X ≈ 72%. Obviously, the situation of partially filled fine channels of water migration may be realized in deformed membranes, which leads to a weakening of the ionomer peak in SANS.

Conclusions

The investigated membranes generally exhibit similar structures, ordered systems of nanoscale channels. The differences between the samples are manifested in the degree of crystallinity and in the ordering on the scale of the distances between channel bundles, which correspond to the matrix knee on the scattering curves at q ∼ 0.3 nm⁻¹, and these differences correlate with the equivalent weight of the polymers.

The most ordered sample, SSC-4, has the largest EW, whereas the least ordered samples, SSC-5 and SSC-1, have the lowest EW. Thus we can consider that an increase in EW increases the correlations and ordering between channel bundles on the scale of ∼20–30 nm. However, a high EW is accompanied by low proton conductivity (the SSC-4 sample as an example). This should be taken into account in selecting a membrane for practical use in fuel cells.

Under orientational stretching, an additional ordering is observed in the form of convergence of adjacent channels, with which the increase in proton conductivity along the stretching direction should be associated. This effect is well defined at 200% stretching, however 100% stretching makes weak effect.

It was found that the conductive channels upon stretching were firstly extended (100% stretching), then became narrow again (200% stretching), which confirms the conclusion¹ that thinner channels contribute to better proton conductivity. Thus two useful factors, reducing the channels thickness and increasing the proton conductivity (the use of short side chains instead of long chains and aqueous emulsion polymerization) are complemented by a third factor, the use of orientational stretching. However, the observed decrease in water content after stretching means the closure of some channels which become inaccessible to water filling.

The effect of the ionomer peak disappearing for some of the stretched samples in D₂O, taking into account various contrast factors for dry and water-filled channels, shows that at the first step of orientational stretching, when water uptake is not reduced, a rearrangement of the opened and closed water channels is observed. Some of the opened channels become closed and a part of the closed channels is opened, i.e. the system of channels becomes mixed, where dry channels adjoin the channels filled with water. This effect is displayed only in membranes with a lower molecular weight. A higher MW contributes to structural preservation under stretching due to greater inertia. Further stretching of the membranes with a lower MW causes water uptake decrease, which means a reduction in the number of cavities, available for water. Generally, orientational stretching causes an increase in proton conductivity in the stretching direction, which is a positive factor for the performance of membranes in fuel cells.

Acknowledgements

The authors are grateful for support by Russian Foundation for Basic Research (grant No. 14-23-01015 ofi_m), and Joint Institute for Nuclear Research staff for SANS measurements assistance.

Notes and references

1. Y. V. Kulvelis, S. S. Ivanchev, V. T. Lebedev, O. N. Primachenko, V. S. Likhomanov and G. Török, RSC Adv., 2015, 5, 73820.
2. S. S. Ivanchev, O. N. Primachenko, S. J. Khajkin, V. S. Likhomanov, V. G. Barabanov and A. S. Odinokov, RU Patent 2545182, 2015.
3. S. S. Ivanchev, V. S. Likhomanov, O. N. Primachenko, S. Y. Khaikin, V. G. Barabanov, V. V. Kornilov, A. S. Odinokov, Y. V. Kulvelis and V. T. Lebedev, Pet. Chem., 2012, 52, 453.
4. Y. V. Kulvelis, V. T. Lebedev, V. A. Trunov, O. N. Primachenko, S. Y. Khaikin, D. Torok and S. S. Ivanchev, Pet. Chem., 2012, 52, 565.
5. L. Rubatat, Z. Shi, O. Diat, S. Holdcroft and B. J. Friske, Macromolecules, 2006, 39, 720.
6. E. Allahyarov and P. L. Taylor, J. Phys. Chem. B, 2009, 113, 610.
7. M. Klein, J.-C. Perrin, S. Leclerc, L. Guendouz, J. Dillet and O. Lottin, Diffusion Fundamentals, 2013, 18(7), 1–4.
8. P. Heijden, L. Rubatat and O. Diat, Macromolecules, 2004, 37, 5327.
9. T. J. Peckham, J. Schmeisser, M. Rodgers and S. Holdcroft, J. Mater. Chem., 2007, 17, 3255.
10. A. I. Kuklin, D. V. Soloviov, A. V. Rogachev, P. K. Utrobin, Y. S. Kovalev, M. Balasoiu, O. I. Ivankov, A. P. Sirotin, T. N. Murugova, T. B. Petukhova, Y. E. Gorshkova, R. V. Erhan, S. A. Kutuzov, A. G. Soloviev and V. I. Gordeliy, J. Phys.: Conf. Ser., 2011, 291, 012013.
11. A. I. Kuklin, A. K. Islamov and V. I. Gordeliy, Neutron News, 2005, 16(3), 16.
12. A. G. Soloviev, T. M. Solovieva, A. V. Stadnik, A. K. Islamov and A. I. Kuklin, Commun. Jt. Inst. Nucl. Res., 2003, E10-2003-86.
13. P. V. Komarov, P. G. Khalatur and A. R. Khokhlov, Beilstein J. Nanotechnol., 2013, 4, 567.
14. A. B. Yaroslavtsev, Polym. Sci., Ser. A, 2013, 55, 674.
15. F. Nallet, J. Phys. IV, 1999, 9, pr1-95.
16. D. I. Svergun and L. A. Feigin, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Plenum, New York, 1987, p. 81.
17. S. S. Ivanchev, E. I. Ruppel and A. N. Ozerin, Dokl. Phys. Chem., 2016, 48, 89.
18. A. N. Ozerin, S. S. Ivanchev, S. N. Chvalun, V. A. Aulov, N. I. Ivancheva and N. F. Bakeev, Polym. Sci., Ser. A, 2012, 54, 950.
19. D. Romano, E. Andablo-Reyes, S. Ronca and S. Rastogi, Polymer, 2015, 74, 76.
20. S. Ronca, G. Forte, H. Tjaden and S. Rastogi, Ind. Eng. Chem. Res., 2015, 54, 7373.
21. Y. Zhao, M. Yoshida, T. Osima, S. Koizumi, M. Rikukawa, N. Szekely, A. Radulescu and D. Richter, Polymer, 2016, 86, 157.
22. T. R. Earnest, J. S. Higgins and W. J. MacKnight, Macromolecules, 1982, 15, 1390.
23. E. J. Roche, R. S. Stein, T. P. Russel and W. J. MacKnight, J. Polym. Sci., Polym. Phys. Ed., 1980, 18, 1497.
24. E. J. Roche, R. S. Stein and W. J. MacKnight, J. Polym. Sci., Polym. Phys. Ed., 1980, 10, 1035.
25. B. C. L. Marx, D. F. Caulfield and S. L. Cooper, Macromolecules, 1973, 6, 344.
26. A. Guinier and G. Fournet, Small-Angle Scattering of X-Rays, Wiley, New York, 1955.
27. J.-D. Kim, M. Ohnuma, C. Nishimura and T. Mori, ECS Trans., 2009, 25, 405.
28. B. Yang and A. Manthiram, J. Power Sources, 2006, 153, 29.
29. D. A. Jackson, J. T. Koberstein and R. A. Weiss, J. Polym. Sci., Part B: Polym. Phys., 1999, 37, 3141.
30. Y. S. Chun and R. A. Weiss, Polymer, 2002, 43, 1915.
31. M. Reitman, D. Jaekel, R. Siskey and S. M. Kurtz, PEEK Biomaterials Handbook. A volume in Plastics Design Library. Ch. 4 – Morphology and Crystalline Architecture of Polyaryletherketones, 2012, pp. 49–60.
32. E. Aleksandrova, S. Hink, R. Hiesgen and E. Roduner, J. Phys.: Condens. Matter, 2011, 23, 234109.
33. D. Wu, S. J. Paddison and J. A. Elliott, Macromolecules, 2009, 42, 3358.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra23445c

---