Tuning metal cluster catalytic activity with morphology and composition: a DFT study of O2 dissociation at the global minimum of PtmPdn (m + n = 5) clusters
Abstract
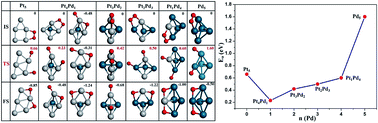
The Pt-based alloyed clusters are the important catalysts in the chemical industry. The global minimum structures of PtmPdn (m + n = 5) clusters were searched for based on the CALYPSO algorithm, and the various properties of the lowest-energy PtmPdn clusters have been studied. The results show that introducing the Pd element can modify the morphology and composition of the pure Pt5 cluster, i.e., from a 2D planar to a 3D trigonal bipyramid structure, except for the Pt4Pd1 (square pyramid). According to the average cohesive energy, the Pt4Pd1 cluster possesses the highest stability among these Pt–Pd alloyed clusters. The O2 molecule prefers to anchor on the clusters by the Yeager mode. The catalytic property for O2 dissociation of the pure Pt5 cluster can be further improved by introducing the Pd atoms. Moreover, the Pt4Pd1 cluster with the high Pt composition and the structure of square pyramid shows the highest catalytic activity. More importantly, the Brønsted–Evans–Polanyi relationship is found to be applicable to the current mini alloyed metal clusters. This study will help to understand the prediction of the global minimum structure of metal cluster by CALYPSO and shed light on the design of the less expensive and more effective alloyed cluster catalysts by controlling the morphology and composition in the fuel cells.


 Please wait while we load your content...
Please wait while we load your content...