Quantum chemistry calculations of technetium and rhenium compounds with application in radiopharmacy: review

Abstract

In the last 15 years, computational quantum chemistry has become an invaluable tool that supports the interpretation of experimental measurements of a broad range of molecular properties of Tc and Re compounds. Among the contemporary computational techniques, density functional theory is the most extended one. This review describes recent computational investigations that illustrate best the promise of quantum chemical calculation in a number of areas of Tc and Re chemistry, such as geometry, stability of complexes, molecular spectroscopic properties and electronic structures and bonding characters. General trends and the prospects for future applications are also discussed.

---

Daniel Hernández-Valdés

Daniel Hernández Valdés is a PhD student at the University of Zurich under the supervision of Prof. Roger Alberto. He received his bachelor in Radiochemistry in 2013 and his master in 2015 from the Higher Institute of Technologies and Applied Sciences (InSTEC), University of Havana. During this time he worked under the supervision of Prof. Ulises Jáuregui Haza in quantum calculations of several chemical systems, including Tc and Re compounds. His currently research concerns topics related with synthesis, characterization and computational studies of new Tc and Re organometallic complexes.

Roger Alberto

Roger Alberto study of and PhD in chemistry at ETH Zürich, Alexander von Humboldt fellow with Prof. W. A. Herrmann TU Munich and with Prof. A. Sattelberger at Los Alamos National Laboratory (LANL), Paul Scherrer Institute (PSI) in 1992–1999, Associate Professor at the University of Zürich 1999–2005, Full Professor in 2006. Main research interests are technetium and rhenium, radiopharmaceutical and bioorganometallic chemistry for molecular imaging. Since 2013, head of “Light to Chemical Energy Conversion” initiative at UZH (LightChEC) for solar light induced water splitting, artificial photosynthesis. Active in vitamin B12 chemistry, in field sensor probes for MR imaging and organometallic chemistry.

Ulises Jáuregui-Haza

Ulises Jáuregui Haza is full professor and researcher at Higher Institute of Applied Technologies and Sciences (InSTEC), University of Havana, Cuba. He received his BSc and MSc in Chemical Engineering at Moscow Institute of Chemical Technology D. I. Mendeleyev, Russia, in 1987 and PhD at National Polytechnic Institute of Toulouse, France, in 2002. He has published over 100 peer-reviewed papers and 4 books chapters. He has been recognized with the Order Carlos J. Finlay and four Awards of the Academy of Sciences. His research interests are wastewater treatment, mathematical modeling of technological processes and quantum chemistry calculations of molecular systems.

---

1 Introduction

The synergy between theory and experiment has vastly accelerated progress in many areas of chemical science. Steeply increased computational power allows the application of various quantum chemical methods to predict molecular properties including equilibrium geometries, energies, spectroscopic properties and reactivities of metal compounds.^1,2

Technetium and rhenium are transition metals with similar chemistry for which many homologous compounds exist. Technetium chemistry is mainly driven by radiopharmaceutical applications and ^99mTc is the most commonly employed radionuclide in diagnostic medicine^3,4 since its nuclear properties, its availability and its low cost are favorable for routine clinical application. Stable rhenium complexes have several applications and the two radionuclides ¹⁸⁶Re and ¹⁸⁸Re, have been suggested for valuable complementary applications in radiotherapy.^4,5 Although the field of radiopharmaceutical design is essentially governed by experimental methods, an important number of computational publications appeared, supporting the experimentalist's work.

The application of computational chemistry to transition metal compounds has been extensively reported in literature, indeed special issues were published in Chemical Reviews^6–18 and Coordination Chemistry Reviews.^19–38 Furthermore, detailed reviews outlining the applications of transition metal complexes and the advances of quantum methods to predict their molecular properties, stabilities, reaction mechanisms, interaction with proteins, etc. can be found over the last years.^39–45 However, it is noteworthy that until to date, publications summarizing the most significant advances in the application of quantum methods to ^99mTc and ^186/188Re radiopharmaceuticals are rare, if ever.

How computational quantum chemistry was used to corroborate experimental results and to evaluate molecular properties of a wide range of Tc and Re complexes is the emphasis of this report. A special focus is put on those studies with a future application in radiopharmacy. Others, although not directly related to radiopharmacy could bring along some knowledge of Tc and Re chemistry and contribute to a future development of radiopharmaceuticals as well. In the first section, we include a brief introduction to technetium and rhenium chemistry for readers not familiar with the topic. Following sections are dedicated to recent computational investigations into the geometric structures, stability analysis of Tc and Re complexes, calculation of spectroscopic properties, electronic structure and bonding character in Tc and Re compounds. The development of new computational methodologies is beyond the scope of this review. With the aim to help the reading, in the remaining part of the paper, ⁹⁹Tc and ^99mTc always refer to experimental compounds.

2 Technetium and rhenium chemistry

Technetium is positioned in the periodic table between manganese and rhenium, but its chemistry is more similar to rhenium. As a transition metal in group VII B, technetium has a d⁷ configuration and +VII is the highest achievable oxidation state (d⁰ configuration) normally in the form of pertechnetate, TcO₄⁻. Pertechnetate is the most stable form of Tc in aqueous solution, technetium compounds have been obtained in oxidation states from −I to +VII.⁴⁶ Tc(V) and (VI) oxidation states can disproportionate to TcO₂ and TcO₄⁻, unless sufficient concentrations of complexing ligand are present.

For radiopharmaceutical purposes, ^99mTc must be converted into complexes, which requires the reduction of pertechnetate into lower oxidation states. The choice of the reducing agent and the specific reduction condition is crucial. Among reducing agents, sodium borohydride (NaBH₄) and sodium dithionite (Na₂S₂O₄) are effective in alkaline pH while stannous chloride (SnCl₂) is typically used under acidic conditions. SnCl₂ is capable to produce high yields of technetium-labeled compounds, excluding the need to remove free ^99mTcO₄⁻. Other stannous salts, such as stannous tartrate, stannous citrate, stannous pyrophosphate and stannous fluoride, are also used in kit formulations.⁴⁷

Tc(V) has a high positive charge and requires good electron-donating ligands to give enough stability to its complexes. The most extensively studied Tc(V) core is the [Tc=O]³⁺ moiety, forming square-pyramidal configurations with a variety of ligands rich in electron-donor atoms such as N, O and S. Amido, amino, thiolate and tetradentate ligands of the N_4−xS_x class have been extensively investigated.³ Other approaches to obtain in vivo stable ^99mTc complexes aimed at a mixed-ligand sphere, in which the equatorial coordination plane is formed by a tridentate and monodentate ligand (3 + 1 approach).⁴⁸ The linear trans-dioxo motif [O=Tc=O]⁺ with a distorted octahedral arrangements is another Tc(V) core present in numerous complexes. In addition, several dinuclear Tc(V) complexes, some of them contain the bridging [O=Tc–O–Tc=O]⁴⁺ unit, have been described.⁴⁶

Depending of the type of nitrogen donor, different Tc–N compounds with oxidation states of Tc from +I to +VII can be formed. Among the most important ones are the Tc(V)–nitrides. ^99mTc–nitrido complexes are generally five-coordinated; one position is always occupied by a nitride N atom and the other positions are available for coordination to four additional donor atoms. Molecular structures for these complexes alter between the two ideal limits of trigonal bipyramidal and square pyramidal geometries. The most widely studied class of coordination ligands for the [Tc≡N]²⁺ core are bidentate chelating ligands.⁴⁹ Along the same line, 6-hydrazino-nicotinic acid (HYNIC) can be considered as a bifunctional chelating agent particularly appropriate for ^99mTc labelling of peptides.⁴⁹ Although no structures exist, it is assumed that the HYNIC group occupies one coordination site on technetium and the remaining sites are completed by various co-ligands such as tricine.^3,49

Reduction of Tc(VII) to Tc(I) generates Tc(I) in a d⁶ configuration that must be stabilized by π acceptor ligands such as phosphines, isonitriles or carbonyls. In this case, the most frequently explored core is the {Tc(CO)₃⁺}. This core is thermodynamically and kinetically stable when six coordination sites are occupied, forming an octahedral 18 e⁻ complex. The development of a fast and easy preparation of the precursor [^99mTc(H₂O)₃(CO)₃]⁺ in excellent radiochemical purity and in high yields allows the preparation of many follow up organometallic tricarbonyl complexes with perspective application in radiopharmacy.^3,49,50

Moreover, Benz and co-workers in 2015 published a new procedure towards bis-arene ^99(m)Tc(I) complexes.⁵¹ This new core, electronically similar to ferrocene, represents a fundamental class of organometallic compounds and displays extraordinarily high stability. Conjugation of biologically active groups to the arene ring opens a path to novel, functionalized and targeting SPECT imaging agents. Fig. 1 shows a selection of common core structures for technetium complexes.

Fig. 1 Technetium cores and the general structures of technetium complexes with ligands.

The two radionuclides of Re, ¹⁸⁶Re and ¹⁸⁸Re, are used as radiotherapeutic isotopes because of their convenient β⁻ emissions and their relatively short half-lives. ¹⁸⁸Re can be obtained from commercially available ¹⁸⁸W/¹⁸⁸Re generators since 1989. Rhenium is attractive because its chemical properties are similar to technetium especially in the low valencies. Therefore, their biological behavior is assumed to be comparable to the ones of ^99mTc which lead to the matched-pair paradigm. This point of view leads potentially to a theranostic approach in which ^99mTc compounds act as imaging agents while its rhenium homologues are used as therapeutic agent. Although the structural features of Re and Tc compounds are similar, there are still substantial differences in their chemistry with practical consequences. For instance, labeling with rhenium is more difficult than with technetium since it is harder to reduce and, correspondingly, it easier reoxidizes and displays increased instability towards air.⁴

3 Applications of quantum chemistry calculations in the study of Tc and Re compounds

Over the last 15 years, the number of theoretical studies published on the chemistry of Tc and Re complexes greatly increased. The majority of these studies were performed to corroborate assumed structures of complexes and to calculate their properties. Although different computational methods have been used, quantum chemistry based methods, Density Functional Theory (DFT) in particular, are the most popular ones. Compared with other methods, DFT has the advantage of being easily applicable, accurate, and fast enough to permit the study of relatively big systems. Concerning DFT methodology, calculations with different functionals and basis set have been carried out but the combination of the hybrid B3LYP functional⁵² and the LANL2DZ pseudopotential⁵³ as a basis set for Tc and Re atoms are most common.^54–72 The use of other functionals and basis sets are also found in literature to produce also reliable results. An overview of recent progress in quantum chemical method applications to Tc and Re chemistry is presented. It is the intention of the authors to draw a special attention to those calculations with relevance for future application in radiopharmacy. In the next sections, this review refers to recent computational applications to geometric structures, stability analyses, spectroscopic properties, electronic structures and bonding characters of Tc and Re compounds.

3.1. Computational investigations on geometric structures of Tc and Re compounds

In general, DFT calculations have been widely used in the recent years to evaluate Tc and Re complex structures. Among the studied systems, oxo-,^{54,56,65,67,68,71,73–75} nitrido-^61–63 and carbonyl-complexes^{55,57–60,66,69,70,76–85} have been extensively studied. Studies with Tc and Re in other complex types are rarer but also present.^86–92 In the majority of these reports, theoretical calculations are combined with experiments.^{55,58–71,74,76–80,89–91,93}

One of the first and most relevant work published in this field was performed by Gancheff et al.⁵⁴ To evaluate the precision of computational methodologies, they studied the oxides MO₂ (M = Tc or Re), pertechnetate and perrhenate ions MO₄⁻, complexes with the [MO₂]⁺ core and the ionic complexes [MO₂(NH₃)₄]⁺. Different basis sets and methods (HF, MP2 and B3LYP) were involved. They assessed that the combination of B3LYP functional and the LANL2DZ basis sets for Tc and Re atoms gave reasonable performance for geometry structures. Calculations on several complexes with the {ReO₂}⁺ core and simple polyamines as ligands employing the B3LYP method and the LANL2DZ basis set completed this study. The results agreed well with the experimental data. It was confirmed that the ligands stabilized the linear geometry of the {ReO₂}⁺ core since the bent geometry is much higher in energy for an isolated [MO₂]⁺ core.

Hernández-Valdés et al. carried out calculations on Re and Tc complexes comprising the fac-{M(CO)₃}⁺ core with tridentate, N substituted iminodiacetic acid chelators.⁸⁵ Evaluation of the accuracy of the computational level B3LYP/LANL2DZ showed good agreement with the experimental X-ray results. The averages of the relative errors calculated for bond angles and bond lengths were less than 2%. Differences of less than 2% in the geometries were found for the corresponding Re and Tc complexes. Similar computational results were previously obtained in other studies.^57,60,78,79 Although B3LYP sometimes fails to predict molecular properties of metal complexes, these results and others were published,^{54–58,60–68,70,78,91} showing that B3LYP calculations predict geometries which are well in agreement with experimental results.

Schibli and co-workers⁷⁶ synthetized mixed carbonyl–nitrosyl complexes of Re(I) and ⁹⁹Tc(I) (NEt₄)[⁹⁹TcCl₃(CO)₂NO], (NEt₄)[ReBr₂X(CO)₂NO] (X = Br, NO₃) and [⁹⁹TcCl(μ-Cl)(CO)₂NO]₂ directly in water in 2005. The structure of these complexes and their potential facial isomers were studied on the DFT level with the BP86 exchange–correlation energy functional^94,95 and a triple-ζ basis set with one polarization function in the valence shell and double-ζ basis set in the core region. Moreover, scalar relativistic effects were taken into account by the Zeroth Order Regular Approximation (ZORA) approach.^96,97 This calculation level gave good structural agreement with experiment results and is an example about how to use a Generalized Gradient Approximation (GGA) functional less computationally expensive than the classical hybrid functionals. This approach can save computational cost and allows the use of an all-electrons method to explicitly take relativistic effects into account.

3.2. Computational stability analysis of Tc and Re complexes

High thermodynamic stability together with kinetic stability are basic for all radiopharmaceuticals. For the labelling of targeting biomolecules with radionuclides, chelators stabilize the metal center against release from the carrier.⁴ Consequently, the search for more stable ^99(m)Tc and Re complexes is a focus in the development of ^99mTc and ^186/188Re radiopharmaceuticals. Quantum computational methods are helpful tools to support the search for stable complexes and for the design of new and in vivo stable radiopharmaceuticals. Different reports appeared in literature in that respect.^{56–58,78,82,85} Experimental and theoretical studies are commonly combined.^58,78,82 DFT methods are also helpful in the comparison of different configurations of isomers to the stability of Tc and Re complexes.^{55,75,76,79,81}

Xiangyun and co-workers⁸¹ studied the geometries and the total molecular energies of ten species in the system [Tc(CO)_i(H₂O_6−i)]⁺ (i = 0–6) by an ab initio molecular orbital method at the MP2/CEP-121 G level. The calculated free energies of formation follow the sequence: [Tc(H₂O)₆]⁺ > trans-[Tc(CO)₂(H₂O)₄]⁺ > [Tc(CO)(H₂O)₅]⁺ > trans-[Tc(CO)₄(H₂O)₂]⁺ > mer-[Tc(CO)₃(H₂O)₃]⁺ > cis-[Tc(CO)₂(H₂O)₄]⁺ > cis-[Tc(CO)₄(H₂O)₂]⁺ > [Tc(CO)₅(H₂O)]⁺ > fac-[Tc(CO)₃(H₂O)₃]⁺ > [Tc(CO)₆]⁺. The species fac-[Tc(CO)₃(H₂O)₃]⁺ is the dominant product under all three preparation conditions (0.1 MPa CO pressure at 25 °C; 0.1 MPa CO pressure at 75 °C; 3.0 MPa CO pressure at 75 °C) and this is in accordance with the experiments observed by Alberto and co-workers.⁹⁸ Moreover, among these 10 species, the complexes fac-[Tc(CO)₃(H₂O)₃]⁺, cis-[Tc(CO)₂(H₂O)₄]⁺ and [Tc(CO)₆]⁺ are the most likely products under any preparation conditions. Under low CO pressure, the complex cis-[Tc(CO)₂(H₂O)₄]⁺ might become the major product, while in very low water concentration [Tc(CO)₆]⁺ will be predominant. For this system, solvent effects are important. Hydrogen bonds between water coordinated to the metal center and water molecules from the solvent do alter the formation energy, however, the authors decided to not consider this contribution assuming that solvent effects would not affect significantly the general pattern of stability.

In a series of three papers, Safi et al.^56–58 performed a conceptual DFT study on several [3 + 1] and tricarbonyl Tc and Re complexes to get an insight into the stability of these complexes. The relative stability of Tc and Re complexes with various ligands containing combinations of N, O, and S as donating atoms were performed with the B3LYP functional and the LANL2DZ basis set. The results were interpreted in terms of the hard and soft acids and bases principle (HSAB). The stability of the complexes of a given metal, was evaluated using a simple substitution reaction.

For Tc(V) and Re(V) [3 + 1] complexes (Fig. 2a) the stability is increased with donor atoms following the sequence S > N > O. It was also found that for ligands containing identical X, Y, and Z atoms SSS are more stable than OOO ligands. The complex with NNN ligand was not calculated. This result is in agreement with HSAB prediction in terms of increasing stability upon increasing ligand softness. The [M=O]³⁺ core (M = Tc, Re) is considered as soft and it prefers to bind to soft bases such as sulfur.⁵⁶

Fig. 2 Schematic representation of complexes studied by Safi et al.^56–58 (a) Structure of Tc and Re [3 + 1] complexes, (b) structure of Tc and Re tricarbonyl complexes, (c) structure of [RCN(H₂O)₂Tc(CO)₃]⁺ complexes.

The fac-[M(CO)₃]⁺ core (Fig. 2b) is harder and the stability sequence N > S > O supports this finding. The number of nitrogen donors in the ligand determines stability of complexes with the fac-[M(CO)₃]⁺ core.⁵⁷ Different from [3 + 1] complexes, the stability for ligands combining three identical donors, the stability sequence was found to be NNN > SSS > OOO. Overall, the authors showed how the relationship of the softness and hardness properties of the core and the ligands define the opposing stability sequence of [M=O]³⁺ complexes versus the M(I) tricarbonyl complexes.

In a further paper, the stabilities of N-chelating tricarbonyl complexes including alkyl nitriles, HCN and imidazole (existent in VitB12) of technetium(I) and rhenium(I) was compared (Fig. 2c).⁵⁸ The nature of the N-chelating atom was selected to simulate the conditions of the Co³⁺–CN entity in vitamin B12. For both Tc and Re complexes, the stability sequence was imidazole > ^tBuCN > NH₃ ∼ CH₃CN > HCN > H₂O. Within the CN compounds, the stability sequence ^tBuCN > CH₃CN > HCN is in agreement with the electron-donating properties of the nitrogen. Theoretical calculations corroborated the experimental results.

The results were identical for all complexes, when passing from Re to Tc. The relative stabilities of Re and Tc complexes were studied using a simple trans-metalation reaction. It was shown that the rhenium complexes are consistently more stable than their Tc analogues.^56–58 This statement was also obtained with theoretically calculations by other authors in more recently reports.^75,78,82,85 All these studies indicate clearly that conceptual DFT, in the light of the hard and soft acids and bases principle at the local level, offers a tool to understand and systematize theoretical and experimental binding features for metals such as Tc and Re.

Moura et al. studied the influence of different donor atom sets on the in vitro stability of rhenium(I) and technetium(I) complexes with pyrazole-containing chelators.⁷⁸ The complexes were optimized without any symmetry constraints using the local functional Vosko, Wilk and Nusair (VWN)⁹⁹ in combination with non-local permute (Becke88)¹⁰⁰ and correlation (Perdew86) functional.¹⁰¹ Relativistic effects were accounted by the scalar correlation ZORA^96,97 approach and solvent effects were taken into account using conductor-like screening model (COSMO) method.^102–104 The agreement between experimental and calculated structures was acceptable and the solvent effect on bond distances and bond angles was negligible. Nevertheless, the addition of implicit solvent (methanol) in the calculation produced more realistic values of binding energies. Thus, the inclusion of solvent effects is crucial in many cases for a good description of the system. The replacement of nitrogen by sulfur donor atoms resulted in slightly less stable complexes. These differences were however not substantial enough to explicate the lower in vitro stability as observed in experiments for those complexes containing sulfur donor atoms. As an important conclusion, this result suggests that the in vitro behavior is not always controlled by thermodynamic factors but that kinetic stabilities govern the overall behavior.

Fuks and co-workers recently used the MPW1PW functional to model the thermodynamic and electronic properties of ‘2 + 1’ fac-{M(CO)₃}⁺ (M = Tc, Re) complexes. The N-methylpyridine-2-carboxymide served as a bidentate ligand and chloride, water or tert-butyl-3-isocyanopropanoate as the monodentate ligand.⁸² DFT results demonstrated that the in vitro behavior of the studied complexes is controlled by thermodynamic factors. For the complexes containing the tert-butyl-3-isocyanopropanoate ligand, the energy of formation is more negative than for those complexes having a coordinated water molecule. Values of dissociation energies agree with the results of challenge experiments in the presence of sulfur-containing amino acids (cysteine or histidine). From challenge experiments, complexes containing tert-butyl-3-isocyanopropanoate ligand are more stable than those with a coordinated water. Rhenium complexes were again found to be more stable than those with technetium.

Quantum chemistry calculations have not only been used for developing new complexes but also to better understand radiopharmaceuticals in current clinical use. For the renal imaging agent ^99mTc^III–DMSA for instance, the structure is not known and only proposed based on calculations. Hernández-Valdés and co-workers⁷⁵ found recently two structures (Fig. 3a) which are thermodynamically more stable than the structure of ^99mTc^III–DMSA originally proposed by Moretti et al. (Fig. 3b).¹⁰⁵ These new structures of ^99mTc^(III)–DMSA were calculated at the B3LYP/LANL2DZ level using double-ζ with polarization function in all atoms and diffuse functions in all non-hydrogen atoms. Other Tc and Re DMSA complexes were calculated in this work as well. For the tumor imaging agent M^(V)–DMSA the stability of the stereoisomer was theoretically calculated and compared. This agent is a mixture of three mononuclear stereoisomers, anti, syn–endo and syn–exo with square pyramidal structure. The results showed that the stability differences of the three stereoisomers are not governing the final composition of the mixture after the preparation of the radiopharmaceutical, however the kinetic has an important effect.

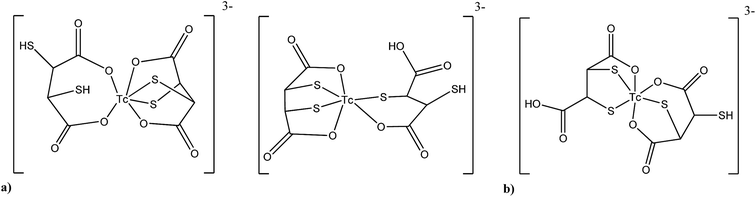Fig. 3 Structure for the renal agent ^99mTc^(III)–DMSA. (a) Structures proposed by DFT calculation more stable than Moretti structure,⁷⁵ (b) structure proposed empirically by Moretti et al. in 1984.¹⁰⁵

3.3. Calculation of spectroscopic properties

Spectroscopy is an essential in inorganic and organic chemistry and experimental spectra are generally analyzed empirically. In more difficult cases, computational techniques based on the electronic structures can strongly support their interpretation. Consequently, quantum chemical methods appeared as an important research instrument over the last years for the calculation of spectroscopic parameters. In regard to Tc and Re chemistry, several examples of applying computational techniques to spectroscopy appeared in literature. The main focus was the analysis of electronic spectra using Time-Dependent Density Functional Theory (TD-DFT) and HOMO–LUMO analysis.^{59–64,66,72,90,93} Examples of NMR calculations^68,74,77,106 with the Gauge-Independent Atomic Orbital (GIAO) methodology and calculations of vibrational spectra⁷⁰ were also reported.

In 2008, Videira and co-workers studied different mercaptoimidazolyl borate complexes of ^99(m)Tc(I) and Re(I) with a special focus on their application in radiopharmacy.⁷⁷ Starting from fac-[Re{κ³-H(μ-H)₂(tim^Me)}(CO)₃] (1) they synthetized three new complexes fac-[Re{κ²-H₂(μ-H)B(tim^Me)}(L)(CO)₃] (L = PPh₃ (2), (^tBuNC) (3), (EtOOCCH₂NC) (4)), (see Fig. 4) which were characterized by IR, NMR spectroscopy. For 2, the X-ray diffraction revealed the structure of the complex. The ¹H NMR spectrum of compound 1 displays two broad resonances at 6.20 and −5.48 ppm, assigned to the terminal and bridging B–H protons, respectively. For 2, 3, and 4, the ¹H NMR spectra depict only one very broad resonance for the B–H protons at −0.47, −0.21, and −0.10 ppm, respectively, clearly implying that the mixed ligand complexes are fluxional in solution. Fast dynamic processes on the NMR time scale at room temperature account for the magnetic equivalence of the terminal and bridging B–H protons. For corroborating these results and as a good example of how computational methods allow to understand experimental spectroscopy behavior, DFT calculations (GIAO method for calculation of chemical shift¹⁰⁷) were carried out for complex 1 and for a model of complex 2 (2m). These calculations showed that the rotation barrier of the B–H₃ group is higher in 1 (20.1 kcal mol⁻¹) than in 2m (8.6 kcal mol⁻¹), assessing thus the different solution behavior of these complexes at room temperature (Fig. 5).

Fig. 4 Schematic representation of complexes synthetized by Videira et al.⁷⁷

Fig. 5 DFT calculated ¹H NMR chemical shifts for the H(B) proton in model complex 2m, as the BH₃ rotates across the B–N bond. Reprinted with permission from ref. 77 Copyright (2008) ACS.

Mancini and co-workers studied theoretically and experimentally the potential of ⁹⁹Tc NMR spectroscopy as a structural characterization technique.¹⁰⁶ Thermal and solvent effects were also computationally studied by DFT/GIAO method (BPW91/aug-cc-pVTZ for Tc and BPW91/IGLO-II for the other atoms). Different implicit and explicit solvent models were included in the calculations. To evaluate the thermal effect, molecular dynamics simulations using the atom-centered density matrix propagation method at BP86/LanL2dz level were carried out. The results show that these effects were important for ⁹⁹Tc chemical shift calculations and that the DFT/GIAO method presents a realistic description of the system in different environments.

Another example of quantum chemical calculations of spectroscopic properties of ^99mTc and Re complexes was performed by Seridi in 2011.⁵⁹ In this report, a B3LYP/LANL2DZ calculation of the electronic absorption spectrum for a rhenium complex prepared with a pyridyltriazole ligand was done using TD-DFT (see Fig. 6). The solvent effect (methanol) was simulated by the polarizable continuum model with the integral equation formalism.^108–110

Fig. 6 Experimental (black) and calculated (red) electronic absorption spectra for the rhenium complex prepared from a pyridyltriazole ligand; λ_max [nm] (ε [dm³ mol⁻¹ cm⁻¹]): 329.9 (3270), 276.8 (11 250), 241.1 (19 650), and 206.1 (39 730). Reprinted with permission from ref. 59 Copyright (2011) Elsevier.

The absorption spectrum of the rhenium complex in methanol is well reproduced by TD-DFT calculations. An HOMO–LUMO orbital analysis (Fig. 7) showed that the longest wavelength experimental band of the UV/vis spectrum of the rhenium complex at 329.9 nm originates from the HOMO−1 → LUMO, HOMO−1 → LUMO+1 and HOMO−4 → LUMO transitions. Consequently, the transitions assigned to the longest wavelength absorptions are interpreted as mixed d_Re → π*(chelate) MLCT and π(Cl)/π(chelate) → π*(chelate) LLCT or a delocalized MLLCT description. The experimental absorption bands at 276.8, 241.1 and 206.1 nm are assigned to metal-to-ligand charge transfers (from the rhenium ion into the π-antibonding orbitals of the chelate ligand or the carbonyl groups), ligand–ligand charge transfer and intra-ligand transitions.

Fig. 7 Energy (eV), character and some contours of the occupied and unoccupied molecular orbitals. Reprinted with permission from ref. 59 Copyright (2011) Elsevier.

A combined experimental and computational study of Schiff base complexes with the {Re(CO)₃}⁺ core and of the general formula fac-[ReCl(CO)₃(L¹/L²)] (L¹ = N-[(2-pyridyl)methyliden]-a-aminonaphthalene and L² = N-[(2-pyridyl)methyliden]-b-aminonaphthalene) was reported by Pramanik et al.⁸⁴ The DFT method at the B3LYP/SDD level and 6-31G(d) basis set for non-rhenium atoms was used. Vertical electronic excitations with a B3LYP optimized geometry was computed by TD-DFT formalism in acetonitrile with a conductor-like polarizable continuum model to take solvent effects into account.¹¹¹ The two weak, vertical electronic transitions at 458 nm and 411 nm correspond to HOMO → LUMO and HOMO−3 → LUMO transitions along with a strong HOMO−1 → LUMO transition at 430 nm. These transitions are attributed as a mixture of dπ(Re) → π*(L) and pπ(Cl) → π*(L) transitions. The high energy band at 310–315 nm is π (L) → π*(L), intra-ligand charge transfer transition.

In a combined experimental and theoretical work, Wolff et al.⁶⁰ synthesized recently with click chemistry three new {Re(CO)₃}⁺-based complexes with pyridyltriazole bidentate ligands bearing a nitro-, chloro- or aminophenyl arms. The complexes were fully characterized with IR, NMR and mass spectrometry. An X-ray structure analyses confirmed the authenticity for two of these complexes. Geometries and spectroscopic properties for all complexes were reproduced by DFT methods. The calculations were carried out with the hybrid B3LYP functional and the pseudopotential LANL2DZ, simulating the solvent effect with the Polarizable Continuum Model (PCM).¹¹² Electronic transitions for the three complexes were calculated using TD-DFT. Excited state structures were calculated, evidencing that the complexes keep nearly octahedral conformations albeit different from the ground state structures e.g., shorter rhenium–nitrogen but longer rhenium–carbonyl in the excited state S₁ as compared to the ground state S₀. This indicates that CO ligands tend to dissociate from rhenium in the excited state whereas the chelate ligand is more tightly bound. This calculation confirms numerous experimental results in which light irradiation lead to smooth cleavage/substitution of at least one CO from such complexes. For complexes bearing a nitro or chloro group on the ligand, the same trend is observed for the lowest lying triplet T₁ states. For complexes with an amino group however, the Re–N(2) bond distances are shortened, while the Re–C and Re–N(1) have similar values in the T₁ state triplet as compared to S₀. As a conclusion, this combined experimental and DFT study indicated that the nature of the pendant arm (X = NO₂, NH₂ or Cl) has decisive effects for the electronic properties of the Re-complexes.

Finally, Noor and co-workers synthesized a family of bioconjugated tridentate pyridyl-1,2,3-triazole macrocycles via “click” reactions⁸³ and compared experimental absorption spectra with TD-DFT calculated models using a number of hybrid functionals with varying amounts of Hartree–Fock exchange (B3LYP (20%), PBE0 (25%), M06 (27%), M062X (54%), CAM-B3LYP (19–65%)). The good agreement between calculations and experiments was determined by comparing calculated data with X-ray crystallographic data and experimental spectroscopy. Although the energies vary significantly, all five functionals predict qualitatively similar transitions. A relatively weak transition at lower (CT1) and a stronger one at slightly higher energy (CT2) were predicted. The functionals M062X and CAM-B3LYP overestimate the energy of these transitions while the functionals with low % HF underestimate them. Regarding the donor orbital for the weaker transition, there is also a slight variation in composition. Those functionals that overestimate the energy predict a contribution from the benzyl alcohol moiety to the donor orbital of CT1. In the case of CAM-B3LYP, this coefficient is negligible (0.13) but in the case of M062X is significant (0.41).

3.4. Electronic structure and bonding character in Tc and Re compounds

The understanding of metal–metal and metal–ligand interactions in Tc and Re complexes focuses mainly on the electronic nature of molecules and the bond character between two participating atoms. Several theoretical methods have been developed to provide information about the electronic properties and strengths of bonds. Various population analysis methods such as Mulliken Population Analysis (MPA)⁷² and the Natural Population Analysis (NPA) combined with the Natural Bond Orbital (NBO) method^{62,63,65,67,68,71,82,88,93} are among the most popular computational methods for analyzing electronic structures and bonding characters of Tc and Re complexes. Further theoretical tools to analyze the topology of the electronic density of molecular systems such as atom in molecules (AIM) are in use to characterize molecular interactions.^74,75,82,85 Moreover, the concept of density of states (DOS), which represents the number of states in unit energy interval, was successful for characterizing ⁹⁹Tc crystal structures.^87–89 A few selected examples are presented in the following section.

The formation of ethene during the cleavage of two C–S bonds in trithia–cyclononane complexes [M(9S3)₂]ⁿ⁺ (with 9S3 = 1,4,7-trithiacyclononane and M = Re, Tc; n = 1, 2) was studied by Maurer and co-workers in 2004.⁸⁶ The static and dynamic calculations were performed with the program CPMD based on DFT. Periodic boundary conditions, plane wave basis sets and a pseudopotential approach were applied in the calculations. The influence of the oxidation state of the metal center on the structural and electronic properties of the reactant and the products was analyzed in detail. Small structural changes upon reduction of the metal centers was evidenced. Dissociation energies and the related activation energy barriers for the dissociation of ethene from the d⁶ and d⁵ complexes were found to be 10 kcal mol⁻¹ (d⁶) and 30 kcal mol⁻¹ (d⁵) respectively for the technetium compounds. For rhenium, the activation energies are smaller, 4 kcal mol⁻¹ for the d⁶ and 22 kcal mol⁻¹ for the d⁵ system. The increase in reactivity of the reduced compounds is caused by a general effect of the lower overall charge and the associated higher eigenvalues of reactant molecular orbitals and not because of the strong activation of the C–S bonds through the addition of one electron. This means that less energy is needed to promote electrons from molecular orbitals of the reactant to those of the dissociating ethene.

In 2009, Weck et al.⁸⁷ predicted the existence of ⁹⁹TcF₄ and ⁹⁹TcI₄ based on DFT calculations. A series of technetium halides ⁹⁹TcX₄ [X = F, Cl, Br, I] was synthesized and their crystal and electronic structures studied. The functional PW91 (ref. 113) and double-ζ basis set with polarization functions on all atoms were used for the calculations. These calculations predict that ⁹⁹TcF₄ is isomorphous with experimentally confirmed ⁹⁹TcCl₄ and ⁹⁹TcBr₄ crystallizing in an orthorhombic system in the centro-symmetric space group Pbca. On the other hand, ⁹⁹TcI₄ crystallizes in the monoclinic space group P2₁/c. In general, the structure [⁹⁹TcX₂-(μ-X)_4/2]_∞ for technetium tetrahalides consist of distorted edge-sharing octahedral groups of composition ⁹⁹TcX₆ linked into endless cis chains. In a population analysis, it was found that the charge on technetium varies from +0.51e (TcF₄) to −0.22e (TcI₄), consistent with the decrease of the electronegativity of the halogens and the increase of their atomic radii. According to DOS calculations, a metallic character for all TcX₄ was obtained. This was supported by the presence of valence and conduction peaks near the Fermi level dominated by Tc 4d orbitals, strongly hybridized with p orbitals from halogens to form σ bonds. Moreover, molecular characteristics vanish as the number of molecular states increases from TcF₄ to TcI₄ (Fig. 8).

Fig. 8 Total and orbital-projected density of states of technetium(IV) halide crystals: (a) TcF₄; (b) TcCl₄; (c) TcBr₄; (d) TcI₄. The Fermi energy is set to zero. Reprinted with permission from ref. 87. Copyright (2009) ACS.

As previously mentioned (Section 3.2.), Fuks and co-workers⁸² investigated thermodynamic and electronic properties of a series of ‘2 + 1’ fac-{M(CO)₃}⁺ (M = Tc, Re) complexes. Atomic charges, the polarization of the CO groups and the effect of transfer of π-electron density between the ligands through the metal were examined. For rhenium and technetium, a significant electron density transfer between the ligand (N-methylpyridine-2-carboxyamide) and the rest of the molecule was found. AIM analysis evidenced a π-electron communication between the CO and other ligands in the trans position through the metal valence shell. This produced an increase in the π character of the C–O bonds. The polarization of bonds in the surrounding of the Re/Tc central atom suggests that a greater stability of the complexes is favored by a lower polarization of the bonds.

Hernández-Valdés et al.⁸⁵ analyzed the metal–ligand bond character for a series of fac-{Tc(CO)₃}⁺ complexes with ligands derived from iminodiacetic acid with the AIM approach. The calculations were carried out with the B3LYP hybrid functional and the LANL2DZ effective core potential for Tc and Re. Solvent effects were taken into account by the PCM.¹¹² All bonds to the metal center presented a closed shell interaction with a character between dative and covalent bond. The strengths of the interactions followed the sequence Tc–CO > Tc–O > Tc–N. Additionally, the π backbonding effect of CO ligands was supported by the electronic density transfer found from the metal center to the ligands.

Machura et al.⁶³ synthetized and characterized (spectroscopically and by X-ray diffraction) three imido rhenium complexes with the biologically relevant 2-hydroxymethylbenzimidazole ligand: [Re(p-NC₆H₄CH₃)Cl₂(hmbzim)(PPh₃)]·CHCl₃ (1), [Re(p-NC₆H₄CH₃)Br₂(hmbzim)(PPh₃)] (2) and [Re(p-NC₆H₄CH₃)(hmbzim)₂(PPh₃)]ReO₄·MeOH (3). To better understand the respective electronic spectra, theoretical calculations based on the B3LYP functional and in combination with LANL2DZ were performed. For obtaining insight into the nature of rhenium–imido ligand interaction in complex 1 and 3, a Natural Bond Orbital analysis was additionally involved. Three Re–N NBOs were detected for complexes 1 and 3. The Re–N bond orbital with σ character was intensely polarized towards the N atom, with an s and p nitrogen orbitals contribution in the bond formation and s, p and d rhenium orbitals. Furthermore, it was observed that NBOs of π-character were the consequence to of overlap the occupied p_x and p_z orbitals of the deprotonated nitrogen of the imido ligand with the empty d_xy and d_yz rhenium orbitals. Finally, assuming that rhenium involves its six valence orbitals, 5d_x²−y², 5d_z², 6s, 6p_x, 6p_y and 6p_z in the formation of σ-bonds with the six ligands, an effective triple bond can be formed if empty 5d_xz and 5d_yz orbitals overlap with 2p_x and 2p_y orbitals on the imido nitrogen.

4 Trends and perspectives

The reported examples highlight the interrelation between computational and experimental studies. In order to improve development of radiopharmaceuticals, the complementary relationship between these two approaches must grow together in the near future. Computational studies of Tc and Re complexes so far focused essentially on their structural characterization with DFT being by far the most popular approach since it allows to take into account the electron correlation with a reasonable computational cost. The selection of the level of calculation, specifically the functional, is a task demanding expertise to find the method that provides the best results for a given system. It is a good practice and time saving to do a thorough literature search for prior calculations on similar systems and properties to straightly select a suitable, well tested functional. It is also recommended to do validation calculations and to compare them with experimental data or high level calculations results. In the context of this review, the most popular functional has been B3LYP, and the choice of basis sets is usually a double or triple ζ with some extra polarization and diffuse functions for main group atoms, and a relativistic ECPs, such as LANL2DZ or SDD for Tc and Re. The choice of this level of theory is usually rewarded by a good agreement between calculated and experimental results (mainly geometry information). This statement about the level of theory is supported by the published results of Tc and Re complexes. One should however take into account that extensive reports over the last years revealed B3LYP functional to have problems to reproduce some transition metal properties. Therefore, the functional has to be chosen with care by considering the systems and the properties to be calculated. On the other hand, the hybrid PBE0 appears as a reliable alternative functional for Tc and Re complexes. Compared with B3LYP, this functional is not frequently found in the literature but has produced good results. Recently, the development of Minnesota functionals (M05 and M06 families) by Zhao and Truhlar,^114–118 which have been applied to metal complexes, appear to be promising for calculations of technetium and rhenium complexes too and it would be interesting to evaluate their performance in this field. Those functionals have extensively been used to successfully study the properties of other transition metal complexes as well.^119–126

The inclusion of solvation effects in the calculation is mandatory for reproducing experimental results such as molecular properties like electronic spectra, NMR parameters and geometries. Solvation models were frequently involved in the calculations of Tc and Re complexes indeed.^{56,57,59–66,68,74,75,78,85,88,106,127} Whereas the PCM family is standard model for the calculation of most solvent effects, the COSMO models was used too. The explicit representation of the solvent is the most realistic way to take the influence of the solvent onto the molecular properties into account. However, these models are computationally more demanding and, at the moment, are less extended towards the calculation of coordination compounds than the implicit models. The ongoing increase of computational power and the development of new methodologies will extend the applications of explicit solvation models into Tc and Re complexes. Nevertheless, due to the importance of the solvation effects for many complex properties, we strongly encourage the readers to perform calculations by using at least implicit solvation models. Considering that PCM family lead to reliable results for Tc and Re compounds, the choice of these models is a viable alternative to the explicit solvation models.

An adequate calculation of the second derivatives of the total energies is extremely important for calculations of Tc and Re complexes. It enables the prediction of vibrational frequencies with concomitant generation of vibrational spectra (infrared and Raman). Vibrational analysis allows quantum chemists to calculate the molecular partition function which enables prediction of thermodynamic functions such as enthalpy, entropy and free energy. The free energy is the thermodynamic criterion to predict stabilities of molecules. Therefore, its calculation is essential for comparing stabilities of Tc and Re complexes. Vibrational frequency calculations are also essential to predict transition states and for distinguishing true minima from saddle points in optimization process.

Different from lighter elements, heavy metal complexes display rapidly increasing relativistic effects with the respective nuclear charge. Scalar relativistic effects and the spin–orbit couplings are especially influential in the correct description of the electronic and spectroscopic properties of heavy metal compounds. In NMR spectroscopy, relativistic effects have to be considered for calculating shielding constants since they affect not only the metal atoms, but also the light atoms in close vicinity to the metal center. The use of pseudopotentials has been the most commonly approach for taking the relativistic effects in Tc and Re complexes into account. This approach permits to reduce the computational costs associated with the high number of core electrons. It also allows to incorporate parametrically some relativistic effects. The all-electrons method based on the ZORA approximation are rarely found in the available studies.^76,78,127 ZORA is a viable approach to include accurate relativistic effects in heavy element compounds and will become useful for more accurate calculations of Tc and, principally, Re complexes.

Inter- and intramolecular interactions play a critical role in chemical reactions, solvations, since determining structures and conformations of chemical compounds. Several theoretical methods have been developed to understand the nature of such molecular interactions. AIM and NBO are most common among current computational methods in this respect. They have been extensively reported in the study of transition metal complexes in general and for Tc and Re in particular. Further computational approaches to study molecular interactions such as charge decomposition analysis (CDA), energy decomposition analysis (EDA) and the electron localization function (ELF) could be important for the development of ^99mTc and ^186/188Re radiopharmaceuticals. They could bring us closer to a quantitative interpretation of electronic structures and to do more profound characterizations of molecular interactions.

Spectroscopy is indispensable in the development of new radiopharmaceuticals. Calculations of electronic absorption and emission spectra of Tc and Re complexes complement experimental spectroscopic results. Unambiguous ground and excited state description is fundamental for predicting metal complex spectra and multi-configurational self-consistent field methods are most appropriate for this purpose. At present, the size and the electronic complexity of the current systems make the use of these methods computationally expensive and impracticable especially for the majority of cases with Tc and Re. A suitable alternative is TD-DFT^1,2 method which has been extensively used to simulate the electronic spectra of Tc and Re complexes. Although the TD-DFT is formally an exact theory, the selection of a suitable functional is always compulsory to obtain good correlations with experimental results. Some hybrid functionals such as B3LYP, PBE0 and the GGA BP86 have been described in literature for the calculation of electronic spectra of Tc and Re complexes. Promising results were obtained. In the majority of published studies, the hybrid B3LYP functional revealed good performance. The inclusion of solvent effects, explicitly or implicitly, is vital to accomplish best consistency between theoretical and experimental results.

Computational methods are tremendously important for developing new and characterizing known ^99mTc and ^186/188Re radiopharmaceuticals. The design of new compounds should rely on the support of computational techniques in future. As in other fields of science, design of compounds based on theoretical approaches will allow for a better selection of suitable candidates, will support driving synthesis processes and will predict binding properties with biological targets. The overarching applicability of theoretical chemistry predictions is a promise for the next years. As is the case for other areas of coordination chemistry, pure theoretical or combined experimental and theoretical works in ^99mTc and ^186/188Re radiopharmaceuticals will increase.⁴⁴ Interesting subjects such as prediction of barriers and reaction paths (reaction mechanisms and kinetic stability), a more detailed description of electronic and molecular orbital properties, calculation of UV, NMR, EPR, IR and Raman spectra can be performed in on a reliable base in future works. Characterization of molecular interactions between technetium and rhenium complexes and their respective targets support the future development of radiopharmaceuticals. Computational evaluation of main interactions between receptor sites and prospective radiopharmaceuticals will allow a careful selection of suitable biomolecules that may function as effective vectors for in vivo delivery of activity to more specific biological targets. The quantum mechanics-molecular mechanics (QM/MM) approach could solve problems related to the size of the biomolecular systems by explicitly taking the whole system into account while describing it at different levels of accuracy, according to the relative importance of the different parts. The use of Density Functional based Tight-Binding (DFTB) could also answer the problem of size permitting calculations of large systems, even on a normal PC. Systems that are limited for the time using the common DFT can be calculated using DFTB. Additionally, DFTB can be used in previous step as a pre-screening tool before a higher level method is performed.

5 Conclusions

In recent years, computational chemistry has emerged as powerful tool to complement experimental investigations in the development of new ^99mTc and ^186/188Re radiopharmaceuticals. Computational chemistry in this field is based on several quantum chemical methods. Their accuracy and versatility to predict and explain molecular properties is a valuable, economic and fast enough tool to study molecular systems. Density functional theory is the most commonly used method in the calculation of Tc and Re compounds. A clear focus is set on investigating the influence of different ligand motives on the electronic structures, the spectroscopic properties and the relative stability of Tc and Re complexes. Theoretical calculations will drive the design of new radiopharmaceuticals in future but are currently not considered to the sufficient extent they deserve. Overall combinations of several computational modalities and the calculation of different molecular properties must address this. Moreover, the synergy between theory and experiment is crucial to accelerate the urgently needed development of new radiopharmaceuticals. Quantum calculations help to discover and develop more thermodynamically stable radiopharmaceuticals. The calculation of reaction mechanisms for predicting reaction products and kinetic stabilities relies on theory. The characterization of molecular interactions, the environment effect and biological activity determination by computational methods will be crucial in future studies. Although most of this is already possible right now, the increase of computational power and the development of new or improved methods will make it more convenient in the near future.

Acknowledgements

The authors wish to thank the InSTEC project “Theoretical and experimental studies of compounds of interest to the Radiopharmacy” for the financial support.

References

1. F. Jensen, Introduction to computational chemistry, Wiley & Sons, Chichester, 2nd edn, 2007.
2. C. J. Cramer, Essentials of computational chemistry: theories and models, Wiley & Sons, Chichester, 2nd edn, 2004.
3. M. D. Bartholoma, A. S. Louie, J. F. Valliant and J. Zubieta, Chem. Rev., 2010, 110, 2903–2920.
4. R. Alberto, in Bioinorganic medicinal chemistry, ed. E. Alessio, Wiley-VCH, Weinheim, 2011, ch. 9, pp. 253–282.
5. R. Alberto, Cosmos, 2012, 8, 83–101.
6. T. R. Cundari, Chem. Rev., 2000, 100, 807–818.
7. A. Ceulemans, L. F. Chibotaru, G. A. Heylen, K. Pierloot and L. G. Vanquickenborne, Chem. Rev., 2000, 100, 787–806.
8. N. S. Hush and J. R. Reimers, Chem. Rev., 2000, 100, 775–786.
9. G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717–774.
10. J. F. Harrison, Chem. Rev., 2000, 100, 679–716.
11. J. A. Alonso, Chem. Rev., 2000, 100, 637–678.
12. F. Maseras, A. Lledós, E. Clot and O. Eisenstein, Chem. Rev., 2000, 100, 601–636.
13. M.-M. Rohmer, M. Bénard and J.-M. Poblet, Chem. Rev., 2000, 100, 495–542.
14. M. Torrent, M. Solà and G. Frenking, Chem. Rev., 2000, 100, 439–494.
15. P. E. M. Siegbahn and M. R. A. Blomberg, Chem. Rev., 2000, 100, 421–438.
16. G. H. Loew and D. L. Harris, Chem. Rev., 2000, 100, 407–420.
17. S. Niu and M. B. Hall, Chem. Rev., 2000, 100, 353–406.
18. E. R. Davidson, Chem. Rev., 2000, 100, 351–352.
19. P. Day, Coord. Chem. Rev., 2003, 238–239, 3–8.
20. P. Comba and R. Remenyi, Coord. Chem. Rev., 2003, 238–239, 9–20.
21. P. Comba and W. Schiek, Coord. Chem. Rev., 2003, 238–239, 21–29.
22. D. E. Ellis and O. Warschkow, Coord. Chem. Rev., 2003, 238–239, 31–53.
23. G. Frenking, K. Wichmann, N. Fröhlich, C. Loschen, M. Lein, J. Frunzke and V. C. M. Rayón, Coord. Chem. Rev., 2003, 238–239, 55–82.
24. J. Autschbach and T. Ziegler, Coord. Chem. Rev., 2003, 238–239, 83–126.
25. A. Ferretti, Coord. Chem. Rev., 2003, 238–239, 127–141.
26. C. Daniel, Coord. Chem. Rev., 2003, 238–239, 143–166.
27. M. D. Newton, Coord. Chem. Rev., 2003, 238–239, 167–185.
28. I. Ciofini and C. A. Daul, Coord. Chem. Rev., 2003, 238–239, 187–209.
29. T. Lovell, F. Himo, W.-G. Han and L. Noodleman, Coord. Chem. Rev., 2003, 238–239, 211–232.
30. H. Erras-Hanauer, T. Clark and R. van Eldik, Coord. Chem. Rev., 2003, 238–239, 233–253.
31. I. P. Georgakaki, L. M. Thomson, E. J. Lyon, M. B. Hall and M. Y. Darensbourg, Coord. Chem. Rev., 2003, 238–239, 255–266.
32. R. A. Friesner, M.-H. Baik, B. F. Gherman, V. Guallar, M. Wirstam, R. B. Murphy and S. J. Lippard, Coord. Chem. Rev., 2003, 238–239, 267–290.
33. A. J. Boone, C. H. Chang, S. N. Greene, T. Herz and N. G. J. Richards, Coord. Chem. Rev., 2003, 238–239, 291–314.
34. C. E. Webster and M. B. Hall, Coord. Chem. Rev., 2003, 238–239, 315–331.
35. J. Reinhold, A. Barthel and C. Mealli, Coord. Chem. Rev., 2003, 238–239, 333–346.
36. J. N. Harvey, R. Poli and K. M. Smith, Coord. Chem. Rev., 2003, 238–239, 347–361.
37. V. N. Sapunov, R. Schmid, K. Kirchner and H. Nagashima, Coord. Chem. Rev., 2003, 238–239, 363–382.
38. P. Macchi and A. Sironi, Coord. Chem. Rev., 2003, 238–239, 383–412.
39. C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 1057–10816.
40. F. Neese, Coord. Chem. Rev., 2009, 253, 526–563.
41. J. Harvey, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 203–226.
42. C. Platas-Iglesias, A. Roca-Sabio, M. Regueiro-Figueroa, D. Esteban-Gómez, A. de Blas and T.-B. Rodriguez, Curr. Inorg. Chem., 2011, 1, 91–116.
43. K. P. Kepp, Coord. Chem. Rev., 2013, 257, 196–209.
44. A. C. Tsipis, Coord. Chem. Rev., 2014, 272, 1–29.
45. C. A. Tsipis, Comments Inorg. Chem., 2004, 25, 19–74.
46. K. Schwochau, Technetium: chemistry and radiopharmaceutical applications, Wiley-VCH, Weinheim, 2000.
47. G. B. Saha, Fundamentals of nuclear pharmacy, Springer, New York, 6th edn, 2010.
48. H.-J. Pietzsch, H. Spies and S. Hoffmann, Inorg. Chim. Acta, 1989, 165, 163–166.
49. I. A. E. Agency, Labelling of small biomolecules using novel technetium-99m cores, IAEA, Viena, 2007.
50. G. R. Morais, A. Paulo and I. Santos, Organometallics, 2012, 31, 5693–5714.
51. M. Benz, H. Braband, P. Schmultz, J. Halter and R. Alberto, Chem. Sci., 2015, 6, 165–169.
52. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
53. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
54. J. Gancheff, C. Kremer, E. Kremer and O. N. Ventura, J. Mol. Struct.: THEOCHEM, 2002, 580, 107–116.
55. M. Lipowska, R. Cini, G. Tamasi, X. Xu, A. T. Taylor and L. G. Marzilli, Inorg. Chem., 2004, 43, 7774–7783.
56. B. Safi, J. Mertens, F. D. Proft, R. Alberto and P. Geerlings, J. Phys. Chem. A, 2005, 109, 1944–1951.
57. B. Safi, J. Mertens, F. De Proft and P. Geerlings, J. Phys. Chem. A, 2006, 110, 9240–9246.
58. B. Safi, J. Mertens and P. Geerlings, Nucl. Med. Biol., 2008, 35, 747–753.
59. A. Seridi, M. Wolff, A. Boulay, N. Saffon, Y. Coulais, C. Picard, B. Machura and E. Benoist, Inorg. Chem. Commun., 2011, 14, 238–242.
60. M. Wolff, L. Munoz, A. François, C. Carrayon, A. Seridi, N. Saffon, C. Picard, B. Machura and E. Benoist, Dalton Trans., 2013, 42, 7019–7031.
61. B. Machura, M. Wolff, A. Świtlicka, R. Kruszynski and J. Mroziński, Struct. Chem., 2010, 21, 761–769.
62. B. Machura, M. Wolff and I. Gryca, Inorg. Chim. Acta, 2011, 370, 7–17.
63. B. Machura, I. Gryca and M. Wolff, Polyhedron, 2012, 31, 128–135.
64. B. Machura, M. Wolff, D. Tabak, Y. Ikeda and K. Hasegawa, Polyhedron, 2012, 39, 76–84.
65. B. Machura, M. Wolff, W. Kowalczyk and R. Musiol, Polyhedron, 2012, 33, 388–395.
66. B. Machura, M. Wolff, E. Benoist and Y. Coulais, J. Organomet. Chem., 2013, 724, 82–87.
67. R. Mahfouz, E. Al-Frag, M. R. H. Siddiqui, W. Z. Al-kiali and O. Karama, Arabian J. Chem., 2011, 4, 119–124.
68. A. A. Dahy, E. S. Al-Farrag, N. S. Al-Hokbany and R. M. Mahfouz, J. Coord. Chem., 2016, 1088–1099.
69. A. Brink, H. G. Visser and A. Roodt, J. Coord. Chem., 2011, 64, 122–133.
70. A. Brink, H. G. Visser and A. Roodt, Polyhedron, 2013, 52, 416–423.
71. N. S. Al-Hokbany, Radiochemistry, 2012, 54, 284–290.
72. L. Qiu, J. G. Lin, X. D. Gong, W. Cheng and S. N. Luo, Bull. Korean Chem. Soc., 2012, 33, 4084–4092.
73. D. W. Demoin, Y. Li, S. S. Jurisson and C. A. Deakyne, Comput. Theor. Chem., 2012, 997, 34–41.
74. Y. Li, V. Gaddam, F. Gallazzi, H. M. Hennkens, M. Harmata, M. R. Lewis, C. A. Deakyne and S. S. Jurisson, Inorg. Chem., 2016, 55, 1124–1133.
75. D. Hernández-Valdés, A. Blanco-González, A. García-Fleitas, Z. Rodríguez-Riera, G. Meola, R. Alberto and U. Jáuregui-Haza, J. Mol. Graphics Modell., 2016, 22, 1–12.
76. R. Schibli, N. Marti, P. Maurer, B. Spingler, M. L. Lehaire, V. Gramlich and C. L. Barnes, Inorg. Chem., 2005, 44, 683–690.
77. M. Videira, L. Maria, A. Paulo, I. C. Santos, I. Santos, P. D. Vaz and M. J. Calhorda, Organometallics, 2008, 27, 1334–1337.
78. C. Moura, C. Fernandes, L. Gano, A. Paulo, I. C. Santos, I. Santos and M. J. Calhorda, J. Organomet. Chem., 2009, 694, 950–958.
79. A. Boulay, A. Seridi, C. Zedde, S. Ladeira, C. Picard, L. Maron and E. Benoist, Eur. J. Inorg. Chem., 2010, 5058–5062.
80. L. Fuks, E. Gniazdowska and P. Koźmiński, Polyhedron, 2010, 29, 634–638.
81. W. Xiangyun, W. Yi, L. Xinqi, C. Taiwei, H. Shaowen, W. Xionghui and L. Boli, Phys. Chem. Chem. Phys., 2003, 5, 456–460.
82. L. Fuks, E. Gniazdowska and N. Sadlej-Sosnowska, Struct. Chem., 2010, 21, 827–835.
83. A. Noor, G. S. Huff, S. V. Kumar, J. E. M. Lewis, B. M. Paterson, C. Schieber, P. S. Donnelly, H. J. L. Brooks, K. C. Gordon, S. C. Moratti and J. D. Crowley, Organometallics, 2014, 33, 7031–7043.
84. A. K. Pramanik, M. S. Jana, S. Kundu and T. K. Mondal, J. Mol. Struct., 2012, 1017, 19–25.
85. D. Hernández-Valdés, Z. Rodríguez-Riera, A. Díaz-García, E. Benoist and U. Jáuregui-Haza, J. Mol. Model., 2016, 22, 1–12.
86. P. Maurer, A. Magistrato and U. Rothlisberger, J. Phys. Chem. A, 2004, 108, 11494–11499.
87. P. F. Weck, E. Kim, F. Poineau, E. E. Rodriguez, A. P. Sattelberger and K. R. Czerwinski, Inorg. Chem., 2009, 48, 6555–6558.
88. F. Poineau, C. D. Malliakas, P. F. Weck, B. L. Scott, E. V. Johnstone, P. M. Forster, E. Kim, M. G. Kanatzidis, K. R. Czerwinski and A. P. Sattelberger, J. Am. Chem. Soc., 2011, 133, 8814–8817.
89. F. Poineau, E. V. Johnstone, P. F. Weck, P. M. Forster, E. Kim, K. R. Czerwinski and A. P. Sattelberger, Inorg. Chem., 2012, 51, 4915–4917.
90. E. V. Johnstone, P. F. Weck, F. Poineau, E. Kim, P. M. Forster, A. P. Sattelberger and K. R. Czerwinski, Eur. J. Inorg. Chem., 2013, 1097–1104.
91. S. M. Balasekaran, J. Spandl, A. Hagenbach, K. Köhler, M. Drees and U. Abram, Inorg. Chem., 2014, 53, 5117–5128.
92. F. Poineau, P. F. Weck, K. German, A. Maruk, G. Kirakosyan, W. Lukens, D. B. Rego, A. P. Sattelberger and K. R. Czerwinski, Dalton Trans., 2010, 39, 8616–8619.
93. E. V. Johnstone, D. J. Grant, F. Poineau, L. Fox, P. M. Forster, L. Ma, L. Gagliardi, K. R. Czerwinski and A. P. Sattelberger, Inorg. Chem., 2013, 52, 5660–5662.
94. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
95. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
96. C. Ch, M. Pelissier and D. Ph, Phys. Scr., 1986, 34, 394.
97. E. V. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
98. R. Alberto, R. Schibli, R. Waibel, U. Abram and A. P. Schubiger, Coord. Chem. Rev., 1999, 190–192, 901–919.
99. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
100. A. D. Becke, J. Chem. Phys., 1988, 88, 1053–1062.
101. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
102. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805,  10.1039/p29930000799.
103. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
104. C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408.
105. J. L. Moretti, J. R. Rapin, J. C. Saccavini, A. Lageron, M. Le Poncin and A. Bardy, Int. J. Nucl. Med. Biol., 1984, 11, 270–274.
106. D. T. Mancini, E. F. Souza, M. S. Caetano and T. C. Ramalho, Magn. Reson. Chem., 2014, 52, 129–137.
107. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
108. E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041.
109. B. Mennucci, E. Cancès and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506–10517.
110. E. Cancès and B. Mennucci, J. Math. Chem., 1998, 23, 309–326.
111. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
112. S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
113. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
114. Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Phys., 2005, 123, 161103.
115. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130.
116. Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382.
117. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
118. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
119. L. Vigara, M. Z. Ertem, N. Planas, F. Bozoglian, N. Leidel, H. Dau, M. Haumann, L. Gagliardi, C. J. Cramer and A. Llobet, Chem. Sci., 2012, 3, 2576–2586.
120. M. Z. Ertem, L. Gagliardi and C. J. Cramer, Chem. Sci., 2012, 3, 1293–1299.
121. G. Huang, B. Cheng, L. Xu, Y. Li and Y. Xia, Chem.–Eur. J., 2012, 18, 5401–5415.
122. K. Lee, W. C. Isley, A. L. Dzubak, P. Verma, S. J. Stoneburner, L.-C. Lin, J. D. Howe, E. D. Bloch, D. A. Reed, M. R. Hudson, C. M. Brown, J. R. Long, J. B. Neaton, B. Smit, C. J. Cramer, D. G. Truhlar and L. Gagliardi, J. Am. Chem. Soc., 2014, 136, 698–704.
123. D. Yang, S. O. Odoh, T. C. Wang, O. K. Farha, J. T. Hupp, C. J. Cramer, L. Gagliardi and B. C. Gates, J. Am. Chem. Soc., 2015, 137, 7391–7396.
124. X. Yan, X. Li, Z. Sun, Q. Li and L. Meng, New J. Chem., 2016, 40, 1988–1996.
125. E. D. Sosa Carrizo and I. Fernandez, Phys. Chem. Chem. Phys., 2016, 18, 11677–11682.
126. Y. Liu, Z. Luo, J. Z. Zhang and F. Xia, J. Phys. Chem. A, 2016, 120, 6485–6492.
127. S. Záliš, C. J. Milne, A. E. Nahhas, A. M. Blanco-Rodríguez, R. M. van der Veen and A. Vlček Jr, Inorg. Chem., 2013, 52, 5775–5785.

---