Online parameter identification of a giant magnetostrictive actuator based on the dynamic Jiles–Atherton model
Ce Rong*,
Zhongbo He,
Dongwei Li,
Guangming Xue and
Zhaoshu Yang
Department of Vehicle and Electrical Engineering, Shijiazhuang Mechanical Engineering College, Shijiazhuang, People's Republic of China. E-mail: rongc1102@sohu.com
First published on 28th November 2016
Abstract
Giant magnetostrictive actuator (GMA) suffers dominant hysteresis nonlinearity while working. In order to better predict its output, a dynamic model of GMA based on the J–A model is established. On the foundation of the model, an online parameter identification method is proposed. Classified into two types, some parameters are determined by physical theories, while the others are identified by a sensitivity-based identification method. Serving as the identification algorithm, the particle swarm optimization (PSO) algorithm is modified to accelerate the identification process. Moreover, to validate the effectiveness of the proposed method, an online parameter identification system is designed as well as identification software. Experimental results prove that the proposed system performs well and is fit for online identification.
1 Introduction
Giant magnetostrictive material (GMM) is an intelligent material firstly invented by A. E. Clark in the 1970s.1 Compared with other smart materials, GMM has many excellent features such as large deformation, great output force as well as high energy density.2 Due to its good performance, actuators based on giant magnetostrictive materials, usually called GMAs, have been widely applied in many areas stretching from sonar systems3 to precision machining.4,5 However, just like actuators based on piezoelectric materials and shape memory alloys, GMAs also possess some inherent defects: strong nonlinearity, multi-field coupling and vulnerability to outside factors. These properties are detrimental to improve their control precision.6 Therefore, it is of significant importance to establish an accurate model and identify parameters precisely.As hysteresis nonlinearity exists in GMA between the input current and the output displacement, a thorough depiction of the hysteresis property helps to better predict its final displacement. At present, hysteresis model of GMA can be roughly classified into two types: namely, mathematical model and physical model.6 Mathematical model is a kind of black box model, which only cares about the relationship between input and output. Preisach model is one of the most famous mathematical models.7 Due to its general applicability and good performance in fitting hysteresis curves, it is widely used to depict the hysteresis loop of GMA. Similar to Presaich model, Prandtl–Ishlinskii model (P–I model) and Bouc–Wen model are other representative mathematical models.8–10 Since their inverse can be obtained analytically, they have been applied to control of GMA. However, mathematical model usually fails to match the hysteresis loop well in dynamic conditions, even if the eddy-current loss and abnormal loss are counted. Moreover, identification of the parameters in these models often relies on large quantities of experiment data, making it sensitive to experiment error inevitably. Different from mathematical model, physical model is set up based on correlative physical process, which can reveal the mechanism of hysteresis. Therefore, physical model not only describes the hysteresis loop, but also contributes to design, optimizing and control of GMA. Established depending on micromagnetics and Weiss molecular field theory, Jiles–Atherton model (J–A model) has some advantages over the other models such as relatively simple expressions and high precision.11 So it is widely used to predict both static and dynamic output of GMA.
Advantages as J–A model has, it can't be neglected that the parameters of J–A model are strongly coupled, making them difficult to determine. Jiles first established five implicit equations via five special points in the hysteresis loop, and parameters of J–A model can be identified by iterative algorithm through these equations.12 Calkins divided the identification process into two step: in the first step, sequential quadratic programming was used to fit the magnetization model, and the second step attempted to get reasonable estimation of parameters in the magnetostrictive model.13 In recent studies, many efforts are made to identify the J–A model including adjoint method,14 Taguchi method15 and several intelligent algorithms.16–18 These methods get good results in the offline case. Among them, particle swarm optimization (PSO) algorithm possesses its own advantages such as fast convergence speed, high precision and insensitivity to initial values.19,20
Nevertheless, when GMA works in dynamic status, the problem becomes more complicated. The parameters in J–A model may vary in real time. The reasons can be summarized as follows.
(1) Change of working temperature may cause parameter altering.
Aiming to provide excitation magnetic field, coil is an essential part of GMA. In dynamic condition, a large amount of heat is generated by coil. Enclosed by a housing, GMA performs poorly in heat dissipation. So the temperature of GMM may rise a lot while working. Although self-cooling system is designed,21 the temperature still can't remain constant for the space inside the GMA is too small. Literatures published before show that the saturation magnetization, coercivity and remanence of GMM may change with temperature, similar to most of the ferromagnetic materials. This phenomenon leads to four temperature dependent parameters in J–A model, which are Ms, k, α and c.22
(2) Change of excitation frequency may cause parameter altering.
Sensitive to the outside factors, GMM can be easily influenced by the mechanical structure of GMA in high frequency. In turn, the mechanical properties of GMM may also exert a tremendous influence on the mechanical structure. The two components of GMA interact with each other, leading to a result that the parameters change along with the altering of excitation frequency. Some scholars discover a phenomenon while conducting experiments: if the parameters are kept constant, the model of GMA can't fit the experiment data well with frequency altering even though eddy current loss and abnormal loss are considered.23,24
Therefore, constant parameters can't predict the output of GMA precisely. Online identification and adjustment of these parameters is important and necessary. As far as we are concerned, there are still few literatures concerning this issue.
The framework of our work is set as follows: Section 1 introduces the background and necessity of this work; Section 2 describes the structure and working principle of GMA; Section 3 establishes the model of GMA considering the dynamic properties of both the GMM and the mechanical structure; Section 4 analyzes each parameter of the established model and proposes an online identification method; in Section 5, an improved PSO algorithm suitable for online identification is introduced; in Section 6, an online parameter identification system is set up; in Section 7, experimental validation is conducted and the results are discussed; in Section 8, some conclusions are drawn.
2 Structure of GMA
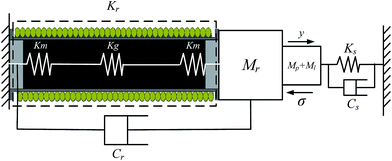
The structure of GMA is detailed in Fig. 1. It mainly contains excitation coil, GMM rod, permanent magnets, housing, disc spring and push-rod. When the GMA works, working current, flowing in excitation coil, generates driving magnetic field along the axial dimension of GMM rod. Under the action of the magnetic field, the GMM rod is deformed, which is called magnetostrictive effect. Followed with the GMM rod, the push-rod outputs displacement and force. Permanent magnets, pasted on both ends of the GMM rod, are used to provide a bias magnetic field so as to avoid frequency doubling of GMM. Disc spring exerts pre-pressure on GMM rod, since larger deformation can be obtained on condition that the GMM rod is preloaded. The housing provides a container for other components and ensures each element has its fixed position in it.3 Dynamic model of GMA
3.1 Magnetic field model
Magnetic field model describes the relationship between excitation current I and magnetic field H, which can be expressed as
 | (1) |
3.2 Magnetization model
The hysteresis between magnetic field H and magnetization M can be described by dynamic J–A model, which is established based on the energy principle. The total energy available to the material can be decomposed into two parts including the energy that the GMM rod absorbs and the energy dissipated, shown as follows.| Etol = Eabs + Edis | (2) |
The total energy can be calculated by
 | (3) |
 | (4) |
 | (5) |
The first term on the right hand denotes the hysteresis loss the same as that in static J–A model. The second one denotes the eddy current loss and the third one denotes the abnormal loss. In this equation, k is a parameter quantifying the energy needed to break pinning sites, c is the reversible coefficient, δ is 1 when Ḣ > 0 and is −1 when Ḣ < 0, ρ is the resistivity of excitation coil, d is the diameter of the cross section, β is a geometrical factor, for cylinder it is 16, G is a constant independent of dimension, w is the width of laminations, and H0 is a parameter related to domain walls.
Combine eqn (5) with other equations in J–A model shown as eqn (6).
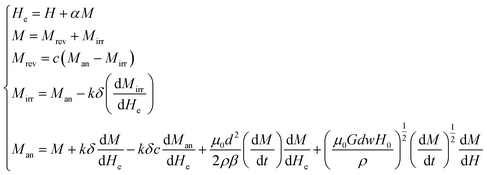 | (6) |
The dynamic J–A model can be finally simplified down to a differential equation
 | (7) |
To solve the differential equation, 4-order Runge–Kutta method needs to be used, with Newton–Raphson method applied to solve the step length of Runge–Kutta.
3.3 Magnetostriction model
The magnetostriction of GMM rod along the axial dimension can be calculated by the quadratic domain rotation model expressed as follows
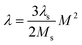 | (8) |
3.4 Dynamics model
To describe the relationship between magnetostriction λ and output displacement y, GMA is often regarded as a second-order system,25 and the transfer equation can help to express its final output.
 | (9) |
In conclusion, there are eleven parameters need identifying in total. To list them out, they are α, a, k, c, λs, Ms, H0, E, M, C, and K.
4 Reduction of parameters to be identified
According to the previous researches, if the driving frequency or the working temperature of GMA alters, the parameters of the model may change. And the output of the GMA may vary a lot as well.26 As a result, while working in dynamic condition, it is necessary to identify and adjust the parameters online to better predict the output of the GMA. However, identification methods available usually rely on a large number of iterations to obtain a satisfactory solution, especially intelligent algorithms, which have relatively high precision. Thus, if there is one more parameter to be identified, a large quantity of excess calculation is needed. Therefore, to realize online identification, these parameters have to be reduced in number. For the sake of this target, two methods are proposed in this section, one of which is to determine some parameters by calculation, and the other one is to select out parameters that have little influence on the output.4.1 Reducing parameters by calculation
As is mentioned above, ascribed to the modeling method based on physical process, each parameter in dynamic model of GMA has its own physical meaning. Hence, some parameters are not difficult to be calculated by basic physical theories such as equivalent mass M, Young's modulus E and equivalent stiffness K.
 | (10) |
 | (11) |
As for Kg, with the assumption that magnetic field inside the excitation coil is uniform, Kg can be represented by
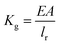 | (12) |
 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 A m−1 with preload of 10 MPa.
000 A m−1 with preload of 10 MPa.
4.2 Selection of non-sensitive parameters
Even though some parameters can be calculated by methods discussed above, there are still too many parameters need identifying, resulting in large computing amount and impossibility of online identification and adjustment of these parameters.To reduce the parameters further, every parameter left is analyzed to estimate its influence on the final displacement of the GMA, so that the parameters, which have little influence on the output, will be identified only once and fixed during the process of online identification. Based on the idea, three steps are employed as follows:
Step 1: build a reference model based on the parameters displayed in the Table 1, which is obtained by us through offline identification.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Ms | 800 kA m−1 | M | 0.06 kg |
| λs | 1000 ppm | C | 3305 Ns m−1 |
| a | 7800 A m−1 | G | 0.1356 |
| c | 0.18 | d | 8 mm |
| α | −0.001 | w | 3.6 |
| k | 3200 A m−1 | β | 16 |
| H0 | 225.1 A m−1 | ρ | 0.0172 Ω mm−2 m−1 |
| f | 100 Hz |
Step 2: alter the value of each parameter successively with the range of ±15%, plot comparative graph via Matlab and calculate the output displacement deviation for a certain parameter by the following equation
 | (14) |
| Parameter | θmax | Parameter | θmax |
|---|---|---|---|
| Ms | 2.0311 × 10−14 | α | 6.1039 × 10−15 |
| λs | 7.2940 × 10−12 | k | 3.2521 × 10−13 |
| a | 7.9395 × 10−12 | C | 6.8836 × 10−14 |
| c | 2.9813 × 10−15 | H0 | 8.964 × 10−15 |
The comparative graphs are shown as Fig. 4.
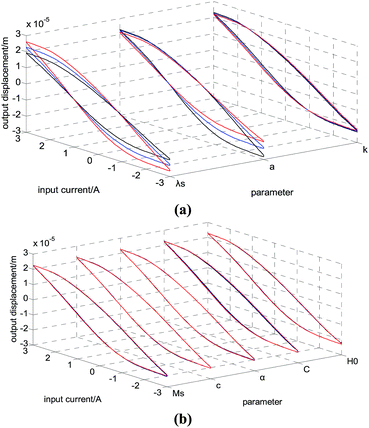 | ||
| Fig. 4 Influence of each parameter on output of GMA (a) parameter λs, a and k (b) parameter Ms, c, α, C and H0. | ||
In Fig. 4, it should be noted that there are three curves in every group. The red one represents the input–output curve determined by the parameters displayed in Table 1. With a certain parameter minus or plus 15%, the black and blue curves are obtained respectively. The curves colored red, black and blue may not be distinguished in Fig. 4(b) for they coincide with each other.
Judging from the figures and calculation above, the parameters can be divided into two types. The first type contains λs, a, and k, which have a significant impact on the final output of GMA, while the rest, classified as the other type, have little influence.
Step 3: for the suspected non-sensitive parameters selected out, alter the value of them further so as to confirm their effects on output of GMA. The variation range of the suspected non-sensitive parameters and their deviation to reference model is shown in Table 3.
| Parameter | Value | θmax |
|---|---|---|
| Ms | [600, 1000] kA m−1 | 6.1202 × 10−14 |
| c | [0.05, 0.40] | 9.1527 × 10−14 |
| α | [−0.01, 0.01] | 3.0059 × 10−11 |
| C | [2000, 4500] Ns m−1 | 1.2278 × 10−13 |
| H0 | [100, 350] A m−1 | 7.952 × 10−14 |
According to Table 3, Ms, c and H0 have much less influence on output of GMA than λs, a, α, C and k. To summary up, λs, a, α, C and k need to be identified and adjusted online, while the others can be fixed to reduce the computation amount of online identification.
5 Identification method based on modified PSO
Particle swarm optimization (PSO) algorithm is an intelligent algorithm widely applied in parameter identification and structure optimization.29 Imitating the feeding behavior of birds, PSO searches optimal solution by moving numerous of searching points, called particles, across the searching space to minimize the fitness function which can be represented as follows.
 | (15) |
Every particle in PSO, which is a potential solution, is attached to two vectors, called velocity vector vi = [vi1, vi2…viD] and position vector Xi = [xi1, xi2, … xiD], where D is the dimension of solution space. As for identification problems, it is the number of parameters to be identified. Particles are initialized by a group of random solutions and search solution space for the best solution adhering to the following equation.
 | (16) |
The new position of particle is substituted into fitness function, and if the fitness value J(Xi) is less than that of pbest, pbest is updated by Xi. The update of gbest follows the same rule mentioned above.
Despite its faster convergence speed than other intelligent algorithms, traditional PSO still can't meet the requirements of online identification. Therefore, some improvements are needed to accelerate it.
(1) A trigonometric function operator is introduced to searching process of the particles. Then, the algorithm can be modified as follows.30
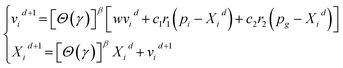 | (17) |
 | (18) |
(2) An error-varying inertia factor is introduced. It is reported that a large inertia factor has a good performance of global searching, while a small one converges to optimal solution more easily. Therefore, a varying inertia factor is necessary in different phase of the algorithm. The error-varying inertia factor can be represented as follows.
 | (19) |
To compare the convergence speed of the modified PSO with traditional one, numeric simulations are conducted in Matlab. It can be detected from Fig. 5 that PSO with improvements converges within 50 iterations, faster than traditional one, and the precision also performs better.
(3) The previous optimized parameters are used as the initial values of the next identification process. In spite that parameters change during the operating procedure of GMA, the range may not be great. Therefore, if the previous optimized parameters are employed as the initial value, the improved PSO may tend to converge in fewer iterations. To validate it, numeric simulations are carried out by Matlab considering the following six conditions as Table 4.
| Condition | Altering range of excitation frequency |
|---|---|
| 1 | 25 Hz → 75 Hz |
| 2 | 125 Hz → 175 Hz |
| 3 | 225 Hz → 275 Hz |
| 4 | 25 Hz → 125 Hz |
| 5 | 125 Hz → 225 Hz |
| 6 | 25 Hz → 225 Hz |
In Table 4, the first three conditions represent where the excitation frequency alters no more than 50 Hz; the conditions numbered 4 and 5 represent where the excitation frequency alters between 50 and 100 Hz; and the last one represents where the excitation frequency alters between 100 and 200 Hz. The simulation results are shown in Fig. 6. The convergence curve can be divided into six parts from left to right. They correspond to the six conditions respectively.
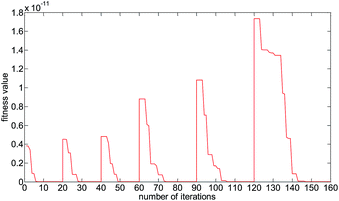 | ||
| Fig. 6 Converge speed of identification algorithm with different altering range of excitation frequency. | ||
Since the previous optimized parameters are near to the current ones, the number of iterations reduces a lot by using them as initial values. According to the results in Fig. 5, when the excitation frequency changes, the iteration number of PSO can be determined as Table 5.
| Range (Hz) | Number of iterations |
|---|---|
| [0, 50] | 10 |
| [50, 100] | 20 |
| [100, 200] | 30 |
| [200, ∞] | 50 |
6 Design of online parameter identification system
To validate the proposed method, online parameter identification system is established. Compared with the offline case, online identification is much more difficult to realize. Many more issues need to be considered. We establish our system centering on data acquisition card (DAQ), which possesses advantages of low cost, high precision and good transplantability.6.1 Design of hardware
As is shown in Fig. 7, the hardware of the identification system mainly consists of four parts: that is, power supply module, GMA, sampling module and master computer.The power supply module is designed aiming to provide excitation current for GMA. It is mainly made up by signal generator and power amplifier. While working, it can drive GMA to generate magnetostriction under the required signal.
The sampling module concerns data acquisition of the input excitation current and the output displacement. It mainly contains a current clamp and an eddy current displacement sensor, both of which have high measurement precision and sensitivity.
The master computer, as the core of the system, is employed to get data from the sampling module and run the software developed to complete the identification process. Inside the computer, DAQ, acting as a bridge between the sensors and the master computer, is embedded, which has a precision of 16 bit.
6.2 Design of software
Whether online identification can be conducted effectively relies on not only hardware but also software. And the software, regarded as a bridge between users and hardware, is developed based on Labwindows/CVI and Matlab, for the reason that CVI is convenient for data acquisition and Matlab has powerful features of numeric computing. With modular design thinking, the software is made up of three parts: namely, data acquisition part, data processing part and user interface part. Main flow chart of the software is shown in Fig. 8.As for identification part alone, if it is the first time to identify, it calls for first-time identification program. All parameters except those can be determined by calculation should be identified and the iteration number of the improved PSO is set as 50. After that, online identification program is called for. With non-sensitive parameters fixed, the others should be identified and adjusted online. The main flow chart of online identification program is shown as Fig. 9. According to the altering range of frequency, the number of iterations is determined following the results in Section 5.
7 Experiment and discussion
With the help of the proposed system, online parameter identification experiments are conducted. According to the operating conditions of GMA, the experiments are classified into two types. In one case, the GMA works in constant frequency and in the other case, the driving frequency changes during the operating procedure of GMA. Besides, it should be noted that both types of experiments are conducted based on the following conditions: (1) the working current is between −3 A and 3 A; (2) the master computer is a workstation with an eight core processor inside. The results are discussed in detail as follows.7.1 Discussion of identification time
The consequences of parameter identification in constant frequency are shown as Fig. 11. It can be observed from Fig. 11(a) that the predicted output is not displayed until about 12 seconds later, for the parameters are not determined until the first identification process is complicated. Moreover, when the deviation is out of the preset threshold due to raised temperature or other causes, the identification algorithm starts again shown as Fig. 11(b). Since the software can only exhibit data within 0.1 second, Fig. 11(b) just displays part of the identification process. The second-time identification process, owing to good initial values of PSO, costs less than 1.5 second to identify, much less than the first-time identification process. | ||
| Fig. 11 Experiment results in constant driving frequency (a) experiment results of first-time identification (b) experiment results of second-time identification. | ||
Fig. 12 shows the experiment results when the driving frequency of GMA changes. The four figures respectively represent the experiment results when the altering range of frequency is 50 Hz, 100 Hz, 200 Hz and more than 200 Hz. To compare the results intuitively, frequency changes are all conducted at the same time, 50 seconds after the beginning of experiments. Observed from the figures, the identification time varies a lot due to different change of frequency. When the frequency alters from 20 Hz to 300 Hz, the identification time is about 6.5 seconds, which is the longest among the experiments.
7.2 Discussion of identification precision
The identification precision, acting as another important assessment index, will be discussed in this section. Since the developed software can store the experiment data, it is convenient to draw the hysteresis loop using the data acquired during the experiment. The results are shown as Fig. 13.Learned from Fig. 13, the displacement output predicted by the identified model of GMA matches the test curves well along the frequencies from 50 Hz to 300 Hz despite some deviations in certain points. And the calculation time, which has been discussed before, is much shorter than previous method. Therefore, it is proved that the identification method proposed in this work is suitable for online system.
8 Conclusion
In this paper, a dynamic model of GMA based on J–A model is established. Considering the dynamic properties of GMM and the mechanical structure, the model can better predict the output displacement of GMA in high excitation frequency.Based on the established model, an online parameter identification method is proposed. Some parameters are determined by calculation through physical theory, and the others are classified into two types according to their sensitivity on final output of GMA. With different identification methods conducted to different type of parameters, the identification time is reduced.
An improved PSO is introduced to complete the process of identification. With some modifications specially for online case, the improved PSO has faster convergence speed than previous ones.
An online parameter identification system is set up to realized online parameter identification for GMA. Both of the hardware and software are developed. Learned from the results, the proposed system performs well and proves its advantage in online identification.
Acknowledgements
The authors acknowledge the financial support from the National Science Foundation of China (Project no. 51275525).Notes and references
- Z. Jia and D. Guo, Theory and Applications of Giant Magnetostrictive Microdisplacement Actuator, Science Press, Beijing, 2008 Search PubMed.
- C. C. Hong, Application of magnetostrictive actuator, Mater. Des., 2013, 46, 617–621 CrossRef.
- L. Sandlund, et al. Giant magnetostrictive composite material for ultrasonic application, Mater. Des., 1992, 13, 246 Search PubMed.
- F. Braghin, S. Chquemani and F. Resta, A low frequency magnetostrictive inertial actuator for vibration control, Sens. Actuators, A, 2012, 180, 67–74 CrossRef CAS.
- C. Yu, C. Wang, H. Deng, T. He and P. Mao, Hysteresis nonlinearity modeling and position control for a precision positioning stage based on a giant magnetostrictive actuator, RSC Adv., 2016, 6, 59468–59476 RSC.
- B. Wang, S. Cao, W. Huang and Y. Sun, Mathematical model and control technology of giant magnetostrictive actuator, J. Hebei Univ. Technol., 2013, 42(1), 6–13 Search PubMed.
- G. Bertotti, Dynamic generalization of the scalar Preisach model of hysteresis, IEEE Trans. Magn., 1992, 28(5), 2599–2601 CrossRef.
- M. A. Zaman and U. Sikder, Bouc–Wen hysteresis model identification using modified firefly algorithm, J. Magn. Magn. Mater., 2015, 395, 229–233 CrossRef CAS.
- P. Zhai, B. Xiao, K. He and K. Zhang, Composite backward control for GMA and its application in high precision machining of variable ellipse pinhole, Opt. Precis. Eng., 2016, 24(6), 1389–1398 CrossRef.
- F. Ikhouane, V. Mañosa and J. Rodellar, Dynamic properties of the hysteretic Bouc–Wen model, Syst. Contr. Lett., 2007, 56(3), 197–205 CrossRef.
- F. Fulginei, G. Lozito, S. Gaiotto and A. Salvini, Improving the Jiles–Atherton model by introducing a full dynamic dependence of parameters, in Research and Technologies for Society and Industry Leveraging a better tomorrow (RTSI), 2015 IEEE 1st International Forum on Date of Conference 2015 Search PubMed.
- D. C. Jiles, Theory of the magnetostrictive effect, J. Phys. D: Appl. Phys., 1995, 28, 1537–1546 CrossRef CAS.
- F. T. Calkins, R. C. Smith and A. B. Flatau, Energy-Based Hysteresis Model for Magnetostrictive Transducers, IEEE Tansactions on Magnetics, 2000, 36(2), 429–439 CrossRef.
- M. A. Zaman, et al. Adjoint method for estimating Jiles–Atherton hysteresis model parameters, J. Appl. Phys., 2016, 120(9), 093903 CrossRef.
- M. A. Zaman and M. A. Matin, Optimization of Jiles–Atherton hysteresis model parameters using Taguchi's method, IEEE Trans. Magn., 2015, 51(5), 1–4 CrossRef.
- A. Meng, J. Zhu, C. Liu, W. Chen and F. Luo, Parameter Identification of Hysteresis Model gor GMA Based on Improved PSO Algorithm, Control Engineering of China, 2014, 21(5), 735–739 Search PubMed.
- M. Hammid, S. M. Mimoune and M. Feliachi, Minor hysteresis loops model based on exponential parameters scaling of the modified Jiles–Atherton model, Phys. B, 2012, 407(13), 2438–2441 CrossRef.
- M. Toman, G. Stumberger and D. Dolinar, Parameter identification of the Jiles–Atherton hysteresis model using differential evolution, IEEE Trans. Magn., 2008, 44(6), 1098–1101 CrossRef.
- X. Yang, J. S. Yuan, J. Y. Yuant and H. Mao, A modified particle swarm optimizer with dynamic adaptation, Applied Mathematics and Computation, 2007, 189(2), 1205–1213 CrossRef.
- Y. Shi, Particle swarm optimization: developments, applications and resources, the 2001 Congress on Evolutionary Computation, 2001, pp. 81–86 Search PubMed.
- Z. Jia, X. Yang, D. Guo and L. Hou, Theories and methods of designing microdisplacement actuator based on giant magnetostrictive materials, Chin. J. Mech. Eng., 2001, 37(11), 46–49 CrossRef.
- A. Nouicer, E. Nouicer and F. Mouloud, A neural network for incorporating the thermal effect on the magnetic hysteresis of the 3F3 material using the Jiles–Atherton model, J. Magn. Magn. Mater., 2015, 373, 240–243 CrossRef CAS.
- W. Huang, B. Wang, S. Cao, Y. Sun and L. Weng, Dynamic model of giant magnetostrictive transducer considering eddy current effects and variational stress, Proceedings of the CSEE, 2005, 25(16), 132–136 Search PubMed.
- S. Cao, B. Wang, R. Yang, W. Huang and L. Weng, Dynamic model with hysteresis nonlinearity for a giant magnetostrictive actuator, Proceedings of the CSEE, 2003, 23(11), 145–149 Search PubMed.
- J. Zheng, S. Cao, H. Wang and W. Huang, Hybrid genetic algorithms for parameter identification of a hysteresis model of magnetostrictive actuators, Neurocomputing, 2007, 70(4–6), 749–761 CrossRef.
- L. Li, B. Yan and C. Zhang, Influence of frequency on characteristic of loss and temperature in giant magnetostrictive actuator, Proceedings of the CSEE, 2011, 31(18), 124–129 Search PubMed.
- X. Tan and J. S. Baras, Modeling and control of hysteresis in magnetostrictive actuators, Automatica, 2004, 40, 1469–1840 CrossRef.
- X. J. Zheng and X. E. Liu, A nonlinear constitutive model for Terfenol-D rods, J. Appl. Phys., 2005, 053901, 1–8 Search PubMed.
- M. Clerc, Particle Swarm Optimization, ISTE Ltd, London, 2006 Search PubMed.
- Z. Ren and J. Wang, Accelerate convergence particle swarm optimization algorithm, Control and Decision, 2011. vol. 26(2), pp. 201–206 Search PubMed.
| This journal is © The Royal Society of Chemistry 2016 |