Effect of the substitution position (2, 3 or 8) on the spectroscopic and photophysical properties of BODIPY dyes with a phenyl, styryl or phenylethynyl group†
Abstract
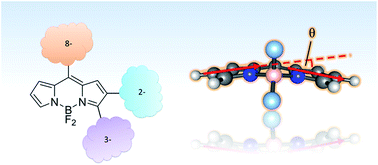
A very active branch of organic chemistry is putting great effort into tailoring fluorescent dyes for a myriad of applications, from technological to bioanalytical and biomedical applications. Among the major families of fluorophores, those derived from 4,4-difluoro-4-bora-3a,4a-diaza-s-indacene (BODIPY dyes) are undergoing a recent boost thanks to the simplicity and robustness of the chemistry involved. The BODIPY core can be modified with numerous side groups, the 8-position being a modification place with important effects on the spectroscopic and photophysical properties of the resulting dyes. Likewise, previous work has shown that the addition of groups attached at the 3- and 2-positions can result in dyes with very different properties. Herein, we generalize the effect of the substituent side groups by studying nine BODIPY dyes substituted with a phenyl, styryl or phenylethynyl moiety at the 2-, 3- or 8-position of the BODIPY scaffold. Within the class of phenyl- or phenylethynyl-substituted dyes, substitution at the 2-position always leads to dyes with the broadest bandwidths and the largest Stokes shifts. We investigate the solvent effect on the spectroscopic properties of the dyes, using four empirical solvent scales (dipolarity, polarizability, acidity and basicity: Catalán, J. Phys. Chem., 2009, 113, 5951). These analyses identify solvent dipolarity and polarizability as critical parameters accounting for the observed solvent-dependent shifts of the absorption and emission maxima. Finally, time-dependent density functional theory calculations provide insights into the structural and energetic issues concerning the spectroscopic properties of these fluorophores.


 Please wait while we load your content...
Please wait while we load your content...