Philippe F. Weck and Eunja Kim
RSC Adv., 2016,6, 107286-107292
DOI:
10.1039/C6RA22249H,
Paper
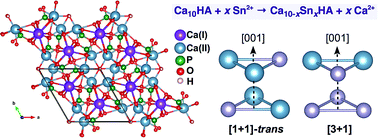
The energetics of Sn2+ substitution into the Ca2+ sublattice of hydroxylapatite (HA), Ca10(PO4)6(OH)2, has been investigated within the framework of density functional theory. Calculations reveal that Sn2+ incorporation via coupled substitutions at Ca(II) sites is energetically favourable up to a composition of Sn6Ca4(PO4)6(OH)2, and further substitutions at Ca(I) sites proceed once full occupancy of Ca(II) sites by Sn2+ is achieved. Compositions of SnxCa10−x(PO4)6(OH)2 (x = 4–9) are predominant, with an optimal stoichiometry of Sn8Ca2(PO4)6(OH)2, and Sn-substituted HA follows approximately Vegard's law across the entire composition range.