Transport properties of the n-type SrTiO₃/LaAlO₃ interface

Abstract

The thermoelectric properties of the (001) n-type 6.5STO/1.5LAO interface were investigated by means of the all-electron full-potential method based on the semi-classical Boltzmann theory. Calculations show that the n-type 6.5STO/1.5LAO interface exhibits non-zero density of states at the Fermi level (E_F), which leads to unusual transport properties and enhances the electrical conductivity. The influence of the temperature on the carrier mobility and the carrier concentration has been investigated. The calculated carrier concentration as a function of temperature is in concordance with previous experimental and theoretical work. At above the E_F, a significant increase in the electrical conductivity occurs to reach the maximum value 1.98 × 10²⁰ (Ω m s)⁻¹ at µ − E_F = 0.05 eV for 300 K, confirming that the 6.5STO/1.5LAO interface is an n-type conduction. The Seebeck coefficient has a negative sign, which confirms that the 6.5STO/1.5LAO interface is an n-type conduction in the vicinity of E_F. It has been found that the power factor is zero at low temperature, which rapidly increases to reach its maximum value 8.1 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at 900 K. Furthermore, the transport coefficients were investigated as a function of chemical potential at three constant temperatures (300, 600 and 900 K). We would like to highlight that our calculated Seebeck coefficient and carrier concentration are in concordance with previous experimental and theoretical work on 4, 5 and 6 u.c. STO/LAO interfaces. The large Seebeck coefficient is attributed to the non-zero density of states at the E_F. The increase of the Seebeck coefficient also leads to a maximum of the power factor.

---

1. Introduction

Recently, it has been found that the LaAlO₃ (LAO) and SrTiO₃ (STO) interfaces show numerous promising applications, for instance as quasi-two-dimensional (2D) electron transport with high electron mobility,¹ for novel devices and technology, 2D superconductivity at low temperatures,² electric field-tuned metal insulators and superconductor insulator phase transitions.³ One of the notable examples is the interface between two band insulators with the perovskite ABO₃ structure, LaAlO₃ (LAO), and SrTiO₃ (STO).⁴ In the [001] direction, two different interfaces can be formed between the polar LaAlO₃, which consists of alternating (LaO)⁺–(AlO₂)⁻ layers, and the nonpolar SrTiO₃, which consists of alternating (SrO)⁰–(TiO₂)⁰ layers. These are LaO/TiO₂ stacking configuration (n-type) and AlO₂/SrO configuration (p-type).⁵ The conductivity occurs only at n-type interfaces when the LaAlO₃ film thickness (n_LAO) is larger than three unit cells (u.c.).^6,7 The n-type interface, in which the LAO layer is grown on top of TiO₂-terminated STO, has highly mobile carriers, while the p-type interface, in which the LAO layer is grown on top of SrO-terminated STO, is totally insulating.¹ The emergence of conductivity at the SrTiO₃/LaAlO₃ interface could be attributed to intrinsic electronic reconstruction due to the polar discontinuity at the interface.⁸ This could be understood in perovskite oxides that have a generic ABO₃ structure, where A and B are metal cations. For STO, A is Sr²⁺ and B is Ti⁴⁺ where AO and BO₂ planes are charge-neutral leads to make STO a non-polar material. Whereas for LAO, A is La³⁺ while B is Al³⁺, AO and BO₂ planes have +1 and −1 charges, respectively, which causes the material to be polar.⁹ At the interface of the polar and non-polar materials, the electronic reconstruction could explain the mechanism of electronic conduction.¹⁰

To understand the SrTiO₃/LaAlO₃ interface activity, it is important to describe the perovskites in terms of their AO and BO₂ layering sequence. In SrTiO₃ the SrO and TiO₂ layers are charge-neutral, while the charge states in the LaAlO₃ are (LaO)⁺ and (AlO₂)⁻, respectively.¹¹ It has been reported that the AO–BO₂ stacking sequence is maintained and consequently a polarity discontinuity arises at the LaAlO₃–SrTiO₃ interface. Therefore, the LaO:TiO₂ interface becomes conducting, and it is suggested that the conduction is governed by electron transfer from LaAlO₃ into the TiO₂ bonds of the SrTiO₃.¹ The complementary AlO₂:SrO interface, with the AlO₂ possibly acting as an electron acceptor, remains insulating.¹ Such conducting interfaces are identical to 2D electron (hole) gases in semiconductors.

The other probability for the emergence of conductivity at the interface is based on oxygen vacancies^12–16 in the STO, which lead to the conductivity at the SrTiO₃/LaAlO₃ interface. Oxygen vacancies are also proposed³ to account for the observed insulating-to-metallic transition, via a mechanism involving the creation and annihilation of oxygen vacancies on the LAO surface. The oxygen vacancy adds two extra electrons to the interface to preserve charge neutrality. Adding an 1 e per unit cell or 0.5 e per unit cell to the interface is enough to maintain overall neutrality. Furthermore, the observed intermixing of cations across the SrTiO₃/LaAlO₃ interface¹⁷ is another probability for the emergence of conductivity at the interface. The orientation of the channels and their thermal behavior suggest that LaAlO₃/SrTiO₃ (LAO/STO) interface originates as a consequence of the STO tetragonal domain formation, which sets in below 105 K.^18,19 The study of the domain structure confirms that the channel-like conductivity in LAO/STO is due to the STO tetragonal domain structure and emphasizes the importance of STO to the interfacial properties.

Drera et al.²⁰ reported that a set of LaAlO₃/SrTiO₃ (LAO–STO) interfaces has been probed by X-ray photoemission spectroscopy in order to contrast and compare the effects of LAO over layer thickness and of the growth conditions on the electronic properties of these heterostructures. These effects are tracked by considering the band offset and the density of Ti+3 states, respectively. Drera et al.²¹ have investigated the origin of electronic states on the basis of the 2DEG found in conducting LaAlO₃/SrTiO₃ interfaces (5 u.c. LaAlO₃) by resonant photoemission experiments at the Ti L_2,3 and La M_4,5 edges. As shown by the resonant enhancement at the Ti L_2,3 edge, electronic states at the Fermi level receive a dominant contribution from Ti 3d states. Both Ti and La resonance effects in the valence-band region are used to estimate the valence-band maxima at the two sides of the junction. Recently, Salvinelli et al.²² reported that the layer-resolved cation occupancy for different conducting and insulating interfaces of LaAlO₃ (LAO) thin films on SrTiO₃ (STO) has been determined by angle-resolved X-ray photoelectron spectroscopy. Three STO interfaces with LAO have been considered, namely, a conducting interface with a five unit cell (u.c.) LAO layer, an insulating interface with a five u.c. LAO layer, and an insulating interface with a three u.c. LAO layer.

Recently, Dai et al.²³ have reported that an oxygen surface adsorbates induced metal–insulator transition at the LaAlO₃/SrTiO₃ interfaces. Kim and Bark²⁴ demonstrated the capability of growing conductive interfaces through large-scale deposition. Adhikari et al.²⁵ reported that the electronic properties of low dimensional systems are particularly sensitive to surface adsorbates. Frenkel et al.²⁶ have observed strong anisotropy in the resistance of LAO/STO devices, that dramatically changed across thermal cycles. Cancellieri et al.²⁷ have reported experimentally and theoretically, that the interplay of spin, charge, orbital and lattice degrees of freedom in oxide heterostructures results in a plethora of fascinating properties. Stephanovich and Dugaev²⁸ have proposed a simple theoretical analytical model to explain the possible appearance of the metallic conductivity in 2D-LaAlO₃/SrTiO₃ interface. Shubhankar et al.²⁹ reported a study of modulation of spin–orbit interaction at the LaTiO₃/SrTiO₃ interface by delta-doping with an iso-structural ferromagnetic perovskite LaCoO₃. They found that, the sheet carrier density at the interface decreases exponentially with delta-doping thickness.

The LAO/STO interface has been extensively investigated experimentally^{5–7,11–13,20–39} and theoretically^{25,27,28,37–39} due to the existence of two kinds of interfaces, LaO/TiO₂/SrO and SrO/AlO₂/LaO. Therefore, this system has attracted a lot of interest.^1–41 To the best of knowledge of the present author, most investigations on the electronic properties of the SrTiO₃/LaAlO₃ interface have been done experimentally and theoretically,^{5–7,11–13,20–39} while measurements of thermoelectric power for the SrTiO₃/LaAlO₃ interface are still sparse.^42–44 Some literature reports the electronic properties of n-type 6.5STO/1.5LAO interfaces;^45–49 unfortunately, none of them report the transport properties of 6.5STO/1.5LAO. Therefore, in a step forward to understand the origin of the conductivity in the interface of 6.5STO/1.5LAO, comprehensive theoretical investigations have been performed based on the all-electron full-potential method within the semi-classical Boltzmann theory as incorporated in the BoltzTraP code⁵⁰ to calculate the transport properties of the n-type 6.5SrTiO₃/1.5LaAlO₃ interface, which possesses strong density of states at E_F, and thus unusual transport properties. Simulations of the thermoelectric properties is a transition from first- to second-principles methods. The first-principles method used here is an all-electron full-potential linear augmented plane wave (FPLAPW+lo) method, whereas the second-principles is the BoltzTraP code,⁵⁰ which solves the semi-classical Bloch–Boltzmann transport equations within the constant relaxation time approximation.⁵⁰

2. Details of calculations

Based on the calculated electronic band structures using the all-electron full-potential linear augmented plane wave (FPLAPW+lo) method in a scalar relativistic version, as embodied in the Wien2k code,⁵¹ the electronic transport properties of the n-type 6.5SrTiO₃/1.5LaAlO₃ interface have been calculated, utilizing the semi-classical Boltzmann theory as incorporated in the BoltzTraP code.⁵⁰ The crystal structure of the n-type 6.5STO/1.5LAO interface is shown in Fig. 1a. A symmetric supercell with one AlO₂ layer in the middle and two LaO layers around it as well as alternating layers of TiO₂ with SrO on both sides has been built, as shown in Fig. 1a. A feature of the symmetry-supercell method is that no vacuum is needed in the simulation of the supercell, making its calculation easier. However, and because of the imposed symmetry and nonstoichiometry of the LAO film, this geometry does not lead in a polar field, meaning that a polar catastrophe can be obviated. The nonstoichiometry of the LAO also creates fixed carrier doping; at the ionic limit, an LAO layer has a charge of +1, and there is an additional one electron that exists in the conduction band of LAO, which is divided evenly by the two interfaces. Therefore, each n-type interface is doped by 1/2 electron per 2-dimensional unit cell, enough to totally compensate for the polar field of LAO; thus the symmetric supercell method is comparable to researching the characteristics of the interfaces when the LAO film is very thick.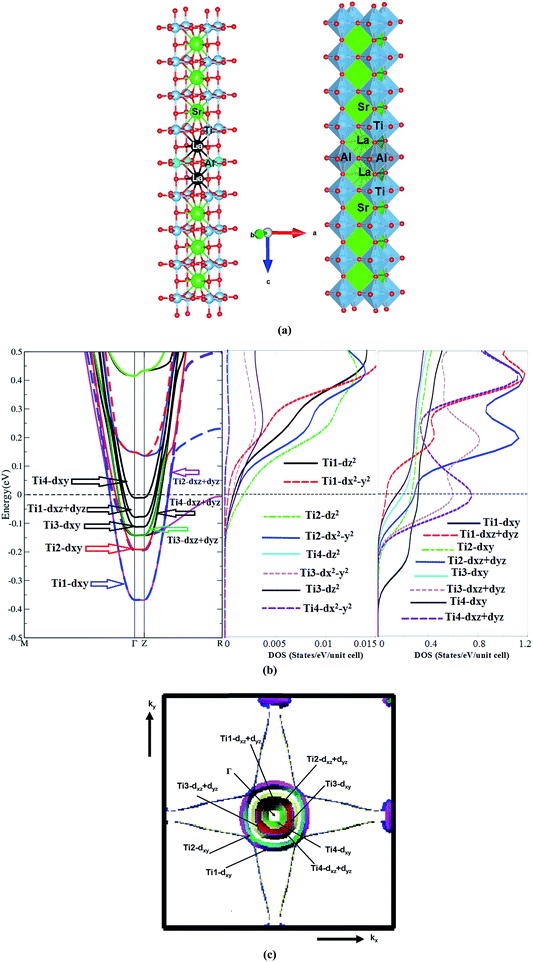

Fig. 1 (a) The crystal structure of the n-type 6.5STO/1.5LAO interface. We have built a symmetric supercell with one AlO₂ layer in the middle and two LaO layers around it and alternating TiO₂ with SrO layers on both sides. In this case, the supercell has two symmetric n-type interfaces and there is no potential buildup due to symmetry. This approach automatically guarantees the doping of 1 electron in the supercell. The doped charge accumulates at the TiO₂ layers at the interface and results in a doping of 0.5 e per u.c.; (b) the electronic band structure of 6.5STO/1.5LAO interface in the vicinity of Fermi level. The electronic band structure show that the n-type 6.5STO/1.5LAO interface exhibit non-zero density of states at E_F which leads to unusual transport properties. Also we have plotted the partial density of states for Ti-d_xy, Ti-d_xz, Ti-d_yz, Ti-d_z² and Ti-d_x²−y² side to side with the electronic band structure. We would like to mention that the colors mean nothing just to illustrated the bands in clear way. (c) Calculated Fermi surface along Γ, X, M, Γ, Z, R, A, Z directions, it consists of several sheets, these sheets is mainly composed of d_xy, d_xz and d_yz orbitals. The calculated Fermi surface show good agreement with previous work.⁴⁵

In the BoltzTraP code, the constant relaxation time approximation and the rigid band approximation were used.⁵⁰ In this code the relaxation time is taken to be direction independent and isotropic.^50,52 To understand the electronic transport properties of the n-type 6.5SrTiO₃/1.5LaAlO₃ interface, the carrier concentration (n), Seebeck coefficient (S), electrical conductivity (σ/τ), electronic thermal conductivity (κ_e), and electronic power factor (S²σ/τ) as a function of temperature at a certain value of chemical potential (µ = E_F), as well as a function of chemical potential at three constant temperatures (300, 600 and 900 K), were investigated. It should be emphasized that the BoltzTraP code depends on a well-tested smoothed Fourier interpolation to obtain an analytical expression of bands. This is based on the fact that the electrons contributing to transport are in a narrow energy range due to the delta-function like Fermi broadening.⁵⁰ For such a narrow energy range the relaxation time is nearly the same for the electrons. The accuracy of this method has been well tested earlier, and the method actually turns out to be a good approximation.⁵³ The formulas of the transport coefficients as a function of temperature and chemical potential were given elsewhere.^50,54 To solve the exchange-correlation potential, the generalized gradient approximation (PBE-GGA)⁵⁵ was used. In FPLAPW+lo, the unit cell is divided into two regions, the spherical harmonic expansion is used inside the non-overlapping spheres of the muffin-tin radius (R_MT) and the plane wave basis set was chosen in the interstitial region (IR) of the unit cell. The R_MT was chosen to be 2.5, 2.46, 1.83, 1.74 and 1.62 a.u. for La, Sr, Ti, Al, and O, respectively. The R_MT × K_max parameter was taken to be 7.0 to determine the matrix size, R_MT is the smallest radius of the muffin-tin sphere, while K_max is the maximum modulus for the reciprocal lattice vectors K. The valence wave functions inside the muffin-tin spheres were expanded up to l_max = 10, while the charge density is Fourier expanded up to G_max = 12 (a.u)⁻¹. Self-consistency is obtained using 1000 k⇀ points in the irreducible Brillouin zone (IBZ). The self-consistent calculations are converged, since the total energy of the system is stable within 0.00001 Ry. The electronic band structure calculations are performed within 3000 k⇀ points and the transport properties within 30 000 k⇀ points in the IBZ.

3. Results and discussion

3.1. Salient features of the electronic band structures

To ascertain the influence of the interface mechanism on the transport properties, we recall the calculated electronic band structure of the n-type 6.5STO/1.5LAO interface. Since the area around the Fermi level plays an important role for the carrier transportation, the attention was concentrated on the area in the vicinity of E_F. Fig. 1b illustrates the calculated electronic band structure above and below E_F in the energy region between −0.5 eV and +0.5 eV. Also, the partial density of states for Ti-d_xy, Ti-d_xz, Ti-d_yz, Ti-d_z² and Ti-d_x²−y² side by side with the electronic band structure (Fig. 1b) have been plotted. The calculated electronic band structure and the density of states show good agreement with previous results.⁵⁶ It is clear that the interface causes significant influence on the bands' locations below and above E_F, resulting in some modification in the ground state properties. It causes the increase/reduction of the parabolic shape of the bands in the vicinity of E_F, resulting in low/high effective mass and hence high/low mobility. Also it causes strong hybridization between the orbitals, which may lead to the formation of covalent bonding. Covalent bonding is more favorable for the transport of the carriers than ionic bonding.⁵⁷ The bonds can significantly influence the carrier's mobility and hence the electrical conductivity.⁵⁷

It has been noticed that the largest contribution to the occupied states close to the Fermi level comes from the interfacial Ti ions, and the rest of the Ti atoms contribute less as distance to the interface increases. It has also been noticed that there is no contribution from the interfacial La ions to the occupied states. There is one electron per n-type interface that contributes to the two dimensional electron gas (2DEG) and this electron is spread over five Ti layers on either side of the interface. It has been found that for 2D electron systems in STO, the Ti-d_xy as well as Ti-d_xz(d_yz) bands cross the Fermi level (see Fig. 1b). The calculated density of states at E_F, N(E_F) and the bare electronic specific heat coefficient (γ) for these bands are listed in Table 1. This shows that these orbitals posses different N(E_F) and γ values, and hence different contributions to the transport properties. It is well known that the non-zero density of states at E_F leads to unusual transport properties,⁵⁸ and the bands which cross E_F are responsible for the transport properties of the compound and those bands which are not crossing E_F will contribute negligibly to the transport properties.⁵⁹ Therefore, we recall the calculated Fermi surface of the 6.5STO/1.5LAO interface⁶⁰ to gain deep insight about the charge transfer. Fig. 1c shows the calculated Fermi surface along Γ, X, M, Γ, Z, R, A, Z directions of first BZ. It consists of several sheets; these sheets are mainly composed of d_xy, d_xz and d_yz orbitals. The calculated Fermi surface of the 6.5STO/1.5LAO interface shows good agreement with previous work.⁴⁵ The origin of the high concentration of electronic charge carriers at the interface between STO and LAO is still under controversial debate.^3,61,62 The effective mass of electrons 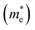have been calculated from the electronic band structure of the n-type 6.5STO/1.5LAO interface. Usually, the value of the effective mass of electrons is estimated from the conduction band minimum curvature. The diagonal elements of the effective mass tensor for the electrons in the conduction band are calculated following this equation;

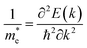Table 1 The calculated density of states at E_F, N(E_F) in (state per eV per unit cell) and the bare electronic specific heat coefficient (γ) in mJ per mol cell per K² for the orbitals of Ti-d atoms

	N(EF)	γ		N(EF)	γ
Total	101.15	17.52	Ti3-d	13.24	2.29
Ti1-d	5.36	0.93	Ti3-dz^2	0.02	0.00
Ti1-dz^2	0.01	0.00	Ti3-dxy	2.90	0.50
Ti1-dxy	4.33	0.75	Ti3-dx^2−y^2	0.01	0.00
Ti1-dx^2−y^2	0.02	0.00	Ti3-dxz+dyz	10.31	1.79
Ti1-dxz+dyz	1.01	0.18	Ti4-d	14.80	2.56
Ti2-d	8.45	1.46	Ti4-dz^2	0.01	0.00
Ti2-dz^2	0.03	0.00	Ti4-dxy	1.77	0.31
Ti2-dxy	3.56	0.62	Ti4-dx^2−y^2	0.01	0.00
Ti2-dx^2−y^2	0.02	0.00	Ti4-dxz+dyz	13.03	2.26
Ti1-dxz+dyz	4.84	0.84

---

The effective mass of electrons is assessed by fitting the electronic band structure to a parabolic function eqn (1). The calculated electron effective mass ratio 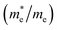around Γ point of BZ is about 0.729, 0.651, 0.520, 0.485, 0.489, 0.729, 0.630, 0.651 for Ti1-d_xy, Ti2-d_xy, Ti3-d_xy, Ti4-d_xy, Ti1-d_xz+d_yz, Ti2-d_xz+d_yz, Ti3-d_xz+d_yz and Ti4-d_xz+d_yz, respectively. It is clear that the d_xy bands have larger effective mass than the d_xz and d_yz bands, in good agreement with previous work.^56,63 This leads to enhancement of the electrical conductivity in good agreement with previous work.^45,64

3.2. Transport properties

3.2.1. Charge carrier concentration and electrical conductivity. In this section, the influence of charge carrier concentration of the n-type 6.5STO/1.5LAO interface on the transport properties has been investigated. Usually, the temperature difference between two materials (here 6.5STO/1.5LAO) is responsible for producing thermoelectric voltage. To gain high thermoelectric efficiency, it is necessary that the material possesses high electrical conductivity, a large Seebeck coefficient and low thermal conductivity.⁶¹ Therefore, to achieve the highest electrical conductivity, high mobility carriers are required. The charge carrier concentration of the n-type 6.5STO/1.5LAO as a function of the carriers' mobility is illustrated in Fig. 2a. It has been found that the charge carriers possess the highest mobility at the vicinity of E_F. We have investigated the influence of the temperature on the carriers' mobility and found that at low temperature (less than 100 K) the mobility decreases with increasing temperature, which shows good agreement with the experimental data.^{1,4,14,16,65,66} At a temperature below 300 K, the carriers' mobility decreases with increasing temperature, in general the trend of our calculated carriers' mobility is comparable with the experimental data.^14,16 We should emphasize that the calculated carriers' mobility show a deviation from the experimental data due to the DFT and BoltzTraP code limitations. In this code, the constant relaxation time approximation and the rigid band approximation were used and the relaxation time is taken to be direction independent and isotropic.^50,52 In the temperature range between 350–450 K, the carriers' mobility fluctuated around zero, as shown in Fig. 2b. Further, the influence of the temperature on the carriers' concentration has been investigated, Fig. 2c illustrates that at low temperature (below 100 K), the carriers' concentration slightly increases with increasing temperature; then it shows almost constant values between 100–300 K, this behavior is comparable with the experimental data^14,16,43 within the limitation of the DFT and BoltzTraP code. Above 300 K, the n-type conduction significantly increases with increasing temperature. It is also important to mention that the calculated carriers' concentration as a function of temperature is in concordance with previous experimental and theoretical work on 4 and 6 u.c. STO/LAO interfaces.⁴³

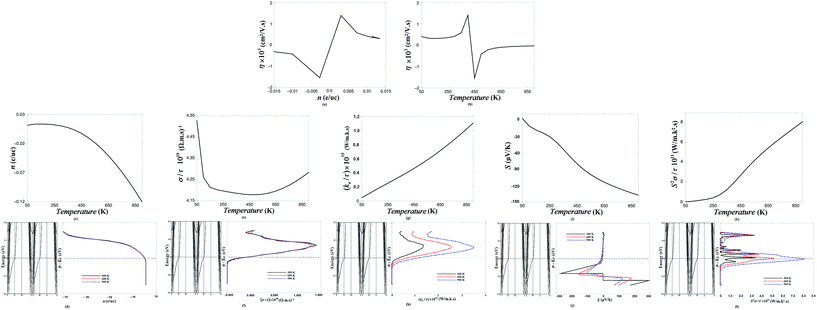Fig. 2 (a) The charge carriers concentration in e per u.c. (electrons (e) per unit cell (u.c.)) of the n-type 6.5STO/1.5LAO as a function of the carriers mobility; (b) the charge carriers mobility of the n-type 6.5STO/1.5LAO as a function of temperature which show the influence of the temperature on the carriers mobility; (c) the charge carriers concentration in e per u.c. of the n-type 6.5STO/1.5LAO as a function of temperature, which illustrated that the carriers concentration decreases with increasing the temperature and the highest carriers concentration is achieved at the temperature range between 100–250 K. Therefore, 100–250 K is the optimal temperature range to gain the highest carriers concentration. We should emphasize that our calculated Seebeck coefficient in concordance with the previous experimental and theoretical work of a 4 and 6 u.c. STO/LAO interfaces, see Fig. 3 in ref. 38; (d) the electronic band structure of the n-type 6.5STO/1.5LAO interface in the vicinity of Fermi level is plotted together with the carriers concentration at three constant temperatures (300, 600 and 900) K; (e) the electrical conductivity (σ/τ) of the n-type 6.5STO/1.5LAO interface at Fermi level (a certain chemical potential value µ = E_F = 0.75252 eV) as a function of temperature; (f) the electronic band structure of the n-type 6.5STO/1.5LAO interface in the vicinity of Fermi level plotted together with the electrical conductivity as a function of chemical potential at three constant temperatures (300, 600 and 900) K; (g) the electronic thermal conductivity of the n-type 6.5STO/1.5LAO interface at Fermi level (a certain chemical potential value µ = E_F = 0.75252 eV) as a function of temperature. It is clear that κ_e/τ increases lineally with increasing the temperature; (h) the electronic band structure of the two symmetric n-type 6.5STO/1.5LAO interface in the vicinity of Fermi level is plotted together with the electronic thermal conductivity (κ_e/τ) as a function of chemical potential at three constant temperatures (300, 600 and 900) K, it is clear that the lowest κ_e/τ is achieved at 300 K therefore, 300 K is the optimal temperature where the n-type 6.5STO/1.5LAO interface expected to give the highest efficiency; (i) the Seebeck coefficient of the n-type 6.5STO/1.5LAO interface at Fermi level (a certain chemical potential value µ = E_F = 0.75252 eV) as a function of temperature. We should emphasize that our calculated Seebeck coefficient in concordance with the previous experimental and theoretical work of a 4, 5 and 6 u.c. STO/LAO interfaces, see Fig. 3 in ref. 38 and Fig. 2 in ref. 39; (j) the electronic band structure of the n-type 6.5STO/1.5LAO interface in the vicinity of Fermi level is plotted together with the Seebeck coefficient as a function of chemical potential at three constant temperatures (300, 600 and 900) K; (k) the calculated the power factor of the n-type 6.5STO/1.5LAO interface at Fermi level (a certain chemical potential value µ = E_F = 0.75252 eV) as a function of temperature; (l) the electronic band structure of the n-type 6.5STO/1.5LAO interface in the vicinity of Fermi level is plotted together with the calculated the power factor at three fixed temperatures (300, 600 and 900) K as a function of chemical potential (µ − E_F) between −0.2 and +0.2 eV.

In Fig. 2d the electronic band structure of the n-type 6.5STO/1.5LAO interface in the vicinity of the Fermi level is plotted together with the carriers' concentration at three constant temperatures (300, 600 and 900 K). It is clear from the electronic band structure that the n-type 6.5STO/1.5LAO interface has parabolic bands in the vicinity of the Fermi level with different k-dispersion. It has been found that the n-type 6.5STO/1.5LAO interface exhibits a maximum carrier concentration in the vicinity of the Fermi level and confirmed that the material is n-type conductions in the region where the 6.5STO/1.5LAO interface is expected to give maximum efficiency, i.e. µ − E_F = ±0.2 eV.

The electrical conductivity (σ/τ) of the two symmetric n-type 6.5STO/1.5LAO interface at the Fermi level (a certain chemical potential value µ = E_F = 0.75252 eV) as a function of temperature is presented in Fig. 2e. It has been found that at a fixed value of the chemical potential (µ = E_F), a rapid reduction in the electrical conductivity occurs with increasing temperature up to 150 K. Above this temperature, σ/τ exhibits an almost constant value up to 500 K, then rises again to reach 4.28 × 10¹⁹ (Ω m s)⁻¹ at 900 K.

To ascertain that the 6.5STO/1.5LAO interface is an n-type conduction in the region where it is expected to give maximum efficiency, the electrical conductivity as a function of chemical potential at three constant temperatures (300, 600 and 900 K) has been investigated. Fig. 2f illustrates the electronic band structure of the two symmetric n-type 6.5STO/1.5LAO interface in the vicinity of the Fermi level plotted together with the electrical conductivity. It is clear that above E_F (at the conduction bands), a significant increase in the electrical conductivity occurs to reach the maximum value of about 1.98 × 10²⁰ (Ω m s)⁻¹ at µ − E_F = 0.05 eV for 300 K, confirming that the 6.5STO/1.5LAO interface is an n-type conductions. It has been noticed that the temperature has an insignificant influence on the electrical conductivity when we vary the chemical potential (µ − E_F) between −0.2 and +0.2 eV, and 300 K is the optimal value to achieve the highest electrical conductivity.

3.2.2. Electronic thermal conductivity. Materials with low thermal conductivity are favorable for designing efficient thermoelectric devices, which are important to maintain a temperature gradient. In general, the thermal conductivity (κ) consists of electronic contribution κ_e (electrons and holes transporting heat) and phonon contribution κ_l (phonons traveling through the lattice). The BoltzTraP code calculates only the electronic part κ_e/τ. Using the BoltzTraP code, the electronic thermal conductivity of the n-type 6.5STO/1.5LAO interface at the Fermi level (at a certain chemical potential value µ = E_F = 0.75252 eV) as a function of temperature has been calculated, as shown in Fig. 2g. It is clear that κ_e/τ increases linearly with increasing temperature. To ascertain that the electronic thermal conductivity increases with the temperature, κ_e/τ as a function of chemical potential at three constant temperatures (300, 600 and 900 K) is shown in Fig. 2h. It is clear that the lowest κ_e/τ is achieved at 300 K along the whole chemical potential range (µ = E_F = ±0.2 eV); therefore, 300 K is the optimal temperature where the n-type 6.5STO/1.5LAO interface is expected to give the highest efficiency.

It should be emphasized that the thermal conductivity of any material is dependent on the motion of the free electrons and the molecular vibrations. For metals (the present case), the thermal conductivity is mainly a function of the motion of free electrons, which implies that the κ_e contribution is dominant. As the temperature increases, the molecular vibrations increase (in turn increasing the mean free path of molecules). Therefore, they obstruct the flow of free electrons, thus reducing κ_l. In high-purity metals, the electron mechanism of heat transport is much more efficient than the phonon contribution because electrons are not as easily scattered as phonons and have higher velocities. Furthermore, metals are extremely good conductors of heat because relatively large numbers of free electrons exist that participate in thermal conduction. Since free electrons are responsible for both electrical and thermal conduction in pure metals, theoretical treatments suggest that the two conductivities should be related according to the Wiedemann–Franz law (L = κ/σT), where σ is the electrical conductivity, T is the absolute temperature, and L is a constant. The theoretical value of L, 2.44 × 10⁻⁸ Ω W K⁻², should be independent of temperature and the same for all metals if the heat energy is transported entirely by free electrons.⁶⁷ Consequently, it has been observed that κ_e increases with increasing temperature (Fig. 2g).

3.2.3. Seebeck coefficient (thermopower). The Seebeck coefficient (S) is an important quantity which is related to the electronic band structure of materials. The calculated Seebeck coefficient of the n-type 6.5STO/1.5LAO interface at the Fermi level (a certain chemical potential value µ = E_F = 0.75252 eV) as a function of temperature is presented in Fig. 2i. The sign of S indicates the type of dominant charge carriers: S with a positive sign represents the p-type materials, whereas n-type materials have a negative S.^50,52,54 Following Fig. 2i, it is clear that the Seebeck coefficient has a negative sign which confirms that the 6.5STO/1.5LAO interface is an n-type conductions at Fermi level. It has been noticed that the Seebeck coefficient exhibits a significant increase in the negative values with increasing temperature. It should be emphasized that the calculated Seebeck coefficient is in concordance with previous experimental and theoretical work on 4, 5 and 6 u.c. STO/LAO interfaces.^43,44 Both experiment and theory coherently report Seebeck coefficients larger in bulk SrTiO₃ than in SrTiO₃/LaAlO₃.

In further investigation, the Seebeck coefficient as a function of chemical potential at three constant temperatures (300, 600 and 900 K) has been calculated. In Fig. 2j, S is illustrated along with the electronic band structure in the energy region between 0.2 and −0.2 eV. One can see that in the vicinity of E_F, the Seebeck coefficient exhibits two pronounced structures below E_F (µ − E_F between 0.0 and −0.2 eV), with the highest value of the Seebeck coefficient at 300 K (−290 and 300 µV K⁻¹). It is important to mention that the large Seebeck coefficient is attributed to the non-zero density of states at E_F.^58,59 The increase of the Seebeck coefficient also leads to a maximum of the power factor.

3.2.4. Power factor. The power factor is defined as (P = S²σ/τ), where S² is the Seebeck coefficient's square, σ the electrical conductivity and τ the relaxation time. Following this formula, one can see that P is directly proportional to S² and σ/τ. Therefore, in order to gain a high power factor one needs to maintain the values of S² and σ/τ. It is well known that the figure of merit is a very important quantity for calculating the transport properties of materials. The dimensionless figure of merit is written as (ZT = S²σT/κ),^68,69 which shows that the power factor comes in the numerator of the figure of merit. Thus, the power factor is an important quantity and plays a principle role in evaluating the transport properties of materials. The power factor of the n-type 6.5STO/1.5LAO interface at the Fermi level (a certain chemical potential value µ = E_F = 0.75252 eV) as a function of temperature, as shown in Fig. 2k, has been calculated. It has been found that the power factor is zero at low temperature; then a rapid increase occurs when the temperature rises to reach its maximum value of about 8.1 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at 900 K. In order to ascertain the influence of varying the chemical potential on the power factor of the 6.5STO/1.5LAO interface, the power factor at three fixed temperatures (300, 600 and 900 K) as a function of chemical potential (µ − E_F) between −0.2 and +0.2 eV, as shown in Fig. 2l, has been calculated. It has been found that at 300 K the investigated material exhibits the highest power factor of about 3.31 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at µ = E_F = 0.005 eV, 3.35 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at µ = E_F = 0.002 eV and 3.25 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at µ = E_F = 0.13 eV. It is interesting that all these values are situated in the conduction bands (see Fig. 2l), confirming that the 6.5STO/1.5LAO interface is an n-type conduction. In contrast, for 600 K and 900 K the highest P value is achieved at µ = E_F (see Fig. 2l). This implies that the temperature has a significant influence on P. Therefore, 300 K is the optimal temperature for the n-type 6.5STO/1.5LAO interface to achieve the maximum efficacy.

It is important to highlight that in the previous works,^70–73 the transport properties using FPLAPW method within BoltzTraP code on several systems whose transport properties are known experimentally have been calculated. In those previous calculations, very good agreement with the experimental data has been found. Thus, we believe that the calculations reported in this paper would produce very accurate and reliable results.

4. Conclusions

An ab initio calculation based on the all-electron full-potential linear augmented plane wave (FPLAPW+lo) method, as embodied in the Wien2k code, is used to obtain the electronic band structure of the n-type 6.5STO/1.5LAO interface. The BoltzTraP code, based on the rigid band approximation, is used to calculate the thermoelectric properties of the n-type 6.5STO/1.5LAO interface. The calculated electronic band structure reveals that the 6.5STO/1.5LAO interface exhibits strong parabolic bands in the vicinity of the Fermi level (E_F) with different k-dispersion. The calculated carrier concentration as a function of temperature shows good agreement with reported experimental and theoretical work. It has been found that the 6.5STO/1.5LAO interface exhibits a negative sign Seebeck coefficient, which confirms that the 6.5STO/1.5LAO interface is an n-type conduction at the Fermi level. The power factor increases with increasing temperature to reach its maximum value of about 8.1 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at 900 K. In order to ascertain the influence of varying the chemical potential on the carrier concentration, electronic conductivity, Seebeck coefficient and power factor, these parameters have been investigated as a function of chemical potential at three constant temperatures (300, 600 and 900 K). It is interesting to mention that the calculated Seebeck coefficient and carrier concentration as a function of temperature is in concordance with previous experimental and theoretical work on 4, 5 and 6 u.c. STO/LAO interfaces. It is important to mention that the large Seebeck coefficient is attributed to the non-zero density of states at E_F. The increase of the Seebeck coefficient also leads to a maximum of the power factor.

Important note

The standard symbol for mobility is µ but here we have used the symbol η for mobility in order to discriminate the mobility from the chemical potential µ.

Acknowledgements

The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, cofunded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI programme and, in the follow-up sustainability stage, supported through CENTEM PLUS (LO1402) by financial means from the Ministry of Education, Youth and Sports under the National Sustainability Programme I. Computational resources were provided by MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/08.0144) infrastructures.

References

1. A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423.
2. D. A. Dikin, M. Mehta, C. W. Bark, C. M. Folkman, C. B. Eom and V. Chandrasekhar, Phys. Rev. Lett., 2011, 107, 056802.
3. C. Cen, S. Thiel, G. Hammerl, C. W. Schneider, K. E. Andersen, C. S. Hellberg, J. Mannhart and J. Levy, Nat. Mater., 2008, 7, 298.
4. M. Huijben, A. Brinkman, G. Koster, G. Rijnders, H. Hilgenkamp and H. A. Blank, Adv. Mater., 2009, 21, 1665.
5. L. Yu and A. Zunger, Nat. Commun., 2014, 5, 5118.
6. S. Thiel, G. Hammerl, A. Schmehl, C. W. Schneider and J. Mannhart, Science, 2006, 313, 1942.
7. A. Brinkman, M. Huijben, M. van Zalk, J. Huijben, U. Zeitler, J. C. Maan, W. G. van der Wiel, G. Rijnders, D. H. A. Blank and H. Hilgenkamp, Nat. Mater., 2007, 6, 493.
8. N. Nakagawa, H. Y. Hwang and D. A. Muller, Nat. Mater., 2006, 5, 204.
9. H. Wadati, J. Geck, D. G. Hawthorn, T. Higuchi, M. Hosoda, C. Bell, Y. Hikita, H. Y. Hwang, C. Schussler-Langeheine, E. Schierle, E. Weschke and G. A. Sawatzky, IOP Conf. Series: Materials Science and Engineering, 2011, vol. 24, p. 012012.
10. R. Hesper, L. H. Tjeng, A. Heeres and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 16046.
11. M. Huijben, G. Rijnders, D. H. A. Blank, S. Bals, S. V. Aert, J. Verbeeck, G. V. Tendeloo, A. Brinkman and H. Hilgenkamp, Nat. Mater., 2006, 5, 556.
12. W. Siemons, G. Koster, H. Yamamoto, W. A. Harrison, G. Lucovsky, T. H. Geballe, D. H. A. Blank and M. R. Beasley, Phys. Rev. Lett., 2007, 98, 196802.
13. A. Kalabukhov, R. Gunnarsson, J. Borjesson, E. Olsson, T. Claeson and D. Winkler, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 121404.
14. Z. Q. Liu, C. J. Li, W. M. Lu, X. H. Huang, Z. Huang, S. W. Zeng, X. P. Qiu, L. S. Huang, A. Annadi, J. S. Chen, J. M. D. Coey, T. Venkatesan and Ariando, Phys. Rev. X, 2013, 3, 021010.
15. Z. Q. Liu, D. P. Leusink, X. Wang, W. M. Lü, K. Gopinadhan, A. Annadi, Y. L. Zhao, X. H. Huang, S. W. Zeng, Z. Huang, A. Srivastava, S. Dhar, T. Venkatesan and Ariando, Phys. Rev. Lett., 2011, 107, 146802.
16. Ariando, X. Wang, G. Baskaran, Z. Q. Liu, J. Huijben, J. B. Yi, A. Annadi, A. Roy Barman, A. Rusydi, S. Dhar, Y. P. Feng, J. Ding, H. Hilgenkamp and T. Venkatesan, Nat. Commun., 2011, 2, 1–8.
17. P. R. Willmott, S. A. Pauli, R. Herger, C. M. Schlepütz, D. Martoccia, B. D. Patterson, B. Delley, R. Clarke, D. Kumah, C. Cionca and Y. Yacoby, Phys. Rev. Lett., 2007, 99, 155502.
18. Z. Erlich, Y. Frenkel, J. Drori, Y. Shperber, C. Bell, H. K. Sato, M. Hosoda, Y. Xie, Y. Hikita, H. Y. Hwang and B. Kalisky, J. Supercond. Novel Magn., 2015, 28, 1017.
19. M. Salluzzo, J. C. Cezar, N. B. Brookes, V. Bisogni, G. M. De Luca, C. Richter, S. Thiel, J. Mannhart, M. Huijben, A. Brinkman, G. Rijnders and G. Ghiringhelli, Phys. Rev. Lett., 2009, 102, 166804.
20. G. Drera, G. Salvinelli, A. Brinkman, M. Huijben, G. Koster, H. Hilgenkamp, G. Rijnders, D. Visentin and L. Sangaletti, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075435.
21. G. Drera, G. Salvinelli, F. Bondino, E. Magnano, M. Huijben, A. Brinkman and L. Sangaletti, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035124.
22. G. Salvinelli, G. Drera, A. Giampietr and L. Sangaletti, ACS Appl. Mater. Interfaces, 2015, 7, 25648.
23. W. Dai, S. Adhikari, A. Camilo Garcia-Castro, A. H. Romero, H. Lee, J.-W. Lee, S. Ryu, C.-B. Eom and C. Cen, Nano Lett., 2016, 16, 2739.
24. D. H. Kim and C. W. Bark, J. Korean Phys. Soc., 2016, 68, 1395.
25. S. Adhikari, A. C. Garcia-Castro, A. H. Romero, H. Lee, J.-W. Lee, S. Ryu, C.-B. Eom and C. Cen, Adv. Funct. Mater., 2016, 26, 5453.
26. Y. Frenkel, N. Haham, Y. Shperber, C. Bell, Y. Xie, Z. Chen, Y. Hikita, H. Y. Hwang and B. Kalisky, ACS Appl. Mater. Interfaces, 2016, 8, 12514.
27. C. Cancellieri, A. S. Mishchenko, U. Aschauer, A. Filippetti, C. Faber, O. S. Barisic, V. A. Rogalev, T. Schmitt, N. Nagaosa and V. N. Strocov, Nat. Commun., 2016, 7, 10386.
28. V. A. Stephanovich and V. K. Dugaev, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 045302.
29. S. Das, Z. Hossain and R. C. Budhani, Phys. Rev. B: Condens. Matter Mater. Phys., 2016 , accepted.
30. N. Nakagawa, H. Y. Hwang and D. A. Muller, Nat. Mater., 2006, 5, 204.
31. G. Herranz, M. Basletic, M. Bibes, C. Carretero, E. Tafra, E. Jacquet, K. Bouzehouane, C. Deranlot, A. Hamzic, J.-M. Broto, A. Barthelemy and A. Fert, Phys. Rev. Lett., 2007, 98, 216803.
32. P. R. Willmott, S. A. Pauli, R. Herger, C. M. Schleputz, D. Martoccia, B. D. Patterson, B. Delley, R. Clarke, D. Kumah, C. Cionca and Y. Yacoby, Phys. Rev. Lett., 2007, 99, 155502.
33. M. Balestic, J.-L. Maurice, C. Carretero, G. Herranz, O. Copie, M. Bibes, E. Jacquet, K. Bouzehouane, S. Fusil and A. Barthelemy, Nat. Mater., 2008, 7, 621.
34. K. Yoshimatsu, R. Yasuhara, H. Kumigashira and M. Oshima, Phys. Rev. Lett., 2008, 101, 026802.
35. M. Salluzzo, J. C. Cezar, N. B. Brookes, V. Bisogni, G. M. D. Luca, C. Richter, S. Thiel, J. Mannhart, M. Huijben, A. Brinkman, G. Rijnders and G. Ghiringhelli, Phys. Rev. Lett., 2009, 102, 166804.
36. M. Sing, G. Berner, K. Goss, A. Muller, A. Ru_, A. Wetscherek, S. Thiel, J. Mannhart, S. A. Pauli, C. W. Schneider, P. R. Willmott, M. Gorgoi, F. Schafers and R. Claessen, Phys. Rev. Lett., 2009, 102, 176805.
37. R. Pentcheva and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035112.
38. M. S. Park, S. H. Rhim and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 205416.
39. S. Ishibashi and K. Terakura, J. Phys. Soc. Jpn., 2008, 77, 104706.
40. N. Reyren, S. Thiel, A. D. Caviglia, L. F. Kourkoutis, G. Hammer, C. Richter, C. W. Schneider, T. Kopp, A.-S. Ruetschi, D. Jaccard, M. Gabay, D. A. Muller, J.-M. Triscone and J. Mannhart, Science, 2007, 317, 1196.
41. A. Brinkman, M. Huijben, M. V. Zalk, J. Huijben, U. Zeitler, J. C. Maan, W. G. V. D. Wiel, G. Rijnders, D. H. A. Blank and H. Hilgenkamp, Nat. Mater., 2007, 6, 493.
42. S. Lerer, M. Ben Shalom, G. Deutscher and Y. Dagan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075423.
43. I. Pallecchi, M. Codda, E. Galleani dAgliano, D. Marŕe, A. D. Caviglia, N. Reyren, S. Gariglio and J.-M. Triscone, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085414.
44. A. Filippetti, P. Delugas, M. J. Verstraete, I. Pallecchi, A. Gadaleta, D. Marŕe, D. F. Li, S. Gariglio and V. Fiorentini, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195301.
45. P. Delugas, A. Filippetti, V. Fiorentini, D. I. Bilc, D. Fontaine and P. Ghosez, Phys. Rev. Lett., 2011, 106, 166807.
46. Z. Zhong, A. Toth and K. Held, arxiv.org/pdf/1209.4705v2, 29 Nov. 2012.
47. Z. Zhong, P. Wissgott, K. Held and G. Sangiovanni, Europhys. Lett., 2012, 99, 37011.
48. R. Arras, V. G. Ruiz, W. E. Pickett and R. Pentcheva, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125404.
49. Z. S. Popovic, S. Satpathy and R. M. Martin, Phys. Rev. Lett., 2008, 101, 256801.
50. G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67.
51. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, an augmented plane wave plus local orbitals program for calculating crystal properties, Vienna University of Technology, Austria, 2001.
52. B. Xu, X. Li, G. Yu, J. Zhang, S. Ma, Y. Wang and L. Yi, J. Alloys Compd., 2013, 565, 22.
53. D. Wang, L. Tang, M. Q. Long and Z. G. Shuai, J. Chem. Phys., 2009, 131, 224704.
54. T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B., 2003, 68, 125210.
55. J. P. Perdew, S. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
56. A. Joshua, S. Pecker, J. Ruhman, E. Altman and S. Ilani, Nat. Commun., 2012, 3, 1129.
57. F. Wu, H. Z. Song, J. F. Jia and X. Hu, Prog. Nat. Sci.: Mater. Int., 2013, 23(4), 408.
58. J. Kübler, A. R. Williams and C. B. Sommers, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1745.
59. S. Sharma and S. K. Pandey, J. Phys.: Condens. Matter, 2014, 26, 215501.
60. A. H. Reshak, M. S. Abu-Jafar and Y. Al-Douri, J. Appl. Phys., 2016, 119, 245303.
61. S. A. Pauli and P. R. Willmott, J. Phys.: Condens. Matter, 2008, 20, 264012.
62. J. Mannhart, D. H. A. Blank, H. Y. Hwang, A. J. Millis and J. M. Triscone, MRS Bull., 2008, 33, 1027.
63. G. Khalsa and A. H. MacDonald, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125121.
64. W.-joon Son, E. Cho, B. Lee, J. Lee and S. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245411.
65. M. Huijben, G. Rijnders, D. H. A. Blank, S. Bals, S. V. Aert, J. Verbeeck, G. V. Tendeloo, A. Brinkman and H. H. Hilgenkamp, Nat. Mater., 2006, 5, 556.
66. J. Nishimura, A. Ohtomo, A. Ohkubo, Y. Murakami and M. Kawasaki, Jpn. J. Appl. Phys., 2004, 43, L1032.
67. http://www.engin.brown.edu/organizations/EWB/GISP/Callster%20-%20chapter_17.pdf.
68. C. C. Hu, Modern Semiconductor Devices for Integrated Circuits, Part I: Electrons and holes in a semiconductor, 2011.
69. J.-H. Lee, J. Wu and J. C. Grossman, Phys. Rev. Lett., 2010, 104, 016602.
70. A. H. Reshak and S. Auluck, Comput. Mater. Sci., 2015, 96, 90.
71. A. H. Reshak, J. Phys. Chem. Solids, 2015, 78, 46.
72. A. H. Reshak, Renewable Energy, 2016, 76, 36.
73. A. H. Reshak, RSC Adv., 2014, 4, 63137 (RSC Adv., 2015, 5, 47569).

---