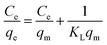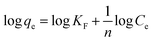Synthesis, characterization and application of cyclam-modified magnetic SBA-15 as a novel sorbent and its optimization by central composite design for adsorption and determination of trace amounts of lead ions†
Rouholah Zare-Dorabei*a,
Maryam Shamsedini Darbandsariab,
Ali Moghimib,
Mahnaz Saghanejhad Tehrania and
Samaneh Nazerdeylamia
aResearch Laboratory of Spectrometry & Micro and Nano Extraction, Department of Chemistry, Iran University of Science and Technology, Tehran 16846-13114, Iran. E-mail: zaredorabei@iust.ac.ir; Fax: +98 21 77491204; Tel: +98 21 77240646
bDepartment of Chemistry, Varamin (Pishva) Branch, Islamic Azad University, Varamin, Iran
First published on 7th November 2016
Abstract
A novel adsorbent based on 1,4,8,11-tetraazacyclotetradecane (cyclam) loaded in mesoporous silica (cyclam-SBA-15) was synthesised and modified by Fe3O4 magnetic nanoparticles (Fe3O4@cyclam-SBA-15). Characterization was performed by scanning electron microscopy (SEM), Fourier transform infra-red spectroscopy (FT-IR) and X-ray powder diffraction (XRD). The application of this sorbent was analyzed in magnetic solid phase extraction (MSPE) and adsorption of trace amounts of lead ions (Pb2+). The effects of various factors, such as adsorbent dosage, initial concentration of the lead ion, contact time and pH of the solution, on the removal efficiency were simultaneously evaluated by central composite design (CCD) under response surface methodology (RSM). The optimized conditions were found to be 0.004 g, 20 mg L−1, 40 min and 4.8, for adsorbent dosage, initial Pb concentration, contact time and pH, respectively. For the extraction experiments, the nature and volume of the eluent were also investigated to obtain the optimum conditions for the enrichment factor. Due to the high stability of the magnetic adsorbent, it can be used several times with only a slight decrease in the recovery of Pb(II) ions. The effects of matrix ions on the retention of the Pb2+ ions were also studied in order to examine the selectivity of this sorbent toward Pb(II) ions. Under the optimal conditions, the proposed method exhibited a high adsorption capacity of 625 mg g−1, a detection limit of 2.02 μg L−1 and an enrichment factor of 200 with a relative standard deviation (RSD%) of 4.14%. Finally, the application of the synthesized material was evaluated for adsorption and preconcentration of lead ions from foods and environmental water samples.
Introduction
Heavy metal ions, generally having a density greater than 5 kg L−1, are regarded as one of the main sources of contamination in the environment. In recent years, the concentration levels of these dangerous metals such as chromium, cobalt, copper, cadmium, mercury and lead, especially in natural and waste waters, have increased dramatically due to agricultural and industrial activities as well as enlargement of urban regions. Lead (Pb) is one of the most numerous toxic heavy metals utilized in many industries such as paints, lead–acid batteries, lead glasses and related chemical industries.1–3 The introduction of lead contamination into the environment can have serious effects on human health as a low level of lead ions in the body leads to a number of adverse health effects especially in the brain and central nervous system (CNS).4,5 However, monitoring of these toxic pollutants at ultra-trace level is not possible due to the matrix effect and low concentration of metal ions in most real samples with high complexity of the matrices such as biological and industrial systems. Therefore, preconcentration and/or adsorption of trace metal ions from the matrix are frequently necessary before analysis by instrumental techniques like those of atomic absorption and atomic emission spectroscopy in order to achieve a favorable detection limit, selectivity and sensitivity of measurement.6 Up to now, various methods including liquid–liquid extraction, co-precipitation, single drop microextraction, membrane extraction, ion exchange and solid phase extraction are reported for preconcentration.7,8 Solid phase extraction as a promising technique is on the basis of sorption of metal ions on various supports. This procedure have been widely applied due to its several advantages over other adsorption techniques in terms of the ability to remove trace amounts of metal ions present in complicated samples, higher enrichment or preconcentration factors, ease of operation and low consumption of reagents and reusability of the adsorbent.9,10In the two past centuries different supports, reagents and chelating ligands including activated carbon,11,12 Amber-lite XAD-2000,13 porphyrins,14 surfactants,15 silica gel,16 polymers,17 graphene and graphene oxide (GO),18–20 biological molecules,21 Dowex M4195 chelating resin22 and alumina23 have been proposed in order to design of suitable sorbents for efficient preconcentration and removal of metal ions from various matrices. Nowadays, porous adsorbents possessing large surface area with more binding sites have considered a lot of attention as ideal adsorbents due to their significant affinity to heavy metals removal. Mesoporous materials specifically with high surface area and uniform pore distribution ranging from 2 to 50 nm (ref. 24) have been extensively used in different fields including adsorption, sensors, catalysis and semiconductor. Mesoporous silica based materials like Santa Barbara Amorphous (SBA-15) are highly ordered mesoporous materials which are benefited from some advantages such as chemically and hydrothermally stable, remarkable pore volume and profusely large surface area with tunable porosity as well as large adsorption capacity.25 Functionalization of SBA-15 as a worthy support by various organic agents and ligands is an attractive approach which allows to introduce more accessible and more selective sites, higher adsorption efficiency and fast binding kinetics as well as showing stronger affinity to target.26–28 In comparison with the labor-consumptive centrifugation, precipitation and filtration conventional methods, magnetic materials are of great value to carry out a convenient and cost-effective separation with fast recovery only by means of an external magnetic field.29 Therefore, incorporating Fe3O4 magnetic nanoparticles as a superparamagnetic material into the synthesized adsorbent is a suitable to overcome the problems of traditional separation steps.30 In this regard magnetic solid phase extraction (MSPE) is introduced as an easy, low-cost, rapid and high-sensitive separation technique in which the magnetic adsorbent can be separated from the solution under an external magnetic field.28,31
In recent years, the statistical design of experiments by using chemometric tools such as Response Surface Methodology (RSM) is widely preferred in order to decrease the number of experiments, while regarding to the interaction between studied parameters and finding the optimum condition.32 Despite the traditional one at the time method, simultaneously evaluation of the factors influencing the experimental process will be possible by this mathematical and statistical technique even in the presence of complex interactions. RSM method is composed of the process modeling step followed by estimation the optimal condition. The modeling is in the form of first or second order polynomial equation to the experimental responses resulted from the experimental design, followed by analysis of the variance (ANOVA) of the model.33 The validated model can be displayed in a tridimensional graph, introducing a surface response can be useful for determination the optimal conditions of the extraction process.34,35
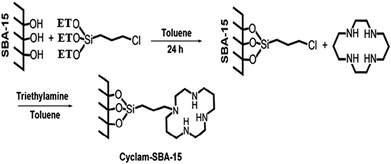
Here authors report a new synthesized material based on 1,4,8,11-tetraazacyclotetradecane (cyclam) loaded in mesoporous silica (cyclam-SBA-15) and modified by Fe3O4 magnetic nanoparticles (Fe3O4@cyclam-SBA-15). SBA-15 have many silanol groups that caused simply reaction with cyclam or other organic compound.36,37 Fig. S1† indicates organic compound cyclam with structural formula C10H24N4. Cyclam with NH group works as a nucleophile and improve selectivity and sensitivity of SBA-15.
Fe3O4@cyclam-SBA-15 was then applied for both adsorption and preconcentration of Pb(II) ions from foods and wastewaters. In the removal step, the influences of some analytical variables such as pH of the analyte solution, adsorbent dosage, contact time, initial Pb(II) concentration were investigated and optimized by experimental design methodology as a mathematical tool. In the preconcentration step, the nature and volume of the eluting solvent on the quantitative recoveries of the analyte was examined by using one at the time approach. Under the obtained optimal condition the performance of the proposed adsorbent in MSPE with regard to linear range, limits of detection, precision and recovery was evaluated in detail.
Experimental
Materials
Pluronic (P123, Mn = 5800, EO20PO70EO20) and cyclam were purchased from Sigma-Aldrich CO. Hydrochloric acid 37%, tetraethylorthosilicate (TEOS), ethanol, toluene, FeCl3 salt, FeCl2·4H2O, chloropropyltriethoxy silane (CPTES, 97%), ethylene diamine tetraacetic acid (EDTA), triethylamine and ammonia solution 25% were used from Merck CO. Double distilled deionized water was used throughout. Nitrate salt of lead (Pb(NO3)2) was of the highest purity available and were applied without any further purification.Instruments
The concentration of Pb ions was measured by using flame atomic absorption spectrometer (FAAS) (AA-6300 Shimadzu, Japan) at the wavelength of 283.3 nm. The pH adjustment of sample solution was performed with a Metrohm 691 pH meter with a combined glass – calomel electrode (Metrohm, Switzerland, Swiss). A shaker (SHO-2D, Wiseshake) was used for synthesis and dispersion of samples. Morphology of the synthesized materials was investigated by field emission scanning electron microscopy (FE-SEM, S4160, Hitachi, Japan) under an acceleration voltage of 30 kV. Low-angle X-ray diffraction (XRD) pattern was collected with an automated Philips X'Pert X-ray diffractometer using Cu Kα radiation (wavelength, λ = 1.5418 Å) for 2θ values over 5–10°. FT-IR spectra were recorded on 8411 S FTIR spectrometer (Shimadzu) at room temperature in KBr pellets under atmospheric conditions in the region 400–4000 cm−1. The textural characterization of the adsorbents was carried out by nitrogen adsorption and desorption isotherms determined at 77 K with a volumetric adsorption analyzer (Micromeritics Instrument, ASAP 2020). Each sample was degassed at 100 °C prior to analysis for 3 h under N2 gas flow. The surface area was calculated by using BET method and the pore size distribution was evaluated from desorption branch of nitrogen isotherms by using the Barrett–Joyner–Halenda (BJH) model.Synthesis of cyclam@SBA-15
SBA-15 was synthesized by hydrothermal method.38,39 4.00 g P123, 90.0 mL HCl 2.0 M and 21.0 mL deionized H2O were stirred for 5 hour at room temperature. 6.8 mL TEOS was add to blend and the mixture was stirred again for 24 h at 400 °C. Thereafter, mixture was aged in autoclave at 1000 °C in oven for 24 h following by washing with deionized water, drying and calcinating for 6 h at 6000 °C in a stove. 1.00 g SBA-15 and 50 mL toluene were stirred for 1 h at room temperature. Then, 1.0 mL CPTES was added and the mixture was refluxed for 24 h at 1200 °C under N2 gas as a neutral gas. After, the product was washed with 10 mL toluene for three times and dried in a vacuum oven for 4 h at 1000 °C. 1 g Cl-SBA-15, 50.0 mL toluene, 1.0 mL triethylamine and 0.10 g cyclam as a ligand were refluxed for 24 h at 1150 °C. The final material was washed with toluene and dried in a vacuum oven for 10 h at 800 °C. The overall steps of SBA-15@cyclam synthesis is indicated in Fig. 1.Synthesis of Fe3O4
Fe3O4 was synthesized by co-precipitation method with a little modification.40 Briefly, 1.7 g FeCl2·4H2O salt and 4.7 g FeCl3 salt with 100 mL deionized H2O were stirred in an ultrasonic bath for 2 h at 60 °C under N2 gas. Then, 10.0 mL NH3 solution 25% was dropwise added to the mixture followed by dispersion for 60 min under ultrasonic irradiation. The black-colored mixture was transferred onto the shaker and shacked for more than 12 h. Fe3O4 nanoparticles were finally gathered with a magnet and washed with deionized water. The product was vacuum-dried at 60 °C overnight and placed in a desiccator before use (Fig. S2†).Synthesis of Fe3O4@cyclam-SBA-15
Fe3O4@cyclam-SBA-15 was synthesized by composite method. Briefly, 0.06 g cyclam-SBA-15 in 20 mL ethanol and 0.02 g Fe3O4 in 20 mL ethanol were stirred separately in an ultrasonic bath and then mixed with each other after complete dispersion. The mixture was shacked for 12 h. The obtained composite of Fe3O4@cyclam-SBA-15 was gathered with magnet and repeatedly washed with deionized water to remove nonmagnetic byproducts. The product was dried at 50 °C overnight.Magnetic solid phase extraction of Pb(III) ions by Fe3O4@cyclam-SBA-15
The extraction process of Pb ions was carried out in batch mode. In the first step, a specific amount of the magnetic sorbent was constantly shaked with 600 mL of Pb(II) ion solution in order to achieve the heterogeneous solution. In the second step, the sorbent was separated by a magnet and washed with deionized water. The adsorbed Pb ions were eluted with 3 mL of a solution containing 0.01 M of EDTA and shacked under a specified time at room temperature. Thereafter, the amounts of lead ions content in the eluent were analyzed by FAAS. For removal experiments, only the first step was performed and after separation by the magnet, the solutions were analyzed for the final concentration of metal ions by using FAAS.Pretreatment and analysis of real samples
In order to determine of the trace Pb ions in real samples and survey reliability and capability of the proposed method, milk sample was purchased from local supermarkets in Tehran and prepared for extraction of lead ions. For this purpose, 7.0 mL of nitric acid (65% HNO3) was added to 25 mL milk and the mixture was heated on a hot plate to 60–70 °C for 30 min. Then 7.0 mL of 65% HNO3 was added and the solution was heated again for 30 min. After cooling at room temperature, 2.0 mL of 30% H2O2 was added and the mixture was heated for 30 min. The final product was separated by centrifuge and the pH of the solution was adjusted to 4.8 by addition of NaOH solution for further experiments. For all preconcentration experiment, the percent of extraction or extraction recovery (ER) was obtained from the following equation:
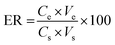 | (1) |
Central composite design (CCD)
As shown in Table 1, five-level CCD was performed to evaluate the significance of the effects of variables on adsorption capacity of the adsorbent (Q, mg g−1) toward Pb(II) ions uptake by using the software Design Expert 7.0.0. Generally, a full design is included Nf = 2f factorial points with Na = 2f axial runs (f is the number of factors) and NC central points. In the current work, the independent variables were adsorbent dosage, initial concentration of the lead ion, contact time and pH of the solution (f = 4 in this study). The total number of design points (N) is obtained by the following equation:| N = 2f + 2f + NC | (2) |
| Factors | Unit | Surface factors | ||||
|---|---|---|---|---|---|---|
| Level | Star point | |||||
| (Low) −1 | (Central) | (High) +1 | −α | +α | ||
| (A) Initial concentration | mg L−1 | 10 | 15 | 20 | 5 | 25 |
| (B) Adsorbent dosage | mg | 4 | 6 | 8 | 2 | 10 |
| (C) pH | — | 3 | 4 | 5 | 2 | 6 |
| (D) Contact time | min | 20 | 30 | 40 | 10 | 50 |
The center points are used to estimate the experimental or pure error and the reproducibility of the data. The independent factors are coded to the (−1, +1) interval as the low and high levels, respectively. The axial points are located at distance of α from center and make the design rotatable.41,42
According to the above explanations, 30 experiments had to be run for the CCD. The experiments were randomized and divided into two blocks. The design matrix and the responses are shown in Table S1.†
The mathematical relationship between the four independent variables can be approximated by the second order polynomial model:
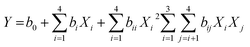 | (3) |
Results and discussions
Characterization
FE-SEM images of SBA-15, cyclam-SBA-15, Fe3O4@cyclam-SBA-15 and Fe3O4@cyclam-SBA-15 after lead ions uptake (Fe3O4@cyclam-SBA-15-Pb) are illustrated in Fig. 2. According to the Fig. 2a, mesoporous SBA-15 has a cylindrical shape with the uniform size distribution and the synthesized structure is in good agreement with the literature.27,38,39 As can be seen from Fig. 2b there was no obvious difference of the morphology between original mesoporous SBA-15 and cyclam functionalized mesoporous composite. Fig. 2c demonstrates tiny spherical nanoparticles of Fe3O4 uniformly distributed throughout the specimen. It is necessary to mention that after Pb(II) adsorption on Fe3O4@cyclam-SBA-15 no significant change was occurred in the structure of the original adsorbent.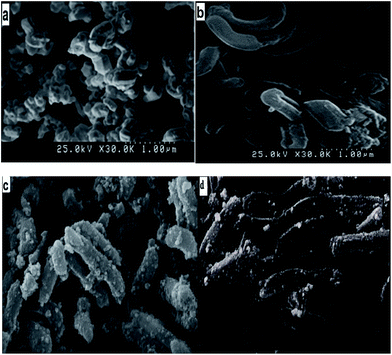 | ||
| Fig. 2 FE-SEM image of (a) SBA-15, (b) cyclam-SBA-15, (c) Fe3O4@cyclam-SBA-15, (d) Fe3O4@cyclam-SBA-15-Pb. | ||
FT-IR spectra shows distinguished peaks at 3344.3 cm−1, 968 cm−1 and 1080.06 cm−1 that are assigned to stretching vibration of O–H band, Si–O and Si–O–Si bands in silanol group (SiOH), respectively (Fig. S3(a)†). Fig. S3(b)† is related to Cl-SBA-15 and reveals a peak at 2925.8 cm−1 which corresponds to C–H bending and stretching vibration in propylene. According to Fig. S3(c),† the strong peaks at 1731.9 cm−1, 1639.38 cm−1 and 1558.38 cm−1 confirm the presence of functional groups like NH group. The peak appearing at 1458 cm−1 is related to C–N in cyclam. Fig. S3(d)† shows a significant peak at 580 cm−1 which is attributed to Fe–O band in Fe3O4.
BET results shows pore diameters of mesoporous silica SBA-15 equal to 85.00 Å. The surface area and total volume pore are 869.00 m2 g−1 and 1.03 m3 g−1, respectively (Table 2). From the sorption/desorption N2 analysis, SBA-15 is categorized as a mesoporous material (Fig. S4†). As is expected, the decrease in BET surface area, the mesoporous volume and average pore diameter was observed after addition of cyclam to mesoporous SBA-15.
| Sample | BET surface area (m2 g−1) | Pore diameter (BJH) (Å) | Total pore volume (m3 g−1) |
|---|---|---|---|
| SBA-15 | 869 | 85 | 1.03 |
| Cyclam-SBA-15 | 374 | 67 | 0.474 |
| Fe3O4@cyclam-SBA-15 | 325 | 61 | 0.469 |
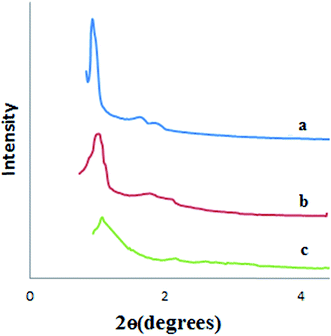
XRD pattern of SBA-15 shows three peaks in (100), (110) and (200) related to the hexagonal mesostructure of SBA-15 (Fig. 3a). The pattern is in good accordance with the literature.44 The low-angle XRD pattern of cyclam-SBA-15 is depicted in Fig. 3b. In compared with the SBA-15, the decrease in the intensities was observed which is attributed to the closeness of the original pores with the cyclam ligand. As is shown in Fig. 3a and b there is no considerable shift in the patterns confirming that cyclam-SBA-15 poses symmetrical structure and the deposition of cyclam onto SBA-15 lead to no obvious change in its surface. According to Fig. 3, after adsorption of Pb(II) onto Fe3O4@cyclam-SBA-15 no significant change or destruction was revealed in the original adsorbent.
Central composite design (CCD)
The data corresponding to the effects of four independent variables (adsorbent dosage (A), Pb(II) initial concentration (B) pH (C) and time (D)) obtained from experiments and the responses for thirty runs are listed in Table 3. The effect of pH was investigated in the range of 2–6 (Table 1). Because at pHs higher than 6, the lead hydroxide precipitates will appear. Therefore the soluble metal ions will removed from the solution leads to a significant error in subsequent analysis of the Pb(II) ions concentration. In order to obtain the most important effects and possible interactions between the variables, analysis of variance (ANOVA) was calculated using Design-Expert 7.0.0 software (Table 3). The quality of the polynomial model equation was evaluated by the coefficient of determination (R2) and the statistical significance of the selected model was judged by F-test. The obtained value of F-value for Pb(II) uptake was 166.38. On the other hand, very low p-values (<0.0001) implied that the model was significant for Pb(II) removal and was considered as a criterion for distinguishing statistically significant parameters. The lack of fit (LOF) is another important expression which is relative to the pure error.| Source | Sum of squares | df | Mean square | F value | p-Value prob > F | |
|---|---|---|---|---|---|---|
| Block | 259.51 | 2 | 129.75 | |||
| Model | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804.35 804.35 |
14 | 4914.60 | 166.38 | <0.0001 | Significant |
| A – adsorbent dosage | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915.32 915.32 |
1 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915.32 915.32 |
809.65 | <0.0001 | |
| B – initial Pb concentration | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521.16 521.16 |
1 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521.16 521.16 |
999.44 | <0.0001 | |
| C – pH | 38.15 | 1 | 38.15 | 1.29 | 0.2763 | |
| D – time | 1749.55 | 1 | 1749.55 | 59.23 | <0.0001 | |
| AB | 1846.24 | 1 | 1846.24 | 62.50 | <0.0001 | |
| AC | 47.99 | 1 | 47.99 | 1.62 | 0.2248 | |
| AD | 143.23 | 1 | 143.23 | 4.85 | 0.0463 | |
| BC | 1251.57 | 1 | 1251.41 | 42.37 | <0.0001 | |
| BD | 29.94 | 1 | 29.94 | 1.01 | 0.3324 | |
| CD | 358.14 | 1 | 358.14 | 12.12 | 0.0041 | |
| A2 | 7499.91 | 1 | 7499.91 | 253.91 | <0.0001 | |
| B2 | 2021.57 | 1 | 2021.57 | 68.44 | <0.0001 | |
| C2 | 104.01 | 1 | 104.01 | 3.52 | 0.0832 | |
| D2 | 1372.41 | 1 | 1372.41 | 46.46 | <0.0001 | |
| Residual | 383.99 | 13 | 29.54 | |||
| Lack of fit | 321.03 | 10 | 32.10 | 1.53 | 0.4013 | Not significant |
| Pure error | 62.96 | 3 | 20.99 | |||
| Cor total | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 447.85 447.85 |
29 |
According to the Table 3, LOF (0.4013) is not significant, confirming the suitability and feasibility of the model for prediction and description of the removal behavior as well as the goodness of the fit. The following semi-empirical predictive equation of adsorption capacity (R) in terms of significant variables can be subsequently obtained by the Design-Expert software for removal of Pb(II) ions (eqn (4)):
| R1 = +232.908 − 48.253A − 3.096B − 0.694C − 0.189D − 1.074AB + 0.865AC − 0.149AD + 1.768BC − 0.027BD + 0.473CD + 4.133A2 + 0.343B2 − 1.974C2 + 0.07D2 | (4) |
From the results obtained by the software, the value of the determination coefficient (R2) for removal of Pb(II) ions is close to 1 (R2 = 0.9945) verifying the response surface quadratic model is the most appropriate model for prediction the adsorption of Pb(II) onto Fe3O4@cyclam-SBA-15. Furthermore, Adeq precision expression which is related to the signal to noise ratio is greater than 4.0 (Adeq precision = 40.350) showing the desirability of the model.
The plot of experimental Q values versus predicted ones calculated from the equation displayed a good fit for Pb removal (Fig. 4).
From eqn (4), it is concluded that the amount of adsorbent and contact time were significant variables and had positive effect on adsorption efficiency. Although pH couldn't be regarded as a significant factor, initial concentration of lead ions was another significant parameter that negatively affects the sorption capacity. Furthermore, the interaction of the amount of adsorbent with sonication time played no significant role in lead metal ions uptake.
Response surface methodology (RSM)
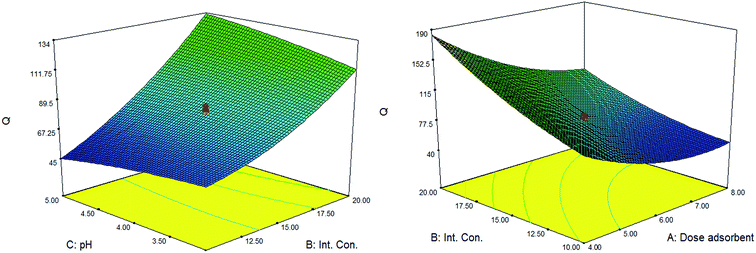
In this section, the three dimensional RSM surfaces corresponding to Q (mg g−1) in the CCD method were applied to give useful information about the possible interaction of parameters as well as optimization the significant variables. According to eqn (4) and ANOVA table, the interactions of AB and BC were remarkable. The RSM plots obtained for these two main interactions are depicted in Fig. 5.From Fig. 5, by changing pH from 3 to 5 the sorption capacity experienced a mild increase. In fact the surface charge of the sorbent plays an important role in electrostatic interaction between the cationic metal ions and surface active sites of the adsorbent. Therefore, at higher pH values, negatively charged surface of the adsorbent resulted into higher Pb(II) ions uptake through the electrostatic attraction. Although pH of the solution presented no significant effect on adsorption efficiency, its interaction with initial concentration of the lead ions (BC) should be considered as an important interaction. The adsorption capacity of metal ions increased at higher initial Pb(II) concentration because the ratio of lead ions to adsorption active sites will increase at high concentrations of the analyte. Furthermore, adsorption capacity of the metal ion was maximum when the initial concentration of Pb(II) was 20 μg L−1 (Fig. 5). As is revealed in Fig. 5, the interaction between initial lead concentration and adsorbent dosage (AB) is also significant and the maximum response was occurred at the adsorbent dosage of 0.004 g. It is clear that the increase in adsorbent dosage can lead to decrease in adsorbent capacity of Pb(II). This phenomenon may be ascribed by the diminishing the ratio of initial lead concentration to available surface area for adsorption as the adsorption capacity is expressed by the following equation (eqn (5)):
| Q = (C0 − Ce)V/W | (5) |
Regarding to the overall results obtained by ANOVA table (Table 3), eqn (4) and Fig. 5, the optimal condition in which the adsorption capacity of lead ions is maximum is proposed by the related statistical software (Table 4). Qe shows the experimental adsorption capacity resulted from the real test under optimum condition of the adsorbent dosage, initial concentration of the analyte, contact time and pH of the solution. Qp is defined as the predicted adsorption capacity obtained by the proposed model (eqn (4)). According to the good agreement between the theoretical response (Qp) and experimental value of adsorption capacity (Qe) it can be inferred that the behavior of Pb(II) removal can be investigated and predicted by the proposed model.
| Optimal conditions | Adsorption capacity (mg g−1) | ||||
|---|---|---|---|---|---|
| Adsorbent dose (g) | pH | Pb(II) concentration (mg L−1) | Contact time (min) | Qp | Qe |
| 0.004 | 4.8 | 20 | 40 | 204.27 | 203.45 |
Effect of type and volume of the eluent
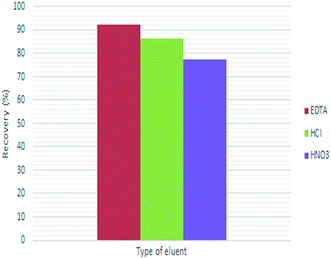
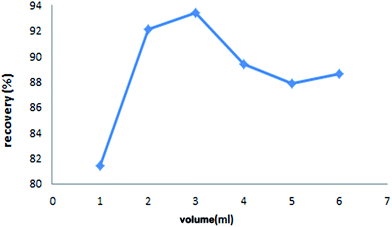
Selection of an appropriate desorbing solutions is a critical factor in order to achieve an ideal extraction recovery with the minimum concentration in order to not affect the accurate study of the analyte and destroy the original structure of solid phase.45 Moreover, the desorbing agent should imply high affinity towards the analyte as well as rapid kinetic for its quantitative recovery.18 In this work, 0.01 M each of EDTA, HCl and HNO3 were attempted to elute the adsorbed lead ions from Fe3O4@cyclam-SBA-15. The results confirmed that EDTA as a chelating agent may be complexed with Pb ions and hence exhibited greater desorption capacity than the other two eluents (Fig. 6). Therefore, EDTA was chosen as the suitable desorbing solution for the further experiments.Subsequently, the effect of EDTA volume on the recoveries of lead ions was studied and optimized within the range of 1–6 mL under optimal condition (adsorbent dose: 0.004 g, contact time: 40 min, pH: 4.8 and initial concentration of Pb(II): 30 μg L−1) at constant concentration of the eluent (0.01 mol L−1). It is necessary to mention that, a satisfactory eluent should effectively desorb the retained analyte with a small volume in order to reach high concentration factor.46 According to the result represented in Fig. 7, the recovery of lead ions was maximum when volume of the desorbing solution was 3.0 mL.
It was found that at higher volumes of EDTA, the recoveries of analyte decrease probably due to the excess amounts of the used eluent with increasing volume above 3 mL. Therefore 3 mL of 0.01 mol L−1 EDTA was employed as the desorbing solution for complete enrichment of lead ions in subsequent analysis.
Effect of desorption time and sample volume
Desorption time is an important parameter influencing the extraction recovery and analytical speed. It should be pointed out that, the preconcentration process should perform in adequate time in order to ensure that the sorption of the metal ions onto the adsorbent is complete as well as full desorption of the retained analyte from the solid phase.In this survey, the dependence of the extraction efficiency of Pb(II) on the desorption time was estimated by extracting lead ions at different elution times ranging from 5 to 30 under optimal condition. It was found that as a result of strong affinity of EDTA group to chelate with metal ions, desorption time is relatively short and 15 min was adequate for the complete elution of the adsorbed lead ions from Fe3O4@cyclam-SBA-15. Thus, desorption time of 15 min was selected for subsequent experiments.
The effect of sample volume (100–1100 mL) on extraction recovery was also investigated under optimal condition to determine the adequacy of the introduced technique for preconcentration of high amounts of lead ions from aqueous solutions. According to our findings (Fig. S5†), the maximum extraction percent was up to the sample volume of 600 mL and then reduced slightly by further increase.
Sorbent capacity
In this section, the sorption capacity which is expressed as the required amount of sorbent for quantitative retention of analyte in solution (eqn (5)) was estimated by several adsorption isotherm models such as Langmuir, Freundlich and Temkin at room temperature and under the optimal conditions of the adsorbent dosage (0.004 g), contact time (40 min) and pH of the solution (4.8) at different initial concentration of the Pb(II) ions (5–100 mg L−1). Adsorption isotherms were undertaken in order to find the maximum adsorption capacity of the synthesized sorbent over batch mode at the room temperature and equilibrium condition with initial concentration of Pb(II) ions varying from 5 to 100 mg L−1. Conventional isotherm models were then applied to fit the experimental data (Fig. S6†). The corresponding equations and the obtained results for each model are summarized in Table 5 In Langmuir model, the values of qm (maximum monolayer adsorption capacity calculated from the isotherm curve, mg g−1) and KL (the Langmuir adsorption constant, L mg−1) were achieved from the slope and intercept of the plot of Ce/qe against Ce, respectively. Ce and qe are concentration of lead ions at equilibrium (mg L−1) and adsorption capacity (the amount of adsorbed analyte on the adsorbent) at equilibrium (mg g−1), respectively. In Freundlich isotherm model, KF (the bonding energy constant related to adsorption capacity, (mg g−1) (mg L−1)−1/n) and n (heterogeneity factor indicative of the adsorption intensity) were calculated from the intercept and slope of the linear plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe against log
qe against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce, respectively. 1/n values reveals the type of isotherm to be irreversible (1/n = 0), favorable (0 < 1/n < 1) or unfavorable (1/n > 1). In Temkin isotherm model, the values of BT and KT related to the heat of adsorption (J mol−1) and equilibrium binding constant (L mol−1) could be defined by the slope and the intercept of plot of qe vs. log
Ce, respectively. 1/n values reveals the type of isotherm to be irreversible (1/n = 0), favorable (0 < 1/n < 1) or unfavorable (1/n > 1). In Temkin isotherm model, the values of BT and KT related to the heat of adsorption (J mol−1) and equilibrium binding constant (L mol−1) could be defined by the slope and the intercept of plot of qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce, respectively. B is obtained from the equation:
Ce, respectively. B is obtained from the equation: 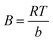 where T is the absolute temperature in Kelvin and R (8.314 J mol−1 K−1) is the universal gas constant35,47,48 According to Table 5, the highest values of correlation coefficients (R2 = 0.9992) is attributed to Langmuir isotherm model, confirming equal affinity of adsorption to lead ions and homogeneous adsorption process. Therefore Langmuir model is applicable for interpretation of the experimental data over the whole concentration range of Pb(II) ions. The maximum adsorption capacity (qm) of Fe3O4@cyclam-SBA-15 calculated by this model was 625 mg g−1 for lead ions indicating the considerable adsorption efficiency of the proposed adsorbent for lead removal.
where T is the absolute temperature in Kelvin and R (8.314 J mol−1 K−1) is the universal gas constant35,47,48 According to Table 5, the highest values of correlation coefficients (R2 = 0.9992) is attributed to Langmuir isotherm model, confirming equal affinity of adsorption to lead ions and homogeneous adsorption process. Therefore Langmuir model is applicable for interpretation of the experimental data over the whole concentration range of Pb(II) ions. The maximum adsorption capacity (qm) of Fe3O4@cyclam-SBA-15 calculated by this model was 625 mg g−1 for lead ions indicating the considerable adsorption efficiency of the proposed adsorbent for lead removal.
For this purpose the adsorption capability of Pb(II) by Fe3O4@cyclam-SBA-15 was analyzed at room temperature and under the optimal conditions of the adsorbent dosage (0.004 g), pH (4.8) and initial Pb(II) concentration (20 mg L−1) at various contact times (5–60 min). The kinetic data was subsequently evaluated by pseudo first-order, pseudo second-order and Elovich models (Table 6). From the pseudo-first-order model, k1 is the pseudo first-order rate constant (min−1). qe (mg g−1) and qt (mg g−1) are the adsorption capacities at equilibrium and at time t (min), respectively. In pseudo-second-order kinetic model, k2 is the pseudo-second order rate constant (g mg−1 min−1). From the Elovich model, the parameters of α (mg L−1 min−1) and β (L mg−1) are constants during one experiment and may be applied for comparison of reaction rates.35 Regarding to the Elovich equation a decrease in the value of β or an increase of α would enhance the reaction rate. Our findings confirmed that the sorption process under optimum condition is surprisingly fast. For Pb(II) uptake in the solution, a contact time of 30 min was enough to reach the equilibrium. Regarding to the high regression coefficient of the pseudo-second-order, the adsorption of Pb(II) on Fe3O4@cyclam-SBA-15 are best evaluated by this kinetic model (R2 = 0.99) (Fig. S7†).
| Models | Parameters | Pb2+ |
|---|---|---|
Pseudo-first-order: ln(qe − qt) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe − k1t qe − k1t |
k1 (min−1) | 0.224082 |
| qe(cal) (mg g−1) | 208.1794 | |
| R2 | 0.9691 | |
| Pseudo-second-order: t/qt = 1/k2qe2 − t/qe | k2 (g mg−1 min−1) | 0.000497 |
| qe(cal) (mg g−1) | 243.9024 | |
| R2 | 0.9948 | |
Elovich: qt = l/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(αβ) + 1/β ln(αβ) + 1/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(t) ln(t) |
β | 0.018842 |
| R2 | 0.9324 |
Regeneration study
Reusability of the adsorbent for further use is a key feature for evaluation its performance.7 In this study, the regenerability and stability of Fe3O4@cyclam-SBA-15 was assessed through the performance of five consecutive adsorption/desorption cycles under the optimal condition. In this regard, some low cost chemicals including HCl (0.01 M), EDTA (0.01 M) and HNO3 (0.01 M) were tested to retrieve the adsorbent loaded previously by Pb(II) solution under the optimum condition. After adsorption, the adsorbent was washed several times by deionized water followed by washing with the eluent. After drying in vacuum at 60 °C for 10 h, the adsorbent was used again for the subsequent run under the same condition. As is depicted in Fig. S8,† EDTA was the best eluent for desorption of metal ions from the adsorbent. The results showed that the removal efficiency decreased through each cycle from its preliminary value of about 95% at first cycle but still remained near 80% at third cycle. Recovery percentage dropped dramatically after the third cycle and reached to about 30%. Therefore, the synthesized sorbent is seemed to be stable and reusable at least for three adsorption/desorption cycles with an approximate 15% loss in sorption efficiency.Effect of interfering ions
To estimate the selectivity of Fe3O4@cyclam-SBA-15 toward Pb ions in the presence of potentially interfering ions, the experiment was performed under optimum condition and in the presence of matrix ions commonly accompany the metal analytes in real samples. The tolerance limit of interfering ions was explained as the as the largest amount causing a change of less than ±5.0% in the extraction recovery of the Pb(II) ions.49 According to the results (Table S2†) the extraction recovery (R%) was not seriously affected by the presence of the examined species at the examined ion concentration. As the synthesized sorbent represented remarkable selectivity toward lead ions, these species found generally in the nature can't interfere with the extraction procedure. To assess the usefulness of the proposed MSPE, it was applied for the removal of Pb(II) ions in various water samples through spiking method and the results are shown in (Table 7). As seen, the amounts of the Pb(II) ions which were added to the water samples could be removed effectively by the introduced magnetic solid phase extraction (Fe3O4@cyclam-SBA-15).| Real sample | Pb(II) found (μg L−1) | Pb(II) added (μg L−1) | Removal of Pb(II) ions Qmax (mg g−1) |
|---|---|---|---|
| Mineral water | <DL | 20.00 | 201.904 |
| Well water | <DL | 20.00 | 198.522 |
| Agricultural water | <DL | 20.00 | 203.014 |
Analytical features
The calibration graph for the Pb(II) solutions under the optimum experimental conditions was linear over the range of 5–100 mg L−1. The corresponded equation was Y = 0.0971X − 0.0487 (where Y is the absorbance and X is the concentration of lead ions (mg L−1) in the initial solution) with correlation coefficient (R2) of 0.9947. The preconcentration factor (defined as the ratio of the maximum volume of the initial solution (600 mL) to the final volume of the extract (3 mL)) were 200. The limit of detection (LOD) which is determined as 3Sb/m (where Sb and m are the standard deviation of the blank and the slope of the calibration graph, respectively) was 2.022 μg L−1, while the dynamic range was 5–50 μg L−1. The relative standard deviation (RSD%) at 30 μg L−1 of Pb(II) under optimum condition and for five experiments was 4.14% which proved the high reproducibility of the proposed method for lead ions extraction and determination.Application to real samples
The introduced procedure was applied for determination of lead ions in milk and water samples. In this process, 4 mg of the synthesized adsorbent was added to the 25 mL of the milk sample spiked with 40 μg L−1 of Pb solution. The mixture was shacked for 15 min followed by separation of the sorbent by using a magnet. The separated solid was eluted with 3 mL of 3 mL EDTA (0.01 M) solution and shacked for 15 min to desorb the metal ions. Finally, the lead ions in the eluent phase were analyzed by FAAS. In order to evaluate the precision of this method three successive experiments were made and the mean values were reported. According to the results summarized in Table 8 the extraction efficiency of the Pb ions in milk sample was about 94.13% which show good reproducibility as well as suitability of the developed adsorbent for determination of lead in real samples without any significant error.| Sample | Spiked (μg L−1) | Found (μg L−1) | Recovery (%) |
|---|---|---|---|
| a ND: not detected. | |||
| Milk sample 1 | 0 | 0 (NDa) | — |
| 40.00 | 39.50 | 98.75 | |
| Milk sample 2 | 0 | 0 (ND) | — |
| 40.00 | 38.02 | 95.05 | |
| Milk sample 3 | 0 | 0 (ND) | — |
| 40.00 | 40.14 | 100.35 | |
| Mineral water | 0 | 0 (NDa) | — |
| 40.00 | 38.70 | 96.75 | |
| Tap water | 0 | 0 (NDa) | — |
| 40.00 | 39.65 | 99.12 | |
| River water | 0 | 0 (NDa) | — |
| 40.00 | 38.40 | 96.00 | |
Comparison of analytical performance with literature
A comparison of the analytical results of the developed method with some reported studies for the extraction of Pb(II) ions is given in Table 9.50–53| Sorbent | Technique | Analyte | LOD (μg L−1) | EF | RSD (%) | Ref. |
|---|---|---|---|---|---|---|
| a LOD, limit of detection; EF, enrichment factor; RSD, relative standard deviation; LDR, linear dynamic range. | ||||||
| Silica gel/zirconium phosphate | FAAS | Pb2+, Cu2+ | 6.1 | — | 3.3 | 50 |
| 1-(2-Pyridylazo)-2-naphthol (PAN) | Solvent-assisted dispersive SPE-FAAS | Pb2+ | 1.3 | 50 | — | 51 |
| Modified silica gel | FIA-FAAS | Pb2+ | 10 | 37 | — | 52 |
| (1-PTSC) + (Triton X-114) | CPE-FAAS | Pb2+, Co2+, Cu2+ | 3.42 | 25 | 4.8 | 53 |
| 3,6-Dithia-1,8-octanediol (modified silica) | FIA-FAAS | Pb2+ | 1.0 | 28 | 3.8 | 54 |
| This work | Magnetic solid phase extraction by FAAS | Pb2+ | 0.02 | 200 | 5.002 | — |
The proposed method revealed significant advantages for enrichment and determination of lead ions from environmental aqueous samples in terms of favorable precision high adsorption capacity, low LOD and satisfactory enrichment factor. The RSD obtained by this method is comparable with most of the other methods reported previously. The results proved that Fe3O4@cyclam-SBA-15 could be considered as an effective magnetic solid phase for extraction of lead ions from complicated matrices.
The comparison between the performance of Fe3O4@cyclam-SBA-15 adsorbent for adsorption and removal of Pb(II) ions with various adsorbents is shown in Table 10.55–59 As shown, the adsorption capacity for Fe3O4@cyclam-SBA-15 is higher than those of corresponding adsorbents reported in the literature.
Conclusion
In the present study, a new, efficient, selective and relatively low cost adsorbent was developed based on Fe3O4 magnetic nanoparticles coated onto mesoporous SBA-15 modified with 1,4,8,11-tetraazacyclotetradecane for adsorption and determination of lead ions as an important toxic heavy metal in aqueous solutions and food samples. The effect of different variables such as adsorbent dosage, initial concentration of the lead ion, contact time and pH of the solution on the removal efficiency were mathematically evaluated by central composite design (CCD) under response surface methodology (RSM). The system represented good adsorption capacity, repeatability and reliability in analytical data, with an RSD value of lower than 4.15% for consecutive five experiments. The synthesized adsorbent could be simply generated by EDTA and reused for at least three adsorption/desorption cycles. According to our findings, the proposed method is effective for extraction and determination of Pb(II) ions at trace levels from large sample volumes (600 mL) and in the presence of complicated matrices.Acknowledgements
The financial support of this study by Iran University of Science and Technology and Iran Nanotechnology Initiative Council are gratefully acknowledged. The author acknowledges financial support from the Iran National Science Foundation (INSF).References
- Y. Lu, X. Li, G. Wang and W. Tang, Biosens. Bioelectron., 2013, 39, 231–235 CrossRef CAS PubMed.
- A. A. Gouda, Int. J. Environ. Anal. Chem., 2014, 94, 1210–1222 CrossRef CAS.
- A. Islam, H. Ahmad, N. Zaidi and S. Kumar, ACS Appl. Mater. Interfaces, 2014, 6, 13257–13265 CAS.
- M. Xu, P. Yin, W. Liu, C. Liu, Q. Tang, R. Qu and Q. Xu, Ind. Eng. Chem. Res., 2013, 52, 14752–14759 CrossRef CAS.
- R. P. Medina, E. T. Nadres, F. C. Ballesteros Jr and D. F. Rodrigues, Environ. Sci.: Nano, 2016, 3, 638–646 RSC.
- F. Jiao and H. W. Gao, Environ. Monit. Assess., 2013, 185, 39–44 CrossRef CAS PubMed.
- M. H. Mashhadizadeh and M. Amoli-Diva, J. Anal. At. Spectrom., 2013, 28, 251–258 RSC.
- O. Sayar, N. Akbarzadeh Torbati, H. Saravani, K. Mehrani, A. Behbahani and H. R. Moghadam Zadeh, J. Ind. Eng. Chem., 2013, 20, 2657–2662 CrossRef.
- S. Sadeghi, H. Azhdari, H. Arabi and A. Zeraatkar Moghaddam, J. Hazard. Mater., 2012, 215–216, 208–216 CrossRef CAS PubMed.
- A. Bagheri, M. Taghizadeh, M. Behbahani, A. A. Asgharinezhad, M. Salarian, A. Dehghani, H. Ebrahimzadeh and M. M. Amini, Talanta, 2012, 99, 132–139 CrossRef CAS PubMed.
- S. Xingguang, W. Meijia, Z. Yihua, Z. Jiahua, Z. Hanqi and J. Qinhan, Talanta, 2003, 59, 989–997 CrossRef PubMed.
- G. Karimipour, M. Ghaedi, R. Sahraei, A. Daneshfar and M. Nejati Biyareh, Biol. Trace Elem. Res., 2012, 145, 109–117 CrossRef CAS PubMed.
- H. B. Senturk, A. Gundogdu, V. N. Bulut, C. Duran, M. Soylak, L. Elci and M. Tufekci, J. Hazard. Mater., 2007, 149, 317–323 CrossRef CAS PubMed.
- L. Wu, L. Y. Feng, J. S. Ren and X. G. Qu, Biosens. Bioelectron., 2012, 34, 57–62 CrossRef CAS PubMed.
- M. Lotya, Y. Hernandez, P. J. King, R. J. Smith, V. Nicolosi, L. S. Karisson, F. M. Blighe, S. De, Z. M. Wang, I. T. Mc Govern, G. S. Duesbeng and J. N. Coleman, J. Am. Chem. Soc., 2009, 131, 3611–3620 CrossRef CAS PubMed.
- S. S. Bozkurt and M. Merdivan, Environ. Monit. Assess., 2009, 158, 15–21 CrossRef CAS PubMed.
- J. J. Liang, Y. F. Xu, Y. Huang, L. Zhang, Y. Wang, Y. F. Ma, F. F. Li, T. Y. Guo and S. Y. Chen, J. Phys. Chem. C, 2009, 113, 9921–9927 CAS.
- E. Kazemi, S. Dadfarnia and A. M. Haji Shabani, Talanta, 2015, 141, 273–278 CrossRef CAS PubMed.
- A. M. Etorki and I. S. Shaban, Am. J. Environ. Prot., 2015, 4, 105–109 CrossRef CAS.
- M. R. Pourjavid, A. Akbari Sehat, M. Haji Hosseini, M. Rezaee, M. Arabieh, S. R. Yousefi and M. R. Jamali, Chin. Chem. Lett., 2014, 25, 791–793 CrossRef CAS.
- S. S. Sabri, P. L. Levesque, C. M. Aguirre, J. Guillemette, R. Martel and T. Szkopek, Appl. Phys. Lett., 2009, 95, 242104 CrossRef.
- M. Tuzen, K. O. Saygi and M. Soylak, J. Hazard. Mater., 2008, 156, 591–595 CrossRef CAS PubMed.
- D. Afzali, Z. Daliri and M. A. Taher, Arabian J. Chem., 2014, 7, 770–774 CrossRef CAS.
- S. M. Holmes, V. L. Zholobenko, A. Thursfield, R. J. Plaisted, C. S. Cundy and J. Dwyer, J. Chem. Soc., Faraday Trans., 1998, 94, 2025–2032 RSC.
- A. Sousa, K. C. Souza, S. C. Reis, R. G. Sousa, D. Windmoller, J. C. Machado and E. M. B. Sousa, J. Non-Cryst. Solids, 2008, 354, 4800–4805 CrossRef CAS.
- Q. Tao, Z. Y. Xu, J. H. Wang, F. L. Liu, H. Q. Wan and S. R. Zheng, Microporous Mesoporous Mater., 2010, 131, 177–185 CrossRef CAS.
- R. Zare-Dorabei, V. Jalalat and A. Tadjarodi, New J. Chem., 2016, 40, 5128–5134 RSC.
- G. Li, Z. Zhao, J. Liu and G. Jiang, J. Hazard. Mater., 2011, 192, 277–283 CAS.
- S. Zhang, Y. Zhang, J. Liu, Q. Xu, H. Xiao, X. Wang, H. Xu and J. Zhou, Chem. Eng. J., 2013, 226, 30–38 CrossRef CAS.
- X. Kong, R. Gaoa, X. He, L. Chen and Y. Zhang, J. Chromatogr. A, 2012, 1245, 8–16 CrossRef CAS PubMed.
- C. Chao, M. He and B. Hu, J. Hazard. Mater., 2011, 187, 379–385 CrossRef PubMed.
- M. Saghanejhad Tehrani and R. Zare-Dorabei, Spectrochim. Acta, Part A, 2016, 160, 8–18 CrossRef PubMed.
- M. Saghanejhad Tehrani and R. Zare-Dorabei, RSC Adv., 2016, 6, 27416–27425 RSC.
- M. Ghaedi, M. Pakniat, Z. Mahmoudi, S. Hajati, R. Sahraei and A. Daneshfar, Spectrochim. Acta, Part A, 2014, 123, 402–409 CrossRef CAS PubMed.
- M. Roosta, M. Ghaedi, A. Daneshfar and R. Sahraei, Spectrochim. Acta, Part A, 2014, 122, 223–231 CrossRef CAS PubMed.
- T. Ben Amor, I. Dhaouadi, B. Lebeau, M. Tlili and M. Ben Amor, Desalination, 2014, 351, 82–87 CrossRef CAS.
- R. Herbert, D. Wang, R. Schomacker, R. Schlçgl and C. Hess, ChemPhysChem, 2009, 10, 2230–2233 CrossRef CAS PubMed.
- A. Tadjarodi, V. Jalalat and R. Zare-Dorabei, Mater. Res. Bull., 2015, 61, 113–119 CrossRef CAS.
- V. Jalalat, A. Tadjarodi and R. Zare-Dorabei, J. Nanostruct. Chem., 2013, 3, 477–482 Search PubMed.
- A. R. Mahdavian and M. Al-Sadat Mirrahimi, Chem. Eng. J., 2010, 159, 264–271 CrossRef CAS.
- M. Roosta, M. Ghaedi, A. Daneshfar, S. Darafarin, R. Sahraei and M. K. Purkait, Ultrason. Sonochem., 2014, 21, 1441–1450 CrossRef CAS PubMed.
- A. Asfaram, M. Ghaedi, S. Hajati, M. Rezaeinejad, A. Goudarzid and M. K. Purkait, J. Taiwan Inst. Chem. Eng., 2015, 53, 80–91 CrossRef CAS.
- M. Ghaedi and S. Nasiri Kokhdan, Spectrochim. Acta, Part A, 2015, 136, 141–148 CrossRef CAS PubMed.
- D. Zhao, J. Feng, Q. Huo, N. Melosh, G. H. Fredrickson, B. F. Chmelka and G. D. Stucky, Science, 1998, 279, 548–552 CrossRef CAS PubMed.
- E. Aliyari, M. Alvand and F. Shemirani, Anal. Methods, 2015, 7, 7582–7589 RSC.
- M. Ghaedi, H. Tavallali, M. Keshavarz and K. Niknam, Chin. J. Chem., 2009, 27, 2066–2072 CrossRef CAS.
- B. K. Jung, Z. Hasan and S. H. Jhung, Chem. Eng. J., 2013, 234, 99–105 CrossRef CAS.
- F. H. Malayeri, M. R. Sohrabi and H. Ghourchian, Int. J. Biomed. Nanosci. Nanotechnol., 2012, 8, 79–86 Search PubMed.
- H. Fazelirad and M. A. Taher, Environ. Technol., 2015, 37, 300–307 CrossRef PubMed.
- E. Matoso, L. T. Kubota and S. Cadore, Talanta, 2003, 60, 1105–1111 CrossRef CAS PubMed.
- R. Reyhaneh and R. Ghadiri, J. Braz. Chem. Soc., 2015, 26, 1642–1647 Search PubMed.
- D. Rodriguez, P. Fernandez, C. Perez-Conde, A. Gutierrez and C. Camara, Fresenius. J. Anal. Chem., 1994, 349, 442–446 CrossRef CAS.
- C. Demirhan and M. Tuzen, Food Chem. Toxicol., 2010, 48, 1399–1404 CrossRef PubMed.
- P. A. B. da Silva, G. C. S. de Souza, D. M. d. S. Leotério, M. F. Belian, W. E. Silva, A. P. S. Paim and A. F. Lavorante, J. Food Compos. Anal., 2015, 40, 177–184 CrossRef CAS.
- J. Goel, K. Kadirvelu, C. Rajagopal and V. K. Garg, J. Hazard. Mater., 2005, 125, 211–220 CrossRef CAS PubMed.
- J. A. Arcibar Orozco, J. R. Rangel Mendez and P. E. Diaz Flores, Water, Air, Soil Pollut., 2015, 226, 1–10 CrossRef.
- J. Hur, J. Shin, J. Yoo and Y. S. Seo, Sci. World J., 2015 DOI:10.1155/2015/836287.
- R. Sitko, P. Janik, B. Feist, E. Talik and A. Gagor, ACS Appl. Mater. Interfaces, 2014, 6, 20144–20153 CAS.
- A. Moghimi, Aust. J. Basic Appl. Sci., 2012, 3, 320–330 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra21895d |
| This journal is © The Royal Society of Chemistry 2016 |