Fe doped LaGaO3: good white light emitters†
Abstract
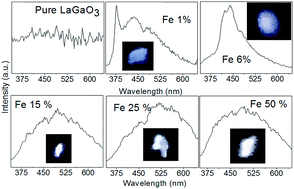
A polycrystalline sample of LaGa1−xFexO3 has been prepared by solid state reaction. The structural, optical and electronic structure of Fe doped LaGaO3 have been investigated. It is observed that with Fe doping the lattice parameter of the prepared samples systematically increases whereas the optical band gap decreases. First-principles density functional theory (DFT) calculations were carried out to understand the effect of Fe doping on the electronic structure and to understand the origin of systematic decrease in optical band gap. DFT studies suggests that there exists an indirect band gap to direct band gap transition with Fe doping which is further confirmed using photoluminescence measurements. Photoluminescence studies suggest that Fe doped LaGaO3 are potential candidates as white light emitting materials.


 Please wait while we load your content...
Please wait while we load your content...