Dispersible cobalt chromite nanoparticles: facile synthesis and size driven collapse of magnetism†
D. Zakutna‡
*ab,
I. Matulkova a,
E. Kentzingerc,
R. Medlind,
Y. Sue,
K. Nemkovskie,
S. Disch
a,
E. Kentzingerc,
R. Medlind,
Y. Sue,
K. Nemkovskie,
S. Disch f,
J. Vejpravova§
f,
J. Vejpravova§
 *ag and
D. Niznansky§a
*ag and
D. Niznansky§a
aDepartment of Inorganic Chemistry, Faculty of Science, Charles University in Prague, Hlavova 2030/8, 12843 Prague 2, Czech Republic. E-mail: zakutna@ill.fr; vejpravo@fzu.cz
bStructural and System Diagnostics, Research Centre Rez s.r.o., Hlavní 130, 25068 Husinec-Rez, Czech Republic
cJülich Center for Neutron Sciences JCNS, Peter Grünberg Institute PGI, JARA-FIT, Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
dNew Technology Research Centre, University of West Bohemia, Univerzitní 8, 306 14 Pilsen, Czech Republic
eJülich Center for Neutron Sciences JCNS at Heinz Maier-Leibnitz Zentrum MLZ, Forschungszentrum Jülich GmbH, Lichtenbergstrasse 1, D-85747 Garching, München, Germany
fDepartment Chemie, Universität zu Köln, Luxemburger Strasse 116, 50939 Köln, Germany
gDepartment of Magnetic Nanosystems, Institute of Physics CAS, v.v.i., Na Slovance 2, 18221 Prague 8, Czech Republic
First published on 4th November 2016
Abstract
Multiferoic oxides have enormous application potential thanks to the mutually coupled magnetic and dielectric response embedded in a standalone material. Among them, the unique case is the cobalt chromite with spin-induced electric polarization locked to the magnetization direction and propagation vector of the spiral magnetic phase. The nature of the ground state magnetic structure gives rise to complex size dependent magnetic behaviour, which collapses when reaching a critical particle size. In our work, we focused on preparation of standalone cobalt chromite nanoparticles (NPs). We introduced hydrothermal decomposition of cobalt(II)/chromium(III) oleates in a water/ethanol system without need of additional thermal treatment, which lead to stable cobalt chromite nanoparticles with diameter of 3.0(1)–4.2(1) nm and log normal size distribution of 12–16%. The size at the edge of the critical limit was tuned by the reaction temperature reaching typically 240 ± 10 °C. The as-prepared NPs are coated with covalently bonded oleic acid and can be easily dispersed in non-polar solvents, which makes them excellent candidates for custom surface modifications. The NPs were studied using a large number of characterization techniques: powder X-ray diffraction, transmission electron microscopy, small-angle X-ray scattering, and vibrational spectroscopies. The impact of the size effect on the magnetic properties was also investigated by temperature and magnetic field dependent magnetization, a.c. susceptibility and diffuse neutron scattering. The onset of the collective glassy state due to the collapse of long range conical magnetic order was observed. The uniform cobalt chromite NPs coated with oleic acid with size of 3–4 nm are excellent prototypes for studying the size effect on magnetic (and feroic) materials, and can be subjected to manifold surface functionalization required for their embedding in smart nanostructures and nanocomposites.
1. Introduction
Nanoparticles (NPs) carrying intrinsic magnetic moments have been intensively investigated due to various applications, of which biomedicine and magnetic recording are the most significant.1,2 With decreasing particle size, the so-called single-domain state, which is a simple consequence of magneto-static to domain wall energy gain governs the magnetic properties of NPs. Consequently, such NPs exhibit superparamagnetic properties at temperatures and magnetic fields high enough to exceed the energy threshold for coherent rotation of the single-particle magnetization. The most prominent magnetic materials studied in the form of NPs are the spinel oxides, especially the ferrites. These materials have attracted significant attention mainly for their biocompatibility hand in hand with convenient magnetic properties making them excellent candidates for use in data storage media, dynamic random access memories, electromagnetic sensors or biomedical imaging and therapies.1–3In addition to the purely magnetic species, NPs of materials with both the intrinsic magnetization and electric polarization entered the scene. The so-called multiferoic compounds with coexistence of at least two types of ferroic order (e.g. magnetic order and electric charge order) emerged as promising successors of the 'just' magnetic NPs. The benefit of such systems is the unambiguous coupling of magnetization to the other macroscopic property, like electric polarization. Consequently, the key ferroic parameters (typically direction of the magnetization and electric polarization) can be controlled by manifold external stimuli, e.g. using magnetic and electric field, mechanical deformation or light. The choice of intrinsic variables and possibility of their multiple control opens door to design of smart sensors and nanoelectronic devices based on multiferroics.4–6
In the family of the spinel oxides, multiferoic properties were reported for several spinel chromite phases. Among them the cobalt chromite is a very unusual multiferroic material with complex magnetic phase diagram. The cobalt chromite crystallizes in a cubic ‘normal’ spinel structure, Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, in which Cr3+ occupy the B sites (16d) and Co2+ the A sites (8a). On cooling the magnetic moments undergo a transition from paramagnetic to collinear ferrimagnetic state at TC ∼ 93 K, followed by additional order-to-order magnetic phase transition to incommensurate spiral (conical) spin structure at TS ∼ 27 K with propagation vector of the spiral component along the [110] direction. Finally, the ground state magnetic phase orders below the so-called lock-in temperature, TL ∼ 14 K. The ferroelectric order coincide with the TS and the direction of the spontaneous polarization is locked to [−110] for magnetization parallel to [001]; both unambiguously fixed to the propagation vector of the spiral component (along [110]). It was also demonstrated that the spontaneous dielectric polarization and magnetization are of purely spin origin.7–12
m, in which Cr3+ occupy the B sites (16d) and Co2+ the A sites (8a). On cooling the magnetic moments undergo a transition from paramagnetic to collinear ferrimagnetic state at TC ∼ 93 K, followed by additional order-to-order magnetic phase transition to incommensurate spiral (conical) spin structure at TS ∼ 27 K with propagation vector of the spiral component along the [110] direction. Finally, the ground state magnetic phase orders below the so-called lock-in temperature, TL ∼ 14 K. The ferroelectric order coincide with the TS and the direction of the spontaneous polarization is locked to [−110] for magnetization parallel to [001]; both unambiguously fixed to the propagation vector of the spiral component (along [110]). It was also demonstrated that the spontaneous dielectric polarization and magnetization are of purely spin origin.7–12
The character of magnetic order projected in the dielectric response is strongly dependent on the particle size, especially when approaching the critical coherence length of the spiral magnetic structure13–17 or varying the B-site occupation.18 Alongside with the fascinating fundamental physical properties, the cobalt chromite phase, especially in sub-micron particles is demanded material and has been already utilized as inorganic pigment and efficient catalyst.19–22 For that purpose, facile preparation of well-defined NPs of cobalt chromite is the key starting point for understanding spin-induced multiferoic properties when emerging critical particle size and consequently development of nanoscale devices with multiple addressing and controls.
Up to date, cobalt chromite NPs were prepared by sonochemistry,23 thermolysis,24 co-precipitation,15,16,25 sol–gel method,26,27 autocombustion,28,29 solvothermal in situ reduction30 and variants of the hydrothermal method.14,31,32 In most of the above-described procedures, the as-prepared products were subjected to annealing at high temperatures in order to get nanocrystalline phase of the cobalt chromite. The final products thus consisted of cobalt chromite NPs in form of nanocrystalline powders. Moreover, the thermal post treatment often lead to aggregation or sintering, so the NPs were finally in direct contact. Consequently, such NPs are not ideal for studies of size-dependent magnetic properties as the direct contact may induce non-negligible changes of the surface spin structure and bring complications to the interpretation of magnetic measurements. Moreover, nanopowders are hardly re-dispersible in solvents, which prevent their further use for surface modification by ligand exchange usually carried out in liquid phase. The versatility of surface functionalization of the NPs is thus as a prerequisite for their incorporation in hybrid nanostructures and nanocomposites, for example using a versatile approach based on sol–gel method33 or the click chemistry art.34–36
Here we present for the first time a facile preparation route yielding pure isolated cobalt chromite NPs without need of thermal post treatment procedure. In order to obtain the ternary spinel phase directly, the high temperature hydrothermal preparation (at reaction temperature about 250 °C) in water–alcohol–oleic acid system at high pressure was carried out. The route leads to uniform NPs capped with covalently bonded oleic acid, which prevents their direct contact and makes the NPs easily dispersible in non-polar solvents; thus suitable for various ligand exchange procedures. Our study is completed with detailed characterization of the NPs by powder X-ray diffraction, transmission electron microscopy, small-angle X-ray scattering, and vibrational spectroscopies. In addition, magnetic properties by means of temperature and magnetic field dependent magnetization and frequency-dependent a.c. susceptibility completed with polarized neutron scattering experiments down to low temperatures are also presented, and the impact of NP size on collapse of the long range magnetic ordering is discussed. Finally, perspectives of using the easily dispersible NPs of the multiferoic cobalt chromite are given.
2. Experimental section
2.1 Materials
The synthesis of cobalt chromite NPs was carried out using commercially available reagents: oleic acid (Sigma-Aldrich, tech. 90%), NaOH (Lach-ner, micropearls, p.a.), FeCl3·6H2O (Sigma-Aldrich, ≥98%), CoCl2·6H2O (Penta-chemicals, p.a.), ethanol (Lach-ner, absolute), hexane (Lach-ner 81.8%), distilled water. All chemicals were used as-received without further purification.2.2 Synthesis of CoCr2O4 NPs
High temperature hydrothermal synthesis was proposed for the preparation of cobalt chromite NPs. First, a solution of sodium oleate was prepared from 10 mmol (0.40 g) of sodium hydroxide, which was dissolved in a small amount of ethanol and water mixture and adding 12 mmol (3.39 g) of oleic acid. A clear, homogeneous solution of sodium oleate was obtained. The water solution of oleate precursors was prepared from chromium and cobalt chlorides (molar ratio Cr3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Co2+ = 2
Co2+ = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The reaction was carried out in total amount of 10 ml of water and 10 ml of ethanol. The water solutions of precursors and sodium oleate were mixed together and put into ultrasonic bath for 5 min. After sonication, the reaction mixture formed two phases (water and organic), and the following reactions took place:
1). The reaction was carried out in total amount of 10 ml of water and 10 ml of ethanol. The water solutions of precursors and sodium oleate were mixed together and put into ultrasonic bath for 5 min. After sonication, the reaction mixture formed two phases (water and organic), and the following reactions took place:| 3Na(oleate) + CrCl3 → Cr(oleate)3 + 3NaCl |
| 2Na(oleate) + CoCl2 → Co(oleate)2 + 2NaCl |
This resulting reaction mixture was put into the autoclave and placed in oven for 16 hours at the desired reaction temperature (the pressure inside autoclave reached 50 bar; all parameters of the preparation for the three samples are listed in Table 1). After cooling down the autoclave, the NPs were isolated from the crude solution by centrifugation in several dispersion/precipitation cycles using solvent–non-solvent pair (n-hexane/ethanol). Finally, the bluish-green dispersion of uniform cobalt chromite NPs capped with oleic acid in hexane was obtained.
| Sample | Temperature (°C) | Time (h) | Pressure in autoclave (bar) |
|---|---|---|---|
| S1 | 247 | 16 | 54 |
| S2 | 240 | 16 | 47 |
| S3 | 237 | 16 | 40 |
2.3 Structural characterization
Powder X-ray diffraction (PXRD) was performed using a PANalytical X'Pert PRO diffractometer with Cu Kα radiation (λ = 1.54 Å) equipped with a secondary monochromator and PIXcel detector. All samples were measured in the 2θ range of 15–80° with a step size of 0.02°. Calibration was done using the powder standard sample LaB6 (SR 660b) purchased from NIST. The particle diameter by means of size of the coherently diffracting domain was determined by the Rietveld analysis using the Full Prof software.37 The instrumental broadening of the diffraction lines was also considered.2.4 Morphological characterization
Transmission Electron Microscopy (TEM) was carried out using the LVTEM device operated at 5 kV with Schottky emitter (Delong) and JEOL JEM 2200FS operated at 200 kV with Schottky emitter using bright field (BF) mode and electron diffraction (ED). The samples were obtained by dropping the dispersion on the coated copper grid. ED was performed at camera lengths of 40 cm or 60 cm.Small-angle X-ray scattering (SAXS) measurements were carried out using the gallium anode low-angle X-ray instrument (GALAXI)38 at JCNS, Forschungszentrum Jülich, equipped with a Pilatus 1M detector, parabolic optics and 4 m long collimation. For the SAXS measurement, dispersions of NPs were filled in glass capillaries. An X-ray wavelength of λ = 1.34 Å and detector distances of 853 and 3548 mm were used for the measurement. The data were collected using a two-dimensional (2D) detector and corrected for contributions of the cell with solvent, thickness and transmission. The scattered intensity was calibrated to absolute units using a FEP 1400A (d = 0.35 mm) standard measurement. The SAXS data were fitted using Beaucage model with two levels, which characterizes the Guinier and Porod regions with smooth transition between them and yields a radius of gyration and Porod exponent.
2.5 Elemental analysis
Thermogravimetric analysis (TGA) was carried out using the device of Setaram. The samples were heated up to 600 °C (heating rate 10 °C min−1) in argon atmosphere with nitrogen 40 ml min−1. A complementary energy dispersive analysis was also performed on the Tescan Mira I LMH device with the energy dispersive X-ray detector (EDX) Bruker AXS. The NP powders were deposited on carbon film to diminish charging during the experiment.2.6 Vibrational spectroscopies
Fourier transform infrared (FTIR) spectra were obtained using Thermo Scientific Nicolet 6700 FTIR spectrometer (resolution 2 cm−1, DTGS detector, KBr beamsplitter, Happ-Ganzel apodization, KBr windows) in the region 400–4000 cm−1 with diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) technique. The nanocrystalline samples were mixed with KBr (for IR spectroscopy, Merck). Raman spectra of nanocrystalline samples were measured using Thermo Scientific DXR Raman Microscope with Olympus microscope (objective 50×) in the spectral range of 50–1900 cm−1 with resolution of 3 cm−1. He–Ne laser or diode lasers (532 and 780 nm) were used for the measurement. The spectrometer was calibrated using multiple neon emission lines and multiple polystyrene Raman bands and standardised by white light.2.7 Magnetization and a.c. susceptibility
The temperature dependence of the zero-field-cooled (ZFC) and field-cooled (FC) magnetization and the magnetization isotherms at selected temperatures were measured using the Quantum Design MPMS7XL device (SQUID magnetometer). The ZFC-FC measurements were carried out between 2 and 300 K with 2 K min−1 sweep in the applied magnetic field of μ0H = 10 mT, after cooling in either applied (FC) or in zero field (ZFC). Temperature dependent a.c. susceptibility was recorded in zero external magnetic field at frequencies of f = 0.1, 1, 10, 102 and 103 Hz with an a.c. magnetic field amplitude of 0.3 mT. The powder samples with mass about 5 mg were put into gelatine capsules and fixed with a piece of polystyrene during the experiments. The magnetization values were corrected to the content of the oleic acid.2.8 Polarized neutron scattering
Polarized neutron scattering with XYZ polarization analysis was carried out at the Diffuse Neutron Scattering (DNS)39 instrument at Heinz Maier-Leibnitz Zentrum. The six polarized scattering contributions by cobalt chromite nanoparticles as well as Ni0.89Cr0.11 standard and vanadium references were measured in a wide scattering momentum range of 0.5 < Q < 3.4 Å−1. The measurements were carried out at aluminium sample holder using a temperature of 4 K and 100 K and a neutron wavelength of λ = 3.3 Å. The magnetic, nuclear and nuclear spin-incoherent scattering contributions were separated from the total scattering cross section by means of XYZ-polarization analysis in the spin flip (SF) and non-spin flip (NSF) channels. Separation of the observed data was performed using DNS polarization analysis algorithm. The reference measurement of a Ni0.89Cr0.11 alloy yields the flipping ratio correction and thus the real polarization of the incident neutron beam. Background correction is performed by measurement of the empty aluminium sample holder and subtraction from the raw data. Vanadium was measured for calibration of the detector efficiency.3. Results and discussion
3.1 Synthesis of nanoparticles
Cobalt chromite NPs with covalently bonded oleic acid were successfully synthesized by hydrothermal decomposition of cobalt(II) and chromium(III) oleates in water/ethanol system. The reaction temperature was adjusted above the range (180 to 200 °C) common for preparation of ferrite NPs40–42 due to the higher decomposition temperature of the chromium(III) oleate in comparison to the iron(II), (III) and cobalt(II) oleates. This hypothesis was tested on two preparation protocols applied to the cobalt ferrite NPs as a reference. First the general route in water–alcohol–fatty acid system introduced by Wang and co-workers40 was carried out using the same parameters of the reaction (reaction temperature: 180–200 °C, amount of oleic acid and solvents, ratio of metal oleates). In this general route the NPs are formed from the in situ generated metal oleates. Using this preparation route, cobalt ferrite NPs with size up to 8 nm were obtained,41 while successful preparation of the cobalt chromite NPs was not possible without additional annealing.14 The same result was obtained when using the hydrothermal decomposition of ex situ prepared metal oleates at the maximum temperature of 200 °C. While decomposition of the cobalt(II) oleate in high pressure autoclave occurs at around 170 °C and cobalt ferrite NPs can be easily prepared,42 the chromium(III) oleate decomposes at higher temperature (240 °C); thus only amorphous residuum is obtained. For this reason the reaction temperature was adjusted close to the decomposition temperature of the chromium(III) oleate. The updated procedure leads directly to the NPs of the desired spinel phase coated with oleic acid. Consequently, the NPs can be easily dispersed in hexane. The greenish dispersion of the cobalt chromite NPs in various non-polar solvents was found to be stable against precipitation for months. Moreover, the size of the NPs can be tuned up to some extend by varying the reaction temperature as with the increase of the reaction temperature, the size of the NPs also increases.3.2 Morphological and structural characterization
First, the morphology of the cobalt chromite NPs was characterized using the TEM and SAXS. Typical TEM micrographs presented in Fig. 1 (top) reveal nearly spherical shape of the NPs with the mean particle diameter of 3.0(1), 3.2(1) and 4.2(1) nm and log normal size distribution of 13.0(2), 12.0(1) and 16.1(1)% for S1, S2 and S3 sample, respectively (for details, please see the ESI†).The results of the SAXS experiment together with the fit of the experimental data are shown in Fig. 1 (bottom). The fitted value of the fractal dimension lies between 1 and 2. According to the study of Bonini43 the Porod exponent equal to 1 suggests formation of chain-like aggregates. In our case the Porod exponent is close to 1.5, which suggests formation of branched assemblies of the NPs. Such structures were also observed in the TEM micrographs (Fig. 1a marked with orange squares) and they are typical for NPs prepared by the variants of the hydrothermal route in water/alcohol/fatty acid system.40,41 At higher Q range the Q−4 asymptotic behaviour was observed, which corroborates the spherical shape of the NPs observed by the TEM. The obtained spherical radius, RS is related to the gyration radius, RG according to RS = (5/3)1/2 × RG. The spherical radii determined from the SAXS data (Table 2) are in good agreement with those obtained by the TEM analysis. A second parameter, which can be obtained at lower Q range corresponds to the size of potential aggregates. The average size of the aggregates is given in Table 2. The tendency to aggregation of the dried NPs was also observed in the TEM (Fig. 1 a marked with orange rectangle).
| Sample | Particle size (nm) | Aggregate size (nm) | ||
|---|---|---|---|---|
| dPXRD | dTEM1 | dSAXS1 | dSAXS2 | |
| a dPXRD is size obtained from Rietveld analysis, dTEM1 is a mean size from log-normal distribution of size from TEM and dSAXS (dSAXS = 2 × RS) from Beaucage fits of SAXS. | ||||
| S1 | 3.5(2) | 4.2(1) | 5.7(1) | 49.1(1) |
| S2 | 2.8(1) | 3.2(1) | 4.4(5) | 72.3(2) |
| S3 | 2.6(1) | 3.0(1) | 4.6(1) | 82.6(1) |
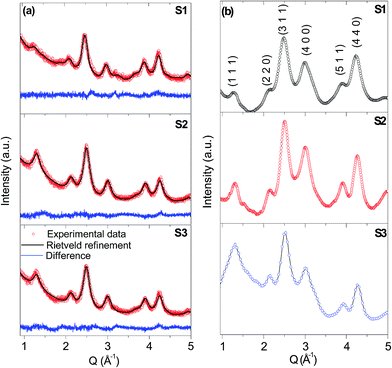
The phase analysis was carried out using powder X-ray and electron diffraction, respectively. Both experiments confirmed the presence of the cobalt chromite spinel structure in the NPs (Fig. 2a and b) with the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (card no. JCPDF 22-1084). The values of the refined lattice parameter a and the particle size (diameter, dPXRD) are summarized in Table 3 and 2, respectively. Both values increase with increasing reaction temperature for all prepared samples as expected. The dPXRD value is somewhat smaller in comparison to the size derived from the TEM and SAXS. This fact is in good agreement with the general expectation that the particle size derived from the PXRD is related to the coherently diffracting domain size, which is usually smaller than the physical size of the whole particle, even for highly crystalline NPs. The Co2+
m (card no. JCPDF 22-1084). The values of the refined lattice parameter a and the particle size (diameter, dPXRD) are summarized in Table 3 and 2, respectively. Both values increase with increasing reaction temperature for all prepared samples as expected. The dPXRD value is somewhat smaller in comparison to the size derived from the TEM and SAXS. This fact is in good agreement with the general expectation that the particle size derived from the PXRD is related to the coherently diffracting domain size, which is usually smaller than the physical size of the whole particle, even for highly crystalline NPs. The Co2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cr3+ ratio was determined using EDX analysis and the values close to the nominal 1
Cr3+ ratio was determined using EDX analysis and the values close to the nominal 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry were found for all samples.
2 stoichiometry were found for all samples.
| Refined parameter | Refined value | ||
|---|---|---|---|
| S1 | S2 | S3 | |
| a Symbol meaning: lattice parameter, a, position of oxygen atoms, u, an overall isotropic displacement, BOV, isotropic particle size broadening contribution, Y, an isotropic Gaussian size parameter, GausSize, zero position and Rietveld agreement factors. | |||
| a (Å) | 8.374(1) | 8.358(1) | 8.337(1) |
| u | 0.2563(1) | 0.2652(2) | 0.2567(1) |
| BOV (Å2) | 0.86(5) | 2.1(1) | 1.9(2) |
| Profile function | pseudo-Voigt function | ||
|---|---|---|---|
| Y (°) | 0.12(2) | 1.16(1) | 0.01(1) |
| GausSize (°) | 3.76(4) | 3.07(3) | 4.65(3) |
| Background function | Chebyshev polynomial (13 refined parameters) | ||
|---|---|---|---|
| Zero (0.01°) | 0.4(1) | 0.2(1) | 0.3(1) |
| RB (%) | 14.6 | 11.7 | 16.8 |
| Rwp (%) | 2.56 | 3.65 | 3.99 |
| Rexp (%) | 2.55 | 2.98 | 3.63 |
| χ2 | 1 | 1.4 | 1.1 |
The content of the oleic acid in the prepared NPs was evaluated using the TGA analysis (Fig. 3a). During the TGA, the decomposition of the prepared samples occurs in two steps. The first step represents the process of dehydration of samples up to 220 °C. The second step corresponds to the decomposition of the oleic acid on the surface of the NPs.
The covalent nature of the bond of the oleic acid to the NPs was then confirmed by the FTIR spectroscopy; the spectra are shown in the Fig. 3b and all assignments are summarized in Table 4. The Raman spectra of the chromite NPs were also measured as a complementary probe of the vibrational states in the spinel chromite phase. They are shown in Fig. 3c for the S1 and S3 samples. All Raman active bands (A1g, F2g, Eg) were assigned according to the theoretical vibrational representation vibrational.14 The explicit positions of the Raman bands were detected as follows: 674, 635, 592, 575, 509, 454 and 191 cm−1 and 671, 634, 589, 578, 523, 507, 461, 447 and 190 cm−1 for the S1 and S3 sample, respectively. In comparison to the bulk sample of the cobalt chromite44 the Raman bands of the NPs show a predominant shift towards lower wavenumbers. However, the values are close to those of the nanosized cobalt chromite particles reported by other authors.32 The overall downshift of the Raman bands can be well understood in terms of the size effect as in oxide materials the size reduction results in the increase of the micro-strain and/or dominance of the phonon confinement.45
| Wavenumber (cm−1) | Assignment | ||
|---|---|---|---|
| S1 | S2 | S3 | |
| 510 vs | 510 vs | δ C–C | |
| 514 vs | 518 vs | F1u (2), δ OCO, δ CCO, δ CC | |
| 618 vs | 618 vs | 618 vs | F1u (1), δ OCO, δ CCO, δ CC |
| 722 w | 722 w | 721 w | ρ CH2 |
| 1062 w | 1066 w | νas –C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C– C–C– |
|
| 1306 wb | 1305 wb | 1307 wb | ν C–O + δ COH |
| 1410 sb | 1410 sb | 1414 s | δ –CH2CO–, ν C–O + δ COH |
| 1437 sb | ν C–O + δ OH | ||
| 1456 sh | 1456 sh | δ –(CH2)n– | |
| 1548 sb | 1548 sb | 1534 sb | νs COO− |
| 1706 mb | 1741 mb | 1707 mb | ν C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
| 2854 s | 2853 s | 2853 s | ν –CH2– |
| 2924 s | 2924 s | 2924 s | ν –CH2– |
| 2955 s | 2955 s | ν –CH3, ν –CH2– | |
| 3006 mb | 3006 mb | 3005 mb | ν –CH3 |
| 3300 mb | 3273 mb | ν OH | |
| 3406 mb | 3420 mb | ν OH | |
3.3 Magnetic properties
Magnetic properties of the S1–S3 samples were finally investigated and interpreted in context of previous studies on NPs prepared by other routes with larger particle size. In order to compare the magnetic behaviour of the NPs to the bulk material, the temperature dependencies of the magnetization recorded in moderate external magnetic field of 10 mT in zero-field cooled (ZFC) and field-cooled (FC) regimes were carried out. The resulting curves are presented in Fig. 4a. The ZFC curves show a clear single maximum for all samples at a temperature termed Tmax (the values for all samples are listed in the Table 5). In addition, a bifurcation point of the ZFC and FC curves was observed at slightly higher temperature. The values of the Tmax are depicted in Fig. 4b in comparison to the values obtained for larger NPs prepared by the same route, but subjected to additional heat treatment, and the Tc of the bulk cobalt chromite. The Tmax values are almost identical for all samples and fall to the monotonous dependence on the particle size. However, the rapid degrees with respect to the decreasing particle size suggests change of the intrinsic magnetic structure in the NPs. The hypothesis is corroborated by the character of the first order derivatives of the ZFC and FC curves, shown in Fig. 4c. In the bulk sample the sharp minimum of the ZFC curve below the Tc is expected,13 while there is a rather broad minimum of the ZFC curve for all investigated samples, which is usually related to the disorder effects in NPs and subsequent reform of the exchange interactions due to the disorder.44 In extreme case, the collapse of the bulk-like magnetic order can be observed, which is characterized by the onset of short-range order or glassy like spin state.46 Moreover no additional sharp extreme in the ZFC curve and the related M(T) derivatives was observed; thus the order-to-order magnetic phase transitions at the TS and TL in the bulk cobalt chromite are not evidenced in the NPs. As reported previously, the disorder effects are significant for cobalt chromite NPs with crystallite size 4–6 nm;14 thus they are expected to dominate the magnetic response of the NPs with crystalline size below 4 nm as is the case of the S1–S3 samples.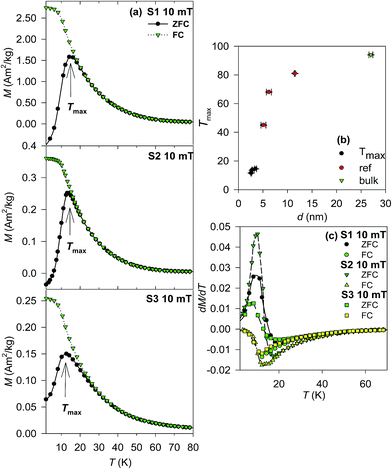 | ||
| Fig. 4 (a) ZFC-FC curves of the S1–S3 samples recorded at 10 mT. (b) Size dependence of the Tmax in comparison to the bulk and previously reported values.14 (c) First derivatives of the ZFC-FC curves for S1–S3 samples. | ||
| Sample | Mr (A m2 kg−1) | μ0 Hc (T) | Ms_2K (A m2 kg−1) | Tmax (K) |
|---|---|---|---|---|
| S1 | 2.6 ± 0.3 | 0.10 ± 0.01 | 4.6 ± 0.3 | 14.5 ± 0.2 |
| S2 | 3.8 ± 0.4 | 0.80 ± 0.08 | 6.5 ± 0.4 | 13.6 ± 0.1 |
| S3 | 2.0 ± 0.2 | 0.70 ± 0.07 | 4.0 ± 0.2 | 11.6 ± 0.1 |
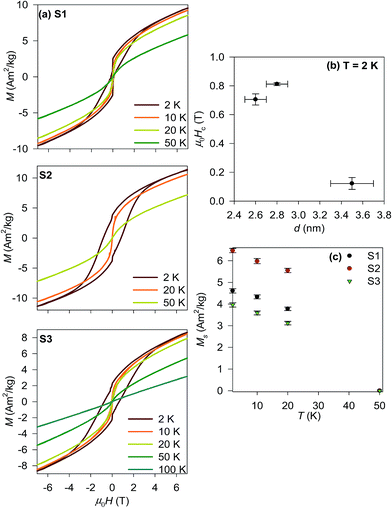
The temperature dependencies of the ZFC-FC magnetization were completed by measurements of magnetization isotherms for all prepared samples in the temperature range 2–100 K in the magnetic field up to ±7 T. The obtained M(H) curves are shown in Fig. 5a. A considerable hysteresis opens below the Tmax reaching the coercivity, μ0Hc about 0.6 T and 0.8 T at 2 K for the S2 and S3 samples, respectively. The hysteresis loop of the S1 sample recorded at 2 K is constricted yielding μ0Hc ∼ 0.1 T. A similar deformation of the hysteresis loops is usually attributed to the coexistence of at least two magnetic phases with very different coercivities (soft and hard magnetic phase).48 As the phase analysis unambiguously confirmed single phase nature of the sample, the constriction of the loop is rather originated by different types of the spin order coexisting within a single NP. This explanation is corroborated by the study of exchange bias in ∼5 nm large cobalt chromite NPs, where the frozen and rotatable spins coexist in a single NP due to the size driven spin disorder.47 The complexity of spin texture in the S1 sample is also coherent with the relative fraction of disordered spinel structure in comparison to the S2 and S3 samples as the spin disorder is closely related to the crystallographic disorder. The value can be estimated by comparison of the volumes of the coherently diffracting domain (crystalline part) to the physical volume derived from the TEM. Therefore in the S1 sample with about 40% of the volume disorder, the deviation of the spin structure and its complexity is more favoured then in the S2 and S3 samples with the structural disorder about 30% of the whole volume.
The complexity of the spin structure is also mirrored in the size dependence of the coercivity determined below the Tmax shown for all samples in Fig. 5b. The S2 and S3 μ0Hc values are more than one order of magnitude higher than the coercive field reported for a bulk single crystal46 (0.1 T), however; there is no clear correlation of the μ0Hc values with the particle size (determined by the PXRD, TEM and SAXS). The constriction of the loop of the S1 sample also prevents any simple size correlation. However; similar observations were reported by Zhu and co-workers for nanopowders of cobalt chromite prepared by hydrothermal decomposition of metal hydroxides.48 Finally, the hysteresis loops show no trend to saturation up to 7 T, likely due to formation of a glassy-like state associated with the overall spin disorder due to the very low particle size.14,49 Above the Tmax, the hysteresis disappears and the magnetization follows the Brillouin-like dependence as expected for paramagnetic state. For completeness, the values of the spontaneous magnetization below the Tmax are depicted in Fig. 5c. They clearly decrease on heating due to increasing spin fluctuations resulting in decrease of the average magnetization values.
The questionable nature of the magnetic state below the Tmax was finally inspected by polarized neutron scattering experiments carried out on the S2 sample. No additional diffraction peaks, which could be associated with long range magnetic order were detected alongside with the diffractions identified in the paramagnetic state (see Fig. 2S in ESI†). Therefore any speculations on persistence of long-range magnetic order in the spinel chromite NPs with size below 4 nm can be unambiguously excluded. Thus the anomaly observed on the ZFC–FC dependencies can be attributed to the glassy state formed due to collapse of the long-range magnetic order as the particle size is lower than the characteristic coherence length of the spiral component in the ground state magnetic structure.46 Our results also exclude hypothesis on formation of the superparamagnetic (SPM) state for such small particles of cobalt chromite, which has similar fingerprints on the ZFC-FC curves. The SPM state requires formation of a single-domain state, which is possible only for materials with long-range ferromagnetic or ferrimagnetic order.
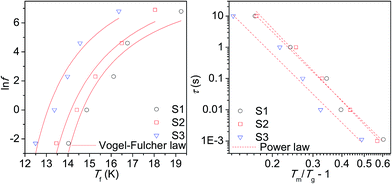
The dynamic spin properties of the glassy state were further investigated by measurements of the real (χ′) and imaginary (χ′′) parts of the a.c. susceptibility with varying frequency (f) of the alternating magnetic field with the amplitude of 3 mT; the results for the real (χ′) component are shown in Fig. 6. The temperature dependence of the χ′ reveals a shift of the characteristic maximum, Tm with increasing f. This phenomenon is deemed as a consequence of the spin relaxation. The spin dynamics was first inspected by evaluating a phenomenological parameter ϕ, which represents a shift of the Tm (ΔTm) per frequency decade:
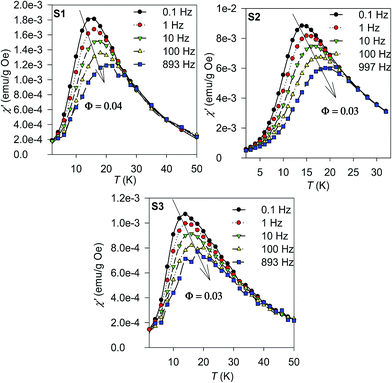 | ||
| Fig. 6 Real part of the a.c. susceptibility, χ′ of the S1–S3 samples measured at various frequencies. | ||
As suggested by the static magnetic experiments, significant disorder resulting in collapse of magnetic order and onset of spin-glass like state is expected. Thus, the a.c. susceptibility data were subjected to analysis by the Vogel–Fulcher law:52
where τ0 is the characteristic relaxation time, Tg represents the temperature of transition to the glassy state and zv is the critical power exponent. The best fits to the experimental data using both approaches are shown in Fig. 7 and the resulting values are listed in Table 6. The τ values are of few orders of magnitude larger then usually reported for canonical spin glasses (τ ∼ 10−12 s), but comparable to the values reported for substituted spinel phases with short-range ferrimagnetic ordering.13,48 Thus strong correlation between the constituent spin units suggests condensation of the collective cluster glass like state in our spinel chromite NPs.
| Sample | Vogel–Fulcher law | Power law | |||
|---|---|---|---|---|---|
| τ (s) | TVF (K) | Tg (K) | zv | τ (s) | |
| a Where τ is the attempt frequency, TVF is Vogel–Fulcher temperature, Tg is glassy transition temperature and zv represents the power law exponent. | |||||
| S1 | (4.4 ± 0.4) × 10−5 | 12 ± 2 | 12 ± 2 | 7.3 ± 0.5 | (2.4 ± 0.4) × 10−5 |
| S2 | (1.5 ± 0.2) × 10−5 | 11 ± 2 | 11.5 ± 2 | 7.8 ± 0.5 | (4.4 ± 0.4) × 10−5 |
| S3 | (8.4 ± 0.8) × 10−6 | 10 ± 2 | 11 ± 2 | 7.3 ± 0.5 | (4.7 ± 0.5) × 10−5 |
4. Conclusions
High temperature hydrothermal synthesis without need of additional thermal treatment has been developed to produce uniform cobalt chromite NPs with size distribution of 12–16%. The optimized route leads to the formation of cobalt chromite NPs capped with covalently bonded oleic acid with mean particles diameter in the range of 3.0(1)–4.2(1) nm. Thanks to the hydrophobic coating, the NPs can be easily dispersed in non-polar solvents; the dispersion was found to be stable over months. The formation of pure spinel cobalt chromite phase was observed by X-ray and electron diffraction. The FTIR measurements confirmed the presence of covalently bonded oleic acid, which causes their hydrophobic properties. The uniform spherical shape of the NPs was confirmed by the TEM and SAXS experiments. The characteristic fractal dimensions obtained from the SAXS point to the formation of branched structures. The investigation of the magnetic properties suggested strongly reformed behaviour in comparison to the bulk material due to the very low particle size. Magnetic phase transitions reported for the bulk cobalt chromite were not observed in the NPs; instead the glassy like state emerges with the transition temperature in the interval of 11.6(1)–14.5(1) K. The collapse of long-range magnetic order was unambiguously confirmed by the neutron scattering experiments. The spin dynamics of the glassy-like state studied by the a.c. susceptibility revealed values of the spin relaxation time typical for collective spin glass behaviour with short-range correlations between the disordered spins, located dominantly in the surface proximity. The successful preparation of the uniform NPs of the cobalt chromite as the archetype multiferoic phase is the important key to understand the mechanism of coupling between the magnetization and polarization when approaching critical NP size, where the magnetic long range order collapses. Moreover, availability of dispersible cobalt chromite NPs opens door to numerous preparation strategies aiming to incorporation of the multiferoic NPs in smart hybrid nanostructures and nanocomposites using general concepts such as the sol–gel chemistry or the click chemistry art, which both require possibility of custom functionalization of the NPs in liquid phase as the kick off point.Abbreviations
| NPs | Nanoparticles |
| PXRD | Powder X-ray diffraction |
| TEM | Transmission electron microscopy |
| SAXS | Small-angle X-ray scattering |
| ED | Electron diffraction |
| EDS | Energy disperse spectroscopy |
| FTIR | Fourier transform infrared |
| DRIFTS | Diffusion reflectance infrared Fourier transform spectroscopy |
| ZFC | Zero-field cooled |
| FC | Field cooled |
| SQUID | Superconducting quantum interference device |
| DNS | Diffuse neutron scattering |
| SF | Spin flip |
| NSF | Non-spin flip |
Acknowledgements
This work was supported by the Czech Science Foundation (project no. 15-01953S). Magnetic measurements were performed in MLTL (see: http://www.mltl.eu), which is supported within the program of Czech Research Infrastructures (project no. LM2011025). We acknowledge JCNS for providing of neutron scattering facility at DNS instrument. The presented work was financially supported by the Ministry of Education, Youth and Sport Czech Republic Project LQ1603 (Research for SUSEN). The results were partially developed within the CENTEM project CZ.1.05/2.1.00/03.0088 through CENTEM PLUS (LO1402) from the Ministry of Education, Youth and Sports under the National Sustainability Programme I.References
- I. Hilger and W. A. Kaiser, Nanomedicine, 2012, 7, 1443 CrossRef CAS PubMed.
- M. E. McHenry and D. E. Laughlin, Acta Mater., 2000, 48, 223 CrossRef CAS.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167 CrossRef CAS.
- J. M. Hu, L. Q. Chen and C. W. Nan, Adv. Mater., 2016, 28, 15 CrossRef CAS PubMed.
- A. Aqeel, N. Vlietstra, J. Heuver, G. Bauer, B. Noheda, B. van Wees and T. Palstra, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 224410 CrossRef.
- R. Ramesh and N. A. Spaldin, Nat. Mater., 2007, 6, 21 CrossRef CAS PubMed.
- V. Tsurkan, S. Zherlitsyn, S. Yasin, V. Felea, Y. Skourski, J. Deisenhofer, H. von Nidda, J. Wosnitza and A. Loidl, Phys. Rev. Lett., 2013, 110, 115502 CrossRef CAS PubMed.
- L. Chang, D. Huang, W. H. Li, S. W. Cheong, W. Ratcliff and J. Lynn, J. Phys.: Condens. Matter, 2009, 21, 456008 CrossRef CAS PubMed.
- I. Kim, Y. S. Oh, Y. Liu, S. H. Chun, J. S. Lee, K. T. Ko, J. H. Park, J. H. Chung and K. H. Kim, Appl. Phys. Lett., 2009, 94, 042505 CrossRef.
- N. Menyuk, K. Dwight and A. Wold, J. Phys., 1964, 25, 528 CAS.
- I. Efthimiopoulos, Z. Liu, S. Khare, V. P. Sarin, T. Lochbiler, V. Tsurkan, A. Loidl, D. Popov and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 064108 CrossRef.
- Y. Yamasaki, S. Miyasaka, Y. Kaneko, J. P. He, T. Arima and Y. Tokura, Phys. Rev. Lett., 2006, 96, 207204 CrossRef CAS PubMed.
- R. N. Bhowmik, R. Ranganathan and R. Nagarajan, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 144413 CrossRef.
- D. Zakutna, A. Repko, I. Matulkova, D. Niznansky, A. Ardu, C. Cannas, A. Mantlikova and J. Vejpravova, J. Nanopart. Res., 2014, 16, 2251 CrossRef.
- C. Rath and P. Mohanty, J. Supercond. Novel Magn., 2011, 24, 629 CrossRef CAS.
- C. Rath, P. Mohanty and A. Banerjee, J. Magn. Magn. Mater., 2011, 323, 1698 CrossRef CAS.
- D. Kumar, J. Galivarapu, A. Banerjee, K. Nemkovski, Y. Su and C. Rath, Nanotechnology, 2016, 27, 175702 CrossRef CAS PubMed.
- D. Kumar, P. Mohanty, V. Singh, J. K. Galivarapu, A. Banerjee, V. Ganesan and C. Rath, Mater. Res. Bull., 2014, 54, 78 CrossRef CAS.
- J. Chen, X. Zhang, H. Arandiyan, Y. Peng, H. Chang and J. Li, Catal. Today, 2013, 201, 12 CrossRef CAS.
- Y. Wang, P. Yang, G. Liu, L. Xu, M. Jia, W. Zhang and D. Jiang, Catal. Commun., 2008, 9, 2044 CrossRef CAS.
- Y. Wang, A. P. Jia, M. F. Luo and J. Q. Lu, Appl. Catal., B, 2015, 165, 477 CrossRef CAS.
- U. Zavyalova, B. Nigrovski, K. Pollok, F. Langenhorst, B. Mueller, P. Scholz and B. Ondruschka, Appl. Catal., B, 2008, 83, 221 CrossRef CAS.
- D. P. Dutta, J. Manjanna and A. Tyagi, J. Appl. Phys., 2009, 106, 043915 CrossRef.
- M. Edrisi and A. R. Keshavarz, Nano-Micro Lett., 2012, 4, 83 CrossRef.
- L. Kumar, P. Mohanty, T. Shripathi and C. Rath, Nanosci. Nanotechnol. Lett., 2009, 1, 199 CrossRef CAS.
- A. Mantlikova, J. P. Vejpravova, P. Holec, J. Plocek and D. Niznansky, IOP Conf. Ser.: Mater. Sci. Eng., 2011, 18, 032022 CrossRef.
- H. T. Cui, M. Zayat and D. Levy, J. Sol-Gel Sci. Technol., 2005, 35, 175 CrossRef CAS.
- I. Matulkova, P. Holec, B. Pacakova, S. Kubickova, A. Mantlikova, J. Plocek, I. Nemec, D. Niznansky and J. Vejpravova, Mater. Sci. Eng., B, 2015, 195, 66 CrossRef CAS.
- R. K. Singh, A. Yadav, A. Narayan, A. K. Singh, L. Verma and R. Verma, J. Therm. Anal. Calorim., 2012, 107, 197 CrossRef CAS.
- S. Lei, L. Liu, C. Wang, X. Shen, C. Wang, D. Guo, S. Zeng, B. Cheng, Y. Xiao and L. Zhou, CrystEngComm, 2014, 16, 277 RSC.
- S. K. Durrani, S. Z. Hussain, K. Saeed, Y. Khan, M. Arif and N. Ahmed, Turk. J. Chem., 2012, 36, 111 CAS.
- M. Maczka, M. Ptak, M. Kurnatowska and J. Hanuza, Mater. Chem. Phys., 2013, 138, 682 CrossRef CAS.
- S. Kubickova, J. Plocek, A. Mantlikova and J. Vejpravova, RSC Adv., 2014, 4, 5113 RSC.
- J. E. Moses and A. D. Moorhouse, Chem. Soc. Rev., 2007, 36, 1249 RSC.
- H. C. Kolb, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004 CrossRef CAS.
- S. A. McCarthy, G. L. Davies and Y. K. Gun'ko, Nat. Protoc., 2012, 7, 1677 CrossRef CAS PubMed.
- J. Rodriquez-Carvajal and T. Roisnel, FullProf.98 and WinPLOTR: New Windows 95/NT Applications for Diffraction. Commission for Powder Diffraction, International Union of Crystallography, 1998 Search PubMed.
- M. K. U. R. Emmanuel Kentzinger, Journal of Large-Scale Research Facilities, 2016, 2, A61, DOI:10.17815/jlsrf-2-109.
- W. Schweika and P. Boni, Phys. B, 2001, 297, 155 CrossRef CAS.
- X. Wang, J. Zhuang, Q. Peng and Y. D. Li, Nature, 2005, 437, 121 CrossRef CAS PubMed.
- A. Repko, D. Niznansky and J. Poltierova-Vejpravova, J. Nanopart. Res., 2011, 13, 5021 CrossRef CAS.
- A. Repko, J. Vejpravova, T. Vackova, D. Zakutna and D. Niznansky, J. Magn. Magn. Mater., 2015, 390, 142 CrossRef CAS.
- M. Bonini, E. Fratini and P. Baglioni, Mater. Sci. Eng., C, 2007, 27, 1377 CrossRef CAS.
- J. Preudhom and P. Tarte, Spectrochim. Acta, Part A, 1971, 27, 1817 CrossRef.
- Z. V. Popovic, Z. Dohcevic-Mitrovic, M. Scepanovic, M. Grujic-Brojcin and S. Askrabic, Ann. Phys., 2011, 523, 62 CrossRef CAS.
- K. Tomiyasu, J. Fukunaga and H. Suzuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 214434 CrossRef.
- C. Zhu, Z. Tian, L. Wang and S. Yuan, J. Magn. Magn. Mater., 2015, 393, 116 CrossRef CAS.
- Z. Tian, C. Zhu, J. Wang, Z. Xia, Y. Liu and S. Yuan, J. Magn. Magn. Mater., 2015, 377, 176 CrossRef CAS.
- R. H. Kodama, A. E. Berkowitz, E. J. Mcniff and S. Foner, J. Appl. Phys., 1997, 81, 5552 CrossRef CAS.
- J. L. Dormann, D. Fiorani and E. Tronc, Adv. Chem. Phys., 1997, 98, 283 CrossRef CAS.
- D. X. Li, S. Nimori, Y. Shiokawa, Y. Haga, E. Yamamoto and Y. Onuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 012413 CrossRef.
- S. Shtrikman and E. P. Wohlfarth, Phys. Lett. A, 1981, 85, 467 CrossRef.
- J. Souletie and J. L. Tholence, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 516 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra21377d |
| ‡ Present address: Department Chemie, Universität zu Köln, Luxemburger Strasse 116, 50939 Köln, Germany. Institut Laue-Langevin, F-38042 Grenoble, France. |
| § These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2016 |