Effect of lead and caesium on the mechanical, vibrational and thermodynamic properties of hexagonal fluorocarbonates: a comparative first principles study

Abstract

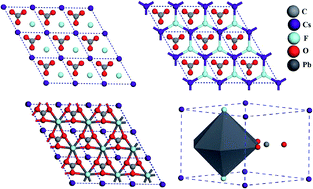
Exploration of the structure–property correlation of fluorocarbon materials has received much interest over recent years due to their extremely strong nonlinear optical (NLO) responses (13.6 times that of KH₂PO₄(KDP)), good ultraviolet (UV) cutoff (<200 nm) with better mechanical and chemical stability. In the present work a novel CsPbCO₃F, ABCO₃F (A = K, Rb; B = Ca, Sr) series is explored using density functional theory (DFT) calculations focusing on their mechanical, vibrational and thermodynamic properties and their Born effective charge (BEC) tensors. The calculated structural properties of lead carbonate fluoride with a semi-empirical dispersion corrected Ortmann Bechstedt Schmidt (OBS) method are found to be in relatively close agreement with experimental data. The obtained single crystal elastic constants satisfy the Born's mechanical stability criteria. The calculated bulk modulus value of lead carbonate (41 GPa) indicates its soft nature compared with other studied carbonates and is observed to be harder than KDP (26 GPa). In addition we have calculated the polycrystalline properties, bulk modulus (B), shear modulus (G), Young's modulus (E) and Poisson's ratio (σ) of CsPbCO₃F and ABCO₃F (A = K, Rb; B = Ca, Sr) using the Voigt, Reuss and Hill approximations. The obtained B/G (>1.75) results reveal the ductile nature of all the studied materials except for KCaCO₃F (1.67) which is found to be brittle. Results of the hexagonal shear anisotropic factors (A₁, A₂, A₃) indicate that all the studied crystals possess considerable mechanical anisotropy. Calculated zone centered vibrational infrared (IR) spectra confirm the higher optical activity of CsPbCO₃F compared with the other carbonates. The obtained high frequency modes are consistent with the experimental values. The obtained BECs reveal the presence of a mixed covalent–ionic character of the compounds. The thermodynamic properties, namely entropy, Debye temperature, heat capacity, enthalpy, thermal expansion and thermal conductivity, have been computed at different temperatures ranging from 5 K to 1000 K. The results show that the lead based compound has the highest thermal conductivity (32.430 W m⁻¹ K⁻¹) of the reported carbonate materials. The results clearly indicate that the material could show better durability than LiNbO₃, α-SiO₂, CaCO₃, and Ba₃B₆O₁₂ hexagonal NLO materials. All the computed thermodynamic properties indicate that CsPbCO₃F might be a potential candidate for second-order NLO applications. The polycrystalline, vibrational and thermodynamic properties of carbonate materials presented in this work could be a step forward in the process of developing new NLO materials.

---

1 Introduction

NLO materials play a crucial role in nonlinear optics, in particular they have a great impact on laser technology, optical storage communications, optical computing systems, information technology and have wide industrial applications.^1,2 These materials also have applications in photochemical synthesis and for the efficient generation and detection of terahertz pulses.³ The search for new efficient materials which are prime candidates for different nonlinear optical processes has become very active ever since the second harmonic generation (SHG) phenomena was first observed in single crystal quartz by Franken and co-workers in 1961.⁴ This discovery turned researchers’ attention towards inorganic anionic groups with π-conjugated systems with a planar triangle structure such as borates [BO₃]³⁻, carbonates [CO₃]²⁻ and nitrates [NO₃]⁻.^5,6 Despite their applications in various fields, the scarcity of new single crystals with excellent optical qualities, large nonlinear coefficients, higher laser damage threshold voltage values, suitable birefringence, good mechanical strength and chemical stability by reliable crystal growth techniques is slowing down the development of new optical devices.^8,10–12 Till now, in accordance with the frequency conversion efficiency & transparency range, there are three types of NLO materials available in the literature which can serve in the visible, ultra violet (UV) and infrared (IR) regions of optical spectra.¹³ Recent experimental and theoretical studies reveal that a new possible carbonate based group of NLO materials can serve as a better candidate, like borates, in the UV and deep-UV frequency window.^5,7–9,16 The idea behind the work is that, ”since borates having [BO₃]³⁻ unit as a anionic group with planar triangular structure, they are found to be promising NLO materials in UV and deep-UV regions according to Chen's anionic group theory”,¹⁵ the crystals possessing a [CO₃]²⁻ unit as an anionic group which also have a similar planar triangular structure arrangement can be expected to show a good non-linear optical response in this frequency window of optical spectra.⁵

It is known that most fluorocarbonates naturally occur in alkaline rock complexes and over the past few decades numerous attempts have made to synthesize these carbonate based crystals at laboratory scales.¹⁴ The A₂A′CO₃F (A, A′ = K, Rb, Cs) fluorocarbonate series obtained by Albert et al.,^17,18 KCaCO₃F^19,20 phase discovered by West Fletcher in 1992, and the lead carbonate fluoride single crystal Pb₂F₂CO₃ reported by Bengt Aurivillius in 1983 (ref. 21) are known as the starting carbonate materials in this field. Recent experimental and theoretical attempts in this direction have yielded many new novel carbonate fluoride crystals with good chemical and mechanical stability and strong nonlinear optical responses up to 530 (ref. 22) times higher than α-SiO₂ which is the highest of all the carbonate fluoride crystals known to date. Fluoride–oxygen based compounds are also found to be useful matrices for bi-doped rare earth compounds.²³ In 2012, Zou et al., synthesized ABCO₃F series carbonate fluoride crystals which were found to be good phase matchable materials in the UV region with nonlinear coefficients which are 3.33 (A = K, Rb and B = Sr), 3.61 (A = K and B = Ca), 1.11 (A = Rb, Cs and B = Ca) and 1.20 (A = Cs and B = Ba) times larger than that of d₃₆ of the KDP crystal with good mechanical stability (bulk modulus of 50 GPa).⁷ Kang et al.,¹⁶ theoretically proposed a new series of ABeCO₃F and AAlCO₃F₂ (A = Li, Na, K, Rb, Cs) compounds with IIA and IIIA light metal cation substitution in ABCO₃F series using density functional theory calculations. This study suggests that the carbonate fluoride materials might have applications in the deep-UV region by further reducing the absorption edges to around 150 nm. Recently, Zou et al.²² synthesized the first lead carbonate fluoride crystal CsPbCO₃F by solid state reactions. It crystallizes in a non-centrosymmetric space group P6̄m2 with a = 5.3888 Å, c = 5.1071 Å with a monomolecular unit cell. The structure consists of alternate stacked PbCO₃ and CsF layers perpendicular to the c-axis connected by Pb–F–Pb chains parallel to the c-axis. More recently in 2014, Thao Tran et al.⁹ synthesized the RbPbCO₃F crystal structure along with CsPbCO₃F through solvothermal and conventional solid state techniques and found that CsPbCO₃F crystallizes in a non-centrosymmetric space group 6̄ with a = 5.393 Å, c = 5.116 Å with Z = 1 formula unit per unit cell. Even though there are some dissimilarities existing between the previously reported structures by Zou et al. and Thao Tran et al., in both cases the observed nonlinear coefficients are 530 and 160 times higher than that of the α-SiO₂ crystal respectively. This seems to be the record value among all the reported carbonate fluoride materials till now. This uniqueness of the material and its promising optical responses known to arise from the p–π interaction between Pb²⁺ and [CO₃]²⁻ within the [Pb (CO₃)] layers strongly motivated us to address the in-depth structure–property correlation issues in this material through a density functional theory approach.

We have focused on addressing the origin of the nonlinear optical response of CsPbCO₃F, ABCO₃F (A = K, Rb; B = Ca, Sr) crystals from a lattice dynamics point of view. In the present study we report the role of van der Waals (vdW) interactions in predicting the stability of the lead carbonate’s crystal structure and single crystal elastic constants. The polycrystalline properties of CsPbCO₃F, RbSrCO₃F, KSrCO₃F, KCaCO₃F materials are also extracted from single elastic constant values using Voigt, Reuss, Hill approximations.^24–26 Zone center vibrational frequencies (infrared (IR) spectra) are calculated using a density functional perturbation theory (DFPT) approach and complete mode assignments are analyzed in detail. We have examined the nature of directional bonding and frequency and intensity variations of vibrational modes in detail based on the calculated Born effective charge (BEC) tensors. We report the thermodynamic properties which are crucial for exploring the practical applicability (durability) of a NLO material. To the best of our knowledge, to date, such studies have not been reported in the literature for the present studied novel carbonate fluorides. In order to explore more about the vibrational nature of the bonds, we further turned our focus to gaining a better understanding of the heat-conduction process. The thermodynamic properties including entropy, Debye temperature, heat capacity, enthalpy, thermal expansion and intrinsic lattice thermal conductivity at different temperatures ranging from 5 K to 1000 K are reported. We have compared the obtained results with experimentally reported thermal conductivity values of several hexagonal types of NLO materials. Since, there are several recent reports on the crystal structures of carbonate fluoride materials, we explore the crucial structure–property correlation in carbonate group compounds based on different aspects. We believe that the properties studied in this work which are related to lattice dynamics parts such as mechanical, vibrational and thermodynamic properties could open up new possibilities in the world of NLO materials.

2 Calculation methods

First principles calculations play a very important role in explaining the structure property correlations of various materials. Details obtained from these simulations are therefore very useful for new developments in the domain of nonlinear optical materials and their possible practical applications. In the present work, we have used a quantum mechanics based Cambridge Series of Total Energy (CASTEP) program,^27,28 which works based on the density functional theory plane-wave pseudo potential (PP) method. In order to calculate various structure dependent properties of the present carbonate materials of interest, we have taken the experimental structural details as given in ref. 5 and 22. Experimental geometries of CsPbCO₃F, ABCO₃F (A = K, Rb; B = Ca, Sr) are optimized with maximum tolerances for energy of 5.0 × e⁻⁶ (eV per atom), stress of 0.02 GPa and displacement of 5.0 × e⁻⁴ Å. Forces between atoms are minimized up to 0.01 eV Å⁻¹. Electron–ion interactions are treated using Vanderbilt Ultrasoft pseudo potentials³³ to calculate the ground state structural and elastic properties with a 380 eV cutoff energy. The only available Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimizer is used for cell parameter optimization.³⁴ Local-density approximation (LDA),^29–31 generalized gradient approximation (GGA) of Predew–Burke–Ernzerhof (PBE),³² and Perdew–Wang 91 (PW91)³¹ are used as exchange correlation functionals to account for the electron–electron interactions. The Ortmann–Bechstedt–Schmidt (OBS)³⁵ correction to PW91 is used to treat the weak van der Waals (vdW) interaction effects. Norm conserving pseudopotentials³⁶ are used with the valance electrons of atoms such as Pb (5s² 5p⁶ 5d¹⁰ 6s² 6p²), Cs (5s² 5p⁶ 6s¹), F (2s² 2p⁵), O (2s² 2p⁴), C (2s² 2p²), K (3s² 3p⁶ 4s¹), Ca (3s² 3p⁶ 4s²), Rb (4s² 4p⁶ 5s¹), and Sr (4s² 4p⁶ 5s²) to calculate the BECs and zone centre vibrational frequencies of CsPbCO₃F and ABCO₃F (A = K, Rb; B = Ca, Sr) within the framework of density functional perturbation theory (DFPT)³⁷ with a 1300 eV cut-off energy. It is well known that, DFPT is an efficient technique over the finite displacement method to calculate vibrational properties with lower computational times. Moreover, it allows calculation of the crystal response to the external electric field and atomic displacements.³⁸ From these results it is possible to obtain various properties like vibrational intensities, Born effective charges etc. These DFTPT and finite element methods are framed within the harmonic approximation.³⁸ The Monkhorst–Pack scheme⁴¹ is used to generate an 11 × 11 × 10 k-point grid with 80 irreducible k-points. A spacing of 0.02 Å⁻¹ between k-points is used for better accuracy. The Born effective charge tensors for the compounds of present interest are obtained using a linear response method through the Gonze approximation.³⁹ The relations between the Born effective charges and vibrational mode intensities are as follows:⁴⁰ I_i = [Σ_j,kF^|_i,jA_j,k]²; A_i,j = ∂E/∂q_i∂μ_i. Here, A is the atomic polar tensor or Born effective charge tensor, E is the total energy, q_i is the Cartesian coordinate, F^| is the eigenvector, and μ_i is the dipole moment. The thermodynamic properties such as lattice heat capacity, Debye temperature, thermal conductivity and thermal expansion are also calculated for four iso-structural crystals (Z = 1) within the quasi-harmonic approximation. For metals at low T, the heat capacity can be represented by a sum of two terms. The electron contribution is proportional to T and the lattice contribution is proportional to T³ (this is the Debye T³ law). Thus, for metals, the Debye model can only be said to be approximate for the specific heat, but it gives a good approximation for the low temperature heat capacity of insulators and semiconductors where other contributions from highly mobile conduction electrons are absent. We computed these properties to have an overview of how these materials would behave under temperature. Our work could be a starting point and motivation for the experimental researchers in future. More details are discussed in the Results and discussion section and the Thermodynamic properties section.

3 Results and discussion

3.1 Structural, elastic and polycrystalline properties

The layered non-centrosymmetric material under investigation, CsPbCO₃F, crystallizes in the P6̄m2 (187) space group with lattice parameters of a = b = 5.3888 Å, c = 5.1071 Å, α = β = 90 (deg) and γ = 120 (deg). The unit cell consists of one formula unit (Z = 1) and the atoms Cs, C, F, Pb and O are situated at the 1a, 1d, 1e, 1f and 6m Wyckoff sites. Moreover, the reported crystal structure of CsPbCO₃F is made up of alternate [Pb(CO₃)] and [CsF] layers along the c-axis in the x–y plane as shown in Fig. 1. The adjacent layers parallel to the c-axis are connected through F–Pb–F bonds. The iso-structural ABCO₃F (A = K, Rb; B = Ca, Sr) compounds are also found to crystallise in the same P6̄m2 space group with a hexagonal crystal structure with Z = 1 formula units. A slight increment in the lattice parameters and volumes is noted upon changing the heavier metal atoms in these structures, which is expected.^5,7 Hereafter we are naming the above mentioned 4 crystals KCaCO₃F, KSrCO₃F, RbSrCO₃F and CsPbCO₃F as KCa, KSr, RbSr and CsPb for simplicity. The atomic sites occupied by different atoms in the KCa, KSr and RbSr phases are as follows: K, K and Rb at 1a, 1e and 1c; Ca, Sr and Sr at 1b, 1f and 1f; C atoms at 1d, 1d and 1b; O atoms at 3k, 3k and 3k; and F atoms at 1a, 1e and 1e respectively. In all the crystals, the oxygen atoms are located with mm2 site symmetry, whereas all other atoms K, Rb, Ca, Sr, C, O and F occupy the 6̄m2 site symmetry out of 5 possible site symmetries for the 187 space group. In this section we verify the effect of these different Wyckoff site occupancy's, chemical composition variations on the structural, mechanical and polycrystalline properties in a detailed manner. As a first step, to obtain the correct lattice parameters and volume, we have optimized the experimental crystal structure of CsPbCO₃F using the LDA functional and GGA (by applying PBE) exchange correlation functionals as implemented in the CASTEP code. The obtained ground state structural properties, lattice parameters and volume are given in Table 1. In comparison with the experimental data, we found that the optimized volume with LDA is underestimated by 6.8%, while the PBE functional overestimates it by 4%, which is a considerable deviation from the experimental values. In order to capture the effect of the non-bonded interactions present between the adjacent layers, one needs to optimize the system with dispersion corrected schemes applied to the standard DFT methods. Since the Grimme (G06)⁴² corrections are not implemented for the Pb and Cs elements in the present case, we performed further structural optimizations with the PW91 functional and the (OBS) correction by Ortmann et al.³⁵ to PW91. The obtained volumes with PW91 (see Table 1) are also overestimated by >3% before including the vdW effects and with PW91 + OBS the unit cell volume is slightly overestimated by 1% and is in relatively good agreement with experimentally reported data. Moreover, after the inclusion of vdW corrections, improvement is observed in the prediction of the lattice parameter ‘a’. Whereas, ‘c’ is well predicted before and after the vdW interactions are taken into account. The percentage of deviations in ‘a’ with the PBE, PW91 and PW91 + OBS functionals are 2.3%, 2.2% and 1.6% with respect to experimental values. With the LDA functional ‘a’ and ‘c’ are underestimated by 1.2%, and 4.5%. Overall the results of structural optimization of CsPb indicate that the OBS correction method has reproduced the experimental results more accurately. The calculated bond lengths with the OBS and PBE functionals are displayed in Table 2. We find that our calculations are in good agreement with experimental data for all of the studied compounds.

Fig. 1 Experimental crystal structure of CsPbCO₃F²² consisting of CsF and PbCO₃ layers.

Table 1 Calculated ground state lattice vectors (a and c, in Å), volume (V, in ų) of CsPbCO₃F, using LDA, PBE, PW91 and dispersion corrected PW91 (PW91 + OBS) along with experimental data²²

Symmetry	Compound	Parameter	LDA	PBE	PW91	PW91 + OBS	Experiment
		a	5.322	5.515	5.507	5.477	5.388
P6̄m2	CsPbCO3F	c	4.876	5.059	5.046	5.011	5.107
(Z = 1)		V	119.648	133.275	132.577	130.215	128.437

---

Table 2 Calculated bond lengths (in Å) for the OBS and PBE theoretical equilibrium structures of CsPbCO₃F and ABCO₃F (where A = K or Rb; B = Ca or Sr) respectively. Experimental data for each bond is taken from ref. 5 and 22 for comparison

KCaCO3F			KSrCO3F			RbSrCO3F			CsPbCO3F
Bond	Cal	Exp	Bond	Cal	Exp	Bond	Cal	Exp	Bond	Cal	Exp
Ca–F	2.248	2.2276	Sr–F	2.367	2.3478	Sr–F	2.405	2.3950	Pb–F	2.481	2.5536
Ca–O	2.585	2.5552	Sr–O	2.662	2.6397	Sr–O	2.686	2.6603	Pb–O	2.717	2.7084
Ca–C	2.977	2.9426	Sr–C	3.062	3.0367	Sr–C	3.088	3.0600	Pb–C	3.122	3.1110
Ca–K	3.731	3.6907	Sr–K	3.870	3.8385	Sr–Rb	3.914	3.8858	Pb–Cs	3.988	4.0250
K–O	2.808	2.7765	K–O	2.951	2.9260	Rb–O	2.998	2.7950	Cs–O	3.080	3.1420
K–F	2.977	2.9426	K–F	3.062	3.0367	Rb–F	3.088	3.0600	Cs–F	3.122	3.1120
C–O	1.295	1.2853	C–O	1.299	1.2910	C–O	1.299	1.2960	C–O	1.296	1.2810

---

At a fundamental level, the material’s response to applied stress can be understood from the magnitude of the elastic constants. The bulk modulus of a material will explain the response to isotropic compression. In order to predict these fundamental mechanical equilibrium properties, which are more sensitive to lattice vectors, we have used optimized crystal structures obtained with the PW91 + OBS functional. According to the symmetry elements, for a hexagonal crystal the 36 independent elastic coefficients of a 6 × 6 tensor matrix will reduce to just 5 independent constants. These C₁₁, C₃₃, C₄₄, C₁₂ and C₁₃ constants for the present studied hexagonal structure and the bulk modulus (B) values are calculated using the stress–strain method. The obtained single crystal mechanical properties with the OBS functional are presented in Table 3 along with the calculated values from the PBE and PW91 functionals for comparison. To the best of our knowledge there are no experimental elastic constants reported in the literature for comparison. The obtained elastic constants before and after the inclusion of vdW interactions satisfy Born's mechanical stability criteria derived for a hexagonal system.⁵²

C_ii > 0 (i = 1, 3, 4), C₁₁ > C₁₂, (C₁₁ + C₁₂)C₁₃ > 2C₁₃².

Table 3 Calculated single crystal elastic constants C_ij and bulk modulus B (in GPa units) of CsPbCO₃F for the PBE, PW91 and PW91 + OBS theoretical equilibrium volumes

Method	Functional	C11	C33	C44	C12	C13	B
DFT	PBE	63.0	71.9	15.7	34.9	24.0	40.4
DFT	PW91	67.1	71.3	15.6	37.3	22.0	40.7
vdW	PW91 + OBS	70.2	80.2	16.3	31.8	22.4	41.5

---

CsPb obeys this criteria, confirming its good mechanical stability. The variations in the calculated elastic constants with the PBE, PW91 and PW91 + OBS functionals are related to the differences in their optimized lattice parameters with each functional as shown in Table 1. Strong anisotropy for the externally applied strain along the ‘a’ and ‘c’ crystallographic directions is observed from the C₁₁ and C₃₃ values (see Table 3). The relation C₃₃ > C₁₁ from the calculated results indicates that the crystal is more compressible along the a-axis direction than the c-axis for the applied strains. This effect arise due to weak bonding interactions between the CO₃ and lead atoms (Pb–O) than the interlayer ionic interactions through the F–Pb–F bonds. The bond lengths of (Pb–O) > (Pb–F) also confirming this (see Table 2). The huge differences in the calculated elastic constants C₁₁ and C₃₃ with DFT and vdW (7.3 GPa; 9 GPa) also indicate that the accurate prediction of interactions between (CO₃ and Pb) and adjacent CsF and PbCO₃ layers plays an important role in explaining the crystal stability. The obtained bulk modulus values with and without the vdW effect, 40 GPa & 41.5 GPa respectively, indicate that CsPbCO₃F is a soft material among all the ABCO₃F (where A = K, Rb or Cs; B = Ca or Sr) carbonate fluoride crystals and is harder than the well-known KH₂PO₄ (KDP) crystal (27 GPa)⁵³ and α-SiO₂ (38 GPa)⁵³ and softer than the β-BaB₂O₄ (BBO) crystal (60 GPa).⁵³ In comparison with our previous study,⁷ we noticed that the presence of a heavy metal Pb atom in its isostructures like CsCaCO₃F (51.1 GPa), KSrCO₃F (47.1 GPa), KCaCO₃F (53.7 GPa), RbSrCO₃F (46.4 GPa) and RbCaCO₃F (52.0 GPa) further reduced the hardness of the material by 22%, 13.5%, 22.7%, 11.8% and 25.3% respectively due to the increase in the atomic radii. The hardness of the studied carbonate fluoride materials follows the trend:

KCaCO₃F > RbCaCO₃F > CsCaCO₃F > KSrCO₃F > RbSrCO₃F > CsPbCO₃F;

The occurrence of carbonate materials in alkaline rock complexes and their availability in powder forms and different size crystals at laboratory scales motivated us to also focus on their polycrystalline properties.¹⁴ Since nonlinear optical materials are subjected to high power lasers for various applications like in high power nonlinear optical devices and frequency conversion applications,⁵³ it is worth knowing their polycrystalline properties. We made an attempt to calculate different polycrystalline properties such as the bulk modulus, shear modulus, Young's modulus, Poisson's ratio, shear anisotropy factors and elastic-Debye temperature from the single crystal elastic constant data. Initially, we have calculated the bulk (B_X) and shear (G_X) moduli of CsPbCO₃F with the Voigt (B_V, G_V), Reuss (B_R, G_R) and Hill (B_H, G_H) approximations^24–26 using the single crystal elastic constants. The average of the obtained values from the Voigt and Reuss methods are taken as the suitable polycrystalline values as suggested by Hill for hexagonal symmetry.^43,44,47 We have also calculated similar properties of other iso-structural compounds ABCO₃F (A = K, Rb; B = Ca, Sr) of lead carbonate fluoride based on the reported single crystal elastic constants from our previous work, Narsimha Rao et al.⁷ The obtained results are compared and shown in Table 3.

It is clear from the results that the upper and lower limits of the bulk moduli (B_V, B_R) are found to be almost similar for the studied materials, whereas the results (Table 4) show considerable variations. Moreover, it is observed that B_H > G_H, which indicates that the mechanical stability of the studied compounds is limited largely by the shear moduli. KCa has a large G_H value, whereas CsPb has the lowest value among the studied carbonates. This indicates that the bond restoring energy for the applied elastic shear strain is decreasing with an increase in the atomic number of the metal atoms in the studied carbonates. In addition, according to the Pugh criterion^45,46 the calculated B_H/G_H ratios > 1.75 indicates the ductile nature of the studied crystals, with the exception of KCa (1.67) which is brittle in nature. It was found that the ductile nature of the studied materials increases with an increase in the atomic radii of the metal atoms. This behaviour is accompanied by the diversity present in the values of the calculated elastic constants. Overall, the Hills approximation of the bulk modulus also confirms that CsPb is the softest material among all the carbonate materials. As a next step, we verified the resistance of the studied materials to the applied uni-axial tensions and stability against the shear strain thereby calculating Young's modulus (E) and Poisson's ratio (σ),⁴⁷ where E = 9GB/(G + 3B) and σ = (E/2G) − 1. It is well known that the magnitude of the Poisson's ratio is 0.1 for covalent and 0.25 for ionic materials.⁴⁸ In the present study, the obtained σ values (0.25) point to the mixed ionic–covalent nature of the studied carbonates. From another point of view, it is known that when the magnitude of σ is 0.5 no change in volume occurs. From the obtained results as shown in Table 4, it is clear that a large volume change can occur with elastic deformation of the studied crystals and it is relatively greater for the CsPb crystal than the other carbonates. Overall the change in volume against the applied uni-axial strain in the studied layered materials increases with the metal atom’s atomic radii from K to Sr and Sr to Pb. These observations are consistent with the calculated anisotropy factors.

Table 4 The calculated bulk (B_X) and shear moduli (G_X) values using the Voigt, Reuss and Hill approximations (X = V, R, H). Also listed are the Poisson's ratio σ and B_H/G_H ratio. All values are calculated at the corresponding theoretical equilibrium volumes

Compound	BV	BR	BH	GV	GR	GH	σ	BH/GH
KCaCO3F	53.7	53.8	53.8	33.2	31.1	32.1	0.25	1.67
KSrCO3F	47.0	47.0	47.0	28.1	23.6	25.9	0.26	1.81
RbSrCO3F	46.5	46.5	46.5	25.8	23.6	25.9	0.26	1.79
CsPbCO3F	41.5	41.7	41.6	19.9	19.1	19.5	0.29	2.13

---

Secondly, three shear anisotropy factors, A₁, A₂ and A₃, and the elastic Debye temperature, Θ_D, for the studied hexagonal materials at crystal density ρ (ref. 49 and 50) are also calculated and analyzed. Where A₁ = 2C₄₄/(C₁₁ − C₁₂); A₂ = C₃₃/C₁₁; A₃ = C₁₂/C₁₃. The obtained values are presented in Table 5 along with c/a ratios. It is observed that the calculated c/a ratios of the studied crystals show increments with the metal atom’s atomic radii. It is clear from the results that all three anisotropy factors show considerable deviation from unity. This indicates that all the studied crystals possess large mechanical anisotropy. For the studied carbonates, the anisotropy factor A₁ increased from about 0.4–0.8 and A₂ shows an almost constant value of 1.1 whereas A₃ shows a decreasing trend from about 1.7–1.2. This is consistent with the obtained decreasing trend of hardness (bulk modulus) of the studied materials upon insertion of heavier metal atoms. This behaviour might be arising due to the variations of inter-layer interactions in the (CO₃ and metal atom) layer and intra-layer interactions between the (CO₃ and metal atom) and K/Rb/Cs–F adjacent layers. Moreover, the decreasing trend of C₁₁ from KCaCO₃F → KSrCO₃F → RbSrCO₃F → CsPbCO₃F indicates that bonding between the CO₃ group and metal atoms is becoming more ionic in nature. The increasing trend of C₃₃ from CsPbCO₃F → RbSrCO₃F → KSrCO₃F → KCaCO₃F indicates that the interactions between alternate layers are strengthened. As a next step, we have moved onto the elastic Debye temperature calculations. It is well known that the Debye temperature is a limit, below which the lattice shows stability mainly due to low electron phonon-coupling. Since at lower temperatures this quantity arises purely because of lattice modes, we made an attempt to calculate the elastic Debye temperatures of the carbonate crystals based on the relations given in ref. 51 between the Young's modulus, shear modulus, bulk modulus and crystal density ρ, and the results are presented in Table 5. The results shows that Θ_D decreases from KCa (479.7 K) to KSr (385.6 K) to RbSr (350.4 K) to CsPb (239.8 K). This trend suggests that the melting point is low for lead carbonate fluoride and high for KCa. Since these crystals are newly synthesised, there are no experimental data available in the literature for the above calculated properties. We expect that our simulated results will be helpful as a reference for engineers in the selection of the studied materials for real time applications.

Table 5 Calculated values of the c/a ratio, shear anisotropy factors (A_i) (i = 1, 2, 3), Young's modulus (E), crystal density (ρ) and elastic-Debye temperature (Θ_D) at the theoretical equilibrium volumes

Compound	c/a	A3	A2	A3	E	ρ	ΘD
KCaCO3F	0.869	0.6	1.1	1.3	80.4	2.538	479.7
KSrCO3F	0.892	0.4	1.1	1.7	65.6	2.935	385.6
RbSrCO3F	0.900	0.6	1.0	1.2	65.5	3.464	350.4
CsPbCO3F	0.914	0.8	1.1	1.4	50.6	5.345	239.8

---

3.2 Born effective charges (BEC) and static polarization

The Born effective charge (BEC or, Z*) is a fundamental quantity that demonstrates the coupling between electrostatic fields and lattice displacements. In order to explore more about the structural distortion, covalent and ionic bonding nature and local dipole moments and resulting polarization^54–57 of the present NLO crystals of interest, we have computed the BEC's of all non-equivalent ions using linear response formalism as implemented in the CASTEP code. The obtained results are shown in Tables 6 and 8. The corresponding percentage of deviations from the corresponding nominal ionic charges are shown in Tables 7 and 9. The obtained results satisfy the acoustic sum rule, which in turn indicates good convergence of our calculations.⁵⁹ Moreover, it is known that the BEC tensors obtained using a linear-response and Berry's phase approach will be at the same level of accuracy.⁵⁸ The obtained large deviations in the Born effective charges from its nominal ionic charge indicates that these studied crystals possess covalent–ionic behaviour. The BECs of CsPbCO₃F show larger deviations when compared to other crystals studied which also confirms that lead carbonate fluoride shows a more covalent nature. Moreover, BEC values are found to be highly direction dependent for the studied hexagonal structures which belong to the P6̄m2 space group. The diagonal elements of the BEC tensors at carbon, fluorine, potassium, strontium and lead follow the relation . Whereas at the oxygen atoms, the effective charges are more asymmetric and follow the relation . We compared the BEC tensors of CsPbCO₃F with the previously reported values by Thao Tran et al.,⁹ and the results were found to be similar.

Table 6 Calculated BECs of the Pb, Ca, Sr, F, Cs, Rb, K and C atoms at the theoretical equilibrium volumes along with previously reported⁹ values in parentheses

Atom	Ionic	KCaCO3F		KSrCO3F		RbSrCO3F		CsPbCO3F
Ca, Sr, Pb	+2	2.42	2.31	2.43	2.36	2.47	2.37	3.63(3.7)	3.17(3.0)
F	−1	−0.94	−1.73	−0.91	−1.81	−0.98	−1.76	−0.87(−0.9)	−2.90(−2.9)
Cs, Rb, K	+1	1.15	1.30	1.18	1.29	1.20	1.40	1.28(1.3)	1.56(1.5)
C	+4	2.86	0.14	2.86	0.10	2.97	0.06	2.87(2.8)	0.05(0.04)

---

Table 7 Calculated percentage of deviations of BECs of the Pb, Ca, Sr, F, Cs, Rb, K and C atoms at the theoretical equilibrium volumes

Atom	KCaCO3F		KSrCO3F		RbSrCO3F		CsPbCO3F
Ca, Sr, Pb	21.05	15.65	21.75	18.15	23.6	18.95	81	58.6
F	−5.7	73.6	−8.2	81.8	−2	75.9	−12.7	190.5
Cs, Rb, K	15.6	30.3	17.8	29.4	20.7	40.6	28.3	56.6
C	−28.5	−96.4	−28.42	−97.47	74.25	−98.52	−28.27	−98.65

---

Table 8 Calculated BECs of the O₁, O₂ and O₃ atoms (which have a nominal ionic charge of −2) at the theoretical equilibrium volumes

KCaCO3F			KSrCO3F			RbSrCO3F			CsPbCO3F
−1.61	−2.04	−0.67	−2.27	−1.43	−0.64	−1.66	−2.11	−0.69	−2.24(−2.3)	−2.36	−0.62 (−0.6)
−2.26	−1.39	−0.67	−1.64	−2.06	−0.64	−2.34	−1.43	−0.69	−2.43(−2.3)	−2.17	−0.62 (−0.6)
−1.61	−2.04	−0.67	−1.64	−2.06	−0.64	−1.66	−2.11	−0.69	−2.24(−2.3)	−2.36	−0.62 (−0.6)

---

Table 9 Calculated percentage of deviations of BECs of the O₁, O₂ and O₃ atoms from their nominal ionic charge of −2

KCaCO3F			KSrCO3F			RbSrCO3F			CsPbCO3F
−19.5	2	66.5	13.5	−28.5	−68	−17	5.5	65.5	12	18	−69
13	−30.5	66.5	−18	3	−68	+17	−28.5	65.5	21.5	8.5	−69
−19.5	2	66.5	−18	3	−68	−17	5.5	65.5	12	18	−69

---

More specifically, the charge anisotropy ‘around metal atoms’ shows increments from Ca → Sr → Pb and it was found that . This informs us that the covalent nature of these crystals is increased drastically upon increasing the atomic size of the metal atom in the carbonate fluoride crystals. However, it is more along the ‘a’ direction (the bond between metal–oxygen atoms of carbonate group (inter -layer interactions)) bond than along the ‘c’ (metal–fluorine bond between adjacent layers (intra-layer interactions)) direction. In case of the CsPb compound these and anisotropies around the metal atoms are found to be ∼60% and ∼30% higher when compared with other KCa, KSr and RbSr crystals. The charge anisotropy ‘around fluorine atoms’ in all the studied crystals along the ‘a’ axis is increased as follows RbSr → KCa → KSr → CsPb. It is clear from the calculated data (as shown in Table 6), that the BEC of the fluorine atom for the studied materials is deviated from its ionic charge −1 as follows: along the a-axis → CsPb (−0.87) < KSr (−0.91) < KCa (−0.94) < RbSr (−0.98); along the c-axis → CsPb (−2.90) > KSr (−1.81) > RbSr (−1.76) > KCa (−1.73). This confirms that the ionic nature of the fluorine bond with Rb, K, K and Cs in the RbSr, KCa, KSr and CsPb compounds increased. Whereas in the ‘c’ direction, anisotropy of fluorine increased from KCa → RbSr → KSr → CsPb. This indicates that the bond between fluorine and Ca (in KCa), Sr (in RbSr), Sr (in KSr) and Pb in (CsPb) is becoming more covalent in nature. Especially in the CsPb phase, the deviation of charge from its ionic value increases along the ‘a’ and ‘c’ directions approximately by 4% and 100% compared with the other KCa, RbSr, KSr phases. The BECs of the O₁, O₂ and O₃ oxygen atoms in all the studied crystals show more or less similar deviation when compared to their nominal ionic charge of −2. This confirms the strong covalent bonding behaviour between the carbon and oxygen atoms inside the anionic group. Overall, it has been found that the BEC values are strongly affected by a change in atoms at the A and B site in ABCO₃F (where A = K, Rb or Cs and B = Ca, Sr or Pb) and the atomic bonds associated with them.

3.3 Vibrational modes and symmetry analysis

Study of the fundamental vibrational properties of functional groups present in the crystal plays a crucial role in understanding the structure details and inter-molecular interactions in the low energy region. In this section we present the zone centre vibrational frequencies of CsPbCO₃F and three other isostructural compounds’ ABCO₃F (A = K or Rb; B = Ca or Sr) crystals. The mode assignments of all the obtained frequencies are analyzed and are shown in Tables 10 and 11. All of these four iso-structural compounds crystallize in the P6̄m2 space group, having a single formula unit (7 atoms per cell). According to the symmetry rules for the D_3h (6̄m2) point group, the atoms of CsPbCO₃F and KSrCO₃F compounds are occupying the Wyckoff positions as (Pb, Sr)-1f, F-1e and (Cs, K)-1a, C-1d, O-3k. A slightly different atomic configuration in the case of KCaCO₃F is K-1e, Ca-1b, F-1a, C-1d and O-3k positions and for RbSrCO₃F the atoms are situated at the Sr-1f, Rb-1c, F-1e, C-1b and O-3k sites. According to the symmetry group theory analysis,⁶⁰ the distribution of 3 acoustic (external) and 18 optical (internal) possible vibrational modes for these sets of compounds are as follows:

Γ_acoustic = A′′₂ ⊕ E′

Γ_optic = A′₁ ⊕ A′₂ ⊕ 4A′′₂ ⊕ 5E′ ⊕ E′′

Table 10 The calculated zone-center high frequency vibrational modes (in cm⁻¹) of CsPbCO₃F and ABCO₃F (where A = K or Rb; B = Ca or Sr) and their assignments [here I = IR active mode, R = Raman active mode]. Experimentally reported frequencies are given in parentheses⁵

Mode	CsPbCO3F	RbSrCO3F	KSrCO3F	KCaCO3F	Symmetry
M21–M20	1379.70(1407)	1396.05	1396.68	1422.84	E′ (I + R)
M19	1038.39(1049)	1034.91	1032.89	1053.59	A′1 (R)
M18	821.06(843)	834.74	835.83	834.78	A′′2 (I)
M17–M16	665.89(689)	676.78	676.94	682.94	E′ (I + R)

---

Table 11 The calculated zone-center low frequency vibrational modes of CsPbCO₃F and ABCO₃F (where A = K or Rb; B = Ca or Sr) and their mode assignments [here Trans. = translation, Asymm. = asymmetric and str. = stretching]

Compound	Mode	PBE	Symmetry	Assignment of modes
KCaCO3F	M15	372.86	A′′2 (I)	Asymm. str. mode of Ca–F
	M14	187.82	A′′2 (I)	Trans. of (CO3), Trans. of (Ca–F)
	M13–M12	173.86	E′ (I + R)	Symm. bending of (Ca–F), Trans. of (CO3)
	M11	158.41	A′′2 (I)	Trans. of (K, CO3)
	M10–M09	157.27	E′ (I + R)	Trans. of (CO3, K), Symm. bending of (Ca–F)
	M08–M07	150.67	E′′ (R)	Libration of (CO3)
	M06–M05	114.07	E′ (I + R)	Symm. bending of (Ca–F), Trans. of (K)
	M04	98.12	A′2 (silent)	Rotation of CO3
KSrCO3F	M15	346.32	A′′2 (I)	Asymm. str. mode of Sr–F
	M14	175.77	A′2 (silent)	Rotation of CO3
	M13–M12	173.09	E′ (I + R)	Trans. of (CO3), symmetric bending of (Sr–F)
	M11	136.06	A′′2 (I)	Rot. mode of CO3 group
	M10–M09	115.33	E′ (I + R)	Trans. of (CO3, K), symmetric bending of (Sr–F)
	M08–M07	112.37	E′′ (R)	Libration of (CO3)
	M06	96.15	A′′2 (I)	Trans. of (CO3, K)
	M05–M04	62.63	E′ (I + R)	Trans. of (F), Symm. bending of (Sr–F)
RbSrCO3F	M15	306.20	A′′2 (I)	Asymm. str. mode of Sr–F
	M14–M13	162.54	E′ (I + R)	Trans. of CO3 group, Symm. bending of (Sr–F)
	M12	161.71	A′2 (silent)	Rotation of CO3
	M11	131.09	A′′2 (I)	Trans. of CO3 group, Asymm. str. of (Sr–F)
	M10–M09	126.58	E′ (I + R)	Symm. bending of (Sr–F)
	M08–M07	118.91	E′′ (R)	Libration of (CO3)
	M06	99.00	A′′2 (I)	Trans. of (CO3, Rb)
	M05–M04	81.32	E′ (I + R)	Trans. of (CO3, Rb), Symm. bending of (Sr–F)
CsPbCO3F	M15–M14	177.53	E′′ (R)	Libration mode of CO3
	M13	158.38	A′′2 (I)	Trans. mode of (CO3, Cs) + Asymm. str. (Pb–F)
	M12	145.61	A′′2 (I)	Asymm. str. of (Pb–F)
	M11	106.75	A′2 (silent)	Rot. mode of CO3
	M10–M09	87.26	E′ (I + R)	Trans. of (CO3, Cs) + Symm. bending of Pb–F
	M08	81.16	A′′2 (I)	Trans. of (CO3, Cs), Asymm. str. (Pb–F)
	M07–M06	65.77	E′ (I + R)	Trans. of Cs, Symm. bending of (Pb–F)
	M05–M04	43.10	E′ (I + R)	Symm. bending of (Pb–F), Trans. of CO3

---

The calculated 21 frequency modes from the present study are in good agreement with the above mentioned group theory representations for all the crystals. Apart from the 3 acoustic modes, among the 18 possible optical modes we observe that four modes (A′′₂) are infra-red (I) active, three modes (E′′, A′₁) are Raman (R) active, and 10 modes (E′) are combined infra-red + Raman active (I + R). Interestingly one silent mode is observed with A′₂ symmetry from our results for all the compounds. A negligible change in polarization and dipole moment due to the CO₃ rotational mode (see Fig. 3) could be the possible origin. However, according to group theory analysis this mode is found to be active only in the hyper-Raman region.

Fig. 2 Calculated zone center vibrational (IR) spectra in the far-IR, mid-IR, near IR regions of CsPbCO₃F and ABCO₃F (where A = K, or Rb; B = Ca or Sr) (from left to right) structures at theoretical equilibrium.

Fig. 3 Snapshots of different vibrational mode animations of carbonate fluoride materials.

The calculated modes in the ‘higher frequency region’ (>600 cm⁻¹) are in good agreement with the available experimental data as shown in Table 10. These modes arise due to the vibration of the CO₃ unit alone for all the studied compounds. The vibrations of the CO₃ unit observed based on animations and in reference to the previous reports^61,62 are assigned as follows: the frequency mode between 660 and 690 cm⁻¹ corresponds to doubly degenerate asymmetric in-plane bending; between 820 and 840 cm⁻¹ is due to symmetric out-of-plane bending; between 1030 and 1060 cm⁻¹ is because of symmetric stretching (breathing mode); between 1370 and 1430 cm⁻¹ is due to doubly degenerate asymmetric stretching. Further, in the ‘lower frequency region’ (<400 cm⁻¹), vibrational modes for all the present investigated compounds mainly arise from librational, translational, rotational motions of the CO₃ group and stretching and bending motions of the metal atom (M)–F (where M = Ca, Sr or Pb) bonds (see Fig. 3). Whereas in the ‘mid frequency region’, in contrast with the experimental results,²² we do not observe any Pb–F vibrational mode at 407 cm⁻¹ in the case of CsPbCO₃F. It is clear from Fig. 2 that the 407 cm⁻¹ mode is further shifted to the lower frequency side. The larger values of BEC suggests that the presence of dominant LO-TO splitting might be the possible reason for this discrepancy. The low frequency mode assignments are analyzed as shown in Table 11 and it is found that at least one silent mode is observed for every studied compound. Snapshots of all these CO₃ vibrations are shown in Fig. 3 for further reference.

It is observed from the calculated IR spectra that all peaks (from 1–8), as shown in Fig. 2, are red shifted with an increase in the atomic number. The changes in intensity of the different frequencies are attributed to variation in the probability of vibrational transition occurrence from the ground state to the exited states. Due to the same symmetry of the studied crystals, an equal number of absorption peaks (8) are found to occur in the spectra. As a starting point we analyzed the reasons for the frequency shifts and the origin of the intensity variations will be discussed based on the obtained BECs later.

In the higher frequency region (>600 cm⁻¹), the peak number 8 (I + R mode) corresponding to the asymmetric vibration of the CO₃ group is red-shifted considerably from KCa to RbSr to CsPb with a slight variation in the intensity. Whereas in case of KSr and RbSr the peak position is almost constant. The existence of directional bonding (covalent/ionic) interactions between the anionic group and metal atoms, causes this frequency shift due to increasing the atomic mass of metal atoms. From Tables 6 and 8 it is clear that anisotropy in the BECs of the carbon and oxygen atoms is almost constant for KCa and KSr and similarly for RbSr and CsPb. This manifests as similar intensities of peak 8 for the (KCa and KSr) and (RbSr and CsPb) compounds. A slight increment in intensity from KCa and KSr → RbSr and CsPb is attributed due to differences in the carbon and oxygen BEC deviations from their respective nominal ionic charges. In addition, the obtained trends in bond lengths between the metal atom and oxygen atoms (Pb–O) > (Sr–O) > (Ca–O) suggests that bending of CO₃ in CsPb occurs at lower frequencies than the other studied crystals. This could be the possible reason behind the soft nature (41.6 GPa) of CsPb compared with KCa (53.8 GPa). Moreover, KSr and RbSr possess almost similar hardness (47.0 GPa and 46.5 GPa) due to similar Sr–O interactions.

The position and intensity of peak number 7 (IR active) which arises from symmetric bending of the CO₃ group, is almost constant for all the studied crystals and in turn suggests that the IR absorption of this mode is less affected with respect to the atomic number of the metal atoms. Peak 6 which is active in the infra-red and Raman regions, arises due to the asymmetric in-plane bending mode of CO₃. This peak shows less shift in peak position but a huge intensity increase in the case of lead carbonate fluoride compared to the other carbonates. This can be due to the larger change in BECs of both the ‘C’ and ‘O’ atoms of lead carbonate fluoride in the xy-plane than other studied crystals. The different effective charges of the C and O atoms in the lead carbonate material makes CO₃ more polarizable. Peak 5 (IR active mode) corresponds to the asymmetric stretching mode of the Ca–F and Sr–F bonds and is red shifted with a constant intensity from KCa → KSr → RbSr. Interestingly, no peak corresponding to the Pb–F bond is observed in this region as reported in the literature. The reason for this shift is attributed to the different bond lengths of Ca–F (2.248 Å) in KCa, Sr–F (2.367 Å) in KSr and Sr–F (2.405 Å) in RbSr.

In the lower frequency range (below 200 cm⁻¹), the spread of the vibrational spectrum is different for each of the studied carbonates as shown in Fig. 2. Even though compounds from KSrCO₃F to CsPbCO₃F are iso-structural, their IR spectra below 200 cm⁻¹ are very different and frequencies are equally spread over the region between 50–200 cm⁻¹. Whereas in case of KCaCO₃F it is between 100 and 200 cm⁻¹ and for RbSrCO₃F lies in-between 75 and 175 cm⁻¹. It is observed from Table 11 that the highest intensity mode in this region (see Fig. 2) arises due to the combination of symmetric bending of the Ca/Sr/Pb–F bond and translation of the CO₃ group. In the cases of KCaCO₃F, KSrCO₃F and RbSrCO₃F the position of this highest intensity peak is almost constant but for lead carbonate fluoride it was red-shifted due to the heavier mass of the lead atom. In the lower frequency window, the higher intensity modes, peaks 5 and 3 in KCa, peaks 4 and 5 in KSr, and peaks 5, 4 and 3 in RbSr are mainly found to arise because of Ca–F, Sr–F and Pb–F vibrations along with CO₃ vibrations. The intensities of the remaining optical modes in this window are found to be higher for the CsPbCO₃F compound which also confirms the effect of higher BECs.

Overall, higher intensities for all the IR modes of lead carbonate fluoride are observed, suggesting that it is a more optically active material in the IR region than the other studied carbonates. The contribution from the CO₃ group vibrations (peaks 6 and 8) in the near IR region to the optical response is greater in the case of CsPb than others. Our results show a similar trend and give a hint about the different optical responses of carbonate fluorides for the same incident light of 1064 nm which was reported in the literature^5,22 as 13.6, 3.61, 3.33 and 3.33 higher nonlinear coefficients than the well-known KDP crystal.

3.4 Thermodynamic properties

Investigation of the thermal behaviour of a nonlinear optical material is important in expanding knowledge about crystal growth issues, solid state physics and chemistry, crystal chemistry and its possible practical applications.⁶⁴ It is known that thermal expansion of the crystal can lead to changes in the shape/dimension of the sample and specific heat can impact the damage threshold thereby limiting the use of the material for industrial applications. Information about the thermal conductivity of a NLO material is very useful in determining its ability to transfer heat into the air thereby affecting the quality of the output beam.^53,63 So we made an attempt to calculate the thermodynamic properties of the present novel carbonate fluoride materials. Here we apply the quasi-harmonic Debye model,⁶⁵ in which the Gibbs free energy (G) of the system takes the following form G(V,P,T) = E(V) + PV − TS where E(V) is the total energy, V is the volume and S is the entropy of the system. Since the electronic structure calculations are performed in the static approximation, i.e., at T = 0 K and neglecting zero-point vibrational effects, the corresponding Gibbs free energy in this case becomes G_stat(V,P) = E(V) + PV which is the enthalpy, H, of the system. According to this quasi-harmonic Debye model, the non-equilibrium Gibbs free energy function is given by G(V,P,T) = E(V) + PV + A_vib(Θ(V), T). Where Θ(V) is the Debye temperature, PV indicates the constant hydrostatic pressure condition and A_vib is the vibrational Helmholtz free energy.⁶⁵ The heat capacity (C_V), entropy (S_V) and vibrational internal energy (U_vib) are calculated using the following relations: C_V = 3nk[4D(Θ/T) − (3(Θ/T)/(e^(Θ/T) − 1))]

S_V = nk[4D(Θ/T) − 3 ln(1 − e^(Θ/T))]

U_vib = nkT[(9/8)(Θ/T) + 3D(Θ/T)]

The Debye temperature is the highest temperature that can be achieved due to a single normal mode of a solid. Its magnitude varies from material to material based on the lattice vibrations. It is a fundamental parameter which correlates with many physical properties of solids, such as entropy, specific heat, thermal expansion and thermal conductivity. Since the Debye temperature shows strong temperature dependence, we have calculated this dependence up to a temperature of 1000 K as shown in Fig. 4. Entropy is a measure of uncertainty in the energy associated with the random arrangement and thermal motion of the atoms. As the temperature increases, the vibrational contribution to the entropy increases and, in turn, entropy increases. For the present studied crystals (see Fig. 4), the plots indicate a slight change in entropy which could be due to the change in atomic arrangements (Wyckoff positions) and with atomic masses. It is observed that CsPb shows higher entropy where as KCa shows a lower entropy response. In the cases of KSr and RbSr, the entropy is almost constant. It is well known that as the temperature rises the contribution of phonons becomes more and more important and one can calculate the free energy, F = U − TS, where U is the vibrational internal energy which contains the static energy and the phonon contribution and S is the entropy which is completely due to phonons and is shown in Fig. 4. The calculated free energy of all the studied crystals decreases with the increase in temperature. This behaviour is due to the fact that both vibrational internal energy U and entropy S increase with temperature and this leads to a decrease in the free energy. The studied systems are found to be thermodynamically stable below 1000 K. We have calculated the coefficient of thermal expansion using the relation α = (γC_V)/(BV) where B, V and C_V are the isothermal bulk modulus, unit formula volume and specific heat at constant volume respectively and γ is the Gruneisen parameter calculated on the basis of a rigid ion model.⁶⁶

Fig. 4 Calculated thermodynamic properties including enthalpy (H), free energy (F), entropy (S_V), heat capacity (C_V) and Debye temperature Θ(V) of carbonate structures at theoretical equilibrium up to 1000 K temperature.

The thermal expansion coefficient is proportional to the specific heat and both the properties exhibit the same temperature dependence. The specific heat and thermal expansion coefficient increase as T³ at low temperatures and gradually approach a linear increase at high temperatures, and then the increasing trend becomes gentler. Specific heat and thermal expansion reach a constant value at high temperature as shown in Fig. 4 and 5. It is to be noted from the results that the lead carbonate material has the lowest thermal expansion coefficient of 2.577 × 10⁻⁶/K compared with α-SiO₂, LiNbO₃, CaCO₃ (calcite) and the ABCO₃F (A = K, Rb; B = Ca, Sr) carbonates as shown in Table 12. In comparison with other studied carbonate fluoride crystals, it is observed that the α value decreases with an increase in atomic number. This could be due to the strengthened atomic bonds in CsPb.

Fig. 5 Calculated thermal conductivity (K) and thermal expansion (α) coefficients of carbonate structures at theoretical equilibrium. The K and α curves of KSr and RbSr are shifted upwards by 1 W m⁻¹ K⁻¹ and 0.5 (10⁻⁶/K) from the preceding curve for clarity.

Table 12 The calculated thermal conductivities k (W m⁻¹ K⁻¹) and thermal expansion coefficients α (10⁻⁶/K) of carbonate fluorides at room temperature along with data from other hexagonal NLO materials

Material	k	α
Present
CsPbCO3F	32.430	2.577
RbSrCO3F	2.634	2.786
KSrCO3F	1.584	2.877
KCaCO3F	0.488	3.178
Previous^53
Ba3B6O12	4.0, 36.0	1.2, 1.6
α-SiO2	12.38, 6.88	6.2, 10.4
LiNbO3	15.4, 5.3	5.4, 5.3
CaCO3	−3.7, 25.1	4.5, 5.4

---

Thermal conductivity (K) plays a critical role in controlling the performance and stability of materials and is one of the fundamental and important physical parameters of materials. It is a critically important parameter in the design of high-power nonlinear optical (NLO) devices such as frequency doublers and optical parametric oscillators (OPO's). On a more fundamental level, the study of the underlying physics of the heat-conduction process has provided a deep and detailed understanding of the nature of lattice vibrations in solids.⁶⁷ The thermal conductivity for the present nonlinear optical crystals is calculated using a phonon relaxation time method.⁶⁸ An important postulate is that if the material is pure then the term accounting for strong defect scattering will be negligible compared to the term for phonon–phonon scattering, so that thermal conductivity k = (K_B²/2π²ħν_s)(Θ_D/CT).

The thermal conductivity of the NLO materials was calculated following the work of Callaway and Baeyer.⁶⁸ The thermal conductivity as a function of temperature for CsPb and other carbonate materials is graphically represented in Fig. 5. It is clear from the plots that the increase in conductivity is initially rapid and reached a constant at higher temperatures. This effect is more pronounced in lead carbonate fluoride than the other studied crystals which gives more of a hint about the possible longest phonon mean free path than in the other crystals.⁵³ The thermal conductivity decreases with temperature due to the fact that the molecular vibrational densities increase with temperature. The obtained ‘K’ values for the KCa, KSr, RbSr and CsPb crystals at room temperatures are 0.0048 W cm⁻¹ K⁻¹, 0.0158 W cm⁻¹ K⁻¹, 0.0263 W cm⁻¹ K⁻¹ and 0.032 W cm⁻¹ K⁻¹. These values are consistent with the experimental observations for other NLO materials.^53,63 All the obtained values along with known values of hexagonal NLO materials are tabulated in Table 12 for better comparison. Importantly, the predicted thermal conductivity of the lead material at room temperature is 0.032 W cm⁻¹ K⁻¹ which is greater than the earlier reported thermal conductivity values for Ba₃B₆O₁₂ which is 0.016 W cm⁻¹ K⁻¹ (ref. 63) and other hexagonal NLO materials.⁵³ Moreover, it shows the largest ‘K’ value among all the studied carbonates. This information tells us that CsPb has better durability than BBO and other carbonate materials. Moreover it is well known that nonlinear media must have sufficiently high thermal conductivities to get better average power outputs in the devices. Present thermal conductivity results clearly infer that the lead based carbonate could be the best suited NLO material, thereby overtaking the other carbonates and borates. We were not able to compare our results due to a lack of experimental and theoretical data as our work is the first to calculate these properties of carbonate fluoride crystals. These results could provide necessary input for the design of high-power optical frequency converters in the near future.

4 Conclusions

In conclusion, we have studied the effect van der Waals (vdW) interactions on the structural properties of CsPbCO₃F by means of density functional theory. The calculated structural properties using a semi-empirical dispersion correction scheme (PW91 + OBS) to treat the van der Waals interactions are found to be in good agreement with the experimental values which indirectly suggests the important role of van der Waals forces in this crystal. In addition, we have also calculated the zone center vibrational frequencies of CsPbCO₃F and ABCO₃F (A = K, Rb; B = Ca, Sr) with a density functional perturbation theory (DFPT) approach and the obtained high frequency modes are in good agreement with the available experimental values. All mode assignments were performed and at least one silent mode was observed in the case of all the studied crystals. This mode arises due to a rotation of CO₃ group and is found to be active only in the hyper-Raman region from group theory analysis. The variations in vibrational mode intensities and optical activity of the studied crystals are broadly analyzed from the obtained Born Effective Charge (BEC) tensor values. We have also calculated the thermodynamic properties such as enthalpy, free energy, entropy, heat capacity, Debye temperature, thermal conductivity and thermal expansion. The room temperature values of heat capacity, thermal expansion and thermal conductivity for all studied NLO materials are different, their overall temperature dependence is very similar. This indicates that all the compounds are characterized by rather similar lattice dynamical and thermal properties. We believe this work sheds light on the (NLO) material CsPbCO₃F as it could be a promising NLO material in near future.

Acknowledgements

ENR would like to thank the DRDO (through the ACRHEM under the DRDO: vide project no. DRDO/02/0201/2011/00060 Phase-II) and GV would like to thank the Department of Science and Technology (DST) (under the grant SR/FTP/PS-096/2010(G)) for financial support. We would also like to acknowledge the CMSD, University of Hyderabad, for providing the computational facilities. ENR would like to thank Dr T. Atahar Parveen for fruitful discussions. AHR would like to acknowledge the CENTEM project, registered number CZ.1.05/2.1.00/03.0088, co-funded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI program and the follow-up sustainability stage, supported through CENTEM PLUS (LO1402) by financial means from the Ministry of Education. AHR is also grateful for the support of the Youth and Sports under the 4National Sustainability Programme I, and MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/08.0144) infrastructures. SA would like to thank the High Performance Facilities (HPC) at the Inter-University Accelerator Centre (IUAC) in New Delhi, the Indian Institute of Mathematical Sciences (IMSC) in Chennai, CSIR-4PI in Bangaluru and the Indian Institute of Technology in Kanpur.

References

1. J. A. Neff, Prog. Cryst. Growth Charact. Mater., 1990, 20, 1–7.
2. C. T. Chen, G. L. Wang, X. Y. Wang and Z. Y. Xu, Appl. Phys. B: Lasers Opt., 2009, 97, 9–25.
3. C. Bosshard, K. Sutter, P. Pretre, J. Hulliger, M. Florsheimer, P. Kaatz and P. Gunter, Organic Nonlinear Optical Materials, Gordon and Breach, Switzerland, 1995.
4. P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118–119.
5. G. Zou, N. Ye, L. Huang and X. Lin, J. Am. Chem. Soc., 2011, 133, 20001–20007.
6. F. Gan and S. Tian, Series on Archaeology and History of Science in China, History Of Modern Optics and Optoelectronics Development in China, World Scientific/World Century, Hackensack, 2014.
7. E. Narsimha Rao, S. Appalakondaiah, N. Yedukondalu and G. Vaitheeswaran, J. Solid State Chem., 2014, 212, 171–179.
8. L. Kang, Z. Lin, J. Qin and C. Chen, Sci. Rep., 2013, 3, 1366.
9. T. T. Tran, P. S. Halasyamani and J. M. Rondinelli, Inorg. Chem., 2014, 53, 6241–6251.
10. P. C. Ray, Chem. Rev., 2010, 110, 5332–5365.
11. M. a. MÃĎâĂęczka, L. Macalik and A. Majchrowski, J. Alloys Compd., 2013, 575, 86–89.
12. R. Arun Kumar, M. Arivanandhan and Y. Hayakawa, Prog. Cryst. Growth Charact. Mater., 2013, 59, 113–132.
13. P. Yu, L.-M. Wu, L.-J. Zhou and L. Chen, J. Am. Chem. Soc., 2014, 136, 480–487.
14. J. D. Grice, V. Maisonneuve and M. Leblanc, Chem. Rev., 2007, 107, 114–132.
15. C. Chen, Y. Wu and R. Li, Int. Rev. Phys. Chem., 1989, 8, 65–91.
16. L. Kang, S. Luo, H. Huang, N. Ye, Z. Lin, J. Qin and C. Chen, J. Phys. Chem. C, 2013, 117, 25684–25692.
17. J. Arlt and M. Jansen, Z. Naturforsch., B: J. Chem. Sci., 1990, 45, 943–946.
18. B. Albert, J. Arlt, M. Jansen and H. Erhardt, J. Inorg. Gen. Chem., 1992, 607, 13–18.
19. X.-L. Chen, M. He, Y.-P. Xu, H.-Q. Li and Q.-Y. Tu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, i50–i51.
20. Y. P. Sun, Q. Z. Huang, L. Wu, M. He and X. L. Chen, J. Alloys Compd., 2006, 417, 13–17.
21. B. Aurivillius, Acta Chem. Scand., Ser. A, 1983, 37, 159.
22. G. Zou, L. Huang, N. Ye, C. Lin, W. Cheng and H. Huang, J. Am. Chem. Soc., 2013, 135, 18560–18566.
23. G. Lakshminarayana, J. A. Torres, T. C. Lin, I. V. Kityk and M. P. Hehlen, J. Alloys Compd., 2014, 601, 67–74.
24. W. Voigt, Ann. Phys., 1889, 38, 573.
25. A. Reuss, J. Appl. Math. Mech., 1929, 9, 49–58.
26. R. Hill, Proc. R. Soc. London, Ser. A, 1952, 65, 350–362.
27. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
28. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
29. D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569.
30. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
31. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
34. T. H. Fischer and J. Almlof, J. Phys. Chem., 1992, 96, 9768.
35. F. Ortmann, F. Bechstedt and W. G. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205101.
36. D. R. Hamann, M. SchlÃČÂijter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494–1497.
37. S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562.
38. V. Milman, K. Refson, S. J. Clark, C. J. Pickard, J. R. Yates, S.-P. Gao, P. J. Hasnip, M. I. J. Probert, A. Perlov and M. D. Segall, J. Mol. Struct.: THEOCHEM, 2010, 954, 22–35.
39. X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10337–10354.
40. E. B. Wilson, J. C. Decius and P. C. Cross, Molecular vibrations: the theory of infrared and Raman vibrational spectra, McGraw-Hill, New York, 1955.
41. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
42. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
43. S. Appalakondaiah, G. Vaitheeswaran, S. LebÃČÂĺgue, N. E. Christensen and A. Svane, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035105.
44. H. M. Ledbetter, J. Phys. Chem. Ref. Data, 1977, 6, 1181–1203.
45. S. F. Pugh, Philos. Mag., 1954, 45, 823–843.
46. V. Kanchana, G. Vaitheeswaran, A. Svane and A. Delin, J. Phys.: Condens. Matter, 2006, 18, 9615–9624.
47. I. R. Shein and A. L. Ivanovskii, J. Phys.: Condens. Matter, 2008, 20, 415218.
48. J. Haines, J. M. Léger and G. Bocquillon, Annu. Rev. Mater. Res., 2001, 31, 1–23.
49. A. M. Liquori, E. Giglio and L. Mazzarella, Il Nuovo Cimento B, 1971–1996, 55, 476–480.
50. E. S. Fisher and L. C. R. Alfred, Trans. Metall. Soc. AIME, 1968, 242, 1575–1586.
51. A. Bouhemadou, Braz. J. Phys., 2010, 40, 52–57.
52. M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, Oxford, Canada, 1998.
53. M. Bass, C. DeCusatis, J. Enoch, V. Lakshminarayanan, G. Li, C. MacDonald, V. Mahajan and E. V. Stryland, Handbook of Optics, MGH, Florida, 2009, 3rd edn, vol. 4.
54. W. Zhong, R. D. King-Smith and D. Vanderbilt, Phys. Rev. Lett., 1994, 72, 3618–3621.
55. P. Ghosez, X. Gonze, P. Lambin and J. P. Michenaud, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6765–6768.
56. G. Amritendu Roy, S. Mukherjee, R. Gupta, S. Auluck, R. Prasad and A. Garg, J. Phys.: Condens. Matter, 2011, 23, 325902.
57. M. Posternak, R. Resta and A. Baldereschi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 8911–8914.
58. S. Yip, Handbook Of Materials Modeling, Springer, The Netherlands, 2005, pp. 195–214.
59. P. Ravindran, R. Vidya, A. Kjekshus, H. FjellvÃČÂěg and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224412.
60. E. Kroumova, M. I. Aroyo, J. M. Perez-Mato, A. Kirov, C. Capillas, S. Ivantchev and H. Wondratschek, Phase Transitions, 2003, 76, 155–170.
61. J. F. Lin, J. Liu, C. Jacobs and V. B. Prakapenka, Am. Mineral., 2012, 97, 583–591.
62. N. Buzgar and A. I. Apopei, Analele Stiintifice ale Universitati Al. I. Cuza, Iasi Geologie, 2009, 55, 97–112.
63. J. Donald Beasley, Appl. Opt., 1994, 33, 1000–1003.
64. H. Wu, H. Yu, Z. Yang, J. Han, K. Wu and S. Pan, Journal of Materiomics, 2015, 1, 221–228.
65. M. A. Blanco, E. Francisco and V. LuaÃČÂśa, Comput. Phys. Commun., 2004, 158, 57–72.
66. A. Parveen and N. K. Gaur, Thermochim. Acta, 2013, 566, 203–210.
67. D. T. Morelli and G. A. Slack, High Thermal Conductivity Materials, ed. S. L. Shinde and J. S. Goela, Springer, New York, 2006, ch. 2, pp. 37–68.
68. J. Callaway and H. C. von Baeyer, Phys. Rev., 1960, 120, 1149–1154.

---