Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
From diffusive to ballistic Stefan–Boltzmann heat transport in thin non-crystalline films†
A.
Makris
,
T.
Haeger
,
R.
Heiderhoff
* and
T.
Riedl
Institute of Electronic Devices, University of Wuppertal, Rainer-Gruenter-Str. 21, 42119 Wuppertal, Germany. E-mail: heiderho@uni-wuppertal.de
First published on 3rd October 2016
Abstract
Today, different theoretical models exist to describe heat transport in ultra-thin films with a thickness approaching the phonon mean free path length. Due to the influence of parasitic effects, the experimental assessment of heat transport in these ultra-thin films with the required sensitivity is extremely challenging. In this work, the heat transport through thin non-crystalline metal-oxide films is studied using scanning near-field thermal microscopy, which allows to minimize parasitic thermal effects and therefore provides uttermost sensitivity even for the study of thermal transport in ultra-thin films. For the first time, we provide experimental evidence of enhanced out-of-plane heat dissipation in these ultra-thin metal-oxide films by ballistic thermal phonon transport according to the Stefan–Boltzmann-like heat transport model.
Introduction
In electrical insulators, phonons are the predominant species for heat transport. For bulk materials the heat flux![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) is classically described by the Fourier law,1 where in general T(
is classically described by the Fourier law,1 where in general T(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is a given temperature distribution and
) is a given temperature distribution and 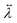 is the tensor of thermal conductivity:2
is the tensor of thermal conductivity:2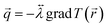 | (1) |
There are steady state as well as transient techniques within the space and time/frequency domain to analyze thermal transport.3–7 If the absorbed power in the sample is known, the thermal conductivity can be directly determined in steady state approaches. In the dynamic case, the density ρ as well as the specific heat c of the material must be considered. Heat flow is described by the general equation of heat conduction:8
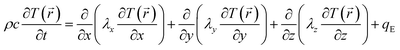 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) appears in this equation, the knowledge of the absolute temperature and the absorbed power is not required. To get access to the three-dimensional material property
) appears in this equation, the knowledge of the absolute temperature and the absorbed power is not required. To get access to the three-dimensional material property 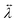 , directional heat transport investigations have been carried out using various experimental techniques.7
, directional heat transport investigations have been carried out using various experimental techniques.7
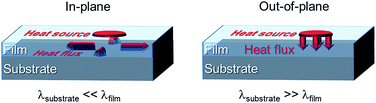
Furthermore, the heat flux strongly depends on the dimensions of the materials and is of growing general interest in the case of a shrinking device size and in thin film technology. Hence, films on substrates with either low or high thermal conductivity have been investigated in order to study in-plane or out-of-plane (also called cross-plane) heat flux (Fig. 1).7
While there is extensive experimental work on the in-plane heat transport in thin films down to film thicknesses of around 20 nm, it must be pointed out that out-of-plane transport is experimentally far less explored and studies are typically limited to film thicknesses larger than 100 nm.9–14 Within these works, a decrease of the thermal conductivity with decreasing film thickness dfilm from 2 μm (ref. 15) to 300 nm (ref. 16) has been found for dielectrics and semiconductors. On the contrary, we have found the thermal conductivity of an organic Alq3 thin film with dfilm down to 20 nm to be constant.17
For ultra-thin films with a film thickness below the phonon mean-free path Λ (i.e. dfilm < Λ), also referred to as Casimir limit,18 some further ambiguities exist. In some reports, these ultra-thin films are considered to be thermal insulators, where phonons are claimed to be trapped between the layer boundaries. Trapped phonons are not able to transport thermal energy.10 In addition the Fourier law is no longer valid in the case of heat source dimensions to values smaller than Λ, which can be hundreds of nanometers in crystalline materials at room temperature.19 A significant decrease in energy transport occurs even into bulk material at nanoscale heated regions compared with Fourier-law predictions due to quasi-ballistic thermal transport effects (quasi-ballistic: with and without scattered phonons). On the contrary could be demonstrated, that surface phonon polaritons excited by a laser beam dramatically enhance energy transfer between two surfaces at small gaps (30 nm) by measuring radiation heat transfer between a microsphere and a flat surface.20 An extremely enhanced heat flux by blackbody radiative transfer of energy from the heater can only be considered under extreme near-field conditions. Although experimental advances have enabled elucidation of heat transfer in gaps as small as 20 nm, quantitative analysis of enhanced radiative heat transfer in the extreme near-field (gaps less than 10 nm) have been carried out just very recently.21 By a similar token, theoretical work based on the Boltzmann transport equation (BTE) for films with dfilm < Λ (below the Casimir limit) considered heat transport to be ballistic and resulted in a description similar to that known from radiative heat transport according to the Stefan–Boltzmann law.22–24 As of yet, the experimental verification of this theory is missing.
In this paper, we study out-of-plane heat transport from a nanoscale heat source through ultra-thin non-crystalline metal-oxide films, e.g. Al2O3 and TiO2, with a thickness down to 4 nm by means of dynamic scanning near-field thermal microscopy (SThM). We have prepared our ultra-thin amorphous like films by atomic layer deposition (ALD), as it is known to allow for uttermost control of layer thickness, conformity, and homogeneity confirmed by former X-ray diffraction and transmission electron microscopy studies.25 For the first time, we provide experimental evidence that the out-of-plane heat transport in ultra-thin films is dominated by ballistic heat transport and can therefore be described by a Stefan–Boltzmann like model.
Experimental
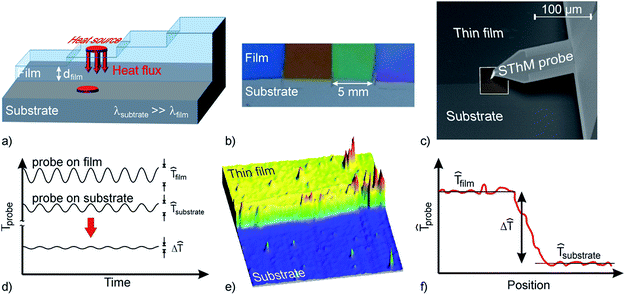
For the out-of-plane heat transport analysis we used silicon as substrate material with a relatively high thermal conductivity of 150 W (m−1 K−1). Non-crystalline Al2O3 and TiO2 films were prepared in a step-like matrix (Fig. 2), where all films exhibited a direct step from the film to the Si-substrate to directly assess the heat flux through the film for each film thickness as described below.The SThM in the present work is installed in the analysis chamber of an Environmental Scanning Electron Microscope (ESEM), thus our SThM measurements are carried out under vacuum (5 × 10−6 mbar).26 Effects of thermal transport due to convection or moisture related interfacial effects can therefore be excluded. The signal detection in our specific setup has been explained in detail elsewhere.27 Briefly, we applied a transient measurement technique within the frequency domain thus only the derivative of T(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , ω) in the swung-in state will be discussed in the following. A constant low force between SThM probe and sample was applied during these measurements to guarantee a constant resulting thermal contact resistance and in order to prevent mechanical influences/damages to the films. Further details can be found in the ESI.†
, ω) in the swung-in state will be discussed in the following. A constant low force between SThM probe and sample was applied during these measurements to guarantee a constant resulting thermal contact resistance and in order to prevent mechanical influences/damages to the films. Further details can be found in the ESI.†
The resistive thermal probe of the SThM is powered by an AC current I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) with angular frequency ω. As demonstrated earlier,28,29 the probe can be considered in far-field as a point like heat source and in close proximity as a line-shaped nanoscale heat source fulfilling the demands for high resolution near-field microscopy30 by generating a heat wave of frequency 2ω with cylindrical symmetry. This wave will diffuse into the substrate and is exponentially damped in the radial direction. According to Carslaw and Jaeger, the resulting amplitude of the temperature oscillations
sin(ωt) with angular frequency ω. As demonstrated earlier,28,29 the probe can be considered in far-field as a point like heat source and in close proximity as a line-shaped nanoscale heat source fulfilling the demands for high resolution near-field microscopy30 by generating a heat wave of frequency 2ω with cylindrical symmetry. This wave will diffuse into the substrate and is exponentially damped in the radial direction. According to Carslaw and Jaeger, the resulting amplitude of the temperature oscillations ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (r) in the sample at a distance r from the heat source depends on the amplitude of the generated heat power
(r) in the sample at a distance r from the heat source depends on the amplitude of the generated heat power ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) per unit length flowing into the sample and the thermal conductivity λ as:31
per unit length flowing into the sample and the thermal conductivity λ as:31
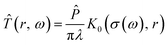 | (3) |
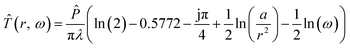 | (4) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) constant and measuring the resulting 3ω component of the voltage drop across the SThM probe Û3ω at two different frequencies ω1 and ω2.
constant and measuring the resulting 3ω component of the voltage drop across the SThM probe Û3ω at two different frequencies ω1 and ω2.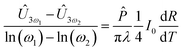 | (5) |
The term 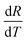 represents the differential thermal coefficient of the probe.
represents the differential thermal coefficient of the probe.
Unfortunately, in SThM ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) depends on the thermal properties (e.g. thermal conductivity)27,33 of both the sample and the probe design. This means that factors like heat dissipation into the supply lines of the thermal probe etc. must also be considered. Furthermore, the heat transfer mechanisms between the probe and the sample must be calibrated. The tip-sample thermal contact resistance can be affected by heat conduction and thermal radiation near the contact region as discussed in detail by Wilson et al.33 in order to perform thermal conductivity measurements in the 3ω mode using a Wollaston wire. This renders the application of the conventional 3ω method difficult for the quantitative determination of thermal conductivity in dependence on the film thickness using VITA-SThM probes. Thus, in order to perform measurements of out-of-plane heat transport from a nanoscale heat source through thin films, we determine the difference of the amplitude of the temperature oscillations of the probe on the film and on the substrate Δ
depends on the thermal properties (e.g. thermal conductivity)27,33 of both the sample and the probe design. This means that factors like heat dissipation into the supply lines of the thermal probe etc. must also be considered. Furthermore, the heat transfer mechanisms between the probe and the sample must be calibrated. The tip-sample thermal contact resistance can be affected by heat conduction and thermal radiation near the contact region as discussed in detail by Wilson et al.33 in order to perform thermal conductivity measurements in the 3ω mode using a Wollaston wire. This renders the application of the conventional 3ω method difficult for the quantitative determination of thermal conductivity in dependence on the film thickness using VITA-SThM probes. Thus, in order to perform measurements of out-of-plane heat transport from a nanoscale heat source through thin films, we determine the difference of the amplitude of the temperature oscillations of the probe on the film and on the substrate Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) film −
film − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) substrate as illustrated in Fig. 2.
substrate as illustrated in Fig. 2.
Out-of-plane heat dissipation in thin non-crystalline metal-oxide films
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) substrate is relatively small (eqn (3)). If the amplitude of electrical power supplied to the probe is kept constant and if only diffusive heat transport in a film with low thermal conductivity is assumed, the temperature oscillation of the probe on top of the film
substrate is relatively small (eqn (3)). If the amplitude of electrical power supplied to the probe is kept constant and if only diffusive heat transport in a film with low thermal conductivity is assumed, the temperature oscillation of the probe on top of the film ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) film is larger than
film is larger than ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) substrate. In the limit where the thermal conductivity of a film would trend to zero, no heat would diffuse into the film. In this case, the generated joule heat would exclusively be transported away from the SThM probe via its supply lines.
substrate. In the limit where the thermal conductivity of a film would trend to zero, no heat would diffuse into the film. In this case, the generated joule heat would exclusively be transported away from the SThM probe via its supply lines.
An exemplary result of Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) vs. dfilm for Al2O3 films is shown in Fig. 3. The uncertainties of temperature and film thickness measurements (for films below 30 nm) are ±0.5 K and ±dfilm 10% nm respectively.
vs. dfilm for Al2O3 films is shown in Fig. 3. The uncertainties of temperature and film thickness measurements (for films below 30 nm) are ±0.5 K and ±dfilm 10% nm respectively.
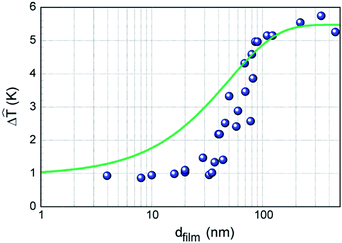 | ||
Fig. 3 Comparison of measured and calculated Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) of Al2O3 films in dependence on the film thickness. The calculated curve is a result of eqn (8) with of Al2O3 films in dependence on the film thickness. The calculated curve is a result of eqn (8) with ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) contact = 1 K. contact = 1 K. | ||
To understand the dependence of Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) vs. dfilm, different regimes of thermal transport must be considered. For dfilm > 100 nm, Δ
vs. dfilm, different regimes of thermal transport must be considered. For dfilm > 100 nm, Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) saturates at a level Δ
saturates at a level Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) max, which indicates that in this regime the Al2O3 layer can be considered as bulk material. Thus, heat transport is diffusive and follows the Fourier law.2 Using the 3ω-technique here (see eqn (5)), we determined the thermal conductivity to λAl2O3 = 0.8 W m−1 K−1 on an average film thickness of 338 nm ± 5 nm using the line source model of the probe. This value is in agreement with previous reports for ALD grown non-crystalline Al2O3 layers.34 The advantages of this 3ω-technique on thermal conductivity analyses of amorphous solids are discussed in detail elsewhere.35 Towards thinner films (dfilm < 100 nm), Δ
max, which indicates that in this regime the Al2O3 layer can be considered as bulk material. Thus, heat transport is diffusive and follows the Fourier law.2 Using the 3ω-technique here (see eqn (5)), we determined the thermal conductivity to λAl2O3 = 0.8 W m−1 K−1 on an average film thickness of 338 nm ± 5 nm using the line source model of the probe. This value is in agreement with previous reports for ALD grown non-crystalline Al2O3 layers.34 The advantages of this 3ω-technique on thermal conductivity analyses of amorphous solids are discussed in detail elsewhere.35 Towards thinner films (dfilm < 100 nm), Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) decays and finally levels off for dfilm < 30 nm.
decays and finally levels off for dfilm < 30 nm.
Lee and Cahill16 used a one-dimensional description to model the out-of-plane heat flow through a film with thicknesses dfilm far less than the thermal penetration depth and much smaller than the width of the heater/thermometer w. If the thermal conductivity of the film is substantially smaller than that of the substrate, this model yields a linear relation of Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and dfilm as follows:
and dfilm as follows:
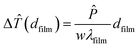 | (6) |
A frequency independent offset of a temperature oscillation amplitude Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is added to the thermal 3ω response of the substrate. Note, as Δ
is added to the thermal 3ω response of the substrate. Note, as Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) scales with dfilm/w, the measurement of ultra-thin films with microscopic probes (dfilm ≪ w) becomes very challenging. This might be the reason why the out-of-plane heat transport is less explored for ultra-thin films using macroscopic probes (with a large w).9,10 On the other hand, in the case of a SThM the ultra-small w on the order of 50 nm (ref. 36) should be perfectly suited to assess thermal transport in ultra-thin films.
scales with dfilm/w, the measurement of ultra-thin films with microscopic probes (dfilm ≪ w) becomes very challenging. This might be the reason why the out-of-plane heat transport is less explored for ultra-thin films using macroscopic probes (with a large w).9,10 On the other hand, in the case of a SThM the ultra-small w on the order of 50 nm (ref. 36) should be perfectly suited to assess thermal transport in ultra-thin films.
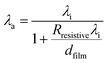
It is not directly obvious from eqn (6) that ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) film would become independent of dfilm for ultra-thin films (dfilm < 30 nm in the example shown in Fig. 3). According to eqn (6), the region of constant Δ
film would become independent of dfilm for ultra-thin films (dfilm < 30 nm in the example shown in Fig. 3). According to eqn (6), the region of constant Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) could be indicative of a thickness dependent thermal conductivity: λfilm ∝ dfilm. This assumption would lead to the conclusion, that ultra-thin films become thermal insulators, as claimed by Lee and Cahill.16 Later Lee and Cahill revised this model by introducing a thermal contact resistance (Rresistive) to be responsible for the observation of
could be indicative of a thickness dependent thermal conductivity: λfilm ∝ dfilm. This assumption would lead to the conclusion, that ultra-thin films become thermal insulators, as claimed by Lee and Cahill.16 Later Lee and Cahill revised this model by introducing a thermal contact resistance (Rresistive) to be responsible for the observation of ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) film becoming constant.16 They assumed an apparent thermal conductivity λa which depends on the film thickness dfilm, the thermal resistance Rresistive and the intrinsic thermal conductivity λi:
film becoming constant.16 They assumed an apparent thermal conductivity λa which depends on the film thickness dfilm, the thermal resistance Rresistive and the intrinsic thermal conductivity λi:
 | (7) |
As we will discuss below this assumption does not allow us to explain our experimental results shown in Fig. 3.
The transition from thin films to bulk materials (including transition from one-dimensional heat transport across the film to three-dimensional heat transport in bulk material) has been described by the introduction of a saturating exponential function,17 that for a given frequency ω finally leads to:
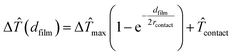 | (8) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) max is the difference of temperature oscillation (
max is the difference of temperature oscillation (![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) film −
film − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) substrate)max found in the limit of thick films, rcontact is the radius of the effective contact area of the probe, and
substrate)max found in the limit of thick films, rcontact is the radius of the effective contact area of the probe, and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) contact is the temperature offset caused by a constant thermal contact resistance, as rcontact and the thermal contact resistance are constant for a certain range of sample thermal conductivity33 which is typically neglected in eqn (6). Note, aside from
contact is the temperature offset caused by a constant thermal contact resistance, as rcontact and the thermal contact resistance are constant for a certain range of sample thermal conductivity33 which is typically neglected in eqn (6). Note, aside from ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) contact, in the limit of ultra-thin films (one-dimensional heat transport) eqn (8) becomes identical to eqn (6) (assuming w = 2rcontact and
contact, in the limit of ultra-thin films (one-dimensional heat transport) eqn (8) becomes identical to eqn (6) (assuming w = 2rcontact and 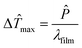 as frequency independent). As the radius of an effective contact area of the probe is known to be on the order of 50 nm and Δ
as frequency independent). As the radius of an effective contact area of the probe is known to be on the order of 50 nm and Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) max was measured to be approximately 5.5 K in the measurement shown in Fig. 3, Δ
max was measured to be approximately 5.5 K in the measurement shown in Fig. 3, Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (dfilm) can be derived from eqn (8). Note,
(dfilm) can be derived from eqn (8). Note, 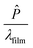 is assumed to be constant and we set
is assumed to be constant and we set ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) contact = 1 K. Obviously, this calculation only fits to the measurement for film thicknesses larger than 80 nm (a similar treatment for TiO2 thin films can be found in the ESI†). The deviation of calculation and measurement indicates a substantially higher heat flux for thinner films (dfilm < 80 nm) than expected by eqn (8). We want to stress that the previous assumption of a thickness dependent thermal conductivity (λfilm ∝ dfilm) as well as a decrease of the effective λfilm calculated recently by a variational approach to solving the BTE24 does not allow for a better fit to the data, but this assumption would rather increase the deviation.
contact = 1 K. Obviously, this calculation only fits to the measurement for film thicknesses larger than 80 nm (a similar treatment for TiO2 thin films can be found in the ESI†). The deviation of calculation and measurement indicates a substantially higher heat flux for thinner films (dfilm < 80 nm) than expected by eqn (8). We want to stress that the previous assumption of a thickness dependent thermal conductivity (λfilm ∝ dfilm) as well as a decrease of the effective λfilm calculated recently by a variational approach to solving the BTE24 does not allow for a better fit to the data, but this assumption would rather increase the deviation.
Note, phonon trapping between the layer boundaries affecting the thermal conductivity at a film thickness on the order of dfilm = 30 nm as well as a decrease of the effective λfilm is not very likely in our samples, as the phonon mean free path is estimated to be approximately two orders of magnitude less for non-crystalline Al2O3 (ΛAl2O3 = 0.47 nm) and ΛAl2O3 = 3.5 nm for sintered polycrystalline Al2O3.37
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) towards ultra-thin films and for the elevated higher heat flow in the region below 80 nm could be related to a constant thermal contact resistance and a significant contribution of Stefan–Boltzmann like heat transport of phonons (which cannot be described by the classical eqn (3)–(8) for diffusive heat transport). It has to be noted, that our measurements are carried out under vacuum conditions, thus heat transport by convection and other parasitic mechanisms related to air and moisture are negligible. Furthermore, effects of radiative blackbody heat transfer are only important in the extreme near-field at a distance far less than 10 nm (ref. 21) and for elevated probe temperatures significantly above those used in our experiment (<400 K).
towards ultra-thin films and for the elevated higher heat flow in the region below 80 nm could be related to a constant thermal contact resistance and a significant contribution of Stefan–Boltzmann like heat transport of phonons (which cannot be described by the classical eqn (3)–(8) for diffusive heat transport). It has to be noted, that our measurements are carried out under vacuum conditions, thus heat transport by convection and other parasitic mechanisms related to air and moisture are negligible. Furthermore, effects of radiative blackbody heat transfer are only important in the extreme near-field at a distance far less than 10 nm (ref. 21) and for elevated probe temperatures significantly above those used in our experiment (<400 K).
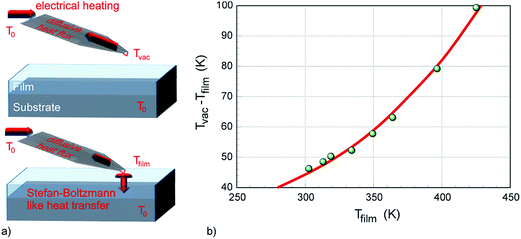
In order to prove Stefan–Boltzmann like heat transfer of phonons the SThM probe temperatures were measured at different applied electrical powers Pelectr to heat the probe. The temperatures were detected under steady state conditions for the SThM probe in vacuum (Tvac) and in contact on a 10 nm thick film (Tfilm), respectively (Fig. 4a). This thickness was used to avoid a thermal flux due to blackbody radiative heat transport (for gaps less than 10 nm), and to guarantee one dimensional heat transport across the film, as well as to keep contributions due to diffusive heat transport (in case of TiO2 for dfilm > 17 nm) negligible.
Thereby, the heat dissipated into the supply lines of the thermal probe can be taken into consideration as the same electrical power Pelectr is supplied to the SThM probe in vacuum and when in contact with the film (more details are available in the ESI†). At moderate temperatures the thermal capacity of the supply line of the thermal probe Csuppl is temperature independent and the radiation heat transfer between our probe and chamber walls is negligible (see ESI†). Finally we derive:
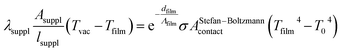 | (9) |
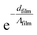 ).22AStefan–Boltzmanncontact is the effective contact area for ballistic heat transport. σ is the Stefan–Boltzmann constant for phonons, which can be related to the specific heat,31 the temperature, and the velocities of sound,38 which depends on the pressure.39 Thus, as described before in the “Experimental” section, the leading force of the probe was kept as low as possible and moderate SThM temperatures were used.
).22AStefan–Boltzmanncontact is the effective contact area for ballistic heat transport. σ is the Stefan–Boltzmann constant for phonons, which can be related to the specific heat,31 the temperature, and the velocities of sound,38 which depends on the pressure.39 Thus, as described before in the “Experimental” section, the leading force of the probe was kept as low as possible and moderate SThM temperatures were used.
Stefan–Boltzmann like heat transport of phonons is becoming more dominant with decreasing film thickness according to the calculations presented in the ESI.† To prove the validity of this Stefan–Boltzmann model for the heat transport in our ultra-thin films we measured Tfilm at varied electrical heating powers Pelectr, applied to the thermal probe (see Fig. 4b). As can be concluded from the graph, which was reproducibly obtained on different scan-areas for an Al2O3 film with dfilm = 10 nm, there is an excellent fit of (Tvac − Tfilm) ∼ Tfilm4. A temperature offset of the SThM probe in vacuum is related to the laser heating of the deflection method for obtaining the topography. In this case the scattering of the measured data is attributed to different scan-areas of our SThM probe on the film. This agreement, for the first time provides clear experimental evidence that the out-of-plane heat transport mechanism from a nanoscale heat source in ultra-thin films is dominated by ballistic heat transport of phonons and can be described by a Stefan–Boltzmann like model. In the discussion of Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) vs. dfilm (Fig. 3), the regime of ultra-thin films is therefore dominated by Stefan–Boltzmann like heat transport. It should be noted that the contribution of ballistic heat transport is dominant even when the probability of Stefan–Boltzmann like transport is relatively small. The
vs. dfilm (Fig. 3), the regime of ultra-thin films is therefore dominated by Stefan–Boltzmann like heat transport. It should be noted that the contribution of ballistic heat transport is dominant even when the probability of Stefan–Boltzmann like transport is relatively small. The ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) contact found in this case is associated with ballistic heat transport through AStefan–Boltzmanncontact. With increasing film thickness, the contribution of ballistic transport decreases exponentially. This will finally lead to a significant increase of Δ
contact found in this case is associated with ballistic heat transport through AStefan–Boltzmanncontact. With increasing film thickness, the contribution of ballistic transport decreases exponentially. This will finally lead to a significant increase of Δ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) >
> ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) contact with increasing film thickness (>30 nm) as observed in our previous measurements (Fig. 3).
contact with increasing film thickness (>30 nm) as observed in our previous measurements (Fig. 3).
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) contact, to the regime where heat transport through the thin film will become increasingly diffusive (Fig. S3†). The film thickness for which the contribution of diffusive and ballistic thermal transport is equal can be determined to be dfilm = 26 nm in the case of Al2O3 and dfilm = 17 nm for TiO2.
contact, to the regime where heat transport through the thin film will become increasingly diffusive (Fig. S3†). The film thickness for which the contribution of diffusive and ballistic thermal transport is equal can be determined to be dfilm = 26 nm in the case of Al2O3 and dfilm = 17 nm for TiO2.
In this context, the contribution of various phonon modes must be taken in to account in the Stefan–Boltzmann like heat transfer, as already discussed especially for amorphous materials.40 Note, in our case is dfilm ≫ Λfilm. Consequently we considered the non-crystalline films with dfilm > 4 nm as bulk materials. Hence, in comparison to acoustic phonons the contribution of optical phonons to the thermal transport is negligible at room temperature.41 Finally, it should be noted that optical phonons, which are usually neglected in thermal conduction for their relatively small group velocities compared with acoustic phonons, can significantly enhance heat transport at room temperature in extremely thin films (dfilm < Λfilm).42
At low temperatures and in isotropic condensed matter, σ was already calculated by Swartz and Pohl38 in studies of thermal boundary resistances and is given by:
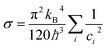 | (10) |
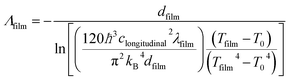 | (11) |
Λ
film has been determined to be 0.63 nm and 0.43 nm at longitudinal sound velocities clongitudinal of 8700 m s−1 (ref. 44) and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 m s−1 (ref. 45) for Al2O3 and TiO2 respectively, in the limit Tfilm → T0. The values for Λfilm of Al2O3 and TiO2 are comparable to that found in literature of 0.47–3.5 nm for Al2O3 (ref. 37) and of 0.4–1 nm for TiO2.46
375 m s−1 (ref. 45) for Al2O3 and TiO2 respectively, in the limit Tfilm → T0. The values for Λfilm of Al2O3 and TiO2 are comparable to that found in literature of 0.47–3.5 nm for Al2O3 (ref. 37) and of 0.4–1 nm for TiO2.46
Conclusions
In summary, we performed out-of-plane heat transport measurements of a nanoscale heat source through thin non-crystalline Al2O3 and TiO2 films for thicknesses from 450 nm down to 4 nm by use of scanning nearfield thermal microscopy (SThM). No change of the thermal conductivity and a pure diffusive heat transport were found for Al2O3 films with a thickness larger than 80 nm. At decreasing film thicknesses a significant enhancement of heat transport was detected, which could not be explained by diffusive thermal transport alone. As we have clearly evidenced for the first time, in this regime heat dissipation has a significant contribution of ballistic Stefan–Boltzmann like heat transport of phonons. From the transition of dominating ballistic out-of-plane heat transport to increasing probability of diffusive mechanism the mean-free path of longitudinal acoustic phonons have been estimated to be 0.63 nm and 0.43 nm for Al2O3 and TiO2 respectively.These results will significantly influence thin film technology and the thermal management of modern devices, as heat dissipation is at this time the key limiting factor for power electronics, including high-power RF devices as well as in high-power laser diodes and high-brightness light-emitting diodes (LEDs). In contradiction to former estimations, that ultra-thin films become thermal insulators, an enhanced heat dissipation by ballistic phonon transport occurs with decreasing film thicknesses even far above the Casimir limit.
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG) under the project number HE2698/7-1.References
- J. B. J. Fourier, Theorié analytique de la chaleur, Chez Firmin Didot, père et fils, 1822 Search PubMed.
- A. Freeman, Theory of heat, Cambridge University Press, London, 1878 Search PubMed.
- R. Heiderhoff, A. Makris and T. Riedl, Mater. Sci. Semicond. Process., 2016, 43, 163–176 CrossRef CAS.
- Z. L. Wu, M. Reichling, X. Hu and K. Balasubramanian, Appl. Opt., 1993, 32, 5660–5665 CrossRef CAS PubMed.
- D. M. Price, M. Reading, A. Hammiche and H. M. Pollock, Int. J. Pharm., 1999, 192, 85–96 CrossRef CAS PubMed.
- B. E. Belkerk, M. A. Soussou, M. Carette, M. A. Djouadi and Y. Scudeller, J. Phys. D: Appl. Phys., 2012, 45, 295303 CrossRef.
- D. G. Cahill, H. E. Fischer, T. Klitsner, E. T. Swartz and R. O. Pohl, J. Vac. Sci. Technol., A, 1989, 7, 1259–1266 CAS.
- J. H. Lienhard IV and J. H. Lienhard V, A Heat Transfer Textbook, Phlogiston Press, Cambridge, Massachusetts, U.S.A., 4th edn, 2015 Search PubMed.
- A. M. Marconnet, M. Asheghi and K. E. Goodson, J. Heat Transfer, 2013, 135, 061601 CrossRef.
- C. J. Gomes, M. Madrid, J. V. Goicochea and C. H. Amon, J. Heat Transfer, 2006, 128, 1114–1121 CrossRef CAS.
- C. Jeong, S. Datta and M. Lundstrom, J. Appl. Phys., 2012, 111, 1–6 CrossRef.
- K. E. Goodson and Y. S. Ju, Annu. Rev. Mater. Sci., 1999, 29, 261–293 CrossRef CAS.
- D. G. Cahill, K. Goodson and A. Majumdar, J. Heat Transfer, 2002, 124, 223–241 CrossRef CAS.
- G. Chen, IEEE Trans. Compon. Packag. Technol., 2006, 29, 238–246 CrossRef CAS.
- J. S. Reparaz, E. Chavez-Angel, M. R. Wagner, B. Graczykowski, J. Gomis-Bresco, F. Alzina and C. M. S. Torres, Rev. Sci. Instrum., 2014, 85, 034901 CrossRef CAS PubMed.
- S.-M. Lee and D. G. Cahill, J. Appl. Phys., 1997, 81, 2590–2595 CrossRef CAS.
- R. Heiderhoff, H. Li and T. Riedl, Microelectron. Reliab., 2013, 53, 1413–1417 CrossRef CAS.
- H. B. G. Casimir, Physica, 1938, 6, 495–500 CrossRef.
- M. E. Siemens, Q. Li, R. Yang, K. A. Nelson, E. H. Anderson, M. M. Murnane and H. C. Kapteyn, Nat. Mater., 2010, 9, 26–30 CrossRef CAS PubMed.
- S. Shen, A. Narayanaswamy and G. Chen, Nano Lett., 2009, 9, 2909–2913 CrossRef CAS PubMed.
- K. Kim, B. Song, V. Fernández-Hurtado, W. Lee, W. Jeong, L. Cui, D. Thompson, J. Feist, M. T. H. Reid, F. J. García-Vidal, J. C. Cuevas, E. Meyhofer and P. Reddy, Nature, 2015, 528, 387–391 CrossRef CAS PubMed.
- A. Majumdar, J. Heat Transfer, 1993, 115, 7–16 CrossRef.
- P. B. Allen, arXiv:1308.2890, 2013, pp. 1–5.
- V. Chiloyan, L. Zeng, S. Huberman, A. A. Maznev, K. A. Nelson and G. Chen, Phys. Rev. B, 2016, 93, 155201 CrossRef.
- J. Meyer, P. Görrn, F. Bertram, S. Hamwi, T. Winkler, H.-H. Johannes, T. Weimann, P. Hinze, T. Riedl and W. Kowalsky, Adv. Mater., 2009, 21, 1845–1849 CrossRef CAS.
- R. Heiderhoff, in 2012 19th IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits, IEEE, 2012, pp. 1–4 Search PubMed.
- A. Altes, R. Heiderhoff and L. J. Balk, J. Phys. D: Appl. Phys., 2004, 37, 952–963 CrossRef CAS.
- A. Altes, R. Tilgner, M. Reissner, G. Steckert and G. Neumann, Microelectron. Reliab., 2008, 48, 1273–1278 CrossRef.
- A.-K. Geinzer, Thermoelastic analysis of devices by scanning near-field thermal microscopy techniques, University of Wuppertal, 2010 Search PubMed.
- R. Heiderhoff and L. J. Balk, in Handbook of Nanoscopy, ed. G. Van Tendeloo, D. Van Dyck and S. J. Pennycook, Wiley-VCH Verlag & Co. KGaA, Weinheim, Germany, 2012, vol. 1, pp. 499–538 Search PubMed.
- D. G. Cahill, Rev. Sci. Instrum., 1990, 61, 802–808 CrossRef CAS.
- G. B. M. Fiege, A. Altes, R. Heiderhoff and L. J. Balk, J. Phys. D: Appl. Phys., 1999, 13, L13–L17 CrossRef.
- A. A. Wilson, M. Muñoz Rojo, B. Abad, J. A. Perez, J. Maiz, J. Schomacker, M. Martín-Gonzalez, D.-A. Borca-Tasciuc and T. Borca-Tasciuc, Nanoscale, 2015, 7, 15404–15412 RSC.
- A. Cappella, J.-L. Battaglia, V. Schick, A. Kusiak, A. Lamperti, C. Wiemer and B. Hay, Adv. Eng. Mater., 2013, 15, 1046–1050 CrossRef CAS.
- D. G. Cahill and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 4067–4073 CrossRef CAS.
- P. Tovee, M. Pumarol, D. Zeze, K. Kjoller and O. Kolosov, J. Appl. Phys., 2012, 112, 114317 CrossRef.
- N. Oka, R. Arisawa, A. Miyamura, Y. Sato, T. Yagi, N. Taketoshi, T. Baba and Y. Shigesato, Thin Solid Films, 2010, 518, 3119–3121 CrossRef CAS.
- E. T. Swartz and R. O. Pohl, Rev. Mod. Phys., 1989, 61, 606–668 CrossRef.
- L. Zhang and A. Chopelas, Phys. Earth Planet. Inter., 1994, 87, 77–83 CrossRef CAS.
- F. F. Freeman and A. C. Anderson, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5684–5690 CrossRef.
- Z. Tian, K. Esfarjani, J. Shiomi, A. S. Henry, G. Chen, Z. Tian, K. Esfarjani, J. Shiomi, A. S. Henry and G. Chen, Appl. Phys. Lett., 2011, 99, 1–3 Search PubMed.
- D. Xiong, Y. Zhang and H. Zhao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052128 CrossRef PubMed.
- A. Mittal and S. Mazumder, J. Heat Transfer, 2010, 132, 52402 CrossRef.
- C. S. Gorham, J. T. Gaskins, G. N. Parsons, M. D. Losego and P. E. Hopkins, Appl. Phys. Lett., 2014, 104, 253107 CrossRef.
- M. A. Caravaca, R. A. Casali, J. C. Miño, L. E. Kosteski and R. B. D. Ambra, e-Proceedings Online Workshop: SimNDT 2010, 2010 Search PubMed.
- C. B. Carter and M. G. Norton, in Ceramic Materials, ed. C. B. Carter and M. G. Norton, Springer New York, New York, NY, 2013, pp. 641–657 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of thin film preparation, scanning near-field thermal microscopy, Stefan–Boltzmann like heat transfer. See DOI: 10.1039/c6ra20407d |
| This journal is © The Royal Society of Chemistry 2016 |