Difference in pi-electron delocalization for monosubstituted olefinic and aromatic systems

Abstract

Application of HOMA (Harmonic Oscillator Model of Aromaticity) to a series of monosubstituted derivatives of cyclohexa-1,3-diene (olefinic) and benzene (aromatic) revealed an increase of the pi-electron delocalization in olefinic systems and a decrease in the case of aromatic systems (in comparison to unsubstituted species). Due to the nature of the system to which the substituents are attached, the range of changes of the electron donating/attracting (ED/EA) properties of the substituents may be as large as 30% of the total variation of ED/EA properties for all substituents considered.

---

Introduction

The chemical and physicochemical properties of olefinic pi-electron systems differ dramatically from those observed in the aromatic ones. The difference lies in their response to perturbation – either external, like attack of chemical reagents, or internal – like substituent effects. Olefinic systems easily undergo chemical reactions with a total destruction of the pi-electron structure (addition reactions), whereas the aromatic ones tend to react maintaining the pi-electron structure (substitution reactions).¹ It was found for monosubstituted benzene derivatives that substituent effect (SE) on aromaticity of the ring is observed in a limited way,^2,3 whereas it is not the case for mono- and disubstituted benzene dications.⁴ In 1,4-disubstituted 1,3,5,7-cyclooctatetraene (COT) pi-electron delocalization depends strongly on the kind of substituent and position of the substitution.⁵ Pi-electron delocalization estimated for the sequence of bonds between C1 and C4 carbon atoms is significant, and much smaller for 1,3- and 1,5-disubstituted COT systems. Similarly, in unsaturated cyclic system, fulvene,⁶ exocyclic substitution leads to dramatic changes in pi-delocalization of the ring in a range of HOMA⁷ between −0.5 and 0.7. Additionally, simple comparison of the HMO⁸ atom–atom polarizabilities between corresponding atoms in benzene and buta-1,3-diene shows that the interactions in the olefinic pi-electron systems are 2–5 times greater.⁷ A new perspective may be achieved by application of novel quantum chemical modelling of SEs and pi-electron delocalization. The charge of substituent active region (cSAR) approach allows to describe the electron attracting or donating (EA or ED) property of the substituent X. cSAR(X) is defined as a sum of atomic charges at the substituent and the ipso carbon atom,⁹ and its values correlate well with substituent constants.^10,11 The aromaticity index HOMA (Harmonic Oscillator Model of Aromaticity)⁷ is used to describe level of pi-electron delocalization in appropriate fragments of molecules.¹²

The purpose of this paper is the comparison of the substituent effect acting in cyclohexa-1,3-diene (olefinic) and benzene (aromatic) systems, both represented by their monosubstituted derivatives. The differences are discussed from the viewpoint of classical and reverse substituent effects.⁸ All objects of this study can be expressed as X–R, where R denotes transmitting moiety: cyclohexa-1,3-diene (CHD) or phenyl (Ph) ring (Scheme 1). The B3LYP/6-311++G** method was used for all calculations as the one which was proven to give fine results.¹³ The vibrational frequencies were calculated at the same level of theory to confirm that all calculated structures correspond to the minima on potential energy surface.

Scheme 1 Substituted derivatives of cyclohexa-1,3-diene (CHD): 1-X–CHD and 2-X–CHD (a) and benzene: X–Ph (b); X = NMe₂, NH₂, OH, OMe, CH₃, H, F, Cl, CF₃, CN, CHO, COMe, CONH₂, COOH, NO₂, NO.

The question to be asked here is what kind of differences are observed while olefinic and aromatic systems are subject of the SE.

Classical substituent effect

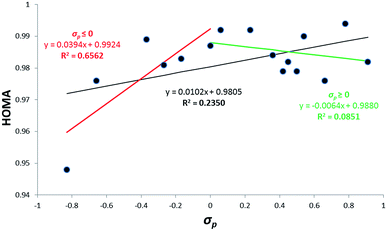
Classical Hammett-like approaches relate EA/ED properties of the substituents X to the properties of a reaction site Y¹⁴ or of the transmitting moiety R¹⁵ in systems like X–R–Y. Traditionally, as the SE characteristics the Hammett's substituent constants have been used. In this report the cSAR(X) characteristics also is applied. Dependences of HOMA on substituent constants for 1-X–CHD and X–Ph are presented in Fig. 1 and 2.

Fig. 1 Dependence of HOMA on substituent constants, σ_p, for 1-X–cyclohexa-1,3-dienes.

Fig. 2 Dependence of HOMA on substituent constants, σ_p, for mono-substituted benzene derivatives.

The relationship shown in Fig. 1 is very characteristic. Delocalization of pi-electrons estimated by HOMA values (obtained for the butadiene unit of the molecule) increases with an increasing of EA/ED strength, i.e. with an increase of the absolute value of the substituent constants. The obtained HOMA value ranges for EA substituents are ∼0.4 and for ED ones ∼0.3. The range of HOMA index variation for 2-X–CHD derivatives is also substantial, Δ = 0.154. These results are much higher than that observed for the benzene derivatives with Δ = 0.046 and indicate that the olefinic systems are much more sensitive to perturbation than benzene derivatives. The dependence of HOMA values on substituent constants for 2-X–CHD series is not conclusive, it presents a rather chaotic set of points. The shape of the dependence observed in Fig. 1 may be qualitatively interpreted by means of using resonance structure description, shown in Scheme 2, where D and A stand for electron donating or attracting substituent, respectively. The stronger D/A property of the substituent the greater contribution of the excited structure and hence greater delocalization of pi-electrons.

Scheme 2 The resonance structures of CHD mono-1-substituted by electron accepting (A) or electron donating (D) groups.

The dependence of HOMA on substituent constants for benzene derivatives, shown in Fig. 2, is substantially different from that for 1-X–CHD.

Despite of a low precision of the regression lines, it may be stated that the picture is opposite to that for 1-X–CHD: an increase of EA/ED strength is associated with a decrease of aromaticity. The reason for this difference may be explained also by means of resonance structures (as shown in Scheme 3). Substituents, either ED or EA, affect full delocalization of the ring by introducing resonance structures with localized double bonds, and hence decreasing aromaticity of the ring.

Scheme 3 The resonance structures of benzene derivatives mono-substituted by electron accepting (A) or electron donating (D) groups.

Reverse substituent effect

This is known from the very beginning, that substituent constant for NO₂ group in para-position estimated from acid–base equilibrium constants of benzoic acids (classical Hammett's σ) differ substantially from that obtained from phenol acid–base equilibrium; the values are 0.778 and 1.227, respectively.¹⁶ Application of cSAR approach allows to estimate charge in the substituent active region of a given substituent X, cSAR(X). The more negative value of cSAR(X) the more EA power of the substituent, and vice versa for ED substituents, the more ED substituent the greater cSAR(X) value.^8,10 It should be noted that for the studied systems cSAR(X) is well correlated with the Hammett σ as presented by the data in Table 1.

Table 1 Regressions of cSAR(X) on σ constant: cSAR(X) = a × σ + b

Series	a	b	R ^2
1-X–CHD	−0.263	0.010	0.906
2-X–CHD	−0.222	−0.057	0.862
X–Ph	−0.244	−0.015	0.901

---

Therefore, the obtained results confirm the statement that cSAR(X) values are reliable characteristics of SE. This allows us to use them as a measure describing how the pi-electron moieties studied in this paper affect the EA/ED properties of substituents. Table 2 presents several values of cSAR(X) in dependence on the kind of the moiety (R).

Table 2 cSAR(X) values for selected substituents in 1-X–CHD, 2-X–CHD and X–Ph derivatives; Δ is a range of variation cSAR(X) values

X	cSAR(X)			Δ
	1-X–CHD	2-X–CHD	X–Ph
NO	−0.207	−0.234	−0.190	0.044
COOH	−0.174	−0.217	−0.186	0.043
F	0.090	0.016	0.055	0.074
H	0.037	−0.033	0.000	0.070
OH	0.141	0.072	0.105	0.069
Me	0.047	−0.031	0.007	0.078
NH2	0.167	0.064	0.131	0.103
Δ	0.374	0.306	0.321

---

In all three cases gathered in Table 2 substituents are attached to pi-electron hydrocarbons. Therefore, the differences between cSAR(X) values express changes in the impact of those pi-electron structures on the EA/ED properties of the substituents. These differences illustrate the ability of the hydrocarbon moieties to accept or pull out the charge from the substituent. The difference Δ for cSAR(X) of a given substituent may be as large as 0.103 (for NH₂) which may be compared with Δ for cSAR(X) between most donating and most attracting substituents in series, that are in the range between 0.306 and 0.374. This means that changes in EA/ED property of a given substituent due to the kind of moiety to which is attached may be ∼30% of the total changeability in cSAR(X) estimated as the difference between the most donating and the most attracting substituents. This is a new information about properties of the pi-electron systems studied qualifying the dependence of their ED/EA properties on the nature of the pi-electron system.

When cSAR(X) for 2-X–CHD and 1-X–CHD derivatives are plotted against cSAR(X) for benzene derivatives, see Fig. 3, the influence of the moiety on SE can be compared. It results from the calculated slopes that sensitivity of the EA/ED properties for the system with substitution in position 1 is greater than in position 2 and with the aromatic one in between.

Fig. 3 Relation between cSAR(X) values for 1-X–CHD and 2-X–CHD derivatives.

Conclusions

It may be concluded, that:

(a) Effect of the substituent on the pi-electron delocalization in olefinic systems is significantly greater than that observed in the aromatic ones;

(b) Substitution of EA or ED groups to olefinic system, 1-X–CHD, increases pi-electron delocalization, contrary to the case of aromatic systems, where decrease of pi-electron delocalization is observed;

(c) Due to the nature of system to which substituent is attached, the range of variability of ED/EA property of the substituent [estimated by means of cSAR(X)] may be up to ∼30% of the overall changes in ED/EA properties observed for all substituents.

Acknowledgements

H. S. and T. M. K. thank the National Science Centre and Ministry of Science and Higher Education of Poland for supporting this work under the grant no. UMO-2013/11/B/ST4/00531.

Notes and references

1. R. O. C. Norman and R. Taylor, Electrophilic substitution in benzenoid compounds, Elsevier Publishing Company, London, 1964.
2. T. M. Krygowski and B. T. Stepien, Pol. J. Chem., 2004, 78, 2213–2217.
3. T. M. Krygowski, K. Ejsmont, M. K. Stepien, J. Poater and M. Sola, J. Org. Chem., 2004, 69, 6634–6640.
4. M. Palusiak, M. Domagala, J. Dominikowska and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2014, 16, 4752–4763.
5. M. Palusiak and T. M. Krygowski, New J. Chem., 2009, 33, 1753–1759.
6. T. M. Krygowski, W. P. Oziminski, M. Palusiak, P. W. Fowler and A. D. McKenzie, Phys. Chem. Chem. Phys., 2010, 12, 10740–10745.
7. T. M. Krygowski, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78.
8. A. Streitwieser Jr, Molecular Orbital Theory for Organic Chemists, J. Wiley & Sons, N.Y., 1961.
9. N. Sadlej-Sosnowska, Chem. Phys. Lett., 2007, 447, 192–196.
10. T. M. Krygowski and N. Sadlej-Sosnowska, Struct. Chem., 2011, 22, 17–22.
11. O. A. Stasyuk, H. Szatylowicz, C. F. Guerra and T. M. Krygowski, Struct. Chem., 2015, 26, 905–913.
12. M. Shahamirian, M. K. Cyrański and T. M. Krygowski, J. Phys. Chem. A, 2011, 115, 550–556.
13. H. Szatylowicz, T. Siodla, O. A. Stasyuk and T. M. Krygowski, Phys. Chem. Chem. Phys., 2016, 18, 11711–11721.
14. L. P. Hammett, Physical Organic Chemistry, McGraw-Hill, New York, 1940, p. 184.
15. A. R. Katritzky, R. F. Pinzelli, M. V. Sinnott and R. D. Topsom, J. Am. Chem. Soc., 1970, 92, 6861.
16. L. P. Hammett, Physical Organic Chemistry, McGraw-Hill, New York, 1940, p. 196.

---