Quantitative X-ray microscopic analysis of individual thermoresponsive microgel particles in aqueous solution

Abstract

High resolution scanning soft X-ray transmission microscopy (STXM) has been employed to investigate individual thermoresponsive microgel particles in aqueous environments. STXM generates 2-dimensional projections with spatial resolutions in the regime of a few 10 s of nm. In the present study we are able to regain a 3D representation of the investigated specimen and observe the deswelling of the microgel particles upon heating, thus offering insight into the thermoresponsive behaviour of individual differently sized particles. We employ a 2-shell model that is able to derive the radial concentration profile of individual microgels particles and thus serves as a complementary method to scattering experiments that average over all particles. Furthermore, we are able to detect the different deswelling behaviour of the particle interior and its interface to the water environment.

---

1. Introduction

Microgels are suspensions of colloidal polymer networks incorporating a significant solvent content and with particle diameters ranging from 100 nm to some micrometres.^1–4 The swelling behaviour and related size of the microgel particles can be influenced by external stimuli that unbalance the osmotic equilibrium of the particles and their solvent matrix resulting in switchable properties of the suspension.^5–8 The most investigated stimuli for swelling and deswelling in microgel particles are temperature and pH.^6,9–11 Switchable microgels have been investigated aiming towards various fields of application, such as drug delivery with controllable release,^12–15 separation processes,¹⁶ sensors^17–19 or biotechnology.^20–22 Composites of microgels and inorganic nanoparticles offer a broad range of unique properties.^7,23–25 Microgel suspensions are very resistant to aggregation, since the polymer particles usually carry covalently bound charged groups that also determine the electrophoresis properties of the gel.^6,26,27 Furthermore, these systems can be non-toxic, non-carcinogenic and biocompatible. The most intensely studied thermoresponsive microgels are those containing poly(N-isopropylacrylamide) (PNIPAM).^7,8,28–31 Below the volume phase transition temperature (VPTT) of 32 °C PNIPAM microgel particles consist of a loose network of cross-linked polymer chains with a comparably high solvent content and dangling surface chains. Above the VPTT the PNIPAM chains coil up, the particles deswell and the solvent is mainly released due to energetically more favourable internal interactions within the polymer network.^31–33 The result is a temperature dependent change in optical and mechanical properties of the microgel^7,8,31,34 and a strong thermophoretic effect.^35,36

Complementary in situ studies of microgel swelling and deswelling are mainly performed by means of dynamic light scattering (DLS) or small-angle neutron scattering (SANS).^7,29,37 While these techniques enable the determination of average particle diameters and pore sizes with high resolution and especially directly in solution (in contrast to, e.g., electron microscopy), it is not possible to investigate individual particles. Therefore these techniques are especially useful for highly monodisperse microgels and with a homogeneous swelling behaviour (i.e., homogeneous crosslinker density).^38,39 However, for a detailed study of inhomogeneous microgels, scattering techniques are stretched to their limits.

Scanning transmission soft X-ray microspectroscopy (STXM) is a powerful technique for high-contrast imaging of soft matter specimens due to resonant imaging.⁴⁰ Employing modern zone plate technology resolutions of 10 nm are accessible.^41,42 Although STXM is limited to rather thin specimens with sufficient transparency, the low absorption of water for photon energies below 530 eV has been successfully employed for in situ investigations of various polymer particles in aqueous solution, e.g., gas filled microspheres,^43,44 microcontainers,^45,46 temperature-dependent phase-change microcapsules⁴⁷ or pH-sensitive polyvinyl composite microgels.⁴⁸ Recent advances resulted in 3D representations of nanoparticle coated microspheres from STXM focal series by means of a digital reconstruction algorithm.⁴⁹ The higher penetration depth of soft X-rays in water is especially advantageous compared to electron microscopy.

In this paper we report on the microscopic characterization of isolated thermoresponsive poly(vinyl alcohol)/poly(methacrylate-co-N-isopropylacrylamide) (PMN-II) based microgel particles in aqueous environment. Aiming on a detailed structural analysis we recorded STXM micrographs and generated quantitative radial profiles of isolated microgel particles. A deconvolution model for rigid gas filled microspheres that respects the influence of the spherical particle geometry on the transmitted signal⁵⁰ was employed to monitor a temperature dependent decrease of the respective particle radius upon thermal treatment. Compared to conventionally used scattering techniques, direct imaging of individual particles provides the opportunity to analyse the shrinking behaviour of differently sized particles. Within the present study we are able to derive radial profiles that consist of a dense interior (“core”) and a less dense regime of dangling surface chains (“shell”). In addition, the comparison of larger and smaller particles indicates relative differences that can hardly be measured with other techniques.

2. Experimental

Thermoresponsive PMN-II microgel particles were synthesized via a water-in-water emulsion technique and cross-linked by photopolymerization according to a procedure described in detail elsewhere.^51,52 The effective amount of NIPAM incorporated in the network was 22% (w/w) and the average diameter of the particles was 1.8 μm according to scanning electron microscopy (dry state), DLS and confocal scanning laser microscopy (CLSM) in solution. The incorporation of NIPAM induces a thermoresponsive deswelling of the PVA-based microgel network above a VPTT of about 33 °C to achieve a new type of switchable microgels for drug transport.⁵¹ Data on the effect of NIPAM content on the swelling degree of the particles are provided in the ESI (Table S1†). An average chemical structure of the PMN-II network and a SEM micrograph of exemplary microgel particles in dry state are depicted in Fig. 1.

Fig. 1 Average structure of PMN-II network (m = 0.05; n = 0.12) and SEM micrograph of exemplary microgel particles in dry state.

Liquid cells for in situ STXM in aqueous environment were prepared by dropping the microgel solution on a 100 nm thin Si₃N₄-membrane (Silson Ltd., United Kingdom) and covering it with a second membrane. The resulting water microbasin was hermetically sealed with varnish.⁵³ To avoid absorption saturation by the aqueous environment only samples with water film thicknesses below 10 micrometres were used. The specimen temperature was controlled with a modified sample holder equipped with a heating resistor and a Pt 200 sensor.⁵⁴

STXM experiments were performed at the PolLux end station at the Swiss Light Source (SLS).⁵⁵ The STXM setup uses synchrotron light from a bending magnet that is focused on the specimen by a Fresnel zone plate. The sample is raster-scanned through the first order focus spot of the zone plate with interferometric control while the transmitted photon intensity is recorded by a photomultiplier tube (Hamamatsu 647P) located behind the specimen. STXM images of isolated microgel particles were recorded at different temperatures with a dwell time of 1 or 2 ms and 520 eV incident photon energy. Within the so-called “water window” (280 eV < hν < 525 eV) the absorption of carbon-containing material is larger than for water, thus offering significant image contrast. Radial transmission profiles of individual microgel particles (with ideal spherical shape) were extracted from the STXM images using the freely available analysis software aXis2000 and their baseline (pure water) was normalized to 1. The profiles were quantitatively analysed in ROOT⁵⁶ by a least-square fitting analysis that takes a finite size of the focused X-ray beam into account (see ESI, Fig. S1†). We ensured that the observed effects were not affected by X-ray irradiation and that the temperature behaviour was fully reversible.

3. Quantitative analysis from 2D radial profiles

The transmitted intensity of monochromatic X-rays through matter (consisting of one chemical component) is described by the Lambert–Beer law:

I_t(x,y) = I₀ exp(−μ(hν)ρD(x,y)) = I₀ exp(k(hν)D(x,y)) (1)

I_t(x,y) represents the local transmitted intensity and I₀ the incident photon intensity. The mass absorption coefficient μ strongly depends on the photon energy hν thus reflecting the high chemical sensitivity in soft X-ray absorption. Density, local thickness and the absorption coefficient of the absorbing material are given by ρ, D(x,y) and k(hν), respectively. In multicomponent systems the image contrast is governed by the specific absorption coefficients. In particular for heterogeneous soft matter samples, the tuneable photon energy enables optimum contrast imaging due to spectroscopic contrast.⁴⁰

To facilitate a quantitative analysis the local transmittance I_t(x,y) from the 2D STXM micrographs of isolated microgel particles is transferred to a radial dependence I(r) by extraction of radial profiles. The geometrical model of the particles is adopted from a previous study of gas-filled microspheres.⁵⁰ The analysis is based on eqn (1) considering ideal spherical core–shell particles with an outer radius R₁ (cf. Fig. 2). We describe the particles by a homogenous interior (core) with radius R₀ and absorption parameter k_core (corresponding to region III, Fig. 2) and a (less dense) shell regime (region II) of thickness h = R₁ − R₀ with absorption parameter k_shell (k_shell < k_core). The shell corresponds to the dangling surface chains of the cross-linked polymer framework. The absorption of the surrounding water matrix is considered by an additional absorption coefficient k_H2O (region I). Note that the water film thickness exceeding the particle diameter (d > 2R₁) only contributes with a small homogenous background that is to be considered in the quantitative analysis. The additional water in the wet-cell as well as the two Si₃N₄ membranes absorbs a constant fraction of the transmitted intensity and is taken into account in I₀ which is also a fitting parameter.

Fig. 2 Top: Schematic model of a spherical microgel particle consisting of a homogenous interior sphere and homogenous particle shell in aqueous surrounding with respective absorption coefficients defining the different radial regimes and variables. Bottom: radial transmission profile and its behaviour in different regimes assuming low absorption of the water matrix (regime I).

Fig. 2 shows the generation of a transmission profile from a spherical microgel particle by convolution. The three regimes (water, shell and core) each are described by equations that include the respective absorption coefficients and component thicknesses. The latter parameters are derived from geometrical considerations. In the present model the mass absorption coefficient μ_i and density ρ_i in the respective regimes are constant and can therefore be replaced by the absorption coefficients k_i. For simplicity, the photon energy dependence of μ and k are neglected. We can thus derive the following equations for the 3 different regimes:

Regime I (H₂O), i.e. |r| > R₁:

I_t = I₀ exp{−k_H2OD_H2O} = I₀ exp{−k_H2O2R₁} (2a)

with

D_H2O = 2R₁ (2b)

Regime II (shell), i.e. R₀ < |r| ≤ R₁:

I_t = I₀ exp{−k_H2OD_H2O − k_shellD_shell} (3a)

with

Regime III, i.e. |r| ≤ R₀:

I_t = I₀ exp{−k_H2OD_H2O − k_shellD_shell − k_coreD_core} (4a)

with

For the quantitative analysis we consider continuity at the regime borders shell/water (r = R₁) and shell/core (r = R₀). Eqn (2)–(4) are used for a least-square fit procedure. k_H2O was kept constant during the iterative process at a value of 0.11 μm⁻¹ in accordance with previous studies.⁵⁰

Most presumably the microgel particles adhere to at least one of the two Si₃N₄-membranes that build up the liquid cell. The effect of membrane interactions on the resulting radial profiles as well as an approach on the deconvolution of such profiles has been discussed for in situ STXM studies of PVA-based microballoons in literature.⁵⁰ We did not find similar profile distortions within the present study and therefore do not expect significant effects of the membrane on the deswelling behaviour.

4. Results and discussion

Fig. 3 shows the STXM micrographs of two exemplary PMN-II microgel particles (size distribution given in ESI, Fig. S2†) in aqueous environment recorded at three different temperatures. During the heating of the specimen the microgel particles show deswelling as expected from their thermoresponsive behavior. Positional changes due to thermal drift were corrected for the quantitative analysis. Note that the stated temperatures are those recorded about 6 mm away from the wet cell sample. While the starting temperature (T₁ = 25 °C) was measured with high accuracy, we may conclude that the actual sample temperatures for 45 °C (T₂) and 55 °C (T₃) measurements are lower at the specimen location and, therefore, closer to the VPTT of PNIPAM. The smaller features close to the investigated particles are either very small microspheres or residuals of the polymerization educts from the solution. However, they are irrelevant for the quantitative analysis since they do not affect the radial profile extraction from the 2D images.

Fig. 3 STXM micrographs of two representative spherical microgel (PMN-II) particles at temperatures of 25 °C (A), 45 °C (B) and 55 °C (C). The dotted circles indicate the borders of the respective extracted radial profiles. The images were recorded at hν = 520 eV to prevent absorption saturation by the surrounding water. The water background is normalized to 1 (cf. profiles in Fig. 4).

The dark dotted circles in Fig. 3 depict the regions that have been defined to extract the respective radial profiles. The resulting profiles for the two representative particles are shown in Fig. 4. Upon heating a reduction in radial size is obvious for both particles and simultaneously the transmitted intensity I_t is decreasing. Since the experiments were performed at 520 eV incident photon energy, the absorption of water does not significantly contribute to the overall transmitted intensity. In contrast, the reduction of I_t is due to stronger absorption within the particles, i.e., higher material density and therefore increased optical density upon the release of water. For both particles inspected in Fig. 3 we observe some minor changes in their diameters upon heating from 45 °C to 55 °C, which is some indication that the particles have not yet reached the state of complete deswelling at 45 °C.

Fig. 4 Least-square fit analysis (solid lines) of the temperature dependent radial profiles (dots) for the larger (A) and smaller particle (B) depicted in Fig. 3, respectively, according to eqn (3) and (4). For details, see text.

Fig. 4 also summarizes the graphic result of the least-square fit analysis of the radial profiles for the larger (Fig. 4A) and smaller particle (Fig. 4B) in the micrographs depicted in Fig. 3. For smaller radii, the radial profiles are well represented by the applied model while for larger radii the fitted curves slightly deviate from the experimental data. In particular for |r| < 0.5 nm the radial profile of the larger particle has no pronounced curvature, but appears flat suggesting a constant absorption. The explanation for this finding is related to the overall thickness of the particle interior. Typically, STXM uses resonant excitation for maximum image contrast and thus, absorption saturation often occurs for film thicknesses of about 200–300 nm (in case of soft materials). Using non-resonant excitation as in the present case (hν = 520 eV), the calculated 1/e penetration depth for carbon is around 680 nm.⁵⁷ Therefore, absorption saturation plays a significant role in the case of larger particles, while for the smaller particle, the experimental curve follows the model (eqn (4a) and (b)) within the shell and core regime. For all analysed microgel particles the flanks of the radial profiles are well represented by the quantitative fits and the deviations are restricted to |r| < R₀. Therefore, the determination of the core–shell border will not be affected and the influence on the absorption coefficients is negligible. The respective fit results for R₀, R₁, k_core and k_shell are denoted in detail in the ESI (Table S2†).

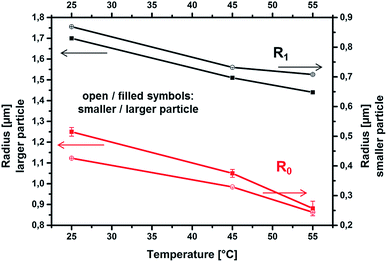
The temperature dependent changes of the diameter of the two selected PMN-II microgel particles are shown in Fig. 5. Upon heating the inner radius R₀ changes for the larger particle by approximately 32% from T₁ to T₃ (T₁ → T₂: 16(±3)% decrease, T₂ → T₃: 16(±5)% decrease with respect to the radius at T₂) while the outer radius R₁ decreases by 15% (−11(±0.5)% and −4.5(±0.2)% for the respective temperature steps). For the smaller particle the situation was comparable: a 43% overall decrease for R₀ during heating from T₁ to T₃ (T₁ → T₂: 23(±0.5)% decrease, T₂ → T₃: 26(±0.5)% decrease with respect to the radius at T₂), and 19% decrease for R₁ (−16(±0.4)%/−3.3(±0.3)%). Simultaneously the respective k values are increasing by about 25% in both regimes for heating from T₁ to T₂ and by 50% from T₁ to T₃. Since smaller particle diameters go along with decreasing X-ray penetrated specimen volume, this finding detects a strong increase in material density. Considering the overall particle diameter, these findings are in accordance with a previous study based on scattering data (dynamic light scattering, neutron scattering) and confocal laser scanning microscopy.⁵² However, according to our results, the particle shrinkage is mainly governed by a deswelling of the highly cross-linked core network. The diameter of the shell (R₁ − R₀) is found to be relatively constant, while this regime also shows a strong increase of polymer density that goes along with solvent release. In other words, the dangling surface chains are moving closer together due to a shrinkage of the particle core, but don't significantly shrink in length. This behaviour goes along with a smoother particle surface and a decrease of pore sizes as it has been detected by SANS, DLS and confocal laser scanning microscopy.^29,52,58 Moreover, our results evidence that the diameter decrease above VPTT is mainly due to the core shrinking more than to the shell. Such details are accessible only to STXM analysis, in which the core and shell regions are directly distinguished. This behaviour can be interpreted in terms of a phase segregation of the two moieties participating to the microgel network, i.e. the PVA and the poly(methacrylate)-co-poly(NiPAAm) chains.

Fig. 5 Temperature-dependent change of the particle radii of two differently sized PMN-II.

5. Conclusions and outlook

Due to their considerable PNIPAM content PMN-II microgel particles show significant deswelling and water release upon heating above the VPTT. Quantitative fitting of radial profiles extracted from in situ recorded high-resolution STXM micrographs allows for a detailed analysis of this shrinking for individual particles of different size and/or density. It should be mentioned that the presented approach presents an elegant way to achieve information of the 3D shape of the investigated specimen from pure 2D data.

The accordance of the applied specimen model with the experimental data supports our approach for the quantitative analysis based on the projected radial profiles considering a simple core–shell particle. Although some deviations from ideal profiles occur for larger particles due to absorption saturation, we obtain valuable insight into the structural modifications in microgel particles induced by temperature increase. Based on the derived fit parameters for two exemplary particles, we are able to confirm the increase in (optical) density in the interior of the particles due to the release of water upon temperature increase above VPTT. This is already obvious from the reduction of intensity in the radial profiles for |r| ≈ 0. Quantification indicates a pronounced increase of k_core for either size. Furthermore, we find no significant shrinkage of the shell regime representing dangling surface chains of the polymer network. This finding is rather surprising, since usually a collapse of the shell is considered in literature based on scattering data.^29,52,58

In summary, STXM microanalysis of individual thermoresponsive microgel particles in water provides detailed insight into morphological changes upon heating. Although the applied model for the radial profile analysis is only based on simple geometric considerations, we are able to observe structural variations with high accuracy. The derived values are in good agreement with complementary studies on the same material. Further model studies will take into account potential concentration gradients in the shell regime to obtain a more detailed insight into radial water gradients within the less dense material. This will require additional experiments in the C1s and O1s photon energy regime to increase chemical sensitivity beyond pure mass absorption by resonant imaging. Furthermore, we want to employ our spectromicroscopic capabilities to gain more insight into the distribution of the polymer moieties in heterogeneous networks where incompatibility of chains can give rise to microscopically phase separated domains.

Acknowledgements

We gratefully acknowledge experimental support by Drs J. Raabe and B. Watts from the PolLux beamline at the Swiss Light Source (SLS). The project was funded by the Bundesminister für Bildung und Forschung (BMBF), contract 05 K16WED. The research leading to these results has received funding from the European Commission's Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 312284 (CALIPSO). A. S. and R. F. acknowledge travelling support through the Graduate School Molecular Science (GSMS) and by the DFG within GRK 1896 “In situ microscopy”.

References

1. W. O. Baker, Ind. Eng. Chem., 1949, 41, 511.
2. R. H. Pelton and P. Chibante, Colloids Surf., 1986, 20, 247.
3. B. R. Saunders and B. Vincent, Adv. Colloid Interface Sci., 1999, 80, 1.
4. N. Sanson and J. Rieger, Polym. Chem., 2010, 1, 965.
5. J. M. Weissman, H. B. Sunkara, A. S. Tse and S. A. Asher, Science, 1996, 274, 959.
6. R. H. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1.
7. M. Karg and T. Hellweg, Curr. Opin. Colloid Interface Sci., 2009, 14, 438.
8. L. A. Lyon and A. Fernandez-Nieves, Annu. Rev. Phys. Chem., 2012, 63, 25.
9. T. Tanaka, S. Ishiwata and C. Ishimoto, Phys. Rev. Lett., 1977, 38(14), 771.
10. T. Tanaka, Phys. Rev. Lett., 1978, 40(12), 820.
11. T. Hoare and R. Pelton, Macromolecules, 2004, 37, 2544.
12. L. Bromberg, M. Temchenko and T. A. Hatton, Langmuir, 2002, 18, 4944.
13. D. Schmaljohann, Adv. Drug Delivery Rev., 2006, 58(15), 1655.
14. T. R. Hoare and D. S. Kohane, Polymer, 2008, 49, 1993.
15. Y. Guan and Y. Zhang, Soft Matter, 2011, 7(14), 6375.
16. R. F. S. Freitas and E. L. Cussler, Chem. Eng. Sci., 1987, 42(1), 97.
17. S. Höfl, L. Zitzler, T. Hellweg, S. Herminghaus and F. Mugele, Polymer, 2007, 48(1), 245.
18. G. R. Hendrickson and L. A. Lyon, Soft Matter, 2009, 5(1), 29.
19. M. R. Islam and M. J. Serpe, Chem. Commun., 2013, 49(26), 2646.
20. H. Kawaguchi, K. Fujimoto and Y. Mizuhara, Colloid Polym. Sci., 1992, 270, 53.
21. B. Jeong and A. Gutowska, Trends Biotechnol., 2002, 20(7), 305.
22. X. Zhu, X. Gu, L. Zhang and X.-Z. Kong, Nanoscale Res. Lett., 2012, 7, 519.
23. S. Nayak and L. A. Lyon, Angew. Chem., Int. Ed., 2005, 44, 7686.
24. P. Schexnailder and G. Schmidt, Colloid Polym. Sci., 2009, 287(1), 1.
25. D. M. Han, Q. M. Zhang and M. J. Serpe, Nanoscale, 2015, 7(6), 2784.
26. W. McPhee, K. C. Tam and R. Pelton, J. Colloid Interface Sci., 1993, 156, 24.
27. A. Fernández-Nieves and M. Márquez, J. Chem. Phys., 2005, 122, 084702.
28. M. Heskins and J. E. Guillet, J. Macromol. Sci., 1968, 2(8), 1441.
29. K. Kratz, T. Hellweg and W. Eimer, Polymer, 2001, 42, 6631.
30. J. Wu, B. Zhou and Z. Hu, Phys. Rev. Lett., 2003, 90(4), 048304.
31. P. J. Yunker, K. Chen, M. D. Gratale, M. A. Lohr, T. Still and A. G. Yodh, Rep. Prog. Phys., 2014, 77, 056601.
32. Y. H. Bae, T. Okano and S. W. Kim, J. Polymer Sci. B Polymer Phys., 1990, 28(6), 923.
33. R. H. Pelton, J. Colloid Interface Sci., 2010, 348(2), 673.
34. C. D. Jones, M. J. Serpe, L. Schroeder and L. A. Lyon, J. Am. Chem. Soc., 2003, 125, 5292.
35. S. Wongsuwarn, D. Vigolo, R. Cerbino, A. M. Howe, A. Vailati, R. Piazza and P. Cicuta, Soft Matter, 2012, 8(21), 5857.
36. A. Koniger, N. Plack, W. Kohler, M. Siebenburger and M. Ballauff, Soft Matter, 2013, 9(5), 1418.
37. B. R. Saunders, Langmuir, 2004, 20(10), 3925–3932.
38. R. Acciaro, T. Gilányi and I. Varga, Langmuir, 2011, 27(12), 7917.
39. T. Still, K. Chen, A. M. Alsayed, K. P. Aptowicz and A. G. Yodh, J. Colloid Interface Sci., 2013, 405, 96.
40. H. Ade and A. P. Hitchcock, Polymer, 2008, 49, 643.
41. J. Vila-Comamala, K. Jefimovs, J. Raabe, T. Pilvi, R. H. Fink, M. Senoner, A. Maassdorf, M. Ritala and C. David, Ultramicroscopy, 2009, 109, 1360.
42. W. Chao, P. Fischer, T. Tyliszczak, S. Rekawa, E. Anderson and P. Naulleau, Opt. Express, 2012, 20, 9777.
43. G. Tzvetkov, B. Graf, P. Fernandes, A. Fery, F. Cavalieri, G. Paradossi and R. H. Fink, Soft Matter, 2008, 4(3), 510.
44. G. Tzvetkov, A. Späth and R. H. Fink, Radiat. Phys. Chem., 2014, 103, 84.
45. C. Déjugnat, K. Köhler, M. Dubois, G. B. Sukhorurov, H. Möhwald, T. Zemb and P. Guttmann, Adv. Mater., 2007, 19, 1331.
46. A. Späth, H. Minami, T. Suzuki and R. H. Fink, RSC Adv., 2014, 4, 3272.
47. G. Tzvetkov, B. Graf, R. Wiegner, J. Raabe, C. Quitmann and R. Fink, Micron, 2008, 39, 275.
48. S. Fujii, S. P. Armes, T. Araki and H. Ade, J. Am. Chem. Soc., 2005, 127(48), 16808.
49. A. Späth, S. Schöll, C. Riess, D. Schmidtel, G. Paradossi, J. Raabe, J. Hornegger and R. H. Fink, Ultramicroscopy, 2014, 144, 19.
50. P. A. L. Fernandes, G. Tzvetkov, R. H. Fink, G. Paradossi and A. Fery, Langmuir, 2008, 24, 13677.
51. S. V. Ghugare, P. Mozetic and G. Paradossi, Biomacromolecules, 2009, 10(6), 1589.
52. S. V. Ghugare, E. Chiessi, R. Fink, Y. Gerelli, A. Scotti, A. Deriu, G. Carrot and G. Paradossi, Macromolecules, 2011, 44(11), 4470.
53. B. Graf-Zeiler, G. Tzvetkov and R. H. Fink, Chem. Phys. Chem., 2011, 12(18), 3503.
54. G. Tzvetkov and R. H. Fink, Scr. Mater., 2008, 59, 348.
55. J. Raabe, G. Tzvetkov, U. Flechsig, M. Böge, A. Jaggi, B. Sarafimov, M. G. C. Vernooij, T. Huthwelker, H. Ade, D. Kilcoyne, T. Tyliszczak, R. H. Fink and C. Quitmann, Rev. Sci. Instrum., 2008, 79, 113704.
56. R. Brun and F. Rademakers, Nucl. Instr. Meth. Phys. Res. A, 1997, 389, 81.
57. B. L. Henke, E. M. Gullikson and J. C. Davis, At. Data Nucl. Data Tables, 1993, 54, 181.
58. A. Fernández-Barbero, A. Fernández-Nieves, I. Grillo and E. López-Cabarcos, Phys. Rev. E, 2002, 66, 051803.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra20142c

‡ Present address: Solvay Research & Innovation Centre, Plot no. 72/73/74, Alindra Extention, G.I.D.C. Estate, Savli, Dist Vadadora, 391770 Gujarat, India.

---