High spectral field enhancement and tunability in core–double shell metal–dielectric–metal spherical nanoparticles†
Luis J. Mendoza Herreraa,
Lucía B. Scaffardiab and
Daniel C. Schincaab
aCentro de Investigaciones Ópticas (CIOp), (CONICET La Plata-CIC), Argentina. E-mail: daniels@ciop.unlp.edu.ar
bDepartamento de Ciencias Básicas, Facultad de Ingeniería, UNLP, Argentina
First published on 15th November 2016
Abstract
In this work we have developed full Mie theory for spherical core–double shell NPs, considering the boundary conditions of the electric and magnetic fields at each interface, to study plasmon resonances, optical extinction and spectral field enhancement of a generalized metal–dielectric–metal NPs. Keeping gold as the outer metal shell, calculations were carried out for different core metals (gold, silver, copper and aluminium) and different intermetallic dielectrics (silica, titanium dioxide, aluminium oxide and water). The metal dielectric function includes free and bound electron size corrections. Theoretical results show that the structures Al–SiO2–Au, Ag–SiO2–Au and Cu–SiO2–Au have field enhancement maxima factors of 33, 30 and 20 respectively in the outer region, all larger than that for Au–SiO2–Au (18). For the intermetallic region, field enhancement factors between 459, 960 and 841 are obtained for the first three structures mentioned before, respectively, also larger than that for Au–SiO2–Au (770). Spatial field enhancement was also calculated for both regions, for different core metals and fixed core–double shell size. A hybridization model specially developed for a core–double shell system allows an insightful interpretation of its plasmon resonances, field enhancement maxima and lack of symmetry in the outer region field distribution.
1 Introduction
Bare-core and single coated metal NPs have found many applications in diverse areas of science and technology.1–10 In recent years, major interest is being devoted to the synthesis and characterization of core–double shell metal–dielectric–metal NPs due to their diverse applications in catalysis,11,12 biocompatible SERS,13 drug-delivery,14 tumor diagnosis and therapy,15 contaminant detection SERS,16,17 near-field enhancement18 and nanoscale optical parametric amplification.19 These core–double shell NPs have been successfully synthesized using chemical and laser assisted methods.13,20,21Recent works about core–double shell metal–dielectric–metal NPs are devoted to theoretically analyze plasmonic response and field enhancement dependence on relative core–shell radii for the particular case of Au–SiO2–Au, mainly interested in the biocompatibility of gold.22–24 For the simulations, the authors use different approximations and metal dielectric function, although not always appropriately corrected for free and bound electrons for describing the studied cases. Besides, no other configurations of metal and dielectric were explored in the literature.
In this paper, plasmonic properties and field enhancement of spherical core–double shell metal–dielectric–gold NPs for different core metals (Ag, Cu and Al) and different intermetallic dielectrics (water, SiO2, Al2O3 and TiO2) are studied for the first time. We show in first place, the difference in plasmon resonances of bare core and core–double shell NPs using the dipolar approximation and full Mie theory, showing that the former may lead to wrong plasmon resonance conclusions, especially when non-noble metals are considered.
We have developed Mie theory for spherical NPs comprising a metal core and two concentric shells, with appropriate boundary conditions, including modifications for free electron and bound electron contributions to the metal dielectric function. This approach is used to calculate spectral and spatial field enhancement for different core metals and intermetallic dielectric, showing high enhancement factors for particular configurations.
Finally, hybridization model was extended for core–double shell NPs and used to explain the location, redshift and intensity increase (decrease) of the maxima in the field enhancement spectra.
2 Theoretical model
To study the extinction of core–double shell spherical NPs, electric and magnetic fields in each of the regions indicated in Fig. 1 must be calculated. Ei,Hi represent the incident electric and magnetic fields, Ej,Hj (for j = 1, 2 and 3) represent the electric and magnetic fields in each of the regions and Es,Hs represent the scattered electric and magnetic fields. represents the complex refractive index of the surrounding media while Nj (for j = 1, 2 and 3) are the complex refractive index of each layer. As it is known,
represents the complex refractive index of the surrounding media while Nj (for j = 1, 2 and 3) are the complex refractive index of each layer. As it is known, 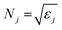 with εj being the complex dielectric function for each region.
with εj being the complex dielectric function for each region.
To obtain the electric and magnetic field of each layer, the vector wave equation in spherical coordinates considering an incident plane wave Ei = E0eikrcosθax must be solved, being ax the unit vector in the x axis. The solution of this problem can be written following the mathematical background given by Bohren and Huffman25 in the form:
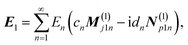 | (1) |
 | (2) |
 | (3) |
 | (4) |
 , j and p subindices correspond to spherical vector function orders (see ESI†). Superscripts (1), (2) and (3) indicate that the spherical Bessel functions used in the expression of the vector functions M and N are
, j and p subindices correspond to spherical vector function orders (see ESI†). Superscripts (1), (2) and (3) indicate that the spherical Bessel functions used in the expression of the vector functions M and N are  ,
,  and hn(kr) = jn(kr) + iyn(kr), respectively, being Jn and Yn the Bessel functions of first and second class. For expressions of magnetic field in each layer, Ampere's law is used (∇ × H = −iωεE). The full definition of M and N vector functions as well as the values of the constants derived from the continuity conditions of electric and magnetic fields at the boundary for each region are described in the ESI.† The expressions for the scattering, extinction and absorption cross sections of spherical particles can be written as:
and hn(kr) = jn(kr) + iyn(kr), respectively, being Jn and Yn the Bessel functions of first and second class. For expressions of magnetic field in each layer, Ampere's law is used (∇ × H = −iωεE). The full definition of M and N vector functions as well as the values of the constants derived from the continuity conditions of electric and magnetic fields at the boundary for each region are described in the ESI.† The expressions for the scattering, extinction and absorption cross sections of spherical particles can be written as:
 | (5) |
 | (6) |
| Cabs = Cext − Csca, | (7) |
When the Nps are small, the dipolar approximation can be used. The above expressions are then reduced to:
 | (8) |
For the determination of the fields and cross sections mentioned above, it is necessary to adequately describe the dielectric function of the different layers. If one or more of these layers are metals with nanometer thickness, their dielectric function can be written as the experimental bulk dielectric function plus two size corrective terms corresponding to the contributions of free and bound electrons as:
| ε(ω,R) = εbulk(ω) + Δεfree(ω,R) + Δεbound(ω,R), | (9) |
 | (10) |
 | (11) |
In the case of metal–dielectric–metal NP, for R < R1, free electron correction takes the form  , while for the layer in which R2 < R < R3,
, while for the layer in which R2 < R < R3,  . In these expressions vF is the Fermi velocity of free electrons and C is a constant whose typical value is considered to be in the order of 0.75 (ref. 26–30) for the case of diffuse electron scattering at the particle's boundary. This type of correction is meaningful for NP sizes smaller than about 40 nm, depending on the metal. For metal core sizes or metal shell thicknesses smaller than 2 nm ((R1 < 2 nm) or (R3 − R2) < 2 nm), bound electron size correction Δεbound(ω,R) must be taken into account. To determine ωp and γfree using the method developed by Mendoza Herrera et al.,30–33 we used the experimental complex refractive index given by Babar et al.34 for Au, Ag and Cu and those given by McPeak et al.35 for Al. The obtained results are summarized in Table 1:
. In these expressions vF is the Fermi velocity of free electrons and C is a constant whose typical value is considered to be in the order of 0.75 (ref. 26–30) for the case of diffuse electron scattering at the particle's boundary. This type of correction is meaningful for NP sizes smaller than about 40 nm, depending on the metal. For metal core sizes or metal shell thicknesses smaller than 2 nm ((R1 < 2 nm) or (R3 − R2) < 2 nm), bound electron size correction Δεbound(ω,R) must be taken into account. To determine ωp and γfree using the method developed by Mendoza Herrera et al.,30–33 we used the experimental complex refractive index given by Babar et al.34 for Au, Ag and Cu and those given by McPeak et al.35 for Al. The obtained results are summarized in Table 1:
| Metal | ωp × 1015 [s−1] | γfree × 1014 [s−1] |
|---|---|---|
| Au | 13.26 | 1.26 |
| Ag | 13.74 | 0.25 |
| Cu | 13.39 | 0.40 |
| Al | 17.44 | 2.38 |
3 Results and discussion
3.1 Considerations about dipolar approach and Mie theory
In recent works about core–double shell Nps,22–24 the authors focus on the plasmonic and field enhancement characteristics of gold–silica–gold NPs. Hu et al.24 studied the spectral response and angular scattering properties of silica–gold and gold–silica–gold multilayer nanoshells. They use Mie code to show similarities and differences between optical properties of both structures, without considering intrinsic size corrections for the metal dielectric function. On the other hand, Wu et al.22 investigated the influence of core size and intermetallic dielectric layer thickness on plasmon resonance properties of gold–silica–gold nanoshells, using Mie theory including only free electron size corrected metal dielectric function. Finally, Zhu et al.23 studied the effect of gold core on the local field enhancement of gold–silica–gold nanoshell using the electrostatic approximation for sizes in the order of several tens of nanometers, where the approximation is not valid.A typical experimental result obtained in our group for increasing size of gold NPs (10 nm to 80 nm, for example), yielded spectra with plasmon resonance strongly redshifted (extrinsic effect). However, dipolar approach expression is capable only to account for the small radii spectra, and keeps the plasmon unshifted for larger radii. This typical example for gold may be somehow misleading, in the sense that all metal NPs under say 20 nm in size can be safely treated in the dipolar approach.
It is necessary to point out that care must be exercised in using this latter approach, since the correct plasmon resonance wavelength (as well as higher order resonances) depends not only on NP size but also on the metal which the NP is made of.
This is related to conditions applied to the so called “size parameter x” (x = 2πRN/λ), where N is the surrounding medium refractive index and λ is the incident wavelength in vacuum. While the condition x ≪ 1 considers only dipolar contributions to the scattered field (dipolar approximation), |m|x ≪ 1, being m the metal relative complex refractive index,25 takes into account higher order multipolar contributions (quasi-static approximation). In both approximations the field in the particle is considered uniform. However, the words quasi-static and dipolar may be often used indistinctively in the literature. To accurately describe the plasmonic characteristics of larger particles, it is necessary to use Mie theory instead.
For comparison purposes, Fig. 2 illustrates this point for the case of extinction spectra of bare core Au (a) and Al (b) NPs for two different sizes. For Au, the expected result that for small radius (15 nm) dipolar and Mie Theory yield similar spectra with coincident plasmon resonances while for larger sizes (35 nm) they produce different results is clearly seen. However, the case of Al NPs shows a dramatic difference: dipolar and Mie approach yield different results even for the 15 nm radius and much more different spectra for the larger particles, including the appearance of higher order resonances.
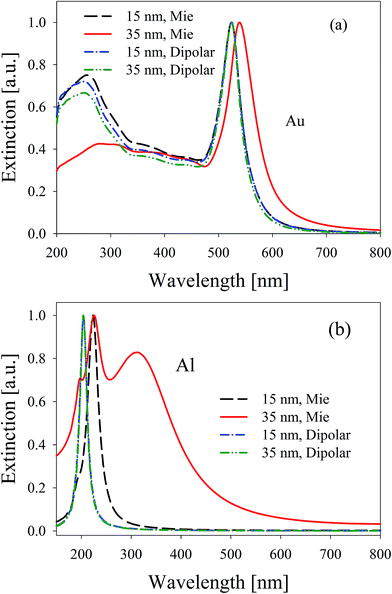 | ||
| Fig. 2 Comparison between extinction spectra of bare spherical NPs calculated using full Mie Theory and its dipolar approximation for (a) gold and (b) aluminum, for two sizes. | ||
The above comparison may be extended to the case of core–double shell type NPs, where also the choice of the core metal implies noticeable differences in the extinction spectra. Let us first consider a core–double shell NP made up of a gold core, a silica layer and an external gold shell, with radii R1, R2 and R3 related by R2 = 1.5R1 and R3 = 2R1. Fig. 3(a) shows a comparison of extinction spectra for R1 = 2 nm and R1 = 22 nm, calculated using the dipolar approximation and full Mie theory. It can be seen that two plasmonic resonances are predicted in both approaches. For small sizes, both spectra are superimposed. However, as the radius is increased, the dipolar approximation still predicts the plasmon peaks at the same wavelengths as before, in contrast to the red shift of both peaks derived when full Mie calculation is used. For spherical NPs, the red shift of plasmon resonance with size is the well-known “extrinsic size” effect.26
If the gold core is replaced by aluminum, striking differences are seen, as depicted in Fig. 3(b). When the dipolar approximation is used to calculate the extinction spectra for the same sizes as in panel (a), two plasmon resonances are seen, which seem to be fixed at approximately λ = 200 nm and λ = 700 nm. However, when full Mie is used for R1 = 2 nm, the large wavelength peak blueshifts to about λ = 400 nm, while the other remains almost fixed. For R1 = 22 nm, Mie approach yields all the multipolar resonances (even the small dipolar shoulder at about λ = 850 nm) while dipolar approximation still wrongly predicts a resonance close to 700 nm.
Taking into account these results, we shall use full Mie theory when calculating the influence of metal core and intermetallic dielectric on the spectral and spatial field enhancement of core–double shell NPs (Sections 3.2 and 3.4, respectively).
3.2 Spectral field enhancement calculations
Using Mie Theory for core–double shell metal–dielectric–metal NPs, the total (Etotal = Es + Ei) electric field spatial distribution inside and outside the particle may be obtained. From this field distribution, the maximum value in the intermetallic dielectric region and in the outer medium may be obtained. When the amplitude of this maximum field is divided by the amplitude of the incident field (|E0|), the so called field enhancement factor can be obtained. This enhancement depends not only on wavelength (due to the plasmon resonances of the compound particle) but on various parameters such as core metal, intermetallic dielectric and layer sizes.Fig. 4 shows the influence of different core metals (Au, Ag, Cu and Al) on the spectral field enhancement both outside the metal shell (panel (a)) and in the intermetallic dielectric (panel (b)).
It is interesting to notice the large difference between the scales in the vertical axes of panels (a) and (b). This is due to the much stronger field enhancement in the intermetallic region with respect to the outer region, where the fields are shielded by the external metal shell. Panel (a) shows that the largest field enhancement factor |Etot|/E0 = 33 corresponds to Al as core metal, while there is a decrease in intensity when core metals Ag, Cu and Au are considered, respectively. Also, there is a general redshifted of these resonances for the considered metals. Field enhancement resonances corresponding to the shorter wavelength plasmon peak appear in inverse order of intensity compared with the large wavelength plasmon resonance. Panel (b) shows that Ag as core metal produces a maximum field enhancement |E2|/E0 = 950 in the intermetallic region.
Fig. 5(b) shows the outer region spectral field enhancement |Etot|/E0 for realistic intermetallic dielectrics: water, SiO2, Al2O3 and TiO2. Their wavelength dependent dielectric function were calculated using the Sellmeier's equation and ordered in increasing values of ε at 600 nm (εwater = 1.77, εSiO2 = 2.13, εAl2O3 = 3.10 and εTiO2 = 6.78). It can be seen that the general behavior follows that of Fig. 5(a). Combining the results shown in Fig 4(a) and 5(a), core–double shell NPs may be engineered to tune field enhancement for specific applications.
The field enhancement spectrum calculated in the intermetallic region (|E2|/E0) for the same Au–dielectric–Au configuration and increasing ε2 values, is dominated by a strong resonance that redshifts as the permittivity increases. However, as can be seen in Fig. 6(a), its intensity increases for ε2 from 1 to 3, and then decreases monotonically for larger values of permittivity.
Summarizing, the attractive characteristic of these kinds of triple spherical structures is that the wavelengths of field enhancement maxima originated by interference of the bare core and nanoshell resonances may be tuned not only through appropriate engineering of NP size ratios,22 but also by selecting specific core metals and specific intermetallic dielectric, as shown in this work.
3.3 Hybridization calculations
The maxima of the spectral field enhancement shown in the previous paragraph are related to the plasmon resonance peaks of the core–double shell NPs. These peaks may be physically interpreted through a relatively simple approach based on the interaction between resonance modes of simpler nanostructures such as spheres, cavities and nanoshells, known as hybridization model. In trying to obtain an explicit expression for the location of plasmon resonances, this model makes use of the simpler expression of quasi-static approximation, avoiding cumbersome mathematics involved in Mie theory. Although plasmon wavelengths are derived with a smaller precision than with Mie's, the strength of this approach relies on the insightful qualitative and quantitative description of the plasmon peaks.Hybridization model was first applied for the particular case of a single metallic nanoshell immersed in vaccum by Prodan et al.,37 showing that the resonances of this structure could be obtained by hybridization of the resonances of a gold core and a cavity in a gold bulk. Following a different path within the quasi-static approximation, we have calculated the solution of Laplace equation for the electric potential for a sphere of radius R3 and dielectric function ε3 immersed in a medium with a permittivity εm and for a cavity of radius R2 and ε2 immersed in a medium ε3, yielding the wavelength dependent resonance conditions F(λ) = lε3 + (l + 1)εm = 0 and F(λ) = (l + 1)ε2 + lε3 = 0, respectively, where l represents the multipolar order. When the metal dielectric function is written in the simple Drude form ε = 1 − ωp2/ω2, the plasmon resonance wavelengths predicted in37 are obtained. However, this expression for the metal dielectric function lacks free and bound electron contribution corrections, the latter being important in the UV-visible range where the plasmon resonances for Au, Ag, Cu and Al are encountered. Some authors22,38 consider the correction of bound electron contribution as an additive constant to the dielectric function, whose value is determined by fitting the extinction spectrum of a NP of known size. However, the method misses the location of plasmon peaks for sizes larger or smaller than that of the known Np. The first resonance condition, corresponding to a bare 10 nm radius Au NP, is plotted in the upper panel of Fig. 7 (blue dot-dashed line). When the curve crosses the F(λ) = 0 line, it yields the plasmon resonance wavelength λs, indicated by a full blue vertical line in the middle panel along with a schematic of the bare Au NP.
For the more general case of a dielectric (ε2)–metal (ε3) nanoshell immersed in a dielectric medium (εm), the resonance condition F(λ) = ε32l(l + 1)(x−2l−1 − 1) +ε3[l(l+ 1)(ε2 + εm) + (ε2l2 + εm(l +1)2)x−2l−1] + ε2εml(l + 1)(x−2l−1 − 1) = 0 is obtained, where  . This condition is also plotted in the upper panel of Fig. 7 (red dashed line), where it can be seen that it crosses the zero line at points corresponding to the two resonance wavelengths λ±. One of them (λ+) is just outside of the wavelength range for which the experimental values of the complex refractive index were measured by Babar et al.34 and Johnson and Christy36 These wavelengths are also shown in the middle panel along with a schematic of a nanoshell.
. This condition is also plotted in the upper panel of Fig. 7 (red dashed line), where it can be seen that it crosses the zero line at points corresponding to the two resonance wavelengths λ±. One of them (λ+) is just outside of the wavelength range for which the experimental values of the complex refractive index were measured by Babar et al.34 and Johnson and Christy36 These wavelengths are also shown in the middle panel along with a schematic of a nanoshell.
Finally, the hybridization of a bare metal NP (ε1) and a dielectric–metal nanoshell yields a resonance condition given by (λ) = x1(ε1 + 2ε2)[3ε3(ε2 − ε3) − (ε3 + 2εm) (ε2 − ε3)] + x2(ε2 − ε1)[3ε3(ε2 − ε3) − (ε3 + 2εm) (ε2 − ε3) − 9ε2ε3 + 3ε2(ε3 + 2εm)] + x3(ε3 + 2εm)(ε2 − ε1)(2ε3 − 2ε2) + (ε3 + 2εm)(ε2 + 2ε3) (ε1 + 2ε2), where  This condition is plotted as a full black line in the upper panel of Fig. 7. This curve crosses the zero line at three points corresponding to wavelengths denoted as λ±±. The shortest wavelength λ++ again falls in the range where no experimental measurements of the refractive index are given.34 The other two wavelengths, λ±−, indicate hybridization resonances that fall in the visible range. Hybridization between λs and λ± gives rise to λ±±, shown with grey vertical lines in the central panel.
This condition is plotted as a full black line in the upper panel of Fig. 7. This curve crosses the zero line at three points corresponding to wavelengths denoted as λ±±. The shortest wavelength λ++ again falls in the range where no experimental measurements of the refractive index are given.34 The other two wavelengths, λ±−, indicate hybridization resonances that fall in the visible range. Hybridization between λs and λ± gives rise to λ±±, shown with grey vertical lines in the central panel.
The extinction spectra of a core–double shell gold–dielectric–gold NP with sizes R1 = 10 nm, R2 = 15 nm and R3 = 25 nm radii as well as that of a dielectric–gold nanoshell of sizes R2 = 15 nm and R3 = 25 nm radii are plotted in the lower panel of Fig. 7, using dipolar approximation and full Mie. As can be expected, the plasmon resonance wavelengths are correctly given by the full Mie approach (which correspond to the vertical black lines in the central panel), while blue-shifted peak values are found in the dipolar approximation. Comparing the lower and middle panels, it can be seen that the peaks for the core–double shell NP given by the dipolar approximation match the resonances derived from hybridization model. This fact supports the goodness of nanoparticle hybridization concept for determining plasmon resonance wavelengths in an approximate way. For the case of a 10 nm radii bare core gold NP with a 5 nm thickness SiO2 shell, hybridization yields a plasmon at λs = 537.0 nm, while full Mie yields λs = 539.0 nm. For the case of a SiO2–Au nanoshell with sizes R2 = 15 nm and R3 = 25 nm radii, dipolar approximation yields λ± = 187.8 nm and 572.2 nm, while full Mie yields λ± = 195.4 nm and 578.0 nm.
Following the same procedure, the visible hybridization wavelengths λ+− and λ−− for core–double shell NPs with Ag, Cu and Al cores may be derived. Their values are: λ+− = 506 nm and λ−− = 645.6 nm for Ag, λ+− = 552.7 nm and λ−− = 665.7 nm for Cu and λ+− = 502.6 nm and λ−− = 620.5 nm for Al.
The characteristics of the spectral field enhancement shown in Fig. 5 concerning redshift and intensity variation with intermetallic dielectric permittivity (ε2) may be now interpreted based on the hybridization model. As ε2 increases, the boundary conditions for the electric and magnetic fields produce a general redshift of all plasmon resonance wavelengths. Particularly, the plasmon wavelength of the bare core λs shows a larger redshift than those corresponding to the nanoshell, λ− and λ+, since the former is largely influenced by the intermetallic dielectric permittivity than the latter. The final result of this situation is an increase in the coupling that gives rise to λ+− (thus increasing the amplitude of the resonance in the extinction spectrum) and a decrease in the coupling that gives rise to λ−− (decreasing the amplitude of the resonance in the extinction spectrum).
3.4 Spatial field enhancement calculations
Spatial field enhancement calculations were carried out for core–double shell metal–dielectric–gold NP with sizes R1 = 10 nm, R2 = 15 nm and R3 = 25 nm radii, for Au, Ag, Cu and Al as core metals, keeping SiO2 fixed as the dielectric layer. Fig. 8–11 show the field enhancement spatial distribution for these core metals, both in the intermetallic (left column) and external (right column) regions, for specific wavelengths corresponding to the two maxima and minimum shown in the field enhancement spectra of Fig. 4(a). The intensity scale in each column is fitted to account for the large difference in field enhancement between the intermetallic region and the outer region. In all cases, circles in dashed lines indicate the geometrical location of the core and the outer shell. For all panels, the incident wave direction is the positive “Y” axis, with the electric field polarized in the plane of the figure in the “X” axis. The data presented corresponds to the plane for which the zenithal angle ϕ = 0.Comparing the right columns, it is interesting to notice the lack of angular symmetry of field enhancement in the surrounding region around the outer metallic shell for the shorter wavelengths. As the wavelength increases, there is a general trend to symmetry. This can be understood bearing in mind that for a bare core NP, the quasi-static approximation is given by |m|x = 2πR|Nmetal|/(λNmedium) ≪ 1, which is better met as λ increases. In this case, the larger contribution to the spatial field enhancement comes from the dipole term producing a symmetric field distribution, while higher order multipoles (asymmetric field distribution) are negligible. Besides, the condition is also dependent on the metal refractive index. For those metals for which its refractive index module is large, a larger wavelength is needed to meet the mentioned condition. For the metals studied in this work, the smallest refractive index module corresponds to Ag (NAg = 0.055 + i4.010 or |NAg| = 2 at 600 nm), while the largest corresponds to Al (NAl = 1.141 + i6.925 or |NAl| = 7 at 600 nm). This behavior is clearly seen in the right columns of Fig. 9 and 11 respectively.
4 Conclusions
We have theoretically studied the tunable optical properties of core–double shell metal–dielectric–metal spherical NPs using full Mie theory, taking into account free and bound electron size corrections to the metal dielectric function. We have shown that care must be taken in using the dipolar approach to describe these properties, since both the location and number of plasmon resonances of these structures may be wrongly yielded if the quasi-static approximation is not fully met, particularly if non noble metals are studied.Spectral field enhancement calculations using Mie theory developed for core–double shell metal–dielectric–metal NPs were carried out for different core metals and different intermetallic dielectric, keeping gold as the fixed outer metal shell. For NPs with fixed dimensions R1 = 10 nm, R2 = 15 nm and R3 = 25 nm, the influence of Au, Ag, Cu and Al as core metals, with SiO2 as the intermetallic dielectric was studied. Field enhancement spectra of these structures show two maxima in the vis-NIR wavelength region and one in the far UV. The wavelengths of these maxima are tunable according to the kind of metal used. Besides, the resonances are also dependent on the intermetallic dielectric permittivity. By changing this parameter, the peaks may be widely tuned across the vis-NIR spectrum. These characteristics yield a wider set of variables that may be used to design NPs with specific plasmonics resonances.
A hybridization model for core–double shell NPs in the quasi-static approach is used to explain the location, redshift and intensity of the peaks in the field enhancement spectrum based on the interaction between resonance modes of simpler nanostructures such as spheres, cavities and nanoshells.
Finally, the influence of the different core metals on the spatial field enhancement of these nanostructures is calculated for incident wavelengths corresponding to the maxima and minimum in the field enhancement spectrum. Plots for inner and outer regions show the symmetric (or asymmetric) angular field enhancement distribution when dipole (or higher order multipoles) describes the field.
The tunability properties of field enhancement, dependent on relative core–double shell sizing, core metal and intermetallic dielectric permittivity, allows designing and engineering NPs with specific plasmonics resonances for enhancing nonlinear response of metallic nanocomposites with potential applications in harmonic generation, SERS and near field optics.
Acknowledgements
This work was granted by PIP 0280 and PIP 0720 of CONICET, PME2006-00018 of ANPCyT, grants 11/I197 of Facultad de Ingeniería, UNLP and X11/680 of Facultad de Cierncias Exactas, UNLP. D. C. Schinca is Member of Comisión de Investigaciones Científicas de la Provincia de Buenos Aires (CICBA), Argentina. L. B. Scaffardi and L. J. Mendoza Herrera are PhD fellows of CONICET, Argentina.References
- P. V. Asharani, S. Sethu, S. Vadukumpully, S. Zhong, C. T. Lim, M. Prakash Hande and S. Valiyaveettil, Adv. Funct. Mater., 2010, 20, 1233 CrossRef CAS.
- M. Takamiya, Y. Miyamoto, T. Yamashita, K. Deguchi, Y. Ohta, Y. Ikeda, T. Matsuura and K. Abe, J. Neurosci. Res., 2011, 89, 1125 CrossRef CAS PubMed.
- Y. Zhang, R. Yuan, Y. Chai, J. Wang and H. Zhong, J. Chem. Technol. Biotechnol., 2011, 87, 570 CrossRef.
- K. Zhao, S. Zhuang, Z. Chang, H. Songm, L. Dai, P. He and Y. Fang, Electroanalysis, 2007, 10, 1069 CrossRef.
- A. Elder, H. Yang, R. Gwiazda, X. Teng, S. Thurston, H. He and G. Oberdörster, Adv. Mater., 2007, 19, 3124 CrossRef CAS.
- F. M. Gutierrez, P. L. Olive, A. Banuelos, E. Orrantia, N. Nino, E. M. Sanchez, F. Ruiz, H. Bach and Y. A. Gay, Nanomedicine, 2010, 6, 681 CrossRef PubMed.
- J. L. Barr, R. L. Axelbaum and M. E. Macias, J. Nanopart. Res., 2006, 8, 11 CrossRef CAS.
- G. Katabi, Yu. Koltypin, X. Cao and A. Gedanken, J. Cryst. Growth, 1996, 166, 760 CrossRef CAS.
- W. De La Cruz, C. Gallardo-Vega, S. Tougaard and L. Cota, Microelectron. J., 2008, 39, 1374 CrossRef CAS.
- H. Kato, T. Minami, T. Kanazawa and Y. Sasaki, Angew. Chem., 2004, 116, 1271 CrossRef.
- P.-P. Fang, A. Jutand, Z.-Q. Tian and C. Amatore, Angew. Chem., 2011, 123, 12392 CrossRef.
- K. Maeda, K. Teramura, D. Lu, N. Saito, Y. Inoue and K. Domen, Angew. Chem., 2006, 118, 7970 CrossRef.
- A. Shen, L. Chen, W. Xie, J. Hu, A. Zeng, R. Richards and J. Hu, Adv. Funct. Mater., 2010, 20, 969 CrossRef CAS.
- J. W. Nah, Y.-I. Jeong, C.-S. Cho and S.-I. Kim, J. Appl. Polym. Sci., 2000, 75, 1115 CrossRef CAS.
- C. Loo, A. Lin, L. Hirsch, M.-H. Lee, J. Barton, N. Halas, J. West, and R. Drezek, Diagnostic and Therapeutic Applications of Metal Nanoshells, in Nanofabrication Towards Biomedical Applications: Techniques, Tools, Applications, and Impact, Wiley-VCH Verlag GmbH & Co. KGaA, 2005 Search PubMed.
- V. I. Shautsova, V. A. Zhuravkov, O. V. Korolik, A. G. Novikau, G. P. Shevchenko and P. I. Gaiduk, Plasmonics, 2014, 9, 993–999 CrossRef CAS.
- P. Guo, D. Sikdar, X. Huang, K. J. Si, W. Xiong, S. Gong, L. W. Yap, M. Premaratne and W. Cheng, Nanoscale, 2015, 7, 2862–2868 RSC.
- V. Mondes, E. Antonsson, J. Plenge, C. Raschpichler, I. Halfpap, A. Menski, C. Graf, M. F. Kling and E. Rühl, Appl. Phys. B: Lasers Opt., 2016, 122, 155 CrossRef.
- Y. Zhang, A. Manjavacas, N. J. Hogan, L. Zhou, C. A. Orozco, L. Dong, J. K. Day, P. Nordlander and N. J. Halas, Nano Lett., 2016, 16(5), 3373–3378 CrossRef CAS PubMed.
- M. Y. Son, Y. J. Hong and Y. C. Kang, Chem. Commun., 2013, 49, 5678 RSC.
- C. Chen, H. Xu, L. Xu, F. Zhang, J. Dong and H. Wang, RSC Adv., 2013, 3, 25010 RSC.
- D. J. Wu and X. J. Liu, Appl. Phys. B: Lasers Opt., 2009, 97, 193 CrossRef CAS.
- J. Zhu, Y.-J. Ren, S.-M. Zhao and J.-W. Zhao, Mater. Chem. Phys., 2012, 133, 1060 CrossRef CAS.
- Y. Hu, R. C. Fleming and R. A. Drezek, Opt. Express, 2008, 16, 19579 CrossRef CAS PubMed.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley & Sons, 1998 Search PubMed.
- U. Kreibig and C. V. Fragstein, Z. Phys., 1969, 224, 307 CrossRef CAS.
- U. Kreibig and C. V. Fragstein, Optical Properties of Metal Clusters, Springer, 1995 Search PubMed.
- O. Cregut, J. Y. Bigot, J. C. Merle and A. Daunois, Phys. Rev. Lett., 1995, 75, 4702 CrossRef PubMed.
- L. B. Scaffardi and J. O. Tocho, Nanotechnology, 2006, 17, 1309 CrossRef CAS.
- L. J. M. Herrera, D. M. Arboleda, D. C. Schinca and L. B. Scaffardi, J. Appl. Phys., 2014, 116, 233105 CrossRef.
- J. M. J. Santillán, F. A. Videla, M. B. Fernández van Raap, D. C. Schinca and L. B. Scaffardi, J. Appl. Phys., 2012, 112, 054319 CrossRef.
- J. M. J. Santillan, F. A. Videla, M. B. Fernández van Raap, D. Muraca, L. B. Scaffardi and D. C. Schinca, J. Phys. D: Appl. Phys., 2013, 46, 435301 CrossRef.
- D. Muñeton, J. M. J. Santillán, L. J. Mendoza, D. Muraca, D. C. Schinca and L. B. Scaffardi, J. Phys. D: Appl. Phys., 2016, 49, 075302 CrossRef.
- S. Babar and J. H. Weaver, Appl. Opt., 2015, 54, 477 CrossRef CAS.
- K. M. McPeak, S. V. Jayanti, S. J. P. Kress, S. Meyer, S. Iotti, A. Rossinelli and D. J. Norris, ACS Photonics, 2015, 2, 326 CrossRef CAS PubMed.
- P. B. Johnson and R. W. Christy, Phys. Rev. Lett., 1963, 11, 4370 Search PubMed.
- E. Prodan and P. Nordlander, J. Chem. Phys., 2004, 120, 5444 CrossRef CAS PubMed.
- E. Massa, S. A. Maier and V. Giannini, New J. Phys., 2013, 15, 063013 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra19349h |
| This journal is © The Royal Society of Chemistry 2016 |










