A theoretical study of DABCO and PPh3 catalyzed annulations of allenoates with azodicarboxylate†
Abstract
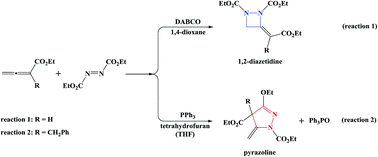
Previous experiments have shown that DABCO-catalyzed annulation of 2,3-butadienoate and diethylazodicarboxylate leads to 1,2-diazetidine (reaction (1)), whereas PPh3-catalyzed 2-benzyl-2,3-butadienoate and diethylazodicarboxylate gives pyrazoline (reaction (2)). To understand the difference, the mechanisms of the two reactions have been studied using density functional theory (DFT) calculations. The calculated results indicate that the two reactions follow different reaction sequences. The favorable mechanism of reaction (1) includes four steps: (i) the nucleophilic attack of DABCO on 2,3-butadienoate forms a zwitterionic intermediate, (ii) the γ-addition of the zwitterionic intermediate to diethylazodicarboxylate, (iii) the intramolecular 4-exo-trig cyclization, and (iv) the catalyst DABCO liberation gives the final product, with Z-1,2-diazetidine being the main product. As for reaction (2), the first step is the formation of a zwitterionic intermediate via the addition of PPh3 to diethylazodicarboxylate. The second step is the addition of the zwitterionic intermediate to the β-carbon atom of 2-benzyl-2,3-butadienoate, followed by the intramolecular cycloaddition. Finally, the elimination of triphenylphosphine oxide OPPh3 affords pyrazoline. Our calculation results are in good agreement with experimental findings. The present study may be helpful not only for rational design of high-efficiency catalysts but also for understanding the reaction mechanism of similar reactions.

 Please wait while we load your content...
Please wait while we load your content...